Примеры деление по математике 4 класс: примеры на умножение и деление 4 класс в столбик карточки: 16 тыс изображений найдено в Яндекс.Картинках

org/BreadcrumbList”>
• Предметы
• Математика
• 4 класс

1. Деление многозначного числа на однозначное число

2. Деление круглого многозначного числа на однозначное

3. Деление многозначного числа на 10, 100, 1000 с остатком

4. Деление многозначного числа с остатком на однозначное число

5. Выполняем деление трёхзначного числа на двузначное число

6. Деление с остатком трёхзначного числа на двузначное число

7. Деление многозначного числа на двузначное число

8. Деление с остатком на двузначное число

9. Выполняем деление на трёхзначное число

10. Деление с остатком на трёхзначное число

11. Деление круглого многозначного числа на круглое число

Урок 58.

Урок № 58. Деление на трёхзначное число.

Перечень вопросов, рассматриваемых в теме:

– Как делить многозначное число на двузначное?

– Как правильно выполнять запись деления?

– Как подобрать пробную цифру частного?

Глоссарий по теме:

Частное – результат деления одного числа на другое.

Неполное частное – результат деления с остатком, который показывает, какое максимальное число раз делитель содержится в делимом.

Основная и дополнительная литература по теме урока:

1. Петерсон Л.Г. Математика. 4 класс. 1 ч. – М.: 2013. – стр. 40-43.

2. Математика. Учебник для 4 кл. нач. шк. В 2 ч./М.И. Моро, М.А. Бантова – М.: Просвещение, 2017.

3. Математика. Проверочные работы. 4 класс. Учебное пособие для общеобразовательных организаций/ С.И.Волкова – М.: Просвещение, 2017. – стр. 78-79.

4. Математика. Тетрадь учебных достижений. 4 класс. Учебное пособие для общеобразовательных организаций/ С.И.Волкова – М.: Просвещение, 2017. – стр. 79-80.

Теоретический материал для самостоятельного изучения

Рассмотрим деление на трёхзначное число. Деление на трёхзначное число выполняется по тем же правилам, что и деление на двузначное число.

936:234.

Первое неполное делимое – это само число 936. Поэтому в частном будет только одна цифра.

Чтобы легче было найти цифру частного, будем делить 936 не на 234, а на 200. Для этого нужно 9 разделить на 2, получим 4. Это пробная цифра. Нужно проверить, подходит ли она. Проверку делаем устно.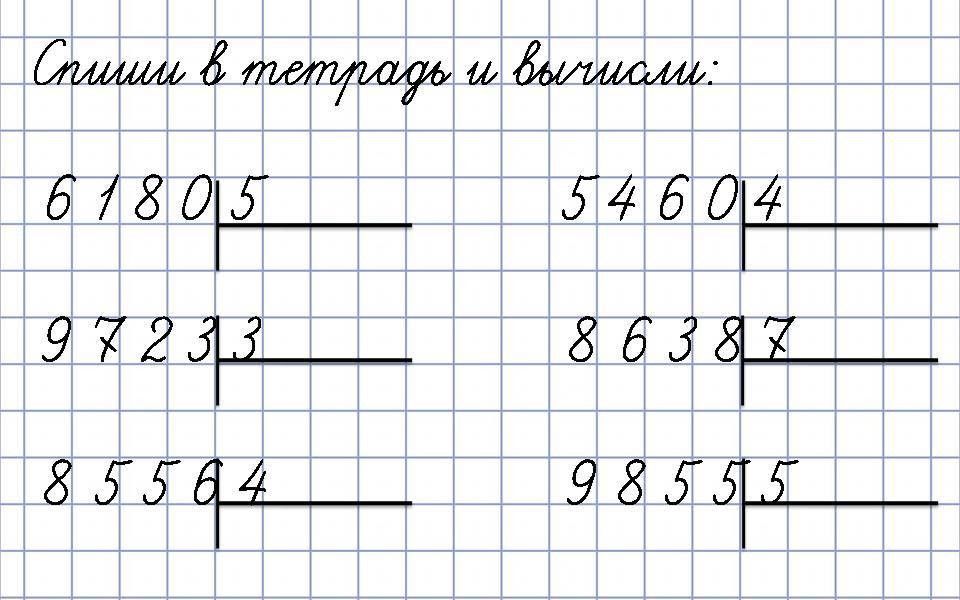

234 · 4 = 200 · 4 + 30 · 4 + 4 · 4 = 936

Полученное число равно делимому, значит, пробная цифра 4 подходит. Записываем ее в частном. Закончим запись деления столбиком. Умножаем 234 на 4, будет 936. Находим остаток от деления. Он равен нулю. Остаток меньше делителя. Деление закончено.

Найдём значение частного 219296 : 352

Выделим первое неполное делимое 2192 сотни.

Так как деление начинаем с сотен, в частном получим 3 цифры. Определяем первую цифру частного: 21:3=7, получили пробную цифру 7.

В запасе сотен нет, а требуется ещё 3 сотни, так как 5 дес. · 7 = 35 десятков. Значит, частное должно быть меньше 7.

Проверим 6.

3 сот. ·6 = 18 сот.

5 дес. ·6 = 30 дес. = 3 сот.

2 · 6 = 12

1800 + 300 + 12 = 2112

2112 < 2192, значит, цифра 6 подходит. Записываем ее в частном.

Умножаем 352 на 6, будет 2112. Вычитаем 2112 из 2192, будет 80. Остаток 80 меньше делителя 352.

Второе неполное делимое 809 десятков.

8 : 3 = 2, получили пробную цифру 2.

Проверяем:

352 · 2 = 704

704 < 809, значит, цифра 2 подходит. Записываем ее в частном.

Умножаем 352 на 2, будет 704. Вычитаем 704 из 809, будет 105. Остаток 105 меньше делителя 352.

Третье неполное делимое 1056 единиц. Определяем цифру частного.

Делим 10 на 3, получаем пробную цифру 3. Проверяем, 352 умножаем на 3. Складываем 900, 150 и 6, получаем 1056. Это число равно третьему неполному делимому. Значит, цифра 3 подходит, записываем ее в частном. Умножаем 352 на 3, будет 1056. Вычитаем 1056 из 1056. Остаток равен нулю. Деление окончено.

Задания тренировочного модуля:

1. Определите значение выражения, используя запись деления столбиком.

92400:462+1386:462

Варианты ответа: 23; 203; 263

Правильный вариант: 203

2. Расшифруйте слово, с которого начинается четверостишие из поэмы М.Ю. Лермонтова.

(40 ∙ 40 ∙ 40 : 2 + 486850 : 650) ∙ 18

_____ воет, дик и злобен,

Меж утёсами громад.

Буре плач его подобен,

Слёзы брызгами летят.

Правильный вариант: Терек

4. Выберите пропущенные числа в записи деления столбиком.

Варианты ответа: 0; 4; 7; 114; 141; 1141

Правильный вариант: 1141; 7; 0

Тест по математике Умножение и деление (4 класс)

Сложность: новичок.Последний раз тест пройден 51 мунуту назад.

Материал подготовлен совместно с учителем высшей категории

Опыт работы учителем математики – более 33 лет.

1. Вопрос 1 из 10

   Чему равен Х в уравнении: 240 : Х = 24?

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 93% ответили правильно
   • 93% ответили правильно на этот вопрос

   В вопросе ошибка?

   Следующий вопросОтветить

2. Вопрос 2 из 10

   Верно ли равенство: 75 х 3 = 235?

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 86% ответили правильно
   • 86% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

3. Вопрос 3 из 10

   Найдите правильный ответ: 250 х 6 =

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 81% ответили правильно
   • 81% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

4. Вопрос 4 из 10

   В овощной магазин привезли 130 мешков картофеля по 80 кг в каждом. Сколько всего кг картофеля привезли в магазин?

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 77% ответили правильно
   • 77% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

5. Вопрос 5 из 10

   Найдите правильный ответ: 3425 : 5 =

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 78% ответили правильно
   • 78% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

6. Вопрос 6 из 10

   Сколько кг в 68 ц?

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 63% ответили правильно
   • 63% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

7. Вопрос 7 из 10

   Найдите частное: 700 : 35 =

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 84% ответили правильно
   • 84% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

8. Вопрос 8 из 10

   Сколько мм в 36 дм ?

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 64% ответили правильно
   • 64% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

9. Вопрос 9 из 10

   Чему равно произведение: 0 х 16?

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 92% ответили правильно
   • 92% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

10. Вопрос 10 из 10

    Сравните выражение: 734 + 865 и 734 + 870

    • Правильный ответ
    • Неправильный ответ
    • Вы и еще 74% ответили правильно
    • 74% ответили правильно на этот вопрос

    В вопросе ошибка?

    Ответить

Доска почёта

Чтобы попасть сюда – пройдите тест.



• Константин Анисимов

  10/10

• Милана Петросян

  10/10

• Надежда Абрамова

  10/10

• Мубина Адхамова

  8/10

• Жмакина Ирина

  10/10

• Артём Мещеряков

  8/10

• Кристина Шаравьёва

  10/10

• Владислав Семьянинов

  9/10

• Игорь Соколов

  9/10

• Роман Тарасов

  10/10

Тест «Умножение и деление» по математике рассчитан на учеников младшей школы. Он поможет закрепить знания по теме, выявить плохо усвоенный материал. Выполнение теста требует понимания самых простых математических действий, знания соответствующих таблиц и правил. Предлагаемые тесты разного уровня сложности, что позволяет объективно оценить знания ребенка. Задания можно проходить в онлайн режиме с любого доступного устройства.

Тест «Деление» (4 класс) с ответами позволяет самостоятельно или с помощью родителей повторить и систематизировать материал для успешного написания текущих и итоговых проверочных работ.

Рейтинг теста

Средняя оценка: 4. Всего получено оценок: 924.

А какую оценку получите вы? Чтобы узнать – пройдите тест.

Деление многозначных чисел на однозначные с нулями в частном

Привет, друзья!

Я рада снова видеть вас. Вы знаете, мне приходит много писем от ребят. Но вот письмо одного мальчика, Вити Считалкина, меня очень расстроило. Он пишет, что получил двойку за самостоятельную работу по математике. И не понимает за что. Ведь Витя назубок знает таблицу умножения и деления, и уверен, что всё решил правильно. В доказательство Витя прислал листок с теми заданиями, которые ему не засчитали. Вот его работа:

Ну что же, ребята, надо помочь Вите Считалкину разобраться, в чём причина такой плохой отметки.

Давайте разберём первый пример. Вы не забыли? При делении многозначных чисел обязательно начинаем с того, что определяем количество цифр в частном. А для этого выделяем первое неполное делимое. Наибольший разряд выражен цифрой один. Один меньше делителя, поэтому не может быть неполным делимым. Возьмём не одну, а две первых цифры. Шестнадцать сотен и будет первым неполным делимым. Ставим точку в частном. После шестнадцати в делимом стоят ещё две цифры, значит и в частном тоже надо добавить две точки. То есть, частное должно быть трёхзначным числом. Начинаем деление. Шестнадцать делим на шесть – это два. Дважды шесть – двенадцать, остаток.… четыре. Он меньше делителя. Переносим вниз к остатку следующую цифру – два. Второе неполное делимое – сорок два десятка. Делим сорок два на шесть, получается семь. Умножаем – сорок два. Вычитаем. Остаток нуль. Действие закончено. Но… Посмотрите, ещё ничего не закончено! Ведь в частном стоит ещё одна точка. Значит, ответ должен быть трёхзначным! А-а, понятно! Деление не закончено, потому что в делимом есть ещё одна цифра, которая не принимала участия в делении.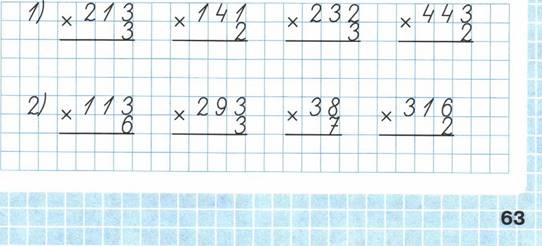 Это нуль. И он будет третьим неполным делимым. Нуль из остатка убираем, так как его в остатке мы пишем только тогда, когда заканчиваем деление. А вот нуль из делимого переносим вниз. Делим его на шесть, получается нуль. Не забываем его записать в частном. Умножаем нуль на шесть. Нуль. Вычитаем. Нуль. Вот теперь мы его записали в остатке, потому что деление закончилось. И ответ этого примера не двадцать семь, а двести семьдесят.

Ребята, видите, какую ошибку допустил Витя Считалкин и могла допустить я? Мы забыли, что нуль, который стоит в конце числа, тоже надо делить. И полученный при этом нуль записывать в частное. Наверное, Витя перед тем как начать деление, не определил количество цифр в частном, и поэтому не смог вовремя заметить ошибку.

Ну что же, с первым примером мы разобрались. Переходим к следующему.

Не забываю определить количество цифр в частном.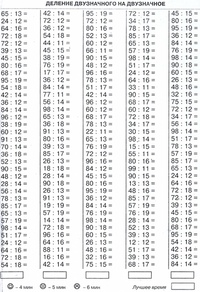 Первое неполное делимое будет четыре? Нет, число маловато. Ведь оно меньше делителя восемь. Значит, первое неполное делимое – сорок. Оно даёт одну цифру в частном. И в делимом после сорока стоят ещё две цифры, поэтому и в частное добавляю ещё две точки. Частное будет трёхзначным числом.

Начинаю деление. Сорок разделить на восемь – пять. Пятью восемь – сорок. Вычитаю. Остаток нуль. Но ведь деление ещё не закончено, поэтому этот нуль я не пишу. Спускаю вниз следующий разряд. Так-так. Семь меньше восьми. Что же делать? Ага, вспомнила! Если делимое меньше делителя, в частном пишем нуль. Умножаем его на восемь, получаем нуль. Вычитаем. Остаток семь. Он меньше делителя. Переносим вниз следующий разряд и делим число семьдесят два. Это третье неполное делимое. Разделили его на восемь, получили девять. Девятью восемь – семьдесят два. И остаток нуль. Деление окончено. Частное равно пятистам девяти.

Вот видите, ребята, как важно определять количество цифр в частном! Если допустили ошибку, точки на месте частного сразу вам об этом просигнализируют.

Ну что же, а теперь я предлагаю вам самостоятельно решить два оставшихся примера, которые неверно решил Витя Считалкин. И, конечно, я тоже их постараюсь решить. А потом мы сверим полученные результаты. Не забудьте, определив первое неполное делимое, подсчитать количество цифр в частном.

Ребята, как вы справились с моим заданием? Проверьте своё решение!

У вас так получилось? Я надеюсь, что Витя Считалкин тоже посмотрел наш урок, и больше не будет пропускать нули в частном.

А мы сегодня попрощаемся с вами. До встречи на следующем уроке! До свидания, друзья!

Математика: уроки, тесты, задания.

1. 1. Пространственные и временные представления

   2. Пары и группы предметов

   3. Нумерация.

      Сколько? От 0 до 10

   4. Нумерация. Сколько? От 11 до 20

2. 1. 02 Точка, прямая линия, кривая и отрезок

   2. Знаки сравнения, знаки действий и знак равенства

   3. Сравнение чисел от 1 до 5

   4. Примеры на сумму

   5. Примеры на разность

   6. Примеры на сложение и вычитание от 1 до 5

   7. Сравнение чисел от 0 до 10 и выражений

   8. Текстовые задачи (сумма)

   9. Текстовые задачи (разность)

   10. Задачи на смекалку (от 1 до 5)

   11. Задачи на смекалку (от 0 до 10)

3. 1. Счёт десятками

   2. Сравнения чисел от 11 до 20

   3. Таблица сложения.

      Числа от 1 до 9

   4. Задачи на смекалку (от 11 до 20)

1. 1. Сложение и вычитание чисел в пределах 20 с переходом через десяток

   2. Таблица сложения. Числа от 0 до 18

   3. Ломаная линия

2. 1. Числа от 20 до 100.

      Нумерация. Числа и цифры

   2. Счёт десятками

   3. Круглые числа

   4. Сложение и вычитание чисел в пределах 100 без перехода через десяток

   5. Сложение и вычитание чисел в пределах 100 с переходом через десяток

   6. Сложение и вычитание чисел в пределах 100

   7. Решение задач в два действия

   8. Метр

3. 1. Скобки.

      Сочетательный закон сложения

   2. Выражения без скобок

   3. Выражения со скобками

   4. Луч

   5. Угол

   6. Прямой, тупой и острые углы

   7. Квадрат, круг, прямоугольник, треугольник

   8. Периметр

4. 1. Понятие умножения

   2. Деление

   3. Чётные и нечётные числа

   4. Переместительный закон умножения

   5. Таблица умножения на 2

   6. Таблица умножения на 3

1. 1. Таблица умножения на 4

   2. Таблица умножения на 5

   3. Таблица умножения на 6

   4. Таблица умножения на 7

   5. Таблица умножения на 8

   6. Таблица умножения на 9

   7. Умножение и деление на 0, 1, 10.

      Деление числа на само себя

   8. Увеличить на… Увеличить в… Уменьшить на… Уменьшить в…

   9. Больше на… больше в… меньше на… меньше в…

   10. Нахождение доли числа

   11. Нахождение числа по доле

   12. Сравнение долей

   13. Уравнения (сумма)

   14. Уравнения (разность)

   15. Нахождение неизвестного множителя

   16. Нахождение неизвестного делителя

   17. Нахождение неизвестного делимого

   18. Умножение суммы на число

   19. Деление суммы на число

   20. Деление круглого числа на круглое число

   21. Умножение и деление круглого числа на однозначное число

   22. Умножение двузначного числа на однозначное число

   23. Деление двузначного числа на однозначное

   24. Деление двузначного числа на двузначное

   25. Деление с остатком

   26. Треугольники

   27. Час.

       Минута. Сутки

2. 1. Нумерация

   2. Сложение и вычитание трёхзначных чисел

   3. Умножение на однозначное число. Распределительный закон умножения относительно сложения

   4. Умножение и деление трёхзначного числа на однозначное число

   5. Километр

   6. Килограмм

   7. Связь между величинами

1. 1. Миллиметр

   2. Площадь фигуры.

      Площадь прямоугольника

   3. Единицы измерения площади

2. 1. Умножение круглого числа на однозначное число

   2. Деление круглого многозначного числа на однозначное

   3. Умножение и деление чисел на 10, 100 и 1000

   4. Умножение на круглое число

   5. Умножение и деление круглых чисел

   6. Умножение круглых чисел

   7. Деление многозначного числа на однозначное число

   8. Умножение на двузначное число

   9. Деление трёхзначного числа на двузначное число

   10. Деление многозначного числа на двузначное число

   11. Умножение на трёхзначное число

   12. Деление на трёхзначное число

   13. Деление многозначного числа на 10, 100, 1000 с остатком

   14. Деление круглого многозначного числа на круглое число

   15. Деление многозначного числа с остатком на однозначное число

   16. Деление трёхзначного числа на двузначное с остатком

   17. Деление на двузначное число с остатком

   18. Деление на трёхзначное число с остатком

   19. Геометрические понятия: окружность и круг

1. Методические рекомендации по использованию в педагогической деятельности ЯКласс

2. 1. Законы арифметических действий.

      Вычисления с многозначными числами

   2. Координатный луч

   3. Отношение “больше”, “меньше”, “равно” между числами на координатном луче

   4. Сравнение натуральных чисел друг с другом

   5. Округление чисел.

      Прикидка и оценка результатов вычислений

   6. Степень с натуральными показателями

   7. Деление с остатком

   8. Делители и кратные числа

   9. Признаки делимости на 2, 3, 5, 9, 10

   10. Простые и составные числа. Разложение натурального числа на простые множители

   11. Наибольший общий делитель и наименьшее общее кратное

   12. Решение текстовых задач арифметическим способом

3. 1. Числовые и буквенные выражения

   2. Формулы. Уравнения. Упрощение выражений

   3. Математический язык и математическая модель

4. 1. Числовые и буквенные выражения

   2. Формулы. Уравнения. Упрощение выражений

   3. Математический язык и математическая модель

5. 1. Понятие дроби

   2. Правильные и неправильные дроби. Смешанные числа

   3. Основное свойство дроби

   4. Сравнение дробей

   5. Сложение, вычитание, умножение и деление обыкновенных дробей и смешанных чисел

   6. Среднее арифмитическое нескольких чисел. Задачи.

6. 1. Начальные геометрические понятия: прямая, отрезок, луч, ломанная, прямоугольник

   2. Угол. Измерение углов

   3. Биссектриса угла. Свойство биссектрисы угла

   4. Свойство углов треугольника. Размеры объектов окружающего мира (масштаб)

   5. Расстояние между двумя точками. Масштаб

   6. Параллельность прямых

   7. Перпендикулярность прямых. Расстояние от точки до прямой. Серединный перпендикуляр

   8. Треугольник. Площадь треугольника

   9. Прямоугольный параллелепипед

   10. Развёртка прямоугольного параллелепипеда

   11. Объём прямоугольного параллелепипеда

7. 1. Угол. Измерение углов

   2. Биссектриса угла. Свойство биссектрисы угла

   3. Параллельные и перпендикулярные прямые

   4. Площадь прямоугольного треугольника и некоторых видов многоугольников.

   5. Переход от одной единицы измерения площади к другой.

   6. Прямоугольный параллелепипед

   7. Объём прямоугольного параллелепипеда

1. 1. Понятие десятичной дроби. Представление десятичной дроби в виде обыкновенной дроби и наоборот

   2. Сравнение десятичных дробей

   3. Рациональные числа. Периодические дроби

   4. Сложение и вычитание десятичных дробей

   5. Умножение десятичных дробей

   6. Среднее арифметическое и деление десятичных дробей на натуральное число

   7. Деление десятичной дроби на десятичную дробь

2. 1. Положительные и отрицательные числа. Координатная прямая

   2. Противоположные числа. Модуль числа

   3. Сравнение чисел

   4. Сложение рациональных чисел с помощью координатной прямой

   5. Алгебраическая сумма и её свойства

   6. Сумма рациональных чисел с одинаковыми знаками

   7. Сумма рациональных чисел с разными знаками

   8. Умножение и деление рациональных чисел

3. 1. Координаты. Координатная плоскость. Координаты точки

4. 1. Начальные понятия и факты курса геометрии

   2. Окружность и круг. Число Пи. Длина окружности. Площадь круга

   3. Осевая и центральная симметрия

5. 1. Проценты. Задачи на проценты: нахождение процента от величины и величины по её проценту

   2. Отношения

   3. Пропорция. Основное свойство пропорции

   4. Решение задач с помощью пропорций

   5. Прямая и обратная пропорциональность

   6. Разные задачи на пропорции

“Деление числа на произведение” урок математики 4 класс

Самоанализ урока по математике в 4 классе

По теме «Деление числа на произведение»

Данный урок по типу является уроком изучения новой темы.

Методы и приемы: здоровьесберегающая технология, электронный образовательный ресурс

Цели: познакомить детей с делением числа на произведение.

Задачи учебного занятия:

Обучающая:

– формировать умение различать понятия «Величина» и «Единицы измерения этой величины», умение соотносить единицы длины, умение пользоваться линейкой;

– совершенствовать навыки устного счёта, приемы письменных вычислений. Совершенствовать умение читать, записывать и сравнивать многозначные числа;

– развивать логическое мышление, память, внимание, познавательные и математические способности, речь;

– прививать любовь к предмету;

– совершенствовать умение читать, записывать, сравнивать многозначные числа;

Воспитывающие:

1. Воспитывать информационную культуру, дисциплинированность, аккуратность, настойчивость в учебе.

2. Воспитывать ответственность за выполняемую работу, аккуратность при работе с компьютером.

Развивающая:

1. Способствовать развитию грамотной речи, взаимодействия между учащимися.

2. Развивать умение работать в паре и умение выстраивать самостоятельную работу.

3. Способствовать развитию умения планировать свою деятельность.

4. Формировать интерес к предмету математики.

5. Развивать логическое мышление, память, внимание, познавательные и математические способности.

Развитие универсальных учебных действий:

Предметные результаты:

– Познакомить учащихся с единицами измерения длины: километр; продолжить работу над обратными задачами; прививать интерес к предмету;

– Усвоить единицы измерения длины: километр; решать обратные и составные задачи; выработать каллиграфическое написание цифр,

Метапредметные результаты:

– Усвоить единицы измерения длины: километр; решать обратные и составные задачи;

– Выработать каллиграфическое написание цифр, навыки работы на ПК, навыки чтения

Регулятивные:

– Анализировать, сравнивать выполненные действия и полученные результаты.

– Определить план выполнения задания на уроке, следовать плану и алгоритму при выполнении задания.

Коммуникативные:

– Участвовать в диалоге на уроке, воспринимать объяснения и инструкции учителя;

– Планировать учебное сотрудничество с учителем и сверстниками, уметь с достаточной полнотой и точностью выражать свои мысли, управлять поведением партнёра, контролировать себя и партнера при работе в паре, в группе

Личностные:

– Оценивать результаты выполненной работы.

– Развивать внимание, вариативность мышления.

– Развивать креативность и творческие качества личности.

– Воспитывать бережливость, аккуратность, привычки ухаживать за своими вещами, экономить своё и чужое время.

Оборудование:

Компьютер, проектор, экран.

Электронное приложение к учебнику Моро. Математика 4 класс. ФГОС М., Просвещение,.2012 г

Таблица «Единицы длины».

Электронная физминутка

Учебник, рабочая тетрадь ученика.

Тип урока: урок открытия нового знания.

Свой урок я строила в соответствии с ФГОС, используя информационно-коммуникативные технологии.

Данный урок представлен по ходу изучения раздела «Величины».

На уроке были учтены возрастные и психологические особенности учащихся В содержание урока я включила элементы обучения школьников универсальным учебным действиям: цели урока определяют сами ученики, исходя из соответствующей проблемной ситуации.

На данном уроке применяется деятельностный метод обучения, который реализуется в следующих видах деятельности: учебной и учебно-исследовательской.

Любой процесс познания начинается с импульса, побуждающего к действию. Необходима мотивация, побуждающая ученика к вступлению к деятельности. Помня об этом, я тщательно продумывала каждый этап урока, составляла задания, подбирала вопросы, использовала различные приёмы активизации учеников.

На всех этапах урока ученики вовлекаются в активную мыслительную и практическую деятельность исследовательского характера, детям надо не только использовать уже имеющиеся знания, но и найти новый способ выполнения уже известного им действия.

Этапы урока тесно взаимосвязаны между собой, чередуются различные виды деятельности. Умственные действия опираются и подкрепляются практическими. Учебный материал на протяжении всего урока направлен на организацию посильного поиска и исследования учеников, соответствует их жизненному опыту.

Для каждого ученика создается ситуация успеха, что также способствует повышению мотивации и поддержанию познавательного интереса к учению.

При постановке вопросов и определении заданий на уроке я учитывала индивидуальные особенности учеников.

Учебный материал урока соответствует принципу научности, доступности и посилен для учеников четвертого класса. Учебная информация привлекательна для детей.

На уроке наблюдается рациональное использование времени, предупреждение перегрузки детей обеспечивается за счёт быстрой смены видов деятельности. Применяются здоровьесберегающие технологии (физминутка общего воздействия). Применяются задания, направленные именно на развитие детей. При проведении урока используются различные формы обучения: индивидуальная и фронтальная работа. При проведении урока используется презентация, как компьютерная поддержка. При подведении итогов и рефлексии применяется самоанализ деятельности учеников.

5

Тема: «Деление многозначного числа на круглое двухзначное число»

Тема: «Деление многозначного числа на круглое двухзначное число»

Цели:

1)Способствовать формированию знанию учащихся по делению многозначного числа на круглое двухзначное число;

2)содействовать развитию навыка деления многозначного числа на круглое двухзначное число, памяти, мышления;

3)создать условия для воспитания  культуры математической речи.

Методическое обеспечение:  Учебник «Математика, 4» (часть 2),карточки с изображением смайликов  для рефлексии, карточки с зашифрованным заданием для организации начала урока, задания для устного счета, алгоритм решения примеров, портрет Пифагора, видеозапись физкультминутки «4 шага»

План урока:

1. Организация начала урока.

1.1 Игра «Разгадай шифр»

2.1 Беседа о значении чисел в жизни

2. Актуализация знаний.

1.2 Фронтальный опрос

4. Устный счёт

1.4 Математический диктант ( самостоятельное решение  письменно у доски и в тетрадях)

2.4 Решение задач

3. Сообщение темы и целей урока.

5. Изучение нового материала.

1.5 Решение примера на доске и в тетради

6. Закрепление изученного материала:

1.6 Решение примеров задания №1 с.78 на доске и в тетради

Физкультминутка

2.6 Решение задачи №4 с.79 на доске (составление чертежа) и в тетради

3.6 Решение задачи №5 с.79 устно с использованием схемы

4.6 Самостоятельное письменное  решение  примеров задания №6 с.79

5.6 Устное решение примеров задания №7 с.79

6.6 Устное решение логической задачи

7. Подведение итогов урока.

8. Домашнее задание.№8,9 с.79

Ход урока:

1.Организация начала урока:

-Здравствуйте, ребята!Садитесь.

-Один из величайших греческих математиков древности,Пифагор, живший с 580-500 годы до нашей эры, считал, что числа очень важны для жизни людей. Попробуйте сами прочитать, что он говорил о числах, расшифровав запись на доске или на карточках, которы находятся у вас на партах. (Приложение 1)

-Дествительно, при помощи чисел мы сможем записать пример, решить задачу или уравнение, оперировать различными величинами, сравнивать, производить вычисления и многое другое. Все эти знания вам пригодятся в жизни, поэтому на уроке будьте внимательными, активными и старательными. И именно тогда у вас всё получится!

2.Актуализация знаний.

3. Устный счёт:

-Давайте напишем математический диктант:

200/50=40

500+1500=2000

250*2=500

100*300=30000

2468+32=2500

630/7=90

0*(1000/800)=0

(100+80)/10=18

69/3=23

56/7=8

-А теперь задачи:
1)Пассажир был в пути двое суток и 6 часов. Сколько часов был в пути пассажир? (54 часа)

2) Сумму чисел 76 и 54 уменьшите в 10 раз. (13)

3)На 70 км автомобиль израсходовал 7 л бензина. Сколько бензина он израсходует на 210 км пути? (21 л)

-Молодцы!

4.Сообщение темы и целей урока .

-Молодцы! Я вижу, что вы справились с домашним заданием, а значит и хорошо усвоили прошлую тему.

-Сегодня мы с вами познакомимся с ещё одной возможность чисел. На прошлом уроке вы познакомились с делением многозначных чисел на двухзначные, а сегодня вы  познакомитесь с делением многозначных чисел на круглое двухзначное число.

-А для того, чтобы наш урок был наиболее продуктивным давайте посчитаем устно.

5. Изучение нового материала:

-Прочитайте выражение, которое записано на доске

+24 780:30

-Давайте вместе с вами решим этот пример.

-Каким будет первое неполное делимое?

+247

-Правильно.Значит в частном будет 3 цифры.

-Делим 247 на 30.Для удобства разделю 24 на 3. Пробная цифра-8

-Умножаю 8 на 30, получаю 240.

-Вычитаю : 247-240=7

-Так как 7<30, то деление выполнено верно.Записываю 8 в частное.

–Второе неполное делимое:78 дес.

-Для удобства делю 7:3, пробная цифра -2.

-Умножаю 2 на 30= 60 (дес)

-Вычитаю: 78-70=18 (дес)

-Сравниваю :18<30, деление выполнено верно.Записываю 2 в частное.

–Третье неполное делимое:180 ед.

-Делю 180 на 30

-Для удобства делю 18:3, пробная цифра-6.

-Умножаю 6 на 30 получаю 180 (ед.)

-Вычитаю 180-180=0.Записываю 6 в частное.

-Читаю ответ:826.

-Кому не понятно?

– Дети, запишите сегодняшнее число, «классная работа» и запишите этот пример в тетради.

VI. Закрепление изученного материала:

-А сейчас выполним задание № 1 на странице 78. Решаем на доски  и в тетрадях с комментированием. К доске пойдет…

-Не забывайте пользоваться алгоритмом, если забыли порядок выполнения действий.

(решение примеров по алгоритму – Приложение 3)

29 340:60=489

43 650:50=873

31 280:80=391

57 680:80=721

124 040:70=1772

103 230:90=1147

– А сейчас немного отдохнем.

Физкультминутка (Приложение 4)

-А сейчас выполним задание № 4 на странице 79.

-Прочитает задачу…

-Что необходимо узнать в задаче?

+Периметр и площадь прямоугольника.

-Как  найти площадь и периметр у прямоугольника. Запишет формулы…

+  P=2(a+b) ,S=a*b

-Что нужно знать, чтобы найти  периметр и площадь прямоугольника?

+Длину и ширину прямоугольника.

-Что знаем?

+Длину прямоугольника?

-Что известно про ширину?

+Ширина составляет одну треть длины.

-Каким действием найдем ширину?

+Делением.

-Зная длину и ширину , можем найти периметр?

+Да.

-Как найдём?

+Периметр равен удвоенной сумме длины и ширины.

-Зная длину и ширину , можем найти площадь?

+Да.

-Как найдём?

+Длину умножим на ширину.

-Во сколько действий решается задача?

+ В 3

-Что найдём в первом действии?

+Ширину прямоугольника

-Каким действием?

+Делением 

-Что найдём в втором  действии?

+Периметр

-Что найдём в третьем  действии?

+Площадь

-Каким действием?

+Умножением.

-Запишите решение  в тетрадях. К доске пойдёт …

-А сейчас выполним задание № 5 на странице 79. (выполняется устно с помощью рассмотрения чертежа в учебнике)

-А сейчас выполним задание № 6 на странице 79. Решите первые 2 примера самостоятельно, а потом проверим .

  2 кг 350 г *5=11 кг 750 г

7т 105 кг*5 =35т 525 кг

-Два человека будут работать за закрытой доской. Кто желает…Первый столбик решает…,  а второй…

-А все остальные выполняют примеры в тетради.

-А сейчас проверим.

-А сейчас выполнив задание № 7 на странице 79 мы проверим вашу смекалку

-Как легче всего вычислить?

+сумма чисел 52 и 18, получим 70. А затем 70 умножим на 376.

(по аналогии выполнение остальных примеров)

-А сейчас проверим вашу математическую смышленость

(решение логических задач –Приложение 5)

VIII. Итог урока. Рефлексия.

-Что нового вы сегодня узнали на уроке?

-Что вызывало некоторые трудности?

-Что было самым интересным? (Ответы детей)

 -Ребята, у вас на столах лежат карточки. Если на уроке всё было понятно и не возникало никаких трудностей – нарисуйте улыбку смайлику, если же возникали какие-то затруднения – грустную улыбку.

– Я рада, что всем было всё понятно.

VIII. Домашнее задание.

–№8,9, ст.79

Что такое дивизия? – Определение, факты и пример

Что такое дивизион?

Разделение – это метод разделения группы вещей на равные части. Это одна из четырех основных операций арифметики, которая дает хороший результат обмена.

Деление – это операция, обратная умножению. Если 3 группы по 4 составляют 12 в умножении; 12 разделенных на 3 равные группы дают по 4 в каждой группе в дивизионе.

Основная цель разделения – увидеть, сколько равных групп или сколько в каждой группе при справедливом распределении.

Например:

Есть 16 шаров и 4 коробки, как положить 16 шаров в четыре коробки одинакового размера?

Итак, 16 разделить на 4 =?

Следовательно, в каждом ящике должно храниться по 4 мяча.

Математическое обозначение деления

Существуют различные знаки, которые могут использоваться для обозначения деления, например, ÷, /.

Например:

Специальные имена для каждого символа в Подразделении

Каждая часть, участвующая в уравнении деления, имеет особое имя.

Дивиденд ÷ делитель = частное

Дивиденд : Дивиденд – это число, которое делится в процессе деления.

Делитель : Число, на которое делится дивиденд, называется делителем.

Частное : Частное – это результат, полученный в процессе деления.

18 ÷ 3 = 6

Дивиденды d Коэффициент пропорциональности

Итак, в приведенном выше процессе мы разделили 16 шаров на 4 равные группы;

Дивиденд равен 16, делитель 4 и, следовательно, частное равно 4.

Введение к остатку

Остаток – это часть дивиденда, оставшаяся после деления. Например, при делении 83 на 2 остается 1.

Значит, 83 ÷ 2 = 41 и r = 1,

Здесь «r» – остаток.

Особенности подразделения

• При делении чего-либо на 1 ответом всегда будет исходное число. Это означает, что если делитель равен 1, частное всегда будет равно деленному, например 10 ÷ 1 = 10.

• Деление на 0 не определено.

• Деление одного и того же дивиденда и делителя всегда равно 1. Например: 4 ÷ 4 = 1.

Рабочие листы деления для 3, 4 и 5 классов

Это бесплатные распечатываемые рабочие листы по разделам, сгенерированные случайным образом для учащихся 3-5 классов.Темы включают факты деления, умственное деление, деление в столбик, деление с остатками, порядок операций, уравнения и факторинг.

Вы можете распечатать их прямо из окна браузера, но сначала проверьте, как это выглядит в «Предварительном просмотре». Если рабочий лист не помещается на странице в режиме предварительного просмотра, настройте поля, верхний и нижний колонтитулы в настройках страницы в браузере. Или же, отрегулируйте «масштаб» до 90% или меньше в предварительном просмотре. В некоторых браузерах может быть опция «Печатать по размеру», которая автоматически масштабирует рабочий лист до такого размера, чтобы он соответствовал области печати.

Все рабочие листы имеют ключ ответа; однако вам необходимо щелкнуть страницу ключа ответа сразу же после создания рабочего листа, , потому что ключ ответа также генерируется «на лету» и не будет существовать позже, если вы придете искать его позже.

Перейти к:

4 класс

Рабочие листы ментального деления

Деление с остатком от 1 до 100 по основным фактам
Деление с остатком в пределах 1-100
Деление с остатком, деление целых десяти
Деление с остатком, делителем на целую сотню

Порядок операций: сложение, вычитание, умножение, деление и скобка – три операции
Порядок операций: сложение, вычитание, умножение, деление и скобка – четыре операции
Порядок операций: сложение, вычитание, умножение, разделение и скобка – пять операций

Листы с длинным делением

Длинное деление, двузначные дивиденды, однозначный делитель, точное деление
Длинное деление, двузначные дивиденды, однозначный делитель, возможны остатки

Длинное деление, трехзначные дивиденды, однозначный делитель, точное деление
Деление в столбик, трехзначные дивиденды, однозначный делитель, возможны остатки

Длинное деление, 4-значные дивиденды, 1-значные делители, точное деление
Длинное деление, 4-значные дивиденды, 1-значные делители, возможны остатки

5 класс

Психическое подразделение

Разделите в уме трех- и четырехзначное число на однозначное

Деление с остатком в пределах 1-100
Деление с остатком, деление целых десяти
Деление с остатком, делитель на целую сотню

Деление в длину

2-значный делитель, 4-значное делимое, делитель от 11 до 35
2-значный делитель, 4-значное делимое, без остатка – (делителем является любое двузначное число)
2-значный делитель, 4-значное делимое, с остатком – (делителем является любое двузначное число)

Умножение уравнения (пропущенный множитель; решить в столбик)
Уравнения деления (пропущенный делимый или делитель; решите путем длинного умножения или длинного деления)
Решите уравнения умножения – используя длинное деление, одно- или двухзначный делитель
Решите уравнения деления – используйте либо длинное деление, либо умножение

Таблицы факторинга

Факторинговые числа в пределах 4-100 на простые множители
Сложный факторинг: числа множителей в пределах 4-500 в простых множителях

Как сделать длинное деление за 6 шагов [с иллюстрациями]

Как выполнить деление в столбик за шесть шагов

1. Обзор

Используйте игры на умножение и другие математические игры, чтобы заинтересовать учащихся в обучении и развить уверенность в математике, прежде чем продолжать.

2. Начните с простого

Давайте начнем с урока лексики. В уравнении деления в столбик есть много разных частей. Убедитесь, что ваши ученики знают, что они имеют в виду и как их идентифицировать. Дивиденд – это число в правой части уравнения под линией. Он представляет собой разделяемую сумму. Делитель – это число слева – оно выполняет деление. Частное – это число вверху. Он представляет собой ответ или количество единиц в каждом значении разряда после того, как уравнение было завершено.Остаток – это номер вверху справа. Он представляет собой оставшиеся единицы, которые нельзя равномерно разделить на частное. Во-первых, введите уравнение, в котором нет остатков, чтобы учащиеся могли привыкнуть к формату и начать понимать новый словарный запас, который они только что выучили: Спросите учащихся, сколько раз 2 вписывается в 4. Это может быть для них непростой концепцией. , поэтому используйте идею совместного использования: если вы хотите поделиться 4 объектами между двумя людьми, сколько объектов получит каждый? Когда они дадут правильный ответ, поставьте 2 над 4.Затем повторите шаг со второй цифрой делимого. Используйте эти простые уравнения, чтобы усилить числовую ценность. Объясните ученикам, что, когда они спрашивают, сколько раз 2 может перейти в 4, они на самом деле спрашивают, сколько раз 2 входит в 40.

3. Оставайтесь в единицах

Попросите ваших учеников практиковать вышеуказанный шаг, пока они не почувствуют себя комфортно с базовым форматом. Тогда пора двигаться дальше. Вместо того, чтобы сразу переходить к уравнению с остатками, начните с другого наглядного урока .Разделите учащихся на группы по три, четыре или шесть человек и раздайте каждой группе по 50 ватных шариков (или мармелад, или помпоны, или зефир – любой маленький предмет, доступный в вашем классе). Попросите учеников разделить предметы так, чтобы каждый член группы группа имеет равное количество, затем наблюдайте и ждите. В конце концов они поймут, что не могут разделить его поровну, и всегда будут оставаться какие-то объекты. Вот где вы приходите, чтобы спасти положение и объяснить, как выполнить деление в столбик с остатками .Во-первых, покажите студентам задачу, в которой остаток находится в единицах: Теперь начните со столбца десятков и проработайте задачу: 5 переходит в 5 ровно один раз, поэтому там ничего не остается. Но сколько раз 5 превратится в 7, и что вы будете делать с остатками? Покажите студентам новые шаги:

• Разделите делимое столбца единиц на делитель
• Умножьте делитель на частное справа поместить столбец
• Вычтите произведение из столбца единиц

Число, с которым они остались, и есть остаток.Обязательно смоделируйте несколько задач в классе, чтобы учащиеся могли начать понимать шаги и как правильно писать свои ответы. Это хорошее время на уроке, чтобы научить студентов проверять свои ответы. Попросите их умножить делитель на частное и сложить остаток – ответ должен быть таким же, как и дивиденд, с которого они начали.

4. Остаться в десятках

Теперь ученикам пора заняться задачами, в которых делитель не вписывается точно в столбец десятков или единиц.Шаги более или менее одинаковы, за исключением одного нового добавления:

• • Разделите делимое столбца десятков на делитель
  • Умножьте делитель на частное в столбце разряда десятков
  • Вычтите произведение из делителя
  • Понизьте делимое в столбце единиц и повторите .

Для простоты начните с однозначных делителей и двузначных дивидендов. Помните, что это совершенно новая концепция для учащихся, поэтому не торопитесь моделировать задачи на доске.Обсудите, почему эти шаги работают, и помогите им понять, насколько важную роль в этом процессе играет ценность места.

5. Вводите большие числа, постепенно

Вот и все. Или это так? Пусть студенты освоятся с формулой и поработают над более мелкими задачами. По мере того, как они приобретают уверенность и начинают понимать, как выполнять деление в столбик, начинайте предлагать им задачи с трехзначным делителем, а затем задачи с двузначным делителем. Напомните учащимся, что шаги остаются неизменными независимо от того, насколько велика задача. , и посоветуйте им использовать макулатуру, чтобы «угадывать и проверять» умножение в процессе.Это хорошее место, чтобы убедиться, что они не испытывают затруднений и полностью понимают связь деления с числовой величиной и умножением. Чтобы освежиться, посмотрите это видео из Khan Academy:

6. Как это сделать. деление в столбик с десятичными знаками

Если вы охватили весь свой контент за первые пять шагов, поздравляю! Попросите учащихся продолжать практиковаться в продольном делении больших и малых чисел и укреплять взаимосвязь между делением и другими математическими концепциями, которые они изучают.Но процесс еще не завершен – учащиеся должны понимать, как выполнять деление в столбик с десятичными знаками. Для начала вернемся к одной из фундаментальных концепций деления: числовой стоимости. Однако на этот раз вы будете двигаться назад, а не вперед.

|

Предложите учащимся решить задачу, как они обычно это делают. Когда они дойдут до шага, на котором они обычно останавливаются на остатке, попросите их поставить десятичную точку в конце частного и деленного и записать несколько нулей после делимого.Попросите их продолжить обычные шаги деления на одно или два разряда, сбрасывая нули. Соедините десятичную дробь с дробями. Попросите их преобразовать частное с десятичной дробью в неправильную дробь. Это должно помочь им понять взаимосвязь между дробями и числовой ценностью и может быть хорошей возможностью перейти к основам дробей.

Как выполнить деление в столбик (без деления в столбик)

Поздравляем! Ваш урок подходит к концу, и вы успешно научили своих учеников делать столбики.Но знаете ли вы, что есть несколько способов разделить большие числа? Обучение студентов другим способам проверки своей работы является важной частью общих математических стандартов и может улучшить понимание учащимися того, что на самом деле означает длинное деление в данном контексте.

Квадратные модели

Квадратные модели – отличный способ для учащихся, изучающих визуальное представление, понять и концептуализировать деление, а также улучшить чувство числа. В этом методе используется сетка, чтобы представить процесс разделения как проблему площади: например, 148 ÷ 4 будет разделено на сетку высотой 4 единицы, площадью 148 квадратных единиц и неизвестным количеством единиц шириной.Студенты разбивают сетку на более управляемые области: 100 квадратных единиц, 40 квадратных единиц и 8 квадратных единиц. 100 ÷ 4 равно 25, 40 ÷ 4 равно 10, а 8 ÷ 4 равно 2. Эти числа находятся в верхней части модели площади и могут быть добавлены для получения ответа.

Частные частные

Подобно модели площадей, частные частные побуждают учащихся разбивать вопросы с разделением на «более удобные» части. Это помогает учащимся понять, что деление – это определение того, сколько раз одно число может переходить в другое число.Задайте задачу (в данном случае 450 ÷ 23) как уравнение деления в столбик. Попросите учащихся умножить делитель на 2 и 5, чтобы использовать их в качестве удобной ссылки. Спросите, сколько раз 23 входит в 400, но не ищите точное ближайшее число: сделайте его простым для работы, например 230 (десять раз). Вычтите 230 из 450 и поместите 10 справа, чтобы отслеживать это значение. Возьмите разницу и вычтите ее из дивиденда. Ответ должен быть 220. Спросите, сколько раз 23 переходит в 220. 5 x 23 равно 115, поэтому вычтите это из 220 и запишите 5.Продолжайте умножать и вычитать, пока окончательное число не станет слишком маленьким. Когда вы достигли этого шага, вы нашли остаток! Сложите числа в правом столбце, чтобы найти частное. Частные частные обладают гибкостью, которой нет у длинного деления. Деление в столбик нужно производить точно, но с частными частными можно просто многократно вычесть делитель из дивиденда и все равно прийти к правильному ответу. Используйте этот метод, чтобы усилить числовую ценность и концепцию деления как повторного вычитания.

Упражнения с длинным делением

Лучший способ для студентов научиться делать длинное деление – это практиковаться, практиковаться, практиковаться. Вот список из восьми заданий, которые увлекут ваш класс делением в столбик и помогут им развить твердые математические навыки.

1. Prodigy

Prodigy – это забавный, увлекательный ресурс с нулевой стоимостью для занятий в классе или дома. Учащиеся исследуют мир, наполненный приключениями, где успех зависит от правильных ответов на математические вопросы.С помощью панели управления учителем вы можете доставлять контент, согласованный с уроком, в зависимости от оценки, навыков или учащегося. Затем учащиеся отвечают на эти вопросы в игре и предоставляют вам отзывов в реальном времени о своем обучении и понимании . Поощряйте своих учеников практиковать все математические навыки, которые они изучали в классе, включая деление в столбик. Вот как вы можете использовать Prodigy, чтобы: Студенты любят увлекательную игровую платформу, где они могут собирать домашних животных, выполнять квесты и сражаться с друзьями.А пока они веселятся, вы помогаете им развить математическую уверенность и навыки деления в столбик. Это победа для всех!

2. Полное деление в натуральную величину

Ученики 5-го класса расширили свои навыки проведения #long_division с помощью различных занятий @DawhaHighSchool @FawziehHn #kinesthetic #online_division_calculator ➗✔ pic.twitter.com/vuNnKGu9Uc

– najah shams (@najahshams) 19 декабря 2018 г.

Оживите математику с помощью практической головоломки с делением столбиком. Вырежьте из разноцветной бумаги квадраты со всеми числами, которые нужны учащимся, чтобы решить задачу о длинном делении от начала до конца.Используйте малярную ленту, чтобы провести линии разделения на полу, и раздайте студентам пронумерованные карточки. Начиная с данного уравнения, попросите учащихся разложить все карточки в правильном порядке, чтобы решить уравнение. Это задание побуждает учащихся замедлиться и обдумать свои шаги, и это особенно полезно для класса, который все еще пытается освоить шаги умножения.

3. Бинго с длинным делением

|

Бинго – классика не зря. Каждый номер в листе ученика должен соответствовать вопросу, который стоит у вас в передней части класса.Напишите задачу на доске, а затем дайте учащимся бумагу для заметок и возможность решить ее и посмотреть, есть ли она у них на карточке. Как всегда, побеждает первый ученик, который заполнит целый ряд! Бросьте вызов своим ученикам, но убедитесь, что вы уделяете этому заданию достаточно времени – у некоторых учеников могут возникнуть проблемы с быстрым решением проблем, и они могут расстроиться или совершить ошибки, если они не в состоянии угнаться.

4. Книги по математике

Повысьте уровень грамотности и обучения математике с помощью забавных книг, охватывающих сложные математические концепции.Используйте их, чтобы объяснить учащимся разделение и остатки в увлекательной и увлекательной форме и даже охватить более основные концепции, прежде чем они начнут изучать, как выполнять деление в столбик. Некоторые учебники по математике, посвященные делению, включают: [галерея size = “medium” ids = “3833,3837,3834”]

• Остаток одного Элинор Дж. Пинчес
• Тринадцать Бобов Мэтью Макэллиготт
• Дверной звонок Пэт Хатчинс

5. Проявите творческий подход

У длинного подразделения много ступеней, и у них есть нужно делать в правильном порядке, чтобы получить правильный ответ.Учащиеся могут запутаться или расстроиться, если не запомнят шаги, что отрицательно скажется на их математической уверенности и успеваемости. Предложите учащимся придумать свой собственный уникальный способ запомнить, как выполнять продольное деление – разделите , умножьте , вычтите и сократите – чтобы творческий потенциал проявился в вашем классе. Попросите их создать плакат, песню, мнемоническое устройство или даже небольшую сценку, которую они могут показать своим одноклассникам.Если они стараются запомнить шаги, они с большей вероятностью научатся быстро.

6. Реле с удлиненным разделителем

|

Превратите практику деления в столбик в увлекательную классную игру с помощью эстафеты в столбик. Разделите свой класс на команды и составьте карточки с задачами в столбик. Выстройте учеников в группы. Каждая группа получает карточку для начала, и первые ученики выполняют первый набор шагов для решения возникшей у них проблемы. Когда они это делают, второй ученик ищет ошибки и продолжает решение.Если они решат проблему, они могут позвонить вам, чтобы проверить их работу и обменять правильный ответ на карточку с новой проблемой. Продолжайте, пока каждая группа не ответит на все свои карточки, и посмотрите, какая команда победит!

7. Сундук с сокровищами

Это задание – забавный способ для вашего класса отпраздновать завершение своего подразделения по разделению. Возьмите несколько коробок и наполните их небольшим угощением, которое понравится всем в классе. Включите список задач на умножение, которые ученики должны решать в группах, чтобы «разблокировать» коробку.В качестве дополнительной задачи сделайте код: каждое частное должно совпадать с буквой алфавита, чтобы учащиеся могли правильно расшифровать ключевую фразу, чтобы открыть коробку.

8. Генератор рабочих листов

Рабочие листы – это проверенный временем элемент математического класса. К счастью для вас, существует множество веб-сайтов, которые сделают всю работу за вас и сгенерируют настраиваемый рабочий лист, который даст вашим ученикам возможность попрактиковаться в делении в столбик. Вот некоторые из наших любимых:

Заключительные мысли об обучении студентов делению в столбик

Самое важное, что нужно помнить при обучении учащихся делению в столбик, – это не торопиться с материалом.Это большая концепция, которая отличается от всего, что они изучали раньше, и некоторые (если не все) ваши ученики могут сначала столкнуться с трудностями. Если вам нужно, вернитесь к более простым уравнениям и некоторым из более ранних шагов, которые мы обрисовали в общих чертах. для вас и работайте над ними, пока ваши ученики не почувствуют себя уверенно. Продолжайте ободрять и бросать вызов своим ученикам, и они будут готовы разделять и побеждать в кратчайшие сроки!

---

Создайте или войдите в свою учетную запись учителя на Prodigy – бесплатной игровой платформе для обучения математике, которую легко использовать как преподавателям, так и ученикам.{\ mathrm {th}} $$ в повторяющемся шаблоне формы.

Учащиеся развили базовое понимание деления в 3 классе, когда они пришли к пониманию деления в отношении равных групп, массивов и площадей. Они разработали множество стратегий, чтобы добиться беглости с делением в пределах 100, и они применили эти знания в контексте одно- и двухэтапных задач с использованием четырех операций. Студенты также пришли к пониманию свойства распределения, которое лежит в основе стандартного алгоритма деления.

Так же, как и в начале предыдущего раздела, когда учащиеся расширили свое понимание умножения за пределы понимания 3-го класса, включив в него задачи мультипликативного сравнения, этот модуль начинается с дополнительной сложности задач деления с остатками (4.OA.3). Это, вероятно, знакомо студентам из их собственного реального опыта попыток разделить количества поровну, и поэтому основное внимание уделяется интерпретации этих остатков в контексте различных задач.Затем студенты сосредотачиваются на расширении своих процедурных навыков с делением, чтобы включать до четырехзначных дивидендов с однозначными делителями (4.NBT.6), представляя эти случаи с базовыми десятью блоками, моделью площади, частными частными и, наконец, стандартный алгоритм, устанавливающий связи между всеми представлениями по мере их появления. Использование модели области помогает студентам концептуально понять разделение и как связь с их работой с площадью и периметром (4.MD.3), вспомогательным стандартом кластера.Наконец, вооруженные глубоким пониманием всех четырех операций, охватываемых в последних трех разделах, студенты решают многоэтапные задачи, включающие сложение, вычитание, умножение и деление, включая свои новые проблемные ситуации, такие как мультипликативное сравнение и интерпретация остатков (4.OA .3). Они также исследуют паттерны чисел и форм, используя четыре операции, чтобы сделать выводы о них (4.OA.5).

На протяжении всего раздела студенты по-разному занимаются математической практикой.Например, учащиеся видят и используют структуру (MP.7), когда они «разлагают [e] дивиденд на аналогичные десятичные единицы и находят частное единицу за единицей» (NBT Progressions, стр. 16). Кроме того, «неоднократно рассуждая (МР.8) о связи между математическими рисунками и письменной числовой работой, учащиеся могут увидеть алгоритмы умножения и деления как сокращения или резюме своих рассуждений о количествах» (NBT Progression, стр. 14). Наконец, когда учащиеся решают многоступенчатые задачи со словами, включающие сложение, вычитание и умножение, они моделируют математику (MP.4).

В то время как на протяжении всего модуля учащимся рекомендуется использовать модели, когда это необходимо для решения задач, их глубокий опыт работы с системой разрядных значений и несколькими концептуальными моделями, а также знакомство с алгоритмами деления готовит их к расширению этих моделей до двузначных делителей в Оценках. 5 (5.NBT.6) и свободное владение алгоритмом деления в 6 классе (6.NS.2). Каждый последующий класс зависит от понимания многозначного деления и его алгоритмов, что делает этот модуль важным для учащихся 4-х классов.

Темп: 19 учебных дней (16 уроков, 2 гибких дня, 1 контрольный день)

Инструкции по корректировке темпа обучения на 2020-2021 учебный год в связи с закрытием школ см. В нашем разделе «Рекомендуемые корректировки объема и очередности 4-го класса».

Как помочь вашему ребенку освоить стратегии деления и длинного деления

Когда моя дочь пошла на деление в четвертом классе, я знал, что нас ждут неприятности (и дополнительные домашние занятия по математике).Как родитель, который изучал математику «старым» способом, мне было очень трудно понять процессы, лежащие в основе ее домашнего задания по математике и задач со словами. (Мне стыдно сказать, что задачи по разделению слов для четвертого класса – это не шутка.) Я использовал книгу Эвана-Мура Основы математики , чтобы изучить, попрактиковаться и проанализировать стратегии разделения. Визуальные модели и объяснения предоставили пошаговый процесс обучения, который укрепил то, что моя дочь изучала в школе, и углубил ее понимание. Помогая своей дочери освоить деление в столбик, я даже обнаружил стратегии, лежащие в основе процесса деления, которые углубили мое понимание взаимосвязи между делением и умножением.

Дивизион – один из тех математических навыков, которые заслуживают много внимания, объяснений и практики. Вместо того, чтобы преподавать математику как серию систем / шагов для запоминания, сегодняшняя программа по математике включает в себя фундаментальные мыслительные процессы, лежащие в основе каждого навыка и стратегии, которым обучают детей. Сегодняшняя программа по математике требует, чтобы дети понимали, почему они делают эти шаги, и использовали это понимание числовых соотношений для более эффективного решения задач. Если дети знают, почему они делают определенные шаги, они могут применять это понимание для решения различных математических задач и понимать беглость чисел на более глубоком уровне.

Вот некоторые стратегии и концепции, которые мы практиковали, которые помогли мне и моей дочери лучше понять разделение.

Начало деления и умножения

Когда ваш ребенок начинает изучать деление, ему / ей важно понимать взаимосвязь между делением и умножением. Детям необходимо хорошо знать факты умножения. (Если они не знают фактов умножения, потренируйтесь в беглости несколько недель, прежде чем начинать деление.) Ознакомьтесь с дополнительными ссылками ниже, чтобы получить советы и идеи, чтобы узнать факты умножения.

Связь между умножением и делением

«Начало деления» учит простой концепции: чтобы делить, вы должны умножать. Использование наглядных примеров умножения и деления поможет вашему ребенку научиться распознавать разницу между умножением и делением.

Если вы привыкли к старому методу деления, этот процесс может показаться утомительным, но детям важно понимать разницу между умножением и делением.Когда задачи с числами и словами усложняются, это фундаментальное понимание поможет им узнать, когда делить, а когда умножать.

Смоделируйте, как найти неизвестное число умножением или делением.

Чтобы узнать, понимает ли ваш ребенок основную связь между умножением и делением, спросите его или ее:

Ответ: факты умножения и деления связаны. Если вы знаете один факт, вы можете решить другой связанный факт.

Стратегия трех подразделений

Один из аспектов нынешней учебной программы по математике, который мне нравится, – это акцент на обучении нескольким стратегиям и предоставление детям возможности решать, какая из них лучше всего подходит для них. Такой подход позволяет детям понять и выбрать, какой метод лучше всего подходит для их стиля обучения. Испытание разных подходов может иногда даже иметь значение между неудачей и успехом в математике. Вот три разные стратегии, которым нужно научить, когда начинаете деление.

1. Сделайте связи с помощью шаблонов деления и разбейте числа

Это высшая степень беглости чисел. Обучение детей распознаванию и использованию шаблонов в числовых операциях поможет им эффективно решать проблемы.

6,000 ÷ 3

6 ÷ 3 = 2

6,000 ÷ 3 = 2,000

Просто представьте 6000, разделенные на 3, как 6 тысяч, разделенные на 3, и это 2 тысячи.

2.Разбивка чисел на «дружественные» числа с использованием модели области

260 ÷ 5 = 52

Разбейте числа на «дружественные» числа. Разбиение чисел на числа, которые легко делятся, важно научиться беглому чтению чисел. Это может показаться немного утомительным, но понимание того, как разбить большие числа на числа, которыми проще манипулировать, может развить у детей умственные математические способности.

Разбейте 260 на «дружественные» числа 250 и 10. Я выбрал 250, потому что это делитель 5, умноженный на большое число (50).Я выбираю 10, потому что это разница между 250 и 260. Они входят в рамки модели площади. Разделите каждый на делитель, чтобы получить множители, затем сложите множители.

3. Разделить на группы вычитания

623 ÷ 4

Я могу составлять группы по 4 человека и вычитать их из 623 до тех пор, пока не останется достаточно, чтобы образовать группу. Я начну со 100 групп по 4. Осталось 223. Затем я вычту 50 групп по 4. Теперь у меня осталось 23.5 групп по 4 человека израсходуют большую его часть; осталось недостаточно, чтобы вычесть даже 1 группу из 4. Наконец, я сложу количество групп из 4 и запишу остаток.

Длинное деление: деление многозначных чисел с помощью моделей площади, частичных частных и стандартного алгоритма

Если я только что потерял вас, используя такие фразы, как «частные частные» и «стандартный алгоритм», не пугайтесь. Это просто математическая терминология для пошаговых процессов.Частное – это ответ, а частное – частичное. Стандартный алгоритм – это пошаговый способ решения проблемы. При делении в столбик эти стратегии используются для повторного вычитания, чтобы в конечном итоге найти ответ.

Деление многозначных чисел с использованием модели области

Мы занимались этим ранее, начав деление, но теперь числа становятся больше и немного сложнее.

3,182 ÷ 15 = 212 R2

Деление – это просто повторное вычитание.Я буду группировать по 15 и вычитать их, пока не останется достаточно средств для вычитания. Затем я сложу количество групп. Поскольку у меня получилось число меньше делителя, я запишу его как остаток.

3,182 ÷ 15 = 212 R2

Разделить на частные

Как и в модели площади, я найду группы делителя и вычту их. Затем я сложу количество групп и запишу остаток, если он есть.

Разделить по стандартному алгоритму

Если вы вздохнете с облегчением на этом примере, я полностью понимаю. Это традиционный способ обучения разделению, которому большинство из нас научилось много лет назад.

Этот стандартный алгоритм длинного деления повторяется с шагами:

1. Разделить

2. Умножить

3. Вычтем

4. Перейдите к следующей цифре

5.Повторить

* Многие дети путаются с шагами 2 и 3 , потому что вы на самом деле не делите, а умножаете и вычитаете, чтобы найти остаток.

3,182 ÷ 15 = 212 R2

Посмотрите только на одно место за раз, начиная с левого. Поскольку 15 не делятся на 3, я перейду к следующему месту. Теперь я прикидываю, сколько раз 15 перейдет в 31, и напишу это над 1. Я вычитаю и опускаю цифру со следующего места.Я продолжаю делать это через дивиденд (число). Когда у меня заканчиваются места, я запишу оставшееся число в качестве остатка.

Лучший способ помочь вашему ребенку овладеть трудным навыком деления – это практиковаться, практиковаться и практиковаться. Узнайте, какой метод лучше всего подходит для вашего ребенка, и предложите ему или ей множество практических задач. Кроме того, не забывайте решать проблемы с разделением слов. Решение задач со словами может продемонстрировать, насколько хорошо ваш ребенок понимает концепцию деления и как ее использовать.

Рекомендуемые ресурсы

Все примеры и стратегии были взяты из книги Эван-Мур Основы математики для 1–6 классов. Хотя это учебный ресурс, я обнаружил, что математические модели и практические занятия удобны для использования дома.

Советы по обучению задачам со словами и умножению можно найти в следующих статьях:

---

Хизер Фоуди – сертифицированный учитель начальных классов с более чем 7-летним опытом работы преподавателем и волонтером в классе.Ей нравится создавать содержательные и творческие уроки для учащихся. В настоящее время она работает в отделе маркетинга и коммуникаций Эван-Моора и любит создавать возможности для обучения, которые являются значимыми и творческими как для студентов, так и для учителей.

Категории: Классные стратегии, Идеи для уроков | Теги: математика 3-го класса, математика 4-го класса, разделение 5-го класса, общее ядро ​​деления, стратегии деления, разделение четвертого класса, как преподавать разделение, математика, разделение третьего класса | Постоянная ссылка

Математика 4-го класса: Дивизион – Видео и уроки

Используйте видеоролики и тесты, входящие в эту главу, в дополнение к изучению этой темы в классе вашим 4-классником.Ваш ученик обнаружит, что занимательная анимация, увлекательное повествование и короткие уроки делают изучение деления простым и увлекательным. Поскольку мы знаем, что вам небезразлично, насколько хорошо ваш четвероклассник владеет принципами и методами деления, мы включили в каждый урок и экзамен по главе, чтобы помочь вам оценить его или ее понимание этих тем.

Урок	Цель
Как выполнять деление: шаги и примеры	В уроке описаны шаги, необходимые для деления целых чисел.
Как делить однозначные числа	Учащиеся видят примеры, которые они могут использовать, чтобы научиться делить однозначные числа.
Правила делимости для 2, 5 и 10	На видео показаны правила деления на 2, 5 и 10.
Деление с остатком	На этом уроке инструкторы обучают процессу деления чисел с помощью остаток.
Выполнение длинного деления с большими числами: шаги и примеры	Примеры используются в этом уроке, чтобы научить студентов выполнять длинное деление больших чисел.
Деление трехзначных чисел	В этом уроке используются примеры и задачи со словами, чтобы показать, как делить трехзначные числа.
Как делить числа, оканчивающиеся на нули	Учащиеся могут попрактиковаться в делении чисел, оканчивающихся на ноль.
Как заполнить таблицу деления	Инструкторы показывают процесс, используемый для заполнения таблицы деления.
Работа с таблицами ввода-вывода деления	В этом уроке используются примеры, демонстрирующие, как найти решения с помощью таблицы ввода-вывода.
Решение задач со словами с разделением	Учащиеся узнают, как решать задачи со словами с разделением.
Решение шаблонов деления при увеличении разрядов	Урок знакомит студентов с увеличением разрядов и их использованием для решения шаблонов деления.
Как завершить предложение с разделением	Студенты практикуют завершение предложения с разделением после изучения процесса.

Spectrum Учебное пособие по математике для четвертого класса – умножение, деление, дроби, десятичные дроби по математике с примерами, тестами, ключом ответа для домашнего образования или класса (160 стр.): Spectrum: 9781483808727: Amazon.com: Книги

ОСОБЕННОСТИ УПРАЖНЕНИЯ:

• Возраст 9–10, 4 класс

• 9 глав, 160 страниц, 10,9 дюйма x 8,4 дюйма

• Охватываемые темы: умножение и деление, дроби и десятичные дроби, преобразование единиц измерения , классификация геометрических фигур и подготовка к алгебре

• Предварительные, заключительные, промежуточные и заключительные тесты

• Включает ключ для ответа

ЦЕЛЕВАЯ ПРАКТИКА: Учебное пособие по математике для четвертого класса Spectrum обеспечивает целенаправленную практику в математическом мастерстве для детей от 9 до 10 лет.Эта 160-страничная рабочая тетрадь помогает детям укреплять математические навыки с помощью прогрессивных уроков, упражнений по решению проблем и тестов на протяжении каждого урока, чтобы проверить уровень понимания и знаний каждого ученика по предмету.

СООТВЕТСТВУЕТ ТЕКУЩИМ ГОСУДАРСТВЕННЫМ СТАНДАРТАМ: Эта основанная на стандартах рабочая тетрадь помогает вашему ребенку развить беглость и овладеть основными математическими навыками, включая умножение и деление, дроби и десятичные дроби, преобразование измерений, классификацию геометрических фигур и подготовку к изучению алгебры.

КАК ЭТО РАБОТАЕТ: Учащиеся начинают каждую главу с предварительного теста, чтобы определить текущее понимание, затем переходят к веселым и увлекательным урокам, которые включают пошаговые примеры и обширные практические страницы. Промежуточные и последующие тесты позволяют вашему четверокласснику проверить свои знания и убедиться, что он усвоил навыки, необходимые для перехода по учебной программе к следующей концепции.

РАБОТА ВМЕСТЕ: Родители и учителя могут точно контролировать и оценивать обучение и навыки учащихся в классе или дома, используя ключ для ответа, результаты выставления оценок и оценки.

ПОЧЕМУ SPECTRUM: Уже более 20 лет Spectrum предоставляет решения для родителей, которые хотят помочь своим детям продвигаться вперед, и для учителей, которые хотят, чтобы их ученики достигли поставленных целей обучения и превзошли их; Рабочие тетради также являются отличным ресурсом для домашнего обучения. Spectrum вместе с вами поддерживает образовательный путь вашего ребенка на каждом этапе его пути.