Примеры больше меньше равно: Больше, меньше, равно — урок. Математика, 1 класс.
Комплект карточек (10) “Обучающий калейдоскоп. Больше, меньше, равно”
Навигация:Главная›Для школ›Учебно-наглядные пособия и оборудование›Начальная школа›Математика›Раздаточные пособия›Комплект карточек (10) “Обучающий калейдоскоп. Больше, меньше, равно”
В избранномВ избранное Артикул: 10688 Цена: предоставляется по запросу Задать вопрос по оборудованию | ||||||||||
Назначение Используется вместе с наглядно-дидактическим пособием “Обучающий калейдоскоп” Технические характеристики и комплектность
Пособие состоит из 10 полноцветных, напечатанных на картоне и ламинированных пленкой карточек. Карточки снабжены маркировкой, где буква обозначает предмет, первая цифра – код темы, вторая цифра – порядковый номер (тему) карточки в серии, последняя цифра – вариант (I или II). М4.1.I. Решение простых задач с использованием картинок. М4.1.II. Нахождение на числовой прямой числа, больше или меньше указанного. М4.2.I, М4.2.II. Простые примеры в пределах 10, сформулированные следующим образом: «насколько одно число больше/меньше другого». Рекомендуется записывать условия (математическим языком) и решения в тетрадь. М4.3.I. Нахождение наибольшего числа в рядах чисел (счет в пределах 20). М4.3.II. Простые примеры в пределах 10. Задания на нахождение самого маленького/большого числа из ряда чисел и последующее выполнение вычислений с ним.Рекомендуется записывать решения в тетрадь. М4.4.I, М4.4.II. Карточки, содержащие верные и неверные неравенства. Внимание! На поле справа выставляются только фишки, обозначающие верные неравенства. Фишки, расположенные радом с неверными неравен-ствами, остаются слева или убираются с поля.Рекомендуется использовать при знакомстве учащихся со знаками > <, решении простых примеров в пределах 10. М4.5.I. М4.5.II. Карточка с заданием повышенной сложности. Вычисления в пределах 50. Из ряда чисел требуется найти самое большое/маленькое число; самое маленькое двузначное число; число, которое больше самого маленького на 6, и т.п. Рекомендуется записывать решения в тетрадь. ← Назад |
Инженерные классы
Образовательные робототехнические модули
WS Junior – Мехатроника Festo
Учебно-наглядные пособия и оборудование
- Анатомия
- Биология
- География
- ИЗО, МХК
- Иностранный язык
- История
- Литература
- Математика
- Начальная школа
- НВП
- ОБЖ
- Русский язык
- Труд
- Физика
- Химия
- Музыка
- Черчение
- Астрономия
- Информатика
- Физическая культура
Точки роста
Мультимедийное оборудование
3D Принтеры
Учебное оборудование Phywe.
Учебные лаборатории ФГОС.
Инновационное оборудование. Переносные лаборатории
Инновационное оборудование. Цифровые учебные лаборатории
Национальный проект “Образование”
Сравнение натуральных чисел. – tutomath.ru репетитор по математике
Определение, что такое сравнение натуральных чисел.
Сравнение в жизни мы используем постоянно. Например, длинная дорога или короткая, высокий или низкий человек, много игрушек или мало, большая емкость или маленькая. Так, что же такое сравнение натуральных чисел?
Сравнение натуральных чисел – это определение какое из натуральных чисел больше, а какое меньше.
Способы сравнения натуральных чисел.
Рассмотрим натуральный ряд чисел.
1, 2, 3, 4, 5, 6, 7, 8, 9,10, 11, 12, 13, 14, 15, …
1) Всегда числа, стоящие справа в натуральном ряду больше чисел, стоящих слева.
Например, сравним числа 7 и 9. Число 9 стоит правее числа 7, следовательно, число 9 больше 7.
Единица, является самым маленьким натуральным числом.
Любое натуральное число больше нуля.
2) Всегда больше то натуральное число, у которого разрядов больше.
Сравним два числа 45 и 190. Сразу понятно, что число 190 больше числа 45. Мы сделали такой вывод потому, что число 190 является трехзначным числом, а 45 – двухзначным числом. У числа 190 есть разряд сотен, десятков и единиц, а у числа 45 только разряд десятков и единиц.
3) Если количество разрядов одинаково, то мы будем сравнивать величины цифр разрядов, начиная с высшего разряда (слева направо).
Например, сравним числа 478 и 399. Оба числа являются трехзначными, поэтому подробно рассмотрим высший разряд сотен. У первого числа 478 разряд сотен равен 4, а у второго числа 399 разряд сотен равен 3. Следовательно, первое число 478 больше второго числа 399, потому что 4 больше 3.
Если высшие разряды одинаковые мы сравниваем следующий меньший разряд цифр.
Сравним числа 7890 и 7860. Начинаем сравнивать высший разряд единиц тысяч он у обоих чисел равен 7. Следующий разряд сотен, также равен у обоих чисел 8. А вот разряд десятков различен. У первого числа 7890 разряд десятков равен 9, а у второго числа 7860 равен 6. Далее делаем вывод, первое число 7890 больше 7860, потому что разряд десятков у первого числа больше чем у второго. Проще сказать, 9 больше 6.
\(\left(\begin{array}{c}78 \color{blue} {9}0\\ 78\color{red} {6}0\end{array}\right)\)
4) Если при сравнении все цифры разрядов двух натуральных чисел одинаковы, значит числа равны.
Например, сравним числа 4890765 и 4890765. Видно, что у обоих чисел все цифры разрядов одинаковы, следовательно, они равны.
\(\left(\begin{array}{c}4890765\\ 4890765\end{array}\right)\)
Неравенство и знаки неравенства.
Чтобы не писать словами больше, меньше или равно в математике придумали обозначения. Больше (>), меньше (<), равно (=). Например, 3 больше 2 математическая запись будет выглядеть так 3>2. Или 6 меньше 10, мы запишем как 6<10. 8 равно 8, запишем 8=8.
Больше (>), меньше (<), равно (=). Например, 3 больше 2 математическая запись будет выглядеть так 3>2. Или 6 меньше 10, мы запишем как 6<10. 8 равно 8, запишем 8=8.
Выражения 3>2, 6<10 и 8=8 называются в математики неравенствами.
Такая запись 2<3<4 называется двойным неравенством.
Вопросы к теме:
Назовите наименьшее натуральное число?
Ответ: единица.
Назовите наибольшее натуральное число?
Ответ: натуральный ряд чисел бесконечен, поэтому наибольшего натурального числа не существует.
Какое из чисел больше шестизначное или семизначное число?
Ответ: семизначное число больше шестизначного.
Разобраны примеры с ответами на типичные задания темы.
Пример №1:
Прочитайте неравенство: а) 5<12 б) 6>1 в) 7=7
Ответ: а) пять меньше двенадцати б) шесть больше одного в) семь равено семи.
Пример №2:
Запишите неравенство: а) 4 меньше 8 б) 10 больше 9 в) 11 равно 11.
Ответ: а) 4<8 б) 10>9 в) 11=11.
Пример №3:
Верны ли неравенства? Проверьте знаки сравнения: а) 5<6 б) 7<3 в) 22>23 г) 5=55
Ответ: а) верно б) неверно в) неверно г) неверно.
Пример №4:
Сравните числа, поставьте правильно знаки неравенства (<, >, =): а)3 и 3 б)4 и 9 в)8 и 3
Ответ: а) 3=3 б) 4<9 в) 8>3
Пример №5:
Посмотрите на рисунок и составьте неравенство.
Ответ: 10>2 или 2<10.
Равно, Больше, Меньше
Что такое равенство?
Связь между двумя величинами или математическими выражениями, которые имеют одинаковое значение или представляют различные объекты, называется равенством. Для представления равенства мы используем символ равенства или знак равенства . Следовательно, мы пишем два параллельных горизонтальных символа, таких как «=», чтобы показать равенство.
Таким образом, равенство между A и B записывается как A = B , что читается как A равно B или A равно B .
Что такое неравенство?
Неравенство — это отношение между двумя числами или алгебраическими выражениями, которые не равны. Неравенства иногда могут быть представлены либо как вопрос, который может быть решен, либо как констатация факта в форме теорем. Мы можем использовать четыре члена неравенства для сравнения двух величин: не равно , больше , больше или равно , меньше и меньше или равно .
Не равно
Один из символов, которые мы используем для неравенства, не равен знаку. Он используется, чтобы показать, что одно значение не равно другому. Следовательно, чтобы показать отношение не равно, мы используем две горизонтальные линии и косую черту посередине.
Следовательно, если две величины A и B не равны, это записывается как A ≠ B , что читается как A не равно B .
Больше
Больше чем также является одним из неравенств, используемых, когда количество больше или больше, чем другое количество или количества. Следовательно, чтобы показать, что одно число больше другого, мы используем две штрихи одинаковой длины, которые выглядят как острый угол, направленный вправо.
Следовательно, чтобы показать, что одно число больше другого, мы используем две штрихи одинаковой длины, которые выглядят как острый угол, направленный вправо.
Итак, чтобы сказать, что количество A больше, чем B, мы обозначаем его как A > B , что читается как A больше, чем B .
Больше или равно
Помимо слова больше или равно, мы также используем термин больше или равно, чтобы показать взаимосвязь между двумя или более математическими объектами или неравенствами. Больше или равно предполагает, что значение переменной может быть больше или равно определенному числу. Термин « по крайней мере ” означает, что значение может быть больше или равно. Следовательно, чтобы показать, что число больше другого, мы используем две штрихи одинаковой длины, которые выглядят как острый угол, уходящий вправо, и подчеркивание под ним.
Таким образом, чтобы показать, что A больше, чем B, мы обозначаем его как A ≥ B , что читается как A больше или равно B – что означает, что A может быть больше, чем B, а также может быть равно B.
Меньше
Когда первое значение меньше второго, мы используем термин меньше чем. Меньше используется, чтобы показать отношение между меньшим и большим значением. Чтобы показать неравенство, что одно число меньше другого, мы используем символ, состоящий из двух штрихов одинаковой длины, которые выглядят как острый угол, идущий влево.
Следовательно, чтобы показать, что A меньше B, мы обозначаем его как A < B , что читается как A меньше B .
Меньше или равно
Меньше или равно означает, что переменная меньше или равна другому числу, выражению или термину. Использование терминов «самое большее», «не более», «максимум» и «не превышающий» также означает меньше или равно. Два штриха одинаковой длины, которые выглядят как острый угол, идущий влево, и подчеркивание под ним — это символ, используемый для обозначения того, что одна величина меньше или равна другой.
Следовательно, чтобы показать, что A меньше или больше B, мы обозначаем его как A ≤ B , что читается как A меньше или равно B .
Что такое символы равенства и неравенства?
В таблице ниже собраны все символы, которые мы используем для обозначения равенства и неравенства между двумя величинами.
| СИМВОЛ | ТЕРМИН | ПРИМЕР | КАК ЧИТАТЬ 8102 | |||||
| = | равны | 1 + 1 = 4 | 1 плюс 1 равен 21 плюс 1 равен 2 | |||||
| ≠ | не равны | 2 + 1 c 4 | 2 Plus 10102 | 2 + 1 c 4 2 | 2 Plus 10102 | 2 + 1 c 40102 | 2 плюс 10102 | 2 + 1 c Не равен 4 |
| > | больше, чем | 9> 5 | 9 больше 5 | |||||
| < | Менее | 3 <10 | 9009 3 IS Менее3 <10 | 9009 3 – менее3 <10 | 9009 3 – менее3. |
Почему мы используем символы равенства и неравенства?
Использование символов равенства и неравенства может помочь нам сравнивать числа, устанавливать отношения между двумя или более математическими объектами, в которых мы еще не уверены, и использовать их для математических уравнений или неравенств.
Сравнение чисел
Одной из наиболее важных функций использования символов равенства и неравенства является сравнение двух математических величин. Давайте посмотрим на некоторые из примеров ниже!
Использование знака равенства для сравнения математических объектов
Пример №1
На приведенном рисунке мы видим, что слева у нас есть два леденца на палочке. С правой стороны у нас также есть два леденца на палочке. Поскольку в знаке слева и справа одинаковое количество леденцов, мы будем использовать знак равенства, чтобы показать равенство между двумя разными группами леденцов.
Использование больше или меньше для сравнения математических объектов
Пример #1
Подсчитав количество файлов cookie с обеих сторон, мы узнаем, что количество файлов cookie с левой стороны больше, чем число файлов cookie с правой стороны. Следовательно, мы используем символ «больше», чтобы показать взаимосвязь между файлами cookie.
Пример #2
Во втором примере мы ясно видим, что справа больше мороженого, чем слева. Таким образом, мы используем знак меньше, чтобы показать, что два действительно меньше трех мороженых.
Отношения состояний
Когда есть величины, в которых мы не уверены, мы иногда используем символы равенства и неравенства, чтобы узнать их отношения.
Пример #1
Объяснение:
На данном рисунке, если мы сравним отношения между двумя собаками, мы ясно увидим, что одна выше другой. Следовательно, мы можем сказать, что собака с правой стороны больше, чем собака с левой стороны.
Пример #2
\$1 = 100 центов
В этом примере мы знаем, что для того, чтобы сделать доллар из центов, нужно иметь 100 центов. Следовательно, мы можем сказать
Пример #2
У Джейса было 20 ручек, но он потерял их в школе. Сколько у него сейчас?
Так как Джейс потерял несколько своих ручек, то количество ручек, которое у него сейчас есть, должно быть меньше 20. Следовательно, ручек < 20 .
Следовательно, ручек < 20 .
Пример #3
Анджелина уже потратила $50 и купила еще одежду. Как вы думаете, сколько она потратила?
Уже было сказано, что Анджелина уже потратила 50 долларов, прежде чем добавить больше одежды для покупки. Следовательно, можно сказать, что она потратила больше 50 долларов. Таким образом, расходы Анджелины > 50 долларов.
Пример #4
Даная приготовила 40 кексов для своих посетителей. Первая группа из двадцати человек съела примерно 24 кекса, затем подошла еще одна группа людей. Сколько кексов осталось?
Пока готовилась, Даная приготовила ровно 40 кексов, но потом пришли двадцать человек и съели 24 кекса. Таким образом, мы уже знаем, что кексов теперь меньше 40. Но людей пришло больше, поэтому можно сказать, что кексов тоже может быть 40. Значит, мы можем перевести данное утверждение в 9.0005 0 ≤кексы < 40 , что читается как кексы, может быть больше или равно 0, но меньше 40 кексов.
Как использовать символы равенства и неравенства?
Мы перечислили все возможные причины, по которым мы используем символы равенства и неравенства, такие как знак равенства, знак больше или меньше. Теперь, как мы будем практиковать их использование? Давайте посмотрим на некоторые образцы раньше.
Теперь, как мы будем практиковать их использование? Давайте посмотрим на некоторые образцы раньше.
Пример #1
Укажите взаимосвязь между двумя числами, используя знаки “равно”, “больше” или “меньше”. 9Примеры Мы будем использовать знак равенства. Следовательно, у нас будет утверждение 20 = 20, которое читается как 20 равно 20. Таким образом, ответ = .
 Итак, чтобы сделать утверждение верным, 8 < 17, что читается как 8, меньше 17. Следовательно, ответ равен 9.0005 < .
Итак, чтобы сделать утверждение верным, 8 < 17, что читается как 8, меньше 17. Следовательно, ответ равен 9.0005 < .Пример #2
Укажите взаимосвязь между двумя числами, используя знаки “равно”, “больше” или “меньше”. Примеры
Таким образом, 11 > 9 , которое читается как 11, больше 9. Следовательно, ответ будет > .
Следовательно, 6 = 6 , что читается как 6, равно 6. Следовательно, ответ = .
 . Итак, переписав его, мы получим 35 __ 39. Следовательно, 35 < 39 , что читается как 35, меньше 39. Следовательно, ответ < .
. Итак, переписав его, мы получим 35 __ 39. Следовательно, 35 < 39 , что читается как 35, меньше 39. Следовательно, ответ < .Пример №3
Укажите взаимосвязь между двумя числами, используя знаки “равно”, “больше” или “меньше”.
| Примеры | Объяснение или ответ |
| 20 – 13 __ 35 – 23 | Первый шаг, который нам нужно сделать – это вычесть цифры с левой стороны, соответственно, и вычесть из них числа с левой стороны. Следовательно, 20 – 13 = 7 и 35 – 23 = 12,9.0304 Следовательно, у нас есть новое утверждение 7 __ 12. Таким образом, 7 < 12 , которое читается как 7, меньше 12. Следовательно, чтобы сделать утверждение верным, нам нужно добавить символ < . |
| 21 – 8 __ 39 – 26 | Первое, что нам нужно сделать, это вычесть числа слева и справа от математического выражения. Таким образом, 21 – 8 = 13 и 39 – 26 = 13. Следовательно, 13 = 13 , что читается как 13, равно 13. Следовательно, использование = сделает утверждение верным. |
| 100 – 54 __ 64 – 20 | Вычитая числа слева и справа от математического утверждения, мы получим 100 – 54 = 46 и 64 – 20. Получим новое утверждение 46 __ 44. Следовательно, 46 > 44 , которое читается как 46, больше 44. Следовательно, нам нужно использовать символ больше, > , чтобы утверждение было верным. |
Пример #4
Укажите взаимосвязь между двумя числами, используя знаки “равно”, “больше” или “меньше”. Примеры Следовательно, 0 x 3 = 0, а 1 x 3 = 1. Таким образом, переписав новый оператор 0 __ 1, мы можем легко определить, какой символ использовать.
Таким образом, 0 < 1 , которое читается как 0, меньше 1.
Следовательно, чтобы утверждение было верным, нам нужно использовать знак «меньше».
Следовательно, 6 x 4 = 24, а 3 x 8 = 24. Таким образом, переписав новый оператор 24 __ 24, мы можем легко определить, какой символ использовать.
Таким образом, 24 = 24 , что читается как 24, равно 24,9.0304 Следовательно, чтобы сделать утверждение верным, нам нужно использовать знак равенства.
Таким образом, 84 < 91 , которое читается как 84, меньше 91.
Следовательно, символ “меньше” делает утверждение верным.
Таким образом, переписав новое выражение 50 __ 48, мы можем легко определить, какой символ использовать. Таким образом, 50 > 48 , которое читается как 50, больше, чем 48.
Следовательно, символ больше делает утверждение верным.
Пример №5
Укажите взаимосвязь между 10 метрами и 10 000 сантиметров.
Решение
| Пошаговый процесс | Объяснение |
| 10 метров X 100 сантиметра/1 метр | Contrert 10 Meterters. |
| 10 х 100 = 1000 сантиметров | Упростить. |
| 1000 см __ 10 000 см | Сформулируйте новое математическое утверждение. |
| 1000 сантиметров < 10 000 сантиметров | Поскольку 1000 сантиметров меньше 10 000 сантиметров, нам нужно использовать символ «меньше». |
| Следовательно, 10 метров < 10 000 сантиметров . |
Пример #6
Если у Луны было 150 долларов и она купила сумку стоимостью не более 100 долларов, сколько денег у нее осталось?
Решение
| Пошаговый процесс | Объяснение |
| Деньги Луны = \$150 | 9009na указано, что у Луны было $150 9009na до покупки сумки.|
| стоимость сумки < 100 долларов | Из-за использования слова «не более 100 долларов мы уверены, что стоимость сумки меньше 100 долларов. |
| ~\$100 __ \$150 | Поскольку стоимость сумки меньше \$100, нам нужно написать математическое выражение, которое преобразуется в ~\$100 __ \$150, которое читается как около \$100 равно __ к \ 150 долларов. |
| ~\$100 < \$150 | Чтобы утверждение было верным, мы точно знаем, что $100 меньше, чем \$150. Поэтому поставьте < на пустом месте. Поэтому поставьте < на пустом месте. |
| Осталось денег < \$150 | Мы можем сделать вывод, что после покупки сумки на Luna осталось меньше $150. |
| Следовательно, Деньги Луны < \$150 после покупки сумки. |
Неравенства с одной переменной (временная тематика) Рабочие листы
Понимание и решение неравенств с одной переменной. Рабочие листы по математике для 6-го класса
Сравнение трехзначных чисел. Рабочие листы для 2-го класса по математике. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Что меньше или равно? Определение, символ, примеры
Где уравнения определяют равенство между двумя или более математическими элементами; неравенства дают нам возможность исследования, когда две величины не равны по стоимости, но сравнимы по своей природе. В уравнении используется символ « равно (=)» , чтобы выразить отношение равенства между двумя величинами. В неравенствах используются символы « больше, чем (> )» и « меньше, чем (<)» для сравнения величин, которые не равны по своей природе.
В уравнении используется символ « равно (=)» , чтобы выразить отношение равенства между двумя величинами. В неравенствах используются символы « больше, чем (> )» и « меньше, чем (<)» для сравнения величин, которые не равны по своей природе.
Мы используем «больше чем», когда одна величина больше другой. Например, 7 манго больше, чем 3 манго, что математически выражается как 7 > 3 .
Мы используем «меньше чем», когда одно количество меньше другого. Например, 8 морковок меньше, чем 10 морковок, что математически выражается как 8 < 10.
Однако в некоторых случаях, когда у нас есть только одно количество и мы хотим оценить другое количество, сравнимое с нашим первым, мы используем оператор неравенства, называемый « Меньше или равно ($\leq$)».
Давайте разберемся в этом на примере реальной ситуации. Дэвид ходит с мамой по магазинам, где она разрешает ему купить себе любую игрушку, если ее стоимость не превышает 10 долларов. Это означает, что Дэвид может купить игрушку стоимостью 3, или 4, или 7, или 8, или даже 10 долларов, или любой другой ценой, пока он не превысит лимит в 10 долларов. Мы также можем сказать, что максимальная сумма, которую ему разрешено потратить, составляет 10 долларов.
Это означает, что Дэвид может купить игрушку стоимостью 3, или 4, или 7, или 8, или даже 10 долларов, или любой другой ценой, пока он не превысит лимит в 10 долларов. Мы также можем сказать, что максимальная сумма, которую ему разрешено потратить, составляет 10 долларов.
Тогда математически мы можем либо сказать, что P меньше 10 или
Он дает нам математическое выражение для утверждений «самое большее, не более, максимальное и не превышающее». Его можно использовать для сравнения переменных или любых математических элементов или любых реальных величин.
Давайте посмотрим на неравенство y $\leq$ 15.
Это означает, что переменная y может иметь любое значение, меньшее или равное 15. Это может быть 1 или 2, или 4,5, или 12/5. ; может быть и 15, но не больше.
Давайте посмотрим, как можно представить неравенство вида x $\leq$ 5 на числовой прямой.
Шаг 1: Найдите цифру «5» на числовой строке, отметьте ее большим кружком и закрасьте кружок.
Шаг 2: Неравенство предполагает, что переменная x может принимать любые значения, меньшие или равные 5, то есть все значения слева от этого круга. Начиная отсюда, продлите стрелку до левого конца, обозначающую все значения, которые может иметь переменная x.
Примечание. Если неравенство было просто «меньше»; мы не заполняем круг, как показано в таблице ниже.
Пример 1: Выберите числа, которые меньше или равны 55 из заданного набора чисел.
Пример 2: В магазине есть арбузы весом 5,3 кг, 7,6 кг, 4,5 кг, 7 кг, 6 кг и 6,1 кг. Если Диана хочет купить арбуз весом не более 6 кг, какие у нее возможности?
Вивиан хочет купить игрушку стоимостью меньше или равной 16 долларам. Какие игрушки она может купить?
Какие игрушки она может купить?
Вивиан может купить куклу, мозаику или марионетку, поскольку они стоят меньше или равны 16 долларам.
 *шир.*выс.), см
*шир.*выс.), см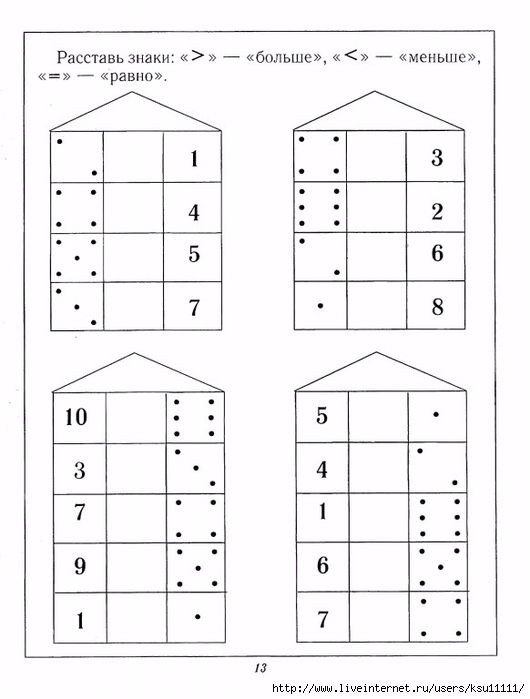
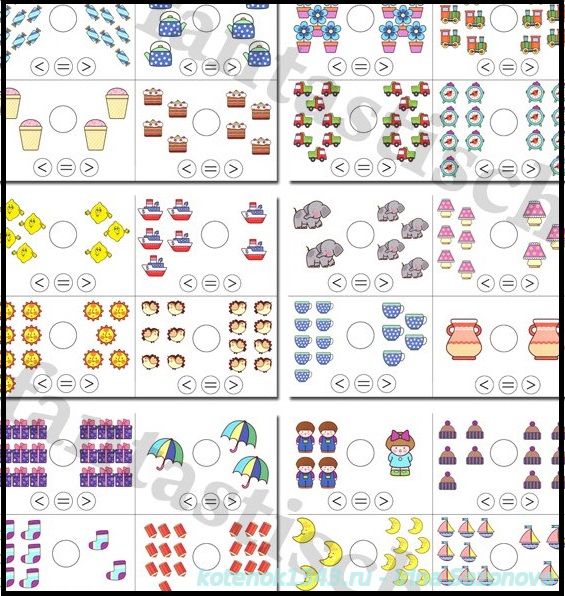 Текстовые задачи с использованием выражений «больше», «меньше». Вычисления в пределах 10.
Текстовые задачи с использованием выражений «больше», «меньше». Вычисления в пределах 10.