Правило умножения суммы на число 3 класс: Умножение суммы на число — урок. Математика, 3 класс.
Умножение суммы на число / Умножение / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Умножение
- Умножение суммы на число
Умножение суммы на число
Чтобы умножить сумму на число, можно вычислить сумму и умножить её на число или умножить на число каждое слагаемое и полученные результаты сложить.
26 • 3 = ?
Рассуждай так:
Число 26 представлю в виде суммы разрядных слагаемых 20 и 6. Эту сумму надо умножить на 3.
26 • 3 = (20 + 6) • 3 = ?
Сначала умножу первое слагаемое 20 на 3, получу 60, потом на 3 умножу второе слагаемое 6, получу 18, теперь полученные результаты 60 и 18 сложу и получу 78.
26 • 3 = (20 + 6) • 3 = 20 • 3 + 6 • 3 = 60 + 18 = 78
Значит, 26 • 3 = 78
(12 + 11) • 4 = ?
Способ 1:
Рассуждай так:
Нахожу сумму чисел 12 и 11, получаю 23.
Теперь 23 умножаю на 4.
| × | 2 | 3 | |
| 4 | |||
| 9 | 2 |
Значит, (12 + 11) • 4 = 92
Способ 2:
(12 + 11) • 4 = ?
Рассуждай так:
Сначала первое слагаемое 12 умножаю на 4, получаю 48, потом на 4 умножаю второе слагаемое 11, получаю 44, теперь полученные результаты 48 и 44 сложу и получу 92. Записываю так:
(12 + 11) • 4 = 12 • 4 + 11 • 4 = 48 + 44 = 92
Значит, (12 + 11) • 4 = 92
Советуем посмотреть:
Табличное умножение
Внетабличное умножение
Умножение на однозначное число в столбик
Умножение на числа, оканчивающиеся нулями
Свойства умножения
Умножение
Правило встречается в следующих упражнениях:
3 класс
Страница 7, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 15, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 20, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 30, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 46, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 48, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 10, Моро, Волкова, Рабочая тетрадь, часть 2
Страница 11, Моро, Волкова, Рабочая тетрадь, часть 2
Страница 27, Моро, Волкова, Рабочая тетрадь, часть 2
Страница 30, Моро, Волкова, Рабочая тетрадь, часть 2
Умножение суммы на число 3 класс | План-конспект урока по математике (3 класс):
Класс: 3
Предмет: Математика
Тема урока: Умножение суммы на число
Цель урока: Формирование умения умножать сумму на число;
Тип урока: Урок открытия новых знаний
Задачи урока:
Личностные: направить обучающихся на осознанное понимание значения математических знаний в собственной жизни;
Метапредметные: развивать умения понимать учебную задачу урока, отвечать на вопросы, обобщать собственные представления, слушать собеседника и вести диалог, оценивать свои достижения на уроке, пользоваться учебником;
Предметные: Способствовать развитию умений умножать сумму на число двумя способами, опираясь на схематические
рисунки, решать составные задачи разными способами, опираясь на знание правил об умножении суммы на число, соблюдать порядок выполнения действий в выражениях;
Ход урока:
1 Мотивация к учебной деятельности
– Ребята, сегодня у нас гости.
Повернитесь к ним. Посмотрите, какие они доброжелательные. Давайте улыбнемся и мысленно пожелаем всем отдохнуть на нашем уроке.
– А мы начнем урок с игры «Добрый день»
Мне очень хочется пожелать доброго дня всем-всем, каждому из вас.
Добрый день, ребята!
Добрый день всем, кто присутствует на нашем уроке!
Я скажу слова «Добрый день…» и назову кого-то из нашего класса. Те, кого я назову, помашут мне рукой – значит, вы услышали меня и отвечаете на приветствие.
Попробуем?
Добрый день всем девочкам!
Добрый день всем мальчикам!
Добрый день всем тем, кто сегодня чистил зубы!
Добрый день всем, кому нравится такая погода, как сейчас за окном!
Добрый день всем, кто любит конфеты!
Добрый день всем, кто сегодня будет хорошо работать на уроке!
Я желаю, доброе и солнечное настроение сопровождало вас в течение всего урока.
Итак, урок математики. Вспомните правила работы на уроке:
- Не выкрикивай.
- Не перебиваем друг друга.
- Мы слышим друг друга.
- Учимся работать сообща.
2. Актуализация знаний
1) Какое сегодня число?
Что вы можете сказать о числе 20.
( двузначное, круглое, четное, записано с помощью двух различных цифр 2 и 0, предшествующее 19, последующее 21, 2 десятка и 0 единиц)
– Запишите число, классная работа. Какую тему изучали на прошлом уроке?
2) На минутке чистописания пишем число 20, далее 20*2, 20*3 и т.д.
Что нужно хорошо знать, чтобы легко решать такие примеры?
(таблицу умножения)
Давайте проверим, как вы ее знаете.
3) Самостоятельная работа
20*6 30*9 40*4 50*2 60*3 70*5 80*1 90*4 20*2 40*7
ВЗАИМОПРОВЕРКА СЛАЙД
120 270 160 100 180 350 80 360 40 280
3 фишки все правильно
2 фишки 1 ошибка
1 фишка 2 ошибки
Встали, у кого все правильно, 1 ошибка, 2 ошибки.
3.
Открытие нового знания. Создание проблемной ситуации.
А сейчас я предлагаю вам решить задачу. Работаете в парах. Я читаю задачу, а вы выложите схему задачи из кругов.
В две корзины собрали по 4 красных и по 3 зеленых мяча. Сколько всего мячей собрали ребята?
Что известно в задаче? Какое требование? (на доске)
Запишите решение задачи разными способами.
Проверка. (Записываю на доске разные способы решения)
Кто составил так же, как …?
Кто по-другому?
4. Целеполагание
Сколько мячей в одной корзине?
Сколько корзин?
Сколько мячей в двух корзинах?
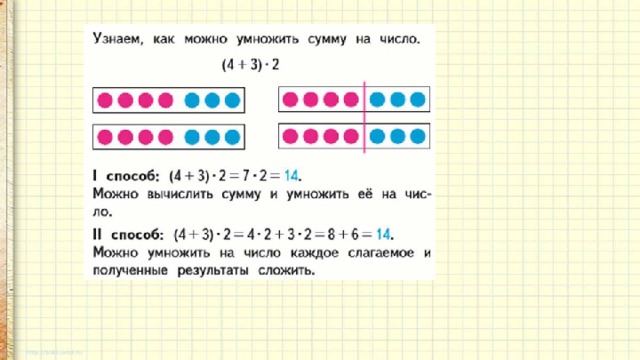
На доске запись (4+3)*2=14
Прочитайте полученное выражение математическим языком
(Сумму чисел 4 и 3 умножить на 2)
Над какой темой будем работать?
Чему будем учиться?
Какую цель поставим перед собой на урок?
Как можно умножить сумму на число?
Откройте учебник.
Вспомните правила работы с книгой.
Как быстро найти нужную страницу? Кто нашел?
Учебник с.
77 правило
5.Первичное закрепление.
1)Кто помнит, где мы уже применяли правило умножения суммы на число?
( периметр)
Я сейчас вам раздам прямоугольники. Измерьте стороны и найдите периметр прямоугольника, применяя правила умножения суммы на число.
(карточка-подсказка)
Рассыпала прямоугольники. Дети собирают по цвету
1 вариант – красные 2см 4 см 12 см
2 вариант – желтые 5см 3см 16см
3 вариант – зеленые 6 см 3см 18 см
Самопроверка
Встаньте те, у кого ответ 12см, 16см, 18 см
(правильный ответ 1 фишка)
2) работа по учебнику № 252 работа у доски
Те, кто затрудняется, работают вместе с нами у доски. Остальные – могут попробовать самостоятельно. Выполнив задание, возьмите карточку и проверьте себя.
3) Дополнительно самостоятельная работа 4 примера
Карточка
6 Оценивание
Ребята, вы сегодня все хорошо работали и пора выставить отметки. Посчитайте свои фишки
4 фишки – 10
3 фишки – 8
2 фишки – 6
7.
Домашнее задание: У. с 78 № 258, № 257*
8. Подведение итогов. Рефлексия
– Вспомните, какие цели мы ставили при изучении новой темы.
– Достигли мы их?
– Какое же правило вы запомнили с нашего урока?
– Где вы можете применить эти знания в жизни?
Оцените свою работу на уроке, выбрав предложения
- Урок полезен, все понятно
- Лишь кое-что чуть-чуть неясно
- Еще придется потрудиться
Да, трудно все-таки учиться.
Все молодцы! Всем спасибо!
Что такое распределительная собственность? Определение, Пример формулы, Факты
Распределение собственности Определение
«Раздать» означает разделить что-то или дать долю или часть чего-то.
Так что же означает распределительная собственность в математике?
Распределительный закон умножения по отношению к основным арифметическим действиям, таким как сложение и вычитание, известен как распределительное свойство.
Связанные игры
Что такое распределительная собственность?
В соответствии с этим свойством умножение суммы двух или более слагаемых на число даст тот же результат, что и умножение каждого слагаемого по отдельности на число с последующим сложением произведений.
Другими словами, согласно дистрибутивному свойству, выражение вида A (B $+$ C) может быть решено как A (B $+$ C) $=$ AB $+$ AC.
Это свойство применимо и к вычитанию.
A (B $–$ C) $=$ AB $–$ AC
Это указывает на то, что операнд A является общим для двух других операндов.
Давайте посмотрим на формулу распределительной собственности:
Где A, B и C — любые действительные числа.
Вот пример того, как результат не меняется при обычном решении и при решении с использованием распределительного свойства:
Это свойство помогает упростить сложные задачи. Вы можете использовать это свойство умножения, чтобы переписать выражение, распределив или разбив множитель на сумму или разность двух чисел.
Связанные рабочие листы
Распределительное свойство умножения над сложением
Когда нам нужно умножить число на сумму двух чисел, мы используем это свойство умножения над сложением. Давайте лучше поймем, как использовать распределительное свойство на примере:
Пример: Решите выражение: $6$ $(20 + 5)$, используя распределительное свойство умножения над сложением.
Воспользуемся этим свойством для вычисления выражения $6$ $(20 + 5)$, число 6 распределено между двумя слагаемыми. Проще говоря, мы умножаем каждое слагаемое на 6, после чего можно складывать произведения.
$6 20 + 6 5 = 120 + 30 = 150$
Возьмем другой пример:
Пример: Решите выражение $2$ $(2 + 4)$, используя распределительный закон умножения над сложением.
Решение: $2 (2 + 4) = 2 2 + 2 4 = 4 + 8 = 12$
Если мы попытаемся решить это выражение с помощью правила PEMDAS, нам придется сложить числа в скобках и затем умножьте сумму на число за скобками. Отсюда следует:
$2 (2 + 4)$ $= 2 \times 6 =$ $12$
Таким образом, мы получаем один и тот же результат независимо от используемого метода.
Распределительное свойство умножения над вычитанием
Распределительное свойство умножения над вычитанием эквивалентно распределительному свойству умножения над сложением, за исключением операций сложения и вычитания.
A(B − C) и AB − AC эквивалентны выражениям.
Рассмотрим приведенные ниже примеры распределительной собственности.
Пример: Решите выражение $6 (20 – 5)$, используя распределительное свойство умножения над вычитанием.
Решение : Использование распределительного свойства умножения над вычитанием
Пример : Решите выражение 2 (4 – 3), используя распределительный закон умножения на вычитание.
Решение : $2 (4 – 3) = 2 4 – 2 3 = 8 – 6 = 2$
Опять же, если мы попытаемся решить выражение с помощью порядка операций или PEMDAS, нам придется вычесть числа в скобках , затем умножьте разницу на число за скобками, что означает:
$2 (4 – 3) = 2 1 = 2$
Распределительное свойство вычитания доказано, поскольку оба метода дают одинаковый результат.
Забавные факты
Несмотря на то, что деление является обратным умножению, закон распределения верен только в случае деления, когда делимое распределяется или разбивается на частичные дивиденды, которые полностью делятся на делитель.
Например, используя распределительный закон для 1326
132, можно разбить его на 60 + 60 + 12 долларов, что упрощает деление.
Мы не можем разбить 132 6 как $(50 + 50 + 32) 6$.
Кроме того, мы не можем разорвать делитель: $132(4+2)$ даст неверный результат.
Заключение
Мы поняли, как свойство дистрибутивности можно использовать для упрощения сложных уравнений и задач. Испытайте новый способ изучения математики с помощью SplashLearn, который представляет собой интерактивную платформу для детей, где каждое понятие превращается в игровое занятие. С интересными таблицами, увлекательными викторинами и простыми для понимания темами измените то, как ваш ребенок понимает математику!
Решенные примеры
Пример 1: решить $(5 + 7 + 3) 4$ .
Решение : Используя распределительное свойство умножения над сложением,
A (B $+$ C) = AB $+$ AC
$(5 + 7 + 3) 4 = 5 4 + 7 4 + 3 4 = 20 + 28 + 12 = 60$
Или,
$(5 + 7 + 3) 4 = 15 4 = 60$
Пример 2: Решите следующее уравнение распределения $−2 (−$ х$ – 7)$ .
Решение : Используя свойство распределения,
A (B $–$ C) $=$ AB $–$ AC
$−2 (−$x$ − 7) = (−2)(−$x$) − (−2)(7) = 2$x$ − (−14) = 2$x$ + 14$
Пример 3. Какое свойство делает уравнение $3 (4 − 9) = 3 4 − 3 9$ показать?
Решение : Приведенное выше уравнение показывает распределительное свойство умножения над вычитанием.
Практические задачи
1
Выражение $7 ($x$ + 6)$ равно
x $+ 42$
$7$x $+ 13$
$7$x $+ 42$
$7$x $+ 6$
Правильный ответ: $7$x $+ 42$
Используя распределительное свойство умножения над сложением,
A (B $+$ C) $=$ AB $+$ AC
7$ ($x $+ 6) = 7($x$) + 7(6) = 7$x $+ 42$
2
Выражение $3 (7$x $– 8)$ равно
$13$x
$7$x$ – 24$
$21$x$ – 24$
$21$x$ – 8$
Правильный ответ составляет: $21$x$ – 24$
Используя распределительное свойство умножения над вычитанием,
A (B $–$ C) $=$ AB $–$ AC
$3 (7$x $– 8) = 3 (7$x$) – 3 (8) = 21$x$ – 24$
3
Выражение m $(3$n $– 9)$ равно
$3$mn $– 9$n
$3$mn $– 9$
$3$mn $– 9$m
$3$ mn$+9$m
Правильный ответ: $3$mn $– 9$m
Используя распределительное свойство умножения над вычитанием,
A (B $–$ C) $=$ AB $–$ AC
m $ (3$n $– 9)$ $=$m $(3$n$) –$m $(9) = 3$mn $– 9m
4
Урожай банановой фермы 355 дюжин бананов.
Сколько бананов было собрано?4260
3550
2130
426
Правильный ответ: 4260
Общее количество собранных бананов определяется выражением $355 x 12$.
Дюжина или 12 могут быть распределены как 10 и 2.
Общее количество собранных бананов $= 355 \times (10 + 2)$
Используя распределительное свойство умножения на сложение,
A (B $+$ C) $=$ AB $+$ AC
$= 355 \times 10 + 355 \times 2$
$= 3550 + 710 = 4260$
Всего на ферме было собрано 4260 бананов.
Часто задаваемые вопросы
Применяется ли раздел имущества также и к разделу?
Свойство распределения применимо к делению так же, как и к умножению. Однако понятие «разбивка» или «распределение» может быть применено к делению только путем деления числителя на более мелкие суммы, которые точно делятся на делитель.
Например, чтобы решить $\frac{125}{5}$, мы можем разделить числитель (125) как: (50 + 50 + 25), поэтому: $\frac{125}{5}$ = $\ frac{50}{5}$ + $\frac{50}{5}$ + $\frac{25}{5}$ = 10 + 10 + 5 = 25,
Каково правило распределительной собственности?
Согласно распределительному свойству, умножение суммы двух или более слагаемых на число дает тот же результат, что и при умножении каждого слагаемого на число по отдельности и сложении произведений.
Как распределительная собственность может помочь в решении сложных вопросов?
Распределяющее свойство распределяет сложные выражения в более простые термины и, таким образом, облегчает решение задач, особенно с несколькими факторами.
Можно ли убрать скобки после распространения?
Да, при применении распределительного свойства внешний множитель умножается на каждое слагаемое в скобках. Это позволяет избавиться от скобок.
Умножение — третий класс мисс Пенс
Правило № 1: Вы умножаете на меня то же самое, что и я на вас
Это правило, более формально известное как рефлексивное свойство умножения, просто означает, что A x B = B x A. Если вы можете научить своего ребенка тому, что 6×7=42, он сможет запомнить и 7×6=42. Это должен быть первый вопрос, который вы задаете, если ваш ребенок застрял на проблеме. Если ваш ребенок не знает ответа на математический факт умножения, поменяйте местами множимое и задайте вопрос еще раз.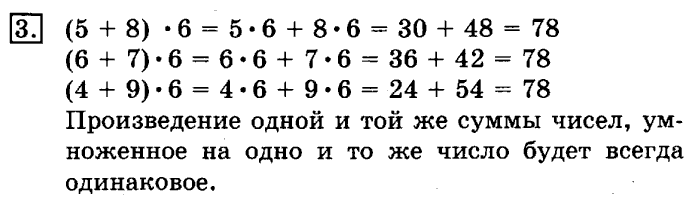
Если учесть эффект идеальных квадратов, одно это правило сокращает количество фактов, которые нам нужно запомнить, почти вдвое, до 55.
Правило № 2: Любое число, умноженное на единицу, является этим числом.
Если умножение — это просто инструкции по сложению, то умножение числа на единицу просто означает сложение одного экземпляра этого числа. В результате всегда получается это число. Это убирает 10 проблем из нашего оставшегося списка фактов, опуская нас уже до 45. Видите, как быстро мы движемся?
Правило №3: Чтобы умножить на десять, прибавь ноль.
Даже если понятия разрядности и смещения десятичных разрядов на данный момент являются новыми, запоминание того, что умножение на десять означает просто добавление нуля к числу, является простым правилом для запоминания. Ноль в конце десятки должен служить спусковым крючком: «Десять заканчивается нулем. Что вы привязываете к другому числу?» Учитывая акцент на повторном использовании фактов сложения в нашей одиссее умножения, я рекомендую избегать фразы «Добавить ноль», иначе вы можете сначала запутаться.
Умножение на десять удаляет из сетки еще девять задач и дает нам 36.
Правило №4: Чтобы умножить на два, удвойте число
Это правило использует факты, полученные во время сложения. 2×7 = 7+7 = 14. Все эти факты уже должны быть выучены наизусть, но даже если это не так, они все еще находятся в диапазоне, где счет на пальцах рук и ног быстро приводит к решению. Поскольку мы уже вычеркнули 2×1 за Правило № 2 и 2×10 за Правило № 3, мы можем вычеркнуть из нашего списка еще восемь, но это все равно опустит нас до 28.
Правило № 5: Умножение на четыре равно удвоению (правило двойного-двойного)
Когда моя дочь останавливается на задаче на умножение на четыре, все, что мне нужно сделать, это сказать «Двойной-двойной», и ответ тут же приходит. 4×6 = 6+6+6+6 = 12 + 12 = 24. Для чисел пять и ниже правило четырех двойных двойных будет работать с добавлением математических фактов и должно выполняться в памяти. Если ваш ребенок может просто складывать две цифры без перегруппировки в памяти, шесть и семь тоже работают.
Это займет некоторое время, но, в конце концов, 4×8 и 4×9 не так уж сложны, но вы можете обнаружить, что эти факты запоминаются до того, как «неси один» начнет происходить в уме. Как бы вы туда ни попали, мы можем вычеркнуть еще семь фактов (пропуская 4×1, 4×2 и 4×10 из приведенных выше правил), что ставит нас в 21 слева!
Правило № 6: Умножение на пять — это просто подсчет на пять
Ваш ребенок должен уже уметь считать пятерками к тому времени, когда он находится в стране умножения, поэтому быстрый способ решить задачу на 5 умножить — просто пропустить счет пятерками до числа. Есть и другие, более сложные стратегии для пятерок (если число четное, разделите его на два и добавьте ноль, так что 8×5 = (8/2) * 10 = 40), но они обычно немного сложны при первом проходе здесь. Правило «Считай пятью» сводит нас к 16 оставшимся фактам.
Правило № 7: Правило девяти. Десятки — это число минус один, единицы — это девять минус десятки
Когда вы умножаете число на девять, сумма цифр результата всегда кратна девяти.
Для основных математических фактов сумма цифр равна девяти, и на самом деле у нее есть некоторые другие интересные свойства. Значение разряда десятков всегда на единицу меньше, чем умножаемое число, и из-за правила девяток разряд единиц всегда равен числу девяти минус значение разряда десятков. Базовый сценарий для изучения этого правила выглядит примерно так: «Умножение на девять? Хорошо, сколько будет один минус другое число? Это цифра десятков. Хорошо, какое число плюс это равно девяти? Это цифра единицы». Опять же, эта стратегия просто опирается на базовые факты сложения и сокращает общее количество математических фактов, которые нужно запомнить, до 10.
