Разное

Правило 1 класс по математике: Презентация по математике “Правила по математике для учащихся 1 класса”

Содержание

ГДЗ по математике 1 класс учебник Моро, Волкова 2 часть

  • Тип: ГДЗ, Решебник.
  • Автор: Моро М. И., Волкова С. И., Степанова С. В.
  • Год: 2020.
  • Серия: Школа России (ФГОС).
  • Издательство: Просвещение.

Решебник – страница 14Готовое домашнее задание

Задание вверху страницы

Сравни рисунки и равенства, записанные под ними. Чем они похожи, чем различаются?

Ответ: Мальчик в левой руке держит 1 красный флажок, а в правой 2 синих флажка. Рисунки различаются тем, что мальчик на втором рисунке перекрестил руки, но так и продолжил держать в левой руке 1 красный флажок, а в правой 2 синих флажка.

На левом рисунке у мальчика 3 флажка в руке, а на правом тоже 3.

Записи похожи тем, что в них находят сумму чисел 1 и 2, но они меняются местами в первом и втором примере, а результат не меняется.

Номер 1.

Ответ: 3 + 2 = 5     1 + 4 = 5     6 + 1 = 7 2 + 3 = 5     4 + 1 = 5     1 + 6 = 7
От перестановки слагаемых результат сложения не изменяется.

Номер 2.

1) Вчера Дима прочитал 4 страницы книги, а сегодня – на 1 страницу меньше. Сколько страниц он прочитал сегодня?
2) Вчера Дима прочитал 4 страницы книги, а сегодня – ☐ страницы. Сколько всего страниц прочитал Дима за эти дни? Дополни условие, используя ответ предыдущей задачи.

Ответ: Задача 1:

4 ‒ 3 = 3 (с.) ‒ прочитал Дима сегодня. Ответ: 3 страницы.
Задача 2:

4 + 3 = 7 (с.) − всего за 2 дня прочитал Дима. Ответ: 7 страниц.

Номер 3.

Ответ: 8 ‒ 3 = 5     6 ‒ 4 = 2 8 ‒ 4 = 4     7 ‒ 4 = 3
10 ‒ 3 = 7     8 ‒ 3 + 4 = 9 10 ‒ 2 = 8     7 + 2 ‒ 4 = 5

Задание внизу страницы

Ответ:

5 + 4 = 4 + 5    8 + 2 = 2 + 8
6 + 3 = 3 + 6

Задание на полях страницы

Сравни:

Ответ:

Рейтинг

👇 Выберите другую страницу 👇

1 часть

Учебник Моро456789101112131415161718192021222324252627282930
31		3233343536373839404142434445464748495051525354555657585960616263646566676869707172 737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113
114		115116117118119120121122123124125126127

2 часть

456789101112131415161718192021222324252627 2829303132333435363738394041424344454647484950515253545556575859606162636465666768
69		707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110 111

Ваше сообщение отправлено!

+

Увеличение числа на несколько единиц

Главная » Для школы » Уроки математики

Дорогой друг! Сегодня тебе предстоит узнать, как увеличивать числа на несколько единиц. Ты будешь сравнивать числа, увеличивать их и складывать. Это будет просто и очень интересно 🙂

У тебя точно все получится!

Если ты хочешь посмотреть видео урок, листай страницу до конца.

Ученик

46.09%

Учитель

19.6%

Родитель

26.67%

Секретный секрет 🙂

7.63%

Проголосовало: 1061

Поделитесь уроком со своими коллегами, одноклассниками и друзьями! Они оценят ваше внимание и будут благодарны за практическую помощь 🙂

Содержание

  1. Узнаем новое!
  2. Закрепляем на практике
  3. Задание 1
  4. Задание 2
  5. Задание 3
  6. Задание 4
  7. Задание 5
  8. Задание 6
  9. Задание 7
  10. Задание 8
  11. Задание 9
  12. Видео урок
  13. Ты молодец!

Узнаем новое!

Посмотри на эту картинку:

Сколько здесь карандашей?

А теперь взгляни на эту картинку:

Что здесь изменилось? Теперь карандашей больше или меньше?

Правильно! Было 4 карандаша. А к ним добавили еще 6. И в итоге карандашей стало на 6 больше. И сколько же их теперь стало? Можешь посчитать?

4 + 6 = 10

В стакане теперь 10 карандашей 🙂

Запомни правило! Чтобы увеличить число на несколько единиц, нужно использовать действие сложения.

Задание 1

У Маши дома живут 5 кроликов. А морских свинок на 4 больше. Сколько морских свинок живет у маши?

5 + 4 = 9

Ответ: 9 морских свинок.

Задание 2

Увеличь каждое число из таблицы на 6 и запиши ответы.

35681011

Правильные ответы: 9, 11, 12, 14, 16, 17

Задание 3

Посмотри на эту картинку:

Придумай на основании этой иллюстрации задачу, которую можно решить в два действия. Какие это должны быть действия?

Подсказка: ответ должен получиться — 17 кг.

Задание 4

Реши задачу: в одном спичечном коробке 5 спички, а в другом на 4 спички больше. Сколько спичек во втором коробке?

Задание 5

Посмотри на эту иллюстрацию. Миша все свои конфеты показывает, А Маша их прячет.

Ответь на следующие вопросы:

  • Можно ли сразу сказать, сколько у друзей конфет? Почему?
  • Как узнать, сколько конфет у Маши? Каким действием?
  • А как теперь узнать, сколько конфет у ребят вместе?

Запиши решение этой задачи.

Ответ: у Маши 10 конфет. А вместе у них 16.

Задание 6

Увеличь все числа на 6 и запиши результат в таблице.

2457910

Проверь себя: в ответах будут использоваться следующие числа — 16, 8, 11, 10, 15, 13. Только их порядок будет отличаться.

Задание 7

Скажи, верны ли следующие утверждения:

  1. Если сложить числа 8 и 2, получится 11
  2. Если к числу 3 прибавить 8, получится 11
  3. Если сложить числа 6 и 4, ответ будет больше 12
  4. Увеличив 8 на 5, получим 13

Подсказка: неправильных здесь 2 утверждения.

Задание 8

В синей тарелке 5 ягодок. В красной — на 3 ягодки больше. Сколько ягод всего?

Задание 9

В каких примерах ошибки? Напиши правильный ответ:

  • 11 — 5 = 7
  • 12 — 8 = 4
  • 16 — 8 = 7
  • 6 + 7 = 13
  • 9 + 7 = 15
  • 7 + 4 = 11

Подсказка: в трех примерах есть ошибки.

Видео урок

Ты молодец!

Ты отлично справился с этим уроком по математике! Теперь ты умеешь увеличивать число на несколько единиц.

Если у тебя остались вопросы, не стесняйся просить помощи у родителей, старшего брата или сестры и учителя. Или пиши здесь в комментариях!

Понравилось?

1 класс

Уроки по математике для 1 класса – полезные материалы для учителя

Главная → Публикации → Математика → Уроки → 1 класс

Уроки по математике для 1 класса и другие полезные материалы для учителя математике, которые вы можете скачать бесплатно Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания.

Математика как предмет формирует устойчивый познавательный интерес и навыки логического мышления. Математические задания способствуют развитию у ребенка мышления, внимания, наблюдательности, строгой последовательности рассуждения и творческого воображения. Сегодняшний мир претерпевает значительные изменения, которые предъявляют новые требования к человеку. Если школьник в будущем хочет активно участвовать во всех сферах жизни общества, то ему нужно проявлять творческую активность, непрерывно самосовершенствоваться и развивать свои индивидуальные способности.

Основными целями математического образования являются:

  • интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых человеку для полноценной жизни в обществе;
  • овладение конкретными математическими знаниями, умениями и навыками, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования;
  • воспитание личности в процессе освоения математики и математической деятельности;
  • формирование представлений об идеях и методах математики, о математике как форме описания и методе познания действительности.

Все категорииАлгебраБиологияГеография, краеведениеГеометрияЕстествознаниеИЗОИностранный языкИнформатикаИсторияКонкурсы для детейЛитератураЛитературное чтениеМатематикаМузыка и пениеМХКНаучная статьяОБЖОбучение грамотеОбществознаниеОкружающий мирОсновы религиозных культурПодготовка к ГИАПодготовка к ЕГЭПрикладное творчествоРабота с родителямиРусский языкСоциальная педагогика, психологияСценарии праздниковТехнология, трудУчителю-дефектологуФизикаФизическое воспитаниеХимияЧерчениеЭкономика

Все разработкиКонспект занятияОценка знанийПланированиеПрезентацииРазноеУрокиФакультативы

Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Через весь урок прослеживается формирующее оценивание. Дети на уроке узнают, как называются компоненты при вычитании; учатся извлекать информацию; – применяют новые термины при составлении и чтении математических выражений на вычитание; – отвечают на …

29 мая 2022 Ольга Вячеславовна Кошелева

79 2 0 0

Конспект урока в 1 классе по программе “Школа России” …

16 мая 2022 Черных Наталья Викторовна

49 1 0 0

МЕТОДИЧЕСКАЯ РАЗРАБОТКА Конспект урока математики По теме «Урок -экскурсия. Занимательные задачи.» Цель: расширить представление о занимательной задаче, определить сходства и отличия в решении простых и занимательных задач; развить научно-познавательн . ..

22 апреля 2022 Кольцов Кирилл Дмитриевич

99 84 2 1

Число и цифра 9. …

20 февраля 2022 Зимина Светлана Александровна

78 3 0 0

С помощью данной статьи, вы сможете узнать приемы и методы, которые позволят повысить мотивацию у учащихся начальных классов …

10 февраля 2022 Смирнова Олеся Евгеньевна

69 1 1 0

Урок проходит в игровой форме. Используются разнообразные виды работ, направленные на обобщение изученного материала. …

04 февраля 2022 Петухова Юлия Николаевна

101 0 2 0

В файле конспект урока и презентация к уроку составлены в соответствии с ФГОС. Слайды содержат материалы для самопроверки и самооценки работ обучающихся. …

12 декабря 2021 Чернышова Ольга Николаевна

103 41 0 0

Технологии: игровая технология, здоровьесберегающая. Формы организации: фронтальная, индивидуальная, работа в паре, в группе. Тип урока: урок закрепления знаний. Цель урока: в результате практических действий и наблюдений закреплять умения выполнять …

02 ноября 2021 Руденко Елена Александровна

181 7 0 0

Данная разработка поможет в интересной форме обобщить знания учащихся по теме “Числа от 1 до 10. Нумерация” …

23 октября 2021 Тихомирова Елена Александровна

132 5 0 0

Данный урок нацелен на формирование представлений у детей о таких терминах как переместительное свойство сложения, на развитие умений оперировать этими знаниями. …

19 октября 2021 Остапенко Елена Борисовна

75 3 0 0

Порядок действий – определение, правила, примеры, задачи

Порядок действий – это набор правил, которым необходимо следовать в определенной последовательности при решении выражения. В математике под словом «операции» мы подразумеваем процесс вычисления любого математического выражения, включающий арифметические операции, такие как деление, умножение, сложение и вычитание. Давайте подробно узнаем о правилах порядка действий и о том, насколько хорошо мы можем запомнить правила, используя короткие трюки.

1. Каков порядок операций?
2. Порядок действий Правила
3. PEMDAS против BODMAS
4. Как использовать порядок операций?
5. способов запомнить
6. Реальные приложения
7. Часто задаваемые вопросы о порядке операций

Каков порядок операций?

Порядок Операций — это правило в математике, которое гласит, что сначала мы вычисляем круглые скобки/квадратные скобки, затем степени/порядки, затем деление или умножение (слева направо, в зависимости от того, что наступит раньше), а сложение или вычитание — в конце.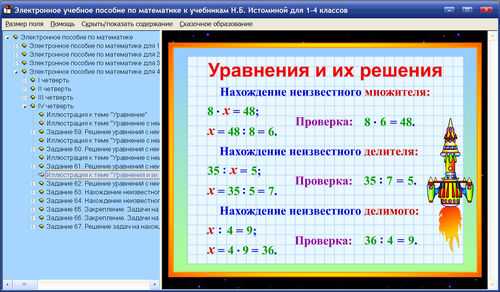 последней (слева направо, в зависимости от того, что наступит раньше). В математике при вычислении выражения может быть выполнено несколько операций, и упрощение в конце дает разные результаты. Однако у нас может быть только один правильный ответ для любого вида выражения. Чтобы определить правильный ответ, мы упрощаем любое заданное математическое выражение, используя определенный набор правил. Эти правила вращаются вокруг всех основных операторов, используемых в математике. Такие операторы, как сложение (+), вычитание (-), деление (÷) и умножение (×). Посмотрите на данное изображение, чтобы получить представление о том, как точно выглядит порядок операций.

Порядок операций Определение

Как мы обсуждали выше, порядок операций можно определить как набор основных правил старшинства, которые мы используем при решении любого математического выражения, включающего несколько операций. Когда подвыражение появляется между двумя операторами, оператор, который идет первым в соответствии со списком, приведенным ниже, должен применяться первым.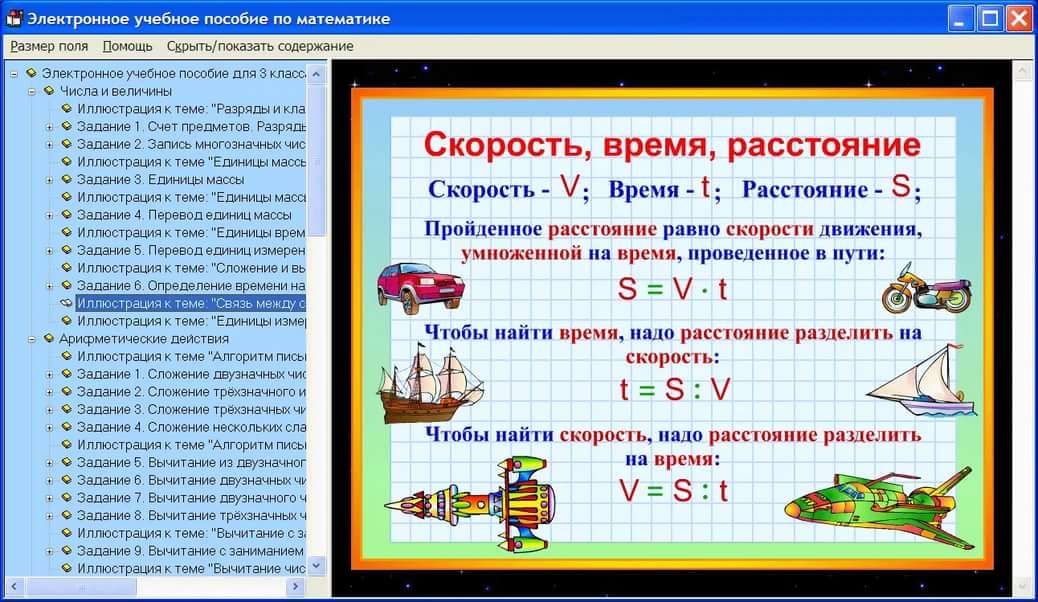 Порядок действий, правила выражены здесь:

  • Скобки ( ), { }, [ ]
  • Показатели
  • Деление (÷) и умножение (×)
  • Сложение (+) и вычитание (-)

Вышеупомянутый набор правил всегда варьируется в зависимости от соответствующих заданных математических выражений.

Порядок действий Правила

При выполнении любой операции над соответствующими числами, присутствующими в выражении, мы будем следовать заданным основным правилам в конкретной последовательности.

Порядок работы Правило 1: Обратите внимание на выражение. Первое правило состоит в том, чтобы решить числа, присутствующие в скобках или скобках. Мы решаем операции группировки изнутри наружу. Обратите внимание на шаблон скобок, присутствующих в выражении, существует особый порядок решения скобок, т. Е. [ { ( ) } ]. Сначала решите круглые скобки ( ) → фигурные скобки { } → квадратные скобки [ ]. Внутри скобок соблюдается порядок действий.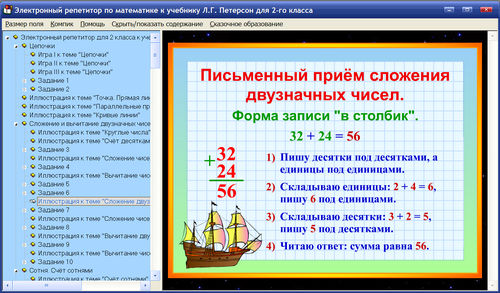
Порядок действий Правило 2: После решения чисел в скобках найдите любой термин, представленный в виде показателей степени, и решите его.
Порядок операций Правило 3: Теперь у нас остались четыре основных оператора. Найдите числа с действием умножения или деления, решите их слева направо.
Порядок действий Правило 4: Наконец, найдите условия со сложением или вычитанием и решите их слева направо.

Эти правила имеют специальное сокращение. Мы называем их PEMDAS или BODMAS. Давайте теперь узнаем, что такое PEMDAS или BODMAS.

Порядок действий – PEMDAS против BODMAS

PEMDAS или BODMAS — это две разные аббревиатуры, используемые для изучения правил. Эти два имени указывают порядок, в котором должны выполняться операции в выражении. Вот подробный термин для каждой буквы, используемой в упомянутых аббревиатурах. Во-первых, мы обсудим PEMDAS.

Порядок действий PEMDAS

  • P означает Скобки ( ), { }, [ ]
  • E означает экспоненты (a 2 ) (Например, здесь a — это число с показателем степени 2 )
  • M означает умножение (×)
  • D означает Раздел (÷)
  • A означает Дополнение (+)
  • S означает вычитание (-)

Порядок действий BODMAS

  • B стойки для кронштейнов ( ), { }, [ ]
  • O означает заказ
    • .
  • D означает Раздел (÷)
  • M означает умножение (×)
  • A означает Дополнение (+)
  • S означает вычитание (-)

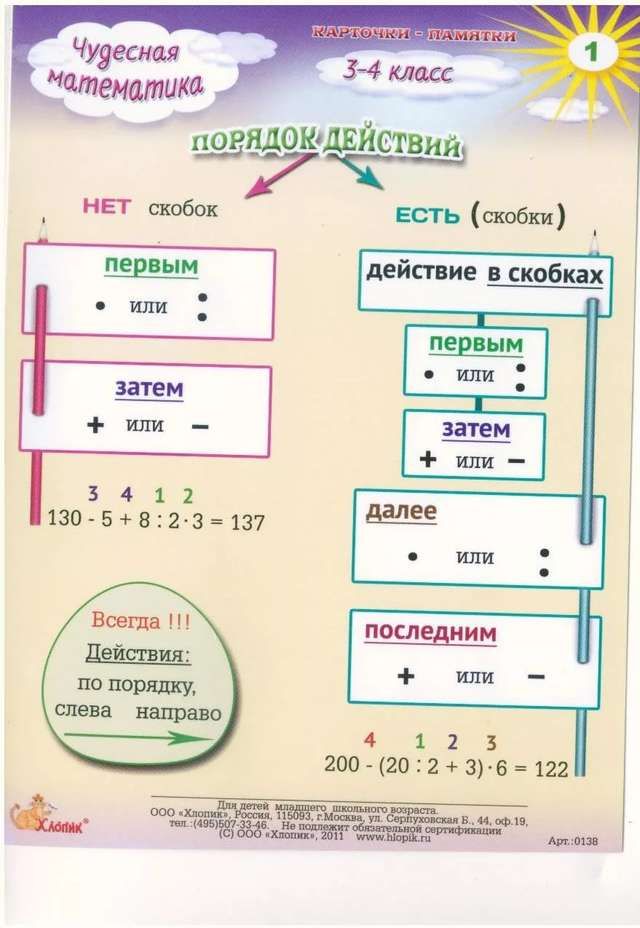
С помощью приведенных выше обозначений мы можем легко решить математические выражения и получить правильный ответ.

Как использовать порядок операций?

Давайте рассмотрим различные примеры, упомянутые ниже, чтобы понять точность правил, используемых в порядке операций.

1) Для решения скобок в порядке операций :

Выражение: 4 × (5 + 2)
Решение: 4 × ( 7 ) = 28 (Верно (✔). правильный способ решить скобки)
Давайте рассмотрим другой подход для того же выражения.
4 × ( 5 + 2) = 20 + 2 = 22 (Неверно (✘). Это неправильный способ решения скобок)

2) Для решения показателей степени в порядке операций

Выражение: 4 × (5 2 )
Решение: 4 × ( 25 ) = 100 (Верно (✔). Это правильный способ решения показателей)
Давайте рассмотрим другой подход для того же выражения.
4 × ( 5 2 ) = 20 2 = 400 ((Неверно (✘). Это неверный способ решения показателей степени)

3) Для умножения или деления и сложения или вычитания

0 Выражение 3 + 5 × 2
Решение: 3 + 5 × 2 = 3 + 10 = 13 (Верно (✔). Это правильный путь.)
Давайте рассмотрим другой подход для того же выражения.
3 + 5 × 2 = 8 × 2 = 16 (Неверно (✘). Это неверный способ.)

Выражение: 3 – 6 ÷ 2
Решение: 3 – 6 ÷ 2 = 2 3 –8 0 (Правильно (✔). Это правильный путь.)
Давайте рассмотрим другой подход для того же выражения.
3 – 6 ÷ 2 = (-3) ÷ 2 = -3/2 (Неверно (✘). Это неверный способ.)

Всегда помните, следуя правилам порядка выполнения операций умножение или деление перед сложением или вычитанием

Способы запомнить порядок действий

Мы только что прочитали о двух разных словах PEMDAS и BODMAS. Это лучший способ запомнить порядок операций. PEMDAS можно запомнить по фразе «Пожалуйста, извините мою дорогую тетю Салли». В порядке операций это означает «круглые скобки, показатели степени, умножение и деление, сложение и вычитание». Здесь умножение и деление, сложение и вычитание вместе. Точно так же мы можем запомнить порядок действий со словом BODMAS (скобки, порядок, деление, умножение, сложение и вычитание).

Самый простой способ узнать порядок действий — выполнить указанные шаги:

  • Сначала начать упрощать термины в скобках
  • Решите экспоненциальные члены.
  • Выполнить деление или умножение.
  • Выполнить сложение или вычитание.

Примечание: Выполняя порядок операций над любым заданным выражением, мы должны соблюдать шаблон операторов.

Реальные приложения порядка операций

Многие действия в нашей жизни требуют определенного порядка действий, чтобы выполнять их хорошо. Возьмем повседневную проблему. Предположим, вы купили пять пицц с пепперони по 20 долларов каждая и хотите поровну разделить общую стоимость на 5 человек. Чтобы узнать, сколько каждый человек должен заплатить, воспользуемся здесь порядком операций.

Общее количество людей = 5
Общее количество пицц = 5
Стоимость одной пиццы = 20
$ Сформулируем выражение, используя PEMDAS:
Выражение: (20 + 20 + 20 + 20 + 20) ÷ 5 или (5 × 20) ÷ 5
Решение: В соответствии с PEMDAS или BODMAS мы сначала решим скобки.
(100) ÷ 5 = 20
Согласно порядку операций, каждый человек должен заплатить 20 долларов.

Подобно вышеупомянутой проблеме, у нас есть много повседневных реальных случаев, когда мы используем порядок операций для решения наших проблем.

☛Связанные статьи о порядке операций

Ознакомьтесь с интересными статьями ниже и узнайте больше о порядке операций и его приложениях.

  • Дополнение
  • Вычитание
  • Умножение
  • Подразделение
  • Порядок действий Рабочие листы 5-й класс

 

Порядок операций Примеры

  1. Пример 1: Помогите Джеку решить следующую задачу с помощью правил порядка действий.
    а) 18 ÷ (9 – 2 × 3)

    Решение: Полученное выражение: 18 ÷ (9 – 2 × 3)
    Согласно правилу порядка операций, мы должны сначала решить скобки. Обратите внимание, что здесь в скобках указаны две операции: умножение и вычитание.
    Сначала умножьте 2 × 3 = 6 
    . 18 ÷ (9 – 6)
    Теперь из 9 вычтите 6,
    . 18 ÷ (3)
    Теперь разделите
    18 ÷ 3 = 6

  2. Пример 2: Упростите данное выражение, используя правила порядка операций.
    ​(6 × 2 – 6 – 1) × 2 2

    Решение: Мы знаем, что порядок операций соответствует либо PEMDAS, либо BODMAS . Соблюдаем правила порядка действий и упрощаем данное выражение.

    Шаг 1: Сначала нам нужно решить числа в скобках. Умножьте 6 на 2 в данном выражении, (6 × 2 – 6 – 1) × 2 2 , получаем, (12 – 6 – 1) × 2 2 .
    Шаг 2. Теперь нам нужно вычесть 6 из 12 внутри скобки, так что мы получаем (6 – 1) × 2 2 .
    Шаг 3- Снимите скобки после вычитания 6 – 1, мы получим, 5 × 2 2 .
    Шаг 4. Решите показатель степени, т. Е. 2 ​​ 2 = 4.
    Шаг 5. Умножьте 5 на 4, чтобы получить окончательный ответ, то есть 5 × 4 = 20.
    ∴ ​(6 × 2 – 6 – 1) × 2 2 = 20 .

  3. Пример 3. Оцените выражение, используя порядок операций: (1 + 20 − 9 ÷ 3 2 ) ÷ ((2 + 1) 2 + 16 ÷ 2)

    Решение: Давайте посмотрим, как мы можем применить правила порядка операций при решении данного выражения.
    Шаг 1: Во-первых, нам нужно упростить самую внутреннюю скобку, (1 + 20 – 9 ÷ 3 2 ) ÷ (3 2 + 16 ÷ 2)
    Шаг 2: Теперь нам нужно вычислить показатели степени (1 + 20 − 9).÷ 9) ÷ (9 + 16 ÷ 2)
    Шаг 3: Теперь нам нужно разделить 9 на 9 и 16 на 2 в скобках, и мы получим (1 + 20 − 1) ÷ (9 + 8)
    . Шаг 4: Складываем 1 и 20, получаем 21. Теперь вычитаем 1 из 21, получаем 20. Теперь (20) ÷ (9 + 8)
    Шаг 5: Добавьте 9 + 8 и разделите результат на 20. 20 ÷ 17 = 20/17
    Шаг 6: ∴ (1 + 20 − 9 ÷ 3 2 ) ÷ ((2 + 1) 2 + 16 ÷ 2) = 20/17

  4. Пример 4. Решите задачу с оператором, используя порядок операций.
    Если 72 разделить на сумму 4 и 5, а затем вычесть из 10, каким будет окончательный ответ?

    Решение:
    Сначала запишем данное утверждение в математической форме. 10 – [72 ÷ (4 + 5)]
    Используя правила порядка операций, это выражение можно упростить как:
    = 10 – [72 ÷ (4 + 5)]
    = 10 – [72 ÷ 9]
    = 10 – 8
    = 2
    ∴ 10 – [72 ÷ (4 + 5)] = 2

перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду

Отличное обучение в старшей школе с использованием простых подсказок С Cuemath вы будете учиться визуально и будете удивлены результатами.

Запись на бесплатный пробный урок

Практические вопросы по порядку действий

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о порядке операций

Каков порядок операций в математике?

Порядок действий в математике представляет собой набор правил, вращающихся вокруг 4 основных операторов. В соответствии с порядком операций существует определенная последовательность, которой мы должны следовать на каждом операторе при решении данного математического выражения.

Как решить порядок операций?

Чтобы решить порядок операций, сначала обратите внимание на выражение и отметьте, какой схеме оно точно соответствует. Теперь начните использовать PEMDAS или BODMAS для решения данного выражения. В соответствии с правилами порядка операций сначала ищите круглые скобки, затем показатели степени, затем переходите к умножению или делению и сложению или вычитанию слева направо.

Как сделать порядок операций с целыми числами?

Мы знаем, что целые числа бывают положительными и отрицательными числами. Мы можем легко выполнить порядок операций с целыми числами, выполнив указанные шаги:

  • Найдите целые числа, находящиеся внутри круглых или квадратных скобок, и решите их.
  • После решения целых чисел в скобках найдите любой целочисленный термин, представленный в виде показателей степени, и решите его.
  • Теперь у нас остались четыре основных оператора, которые нужно выполнять над целыми числами. Найдите целые числа с операцией умножения или деления и решите их слева направо.
  • Наконец, найдите целые числа с помощью сложения или вычитания и решите их.
  • В случае с целыми числами нам нужно убедиться, что мы правильно умножаем знаки. Так что (-) × (-) = + и (+) × (-) = –

Как запомнить порядок действий?

Чтобы запомнить порядок операций, мы используем две известные аббревиатуры, а именно PEMDAS и BODMAS. Мы используем любой из двух в соответствии с правилами порядка операций. PEMDAS или BODMAS помогают запомнить процесс решения любого порядка операций для любого n числа выражений.

Как выполнить порядок операций с экспонентами?

Согласно PEMDAS, буква E обозначает показатели степени, которые идут вторым шагом в порядке операций. Давайте посмотрим на данный пример, чтобы четко понять, как сделать порядок операций с показателями.
Выражение: 7 × (2 2 )
Решение: 7 × ( 4 ) = 28 (Верно (✔). Это правильный способ решения показателей)
Давайте рассмотрим другой подход для того же выражения.
7 × ( 2 2 ) = 14 2 = 196 ((Неверно (✘). Это неправильный порядок действий с показателями)

Каков правильный порядок действий?

Правильный порядок операций можно легко выразить с помощью слова PEMDAS или BODMAS. Эти два слова можно описать как PEMDAS (круглые скобки, показатели степени, умножение или деление и сложение или вычитание). Аналогично, для BODMAS (скобки, порядок , Деление, Умножение, Сложение и Вычитание.)

Какой порядок операций без скобок?

Идем по правилам порядка операций, если убрать скобки, то останется EMDAS. EMDAS означает (экспоненты, умножение или деление, сложение или вычитание). Если в выражении у нас нет экспоненциального члена, то нам нужно сначала выполнить умножение или деление, а затем перейти к сложению или вычитанию. Ситуация может варьироваться в зависимости от операторов, присутствующих в данном выражении

Когда мы используем порядок операций?

Многие случаи в нашей жизни проходят через определенный порядок операций, чтобы выполнить ее хорошо. Каждый день мы сталкиваемся с таким сценарием. Например, отправляясь на продуктовый рынок и покупая вещи, мы быстро проделываем в голове порядок действий. Это помогает нам сократить время работы на кассе.

Какая операция выполняется первой в порядке операций?

В предыдущих разделах мы читали о двух аббревиатурах BODMAS и PEMDAS. Согласно обоим аббревиатурам, в порядке операций мы сначала упрощаем скобки или квадратные скобки.

Для чего нужен калькулятор порядка операций?

Калькулятор порядка операций – это онлайн-инструмент и самый быстрый метод, с помощью которого мы можем вычислить любое заданное числовое выражение с учетом правил порядка операций. Чтобы использовать калькулятор порядка операций, нам нужно ввести числовое выражение в правильном формате. Попробуйте калькулятор порядка операций Cuemath и быстро решите выражения в течение нескольких секунд.

☛Также проверьте:

Для большей практики попробуйте эти:

  • Порядок операций с рабочими листами показателей
  • Рабочие листы расширенного порядка операций
  • Рабочие листы порядка операций

Что такое 4 порядка операций?

4 основных порядка операций:

  • Скобки.
  • Экспоненциальный член.
  • Умножение или деление.
  • В конце сложения или вычитания.

Четыре порядка операций можно легко вспомнить в любой момент времени, заучив аббревиатуры PEMD AS или B ODMAS .

Объяснение правила PEMDAS! (Примеры включены) — Mashup Math

Что такое правило PEMDAS и как оно применяется к математическому порядку операций?

Сообщение от Энтони Персико

Каково правило PEMDAS для математического порядка операций и решения задач? Изучая математику, вы узнаете о процессе, называемом порядком операций . Этот процесс является правилом, которое необходимо соблюдать при решении математических задач с несколькими операциями, такими как вычитание, сложение, умножение, деление, группирование и/или возведение в степень.

Существует множество приемов для запоминания математического порядка операций в правильном порядке, но самым популярным является правило PEMDAS.

Правило PEMDAS представляет собой мнемонику, которая обозначает:

P: Круженная скобка

E: Экспоненты

M: Умножение

D: Разделение

A: Добавление

S = подразделение

9008 . в правиле PEMDAS выполняются слева направо.

Кроме того, правило PEMDAS для запоминания математического порядка операций имеет несколько важных подправил, которые также необходимо соблюдать, если вы хотите правильно использовать PEMDAS (и получать правильные ответы на математические задачи). Эти важные подправила относятся к отношениям между умножением/делением и сложением/вычитанием.

Эти важные подправила правила PEMDAS подробно объясняются в следующем разделе:

Правило PEMDAS: ключевые моменты

Правило PEMDAS существует уже несколько десятилетий как инструмент, помогающий учащимся запомнить математический порядок операций. . Многие предпочитают просто запоминать мнемоническое слово PEMDAS (произносится как PEM-DAHS), в то время как другие предпочитают запоминать фразу , пожалуйста, извините, моя дорогая тетя Салли.

Однако вы предпочитаете помнить, что правило PEMDAS не так важно, как запоминание ранее упомянутых подправил? Почему подправила правила PEMDAS так важны? Потому что подправила часто определяют правильный или неправильный ответ на математическую задачу.

Правило PEMDAS может быть несовершенным, но если вы помните подправила, оно может быть полезным инструментом, помогающим вам правильно применять математический порядок операций и получать правильные ответы как на простые, так и на сложные математические задачи при условии, что вы знаете важные подправила .

Важные подправила правила PEMDAS:

1.) P: Выполняйте операции внутри круглых скобок или групп, прежде чем делать что-либо еще (если нет групп или круглых скобок, вы можете пропустить этот шаг) .

2.) E: Далее, после выполнения операций внутри круглых скобок и группировок (если они есть), применить любые показатели степени (если показатели степени отсутствуют, этот шаг можно пропустить).

3.) M/D: Затем, после круглых скобок и групп и показателей, выполните умножение/деление слева направо в зависимости от того, какая операция была первой).

★ Тот факт, что М стоит перед D в правиле PEMDAS, не означает, что вы всегда будете выполнять умножение перед делением.

4.) A/S: Наконец, после умножения и/или деления выполните сложение/вычитание слева направо в зависимости от того, какая операция была первой).

★ Тот факт, что A стоит перед S в правиле PEMDAS, не означает, что вы всегда будете выполнять сложение перед вычитанием

★ = Чрезвычайно важно

Теперь, когда вы знаете, что означает правило PEMDAS для запоминания математического порядка операций, пришло время узнать, как использовать это правило для решения математических задач и получения правильных ответов.

Почему? Потому что знание того, что означает правило PEMDAS, не имеет никакой образовательной ценности, если вы понятия не имеете, как применить его к математическому порядку операций.

Помните, что правило PEMDAS полезно только в том случае, если вы помните ключевые подправила, показанные в предыдущем разделе.

Имея в виду подправила, в следующем разделе будет рассмотрено несколько примеров того, как правильно применять правило PEMDAS, когда речь идет о математическом порядке операций и решении задач. 92=9

Последний шаг – разделить: 27÷9 = 3

Окончательный ответ: 3

Правило PPEMDAS Пример. 3: 10 x 6 + 1

Обратите внимание, что в этом примере не используются группировки или экспоненты. Поэтому вы можете пропустить P и E в правиле PEMDAS и начать с M/D.

Поскольку умножение/деление предшествует сложению/вычитанию, вы можете решить эту задачу, двигаясь слева направо следующим образом:

 10×6 = 60

60 + 1 = 61

Окончательный ответ: 61

Правило PEMDAS Пример. 4: 75 – 10 x 5

Согласно правилу PEMDAS умножение/деление предшествует сложению/вычитанию, поэтому вы НЕ можете решить эту задачу, двигаясь слева направо.

Правило PEMDAS требует сначала умножить, а затем выполнить вычитание следующим образом:

10 x 5 = 50

75 – 50 = 25

Окончательный ответ: 25

Правило PEMDAS Пример. 5: 8 x 8 ÷ 16

Вы готовы применить важные подправила?

Обратите внимание, что в этом математическом примере есть только две операции: умножение и деление.

Прежде чем двигаться дальше, давайте вернемся к подправилу №3:

3.) M/D: Затем, после круглых скобок, групп и показателей степени, выполните умножение/деление слева направо в зависимости от того, какая операция будет первой).

★ Тот факт, что М стоит перед D в правиле PEMDAS, не означает, что вы всегда будете выполнять умножение перед делением.

Эту задачу можно решить, выполнив сначала умножение (крайняя левая операция), а затем деление второго следующим образом:

8 x 8 = 64.

64 ÷ 16 = 4

Окончательный ответ: 4

Примечание: Если бы вы строго следовали правилу PEMDAS и решали слева направо, вы все равно могли бы получить 4 как правильный ответ. Однако так будет не всегда, как в следующем примере.

Правило PEMDAS Пример. 6: 42 ÷ 7 x 3

Начнем с того, что многие люди неправильно решают эту простую задачу, потому что забывают ключевые подправила правила PEMDAS. Они совершат ошибку, строго следуя правилу PEMDAS и выполняя умножение перед делением (поскольку M стоит перед D в PEMDAS).

Не делайте этой ошибки!

Помните, что ★ Тот факт, что М стоит перед D в правиле PEMDAS, не означает, что вы всегда будете выполнять умножение перед делением.

В этом случае единственными операциями являются умножение и деление. На этот раз деление на первом месте, и это нормально. Вы по-прежнему решаете задачу, двигаясь слева направо следующим образом:

42 ÷ 7=6

6×3=18

Окончательный ответ: 18

Почему 2 не является окончательным ответом? Если вам не удалось правильно применить правило PEMDAS, возможно, вы допустили ошибку, выполнив умножение перед делением следующим образом:

7 x 3 = 21

42 / 21 = 2 (ЭТО ОТВЕТ НЕВЕРНЫЙ!)

( Совет профессионала: Если бы это был вопрос с несколькими вариантами ответов, то оба варианта были бы 18 и 2. Так что будьте осторожны!) (как простые, так и сложные) без понимания того, как применять математический порядок операций, а PEMDAS — эффективный инструмент для их запоминания в правильной последовательности — при условии, что вы также помните важные подправила, описанные выше.

 Правило PEMDAS и математический порядок операций в последние годы привлекли огромное внимание из-за вирусных сообщений в социальных сетях, в которых рассказывались, казалось бы, простые математические задачи, которые собирали тысячи ответов (и неправильных ответов) из-за того, что многие взрослые могут помните «PEMDAS», но не то, как применять фактическое правило PEMDAS (и соответствующие подправила).

Поскольку многие люди не могут найти правильный ответ на эти простые вопросы, они склонны оставлять комментарии и отмечать друзей, что только делает самых популярных в социальных сетях.

Правило PEMDAS для математического порядка операций: Заключение

Правило PEMDAS — популярный инструмент памяти для запоминания математического порядка операций. Правило означает P: скобки, E: экспоненты, M: умножение, D: деление, A: сложение, S = вычитание.

Как правило, операции выполняются слева направо, но есть очень важные ключевые подправила, а именно (1) выполнять умножение/деление слева направо в зависимости от того, какая операция выполняется первой) и выполнять сложение/вычитание слева вправо в зависимости от того, какая операция была первой).

Без понимания этих подправил правило PEMDAS становится крайне ненадежным и может привести к неправильным ответам на простые математические задачи (см. правило PEMDAS, пример 6 выше).

PEMDAS, возможно, не лучший способ запомнить, как правильно применять математический порядок операций, но он может быть надежным инструментом тогда и только тогда, когда вы также помните ключевые подправила.

Дополнительные бесплатные математические ресурсы для классов K-8:

6 комментариев

Подписанный номер

Подписанный номер Назад в математический центр
Добавление целых чисел

ПРАВИЛО 1. Если слагаемые имеют одинаковый знак, сложите два числа и добавьте к их общему знаку префикс.

(+62) + (+14) = +76 (-29) + (-13) = -42

ПРАВИЛО 2. Если слагаемые имеют разные знаки, найдите разницу между двумя числами и поставьте перед ним знак того числа, которое находится на большем расстоянии от нуля.

(+15) + (-8) = +7 (+9) + (-30) = -21

Некоторые практические задачи
1. (-5) + (-6) =
3. (-3) + (-6) =
5. (-2) + (-8) =
7. (-9) + (+10) =
9. (+12) + (+10) =
11. (-29) + (-11) =
13. (+42) + (-19) =
15. (+31) + (-56) =
17. -8 + 10 =
19. 75 + (-25) =
21. 73 + 47 =
23. 78 + (-30) =
25. 75 + (-25) =
27. 200 + 100 =
29. 355 + (-163) =
31. 34 + (-16) =
33. 72 + (-12) =
35. 1/2 + -1/2 =
37. 1/4 + (-1/2) =
39. 1/4 + -1/2 =
41. 16 + 16 =
43. 3 + (-8) + 7 =
45. 12 + 5 + (-8) + 20 + (-16) =
2. (+9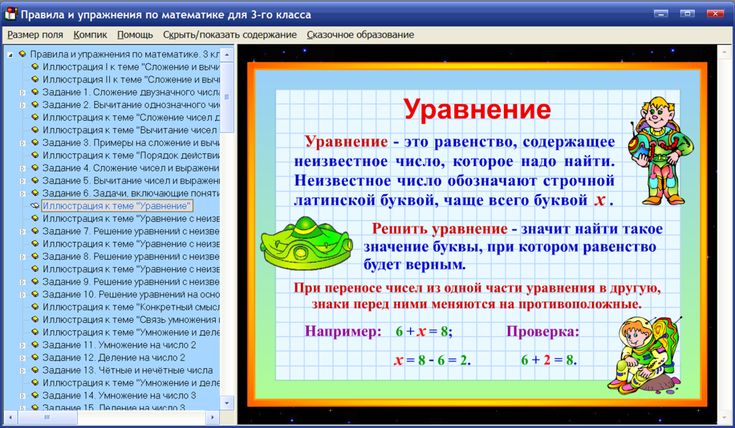) + (-4) =
4. (-4) + (-4) =
6. (-7) + (+1) =
8. (-8) + (-5) =
10. (+13) + (-17) =
12. (-36) + (+24) =
14. (-33) + (+42) =
16. (+65) + (+15) =
18. 7 + (-18) =
20. 33 + (-22) =
22. 86 + (-58) =
24. 100 + 50 =
26. 150 + 50 =
28. 132 + (-181) =
30. 900 + 200 =
32. 14 + 43 =
34. 4 + 17 =
36. 7 + (-7) =
38. -1/4 + 1/4 =
40. 17 + 4 =
42. 2436 + (-1064) =
44. 11+5+(-2)=
45. 12 + 5 + (-8) + 20 + (-16) =
Ключ ответа для сложения целых чисел

 

  1. 11
  2. 5
  3. 9
  4. 8
  5. 10
  6. 6
  7. 1
  8. 13
  9. 22
  10. 4
  11. 40
  12. 12
  13. 23
  14. 9
  15. 25
  16. 80
  17. 2
  18. -11
  19. 50
  20. 55
  21. 26
  22. 28
  23. 108
  24. 50
  25. 100
  26. 200
  27. 100
  28. 49
  29. 192
  30. 1100
  31. 50
  32. 57
  33. 60
  34. 13
  35. 0
  36. 0
  37. 1/4
  38. 0
  39. 3/4
  40. 13
  41. 0
  42. 1372
  43. 2
  44. 14
  45. 13
Правила вычитания целых чисел

ПРАВИЛО 1.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *