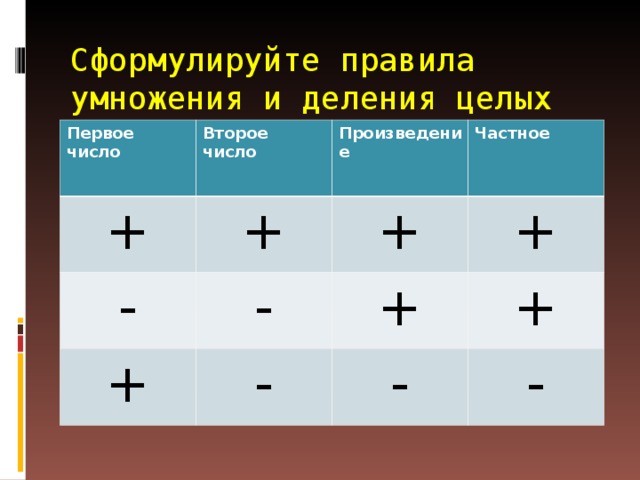
Правила по математике плюс на минус: Правила знаков

Минус на плюс что дает?

Положительные и отрицательные числа придумали математики. Делать им было нечего, вот они и придумали. Правила умножения и деления положительных и отрицательных чисел придумали всё те же математики. Специально для того, чтобы нам жизнь мёдом не казалась. Как же нам быть? Нужно выучить эти правила, чтобы говорить математикам то, что они хотят от нас слышать.

Запомнить правила умножения или деления положительных и отрицательных чисел очень просто. Если два числа имеют разные знаки, в результате всегда будет знак минус.
Если два числа имеют одинаковые знаки, в результате всегда будет плюс.

Рассмотрим все возможные варианты. Что дает минус на плюс? При умножении и делении минус на плюс дает минус. Что дает плюс на минус? При умножении и делении в результате мы тоже получаем знак минус.

Минус на плюс, плюс на минус.

Как вы видите, все варианты умножения и деления положительных и отрицательных чисел исчерпаны, но знак плюс у нас так и не появился.

Это мы сформулировали правило для себя, чтобы запомнить. Что говорить математикам? При умножении или делении положительных и отрицательных чисел в результате получается отрицательное число. Всегда.

Что дает минус на минус? Всегда будет получаться плюс, если мы выполняем умножение или деление. Что дает плюс на плюс? Здесь совсем просто. Умножение или деление плюса на плюс дает всегда плюс.

 

Минус на минус, плюс на плюс.

Надеюсь, это вы запомнили: минус на минус дает плюс, плюс на плюс дает минус. Что говорить математикам? При умножении и делении положительных или отрицательных чисел в результате получается положительное число.

Если с умножением и делением двух плюсов всё понятно (в результате получается такой же плюс), то с двумя минусами ничего не понятно. По логике, если два плюса дают плюс, то два минуса должны давать минус.

Такой большой, жирный минус. Но не тут-то было. Математики думают иначе. Так почему минус и минус превращаются в плюс?

Могу вас заверить, что интуитивно математики правильно решили задачу на умножение и деление плюсов и минусов. Они записали правила в учебники, не особо вдаваясь в подробности. Для правильного ответа на вопрос, нам нужно разобраться, что же означают знаки плюс и минус в математике.

Давайте попробуем применить правило умножениея и деления положительных и отрицательных чисел на практике. Придумаем какой-нибудь пример из нашей жизни. Думаю, вы слышали про бочку мёда и ложку дёгтя, которая может испортить весь мёд. Пусть мёд – это положительные числа, а дёготь – это числа отрицательные. Пробуем. Смотрим на картинки и описываем правила.

Если в бочку дёгтя добавить ложку мёда, получится бочка дёгтя.
Если в бочку мёда добавить ложку дёгтя, получится бочка дёгтя.
Если в бочку дёгтя добавить ложку дёгтя, получится бочка мёда.
Если в бочку мёда добавить ложку мёда, получится бочка мёда.

Первых два примера с натяжкой можно принять. Последний пример вообще не вызывает вопросов. А вот с предпоследним примером возникают очень большие проблемы – в жизни такого не бывает.

Здесь возможны два варианта:
1. Математики не правильно записали свое правило.
2. Мы не правильно применяем математическое правило.

Лично я за второй вариант. Объясню почему. Математику не только нужно знать, но нею ещё нужно уметь пользоваться.

Приведу пример из собственного опыта. Один учитель математики на уроках нам говорил: «математика – это точная наука, два раза соври – получится правда». Это утверждение однажды мне очень пригодилось. Как-то я решал сложную задачу с длинным решением. Я точно знал, какой результат должен быть. Но результат был другим. Я долго искал ошибку в расчетах, но не смог ее найти. Тогда, за несколько действий до итогового результата, я изменил одно число так, чтобы результат получился правильным. Я в расчетах соврал два раза и получил правильный результат.

Математические вычисления в тот раз никто не проверял и я получил хорошую оценку. Это очень похоже на правило «минус на минус дает плюс», не так ли?

Но вернемся к нашим бочкам. Кстати, говорят, именно с бочек с вином математики срисовали знак “минус”. Виноделы этим знаком обозначали пустые бочки. После наполнения бочек вином они перечеркивали знак “минус” и получался знак “плюс”. По сути, знак “минус” заменял виноделам обычный ноль, ведь он обозначал отсутствие вина в бочке. Но математики ловко присобачили знак “минус” к числам и назвали их “отрицательными”.

Так что же не так с мёдом и дёгтем в бочках? Мои четыре примера описывают действие сложения – ведь мы прибавляем одно к другому, а математические правила мы рассматриваем для деления и умножения. Это абсолютно разные вещи, сколько бы математики не повторяли, что умножение это и есть сложение. Сложение – это изменение количества. Умножение – это изменение качества. При добавлении ложки дёгтя в бочку мёда, мёд не превращается в дёготь. 2

В этом примере буква а выполняет роль единицы измерения. Кстати, правило умножения отрицательных чисел наводит на ещё один вопрос математикам: сколько отрицательных чисел нужно сложить, чтобы получилось одно положительное число?

(-2)+(-2)=-4

(-2)*(-2)=+4

Так что же такое знаки “плюс” и “минус” в математике? Существуют ли отрицательные числа? Об этом мы поговорим как-нибудь в другой раз.

Умножения и деление отрицательных чисел. Решение примеров.

• Альфашкола
• Статьи
• Умножения и деление отрицательных чисел

 

 

В этой статье мы будем изучать умножение и деление отрицательных чисел. Существуют определенные правила умножения отрицательных чисел.

• \(“–“-\) при умножении минус на минус результат становится положительным;
• \(“-+”-\) при умножении минуса на плюс результат становится отрицательным;
•  \(“+-“-\) при умножении плюса на минус результат становится отрицательным;
• \(“++”-\)  при умножении плюса на плюс результат становится положительным.

---

Примеры умножения отрицательных чисел. 

Задача 1. Вычислить: \((-4)*(-4)\) и \((-6)*(-5).\)

Решение.

Отрицательное число при умножении на отрицательное станет положительным согласно правилу.

1. \((-4)*(-4)=16\)
2. \((-6)*(-5)=30\)

Ответ: \(16;30.\)

Задача 2. Вычислить: \((-10)*12\) и \((-7)*4.\)

Решение.

Отрицательное при умножении на положительное число станет отрицательным согласно правилу.

-10 * 12= -120

(-7)*4=-28

 

Ответ: \(-120; -28\)

---

Задача 3. Вычислить: \(11*(-11)\) и \(13*(-6).\)

Решение.

Положительное при умножении на отрицательное число станет отрицательным согласно правилу.

1. \(11*(-11)=-121\)
2. \(13*(-6)=-78\)

Ответ: \(-121;-78.\)

Деление отрицательных чисел

 

При делении действуют те же правила знаков, что и при умножении. Делить на ноль нельзя.

• ​\(“–“-\)​ при делении минус на минус результат становится положительным;
•  ​\(“-+”-\)​при делении минуса на плюс результат становится отрицательным;
•  \(“+-“-\)при делении плюса на минус результат становится отрицательным;
• \(“++”-\) при делении плюса на плюс результат становится положительным.

Задача 4. Вычислить: \((-16)*(-4)\) и \((-6)*(-2)\).

Решение.

1. \(-16:(-4)=4\)
2. \((-6):-2=3\)

Ответ: \(4;3.\)

Задача 5. Вычислить: \((-10):5\) и \((-12):6\).

Решение.

1.  \((-10):5=-2\)
2. \((-12):6=-2\)

Ответ: \(-2;-2.\)

Задача 3. Вычислить:  \(121:(-11)\) и  \(169:(-13)\).

Решение.

1.  \(121:(-11)=-11\)
2.  \(169:(-13)=-13\)

Ответ: \(-11;-13.\)

 

 

 

 

 

 

 

 

 

 

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы “Альфа”. Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку “Записаться” принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Надежда Викторовна Хасанова

Репетитор по математике

Стаж (лет)

Образование:

Самаркандский Государственный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Владимир Валерьевич Ковалев

Репетитор по математике

Стаж (лет)

Образование:

Пятигорский государственный педагогический институт иностранных языков

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Павел Юрьевич Осиновой

Репетитор по математике

Стаж (лет)

Образование:

Нижнетагильский государственный социально-педагогический институт (филиал) ФГАОУ ВО

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Предметы

• Математика
• Физика
• Химия
• Русский язык
• Английский язык
• Обществознание
• История России
• Биология
• География
• Информатика

Специализации

• Репетитор по олимпиадной математике
• Подготовка к ЕГЭ по математике (профильный уровень)
• Подготовка к ОГЭ по химии
• Подготовка к олимпиадам по химии
• Подготовка к ОГЭ по русскому языку
• Подготовка к олимпиадам по английскому языку
• Английский язык для начинающих
• Разговорный английский язык
• ВПР по обществознанию
• Подготовка к ОГЭ по географии

Похожие статьи

• Объема конуса
• Эллипс
• Перевод км/час в м/с?
• Биотехнологический факультет МГУ: приёмная комиссия, проходной балл, отзывы
• ЕГЭ по математике, базовый уровень. Текстовые задачи (вариант 5)
• Учимся решать задачи с прикладным содержанием
• Зачем отказываться от чипсов и чем их заменить?
• “Я не знаю, кем мне быть”: ответы на популярные вопросы старшеклассников

Нажимая кнопку “Записаться” принимаю условия Пользовательского соглашения и Политики конфиденциальности

Текст с ошибкой:

Расскажите, что не так

Основные правила для положительных и отрицательных чисел.

• ОПИСАНИЕ. for YourDictionary

• РАЗРЕШЕНИЕ

  Принадлежит YourDictionary, Copyright YourDictionary

Числа больше нуля называются положительными числами, а числа меньше нуля — отрицательными числами. Это означает, что они падают по обе стороны от числовой прямой. Однако то, что они находятся на одной линии, не означает, что они следуют одним и тем же правилам! Продолжайте читать список основных правил использования положительных и отрицательных чисел в математике.

Правила для чисел со знаком

При использовании положительных и отрицательных чисел вы используете правила для чисел со знаком (числа с положительными или отрицательными знаками перед ними). Эти шаги, также известные как операции над числами со знаком, помогут вам избежать путаницы и решить математические задачи как можно быстрее и правильнее.

Следуйте этим правилам, чтобы определить лучший способ сложения, вычитания, умножения и деления положительных и отрицательных чисел. Помните, что если нет знака + или -, число положительное.

Сложение: одинаковые знаки, сложите числа

Когда вы складываете два числа вместе, и они имеют одинаковый знак (два положительных или два отрицательных числа), сложите числа и сохраните знак. Например:

• 1 + 1 = 2
• 51 + 32 = 83
• -14 + (-6) = -20
• -196 + (-71) = -267

Обратите внимание, что уравнения с двумя положительные суммы имеют положительные суммы, а уравнения с двумя отрицательными числами имеют отрицательные суммы. Если вы используете числовую прямую для решения задачи, добавление двух положительных чисел приведет к положительной стороне, а добавление двух отрицательных чисел приведет к отрицательной стороне.

Сложение: разные знаки, вычитание чисел

Если вы складываете положительные и отрицательные числа вместе, вычтите меньшее число из большего и используйте знак из большего числа. Например:

• 6 + (-5) = 1
• -17 + 22 = 5
• -100 + 54 = -45
• 299 + (-1) = 298

Как видите, сложив числа с разными знаками на самом деле является формой вычитания. При использовании числовой прямой ваша сумма будет ближе к нулю.

Вычитание: Переключиться на сложение

Вычитание положительных и отрицательных чисел означает сложение противоположных чисел или аддитивное обратное. Замените знак вычитания на сложение, а следующий за ним знак измените на противоположный. Затем следуйте инструкциям по добавлению. Например:

• -3 – (+5) становится -3 + (-5) = -8
• 9 – (-7) становится 9 + (+7) = 16
• -14 – (+8) становится -14 + (-8) = -22
• 25 – (-90) становится 25 + (+90) = 115

Хороший совет: всякий раз, когда вы видите знак минус и знак минус вместе, например, в 9 – (-7), немедленно делайте их положительными. Отрицательные знаки компенсируют друг друга, и уравнение становится задачей на сложение.

Умножение и деление: одинаковый знак, положительный результат

Кажется, что умножение и деление сложнее, чем сложение и вычитание, но на самом деле они намного проще. Правило умножения положительных и отрицательных чисел с одинаковым знаком (два положительных или два отрицательных) состоит в том, что произведение всегда будет положительным. Например:

• 8 x 4 = 32
• (-8) x (-4) = 32
• 10 x 9 = 90
• (-10) x (-9) = 90

То же правило применяется для деления . При делении числа на другое число с тем же знаком частное (ответ) положительно. Например:

• 12 ÷ 6 = 2
• -12 ÷ (-6) = 2
• 100 ÷ 5 = 20
• -100 ÷ (-5) = 20

числа всегда равны положительному числу? Подобно вычитанию отрицательных чисел, эти операции превращают отрицательные числа в противоположные (обратные). По сути, вы вычитаете отрицательное число несколько раз — и, как показано выше, вычитание отрицательных чисел приводит к положительному уравнению.

• Описание

  Правила для умножения и деления двух чисел положительные и отрицательные

• Источник

  Атрибутив-необратительные производные 4.0 Международный (CC BY-ND 4.0) / Создано Beth Wiggins For Yourdictionary

• Perform

  5555555555555555555

  Принадлежит YourDictionary, Copyright YourDictionary

Умножение и деление: противоположный знак, отрицательный результат

При умножении положительного и отрицательного числа произведение всегда будет отрицательным. Неважно, в каком порядке стоят знаки. Например:

• 6 х (-7) = -42
• -7 х 6 = -42
• 12 х (-11) = -132
• -11 х 12 = -132

Во всех этих случаях вам сначала нужно умножить или разделить числа. Затем решите, является ли произведение или частное положительным (два положительных или два отрицательных в уравнении) или отрицательным (один положительный и один отрицательный в уравнении).

Знаки сходства и отличия в сложении и вычитании

Еще один способ подумать о сложении положительных и отрицательных чисел — посмотреть на знаки в ряду. Два одинаковых знака подряд (++ или –) означают, что вы складываете числа, а два разных знака подряд (+- или –) означают, что вы вычитаете. Например:

• 7 + (+2) = 9 (++ похожи на знаки, поэтому уравнение представляет собой сложение)
• 9 + (-8) = 1 (+- не являются знаками, поэтому уравнение представляет собой вычитание)
• 11 – (+13) = 2 (-+ не похожи на знаки, поэтому уравнение представляет собой вычитание)
• 15 – (-10) = 25 (– похожи на знаки, поэтому уравнение представляет собой сложение)

Этот метод следует те же правила, что и выше, но они могут помочь вам решить проблему быстрее, если вы предпочитаете работать над знаками заранее. Как только вы концептуально поймете положительные и отрицательные числа, вы сможете решить, какой метод лучше всего подходит для вас.

Понимание основ математики

Как только вы познакомитесь с основами математики и ее правилами, перед вами откроется весь математический мир. В отличие от других предметов, в математике нет нюансов или интерпретаций — она просто такая, какая есть! Для дополнительной математической практики ознакомьтесь с инструкциями по решению задач на деление в длину (с примерами). Вы также можете просмотреть различные типы чисел в математике перед следующим заданием по математике.

Правила сложения, вычитания, умножения и деления положительных и отрицательных чисел. [Решено]

Четыре основные арифметические операции, связанные с целыми числами:

• Сложение целых чисел
• Вычитание целого числа
• Умножение целых чисел
• Деление целых чисел

Ответ. Существуют определенные правила сложения, вычитания, умножения и деления положительных и отрицательных чисел.

Прежде чем мы начнем изучать эти методы целочисленных операций, нам нужно запомнить несколько вещей. Если перед числом нет знака, значит, число положительное.

Объяснение:

В следующем содержании показаны правила сложения, вычитания, умножения и деления положительных и отрицательных чисел.

Правило сложения целых чисел:

Случай 1: знаки одинаковые

Если знаки одинаковые, добавьте и сохраните тот же знак.

• (+) + (+) = сложите числа, и ответ положительный

           Пример: 2 + 5 = 7

• (-) + (-) = сложите числа, и ответ будет отрицательным

           Пример: (-5) + (-4) = -9

Случай 2: знаки разные

Если знаки разные, вычтите числа и используйте знак большего числа.

• (+) + (-) = вычесть числа и взять знак большего числа.

           Пример: 7 + (-3) = 4

• (-) + (+) = вычесть числа и взять знак большего числа.

          Пример: (-9) + 6 = -3

Правило вычитания целых чисел:

Чтобы вычесть число из другого числа, нужно изменить знак числа (которое нужно вычесть), а затем это число с измененным знаком прибавить к первому числу.

• (+) – (+) = изменить знак вычитаемого числа и сложить их. Результат принимает знак большего числа.

            Пример: (+6) – (+2)

                                     = (+6) + (-2) = 6 – 2 = 4

• (-) – (-) = Изменить знак вычитаемого числа и сложить их. Результат принимает знак большего числа.

           Пример: (-9) – (-6)

                         = (-9) + (+6) = -9 + 6 = -3

• (+) – (-) = Изменить знак числа для вычитания и сложения их.

           Пример: (+5) – (-3)

                         = (+5) +(+3) = 5 + 3 = 8

• (-) – (+) =  Изменить знак вычесть и сложить их. Результат всегда отрицательный

Пример: (-7) -(+2)

= (-7) + (-2) = -7 -2 = -9

Умножение и разделение целых чисел Правило:

Случай 1: Знаки одинаковы

Если знаки совпадают, ответ всегда положительный.