Особенности понимания детьми дошкольного возраста дробей: Как объяснить ребенку действия с дробями
Как объяснить ребенку действия с дробями
Дроби – одна из самых непростых, но важных тем в математике. Не подготовленному ученику изучить ее и выполнять различные действия бывает сложно, но при правильном подходе самые трудные разделы точной науки становятся понятными и доступными. Для исследования темы дробей нужно применить фантазию, воображение и доносить материал в игровом формате. Чтобы ученик мог самостоятельно выполнять задания, преподавателю понадобится время и терпение.
Термин «дробь» обозначает деление. В рамках школьной программу к изучению этой темы приступают в средней школе, но педагоги рекомендуют начать ее освоение в дошкольном возрасте. Получение базовых знаний о дробях позволяют тренировать навык счета, концентрацию, логическое и пространственное мышление.
С чего начать изучение дробей детям
Начинать изучение темы следует с понятия «долей». Для этого можно использовать наглядные примеры – разделить блюдо или предмет на равные части, объяснив, что такое половина, треть и четверть.
Хорошим упражнением будет сбор конструктора, где дети могут делить целое на части, запоминать одинаковые кубики и пересчитывать различные элементы. Чем большее количество долей получается при делении, тем меньше они будут. Ребенку следует осознать пользу и востребованность дробей повседневной жизни. Когда он это поймет, то процесс понимания темы будет легче и быстрее.
Дробь не является целым числом. Для записи нужного количества долей применяют понятие обыкновенная дробь. Она состоит из двух показателей: знаменателя и числителя, которые разделены наклонной или горизонтальной чертой. Числитель указывается над дробной чертой, а знаменатель записывается снизу и указывает на количество частей от целого.
Виды дробей: правильные и неправильные дроби
Существуют правильные и неправильные обыкновенные дроби. Правильными называют те дроби, в которых показатель числителя меньше знаменателя (3/4). В неправильных дробях значение числителя больше, чем знаменателя, и в них можно выделить целую часть (6/4).
Числитель делится на знаменатель, вследствие чего формируется целая часть и остаток. К неправильным дробям относятся и те, у которых показатели числителя и знаменателя равны (10/10). Составные части такой дроби превращаются в единицу.
Смешанные числа можно трансформировать в неправильные дроби. Для этого нужно часть целого умножить на знаменатель, а к полученной сумме прибавить числитель. Для упрощения дробей необходимо и сокращать. Если обе части дроби равны, то можно их разделить на единое число. При сложении обыкновенных дробей знаменатель остается без изменений, а числители складывают. Если знаменатели различны, то нужно определить наименьшее общее кратное значение. Аналогичным образом проводится и вычитание дробей. Чтобы умножить обыкновенные дроби, необходимо последовательно перемножить знаменатели и числители между собой. При делении дробей необходимо умножить числитель первой на знаменатель второй и наоборот. При сравнении дробей нужно обратить внимание на числитель: больше будет та, у которой его значение.
При одинаковых числителях будет больше та дробь, знаменатель которой меньше. Если при сравнении одна из дробей является неправильной, то она автоматически становится больше. Эти математические операции часто вызывают затруднения у детей, поэтому разбираться в них нужно на практике.
Если в знаменателе дроби есть числа, кратные десяти, то они, соответственно, называются десятичными. Ученики записывают показатель целого, отделяя запятой десятые части (5,2). В математике существуют также дроби без значения целого. Для этого записывают ноль и после запятой указывают значение числителя (0,05). Десятичные дроби особенно удобны в точных вычислительных операциях. Такая система давно доказала свою практичность, она проста и понятна для учеников.
Когда детям нужно изучать дроби
Для того чтобы изучение темы дробей и их места в математической науке было продуктивным, необходимо тщательно разбирать каждые действия с педагогами, закрепляя полученные знания и умения на практике. Обучение математике онлайн развивает способность анализировать, критически мыслить и делать выводы, воспринимать и обрабатывать информацию, обобщать и систематизировать знания.
Дистанционный формат занятий позволяет приобретать навыки в удобном темпе и комфортных условиях, а результаты будут заметны после первых уроков. Чем раньше дети познакомятся с понятием дробей, тем проще им будет в дальнейшем их записывать и совершать математические действия.
Обучение дробям в школе AMAkids
В Академии развития детского интеллекта AMAkids проводится обучение математике в режиме онлайн для детей от шести лет. В штате образовательной организации работают квалифицированные преподаватели с большим опытом, которые могут найти индивидуальный подход к каждому ребенку. Занятия проводятся на специальной интерактивной платформе с применением электронного пособия и игровых тренажеров. Педагоги доносят материал не в форме стандартных лекций, а в процессе увлекательной игры, руководствуясь авторской методикой.
Математика онлайн от Академии AMAkids состоит из нескольких блоков: арифметика, геометрия, основы программирования и финансовой грамотности. На занятиях по арифметики дети изучают меры величин, знакомятся с понятиями целых чисел и обыкновенных дробей, учатся выполнять простые числовые операции.
На уроках геометрии учащиеся знакомятся с основными геометрическими фигурами и их характерными особенностями, исследуют понятия площади и периметра, симметрии и асимметрии.
Финансовая грамотность включает в себя изучение финансовой безопасности, понятий цены и стоимости, знакомятся с историей валютной системы. Ученики узнают о том, как совершать покупки правильно и с максимальной пользой. На основах программирования дети узнают об алгоритмах и множествах. Дети решают логические задачи и примеры разного уровня сложности, выполняют задания на развитие памяти и произвольного внимания.
Как развивать абстрактное мышление ребенка – Развитие ребенка
Для того чтобы осмысливать абстрактные понятия, ребенок должен отвлечься от материальной реальности, связанной с ними, и предметов, которые непосредственно значимы для данных понятий. Ему необходимо вычленить и превратить в самостоятельный объект рассмотрения отдельную сторону, свойство или состояние того, над чем он сейчас размышляет.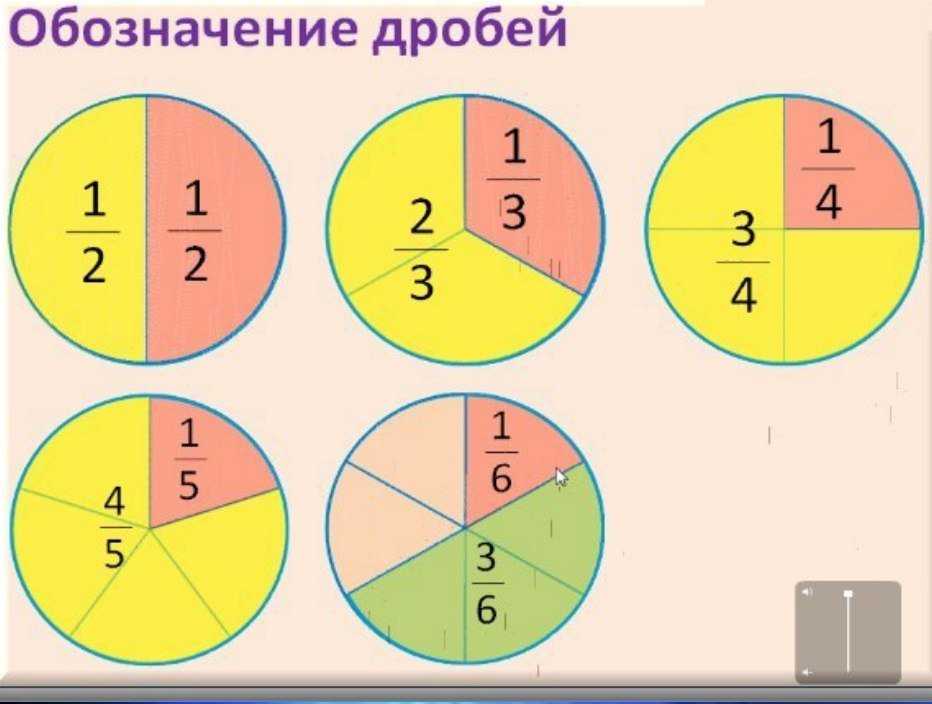
Например, если, после того как ребенок прослушал «Щедрое дерево» Шела Сильверстайна, он сделал заключение, что эта сказка об эгоизме, значит, он способен извлекать и переносить основную тему художественного произведения в свой мир.
Все значительные виды обучения требуют абстрактного мышления. Маленькие дети могут и должны отделять понятия, абстрагировать их от своего мира. Ребенок учится мыслить абстрактно с помощью содержательных игр и обучения взаимодействию, поиска новых способов представления предметов и обобщения полученных впечатлений. Это умение позволяет ему выстраивать теории о его мире.
Абстрактное мышление и числа
Развитие абстрактного мышления идет рука об руку с развивающимися математическими способностями вашего ребенка. Со временем дети развивают более абстрактные идеи о числах и счете. Почти с рождения малыши чувствительны к понятию количества. В возрасте от восьми месяцев до одного года дети, например, могут определять, какая из двух очень маленьких кучек больше, чем другая.
У них начинается долгий процесс познания сложных идей о числах и счете.
Значительное развитие происходит у ребенка в возрасте около двух лет, когда он знакомится с символичными или ролевыми играми: в них он начинает связывать мысли с отношениями и мысленно представлять количество. Например, ребенок может сказать подруге: «Я буду папой, ты будешь сестрой, а эта скала будет собакой». Играя так, он может поставить на стол две тарелки: одну для себя («папы») и одну для своей подруги («сестры»). Затем он берет две ложки – автоматически, не считая – и кладет по одной на каждую тарелку. Ребенок абстрагируется от мысли о числах, играя с конкретными предметами.
Также очень важно развитие понимания слов, обозначающих числа. Эти слова помогают детям осознавать представление о числах и понимать, как можно классифицировать количество. Например, трехлетняя девочка сидит со своей собакой на скамейке и к ним подходит другая собака. Девочка говорит маме: «Мама, смотри, две собачки!» и просит у мамы два лакомства.
Затем она дает по одному лакомству каждой из них. Это важная абстракция, потому что сама идея о числе два – это абстрактное понятие. Девочка смогла использовать слово «два», чтобы рассказать о количестве собак, которых увидела.
Ваш ребенок опирается на эти ранние математические идеи, когда учится считать. Понимание слов, обозначающих числа и навыки счета вместе, позволяет детям конструировать абстрактные сравнения чисел. Например, в возрасте старше трех с половиной лет большинство детей могут точно сравнивать количество в двух группах разнородных предметов, таких как куча кубиков и куча чипсов. Они также могут точно сравнивать группы, которые нельзя увидеть, например, кучу стеклянных шариков и последовательность барабанной дроби. В возрасте от четырех до четырех с половиной лет дети могут сравнивать группы предметов, каждая из которых состоит из разных предметов. Это показывает, что они рассматривают нумерацию в качестве более абстрактной идеи, которая не зависит от размера и природы предметов, которые нужно посчитать.
Ребенок также развивает абстрактные мысли о счете посредством письма. Дошкольники понимают, что письменные знаки на бумаге могут передавать информацию о количестве. Например, трех-, четырехлетние дети могут рисовать на бумаге палочки, чтобы показать, сколько предметов они насчитали.
Понимание форм
Для детей понимание концепции «форма» – это еще один способ осмысления мира и еще один шаг в развитии навыков абстрактного мышления. Это понимание заключается в умении делать обобщения о повседневном окружении. Маленькие дети могут узнавать о формах более глубоко, чем мы думаем. Во-первых, они узнают о формах в «целом»; например, определяя предметы прямоугольной формы, потому что «они похожи на дверь». Когда ваш ребенок может отделять форму от фона, замечать ее и отличать от других предметов, он абстрагирует эту форму.
Позже, проведя множество опытов с формами, ваш ребенок сможет распознавать, скажем, треугольники различных размеров и ориентированности.
Способы развития абстрактного мышления
Вы можете ежедневно помогать ребенку развивать навыки абстрактного мышления, обсуждая его переживания и помогая ему осмыслить их.
- Считайте все вокруг. Считайте вместе с ребенком ступеньки лестницы, по которой вы поднимаетесь; тарелки на столе; изюминки в шоколадке и так далее.
- Учите правила счета. Возьмите куклу (назовите ее, например, Незнайкой) и пусть она посчитает неправильно, попросите ребенка исправить Незнайку. Попросите рассказать, что именно Незнайка сделал не так. Для более уверенного счета ребенка начинайте с маленьких цифр.
- Играйте с маршрутами и картами. С очень маленькими по возрасту детьми обсуждайте достопримечательности, которые вы наблюдаете во время прогулки. Малыш может создавать модели этих достопримечательностей с помощью игрушек. Ребенок постарше может, например, попробовать построить модель своей комнаты или начать рисовать простые карты. Также он может играть дома в такие игры, как поиск спрятанных предметов, с помощью простой карты, которую нарисовали вы. Подчеркните, что модели и карты – это уменьшенные версии настоящего пространства.
- Предоставляйте большое количество возможностей для практического опыта. Счетный материал (детали конструктора, наборы формочек, соединяющиеся и простые кубики) и другие предметы (пуговицы, камешки или бисер) помогают ребенку выстраивать представления о математических идеях. Маленькие дети часто знают числа, но не могут применить это знание; а такие предметы будут помогать им в этом.
- Стройте с помощью различных форм. Дайте ребенку набор блоков (кубиков) различных форм для проектирования и строительства. Находите и показывайте определенные формы в повседневных предметах и пытайтесь воссоздавать их с помощью блоков.
- Поощряйте решение задач. Счетный материал, такой как кубики, можно использовать для счета, арифметики, моделирования и создания геометрических форм. Поощряйте детей использовать эти материалы при решении различных задач и для последующего обдумывания и оценивания своих решений. Это является важным шагом к абстрагированию идей, которые счетный материал помогает развивать.
- Классифицируйте предметы по признакам. Сортируйте и классифицируйте различные предметы. Подчеркните, что для сортировки мы создаем и используем разные категории, признаки. Когда вы убираете комнату ребенка, складывайте вместе детали (кубики) одинаковой формы или классифицируйте детали на те, которые можно катить, и те, которые нельзя.
- Разговаривайте с ребенком.
- Задавайте вопросы: почему? Почему не? Что если? Эти вопросы побуждают ребенка думать и описывать особенности математических объектов, такие, как, например, формы. Они также заставляют смотреть на вещи с различных точек зрения.
- Помогайте ребенку учиться задавать правильные вопросы. Маленькие дети редко просят о дополнительной информации, когда чего-то не понимают, но если их активно поощрять, они будут учиться этому.
- Используйте информацию из книг о математике. Читайте и обсуждайте книги, которые учат математическим понятиям, таким, как счет, соотношение размеров, форм и так далее.
Мы можем ежедневно наблюдать за тем, как наши дети мыслят абстрактно. Они замечательные мыслители и постоянно размышляют о своем мире. Например, ребенок любит наблюдать за птицами и однажды увидев бабочку, он взволнованно говорит: «Птица!». Так он использует абстрактное мышление, чтобы развить теорию о том, что все существа с крыльями, или все, кто может летать и по величине больше чем насекомые, – это птицы.
Как научить вашего ребенка дробям дома
Когда дело доходит до обучения математике дома, это дроби, с которыми ваши дети будут сталкиваться чаще всего. С такими словами, как числитель, неправильное, смешанное число и другими, попадающими в домашние задания и школьные отчеты, иногда даже количество терминов, относящихся к дробям для детей, может показаться немного подавляющим для родителей.
Знать, как научить вашего ребенка дробям дома, может быть сложно. Но, обучая в школах и на дому, мы были там и сделали это, и теперь можем заверить вас — путь есть, вам просто нужно идти по нему шаг за шагом. Этот блог может помочь вам в обучении дробям, помогаете ли вы ребенку в первом или четвертом классе!
Дроби в двух словах – То, что вы, возможно, забыли со школы!Мы понимаем, что дроби могут быть неприятными как для вас, так и для вашего ребенка, поэтому вот все, что вам нужно знать о них вкратце!
Что такое дробь? Дроби используются для представления меньших частей (или частей) целого.
Части могут составлять одну или несколько вещей. Так или иначе, вместе они составляют то, что называется целым.
Важно отметить, что целое может означать несколько вещей. Полезно думать о кондитерской как об аналогии. Чтобы поделиться единой целой суммой, вы можете представить плитку шоколада. Для группировки суммы на дробные части можно представить себе мешок конфет — конфет в мешке много, но нужно, чтобы они все составляли весь мешок.
Какое определение дроби подходит для детей?Простое определение дроби для детей:
Дробь — это любая часть группы, числа или целого числа.
Из каких частей состоит дробь?Дробь состоит из двух частей. Вот они:
Числитель — число над чертой.
Знаменатель , число под чертой.
Что такое дробь? Единичная дробь имеет 1 в числителе (верхнее число) и целое число в знаменателе (нижнее число).
Подробнее: Что такое дробная единица
Что такое правильная дробь?Неединичная дробь — это дробь, у которой число больше единицы в числителе (верхнее число) и целое число в знаменателе (нижнее число), которое больше числителя.
Использование предметов для визуализации дробейКогда вы начинаете учить детей дробям, предметы или изображения предметов — отличный способ понять, как они работают.
Начните с конкретных предметов, таких как еда или прилавки — вместо прилавков вы можете использовать кусочки пасты или сушеные бобы — затем нарисуйте их в виде картинок.
Как только вы это сделаете, вы можете перейти к использованию рациональных чисел (причудливое название дробей) для их представления. Заучивание дробей в таком порядке облегчает впоследствии вычисление дробей натуральных чисел.
Самое важное, что нужно помнить, когда имеешь дело с дробями, — не торопиться.
Столько информации для обработки! Даже если что-то кажется простым, найдите дополнительное время, чтобы действительно понять основные понятия, лежащие в основе дробей.
Это значительно облегчит вам жизнь, когда вы столкнетесь с более сложными задачами, связанными с преобразованием между дробями, десятичными числами и процентами.
Узнайте больше о том, почему мы используем конкретные ресурсы в математике.
Примеры дробей в бытуВы можете даже не замечать, но дроби окружают нас повсюду! Вот некоторые примеры ежедневных дробей:
- Разделение счета в ресторане на половинки, трети или четверти
- Сравнение цен в продуктовом магазине, когда что-то стоит полцены
- Подсчет сумм на кухне, например рецепт может обслужить 10 человек, но едят только 4, а это значит, что вам понадобятся дроби, чтобы вычислить правильное количество
- Суммирование денежных сумм
- Глядя на время! Полчаса и четверть прошедшего — обычное дело, когда речь идет о времени!
В первые годы обучения в школе вы узнаете, как работают числа.
Вы узнаете, как считать, и что число 1 равно одному предмету, 2 равно двум предметам и так далее.
Вы узнаете, что когда вы считаете, числа имеют большее значение. И затем, когда вы думаете, что разобрались с числами, вы узнаете, что существуют и другие типы чисел, например, дроби.
Будучи ребенком, вы все еще познаете мир. Поэтому, когда вы изучаете набор правил (например, как считать с положительными целыми числами), вы придерживаетесь их. Эта проблема? Когда вы сталкиваетесь с вещами, которые не соответствуют правилам, понять их гораздо труднее.
Положительные целые числа (например, 1, 2 или 65) являются простыми. Они приобретают большую ценность по мере роста и всегда означают одно и то же (1 всегда означает 1, а 2 всегда означает 2). Их также называют натуральными числами. Дроби известны как рациональные числа, и они подчиняются другим правилам.
Короче говоря, понимание того, как делать дроби, может быть сложным для детей начальной школы.
Дроби не всегда означают одно и то же.
½ торта — это не то же самое, что ½ из трех тортов или ½ пакета из 12 конфет! Это первое препятствие — значение дроби меняется в зависимости от размера целого.
Во-вторых, если нижнее число (знаменатель) дроби становится больше, значение уменьшается. Вдобавок ко всему, названия дробей не всегда звучат так же, как число, которое они представляют, например, восьмая для ⅛ или четверть/четвертая для ¼.
Самое важное, чем вы можете поддержать своего ребенка, это его понимание того, что дробь — это часть целого, а целое — это несколько частей. А единичная дробь — это равная часть целого. Если они смогут понять это, они смогут двигаться вперед.
Дополнительная поддержка по математике дома:
- Начальный математический словарь для детей и родителей
- Почему математика важна?
С дробями для детей можно многое охватить, но чтобы помочь вам, мы разбили их на отдельные темы.
Они также узнают, что некоторые дроби также эквивалентны, например, 2/4 соответствует ½ или 2/6 соответствует ⅓.
Вот как это объяснить просто с помощью счетчиков (макароны или сушеные бобы – подходящая замена из шкафа).
Чтобы помочь вашему ребенку полностью понять эквивалентные дроби, указывайте на них везде, где можете (особенно на ½ и 2/4 на данном этапе), так как это постоянное повторение поможет им практиковаться, пока они не усовершенствуют свои знания.
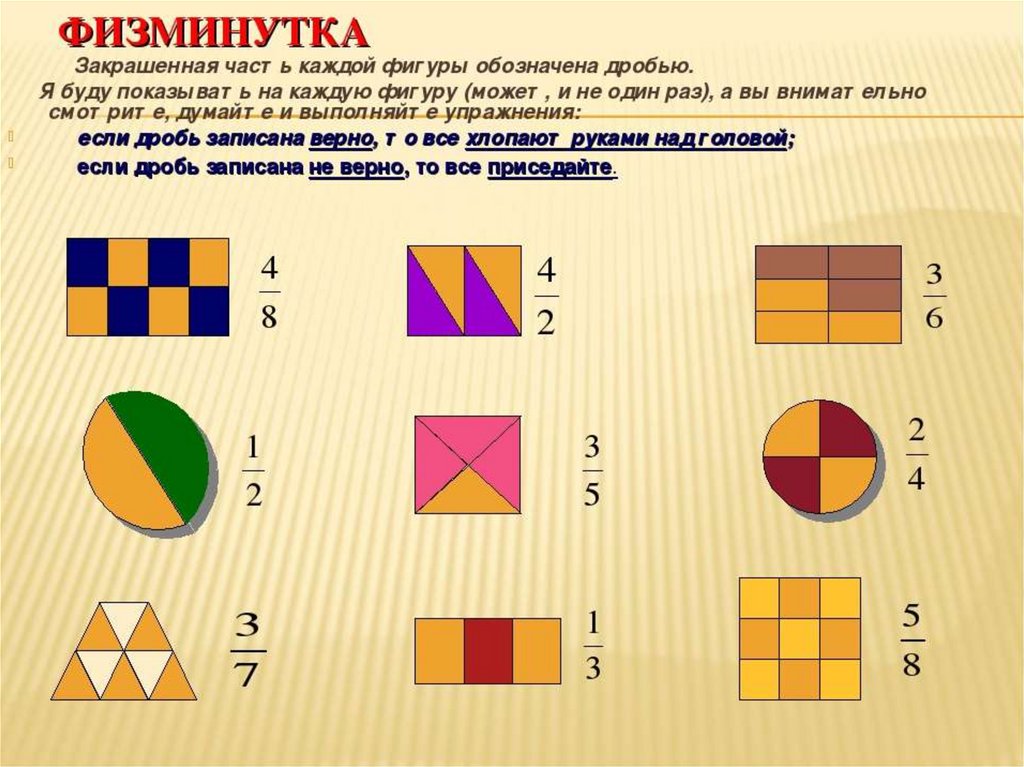
Еще один простой способ попрактиковаться — заштриховывать различные дроби фигур, например:
По мере взросления дети также должны знать несколько эквивалентных дробей с малыми знаменателями и уметь расставлять их по порядку.
Равнозначные дроби – настоящий скачок для многих детей, и большинство учителей считают его настоящим камнем преткновения для многих детей в своих классах.
Однако есть три верных способа помочь вашему ребенку понять, как составлять эквивалентные дроби, и вы можете увидеть их ниже!
Пластилин с эквивалентными дробями
Это простое, но очень эффективное упражнение поможет вашему ребенку визуализировать эквивалентные дроби таким образом, чтобы он понял.
Как проводить задание
- Дайте ребенку три одинаковых по размеру шарика пластилина.
- Попросите их разбить один шар на половинки, другой на четвертинки и третий на восемь частей одинакового размера.
- Теперь используйте шкалу — предпочтительно балансовую шкалу — чтобы показать, что половина равна двум четвертям и четырем восьмым. (Кроме того, что четверть равна двум восьмым, а три четверти равны шести восьмым.)
- Вы можете заставить их снова сформировать три первоначальных шарика пластилина, разбив их на три, шесть и девять равных частей. Опять же, вы можете показать, что треть равна двум шестым и трем девятым, а две трети равны четырем шестым и шести девятым.
Бумажные полоски эквивалентной дроби
Все, что вам нужно для этого занятия, это лист бумаги, ножницы и немного терпения, когда дело доходит до вырезания полосок!
Как выполнить задание
- Сначала нарежьте несколько полосок бумаги. Это должны быть бумажные полоски одинаковой длины.
- Сложите первую полоску пополам.
Сложите вторую полоску вчетверо.
Сложите третью полоску на шесть равных частей или шестых.
Четвертую полоску сложите на восемь равных частей или восьмерок.
Наконец, сложите полоску в двенадцать раз. - Затем поработайте с ребенком, чтобы подписать полоски так, чтобы на каждой части первой полоски было написано ½, на второй полоске было написано ¼s и так далее. Теперь вы/они можете показать, что половина равна двум четвертям, трем шестым, четырем восьмым и шести двенадцатым.
Это должны быть бумажные полоски одинаковой длины.Затем вы можете показать, что четверть равна двум восьмым и трем двенадцатым.
Вы можете повторить процесс еще раз, сложив полоски бумаги одинаковой длины в три, шесть, девять и двенадцать частей, показав, что две шестых, три девятых и четыре двенадцатых равны трети.
Используя сделанные вами полоски, вы можете сделать то же самое для ¾ и ⅔!
Представление дробей Проявите творческий подход, помогая детям вычислять дроби При демонстрации деления на половинки или четвертинки жизненно важно показать, что что-то делится на равные части.
Делая это, ваш ребенок сможет визуализировать то, что происходит, когда вы создаете дробь, и это поможет ему понять. №
Пластилин — отличное средство, с которого можно начать, помогая ребенку вырабатывать дроби в раннем возрасте, так как он податлив и легко адаптируется к различным дробям.
Тем не менее, фаворитом в начальных классах является использование еды для представления дробей, и это то, что вы можете делать со своим ребенком во время ужина, если в меню есть пицца!
Не забудьте подчеркнуть важность того, чтобы все кусочки пиццы были одинакового размера.
Это простое визуальное представление дроби, и вы можете адаптировать его, чтобы попробовать и с ¼.
Вы можете использовать любую пищу, которую легко разделить, но при этом обязательно используйте язык дробей (половинки, четвертинки и деление).
Поначалу ваш ребенок будет в основном сосредотачиваться на числах от 0 до 20, но он также может работать с некоторыми более крупными числами, с которыми в этом возрасте легко справиться.
Например, они могут сказать вам, что половина от 100 — это 50, или что одна четверть от 100 — это 25.
Конечно, значение дроби зависит от числителя (верхнее число) и знаменателя (нижнее число).
Сравнение дробей с одинаковым знаменателем
Так как знаменатели в этой точке одинаковы, вы просто добавляете числители, например:
¼ + 2/4 = ¾
Что снова можно показать с помощью бумажных полосок:
Принцип вычитания на этом этапе тот же.
Пример онлайн-урока по математике Third Space Learning, направленного на то, чтобы учащиеся поняли относительные размеры дробей — распространенное заблуждение, что больший знаменатель означает, что сама дробь больше.Сравнение дробей с разными знаменателями
Ваш ребенок начнет встречать дроби с разными знаменателями, а это значит, что нужно выполнить еще несколько шагов.
Используемый язык также может быть сложным.
Не забывайте часто использовать такие слова, как знаменатель, числитель, делить, сравнивать, упорядочивать, неправильную дробь и смешанное число, чтобы освежить в памяти ребенка ключевую лексику, так как это подготовит его к работе, которую он будет выполнять в более поздних классах.
.
Если ваш ребенок с трудом усваивает принцип сравнения дробей с разными знаменателями, для начала лучше всего воспользоваться калькулятором. Вы можете разделить числитель на знаменатель для каждой дроби, что приведет к десятичной дроби. Затем ваш ребенок может увидеть, какая дробь больше, увидев, какое десятичное число больше!
Бесплатный калькулятор для расчета дробейПроцесс построения дробей без калькулятора может занять немного больше времени, чтобы ребенок освоился, но это то, что ему нужно знать.
На изображении ниже показано, как вычислить порядковые дроби, если у вас нет калькулятора.
Проблемы со словами на дробиПроблемы со словами становятся более распространенными по мере того, как ваш ребенок продвигается вверх по классу, обычно с использованием единиц измерения, таких как метры, ярды, футы, мили, стоуны, фунты и доллары.
Вычислять доли сумм намного проще, если вы используете столбцы для представления различных частей.
Возьмем, к примеру, вопрос:
Что такое 1/6 часть 1200 метров?
Если вы хотите отработать 2/6 от 1200 м, вы просто умножите ответ для 1/6 на 2. Для 3/6 вы должны умножить его на 3.
Брусья очень хорошо подходят для учащихся кто любит видеть вещи изложенными визуально. Их можно использовать и в других областях математики — от деления, умножения, сложения и вычитания до соотношений и пропорций, а не только дробей!
Смешанные числа и неправильные дробиКогда у вас есть целое число и дробь рядом, например 1½ , это называется смешанным числом. Вы можете преобразовать это в дробь, но числитель будет больше знаменателя. В данном случае 3/2. Это называется неправильной дробью.
Сложение и вычитание дробейСкладывать и вычитать дроби с одинаковым знаменателем очень просто, так как вы просто складываете числители и сохраняете знаменатели одинаковыми.
⅛ + ⅜ = 48
Но когда у дробей разные знаменатели, их нужно сделать одинаковыми, прежде чем идти дальше.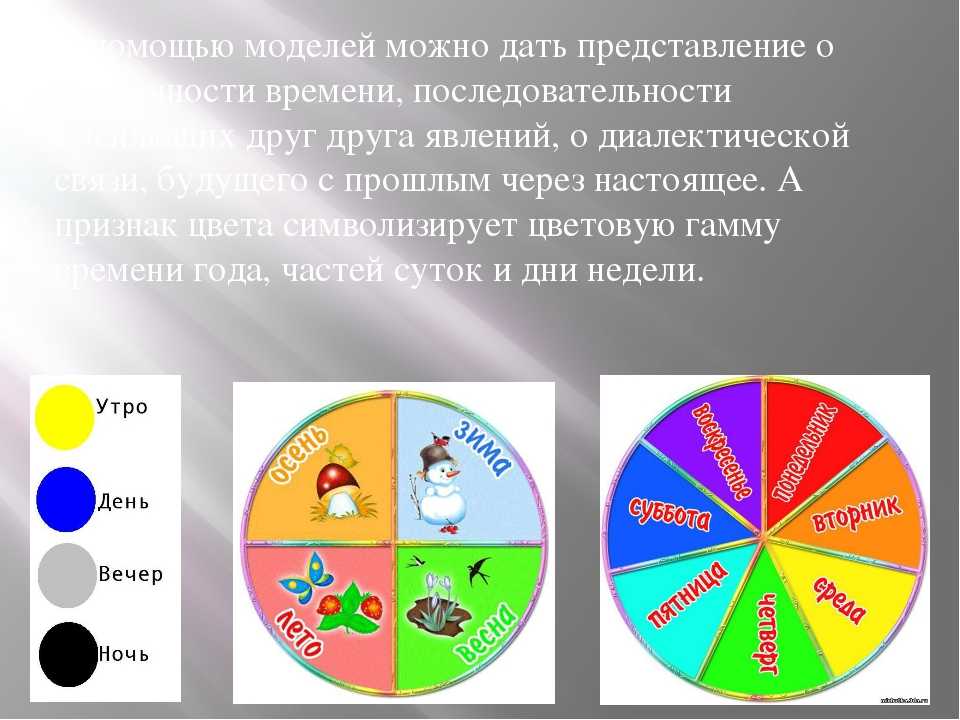
Одна из самых важных вещей, которая поможет вашему ребенку быть уверенным в себе, — это сделать разные знаменатели одинаковыми, и если это так, он будет чувствовать себя намного более уверенным в своих способностях в следующей главе работы с дробями.
Умножение правильных дробей на дробиУзнав уже очень много о дробях, знание того, как умножать дроби, относительно просто по сравнению со всеми другими процессами, которые ваш ребенок усвоил на этом этапе.
Вы просто умножаете числители, а затем умножаете знаменатели, например:
2/4 x 3/5 = 6/20
Умножение дробей на целые числаКогда вас просят умножить целое число на дробь, поначалу это выглядит немного запутанно. Например:
3 x 3/4
Чтобы решить эту пугающую проблему, вы можете начать с возвращения к бумажным полоскам, например:
Здесь важно помнить, что знаменатель остается прежним. Если это оказывается камнем преткновения, вы можете предложить лучшего друга каждого учителя математики: пиццу.
Если запомнить один простой факт, все станет намного проще.
Любое целое число можно превратить в дробь, если присвоить ему знаменатель 1.
3 = 3/1
Это потому, что 3/1 равно 3 ÷ 1, то есть 3.
Полученное уравнение решить намного проще. Просто умножьте числители вместе, а затем знаменатели вместе.
3/1 x 3/4= 9/4
Как упростить дробиПо мере закрепления основ дробей от учащихся часто требуется записывать дроби в их простейшей форме .
Это просто означает, что мы используем наименьшие возможные числа, когда вычисляем наши дроби.
Мы делаем это для простоты — это не дает нам в конечном итоге получить дроби, состоящие из огромных чисел (что может сбивать с толку).
Упрощение дробей — еще одна область, которая подчеркивает важность усвоения детьми фактов умножения.
Например, несмотря на то, что мы знаем, что 2/4 — вполне приемлемая дробь, мы упрощаем ее до 1/2, чтобы упростить задачу (используя наши знания о фактах умножения 2, следовательно, деление пополам).
Вы можете легко упростить дроби, потренировавшись в поиске наибольших общих делителей пар чисел.
Отличным методом поиска факторов являются факторные радуги, пример которых можно увидеть ниже.
Как делить правильные дроби на целые числаДеление дробей — простой процесс, если вы помните, что когда вы используете целые числа в задаче на дробь, вы можете положить это число на 1, чтобы сделать его более простым. тоже дробь, например:
3 = 3/1
Итак, если вы решаете задачу типа 3 ¾ , сначала превратите 3 в дробь.
3/1 / 3/4
Затем переверните вторую дробь (превратив ее в обратную) и измените операцию на умножение.
3/1 x 4/3
Теперь это простая задача на умножение, просто перемножьте числители и знаменатели, чтобы найти ответ.
3/1 x 4/3= 12/3
Не забудьте упростить ответ! В этом случае ответ будет смешанным числом.
12/3= 12 / 3 = 4
Дроби, десятичные дроби и проценты Дроби, десятичные числа и проценты представляют части или части целого, поэтому неудивительно, что они тесно связаны.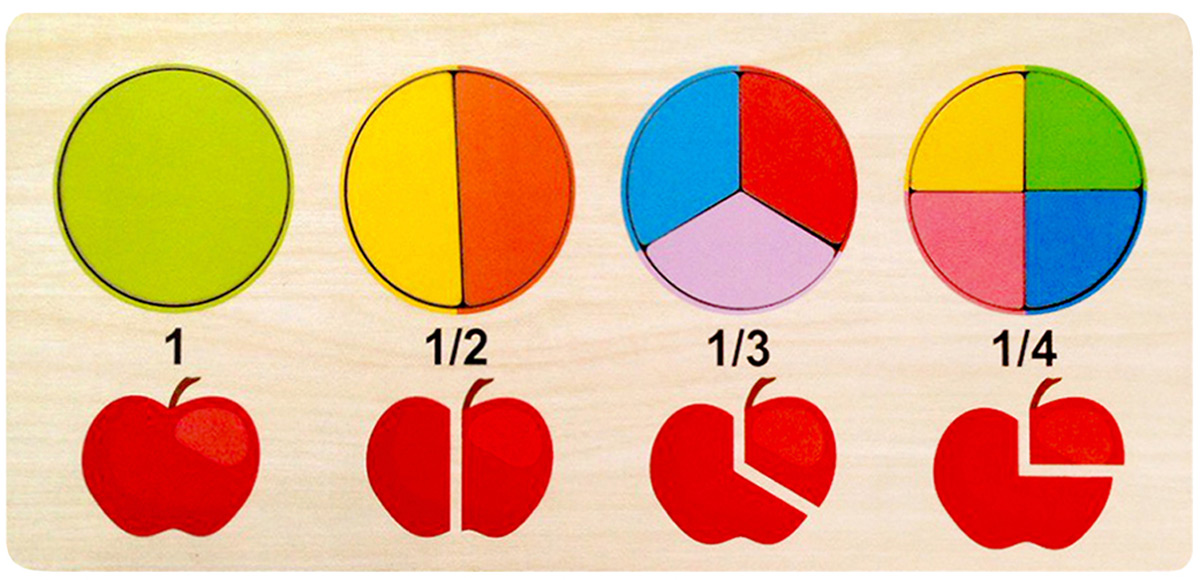
Хорошо знать, как перейти от одного к другому, особенно когда вы заказываете или сравниваете суммы.
Вот несколько полезных эквивалентов для запоминания!
Примечание… символ деления выглядит как ➗, поскольку он показывает черту дроби (или – ее собственное название – винкулум) с точками над и под ней; верхняя точка означает отсутствие числителя, а нижняя точка означает отсутствие знаменателя. Сам символ деления является постоянным напоминанием о связи между дробями и делением!
Ваш ребенок должен выучить наиболее распространенные эквиваленты наизусть и изучить стратегии нахождения общих процентов.
Например, чтобы найти 1%, нужно разделить сумму на 100 или разделить сумму на 10 и результат этого деления снова на 10.
Преобразование дробей Преобразование дробей в десятичныеРазделить числитель на знаменатель.
Если они не знают своих эквивалентов или если это более неясная дробь (что маловероятно), им следует вернуться к использованию короткого деления.
Умножьте десятичную дробь на 100. Например, 0,79 станет 79%.
Преобразование процентов в десятичные числаРазделите проценты на 100. Таким образом, 87% станут 0,87.
Преобразование процентов в дробиПоставьте процентное значение больше 100 (например, 75% = 75/100), затем упростите его – в данном случае ¾ .
Несмотря на то, что существуют письменные методы обратного преобразования десятичных дробей в дроби, на данном этапе лучше всего сосредоточиться на том, что требуется для Common Core в начальной школе по математике, и по большей части простые эквивалентности, такие как 0,25 на ¼, будут всем, что требуется (знание восьмые тоже полезны, например, 0,375 совпадает с тремя восьмыми). Учащиеся также будут много работать с преобразованием десятых и сотых долей из дробей в десятичные и десятичных дробей в дроби.
Также стоит прочитать эту статью о сравнении десятичных дробей и процентов.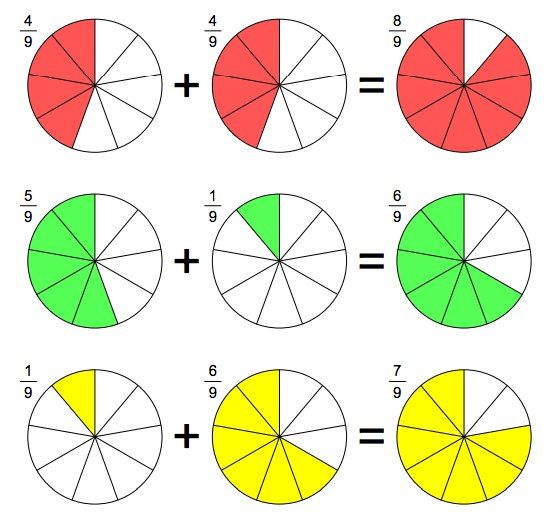
Если вы изо всех сил пытаетесь помочь ребенку понять и изучить дроби дома, помощь всегда рядом. Мы можем предоставить доступное онлайн-обучение математике, идеально соответствующее индивидуальным потребностям вашего ребенка. Если фракции нуждаются в помощи, это то, на что мы можем потратить с ними время.
Есть ли у вас ученики, которым нужна дополнительная помощь по математике?
Предоставьте своим учащимся четвертого и пятого классов больше возможностей для закрепления навыков обучения и практики с помощью индивидуального обучения элементарной математике с их собственным специализированным онлайн-репетитором.
Каждый учащийся получает дифференцированное обучение, предназначенное для устранения индивидуальных пробелов в обучении, а организованное обучение гарантирует, что каждый учащийся учится в нужном темпе. Уроки соответствуют стандартам и оценкам вашего штата, плюс вы будете получать регулярные отчеты о каждом шаге.
Программы доступны для четвертого и пятого классов, и вы можете попробовать 6 уроков абсолютно бесплатно.
Содержание этой статьи изначально было написано учителем начальных классов Софи Бартлетт, а затем было отредактировано и адаптировано для школ США учителем математики начальных классов Жаклин Вассел.
Как учить маленьких детей дробям
«Мне меньшая половинка!»
Сколько раз мы говорили это противоречивое утверждение? Из всех тем элементарной математики дроби вызывают наибольший страх как у детей, так и у взрослых. Учить дроби сложно, потому что для многих детей они представляют собой первый камень преткновения в математике. Фракции могут вести себя таким образом, который на первый взгляд кажется странным. Например, каждый ребенок знает, что 5 больше 4, поэтому он может запутаться, если ему скажут, что 1/5 меньше 1/4.
Думая о том, как познакомить вашего ребенка с дробями, важно сосредоточиться не только на правилах дробей, но и на их значении.
Понимание дробей является целью.
Чтобы понять, как объяснять детям дроби, мы подробно рассмотрим одну конкретную дробь: половину.
Что такое дробь?
Дроби используются для представления меньших частей (или частей) целого. Части могут составлять «целое», которое может быть одной вещью или более чем одной вещью. Звучит запутанно, не так ли? Давайте использовать некоторые вкусные угощения, чтобы обойти все это.
Вот плитка шоколада (ням!), разбитая на две одинаковые части. Каждая часть составляет половину от общей суммы.
Это также может быть записано как 1/2. Давайте разберем эту нотацию — предупреждение: впереди будут какие-то причудливые длинные слова!
Обучение дробям
При написании дроби полезно, чтобы ваш ребенок сначала написал знаменатель, так как это говорит нам, на сколько равных частей делится целое (например, 2 кусочка шоколада). Они могут сказать это вслух, пока пишут. Затем нарисуйте дробную черту (vinculum), которая разделяет числитель и знаменатель.
Наконец, напишите числитель, который является верхним числом в дроби. Это показывает, сколько частей у нас есть (например, 1 целая шоколадка).
Обратите внимание, как дроби строятся на простых упражнениях по счету — главное знать, что вы считаете на каждом этапе. Давайте попробуем другой пример. На этот раз наш вкусный пример включает 12 замороженных бисквитов.
Всего их 12, из них 6 розовых и 6 синих. Мы можем сказать, что 6 из 12, или 6/12, розовые. Это то же самое, что и 1/2, потому что одно из каждых двух печений розовое. Мы говорим, что 6/12 и 1/2 эквивалентны, потому что они представляют одну и ту же сумму.
Использование различных представлений
До сих пор мы использовали группы объектов для представления дробей. Мы также можем использовать длины. Вот поезд, беззаботно идущий по рельсам.
Мы можем измерить всю длину пути и сказать, что поезд прошел половину пути. В этом случае дробь 1/2 обозначает, какую часть пути проехал поезд (на каждые 2 метра, покрывающие весь путь, он прошел 1 метр).
Надеюсь, вы видите, что даже такую простую дробь, как 1/2, можно смоделировать по-разному. Когда детям предоставляется возможность визуализировать дроби (особенно более сложные) в различных ситуациях, они углубляют свое понимание того, как ведут себя эти странные объекты.
Очень скоро ваш ребенок научится распознавать «половину» в повседневных ситуациях: половина торта, полдвенадцатого, стакан наполовину полон. Ключом к пониманию дробей является встраивание их в другие повседневные действия. Еда — фантастический ресурс для фракций. Вы можете использовать кусочки макарон или сушеные бобы вместо счетчиков, а затем пусть ваш ребенок нарисует их в виде картинок, раскрашивая разные части, чтобы обозначить различные дроби.
Увлекательные способы обучения дробям по дому
Вы также можете собрать множество различных предметов по всему дому – галстук от халата, картошку, монету, книгу, стакан воды, гроздь винограда, два яблока, кусок бумаги и т. д.