Разное

Онлайн решение примеров по математике 3 класс: Please Wait… | Cloudflare

Содержание

Задачи и примеры по математике за 3 класс: тренажер по математике для 3 класса онлайн

Ваш ребенок уже перешел в третий класс, но не может похвастаться успехами в решении сложных задач? Мы рекомендуем пройти бесплатные тесты по математике за 3 класс, чтобы выявить проблемы и принять меры к их устранению. Уникальная интерактивная платформа Skills4U поможет в сжатые сроки сформировать устойчивые навыки решения примеров в рамках школьной программы.

Входное тестирование по математике за 3 класс доступно для всех и занимает совсем немного времени. Не потребуется ничего писать и выполнять дополнительные задания кроме тех, что выдает интерактивная платформа. Она анализирует ответы, выбирает правильные и генерирует примеры и задачи в соответствии с уровнем подготовки конкретного ученика.

Наши онлайн тесты по математике за 3 класс включают группу заданий на сложение и вычитание в пределах 100 и 1000, изучение единиц измерения, умножение и деление трехзначных чисел и многое другое.

Вы можете выбрать конкретную тему, которая тяжело дается вашему ребенку, или пройтись по всей школьной программе. В результате тестирования будет поставлена оценка и выведен общий рейтинг.

Но для получения устойчивых навыков, недостаточно просто пройти тест по математике (3 класс), необходимо закрепить пройденный материал, повторив занятие в течение ближайших дней. После получения результатов тестирования система предоставит рекомендации и напомнит, когда следует вновь решить задачи для 3 класса по математике, тренажер при этом не будет полностью повторять задания, ориентируясь на качество ответов.

Мы предлагаем выбрать один из вариантов доступа, который предоставляет комплексный тренажер по математике за 3 класс. Ваш ребенок может тренироваться самостоятельно или под вашим присмотром в течение 1 месяца, полугода или целого календарного года – в этом случае доступ предоставляется на 12 месяцев. Цены вполне умеренные. Результат вас порадует, а школьника заставит поверить в свои силы.

Используйте интеллектуальный тренажер по математике для 3 класса, чтобы улучшить усвоение школьной программы и повысить успеваемость вашего ребенка. Всего 30-40 минут ежедневно могут принести потрясающий результат. Интерактивная платформа Skills4U позволяет прокачать навыки решения задач и примеров различной сложности благодаря продуманному алгоритму, учитывающему индивидуальные особенности ученика и его уровень подготовки.

Как решить уравнение 3 класса онлайн

Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. В 3 классе школьники учатся решать разнообразные простые уравнения с неизвестными методом перебора с учетом связи членов действиями вычитания/сложения. Для решения таких уравнений главное выучить приоритетность выполнения арифметических операций.

Допустим, дано уравнение следующего вида:

\[64 + d = 82\]

Так же читайте нашу статью “Решить уравнения 3 степени онлайн решателем”

В данном уравнении выполняется такая арифметическая операция как сложение двух чисел, одно из которых неизвестное. Оперируя правилом, которое гласит о том, что чтобы найти неизвестное слагаемое необходимо из суммы вычесть известное слагаемое. Выполним это, сделав перенос неизвестной переменной в левую часть, а числа в правую:

\[d = 82 – 64 \]

Выполнив вычитание, мы получим результат решения нашего уравнения:

\[d = 18\]

Если мы подставим \[18\] на место \[d\] в исходное уравнение, то мы увидим, что левая и правая сторона имеют одинаковое значение, что говорит о правильности полученного ответа.

Где можно решить уравнение онлайн с решением 3 класс?

Решить уравнение вы можете на нашем сайте https://pocketteacher. ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать – это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

Решение задач онлайн

Решение Ваших математических задач в онлайн режиме. Бесплатная версия программы предоставляет Вам только ответы. Если вы хотите увидеть полное решение, Вы должны зарегистрироваться для бесплатной полной пробной версии.

Другие программы

Основы математики

Онлайн программа решения математических задач предлагает Вам решение в режиме онлайн задач с дробями, корнями, метрическими преобразованиями.
Вы можете найти площадь и объем прямоугольника, окружности, треугольника, трапеции, куба, цилиндра, конуса, пирамиды, шара.
Вы можете упростить, найти значение, объединять и умножать выражения.

Онлайн программа решения задач курса предварительной алгебры (геометрии)

Вы можете решать все задачи с основного раздела математики а также координатных задач, простых уравнений, неравенств, упрощать выражения.
Вы можете подсчитывать выражения, объединить выражения и умножать / делить выражения.

Онлайн программа решения задач по алгебре

Мы рекомендуем Вам зарегистрироваться для этой онлайн программы.
Решите Ваши задачи (уравнения, неравенства, радикалы, построение графиков, решение полиномов) в онлайн режиме.
Если Ваша домашняя работа включает в себя математические уравнения, неравенства, функции, многочлены, матрицы, значит регистрация для тестовой версии – это правильный выбор.

Онлайн программа решения задач по тригонометрии

Находит значения всех типов выражений (синус, косинус, тангенс, котангенс, секанс, косеканс), уравнений, неравенств.
Строит графики тригонометрических функций.
Тригонометрия прямоугольного треугольника.

Онлайн программа решения задач курса предварительной алгебры

Включает в себя все вышеперечисленное функции плюс нахождение пределов (LIM), сумм, матриц.

Онлайн программа решения задач курса высшей математики

Решение задач c определенными, неопределенными интегралами.

Онлайн программа решения статистических задач

Решайте задач с нахождением вероятности, комбинаторные задачи. Статистические задачи – найти среднее (арифметическое, геометрическое, квадратическое) значение, распределение, нормальное распределение, т-распределение.
Онлайн программа успешно проводит тестирование статистических гипотез

Задачи по математике 3 класс.

Страница 1, 2, 3


Задача 1.

Для приготовления обеда повару понадобилось 24 кг картошки, свеклы в 3 раза меньше, а лука в 2 раза меньше чем свеклы. Сколько килограмм лука потратил повар?

    Решение:
  • 1) 24 : 3 = 8
  • 2) 8 : 2 = 4
  • Выражение: 24 : 8 : 2 = 4
  • Ответ: 4 кг.

Задача 2

Оля вырезала из бумаги 5 квадратов, 7 треугольников, а кругов в 2 раза больше чем треугольников. Сколько всего Оля вырезала фигур?

    Решение:
  • 1) 7 * 2 = 14
  • 2) 5 + 7 + 14 = 26
  • Ответ: 26 фигур.

Задача 3

Первое число 12, второе в 3 раза меньше, а третье в 4 раза больше чем второе. Вычисли сумму этих трех чисел.

    Решение:
  • 1) 12 : 3 = 4 (второе число)
  • 2) 4 * 4 = 16 (третье число)
  • 3) 12 + 4 = 16 (сумма первого и второго чисел)
  • 4) 16 + 16 = 32 (сумма трех чисел)
  • Выражение: 12 : 3 * 4 + 4 + 12 = 32
  • Ответ: 32


Задача 4

В школьную столовую привезли 6 кг, лимонов, яблок на 24 кг больше чем лимонов, а груш на 12 кг меньше чем яблок. Сколько килограмм груш привезли в школьную столовую?

    Решение:
  • 1) 6 + 24 = 30 (в столовую привезли яблок)
  • 2) 30 – 12 = 18 (привезли груш)
  • Выражение: (6 + 24) – 12 = 18
  • Ответ: 18 кг груш привезли в столовую.

Задача 5

Для приготовления обеда повару понадобилось 24 кг картошки, свеклы в 3 раза меньше, а лука в 2 раза меньше чем свеклы. Сколько килограмм лука потратил повар?

    Решение:
  • 1) 24 : 3 = 8 (понадобилось свеклы)
  • 2) 8 : 2 = 4 (понадобилось лука)
  • Выражение: 24 : 3 : 2 = 4
  • Ответ: 4 кг лука понадобилось повару.

Задача 6

Для приготовления крахмала требуется 6 кг картошки. Сколько крахмала получится из 36 кг картофеля?

    Решение:
  • 1) 36 : 6 = 6
  • Ответ: 6 кг крахмала.

Задача 7

В поход пошли 24 мальчика, а девочек в 3 раза меньше, чем мальчиков. Сколько всего детей пошло в поход?

    Решение:
  • 1) 24 : 3 = 8 (девочек пошло в поход)
  • 2) 24 + 8 = 32
  • Выражение: 24 : 3 + 8 = 32
  • Ответ: 32.


Задача 8

Ящик с виноградом и три одинаковых ящика с яблоками весят 45 кг. Сколько весит один ящик с яблоками, если ящик с виноградом весит 15 кг.

    Решение:
  • 1) 45 – 15 = 30 (весят 3 ящика с яблоками)
  • 2) 30 : 3 = 10 (весит один ящик с яблоками)
  • Выражение: (45 – 10) : 3 = 10
  • Ответ: 10 кг.

Задача 9

На детской площадке катались дети на двух и трехколесных велосипедах. Сколько и каких велосипедов было на площадке, если всего было 21 колесо и 8 велосипедов?

    Решение:
  • 1) 8 * 2 = 16 (было бы колес, если бы все велосипеды были двухколесными)
  • 2) 21 – 16 = 5
  • 2) 8 – 5 = 3
  • Ответ: на площадке было 5 трехколесных велосипедов и 3 двухколесных.

Задача 10

В парке выкорчевали 6 орешников, а вместо них посадили 18 орешников. Во сколько раз больше посадили орешников, чем выкорчевали?

    Решение:
  • 1) 18 : 6 = 3
  • Ответ: в 3 раза больше орешников посадили.

Задача 11

Отцу 36 лет, а сыну 9. Во сколько раз отец старше сына и на сколько лет сын моложе отца?

    Решение:
  • 1) 36 : 9 = 4
  • 2) 36 – 9 = 27
  • Ответ: в 4 раза сын моложе отца; на 27 лет отец старше сына.

Задача 12

Автобус за 8 часов работы расходует 48 литров топлива. Сколько литров топлива израсходует автобус за 6 часов работы?

    Решение:
  • 1) 48 : 8 = 6 (литров топлива автобус расходует за 1 час)
  • 2) 6 * 6 = 36 (литров автобус расходует за 6 часов)
  • Выражение: 48 : 8 * 6 = 36
  • Ответ: 36 литров.

Задача 13

В столовую привезли абрикосы. Из них на компот взяли 3 килограмма, а на варенье в 3 раза больше. Сколько всего абрикос привезли в столовую?

    Решение:
  • 1) 3 * 3 = 9 (взяли абрикос на варенье)
  • 2) 3 + 9 = 12 (всего в столовую привезли абрикос)
  • Выражение: 3 * 3 + 3 = 9
  • Ответ: 9 кг абрикос.

Страница 1, 2, 3

Все онлайн калькуляторы для решения задач · Контрольная Работа РУ · Теперь вы можете задать любой вопрос!

Кусочно-заданная функция

Укажите кусочно-заданную функцию и перейдите к нужному вам сервису, например, к одному из: нахождению интеграла, производной, исследованию и построение графика и др.

Решение уравнений

Это сервис позволяет решать уравнения, в том числе получить подробное решение, а также увидеть решение уравнения на графике.

Решение пределов

Этот сервис позволяет найти предел функции. Также рассматривается подробное решение правилом Лопиталя.

Производная функции

Это сервис, где можно вычислить производную функции, частную производную функции, а также производную неявно заданной функции.

Разложение в ряд

Здесь можно выполнить разложение в ряд Тейлора, Фурье, найти сумму ряда.

Системы уравнений

Позволяет решать системы линейных уравнений методом Крамера, методом Гаусса, а также вообще любые системы уравнений.

Решение неравенств

Решает неравенство, а также изображает решённое неравенство на графике.

Решение интегралов

Это сервис, где можно вычислить определённые, неопредёленные интегралы, а также двойные, несобственные, кратные.

График функции

Это сервис построения графиков на плоскости и в пространстве. Приводится подробное решение на исследование функции.

Решение систем неравенств

Вы можете попробовать решить любую систему неравенств с помощью данного калькулятора систем неравенств.

Онлайн уроки по математике для третьего класса

Таблица умножения. Решение задач.

Учимся математике.

Определение объема знаний

Таблица умножения на 2 и 3. Решение примеров и задач.

Таблица умножения. Решение примеров и задач.

Безударные гласные в корне слова.

Умножение трехзначных чисел на однозначное число. Умножение и деление круглых чисел.

Геометрия начальный уровень

Умножение и деление. Решение примеров и задач.

Умножение и деление.

Решение примеров и задач. Повторение.

Решение примеров, задач и уравнений.

Единицы длины. Решение задач и примеров.

Час. Минута. Длина ломаной. Порядок выполнения действий.

Множество и подмножество.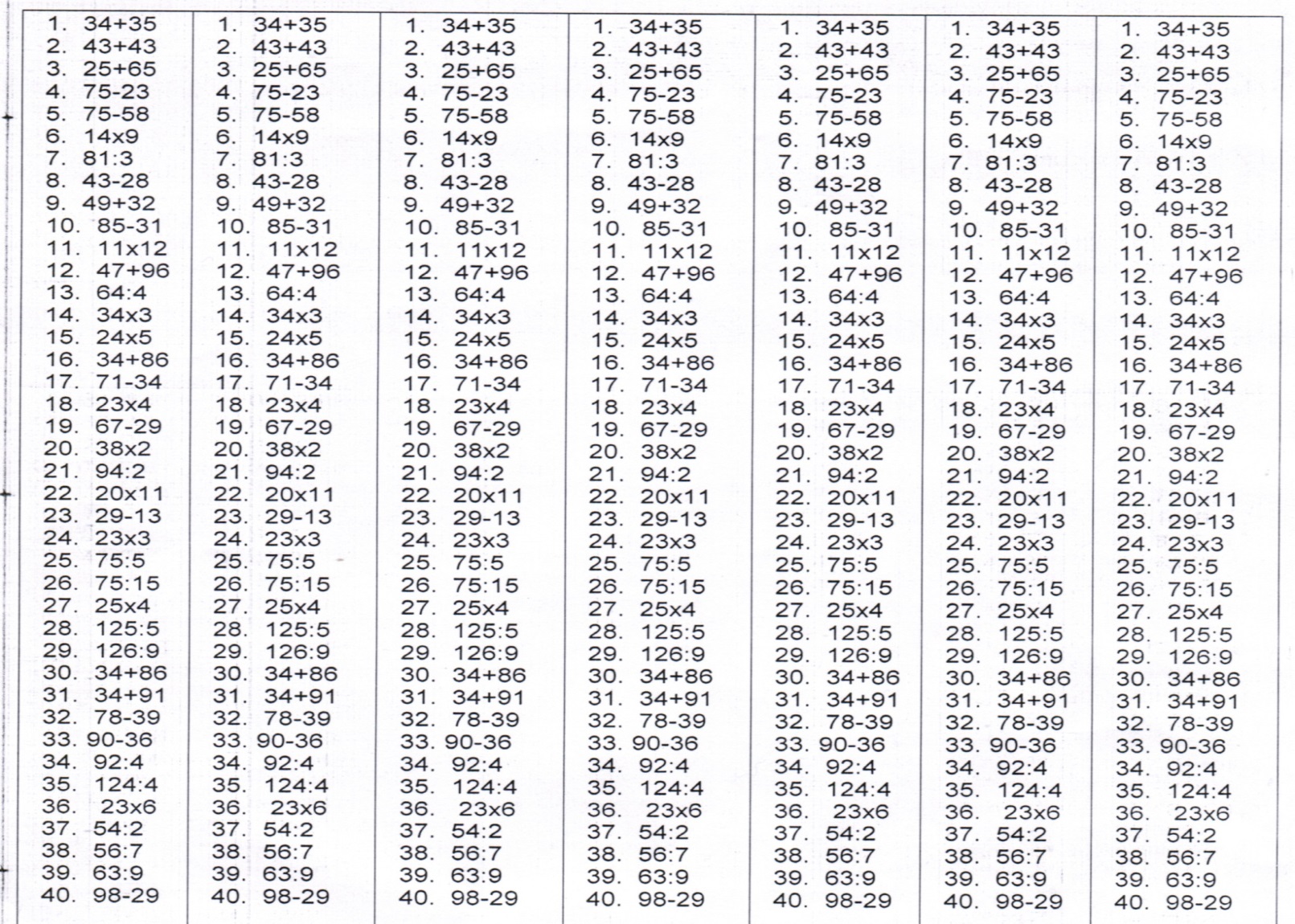

Обозначение геометрических фигур буквами. Повторение и закрепление изученного материала.

Решение задач, примеров, уравнений. Обозначение геометрических фигур буквами. Периметр треугольника.

Обратные задачи. Повторение и закрепление пройденного материала.

Табличное умножение и деление. Таблица умножения на 5.

Числа от 1 до 100. Сложение и вычитание. Решение задач и уравнений.

Числа от 1 до 100. Сложение и вычитание.Решение задач.

Помощь в домашнем задании

Числа от 11 до 100. Десятки и единицы. Однозначные и двузначные числа.

Числа от 1 до 100. Десяток. Счет десятками до 100.

Числа от 1 до 20.

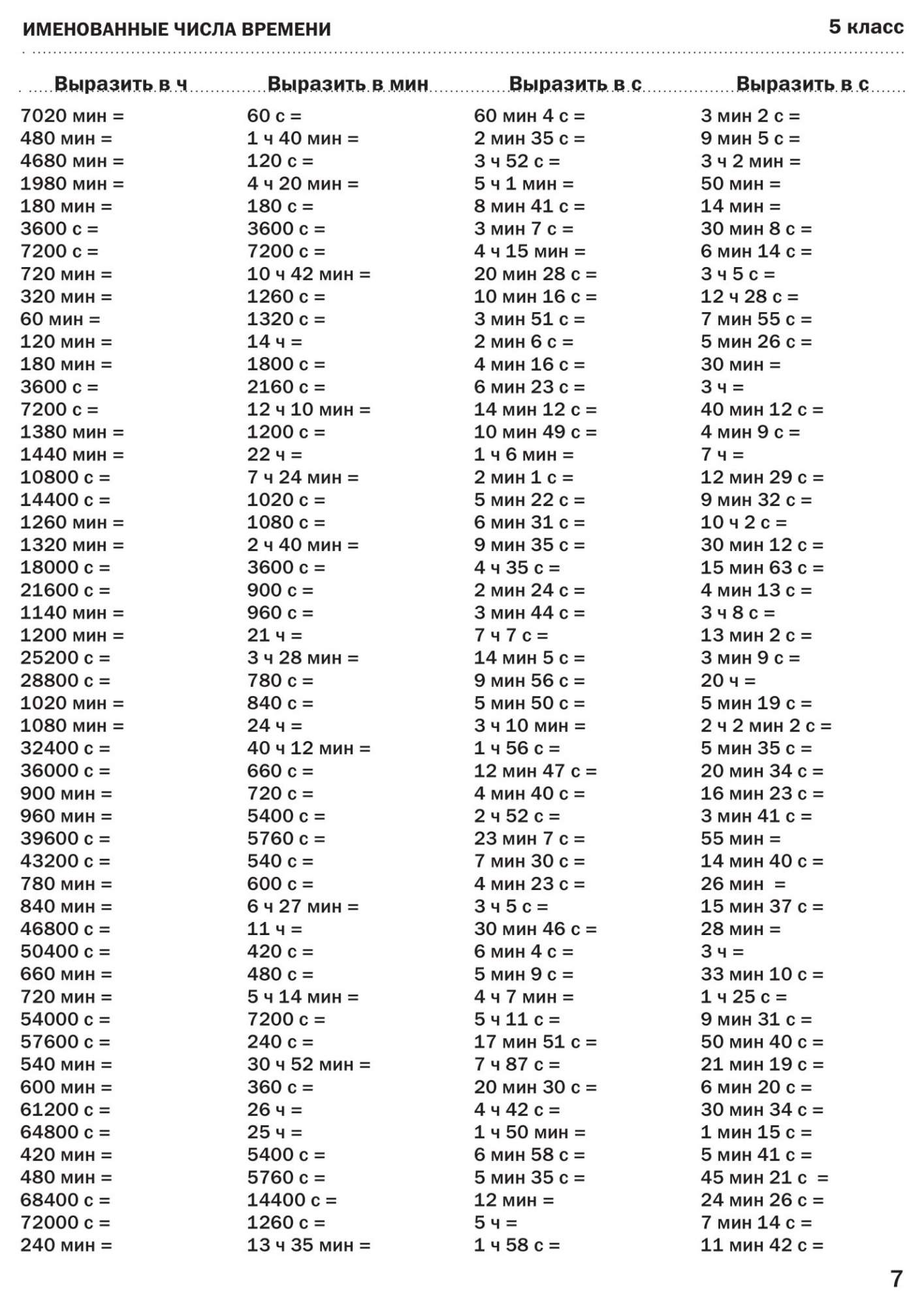
Калькулятор онлайн – Решение показательных уравнений

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать. n} \)

6) an > 0

7) an > 1, если a > 1, n > 0

8) anm, если a > 1, n

9) an > am, если 0

В практике часто используются функции вида y = ax, где a – заданное положительное число, x – переменная. Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.

Определение. Показательной функцией называется функция вида y = ax, где а — заданное число, a > 0, \( a \neq 1\)

Показательная функция обладает следующими свойствами

1) Область определения показательной функции — множество всех действительных чисел.
Это свойство следует из того, что степень ax где a > 0, определена для всех действительных чисел x.

2) Множество значений показательной функции — множество всех положительных чисел.
Чтобы убедиться в этом, нужно показать, что уравнение ax = b, где а > 0, \( a \neq 1\), не имеет корней, если \( b \leqslant 0\), и имеет корень при любом b > 0.

3) Показательная функция у = ax является возрастающей на множестве всех действительных чисел, если a > 1, и убывающей, если 0 Это следует из свойств степени (8) и (9)

Построим графики показательных функций у = ax при a > 0 и при 0 Использовав рассмотренные свойства отметим, что график функции у = ax при a > 0 проходит через точку (0; 1) и расположен выше оси Oх.
Если х x при a > 0.
Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.

График функции у = ax при 0 Если х > 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её). Таким образом, ось Ох является горизонтальной асимптотой графика.
Если х

Показательные уравнения

Рассмотрим несколько примеров показательных уравнений, т. е. уравнений, в которых неизвестное содержится в показателе степени. Решение показательных уравнений часто сводится к решению уравнения ax = ab где а > 0, \( a \neq 1\), х — неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием а > 0, \( a \neq 1\) равны тогда и только тогда, когда равны их показатели.

Решить уравнение 23x • 3x = 576
Так как 23x = (23)x = 8x, 576 = 242, то уравнение можно записать в виде 8x • 3x = 242, или в виде 24x = 242, откуда х = 2.
Ответ х = 2

Решить уравнение 3х + 1 – 2 • 3x – 2 = 25
Вынося в левой части за скобки общий множитель 3х – 2, получаем 3х – 2(33 – 2) = 25, 3х – 2 • 25 = 25,
откуда 3х – 2 = 1, x – 2 = 0, x = 2
Ответ х = 2

Решить уравнение 3х = 7х
Так как \( 7^x \neq 0 \) , то уравнение можно записать в виде \( \frac{3^x}{7^x} = 1 \), откуда \( \left( \frac{3}{7} \right) ^x = 1 \), х = 0
Ответ х = 0

Решить уравнение 9х – 4 • 3х – 45 = 0
Заменой 3х = t данное уравнение сводится к квадратному уравнению t2 – 4t – 45 = 0. {x-2} = 1 \)
x – 2 = 0
Ответ х = 2

Решить уравнение 3|х – 1| = 3|х + 3|
Так как 3 > 0, \( 3 \neq 1\), то исходное уравнение равносильно уравнению |x-1| = |x+3|
Возводя это уравнение в квадрат, получаем его следствие (х – 1)2 = (х + 3)2, откуда
х2 – 2х + 1 = х2 + 6х + 9, 8x = -8, х = -1
Проверка показывает, что х = -1 — корень исходного уравнения.
Ответ х = -1

Решение задач: 3 класс по математике

    Приборная панель

    Математика 3 класс

    Решение проблем

    Перейти к содержанию Приборная панель

    • Авторизоваться

    • Панель приборов

    • Календарь

    • Входящие

    • История

    • Помощь

    Закрывать