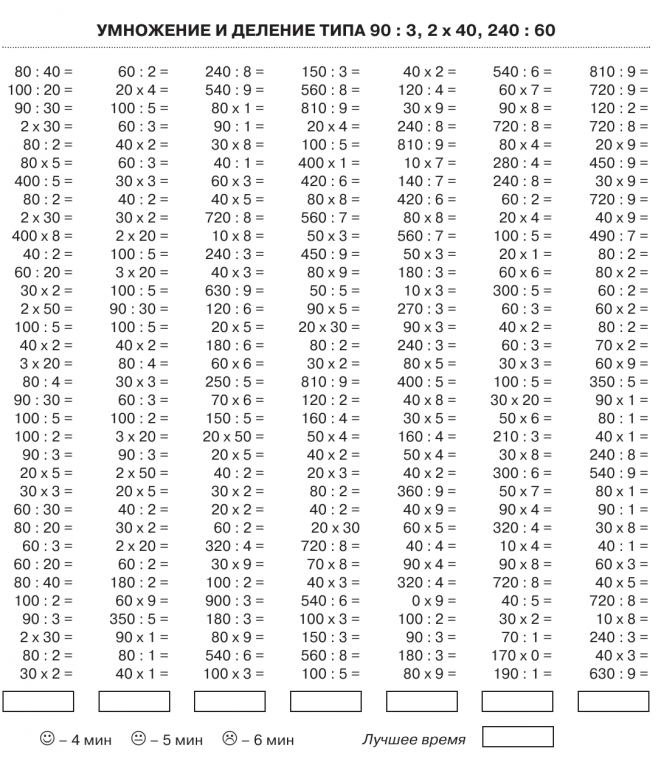
Онлайн решать примеры 4 класс: Тесты по математике для 4 класса онлайн
Домашняя онлайн-школа 4 класс | Онлайн-лицей
Перейти к содержанию
Записаться
Четвертый класс – первый серьезный рубеж в школьной жизни ребенка, момент окончания начальной ступени образования. Здесь очень важно не только углубить и закрепить все необходимые знания, но и сделать так, чтобы процесс первого серьезного испытания в учебе прошел в комфортной обстановке, без стресса. Домашняя онлайн-школа для учеников 4 класса поможет обеспечить и то, и другое. Онлайн-школа — не просто альтернатива привычной классно-урочной системе обучения: она вобрала в себя все преимущества дистанционного обучения. В онлайн-школе ученик занимается самостоятельно, в том темпе, который подходит именно для него, в комфортном месте и в удобное время. При этом домашняя школа обеспечивает индивидуальный подход к каждому учащемуся, делая учебный процесс максимально эффективным. Школа дистанционного обучения в 3 классе вобрала в себя все преимущества классно-урочной и онлайн-систем образования:
- Наши программы полностью соответствуют всем требованиям федеральных образовательных государственных стандартов.

- В уроках мы широко используем разные способы подачи информации – специально разработанные для курса школы дистанционного обучения в 4 классе видеоуроки и электронные учебники.
- Познакомившись с материалами новой темы, ученик проходит тест, который позволяет выявить уровень освоения программы, и выполняет домашнее задание, которое проверяется преподавателем.
- Весь процесс обучения в домашней онлайн-школе сопровождает персональный куратор. Обучающиеся школы дистанционного обучения имеют доступ к еженедельным онлайн-консультациям со всеми преподавателями.
- Обучающийся имеет возможность изучать материалы программы в любое удобное для него время, в любом месте и в том темпе, который комфортен именно для него, без оглядки на школьные уроки и перемены.
Стоимость обученияВопросы родителей
Посмотрите это видео, чтобы узнать, как работает наша Онлайн-школа
- Видеоуроки
- Электронный учебник
- Тесты
- Домашние задания
- Онлайн-занятия
- Личный кабинет
- Поддержка куратора
Видеоуроки
Пример видеоурока по математике
Электронный учебник
Пример учебника физики
Тесты
Пример задания из теста по математике
Домашние задания
Проверка домашнего задания
Онлайн-занятия
Скрин онлайн-занятия по математике
Личный кабинет
Внешний вид личного кабинета
Поддержка куратора
Пример общения с куратором
Продолжается набор на 2022/23 учебный год в 1-11 классы
Скидка 50% на первый месяц обучения при оплате до 28 апреля. Начните обучение уже сегодня!
Записаться
Вверх
Как решать задачи на магические квадраты в 4-5 классе. Как составлять магические квадраты
Магическая константа M – сумма чисел в каждой строке, столбце и на диагоналях.
Для квадрата любой размерности n∙n минимальная магическая константа вычисляется по следующей формуле:
M = n(n2 + 1)/2
I. Магический квадрат 3×3
Для квадрата размера 3×3 минимально возможная магическая константа будет равна:
3(32 + 1)/2 = 3(9 + 1)/2 = 15
Подчеркнём, что 15 – это не единственно возможная магическая константа для квадрата 3×3, а константа, меньше которой других констант для этого квадрата быть не может.
Важное правило, которое вам пригодится при построении магического квадрата 3×3:
Число в центре квадрата 3×3 всегда в три раза меньше магической константы.
То есть, если у нас магическая константа M = 15, то в центре квадрата 3×3 будет стоять
15:3 = 5.
Для дальнейшего составления магического квадрата с магической константой M=15 расставьте по углам чётные числа 2,4,8,6.
Как видим, по сумма чисел на диагоналях квадрата равна 15, то есть магической константе.
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
Зная магическую константу и по два числа в ряду и столбце, мы можем вписать третье число в ряд и столбец. Определить это число очень просто – надо из магической константы вычесть два числа из ряда или столбца.
Применив этот метод, мы получим полностью заполненный магический квадрат:
Ещё одно важное правило построения магических квадратов:
Если у нас есть один магический квадрат, и мы все числа этого квадрата увеличим на одно и то же число или умножим на одно и то же число, то у нас опять получится квадрат. Это правило достаточно очевидно.
Пример 1. К числам в нашем магическом квадрате с M=15 прибавим 3 и 5
Как видим, у первого квадрата сумма чисел по вертикали, горизонтали и диагонали одинакова и составляет 24 (это и есть его магическая константа), а у второго квадрата магическая константа равна 30.
У этих двух квадратов число в центре по прежнему в три раза меньше, чем магическая константа (8 у первого квадрата и 10 у второго).
Пример 2. Числа нашего магического квадрата с M=15 умножим на 2 и на 3
Как видим, в первом случае, после умножения чисел на два, мы получили квадрат с магической константой 30 – та же самая константа, что и после того, как в первом примере мы увеличили все числа на 5. Но при этом, несмотря на то, что у этих двух магических квадратах одинаковые магические константы, числа при этом в клетках разные – а вот число в центральном квадрате одно и то же – это 10.
Так и должно быть, ведь, как было сказано выше, в магическом квадрате 3×3 число в центральной клетке должно быть в три раза меньше магической константы. Т.к. магическая константа у обеих магических квадратов одинаковая, то и центральное число одно и то же.
Задача 1.
Постройте магический квадрат с магической константой 39.
Зная магическую константу, мы легко найдём число, которое должно быть в центральной клетке – нужно магическую константу разделить на 3. 39:3 = 13.
Далее можно или подбирать числа (помня о том, что сумма чисел по диагонали, по горизонтали и по вертикали должна быть равна магической константе) или, для ускорения процесса, воспользоваться знанием чисел магического квадрата с минимальной магической константой M = 15.
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
Напомним этот квадрат:
В центре этого квадрата – число 5. В центре того квадрата, который мы должны построить – число 13.
Разница между этими числами составляет 8. И, как следует из правила, которое мы написали выше, если все числа одного магического квадрата увеличить на одно и то же число, то получится другой магический квадрат.
Достаточно запомнить, что в центре минимального магического квадрата – 5, а по углам – чётные числа 2, 4, 6, 8. Таким образом, нам надо увеличить эти числа на 8. Далее будет легко заполнить оставшиеся клетки (числа в них вычисляются как магическая константа минус числа в ряду или столбце).
Таким образом, нам надо увеличить эти числа на 8. Далее будет легко заполнить оставшиеся клетки (числа в них вычисляются как магическая константа минус числа в ряду или столбце).
В итоге получится вот такой квадрат:
Задача 2.
Достройте магический квадрат
В этом квадрате мы знаем число в центральной клетке (9), а, значит, мы знаем магическую константу, которая в 3 раза больше и равна 27. Ну а зная магическую константу и три первоначальных числа, вписать оставшиеся числа в клетки не составит труда.
Решение:
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
II. Магический квадрат 4×4
Мы не будем подробно останавливаться на магических квадратах 4×4 – они почти не встречаются на математических олимпиадах и вступительных экзаменах в физматшколы, но общее представление о них дадим.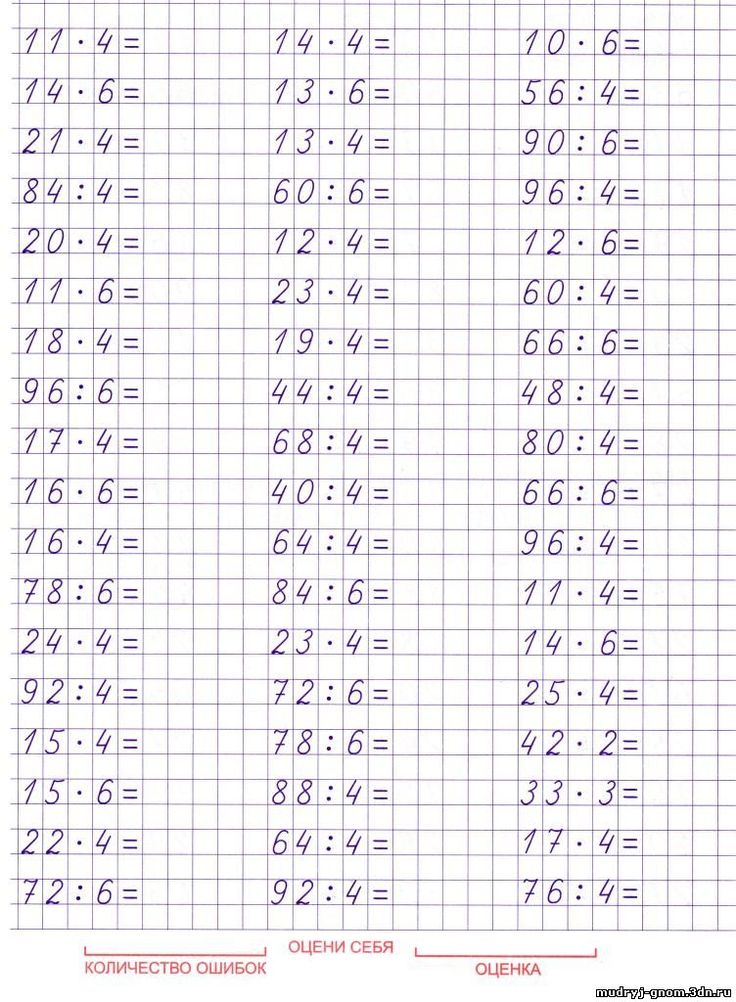
Минимально возможная магическая константа вычисляется всё по той же формуле:
M = n(n2 + 1)/2
M = 4(42 + 1)/2 = 34.
У квадрата 4×4 обе стороны чётные, а это значит, что центральной клетки, в отличие от квадрата 3×3, у него нет, и нет соответствующей закономерности, с ним связанной.
Однако, у этого квадрата есть другие закономерности:
Помимо того, что у магического квадрата 4×4 равна сумма числе по диагонали, вертикали и горизонтали, у него сумма чисел в угловых квадратах 2×2 равна магической константе M, сумма чисел в центральном квадрате 2×2 также равна M, и сумма чисел в углах квадрата тоже равна M.
Сумма чисел в левом верхнем квадрате 2×2: 16+3+5+10 = 34. В трёх других угловых квадратах 2×2 сумма также равна магической константе, о чём и сказано выше.
Сумма чисел в центральном квадрате 2×2 также равна магической константе 34: 10+11+6+7 = 34.
Сумма чисел в углах магического квадрата тоже равна магической константе: 16+13+4+1 = 34
Word Problems Games for 4-Classers Online
Обычно задачи из учебника по математике сосредоточены на числах и не подготавливают вашего ребенка к реальным задачам. С онлайн-играми вы можете предоставить им прекрасный образовательный опыт на всю жизнь. Посетите этот блог, чтобы узнать, как игры со словами могут улучшить процесс обучения вашего ребенка.
С онлайн-играми вы можете предоставить им прекрасный образовательный опыт на всю жизнь. Посетите этот блог, чтобы узнать, как игры со словами могут улучшить процесс обучения вашего ребенка.
Пандемия COVID-19 научила нас тому, что проблемы могут возникнуть в любой момент, и нужно уметь сохранять спокойствие перед лицом невзгод. С помощью обучающих онлайн-игр вы можете передать этот жизненный урок своим детям, научив их тому, что ничто не может помешать их образованию.
Когда вы предоставляете своим малышам увлекательный способ освоить такой сложный предмет, как математика, это помогает им стать увереннее в себе.
Словесные задачи состоят из нескольких предложений, которые объясняют реальную ситуацию, когда задачу необходимо решить с помощью математических вычислений. Давайте перейдем к следующим разделам, чтобы узнать больше о текстовых задачах.
Что такое словесные задачки? Словесные задачи, такие как «Умножение дробей на целое», — это популярные игры, которые проверят понимание вашего ребенка и помогут ему улучшить свои математические навыки. В этой игре перед ребенком будут поставлены задачи, например, если для приготовления рецепта требуется X количества данного ингредиента, ребенку необходимо вычислить долю ингредиента в каждой порции.
В этой игре перед ребенком будут поставлены задачи, например, если для приготовления рецепта требуется X количества данного ингредиента, ребенку необходимо вычислить долю ингредиента в каждой порции.
Несколько словесных задач на сложение, вычитание, умножение и деление денег, которые познакомят вашего ребенка с миром финансов.
Игры охватывают задачи с десятичными дробями, тем самым давая вашему ребенку целостное понимание основных математических понятий. К проблемным играм относятся те, в которых ребенка просят подсчитать общую сумму денег, когда у него изначально было X-сумма, и он потратил Y-сумму из этой суммы.
Некоторые образовательные веб-сайты, такие как SplashLearn, используют забавный подход к обучению математике. Существуют аддитивные и мультипликативные игры со сравнением слов, которые включают сложение и умножение соответственно, чтобы найти неизвестное значение.
Такие игры, как «Умножение дробей на целые», позволяют ребенку практиковать свои навыки, не осознавая, что кто-то оценивает их результаты.
Проблемы со словами часто вызывают беспокойство у младших школьников, и дети часто боятся таких тем. Основная проблема детей заключается в том, что они не понимают языка словесных проблем.
Стратегии поддержки вашего ребенка- Онлайн-игры дадут детям достаточную практику, и в кратчайшие сроки ваш ребенок научится решать проблемы. Эти игры позволяют убедиться, что ваш ребенок в курсе своей кривой обучения.
- Так как ваш ребенок будет получать удовольствие от игры, он захочет делать это дольше. Таким образом, у них будет больше времени на изучение концепций и они станут лучше учиться.
- Когда дети развлекаются, решая задачи со словами, они выясняют, как определять ключевые слова в формулировках задачи, чтобы оценить ожидания. Когда они успешно решают задачу с одним словом за другой, это укрепляет их уверенность.
SplashLearn — это онлайн-платформа, которая помогает вашему ребенку сосредоточиться на аналитической стороне математики.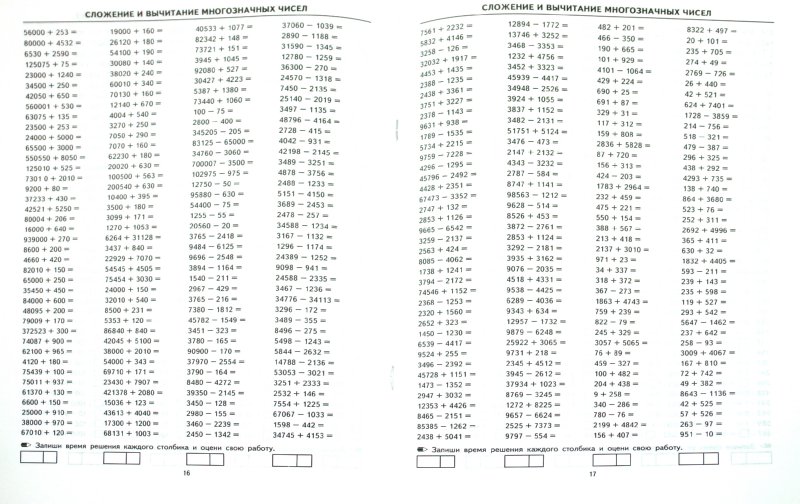 Таким образом, основное внимание уделяется обучению, а не успеваемости ребенка. Тема не кажется однообразной, и ребенок будет более восприимчив к понятиям.
Таким образом, основное внимание уделяется обучению, а не успеваемости ребенка. Тема не кажется однообразной, и ребенок будет более восприимчив к понятиям.
Как вы помогаете своему ребенку в процессе обучения, чтобы сделать его увлекательным? Пишите нам по адресу [email protected] с вашими отзывами и комментариями.
Предложено Текстовые задачи Рабочие листы
Просмотреть все 97 Рабочие листы
Универсальное решение для всех учебных потребностей в классе.
Дайте вашему ребенку страсть и уверенность, чтобы безбоязненно учиться чему-либо самостоятельноРодители, зарегистрируйтесь бесплатно
Учителя, используйте бесплатно
4413+
4567+
Департамент образования штата Орегон: задачи по решению математических задач 3–8 классы: основные навыки: штат Орегон
Перейти к основному содержанию
Официальный сайт штата Орегон.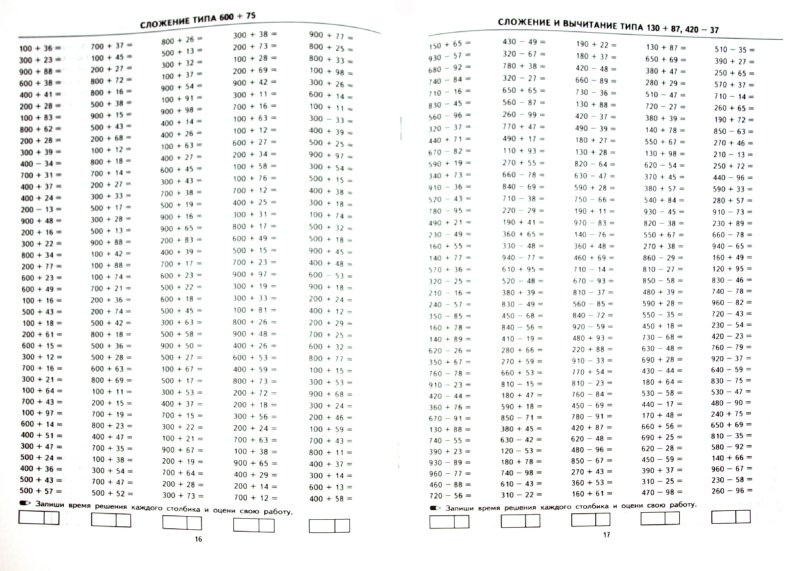 Учиться
Откуда ты знаешь ”
(как определить веб-сайт Oregon.gov)
Официальный сайт штата Орегон »
Учиться
Откуда ты знаешь ”
(как определить веб-сайт Oregon.gov)
Официальный сайт штата Орегон »
Поиск
Требование к оценке результатов на местном уровне
Образцы работ будут более эффективно способствовать обучению учащихся, если они систематически интегрируются в учебную программу округа, а также являются частью обучения в классе (то есть в обычном процессе непрерывной оценки и выставления оценок). Например, когда они используются для подведения итогов учебного модуля или расширения представленных концепций, образцы работ могут стать естественной частью занятий в классе и предлагаться много раз в течение учебного года.