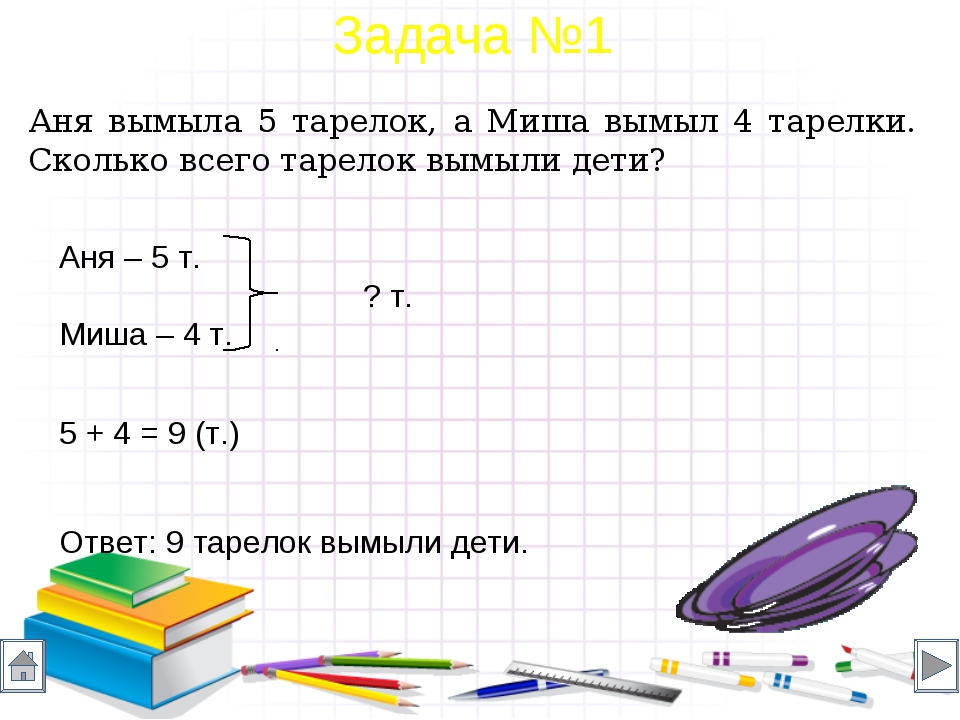
Оформление задач по математике 2 класс: Краткая запись условия задач в 1-4 классе начальной школы
Краткие записи задач для 2 класса по программе “Школа России” | Материал по математике (2 класс) на тему:
МБОУ «СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА
С УГЛУБЛЕННЫМ ИЗУЧЕНИЕМ ОТДЕЛЬНЫХ ПРЕДМЕТОВ
№ 55 имени АЛЕКСАНДРА НЕВСКОГО» г. Курска
ПАМЯТКА
ДЛЯ РЕШЕНИЯ ПРОСТЫХ И СОСТАВНЫХ ЗАДАЧ
ДЛЯ УЧАЩИХСЯ 2 КЛАССА
(программа «Школа России)
Составила:
преподаватель начальных классов
Э.С. Бобрышева
КУРСК 2016 г.
Простые задачи
1. В одной коробке 10 карандашей, а в другой – 6 карандашей. Сколько всего карандашей в двух коробках?
Ιк.–10 к.
ΙΙк.–6 к.
10+6=16(к.)
Ответ: 16 карандашей в двух коробках.
2. У Саши было 12 марок. Он подарил другу 3 марки. Сколько марок осталось у Саши?
Было – 12м.
Подарили–3м.
Осталось – ?м.
12-3=9 (м.)
Ответ: 9 марок осталось у Саши.
3. В одной коробке 10 карандашей, а в другой – 6 карандашей. На сколько больше карандашей в первой коробке, чем во второй?
Ιк.-10 к.
ΙΙк.–6 к.
10-6=4 (к.)
Ответ: на 4 карандаша больше в первой коробке, чем во второй.
4. На прогулку вышли 7 девочек, а мальчиков на 2 больше. Сколько мальчиков вышло на прогулку?
Девочек – 7 ч.
Мальчиков-
7+2= 9 (м.)
Ответ: 9 мальчиков вышло на прогулку.
5. На прогулку вышли 7 девочек, а мальчиков на 2 меньше. Сколько мальчиков вышло на прогулку?
Девочек 7 ч.
Мальчиков –
7-2=5 (м.
)
Ответ: 5 мальчиков вышло на прогулку.
6. На стоянке было несколько машин. Когда 3 машины уехали, осталось 6 машин. Сколько машин было на стоянке сначала?
Было – ? м.
Уехали – 3 м.
Осталось – 6 м.
3+6=9 (м.)
Ответ: 9 машин было на стоянке сначала.
7. В коробке было 10 карандашей. Когда из коробки взяли несколько карандашей, в ней осталось 6 карандашей. Сколько карандашей взяли?
Было – 10 к.
Взяли – ? к.
Осталось – 6 к.
10-6=4 (к.)
Ответ: 4 карандаша взяли.
8. На стоянке стояло 12 машин, из них 5 машин грузовых. Сколько легковых машин стояло на стоянке?
Грузовые – 5 м.
12 м.
Легковые -? м.
12-5=7 (м.)
Ответ: 7 легковых машин стояло на стоянке.
9. У Димы 5 тетрадей в клетку и столько же в линейку. Сколько всего тетрадей у Димы?
В клетку – 5 т.
В линейку – 5 т.
5+5=10 (т.)
Ответ: 10 тетрадей у Димы.
10. На полке стояло несколько книг, когда поставили ещё 3 книги, на полке стало 12 книг. Сколько книг было на полке сначала?
Было-
Поставили – 3 кн.
Стало – 12 кн.
12-3=9 (кн.)
Ответ: 9 книг было на полке сначала.
Составные задачи.
1. На одной полке 10 книг, а на второй на 4 книги больше. Сколько всего книг на двух полках?
Ι п. – 10 кн.
ΙΙ п. – ? кн., на 4 кн. >
1) 10+4=14 (кн.) – на второй полке
2) 10+14=24 (кн.)
10+(10+4)=24 (кн.)
Ответ: 24 книги на двух полках.
2. В гараже 12 грузовых машин, а легковых на 4 машины меньше. Сколько всего машин в гараже?
Грузовые – 12 м.
Легковые – ? м., на 4 м.
1)12-4=8(м)– легковые
2)12+8=20(м.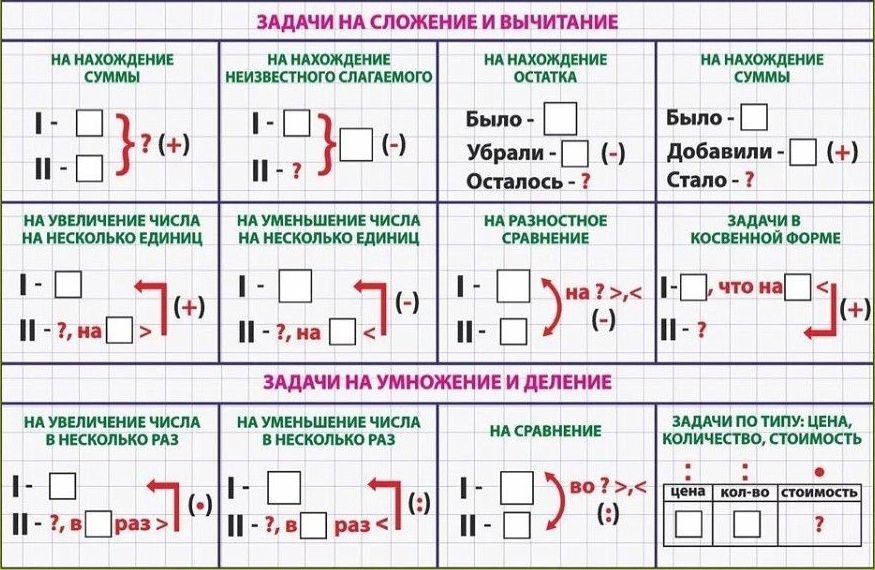
)
Гр.
8
12+(12-4)=20 (м.)
Ответ: 20 машин в гараже.
3. В зоомагазине было 10 волнистых попугайчиков, канареек на 4 больше, чем попугайчиков, а черепах на 6 меньше, чем канареек. Сколько было черепах?
Попугайчики-10 шт.
Канарейки -? к., на 4 к. >
Черепахи – , на 6 ч.
1) 10+4=14 (к.) – было в зоомагазине.
2) 14-6=8 (ч.)
14
(10+4)-6=8 (ч.)
Ответ: 8 черепах было в зоомагазине.
4. В одном ящике 5 кг печенья, а в другом – 8 кг До обеда продали 9 кг печенья. Сколько кг печенья осталось продать?
Было – 5 кг и 8 кг -? кг
Продали – 9 кг
Осталось –
1) 5+8=13 (кг) – печенья было.
2) 13-9=4 (кг)
13
(5+8)-9=4 (кг)
Ответ: 4 кг печенья осталось продать.
5. Во время каникул Витя сделал 18 фотографий. Он подарил 6 фотографий бабушке и 4 фотографии другу. Сколько фотографий осталось у Вити?
Было – 18 ф.
Подарил – 6 ф. и 4 ф. – ?ф.
Осталось –
1) 6+4=10 (ф.) – Витя подарил.
2) 18-10=8 (ф.)
10
18 – (6+4)=8 (ф.)
Ответ: 8 фотографий осталось у Вити.
6. К празднику купили 14 красных воздушных шариков, зелёных на 2 больше, чем красных, а синих столько, сколько красных и зелёных вместе. Сколько синих шариков купили к празднику?
Красные – 14 ш.
Зелёные – ? ш., на 2 ш. >
Синие –
(Можно)
Красных 14 ш.
С –
Зелёных – ? ш., на 2 ш. >
1) 14+2=16 (ш.) – зелёных.
2) 14+16=30 (ш.)
16
14+(14+2)=30 (ш.)
Ответ: 30 синих шариков купили к празднику.
Решение обратных задач
Прямая задача
1. На рябине сидело 8 снегирей и 12 соек. Сколько всего птиц сидело на рябине?
Снегирей – 8 шт. ? пт.
Соек – 12 шт.
8+12=20 (пт.)
Ответ: 20 птиц сидело на рябине.
Обратные задачи
1. На рябине было 20 птиц. Из них 8 снегирей, остальные сойки. Сколько соек сидело на рябине?
Снегири – 8 шт.
Сойки – ? шт. 20 пт.
20-8=12 (с.)
Ответ: 12 соек сидело на рябине.
2. На рябине сидело 20 птиц. Из них 12 соек, остальные снегири. Сколько снегирей сидело на рябине?
Сойки – 12 шт.
Снегири – ? шт. 20 пт.
20-12=8 (с.)
Ответ: 8 снегирей сидело на рябине.
Периметр геометрических фигур
1. Найди периметр треугольника со сторонами
7 см, 4 см, 3 см.
a = 7 см.
в = 4 см.
с = 3 см.
РΔ = а + в +с
7+4+3=14 см
Ответ: 14 см.
2. Найди периметр прямоугольника со сторонами 3см и 2 см.
а = 3 см
в = 2см
Р =а+в+а+в
3+2+3+2=10 см
Ответ: 10см
3. Найди периметр квадрата со стороной 4 см.
а=4 см
Р =а+а+а+а
4+4+4+4=16 см
Ответ: 16 см
Периметр – это сумма длин всех сторон.
ДЛЯ ЗАМЕТОК
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
ЖЕЛАЮ УДАЧИ
И
ВЕРНОГО РЕШЕНИЯ .
Урок 11. модели задачи: краткая запись задачи, схематический чертёж – Математика – 2 класс
Математика, 2 класс
Урок № 11. Модели задачи: краткая запись задачи, схематический чертёж
Перечень вопросов, рассматриваемых в теме:
- Как составить краткую запись и схематический чертеж к задаче?
- Как различать задачи на нахождение неизвестного уменьшаемого и на нахождение неизвестного вычитаемого?
Глоссарий по теме:
Компоненты вычитания – уменьшаемое, вычитаемое, разность.
Задача на нахождение неизвестного вычитаемого, в этой задаче находится вычитаемое (из уменьшаемого отнять разность)
Задача на нахождение неизвестного уменьшаемого, в этой задаче находится уменьшаемое (к разности прибавить вычитаемое)
Краткая запись – это коротко записанное условие задачи, последним в краткой записи пишется вопрос к задаче.
Схематический чертеж к задаче – это чертеж «в отрезках», схематическое изображение отношений между данными и искомым
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –8-е изд. – М.: Просвещение, 2017. – с.28-29
2. Математика. Проверочные работы. 2 кл: учебное пособие для общеобразовательных организаций/ Волкова А.Д.-М.: Просвещение, 2017, с. 18, 19
Теоретический материал для самостоятельного изучения
Научимся решать новые виды задач. Задача первая. На ветке было несколько птиц. Когда пять птиц улетели, на ветке осталось семь птиц.
Сделаем краткую запись задачи. Было- ? Улетели- 5 пт. Осталось- 7 пт.
Сделаем схематический чертеж к задаче.
Начертим отрезок, который показывает, сколько птиц осталось, подпишем 7 птиц. Причертим к концу отрезка еще один отрезок, обозначающий улетевших птиц, подпишем 5 птиц. Сколько было птиц на ветке, неизвестно, поставим знак вопроса.
Рассмотрим краткую запись и чертёж к задаче
Каким действием будем решать задачу?
Правильно, чертёж нам подсказывает, что задача решается сложением, так как надо найти сумму отрезков.
Часть птиц улетели и часть осталось. Значит, мы находим уменьшаемое. А уменьшаемое находится действием сложением.
Запишем решение задачи.
7+5=12(пт.)
Ответ: 12 птиц.
Этот вид задачи называется на нахождение неизвестного уменьшаемого. Так как в этой задаче находим уменьшаемое.
Решим вторую задачу.
На клумбе было одиннадцать тюльпанов. Когда несколько тюльпанов завяло, то осталось шесть тюльпанов. Сколько тюльпанов завяло?
Сделаем краткую запись условия задачи и чертёж.
Было-11т. Завяло-? Осталось-6т.
Сделаем схематический чертеж.
6т. ?
11 т.
Начертим отрезок, обозначающий все тюльпаны.
Подпишем его 11 тюльпанов. Отложим на отрезке отрезок равный оставшимся тюльпанам, подпишем 6 тюльпанов. Другой отрезок, обозначает, сколько тюльпанов завяло, это неизвестно, ставим знак вопроса.
Решим задачу. Узнать сколько тюльпанов завяло, значит надо узнать, на сколько тюльпанов стало меньше. Задача решается вычитанием. По чертежу видно, что неизвестна разность отрезков. Как называется число 11? Уменьшаемое. Как называется число 6? Разность. Неизвестно в задаче вычитаемое. Как найти вычитаемое? Из уменьшаемого вычесть разность.
11-6=5 (т.)
Ответ: 5 тюльпанов завяло.
Такой вид задач называется “
Сделаем вывод: правильно составленная краткая запись задачи подсказывает, каким компонентом является каждое число в задаче: уменьшаемым или вычитаемым. Правильно начерченный схематический чертеж подсказывает, каким действием решать задачу. По чертежу видно, что находим сумму или разность отрезков.
Тренировочные задания.
1. Решите задачу, выберите правильное решение
На стоянке было несколько машин. Когда уехало 8 машин, то осталось 7 машин. Сколько машин было на стоянке?
Варианты ответов:
1. 8-7=1 (м.)
2. 8+7=16 (м.)
3. 8+7=15 (м.)
Правильный вариант:
3. 8+7=15 (м.)
2. Вставьте подходящие слова в предложения
Чтобы найти неизвестное слагаемое, надо ______ вычесть известное слагаемое. Чтобы найти неизвестное __________, надо к разности прибавить вычитаемое. Чтобы найти вычитаемое, надо ________вычесть разность
Правильный вариант:
Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
Чтобы найти вычитаемое, надо из уменьшаемого вычесть разность.
Тип задачи | Пример задачи | Краткая запись | |
1. | Составные задачи на нахождение суммы | Хозяйка купила 3 кг яблок, а груш на 2 кг больше. Сколько всего кг фруктов купила хозяйка? | | – || – ? , на б. |
2. | Составные задачи на нахождение суммы | Валя решила 7 примеров на сложение, а на вычитание на 5 примеров меньше. Сколько всего примеров решила Валя? | | – || – ? , на м. |
3. | Составные задачи на нахождение остатка | На первой полке было 7 книг, а на второй 4 книги. Убрали 5 книг. Сколько книг осталось на полке? | Было – и Убрали – Осталось – ? |
4. | Составные задачи на нахождение слагаемого | На озере плавало 4 утки и 3 лебедя. Когда несколько птиц прилетело, их стало 10. Сколько птиц прилетело? | Было – и Прилетело – ? Стало – |
5. | Составные задачи на нахождение уменьшаемого | Из вазы взяли 3 персика и 2 груши. Сколько фруктов было в вазе сначала, если в ней осталось 3 фрукта? | Было – ? Взяли – и Осталось – |
6. | Составные задачи на нахождение вычитаемого | У хомяка было 6 земляных и 4 грецких ореха. Когда несколько орехов хомяк сгрыз, у него осталось 7 орехов. Сколько орехов сгрыз хомяк? | Было – и Сгрыз – ? Осталось – |
7. | Составные задачи на разностное сравнение | В саду росло 10 деревьев. Из них 8 яблонь, остальные груши. На сколько больше росло яблонь, чем груш? | Яблони – на Груши –? ? б |
Тип задачи | Пример задачи | Краткая запись | |
1. | Составные задачи на нахождение суммы | Хозяйка купила 3 кг яблок, а груш на 2 кг больше. Сколько всего кг фруктов купила хозяйка? | | – || – ? , на б. |
2. | Составные задачи на нахождение суммы | Валя решила 7 примеров на сложение, а на вычитание на 5 примеров меньше. Сколько всего примеров решила Валя? | | – || – ? , на м. |
3. | Составные задачи на нахождение остатка | На первой полке было 7 книг, а на второй 4 книги. Убрали 5 книг. Сколько книг осталось на полке? | Было – и Убрали – Осталось – ? |
4. | Составные задачи на нахождение слагаемого | На озере плавало 4 утки и 3 лебедя. | Было – и Прилетело – ? Стало – |
5. | Составные задачи на нахождение уменьшаемого | Из вазы взяли 3 персика и 2 груши. Сколько фруктов было в вазе сначала, если в ней осталось 3 фрукта? | Было – ? Взяли – и Осталось – |
6. | Составные задачи на нахождение вычитаемого | У хомяка было 6 земляных и 4 грецких ореха. Когда несколько орехов хомяк сгрыз, у него осталось 7 орехов. Сколько орехов сгрыз хомяк? | Было – и Сгрыз – ? Осталось – |
7. | Составные задачи на разностное сравнение | В саду росло 10 деревьев. Из них 8 яблонь, остальные груши. На сколько больше росло яблонь, чем груш? | Яблони – на Груши –? ? б |
Когда несколько птиц прилетело, их стало 10. Сколько птиц прилетело?Советы учителя – Требования к оформлению письменных работ по математике в начальной школе, учитель начальных классов в Москве
Все записи в тетрадях следует оформлять аккуратным каллиграфическим почерком.В 1 классе в период обучения грамоте запись даты ведется учителем или учащимися по центру рабочей строки в виде числа и первых букв названия месяца (1 с.). По окончании периода обучения грамоте дата записывается полностью (1 марта.). Со 2 класса допускается запись даты выполнения работы на полях, с указанием числа и месяца (01.09.).
Запись названия работы производится на следующей рабочей строке по центру с пропуском 1 клетки от числа и оформляется как предложение (Классная работа.
После выполнения работы (классной или домашней) следует отступать 4 клетки, начиная выполнять очередную работу на пятой клетке. В ходе выполнения работы не допускается необоснованный пропуск строк или наличие пустых мест на строке. Использование правил переноса, принятых в математике, обязательно.
При выполнении работы на странице требуется соблюдать внешние и внутренние поля. Между столбиками выражений, уравнений, неравенств и другими видами заданий отступаются три клетки вправо. Запись нового столбика начинается с четвертой клетки.
При оформлении письменных заданий по математике рекомендуется указывать его номер (No 5) без уточнения вида (Задача, Неравенства, Выражения) Краткая запись условия задачи оформляется в соответствии с их видом (краткая запись, схема, чертеж, таблица, диаграмма, рисунок). Ключевые слова в краткой записи пишутся с большой буквы.
В 1 классе допускается их сокращение по первым буквам: М. – 7 м. Б. – 3 м.
Начиная с 2 класса по усмотрению учителя ключевые слова в краткой записи могут быть зафиксированы полностью: Маленькие – 7 м. Большие – 3 м.
При записи решения задачи по действиям с письменными пояснениями (с записью вопроса) или выражением после каждого действия ставится наименование в круглых скобках с использованием правил сокращения слов. Слово «Ответ» пишется под решением с заглавной буквы с отступлением 1 клетки вниз.
В первом классе ответ задачи может быть записан в краткой форме (От. 10 ябл.).
Со 2 класса слово «Ответ» записывается полностью (Ответ: 10 яблок.).
Оформление условия задачи при помощи схемы, чертежа, таблицы, диаграммы или рисунка осуществляется с использованием линейки и простого карандаша.
Краткую запись не следует делать громоздкой, она должна быть удобной, отображать все числовые данные задачи и взаимоотношения между величинами.
- чертежи выполнять простым карандашом по линейке;
- геометрическую фигуру чертить в тех случаях, когда этого требует условие задачи;
- результаты измерений подписывать ручкой;
- обозначения выполнять прописными буквами латинского алфавита.
При оформлении математического диктанта следует записывать только ответы в строчку, отступая одну клетку.
Задачи в два действия — урок. Математика, 2 класс.
Карлсон за один день съел \(10\) банок варенья, а за второй день съел на \(3\) банки меньше. Сколько всего банок варенья съел Карлсон за два дня вместе?
По условию составим запись и выработаем план решения:
1 день −10 банок 2 день −? на 3 банки меньше, чем в 1 день − за 2 дня вместе?
Обрати внимание!
Анализируя эту схему, делаем вывод, что задача решается двумя действиями.
Сначала найдём ответ на вопрос:
1) сколько банок варенья съел Карлсон за второй день?
На \(3\) банки меньше — это значит, следует отнять \(3\)!
\(10 – 3 = 7\) (б.) — столько банок варенья съел Карлсон за второй день.Теперь знаем количество банок варенья, которое съел Карлсон за первый день и за второй день. Поэтому можно ответить на вопрос задачи.
2) Сколько всего банок варенья съел Карлсон за два дня вместе?
Вместе — это значит, следует сложить!
\(10 + 7 = 17\) — столько банок варенья съел Карлсон за два дня вместе.
Ответ: за \(2\) дня Карлсон съел \(17\) банок варенья.
Можно решение этой задачи записать и одним примером:
\((10 – 3) + 10 = 17\).
Первым действием в скобках ответим на первый вопрос, а вторым действием ответим на вопрос задачи.
Пример:
в клетке было \(7\) синих попугаев и \(8\) зелёных попугаев.
Продали \(5\) птиц. Сколько попугаев осталось в клетке?
Сразу на вопрос задачи ответить нельзя.
В ходе решения составим такую запись:
1) \(7 + 8 = 15\) п.,
2) \(15 – 5 = 10\) п.
Ответ: \(10\) попугаев осталось в клетке.
Первым действием узнали общее количество птиц в клетке.
Вторым действием ответили на вопрос задачи, т. е. узнали количество попугаев, оставшихся в клетке.
Задачи в два действия — это составные задачи, в которых для нахождения искомого ответа нужно сначала вычислить одно неизвестное по имеющимся данным.
|
|
..» родителямКраткая запись задачи и её схематический чертёж
-
Охо-хо-хо-хо… И куда этот Плюс подевался? Я один с этим заданием не справлюсь.
Ну, царица! Каждый раз какое-нибудь новенькое задание подкинет.
- Добрый день, Минус! Прости, я задержался – на природу загляделся. Уж такой сегодня день красивый! Я набрал целую охапку листьев – здесь листья клёна и каштана.
- А что ты с ними делать собираешься?
- Как что – составлю осенний букет. А еще, они помогут нам разобраться в том задании, которое дала нам царица-Математика – научиться выполнять краткую запись задачи и её схематический чертёж.
- Давай скорее начнём, а то ты и так опоздал.
- Ну что же, приступим. Вот смотри – у меня несколько листьев клёна. 5 из них я поставлю в вазу и осталось ещё 4 листа.
- Да-да, я знаю. Если задать вопрос, то получится вот такая задача:
Плюс собрал несколько листьев клёна. 5 из них он поставил в вазу. После этого осталось ещё 4 листа. Сколько всего листьев собрал Плюс?
Ну, и что дальше?
- А дальше составляем краткую запись.
- И как мы это сделаем?
- Выбираем главные, опорные слова. Что происходило в задаче?
- Сначала ты собрал листья, а потом 5 из них поставил в вазу. И у тебя остались 4 листа.
- Вот именно – собрал, поставил, осталось. Вот они, опорные слова. Запишем их:
- Да, но, сколько собрал, в задаче неизвестно. В ней сказано, что собрал несколько листьев.
- Ну, раз неизвестно, мы поставили вопросительный знак. Ведь именно это и надо узнать в задаче. Её вопрос звучит так: «Сколько всего листьев собрал Плюс?» А, чтобы не писать полностью слово листьев, мы поставим только первую букву л. Ведь, если вместо слова ставится одна или, допустим, две буквы, то говорят, что слово сократили, и подсказывает нам это маленькая точка.
Ну,
вот. У нас получилась краткая запись задачи. Глядя на неё мы можем
вспомнить всё условие задачи.
- Но ведь нам еще надо сделать и схематический чертёж!
- Ну что же. В этом нам помогут отрезки. Мы ведь их уже отлично рисовать научились. Итак, вот первый отрезок.
Он показывает, сколько листьев я поставил в вазу. Второй отрезок мы начнем рисовать от той точки, которая является концом первого отрезка.
Этот отрезок показывает, сколько листьев у меня осталось. То есть, нам известна та часть листьев, которую я поставил в вазу и та часть листьев, которая осталась. А вот, если объединить все листья вместе, то получится уже не часть, а все листья, то есть целое.
Когда мы объединяем, то есть собираем что-то вместе, находим целое, то, конечно, используем действие сложения. И без меня, Плюса, здесь не обойтись!
Записываю ответ задачи: Плюс собрал 9 листьев клёна.
- Так, отлично, с этой задачей мы справились. Но ведь есть и ещё одна задача.
- Что еще за задача?
- А вот она: На лесной поляне росло 7 мухоморов. Несколько мухоморов съел лось. После этого на поляне осталось 2 мухомора. Сколько мухоморов съел лось?
Теперь моя очередь составлять краткое условие и схематический чертёж. Итак, выделяю числа и опорные слова. Что в задаче происходило? Росло 7 мухоморов. Несколько мухоморов съел лось. Раз несколько, значит, мы не знаем сколько. Дальше написано, что осталось 2 мухомора.
Ну вот, с кратким условием я справился. Так ведь, Плюсик?
- Да, молодец!
- Теперь надо выполнить схематический чертёж.
Росло 7 мухоморов. Рисуем отрезок:
Лось съел, это неизвестно. Пока рисовать не буду, осталось 2 мухомора. Как мне их нарисовать? Откуда начинать? С конца первого отрезка?
Не-е-ет.
Ведь семь – это все мухоморы, то есть целое, а два – это часть этих
семи.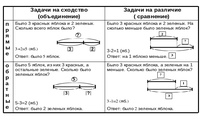
Поэтому откладываем отрезок, обозначающий эти два мухомора от начала
первого отрезка. Мы как бы отделим оставшиеся мухоморы от съеденных. А вот тот
отрезок, который является второй частью целого отрезка и будет съеденными
мухоморами.
Как известно, часть чего-то целого находим действием вычитания. Так что, теперь моя очередь встать в действие:
Ответ: 5 мухоморов съел лось.
- Это у тебя отлично получилось, Минус. Лихо ты справился с такой трудной задачей.
- И ничего трудного тут нет. Чтобы решить любую задачу, надо сначала представить себе все, что в ней происходит. Затем составить краткое условие, выделив опорные слова, которые нам подскажут, что именно происходит в задаче. А потом нарисовать схематический чертёж. Только надо очень внимательно разобраться, что в задаче целое, а что части.
- Если мы находим наибольшее число, то есть целое, из известных частей, то отрезки рисуем так: сначала первый отрезок, затем второй. При этом, конец первого отрезка одновременно является началом второго отрезка. И такую задачу решаем действием сложения. То есть используем знак плюс.
- А если в задаче надо узнать часть чего либо, то сначала рисуем отрезок, обозначающий самое большое число, то есть целое. Затем от начала первого отрезка рисуем второй отрезок, обозначающий меньшее известное число. Мы как бы разрезаем больший отрезок на части, одна из которых известна, а вторую нужно узнать. И, конечно, если надо узнать часть, то задачу решаем действием вычитания. То есть используем знак минус.
- Ну что, пойдем к царице сдавать задание?
- Ну да! Побежали! Урра!
Распечатанные рабочие листы для задач по математике для второго класса
Проблемы со словами могут быть сложной задачей для учащихся, особенно для второклассников, которые, возможно, еще учатся читать.
Но вы можете использовать базовые стратегии, которые будут работать практически с любым учеником, даже с теми, кто только начинает изучать письменные навыки.
Инструкции и стратегии
Чтобы помочь второклассникам научиться решать задачи со словами, научите их выполнять следующие действия:
- Изучите математическую задачу: Прочтите слово «задача», чтобы понять ее общий характер.Поговорите со своими учениками о проблеме и обсудите, какие части являются наиболее важными.
- Прочтите математическую задачу: Прочтите вопрос еще раз. На этот раз сосредоточьтесь на конкретных деталях проблемы. Какие части проблемы связаны друг с другом?
- Задайте вопросы о задействованных операциях: Поразмышляйте еще раз. Определите конкретные математические операции, которые вам нужно выполнить, и перечислите их на бумаге в порядке их выполнения.
- Спросите себя о предпринятых шагах: Просмотрите каждый сделанный шаг.Определите, кажется ли ваш ответ разумным. Если возможно, сверьте свой ответ с ответами в книге, чтобы определить, на правильном ли вы пути.
- Завершите: Просмотрите текст словесных задач, которые вы будете решать, чтобы определить любые слова, которые вы не узнаете. Перечислите их и определите их значение, прежде чем решать проблемы. Напишите краткие определения терминов для справки при решении проблем.
Решение проблем
Изучив эти стратегии, используйте следующие бесплатные распечатки задач со словами, чтобы студенты могли практиковать то, что они узнали.Есть только три рабочих листа, потому что вы не хотите перегружать своих второклассников, когда они только учатся решать задачи со словами.
Начните медленно, при необходимости повторите шаги и дайте своим ученикам возможность усвоить информацию и освоить словесные методы решения проблем в расслабленном темпе. В печатных материалах содержатся термины, которые будут знакомы молодым студентам, такие как «треугольник», «квадрат», «лестница», «десять центов», «пятак» и дни недели.
В эту распечатку включены восемь математических задач, которые покажутся второклассникам многословными, но на самом деле они довольно просты.Задачи на этом листе включают задачи со словами, сформулированные в виде вопросов, например: «В среду вы видели 12 малиновок на одном дереве и 7 на другом дереве. Сколько всего малиновок вы видели?» и «У всех ваших 8 друзей есть двухколесные велосипеды, сколько всего это колес?»
Если студенты озадачены, прочитайте задачи вслух вместе с ними. Объясните: если вы вычеркнете слова, это будут простые задачи на сложение и умножение, где ответ на первый будет следующим: 12 робинов + 7 робинов = 19 робинов; а ответ на второй будет: 8 друзей x 2 колеса (для каждого велосипеда) = 16 колес.
Д. РасселЭта последняя печатная форма в наборе содержит немного более сложные задачи, такие как эта, связанная с деньгами: «У вас есть 3 квартала, и ваша выписка обошлась вам в 54 цента. Сколько денег у вас осталось?»
Чтобы ответить на этот вопрос, предложите учащимся изучить проблему, а затем прочитать ее всем классом. Задайте такие вопросы, как: «Что может помочь нам решить эту проблему?» Если учащиеся не уверены, возьмите три четверти и объясните, что они равны 75 центам. Тогда задача превращается в простую задачу вычитания, поэтому завершите ее, указав числовую операцию на доске следующим образом: 75 центов – 54 цента = 21 цент.
Стандарты | Пояснения и примеры |
1. Осознавайте проблемы и настойчиво их решайте. | Учащиеся 2-го класса с математическими знаниями изучают задачи (задания), могут понять смысл задания и найти точку входа или способ начать выполнение задания. |
2. Рассуждайте абстрактно и количественно. | Учащиеся 2-го класса с математическими знаниями понимают величины и взаимосвязи при решении задач. Это включает в себя два процесса – деконтекстуализацию и контекстуализацию.Во 2 классе учащиеся представляют ситуации, деконтекстуализируя задачи в числах и символах. Например, в задаче «В столовой 25 детей, и к ним присоединяются еще 17 детей. Затем, если 19 из этих детей уйдут, сколько их еще там?» Ожидается, что учащиеся 2-х классов переведут эту ситуацию в уравнение: 25 + 17-19 = __, а затем решат задачу. Студенты также контекстуализируют ситуации в процессе решения проблем. Например, при решении вышеуказанной задачи учащиеся могут обратиться к контексту задачи, чтобы определить, что им нужно вычесть 19, поскольку 19 детей ушли.Процессы рассуждений также применимы ко 2 классу, поскольку учащиеся начинают измерять со стандартными единицами измерения, определяя длину величин на основе определенных единиц измерения. |
3. Придумывайте жизнеспособные аргументы и критикуйте рассуждения других. | Учащиеся 2-го класса со знанием математики точно используют определения и ранее принятые решения для построения жизнеспособных аргументов по математике.Во 2 классе во время обсуждения стратегий решения проблем учащиеся конструктивно критикуют стратегии и рассуждения своих одноклассников. Например, решая 74 + 18 – 37, учащиеся могут использовать различные стратегии, а после работы над задачей могут обсуждать и критиковать рассуждения и стратегии друг друга, ссылаясь на сходства и различия между стратегиями. |
4. Модель с математикой. | Учащиеся 2-го класса с математическим образованием моделируют реальные математические ситуации с помощью числового предложения или уравнения и проверяют, точно ли их уравнение соответствует контексту задачи. Учащиеся 2-х классов по-прежнему будут полагаться на конкретные манипуляции и графические изображения при решении задач, но ожидается, что они также напишут уравнение для моделирования проблемных ситуаций. Точно так же ученики 2-х классов должны создать соответствующую проблемную ситуацию из уравнения.Например, ожидается, что учащиеся создадут задачу-рассказ для уравнения 24 + 17-13 = ___. |
5. Стратегически используйте соответствующие инструменты. | Учащиеся 2-х классов со знанием математики имеют доступ к инструментам и правильно их используют. Эти инструменты могут включать в себя блоки с числовыми значениями (основание десять), доски с сотнями номеров, числовые линии и конкретные геометрические фигуры (например,g., узоры, трехмерные тела). Студенты также должны иметь опыт работы с образовательными технологиями, такими как калькуляторы и виртуальные манипуляторы, которые поддерживают концептуальное понимание и навыки мышления более высокого порядка. |
6.Обратите внимание на точность. | Учащиеся 2-х классов с математическими навыками точны в общении, расчетах и измерениях. При выполнении всех математических задач учащиеся 2-х классов четко общаются, точно используют словарный запас, соответствующий их классу, а также дают точные объяснения и аргументы в отношении своего процесса поиска решений. Например, при итеративном измерении объектов (многократно) учащиеся проверяют, нет ли пропусков или перекрытий.При выполнении задач, связанных с числовым восприятием, студенты проверяют свою работу, чтобы убедиться в точности и разумности решений. |
7. Ищите и используйте структуру. | Учащиеся 2-х классов с математическими знаниями внимательно ищут закономерности и структуры в системе счисления и других областях математики.При решении задач на сложение и вычитание учащиеся могут применять схемы системы счисления, чтобы пропускать счет на 10 секунд после декады. Например, ожидается, что ученики 2-х классов мысленно рассудят, что 33 + 21 – это 33 плюс 2 десятка, что равняется 53, а затем прибавить к сумме, равной 54. Работая в области «Числа по основанию 10», ученики работают с идеей, что 10 единица равняется десятке, а 10 десятков равняются 1 сотне. Кроме того, учащиеся 2-х классов также используют структуру, когда они работают с вычитанием, как проблемы с отсутствием сложения, например, 50-33 = __ можно записать как 33+ __ = 50 и можно представить, сколько еще мне нужно добавить. до 33, чтобы добраться до 50? |
8.Ищите и выражайте закономерность в повторяющихся рассуждениях. | Математически развитые ученики 2-х классов начинают искать закономерность в структуре задач при решении математических задач. Например, после решения задач сложения двух цифр путем разложения чисел по местам (33+ 25 = 30 + 20 + 3 +5) учащиеся могут начать обобщать и часто применять эту стратегию независимо от будущих задач. Кроме того, учащиеся начинают искать стратегии для повышения эффективности вычислений, в том числе стратегии удвоения и получения десятки.Наконец, при решении всех задач ученики 2-х классов тщательно проверяют разумность своих решений во время и после выполнения задания. |
Учащиеся 2-х классов также развивают основы стратегий решения проблем и самостоятельно приобретают навыки использования этих стратегий для решения новых задач. Во 2-м классе работа учащихся по-прежнему опирается на конкретные манипуляции и графические изображения, когда учащиеся решают задачи, если в CCSS не упоминается слово свободно, которое обозначает мысленную математику. Ученики 2-х классов также должны проявлять настойчивость при решении задач; то есть, если учащиеся достигают точки, в которой они застряли, они могут пересмотреть задачу по-другому и продолжить ее решение.Наконец, математически опытные ученики выполняют задание, задавая себе вопрос: «Имеет ли мой ответ смысл?»
Во время обучения в классе студенты должны иметь доступ к различным математическим инструментам, а также к бумаге, и определять, какие инструменты наиболее подходят для использования. Например, решая 28 + 17, учащиеся могут объяснить, почему блоки значений больше подходят, чем счетчики.Олимпиада по математике для учащихся начальной и средней школы
Что говорят учителя О НЛМК
«Соревнования по математике были поистине замечательными. практические задачи вплоть до финиша получения медали! Качество, которое вы предлагаете, непревзойденное во всех отношениях.Результаты были своевременными и легко интерпретируемыми. Мои студенты или ученики искренне извлекла пользу из этого опыта, и в будущем я буду входить в другие группы ».
Юлия М.
Hilldale Elementary, OK
” Спасибо за предложение этого конкурса. Растет популярность в нашей школе и конечно помогая нам сосредоточиться на проблеме решение. С нетерпением ждем следующего участия в конкурсах. год.”
Кейт Р.
Мария, Мать Школы Спасителя, PA
” Этот опыт очень хорош для моих учеников. Мне нравится слышать, как они делятся различными проблемами стратегии решения, когда мы вернулись к тесту. Спасибо, что сделали конкурс доступным! »
Vicki F., Creekmoor Elementary, MO
«Нам очень понравился и гордимся тем, что наши ученики так хорошо справились с ним.Я провожу групповой класс GATE, и этот конкурс – прекрасная возможность обогатить всех. “
Люба С., Рече Каньон Элементарно, Калифорния
«В нашей школе я преподаю математику одаренным ученикам. Моим ученикам понравился конкурс. Мои ученики хотели, чтобы на следующий день я поставил им больше задач. Большинству из них нравилось пытаться выяснить, что их ставило в тупик. Они не хотели, чтобы я отвечал им. Они хотели продолжать работать, пока не выяснили их сами.”
Дженнифер М., Элементарная школа Кросс-Крик, Джорджия
” В конкурсе было просто зарегистрироваться, и у него был легкий доступ к материалам, необходимым для проведения теста. Сертификаты, которые были загружены для участия в тестировании, также были легко доступны и выглядели очень профессионально! Я был очень горд вручить каждому участнику сертификат за их время и талант. Когда пришли медали, Нойтик даже превзошел все мои ожидания.Медали были потрясающими! Я был так взволнован, чтобы раздать их. Спасибо за эту прекрасную возможность для студентов! ”
Мишель К., Big Hollow School, IL
«Мне больше всего понравилось то, как результаты теста записывались и заносились в таблицу. Мне также нравятся медали, которые были отправлены команде-победителю. Хотя у нас не было ни одного ученика, который мог бы забить в верхней национальной сетке. студенты очень гордились тем, что были отмечены наградами / победителями в команде.”
Мелисса Ф., Элементарно-Крик Вью, Алабама
” Большое спасибо за возможность увлечь детей математикой. Во 2-м классе у нас было 30 человек. Они предпочитают приходить в школу два раза в неделю в 7:30, чтобы подготовиться к экзамену. Они всегда так взволнованы, а мы поражены. Они всегда так взволнованы, а мы поражены. . ”
Gidget A, Celebration K-8, FL
” Конкурс понравился.Мне очень понравилось волнение, которое испытали мои ученики, и признание того, что они подумали: «Математика – это круто». ”
Викки, классный руководитель, Северная Каролина
” Мы участвовали во многих разных, но ваш – один из самых организованных, где все логистические детали объясняются руководителям групп, все результаты ясны, и все студенты награждаются очень хорошими наградами, как сертификатами, так и медалями. .Большое спасибо за внимание к деталям конкурса! ”
Элеонора Н., Тихоокеанская академия Сан-Франциско, Калифорния
” Я хотел поблагодарить вас за эту прекрасную возможность бросить вызов нашим студентам. Наша школа участвует уже 4 года. Каждый год вы улучшали веб-сайт, и теперь распечатать сертификаты для студентов стало еще проще! Для меня это огромная экономия времени. Приятно видеть волнение, когда студенты получают свои награды.”
Винни С., Школа Сикамор-Каньон, Калифорния
” В этом было так легко участвовать! Вы дали достаточно инструкций, чтобы помочь нам, но также и достаточно гибкости, чтобы заставить их работать. Спасибо, ”
Лаэль М., начальная школа Кальвина Кристиана, Мичиган
” Да, понравилось! Ранее в этом году у нас был приглашенный лектор, который сказал нам, что мы должны начинать математические соревнования заранее, чтобы подготовиться к математическим соревнованиям в колледже, таким как Патнэм (в котором он участвовал), поэтому мои ученики захотели это сделать, и поэтому я поискал его и нашел ты.Моим студентам понравилась идея подготовиться к тому, чем они будут заниматься в колледже, и получить национальный рейтинг! ”
Кэтлин Ф. , Buel Elementary, ИЛИ
” Конкурс мне очень понравился! Родители сказали, что это похоже на математику, которую они делают в Германии. Это казалось значимым. Это был отличный способ сравнить наших учеников с другими учениками того же возраста. Обожаю новости и награды по электронной почте. Медали были особенными. Сертификат был хорош для усилий студентов, но впереди.Спасибо!”
Учитель
” Отличные проблемы! Я купил предыдущие соревнования, чтобы потренироваться, и мне понравилось, что у младших школьников есть проблемы, над которыми они могли бы работать. Мои старшие ученики занимаются MathCounts, но мне было трудно найти подходящий решение проблем для детей младшего возраста. я думаю ключом является обуздание их интереса, пока они молодой и взволнованный.Большое спасибо за все эта работа для нас в строю! »
Одаренный учитель
Задачи с денежным словом
Эти рабочие листы с задачами с денежным словом привлекают учащихся к реальным задачам и применению математических навыков. Задачи сгруппированы по сложению и вычитанию (подходит для учеников второго или третьего класса), или умножению и делению (подходит для учеников четвертого или пятого класса, которые освоили десятичное деление), или комбинации всех четырех операций.Нажмите одну из кнопок ниже, чтобы просмотреть отдельные рабочие листы в каждом наборе.
Умножение и деление
Проблемы с денежным словом смешанной операции
Сложение и вычитание с дополнительными фактами
Умножение и деление с дополнительными фактами
Смешанная операция Money Word Задачи с дополнительными фактами
Задачи Word для ознакомления с навыками работы с деньгами
Деньги – это мощное и знакомое приложение для выполнения основных математических операций, а рабочие листы задач с денежными историями на этой странице идеально подходят для детей младшего школьного возраста, чтобы они начали применять свои базовые арифметические навыки.
Рабочие листы начинаются с наборов, которые содержат именно ту информацию, которая необходима для решения конкретных задач с денежным словом, но важным навыком является научиться определять лишние или неиспользуемые факты в описании проблемы. Поскольку денежные проблемы в реальном мире возникают в контексте большого количества информации, которая может не понадобиться для решения проблемы, понимание того, какая информация важна, часто является таким же важным навыком, как и способность выполнять базовые арифметические операции. Рабочие листы задач с денежным словом, отмеченные на этой странице как «лишние факты», подходят для учащихся 3–4 классов, которые могут уверенно решать другие задачи.
Задачи со словами сгруппированы в наборы, посвященные сложению и вычитанию, или умножению и делению, или комбинации всех четырех операций. Если вы изучаете основные математические факты, рабочие листы, соответствующие операциям, над которыми вы работаете, могут помочь укрепить концепции и могут использоваться вместе с практикой математических фактов для дополнительной поддержки. Поскольку все это задачи с денежными историями, они обычно включают в себя и доллары, и центы, поэтому для их решения студентам потребуется некоторое знакомство с десятичной арифметикой.
Для наглядного ознакомления с деньгами посетите страницу «Денежные рабочие листы», которая включает в себя «Внесение сдачи» и действительно хороший набор печатных игровых денег, которые могут быть отличным помощником при решении задач с денежными словами и многого другого!
Первый в математике Онлайн-математическая практика
После закрытия школ учащиеся решили 1 001 947 058 задач дома.Решено 26 167 217 187 задач по математике – и их количество растет!
«Я был действительно поражен интересом и целеустремленностью, которые впервые возникли у моих учеников по математике, мотивация не была проблемой! цели, чтобы в конечном итоге достичь того, что вначале было лишь мечтой.«
Джоэл Стоктон – учитель 5-го класса, начальная школа Кавасос, Ла-Хойя, штат Техас ПОДРОБНЕЕ
Программа First In Math предназначена для всех учеников K-8, от интервенции до одаренных, и всех демографических групп, что делает ее бесценной.
дополнение к любой учебной программе.
ПОДРОБНЕЕ >>
Более 200 упражнений для самостоятельного изучения предлагают немедленную обратную связь, чтобы помочь студентам овладеть процедурными навыками и помочь
Педагоги оценивают, где необходимо вмешательство.
ПОДРОБНЕЕ >>
«Есть такая ценность в программе First In Math. Это дает детям, которым нужна небольшая дополнительная помощь, шанс поработать над своими навыками, и это позволяет детям, которые преуспевают, выходить за рамки того, чему учат в классе».
Доктор Франк Фишель – директор начальной школы Маунтин-Вью, Фландрия, штат Нью-Джерси,
Постановка и достижение целей, а также постоянные возможности для признания позволяют учащимся поддерживать в них ускоренные усилия с течением времени.
ПОДРОБНЕЕ >>
© 2021 Suntex International Inc., все права защищены.
24®, First In Math®, Skill Set® и VIFs® являются зарегистрированными товарными знаками, Family Link ™ является товарным знаком Suntex International Inc.
Почему бы вам не попробовать сегодня игру lorem ipsum?
Серия«Математика на практике» для тренеров и учителей математики классов K-5
Каждая учебник для уровня класса организован в модули, которые тщательно раскрывают конкретный материал по математике, преподаваемый в каждом классе, K – 5.Вместо того, чтобы использовать их по порядку, учителя могут выбирать модули по мере необходимости, исходя из своей карты учебного плана, областей, в которых уделяется внимание преподаванию, или потребностей в повторном обучении.
Каждый модуль содержит:
- идеи о ключевых математических идеях
- учитель отмечает подходы к пониманию учеников
- множество классных заданий и мероприятий, иллюстрирующих конкретные стратегии
- обширная коллекция соответствующих интернет-ресурсов
Предварительный просмотр шести модулей K-5
Щелкните ниже, чтобы увидеть полный список модулей в каждой книге об уровне обучения:
Модули детского сада
Подсчет и количество элементов: числа 1–5
Подсчет и количество элементов: числа 0–10
Подсчет, количество элементов и разряд: числа 0–20
Подсчет чисел
Сравнение чисел 1–10
Разложение чисел
Понимание сложения
Понимание вычитания
Понимание фактов
Исследование измерений
Сортировка и классификация объектов
Знакомство с геометрией
Изучение геометрии
Модули 1-го класса
Сложить задачи со словами с суммой до 20
Соединение вычитания и сложения для решения задач со словами
Понимание математических фактов и свободное владение языком: расширение на +/- 1, +/- 0
Понимание математических фактов и свободное владение языком: +/- 2
Сложить и вычесть +/- 10
Сложить и вычесть двойные
Делаем десять
Подсчет и понимание разметки
Исследование сложения и вычитания с помощью двузначного числа
Измерение длины с косвенным сравнением
Определение времени до часа и получаса
Работа с деньгами
Представление и интерпретация данных
Понимание и описание форм и определение атрибутов
Разделение фигур на половинки и четверти
Модули 2-го класса
Решение проблем
Понимание математических фактов и свободное владение языком
Основы умножения: равные группы
Значение места
Сравните два трехзначных числа
Общие сведения о сложении многозначных чисел
Понимание многозначного вычитания
Расширьте понимание сложения многозначных чисел
Расширьте понимание многозначного вычитания
Измерение длины
Время
Деньги
Представление и интерпретация данных
Описание геометрических фигур
Формы разделов
Модули 3-го класса
Понимание умножения и деления
Понимание свойств умножения и деления
Свободно умножать и делить
Решение одно- и двухэтапных задач со всеми четырьмя операциями
Округление чисел до десяти или ста
Свободно добавлять в пределах 1000
Свободно вычесть в пределах 1000
Понимание дробей и обозначений дробей
Дробная эквивалентность
Сравнение дробей
Время
Масса и объем
Представление и интерпретация данных
Понять понятие площади
Периметр
Понимание и описание фигур
Модули 4-го класса
Понимание и решение проблем с мультипликативным сравнением
Множители, кратные, простые и составные числа
Понимание системы ценностей
Свободно складывайте и вычитайте многозначные числа, используя стандартный алгоритм
Используйте разрядное значение для выполнения многозначного умножения
Используйте разряд для выполнения многозначного деления
Эквивалентность и порядок дробей
Сложение и вычитание дробей с одинаковыми знаменателями
Умножение дробей на целые числа
Понимание десятичной записи для дробей
Измерение и преобразование в измерения
Площадь и периметр
Представление и интерпретация данных
Геометрия и геометрические измерения
Решение сложных проблем
Модули 5-го класса
Место значение
Запись и интерпретация числовых выражений
Умножение на многозначные числа
Деление с многозначными целыми числами
Сложение и вычитание десятичных знаков
Умножение и деление с десятичными знаками
Сложение и вычитание дробей с разными знаменателями
Дроби как деление
Умножение дробей на дроби и целые числа
Деление целых чисел и дробей
Преобразование одинаковых единиц измерения
Представление и интерпретация данных
Геометрические измерения: исследование объема
Система координат
Классифицируйте двумерные фигуры
Иллюстративная математика 1 класс, Раздел 2 – Семья
В этом разделе учащиеся решают новые типы сюжетных задач в пределах 10.Они развивают понимание значения знака равенства и связывают сюжетные задачи с уравнениями.
Раздел A: Добавить / убрать проблемы из истории
В этом разделе учащиеся возвращаются к знакомым типам задач рассказов. Студенты впервые работают формально с уравнениями. Они пишут уравнения, такие как \ (2 + 7 = \ boxed {9} \), и учатся рисовать рамкой ответ на вопрос в задаче рассказа. Студенты работают с задачами, где им нужно выяснить, сколько добавляется:
У Диего было 7 карандашей.
Его сестра дала ему несколько карандашей.
Теперь у Диего 9 карандашей.
Сколько карандашей дала ему сестра Диего?
Студенты видят, что эти задачи можно решить сложением или вычитанием. Они могут решить эту проблему, считая от 7 до 9 и записав уравнение \ (7 + \ boxed {2} = 9 \). Учащиеся также могут решить эту задачу, убрав 7 из 9 и записав уравнение \ (9-7 = \ boxed {2} \).
Раздел B: проблемы вместе / разобрать
В этом разделе учащиеся решают задачи, состоящие из двух групп.В некоторых задачах они находят общую сумму, а в других задачах дается сумма, и они находят недостающую группу. Учащиеся решают задачи в контексте игры Shake and Spill, в которой используются двухцветные фишки. Счетчики кладут в чашку и разливают. Студенты наблюдают за тем, что они видят, или за различными комбинациями, которые могут произойти.
Тайлер играет Shake and Spill. Во время своего первого раунда он пролил эти фишки.
Напишите 2 уравнения для обозначения его счетчиков.
Покажите другие комбинации красных и желтых фишек, которые Тайлер мог пролить.
С помощью этого типа задач учащиеся могут рассматривать различные виды уравнений, например, с суммой перед знаком равенства (\ (7 = 4 + 3 \)).
Раздел C: Проблемы сравнения историй
В этом разделе учащиеся решают задачи-рассказы, в которых они находят «на сколько больше» или «на сколько меньше» в одной группе, чем в другой, например:
На арт-станции 8 клеевых стержней и 3 ножницы.
