Обучение количественному и порядковому счету: Количественный и порядковый счет. Обучение детей. Игры и упражнения

Консультация для воспитателей на тему: «Обучение детей количественному и порядковому счету»

 

План

1. Счет предметов.
2. Понятия количественные и порядковые числа.
3. Методика ознакомления с порядковым и количественным значением числа в детском саду.
4. Примеры заданий.

 

Как часто мы задаем ребёнку такие вопросы: Сколько тебе лет? Сколько у тебя друзей? Сколько лап у кота?

Чтобы все это посчитать, нужно знать цифры.

А вы не задумывались, откуда пришли числа? Первобытные люди, так же как и современные дети не знали счета. Детей теперь учат, а первобытных людей некому было учить. Их учила сама жизнь. Наблюдая окружающую природу, от которой он полностью зависел, он научился выделять отдельные предметы. Из стаи волков – вожака, из колоса – одно зерно. Поначалу они определяли это соотношение один – много. Частые наблюдения множества, состоящие из пары предметов (глаза, уши, руки, ноги, крылья) привели человека к представлению о числе. Наш далекий предок, когда видел пару уток, он сравнивал их с парой глаз. А если видел больше, то говорил «много». Лишь постепенно человек научился выделять три предмета, ну а потом 4, 5.

Числа были придуманы людьми для счета, а также для фиксирования результатов измерения величин.

Добывая добычу, обменивая её на предметы своего труда, древние люди показывали нужное число на пальцах. Следы счета на пальцах сохранились во многих странах. Например, в Китае и Японии предметы домашнего обихода считают не дюжинами, а пятерками и десятками.

После того как понятия числа сформировалось, числа стали самостоятельными объектами науки «математика» и появилась возможность изучать числа и действий с ними. Наука изучающая числа и действия с ними, получила название «арифметика» (в переводе с греческого число).

Каждое множество равномощно только одному числу. Поскольку число означает количественную характеристику, его называю количественным.

При количественном счете результат не зависит от того, в каком порядке пересчитывались элементы.

Важно только не пропустить элементы при счете и не пересчитывать один и тот же элемент дважды. Количественный счет отвечает на вопрос: «Сколько?»

При счете элементов множества происходит процесс их нумерации. Счет – это процесс упорядочивания множества путём присвоения каждому элементу множества определенного номера. В этом случаи натуральное число обозначает свой порядковый номер некоторого элемента и называется – порядковым.

При порядковом счете результат зависит от того, при какой последовательности пересчитывались элементы. Порядковый счет отвечает на вопрос: «Который по счету?»

Счет – это процесс нумерации элементов множества. Этот процесс подчиняется определенным правилам:

– первому отмеченному предмету ставится в соответствии число 1;

– на каждом следующем шаге, выбирается предмет ещё не отмеченный ранее;

– ему ставится в соответствии число, следующее за последующим из уже названных.

В основу заложен принцип, что каждое последующие число, начиная со второго, на единицу больше предыдущего.

После того, как ребёнок научился считать, то есть знание счета подразумевает знание слов числительных, названия их порядка при счете, понимания смысла процесса нумерации предметов нужно ввести активное использование приема пересчета каких-либо конкретных предметов. Это ему позволит соотносить название числа с определенным предметом или группой предметов, и определения общего количества предметов. Понимание того, что последний названный номер является характеристикой количественного состава множества, и умение соблюдать правила счета.

Большая нагрузка при освоении счета приходится на механическую память, а не мыслительную операцию. Для того чтобы ребёнок не осваивал его на формальном уровне, на первых порах этот процесс следует обязательно сопровождать предметными действиями: откладыванием, показыванием, а также проговариванием вслух.

При формировании операции счета полезно такое задание. Посчитать круги на фланелеграфе так, чтобы красный круг был первым, а теперь так, чтобы красный был вторым, последним. При этом упражнении процесс нумерации не затрагивается и поэтому ребёнком не осмысливается. Дети незнакомые с приведённой выше формой упражнения обычно спрашивают: «С какой стороны считать?» – и ещё пытаются расположить предметы в ряд будучи убеждены, что считать можно только считать можно только в таком положении, и причем только слева на права. Это показывает, что процесс счета у ребенка сформирован только в механическом виде и им не понят, не осмыслен.

В средней группе детского сада детей учили вести счет в пределах 5. Закрепление соответствующих представлений и способов действий служит дальнейшей основой для развития деятельности счета. Большое внимание уделяется навыкам счета; детей, учат вести счет предметов, слева на право, указывая на предмет по порядку, согласовывать числительные с существительными в роде числе, именовать итог счета. Если кто-то не понимает итогового значения последнего названого при счете числа, то ему предлагается обвести сосчитанные предметы рукой. Круговой обобщающий жест, помогает ребёнку соотнести последнее числительное со всей совокупностью предметов.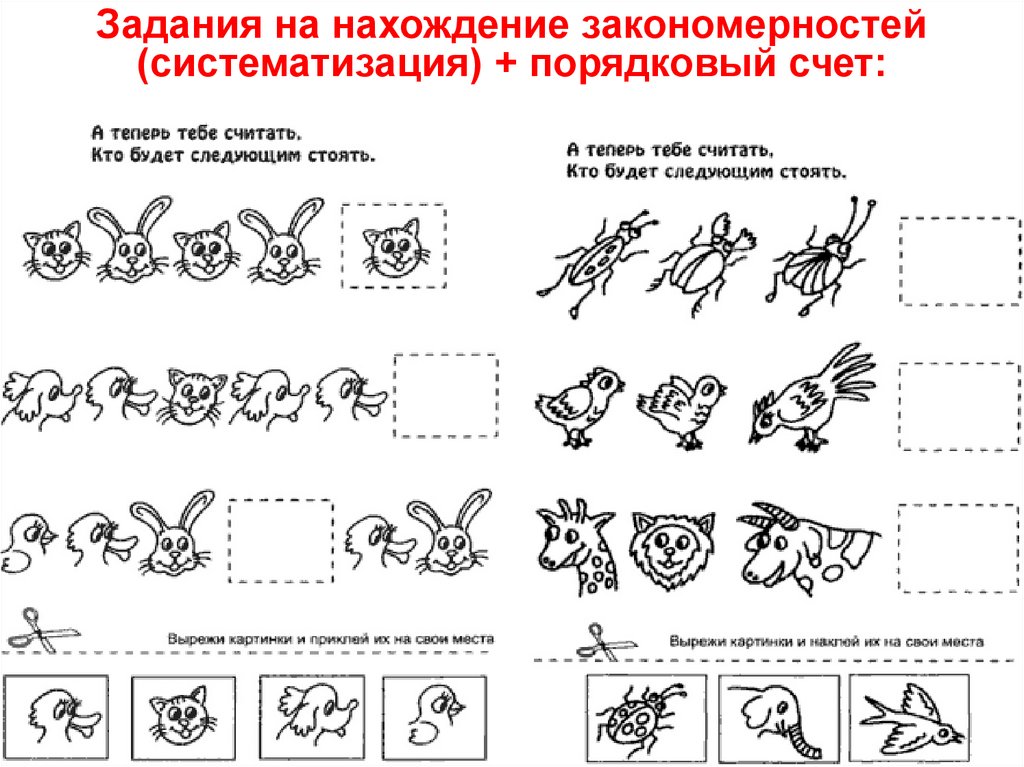 Но в работе с детьми пяти лет он как правило уже не нужен. Детям теперь нужно сосчитать предметы на расстоянии, молча, т.е. про себя. В старшей группе начинает развиваться память на числа. При обучении пятилетних детей количеству детей учат видеть, независимость числа предметов от их пространственных свойств. Предметы могут быть разные по цвету, по форме, но количество остаётся прежним. Детям старшей группы показывают разные приёмы счета. Убеждают, что начинать можно с любого предмета, и вести его в любом направлении, главное не пропускать предметы при счете и не считать один предмет дважды.

Смена дидактического материала, варьирование заданий помогают детям лучше понять способы получения числа и их количественный состав.

В старшей группе детей учат пользоваться порядковыми числительными. Пятилетние дети пользуются числительными, но еще употребляют их не уверенно и часто не верно. Поэтому необходимо раскрыть значение порядковых числительных. Раскрыть порядковое значение числа позволяет сопоставление его с количественным значением.

Когда хотят узнать, сколько предметов их считают: один, два, три, четыре, считая так, находят ответ на вопрос сколько? Но когда нужно найти очередность, место предмета среди других, считают по-иному. Отвечая на вопросы: который? какой по счету? считают: первый, второй, третий, и т.д.

Дети часто путают вопросы который? и какой? Последний требует выделения качественных св-в. предметов: цвета, размера и др. Чередования вопросов: сколько? который? какой по счету? какой? Позволяет раскрыть их значение.

Детям уже не раз показывали. Что для ответа на вопрос сколько? Не имеет значения, в каком порядке считать предметы. Теперь они узнают, что для определения порядкового места предметов среди других направление счета имеет существенное значение. Педагог демонстрирует это, пересчитывая одни и те же предметы в разных направлениях. Он выясняет, например, что среди 7 флажков синий – на пятом месте, если вести счет слева на право, а если считать справа налево, то он на 3 месте.

Дети пробуют определить место предмета среди других, ведя счет в разных направлениях. Делают вывод, что, определяя на котором по счету месте предмет, надо указать направление счета (третий, пятый справа, и.д.).

В качестве счетного материала используют однородные предметы, отличающие цветом и размером, например разноцветные флажки и кружки, елочки разной высоты и т.д., а позднее – совокупности предметов разного вида, например, игрушки (персонажи сказки «Теремок», «Репка»). В порядковом счете детей упражняют на бессюжетном материале, например, на моделях геометрических фигур, полосок разных размеров и т.п. Тренируясь в порядковом счете, они определяют место предмета среди других, находят предмет, занимающий определенное порядковое место (Какой предмет на первом месте, на третьем, пятом месте?), располагают предметы в указанном порядке.

Некоторые дети, определяя место предмета, заменяют порядковые числительные количественными. Педагог прислушивается к тому, как дети ведут счет, указывает на ошибки.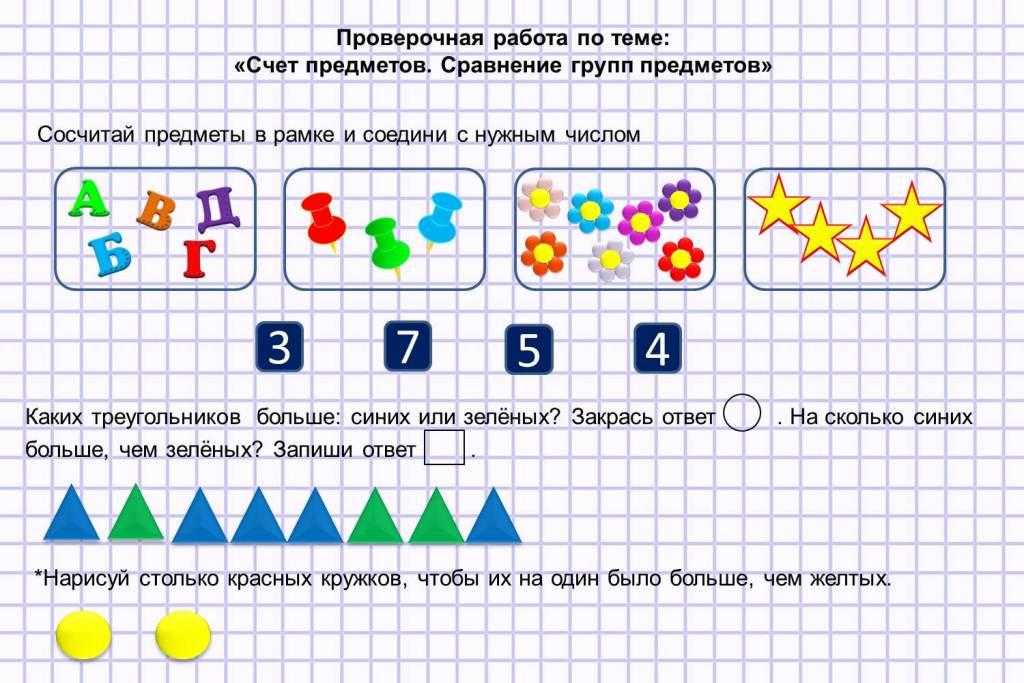 Особенно эффективны так называемые комбинированные упражнения, в которых порядковый счет сочетается с сопоставлением двух и более совокупностей предметов, группировкой геометрических фигур, упорядочиванием предме6тов по размеру.

Обучение порядковому счету, является основной задачей 3-4 занятия, в дальнейшем навыки порядкового счета закрепляются в ходе работы над новым материалом.

М.Монтессори предлагает выполнять методические упражнения, пользуясь в качестве дидактического материала одною из систем брусков.

В какой ни будь день, когда ребенок разложит палочки. Можно предложить пересчитать красные палочки, сини палочки, начать нумерацию от красной палочки или от синей палочки. Эти упражнения позволяют давать порядковое название каждой палочки: палочка номер первый, второй и. т. д.

Умение соотносить число, его название и знак является важным мыслительным действием. Психологи с давних пор вводят этот параметр в определения степени развития мышления человека.

Для закрепления понятия количества по программе Монтессори предлагается детям следующие упражнение:

«Стаканчики с фасолью»

На подносе стоят 10 прозрачных стаканчиков и плошка с крупной фасолью. На каждом стаканчике написана цифра. На последнем стаканчики написано 10. Ребенок раскладывает в стаканчик такое число фасоли, какое написано на стаканчике. Если он выполнит работу правильно, то ни одной фасоли на подносе не останется.

«Математические матрёшки»

В одном отделении лежат 55 маленьких матрешек, а другом гладкие квадратные дощечки с написанными на них крупным шрифтом цифры. Ребенок раскладывает дощечки и на них ставит матрешки, количество должно соответствовать написанным цифрам.

В младшей группе можно провести следующее упражнение:

«Оладушки»

Цель: учить соотносить слово с числительным, числительное с количественным составом множеств.

Способ выполнения.

Используем коробку с большими пуговицами, педагог играет с детьми в «Оладушки».

Читает текст потешки, раздавая детям, играющим по пуговице, называя детей по имени.

Бабушка, бабушка

Испекла оладушки.

Один – Ванечке,

Один – Машеньке и т.д.

Затем пуговицы возвращаются в коробку (Съели оладушки), при этом их можно считать. В другом варианте этого упражнения ребенку дают столько пуговиц, сколько он попросит.

Бабушка, бабушка,

Испекла оладушки.

Ване? (сколько Ване?)

Мише?

И т.д.

Для отработки порядкового счета можно использовать иллюстрацию из произведения К.Чуковского «Тараканище»:

«Ехали медведи

На велосипеде.

А за ними кот

Задом наперед.

А за ним комарики

На воздушном шарике.

 

А за ним раки

На хромой собаке.

Волки на кобыле.

Львы в автомобиле.

Зайчики в трамвайчике.

Жаба на метле…»

Прочитав это произведение, следует показать иллюстрацию.

Необходимо убедиться в том, что ребенок хорошо ориентируется в порядковых отношения, которые в устной речи надо выделять интонацией.

• Сколько персонажей ехало?
• Кто ехал первым?
• Кто ехал четвертым?
• Кто ехал за зайчиками, каким по счету?
• Кто ехал между раками и львами?

 

Используемая литература:

1. А. В. Белошистая. Формирование и развитие математических способностей дошкольников.
2. В. Волина. Праздник числа.
3. В.В.Зайцев. Математика для дошкольников.
4. Л.С. Метлина. Математика в детском саду.
5. Е. Хилтунен. Считаю сам.

Порядковый и количественный счет для дошкольников

24.11.2020

Научить ребенка считать еще до того, как он станет первоклассником? Легко! Для этого нужно разбудить в дошкольнике интерес к математике и простым вычислениям. Конечно же, поможет в этом игра! Играючи можно научиться не только считать, но и отличать количественный счет от порядкового. Забыли, что это и в чем разница? Предлагаем освежить знания.

Математический счет — действие для подсчета чего-либо. В школе учат порядковый и количественный счет. О них и поговорим.

Содержание:

• Что такое количественный счет
• Что такое порядковый счет
• Счета порядковый и количественный — 5 отличий
  • Цели
  • Числительные
  • Вопросы и ответы
  • Направление
  • Значение
• Игры для закрепления материала
  • “На облаках” с порядковым счетом
  • Игра для количественного и порядкового счета — Радуга-дуга
  • Игра — день рождения Лунтика
• Полезные рекомендации

Что такое количественный счет

Количественный счет подразумевает собой ответ на вопрос: “Сколько?”.

Как только ребенок запомнит вопрос, он поймет, что от него требуется. Конечно же, информация лучше всего усваивается в виде игровых упражнений.

Пример: разложите перед малышом предметы. Задайте ему вопрос, дайте возможность посчитать и ответить.

Игру можно постепенно усложнять. Например, добавляя или удаляя некоторые из предметов, группируя по признакам и пр.

Что такое порядковый счет

Порядковый счет связан с вопросом: “Какой по счету?”.

Все просто. Снова игра и предметы, желательно чем-то между собой отличающиеся, например, фломастеры. Порядковый от слов “порядок, по порядку”, это поможет ребенку запомнить главный вопрос. Попросите его определить порядковый номер любого из предметов.

Усложняя игровые задания, меняйте предметы местами, забирайте или добавляйте новые, предлагая ребенку объяснить, как и почему меняется порядковый номер.

Счета порядковый и количественный — 5 отличий

Общего между ними только счет. Придется считать, чтобы получить в конечном итоге ответ на вопрос. Все остальное — отличия:

• цели;
• числительные;
• вопросы;
• направление;
• значение.

На первый взгляд сложно. Для малыша дошкольника может быть даже непостижимо, но стоит немного поиграть и все станет ясно!

Цели

Количественным счетом пользуются для подсчета чего-либо. Конечная цель — определить общее число. Порядковый счет нужен для определения номера предмета в упорядоченном множестве.

Простой пример. Разложите в ряд фрукты: яблоко, грушу, мандарин, апельсин и гранат. Количественный счет нам поможет посчитать сколько всего фруктов на столе — 5.

Порядковый нужен, чтобы определить порядковый номер каждого фрукта в ряду. Яблоко — первое, груша — вторая, мандарин — третий, апельсин — четвертый и гранат — пятый. То же самое можно сделать справа налево, порядковые номера фруктов в таком случае поменяются.

Числительные

Порядковый счет невозможен без числительных порядковых (указывают на порядок предмета в ряду последовательности), а количественный — количественных (указывают на количество).

Например, один, два, три — количественные, первый, второй, третий — порядковые числители.

Вопросы и ответы

Запомнить, чем отличается порядковый счет от числительного детям проще всего по вопросам. “Сколько?” — числительный, “какой, какую по счету?” — порядковый.

В эту игру с примерами можно играть целый день, пока ребенок не запомнит информацию. Задавайте вопросы обо всем, что его окружает. Например:

Сколько ножек у табуретки?

Сколько пальчиков на руке?

Сколько комнат в квартире?

или

Какой у нас этаж?

Какую по счету конфету ты ешь?

Направление

Чтобы посчитать сколько всего предметов не важно, как это делать справа налево или наоборот. Цель — определить общее количество. Узнать номер предмета в множестве можно только после указания направления. Порядковые номера меняются в зависимости от того, считать справа налево или наоборот.

Пример:

Покажешь третью птичку справа?

Какого цвета второй домик слева?

Это задачи для определения порядкового номера с указанием направления. Объясните ребенку, что общее число предметов от изменения направления не меняется.

Значение

Количественный счет указывает на совокупность предметов, а порядковый помогает определить место каждого.

 

Игры для закрепления материала

“На облаках” с порядковым счетом

Интересная игра для закрепления порядкового счета с самыми маленькими. Для игры вам понадобится любая небольшая игрушка меньше листа формата А4. Игрушка — главный герой игры. Она будет кататься на пушистых облаках.

На роль облаков подойдут обычные белые листы формата А4. Кстати, предлагая ребенку представить листы в виде забавных облаков, вы подтолкнете его немного пофантазировать.

Итак, что нужно сделать. Разложите листы-облака в ряд. Усадите игрушку на любой из них. Начинайте задавать вопросы:

Сколько всего облаков, посчитаем?

Все облака одинаковые?

Покажешь, где сидит игрушка?

А как нам узнать на каком облаке она катается?

Отвечая на вопросы, ребенок будет считать облака, сможет выяснить для себя, что игрушка сидит на первом, втором или третьем. Играть в эту игру можно долго. Игрушке скоро станет скучно на своем облаке, она захочет пересесть на другое, а потом на следующее и т.д. Играя, продолжайте задавать ребенку наводящие вопросы.

Игра для количественного и порядкового счета — Радуга-дуга

Вам нужны будут разноцветные одинаковые предметы. В идеале 5-7 цветов. Это может быть все, что угодно — от элементов конструкторов и кубиков до вырезанных фигур из картона, мячей, пластиковых тарелок и пр.

Чтобы закрепить количественный счет, просто предлагайте ребенку считать предметы. Усложняйте задания, группируя их по цветам или каким-то отдельным признакам.

Упражняясь в порядковом счете, предлагайте малышу назвать номер предмета по цвету и наоборот. Например:

Какого цвета третий мячик по счету?

Синий кубик справа какой по счету?

Покажи вторую прищепку слева, какого она цвета?

Меняйте предметы, направление счета, количество до того, как ребенок начнет терять интерес к происходящему.

Игра — день рождения Лунтика

Если ребенок не знает или не любит Лунтика, можете заменить его любым другим героем из мультика. Итак, как играть.

Вместе с ребенком или самостоятельно нужно вырезать из картона 5 одинаковых воздушных шаров на палочке. Под одним нарисуйте праздничный торт. Цель игры — закрепить в сознании ребенка мысль о том, что порядковый номер всегда указывает на конкретный предмет и зависит от направления счета.

Суть истории в следующем. У Лунтика день рождения. Все гости решили подарить ему по воздушному шару. Но кое-кто не смог удержаться и приготовил для именинника праздничный торт. Лунтик знает, что его ждет сюрприз. Об этом ему по секрету рассказали гусеницы. Но кроме того, что сюрприз будет у гостя, который принесет второй шарик, ему ничего не известно!

Задание: Найти второй шарик и убедиться, что вместе с ним Лунтик получит торт. Для начала попробуйте это сделать за именинника. Пусть для видимости он начнет считать не с того конца, пропускать шарики или менять их местами. Главное — наглядно показать малышу, что направление счета влияет на конечный результат.

Вариации игры разные. Можно менять шарики местами, забирать, добавлять и т.д. Каждый раз ребенок должен определять, что поменялось, почему, каким стал порядковый номер шара с праздничным тортом.

Полезные рекомендации

Чтобы заинтересовать малышей до 4-х летом счетом, расскажите им что это поможет узнать общее число предметов и найти место для каждого. Впрочем, не стоит ждать от дошколят слишком многого. Они будут путаться, иногда откровенно скучать и даже вредничать. В силу возраста им не так просто понять математическую разницу между порядковыми и количественными числительными даже если это просто игра.

Проявите терпение и доброжелательность. Не бросайте попыток помочь ребятам усвоить материал в игровой форме, мягко поправляйте, если они ошибаются. Постарайтесь выучить с крохой, что “один, два, три” нужны для того, чтобы узнать сколько всего предметов, а “какой” — для определения места.

Пользуйтесь подручными предметами, фантазируйте и взаимодействуйте с ребенком в удовольствие. Это самый простой способ с раннего детства привить если не любовь, то интерес к математике. Играйте в игры, описанные выше, придумывайте свои сценарии и не забывайте отмечать прогресс, постепенно усложняя занятия.

Номинальный, порядковый, интервальный и относительный: простое объяснение

Если вы новичок в мире количественного анализа данных и статистики, вы, скорее всего, столкнулись с четырьмя всадниками уровней измерения : номинальный, порядковый, интервал и отношение . И если вы попали сюда, вы, вероятно, немного сбиты с толку или не уверены в них.

Не напрягайтесь — в этом посте мы объясним номинальный, порядковый, интервальный и относительный уровни измерения в простых терминах , с загрузками практических примеров .

Обзор: уровни измерения

Вот что мы рассмотрим в этом посте. Нажмите, чтобы перейти непосредственно к этому разделу.

• Что такое уровни измерения в статистике?
• Номинальные данные
• Порядковые данные
• Интервальные данные
• Данные соотношения
• Почему это важно?
• Резюме и визуальное резюме

Уровни измерения 101

Когда вы собираете данные опроса (или любые количественные данные) для своего исследовательского проекта, вы столкнетесь с двумя типами данных — категориальными и/или числовыми . Они отражают разные уровни измерения.

Категориальные данные  – это данные, отражающие характеристики или категории (это неудивительно!). Например, категориальные данные могут включать такие переменные, как пол, цвет волос, этническая принадлежность, предпочтение кофе и т. д. Другими словами, категориальные данные — это, по сути, способ присвоения чисел качественным данным (например, 1 для мужчин, 2 для женщин и т. д.). на).

Числовые данные , с другой стороны, отражают данные, которые по своей природе основаны на числах и количественны. Например, возраст, рост, вес. Другими словами, это вещи, которые естественным образом измеряются числами (т. е. количественными), а не категориальными данными (которые предполагают присвоение чисел качественным характеристикам или группам).

В каждой из этих двух основных категорий есть два уровня измерения:

1. Категория данные – номинальные и порядковые
2. Числовые данные – интервал и соотношение

Давайте рассмотрим каждый из них вместе с некоторыми практическими примерами.

Что такое номинальные данные?

Как мы уже говорили, номинальные данные — это категориальный тип данных, поэтому они описывают качественные характеристики или группы без порядка или ранга между категориями. Примеры номинальных данных включают:

• Пол, этническая принадлежность, цвет глаз, группа крови
• Марка холодильника/автомобиля/телевизора в собственности
• Предпочтения политического кандидата, предпочтение шампуня, любимая еда

Во всех этих примерах параметры данных категориальные , и нет ранжирования или естественного порядка . Другими словами, все они имеют одинаковую ценность — один не стоит выше другого. Таким образом, вы можете просматривать номинальные данные как самый базовый уровень измерения , отражающий категории без ранга или порядка.

Что такое порядковые данные?

Порядковые данные поднимают ситуацию на новый уровень. Это то же самое, что и номинальные данные, в том, что они рассматривают категории, но в отличие от номинальных данных, между вариантами также есть значимый порядок или ранг. Вот несколько примеров порядковых данных:

• Уровень дохода (например, низкий доход, средний доход, высокий доход)
• Уровень согласия (например, категорически не согласен, не согласен, нейтрально, согласен, полностью согласен)
• Политическая ориентация (например, крайняя левая, левая, центральная, правая, крайне правая)

Как вы можете видеть в этих примерах, все опции по-прежнему являются категориями, но между опциями есть разница в порядке или ранжировании . Вы не можете численно измерить различия между вариантами (потому что это, в конце концов, категории), но вы можете упорядочить и/или логически ранжировать их. Таким образом, вы можете рассматривать порядковый номер как несколько более сложный уровень измерения, чем номинальный.

Что такое интервальные данные?

Как мы обсуждали ранее, интервальные данные представляют собой числовые данные тип. Другими словами, это уровень измерения, который включает в себя данные, которые являются естественно количественными (обычно измеряются в числах). В частности, интервальные данные имеют порядок (как и порядковые данные), плюс промежутки между точками измерения равны (в отличие от порядковых данных).

Звучит немного пушисто и концептуально? Давайте взглянем на несколько примеров интервальных данных:

• Кредитные баллы (300 – 850)
• Баллы за GMAT (200–800)
• балл IQ
• Температура по Фаренгейту

Важно отметить, что во всех этих примерах интервальных данных точки данных являются числовыми , но нулевая точка является произвольной . Например, температура в ноль градусов по Фаренгейту не означает, что температуры нет (или вообще нет тепла) — это просто означает, что температура на 10 градусов меньше, чем 10. Точно так же вы не можете получить нулевой балл за баллы или балл за GMAT. .

Другими словами, интервальные данные — это уровень измерения, равный числовое (и можно измерить расстояние между точками), но что не имеет осмысленной нулевой точки — ноль произвольный.

Короче говоря, данные интервального типа предлагают более сложный уровень измерения, чем номинальные и порядковые данные, но он все же не идеален. Введите данные соотношения…

Что такое данные соотношения?

Данные отношения являются наиболее сложным уровнем измерения. Как и интервальные данные, это упорядочено/ранжировано , а числовое расстояние между точками постоянно (и может быть измерено). Но что делает его королем измерения, так это то, что нулевая точка отражает абсолютный нуль (в отличие от произвольной нулевой точки интервальных данных). Другими словами, измерение нуля означает, что эта переменная не существует.

Вот несколько примеров данных соотношения:

• Вес, рост или длина тела
• Температура в Кельвинах (поскольку ноль Кельвинов означает нулевое тепло)
• Длина времени/продолжительность (например, секунды, минуты, часы)

Во всех этих примерах вы можете видеть, что нулевая точка является абсолютной . Например, ноль секунд буквально означает нулевую продолжительность. Точно так же нулевой вес означает невесомость. Это не какое-то произвольное число. Это то, что делает данные типа отношения наиболее сложным уровнем измерения.

С помощью данных соотношения вы можете не только осмысленно измерять расстояния между точками данных (т. е. складывать и вычитать), но и осмысленно умножить и разделить . Например, 20 минут действительно в два раза больше времени, чем 10 минут. Вы не могли бы сделать это с кредитными баллами (т.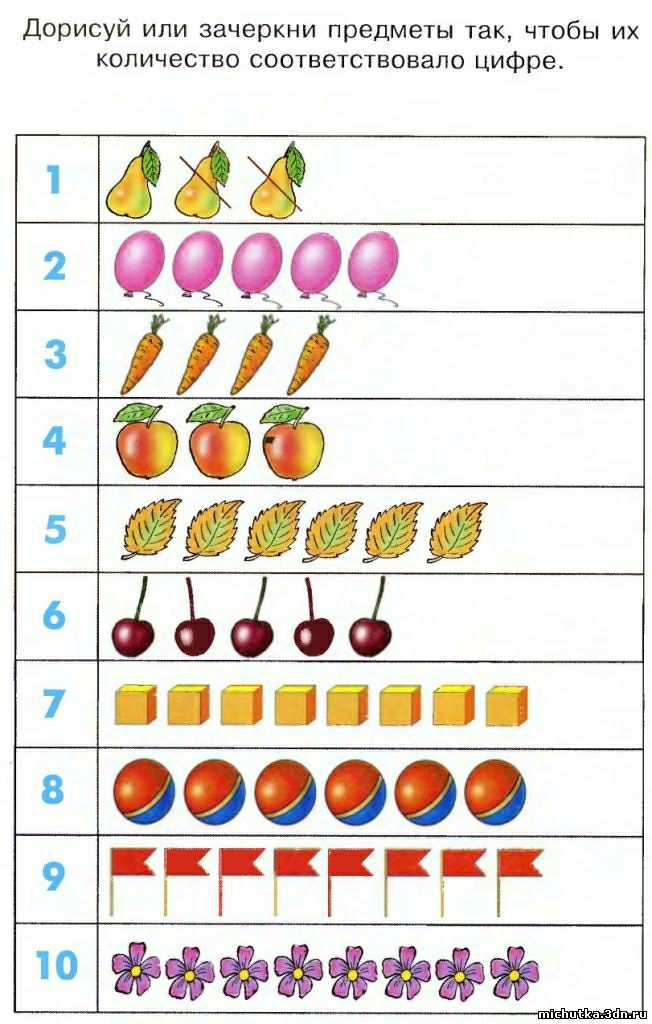 е. интервальными данными), поскольку не существует такого понятия, как нулевой кредитный рейтинг. Вот почему данные отношения являются королем в мире уровней измерений.

Почему это важно?

В этот момент вы, вероятно, думаете: «Ну, Дерек, это милые придирки, но какое это имеет значение?». Это хороший вопрос. И есть хороший ответ .

Причина, по которой важно понимать уровни измерения в ваших данных — номинальный, порядковый, интервальный и относительный — заключается в том, что они непосредственно влияют на то, какие статистические методы вы можете использовать в своем анализе. Каждый статистический тест работает только с определенными типами данных. Некоторые методы работают с категориальными данными (т. е. номинальными или порядковыми данными), в то время как другие работают с числовыми данными (т. е. с интервальными или относительными данными), а некоторые работают с смесь . Хотя статистическое программное обеспечение, такое как SPSS или R, может «позволить» вам провести тест с неправильным типом данных, ваши результаты будут в лучшем случае ошибочными , а в худшем — бессмысленными.

Вывод: убедитесь, что вы понимаете различия между различными уровнями измерения, прежде чем принимать решение о методах статистического анализа. Более того, подумайте о том, какой тип данных вы хотите собрать на этапе разработки опроса (и соответствующим образом разработайте свой опрос), чтобы вы могли проводить самый сложный статистический анализ, как только вы получите свои данные.

Подведем итоги.

В этом посте мы рассмотрели четыре уровня измерения – номинальное, порядковое, интервальное и отношение . Вот визуальное резюме каждого.

Помните, что уровень измерения напрямую влияет на то, какие статистические методы вы можете использовать в своем анализе, поэтому убедитесь, что вы всегда классифицируете свои данные, прежде чем применять тот или иной метод.

Номинальный, порядковый, интервальный и относительный

При выполнении любого вида сбора или анализа данных важно понимать природу данных, с которыми вы имеете дело. В вашем наборе данных у вас будут разные переменные, и эти переменные могут быть записаны с разной степенью точности. Это то, что известно как уровень измерения.

Существует четыре основных уровня измерения: номинальный , порядковый , интервальный и коэффициент . В этом руководстве мы объясним, что именно подразумевается под уровнями измерения в области данных и статистики, и почему это важно. Затем мы подробно рассмотрим четыре уровня измерения, предоставив несколько примеров для каждого из них.

Хотите пропустить? Просто воспользуйтесь интерактивным меню.

1. Каковы уровни измерения в данных и статистике?
2. Почему важны уровни измерения?
3. Каковы четыре уровня измерения?
4. Номинальный уровень
5. Порядковый уровень
6. Интервальный уровень
7. Уровень отношения
8. Уровни измерения: FAQ
9. Ключевые выводы

Приступим!

При сборе данных вы собираете различные типы информации, в зависимости от того, что вы хотите исследовать или выяснить. Например, если вы хотите проанализировать покупательские привычки людей, живущих в Токио, вы можете разослать опрос 500 людям с вопросами об их доходах, их точном местонахождении, возрасте и том, сколько они тратят на различные продукты и услуги. Это ваши переменные: данные, которые можно измерить и записать, и значения которых будут отличаться от одного человека к другому.

Когда мы говорим об уровнях измерения, мы говорим о том, как измеряется каждая переменная, и о математической природе значений, присвоенных каждой переменной. Это, в свою очередь, определяет, какой тип анализа может быть выполнен.

Предположим, вы хотите собрать данные о доходах людей. Существуют различные уровни измерения, которые вы можете использовать для этой переменной. Вы можете попросить людей указать точную цифру или попросить их выбрать ответ из множества диапазонов, например: (а) 10–19.к, (б) 20-29к, (в) 30-39к и так далее. Вы можете попросить их просто классифицировать свой доход как «высокий», «средний» или «низкий».

Видите, как различаются по точности эти уровни? Если вы спросите у участников точную цифру, вы сможете рассчитать, насколько сильно различаются доходы по всему вашему набору данных (например). Однако, если у вас есть только классификации «высокий», «средний» и «низкий», вы не сможете точно увидеть, сколько зарабатывает один участник по сравнению с другим. Вы также не имеете представления о том, какая зарплата считается «высокой», а какая «низкой» — эти классификации не имеют числового значения. Таким образом, последний представляет собой менее точный уровень измерения.

Итак, в двух словах: Уровень измерения относится к тому, насколько точно была измерена переменная .

2. Почему важны уровни измерения?

Уровень измерения важен, поскольку он определяет тип статистического анализа, который вы можете выполнить. В результате это влияет как на характер, так и на глубину понимания, которое вы можете извлечь из своих данных. Некоторые статистические тесты могут быть выполнены только при использовании более точных уровней измерения, поэтому важно заранее спланировать, как вы будете собирать и измерять свои данные.

3. Какие существуют четыре уровня измерения? Объяснение номинальных, порядковых, интервальных и относительных шкал

Существует четыре уровня измерения (или шкал), о которых следует знать: номинальный , порядковый , интервальный и относительный . Каждая шкала основывается на предыдущей, а это означает, что каждая шкала не только «отмечает те же поля», что и предыдущая шкала, но также добавляет еще один уровень точности.

Итак:

• Номинальная шкала просто классифицирует переменные в соответствии с качественными метками (или именами). Эти метки и группы не имеют никакого порядка или иерархии, и они не передают никакого числового значения. Например, переменная «цвет волос» может быть измерена по номинальной шкале в соответствии со следующими категориями: светлые волосы, каштановые волосы, седые волосы и так далее. Узнайте больше в этом полном руководстве по номинальным данным.
• Порядковая шкала также классифицирует переменные по маркированным группам, и эти категории имеют порядок или иерархию для них. Например, вы можете измерить переменную «доход» по порядковой шкале следующим образом: низкий доход, средний доход, высокий доход. Другим примером может быть уровень образования, классифицируемый следующим образом: средняя школа, степень магистра, докторская степень. Это все еще качественные метки (как и в случае с номинальной шкалой), но вы можете видеть, что они следуют иерархическому порядку. Узнайте больше в этом руководстве по порядковым данным.
• Интервальная шкала — это числовая шкала, которая маркирует и упорядочивает переменные с известным, равноотстоящим интервалом между каждым из значений. Часто цитируемым примером интервальных данных является температура в градусах по Фаренгейту, где разница между 10 и 20 градусами по Фаренгейту точно такая же, как разница, скажем, между 50 и 60 градусами по Фаренгейту. Узнайте больше об интервальных данных в этом руководстве.
• Шкала отношений точно такая же, как шкала интервалов, с одним ключевым отличием: Шкала отношений имеет так называемый «истинный ноль». Хорошим примером данных соотношения является вес в килограммах. Если что-то весит ноль килограммов, оно действительно ничего не весит — по сравнению с температурой (интервальные данные), где значение ноль градусов не означает, что «температуры нет», это просто означает, что здесь очень холодно! Полное руководство по соотношению данных вы найдете здесь.

Еще один способ представить уровни измерения — это отношения между значениями, присвоенными данной переменной . При номинальной шкале нет связи между значениями; нет никакой связи между категориями «светлые волосы» и «черные волосы», например, при взгляде на цвет волос. Шкала отношений, с другой стороны, очень красноречиво говорит о взаимосвязи между значениями переменных.

Например, если вашей переменной является «количество клиентов» (которая представляет собой данные об отношении), вы знаете, что значение четырех клиентов в два раза превышает значение двух клиентов. Таким образом, вы можете получить гораздо более точное и точное понимание взаимосвязи между значениями в математических терминах.

В этом смысле существует неявная иерархия четырех уровней измерения. Анализ номинальных и порядковых данных, как правило, менее чувствителен, в то время как шкалы интервалов и отношений поддаются более сложному статистическому анализу. Имея это в виду, как правило, предпочтительнее работать с интервальными и относительными данными.

Теперь мы ввели четыре уровня измерения, давайте рассмотрим каждый уровень более подробно.

4. Номинальный уровень

Что такое номинальный уровень?

Номинальный уровень — это первый уровень измерения, самый простой. Он качественно классифицирует и маркирует переменные. Другими словами, он делит их на именованные группы без какого-либо количественного значения. Важно отметить, что даже если числа используются для обозначения различных категорий, эти числа не имеют никакого числового значения.

Например: если вы собирали данные о цвете волос, при вводе данных в электронную таблицу вы можете использовать цифру 1 для представления светлых волос, цифру 2 для обозначения седых волос и т. д. Эти цифры — просто ярлыки; они не передают никакого математического смысла.

При использовании номинальной шкалы помните, что группы, которые вы используете для классификации переменных, не имеют порядка. Одна категория не выше, не лучше и не выше другой.

Примеры номинальных данных

Некоторые примеры номинальных данных включают:

• Цвет глаз (например, голубой, карий, зеленый)
• Национальность (например, немец, камерунец, ливанец)
• Тип личности (например, интроверт, экстраверт, амбициозный) )
• Статус занятости (например, безработный, неполный рабочий день, пенсионер)
• Политическая партия, за которую голосовали на последних выборах (например, партия X, партия Y, партия Z)
• Тип принадлежащего смартфона (например, iPhone, Samsung, Google Pixel)

Как видите, номинальные данные описывают определенные атрибуты или характеристики.

Как анализировать номинальные данные

1. Описательная статистика для номинальных данных

Описательная статистика описывает или обобщает характеристики вашего набора данных. Две полезные описательные статистики для номинальных данных:

• Частотное распределение
• Мода

Таблица частотного распределения (например, сводная таблица) суммирует, сколько ответов было получено для каждой категории, например, сколько людей выбрали «каштановые волосы», как многие выбрали «блондинку» и так далее. Вы также можете использовать проценты, а не количество, и в этом случае ваша таблица покажет вам, какой процент от общей выборки имеет волосы какого цвета.

Вот как могла бы выглядеть сводная таблица для нашего примера цвета волос с количеством и процентами:

Режим — это мера центральной тенденции, и это значение, которое чаще всего встречается в вашем наборе данных. Итак, если 38 из 129 респондентов имеют седые волосы, а это максимальное количество, то это ваш режим.

2. Статистические тесты для анализа номинальных данных

Вы можете анализировать номинальные данные, используя определенные непараметрические статистические тесты, а именно:

• Критерий согласия хи-квадрат , если вы смотрите только на одну переменную. Это позволяет вам оценить, являются ли собранные вами выборочные данные репрезентативными для всего населения. Он делает это, оценивая степень, в которой ваши наблюдения отклоняются от того, что вы ожидали или предположили.
• Критерий независимости Хи-квадрат используется для изучения взаимосвязи между двумя номинальными переменными. Это делается путем сравнения частоты каждой категории одной номинальной переменной с категориями второй номинальной переменной, что позволяет вам увидеть, есть ли какая-то корреляция.

5. Порядковый уровень

Что такое порядковый уровень?

Порядковый уровень измерения группирует переменные по категориям, как и номинальная шкала, но также передает порядок переменных. Например, оцените, насколько сильно вы испытываете боль, по шкале от 1 до 5 или классифицируйте свой доход как высокий, средний или низкий.

Как видно из этих примеров, существует естественная иерархия категорий, но мы не знаем, какова количественная разница или расстояние между каждой из категорий. Мы не знаем, сколько зарабатывает респондент А в категории «высокий доход» по сравнению с респондентом Б в категории «средний доход»; также невозможно сказать, насколько болезненнее оценка 3 по сравнению с оценкой 1.

Таким образом, хотя порядковый уровень измерения более точен, чем номинальная шкала, это все же качественная мера и, следовательно, не такая точная. или информативными, как шкалы интервалов и отношений.

Примеры порядковых данных

Некоторые примеры порядковых данных включают:

• Академические оценки (A, B, C и т. д.)
• Счастье по шкале от 1 до 10 (это то, что известно как шкала Лайкерта). )
• Удовлетворенность (чрезвычайно удовлетворена, вполне удовлетворена, слегка не удовлетворена, крайне не удовлетворена)
• Доход (высокий, средний или низкий). Обратите внимание, что по умолчанию доход не является порядковой переменной; это зависит от того, как вы решите его измерить.
• Уровень законченного образования (средняя школа, бакалавриат, магистратура)
• Стаж работы (младший, средний, старший)

Как видно из наших примеров, порядковая шкала естественным образом ранжирует переменные в значимом порядке или иерархии.

Как анализировать порядковые данные

1. Описательная статистика для порядковых данных

Для обобщения порядковых данных можно использовать следующие описательные статистики:

• Частотное распределение
• Диапазон

Частотное распределение описывает, обычно в табличном формате, как распределяются ваши порядковые данные со значениями, выраженными либо в виде числа, либо в процентах. Давайте представим, что вы провели опрос, спрашивая людей, насколько болезненным для них было нанесение татуировки (по шкале от 1 до 5). Вот как может выглядеть ваша таблица распределения частот:

Мода и медиана — это меры центральной тенденции (другой возможной мерой центральной тенденции является среднее значение, но это не относится к порядковым данным). Мода — это просто значение, которое чаще всего появляется в вашем наборе данных. В наших сводных таблицах мы видим, что рейтинг боли «5» получил наибольшее количество баллов, так что это режим.

Медиана — это среднее значение в вашем наборе данных, и оно полезно, поскольку дает представление о среднем ответе или предоставленном значении. Если вы упорядочите ответы всех респондентов (т. е. их рейтинг боли) в порядке возрастания, вы сможете вычислить медианное (среднее) значение. В следующем примере мы выделили медиану красным цветом:

В наборе данных с нечетным числом ответов (как в нашем случае, когда мы представили небольшую гипотетическую выборку из тридцати), медианой является среднее число. В наборе данных с четным числом ответов медиана представляет собой среднее значение двух средних чисел. Однако имейте в виду, что с порядковыми данными не всегда возможно или целесообразно вычислять медиану. Например, если вашими средними значениями были «согласен» и «полностью согласен», вычислить среднее значение было бы невозможно; поэтому в этом случае у вас не будет медианного значения.

Последнее описание, которое вы можете использовать для порядковых данных, это изменчивость . Изменчивость определяет самые высокие и самые низкие значения в вашем наборе данных и сообщает вам диапазон, т.е. Насколько самые высокие и самые низкие значения отличаются друг от друга. При рассмотрении изменчивости важно убедиться, что ваши переменные имеют числовое кодирование (т. е. представлены числовыми метками). В нашем примере с оценкой боли при татуировке это уже так: респонденты оценивают свою боль по шкале от 1 до 5. Однако, если бы вы попросили участников выбрать из ряда категорий, таких как «безболезненный», «слегка болезненный», «болезненный», «очень болезненный» и «мучительный», вам нужно было бы преобразовать эти оценки в числа ( например, 1 = безболезненно, 2 = слегка болезненно и т. д.).

После числового кодирования данных вы просто ищете самые высокие и самые низкие значения, которые появляются в вашем наборе данных. Если самая высокая оценка боли была «очень болезненная», ваше максимальное значение будет равно 4. Но если хотя бы один респондент ответил «мучительно», ваше максимальное значение будет равно 5.

После того, как вы определили самую высокую и самую низкую значений, просто вычтите наименьшее из самого высокого, чтобы получить диапазон. Так, например: 5 − 1 = 4, что означает, что 4 — это ваш диапазон. Это полезно, поскольку сразу показывает, что по крайней мере один респондент дал оценку боли на любом конце шкалы.

2. Статистические тесты для анализа порядковых данных

То, как вы анализируете порядковые данные, зависит как от ваших целей (что вы надеетесь исследовать или достичь?), так и от количества и типа выборок данных, с которыми вы работаете. Как и номинальные данные, порядковые данные анализируются с использованием непараметрических тестов. Некоторые возможные варианты включают:

• Медианный тест настроения , который позволяет сравнивать медианы двух или более выборок данных.
• U-тест Манна-Уитни для сравнения суммы рейтингов баллов по двум независимым выборкам данных. Например: как показатели счастья людей, живущих в Берлине, соотносятся с показателями счастья людей, живущих в Нью-Йорке?
• Тест Уилкоксона на соответствие пар со знаком . Это рассматривает распределение оценок в двух зависимых выборках данных, сравнивая, насколько они различаются (направление различия) и в какой степени (величина различия). Например: как отличаются показатели счастья среди жителей Нью-Йорка для тех, кто живет в центре города, по сравнению с теми, кто живет в пригороде?
• Тест Крускала-Уоллиса H , который сравнивает среднее (среднее) ранжирование оценок по трем или более выборкам данных. Например: как различаются показатели счастья между работающими полный рабочий день, частично занятыми и безработными людьми в возрасте 30 лет?
• Ро Спирмена (эффективная ранговая корреляция) . Это исследует, есть ли связь (или корреляция) между двумя порядковыми переменными. Например: существует ли связь между оценкой счастья (1–5) и уровнем дохода (высоким, средним и низким)?

6. Уровень интервала

Что такое уровень интервала?

Интервальный уровень — это числовой уровень измерения, который, как и порядковая шкала, упорядочивает переменные. Однако, в отличие от порядковой шкалы, интервальная шкала имеет известное и равное расстояние между каждым значением на шкале (представьте себе точки на термометре).

В отличие от шкалы отношений (четвертый уровень измерения), интервальные данные не имеют истинного нуля; другими словами, значение нуля на шкале интервалов не означает, что переменная отсутствует. Это лучше всего объяснить на примере температуры. Температура в ноль градусов по Фаренгейту не означает, что «температура не измеряется», скорее, это означает очень низкую или холодную температуру.

Примеры интервальных данных

Некоторые примеры интервальных данных включают:

• Температура в градусах Фаренгейта или Цельсия (но не в Кельвинах) 59k и т. д.)

Как анализировать интервальные данные

1. Описательная статистика для интервальных данных

Одним из первых шагов в процессе анализа данных является суммирование ваших данных. Для интервальных данных можно получить следующую описательную статистику:

• Распределение частот
• MODE , Медиана и среднее значение
• Диапазон , Стандартное отклонение и DISACE частотное распределение представляет сводку данных в виде таблицы, позволяющей увидеть, как часто встречается каждое значение (либо в виде количества, либо в процентах).

  Режим , медиана и среднее значение являются мерами центральной тенденции. Мода — это наиболее часто встречающееся значение; медиана — это среднее значение (обратитесь к разделу об порядковых данных для получения дополнительной информации), а среднее — это среднее значение всех значений. Итак, чтобы вычислить среднее значение, сложите все значения вместе, а затем разделите на общее количество значений.

  Диапазон , стандартное отклонение и дисперсия — все это меры изменчивости в вашем наборе данных. Вы можете рассчитать диапазон, вычитая наименьшее значение в вашем наборе данных из наибольшего. Стандартное отклонение вычисляет в среднем, насколько каждая отдельная оценка отклоняется от среднего значения, что позволяет вам оценить, как распределяются ваши данные.

  Дисперсия показывает, насколько далеко и широко разбросаны числа в заданном наборе данных от их среднего значения. Эти концепции могут сбивать с толку, поэтому стоит глубже изучить разницу между дисперсией и стандартным отклонением. А пока давайте посмотрим, как можно анализировать интервальные данные.

  2. Статистические тесты для анализа интервальных данных

  Если ваши интервальные данные имеют нормальное распределение, вы можете запускать как параметрические, так и непараметрические тесты. Однако параметрические тесты более мощные, поэтому мы сосредоточимся на них. Вот некоторые из наиболее распространенных параметрических тестов, которые вы можете использовать:

  • Т-тест для сравнения средних значений двух выборок данных. Например: какова разница в среднем показателе IQ сорокапятидесятилетних, живущих в Лондоне и Лидсе?
  • ANOVA тест для сравнения средних значений по трем или более выборкам данных. Например: какова разница в среднем показателе IQ сорокапятидесятилетних, живущих в Лондоне, Лидсе и Бирмингеме?
  • Пирсона r , чтобы увидеть, существует ли корреляция между двумя переменными. Например: существует ли связь между диапазоном доходов человека и его показателем IQ?
  • Простая линейная регрессия для моделирования или прогнозирования связи между двумя переменными или влияния одной переменной на другую. Например: можно ли использовать показатель IQ человека для прогнозирования диапазона его заработной платы?

  7.

  Уровень коэффициента

  Что такое уровень коэффициента?

  Четвертый и последний уровень измерения — это уровень отношения. Как и шкала интервалов, шкала отношений представляет собой количественный уровень измерения с равными интервалами между каждой точкой. Что отличает шкалу отношений, так это то, что она имеет истинный ноль. То есть значение нуля на шкале отношений означает, что измеряемая вами переменная отсутствует. Население является хорошим примером данных отношения. Если у вас нулевой подсчет населения, это означает, что людей нет!

  Итак, каковы последствия «истинного нуля»? Как следует из названия, наличие истинного нуля позволяет вам рассчитать соотношение ваших значений. Например, если у вас есть население в пятьдесят человек, вы можете сказать, что это половина размера страны с населением в сто человек.

  Примеры данных отношений

  Переменные отношений могут быть дискретными (т. е. выражаться в конечных счетных единицах) или непрерывными (потенциально принимающими бесконечные значения). Вот несколько примеров данных соотношения:

  • Вес в граммах (непрерывно)
  • Количество сотрудников в компании (дискретно)
  • Скорость в милях в час (непрерывно)
  • Длина в сантиметрах (непрерывно)
  • Возраст в годах (непрерывно)
  • Доход в долларов (непрерывно)
  • Объем продаж за один месяц (дискретно)

  Как анализировать данные об отношениях

  Самое замечательное в данных, измеренных на шкале отношений, заключается в том, что для их анализа можно использовать почти все статистические тесты. Так как же анализировать данные о соотношении? Давайте взглянем.

  1. Описательная статистика для данных отношений

  Вы можете использовать ту же описательную статистику для суммирования данных отношений, что и для интервальных данных (с добавлением коэффициента вариации ). Мы кратко повторим здесь, но для полного объяснения вернитесь к пятому разделу.

  • Распределение частот: Это показывает, как часто каждое значение встречается в вашем наборе данных, и часто представляется в виде таблицы. Частота может быть выражена либо в количестве, либо в процентах.
  • Мода , медиана или среднее значение: Мода — это значение, которое чаще всего встречается в вашем наборе данных, а медиана — это среднее значение. Среднее значение — это среднее значение всех значений в вашем наборе данных. Мода, медиана и среднее — все это меры центральной тенденции, помогающие оценить распределение данных.
  • Диапазон , стандартное отклонение , дисперсия, и коэффициент вариации показывают изменчивость в вашем наборе данных. Коэффициент вариации уникален для данных отношений, потому что это дробь, рассчитанная путем деления стандартного отклонения на среднее значение.

  2. Статистические тесты для анализа данных соотношения

  Как и в случае с интервальными данными, для анализа данных можно использовать как параметрические, так и непараметрические тесты. Тем не менее, как мы знаем, параметрические тесты более эффективны и, следовательно, позволяют вам делать более значимые выводы из вашего анализа. Вот некоторые распространенные параметрические тесты, которые можно использовать для анализа данных соотношения:

  • T-тест для сравнения средних значений двух выборок данных. Например: какова разница в среднем доходе 40-50-летних, проживающих в Лондоне и Лидсе?
  • Тест ANOVA для сравнения средних значений трех или более выборок данных. Например: какова разница в среднем доходе 40-50-летних, проживающих в Лондоне, Лидсе и Бирмингеме?
  • Pearson’s  r   , чтобы увидеть, существует ли корреляция между двумя переменными. Например: существует ли связь между возрастом человека в годах и его доходом?
  • Простая линейная регрессия для моделирования или прогнозирования связи между двумя переменными или влияния одной переменной на другую. Например: можно ли использовать возраст человека в годах для прогнозирования его дохода?

  8. Уровни измерения: FAQ

  Какие существуют 4 уровня измерения?

  4 уровня измерения, также известные как шкалы измерения: номинальный, порядковый, интервальный и относительный. Эти уровни используются для классификации и описания данных на основе их характеристик и свойств.

  Что такое уровень измерения в статистике?

  Уровень измерения, также известный как шкала измерения, относится к процессу категоризации данных на основе характеристик и свойств данных. Это важно в статистике, потому что помогает определить соответствующие статистические методы и тесты, которые можно использовать для анализа данных.

  Возраст – это интервал или соотношение?

  Обычно считается, что возраст измеряется по шкале отношений. Это связано с тем, что возраст имеет истинную нулевую точку, а это означает, что нулевое значение представляет отсутствие возраста.