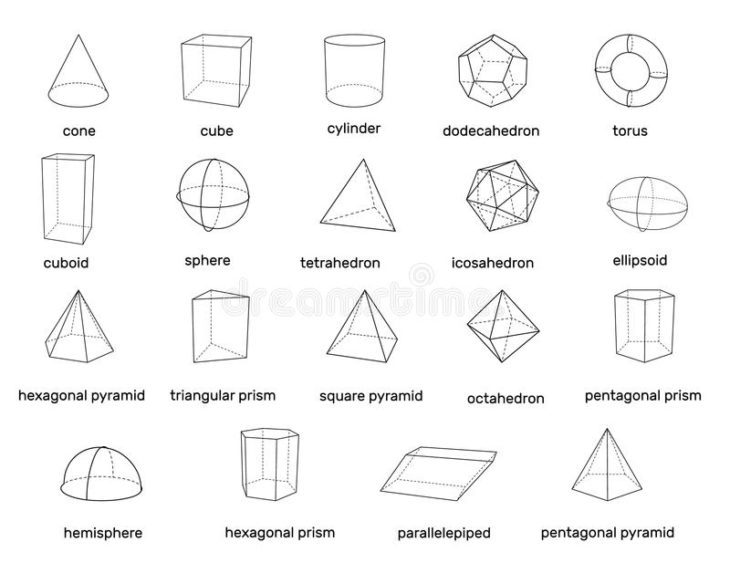
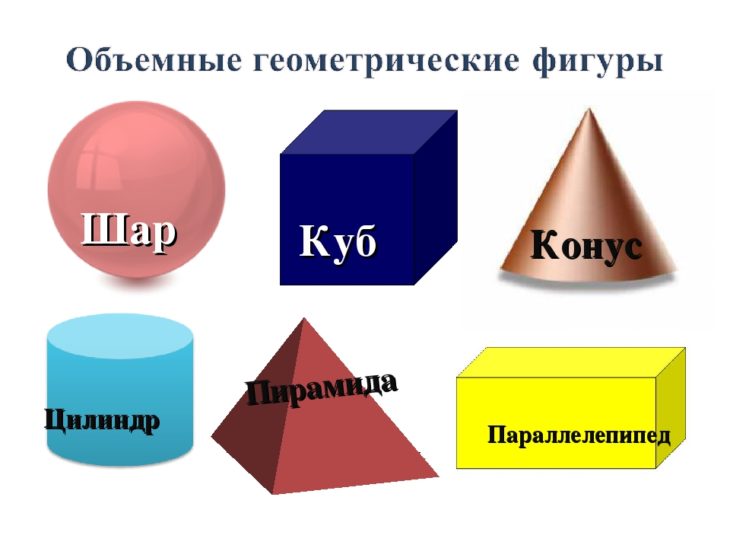
Объемные геометрические фигуры и их названия: Основные геометрические фигуры 🟢🟨🔺 и их названия

шар, куб, пирамида, призма, тетраэдр. Удивительные фигуры в геометрии Что значит плоские геометрические фигуры

Геометрические фигуры представляют собой комплекс точек, линий, тел или поверхностей. Эти элементы могут располагаться как на плоскости, так и в пространстве, формируя конечное количество прямых.

Термин «фигура» подразумевает под собой несколько множеств точек. Они должны располагаться на одной или нескольких плоскостях и одновременно ограничиваться конкретным числом оконченных линий.

Основными геометрическими фигурами считаются точка и прямая. Они располагаются на плоскости. Кроме них, среди простых фигур выделяют луч, ломаную линию и отрезок.

Точка

Это одна из главных фигур геометрии. Она очень маленькая, но ее всегда используют для построения различных форм на плоскости. Точка – это основная фигура для абсолютно всех построений, даже самой высокой сложности. В геометрии ее принято обозначать буквой латинской алфавита, к примеру, A, B, K, L.

С точки зрения математики точка – это абстрактный пространственный объект, не обладающий такими характеристиками, как площадь, объем, но при этом остающийся фундаментальным понятием в геометрии. Этот нульмерный объект просто не имеет определения.

Прямая

Это фигура полностью размещается в одной плоскости. У прямой нет конкретного математического определения, так как она состоит из огромного количества точек, располагающихся на одной бесконечной линии, у которой нет предела и границ.

Существует еще и отрезок. Это тоже прямая, но она начинается и заканчивается с точки, а значит, имеет геометрические ограничения.

Также линия может превратиться в направленный луч. Такое происходит, когда прямая начинается с точки, но четкого окончания не имеет. Если же поставить точку посредине линии, то она разобьется на два луча (дополнительных), причем противоположно направленных друг к другу.

Несколько отрезков, которые последовательно соединяются друг с другом концами в общей точке и располагаются не на одной прямой, принято называть ломаной линией.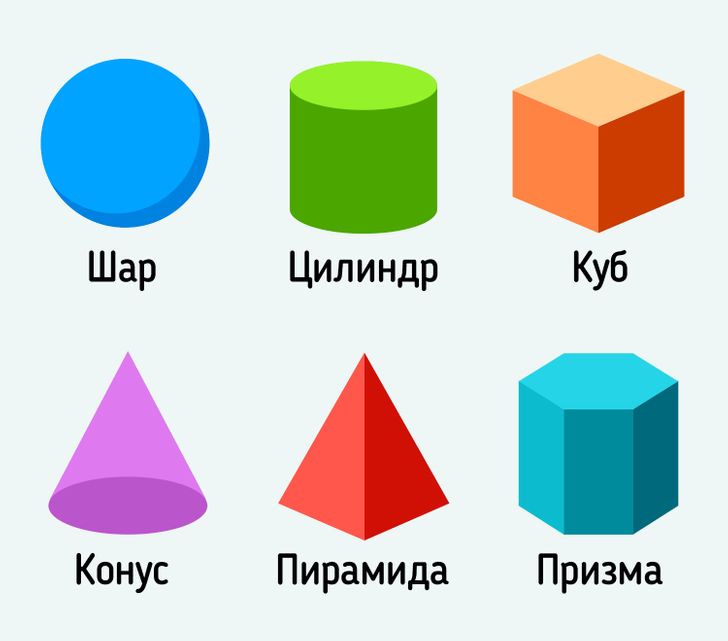

Угол

Геометрические фигуры, названия которых мы рассмотрели выше, считают ключевыми элементами, использующимися при построении более сложных моделей.

Угол – это конструкция, состоящая из вершины и двух лучей, которые выходят из нее. То есть стороны этой фигуры соединяются в одной точке.

Плоскость

Рассмотрим еще одно первичное понятие. Плоскость – это фигура, у которой нет ни конца, ни начала, равно как и прямой, и точки. Во время рассмотрения этого геометрического элемента во внимание берется лишь его часть, ограниченная контурами ломаной замкнутой линии.

Любую гладкую ограниченную поверхность можно считать плоскостью. Это может быть гладильная доска, лист бумаги или даже дверь.

Четырехугольники

Параллелограмм – это геометрическая фигура, противоположные стороны которой параллельны друг другу попарно. Среди частных видов этой конструкции выделяют ромб, прямоугольник и квадрат.

Прямоугольник – это параллелограмм, у которого все стороны соприкасаются под прямым углом.

Квадрат – это четырехугольник с равными сторонами и углами.

Ромб – это фигура, у которой все грани равны. При этом углы могут быть совершенно разными, но попарно. Каждый квадрат считается ромбом. Но в противоположном направлении это правило действует не всегда. Далеко не каждый ромб является квадратом.

Трапеция

Геометрические фигуры бывают совершенно разными и причудливыми. Каждая из них имеет своеобразную форму и свойства.

Трапеция – это фигура, которая чем-то схожа с четырехугольником. Она имеет две параллельные противоположные стороны и при этом считается криволинейной.

Круг

Эта геометрическая фигура подразумевает расположение на одной плоскости точек, равноудаленных от ее центра. При этом заданный ненулевой отрезок принято называть радиусом.

Треугольник

Это простая геометрическая фигура, которая очень часто встречается и изучается.

Треугольник считается подвидом многоугольника, расположенным на одной плоскости и ограниченным тремя гранями и тремя точками соприкосновения.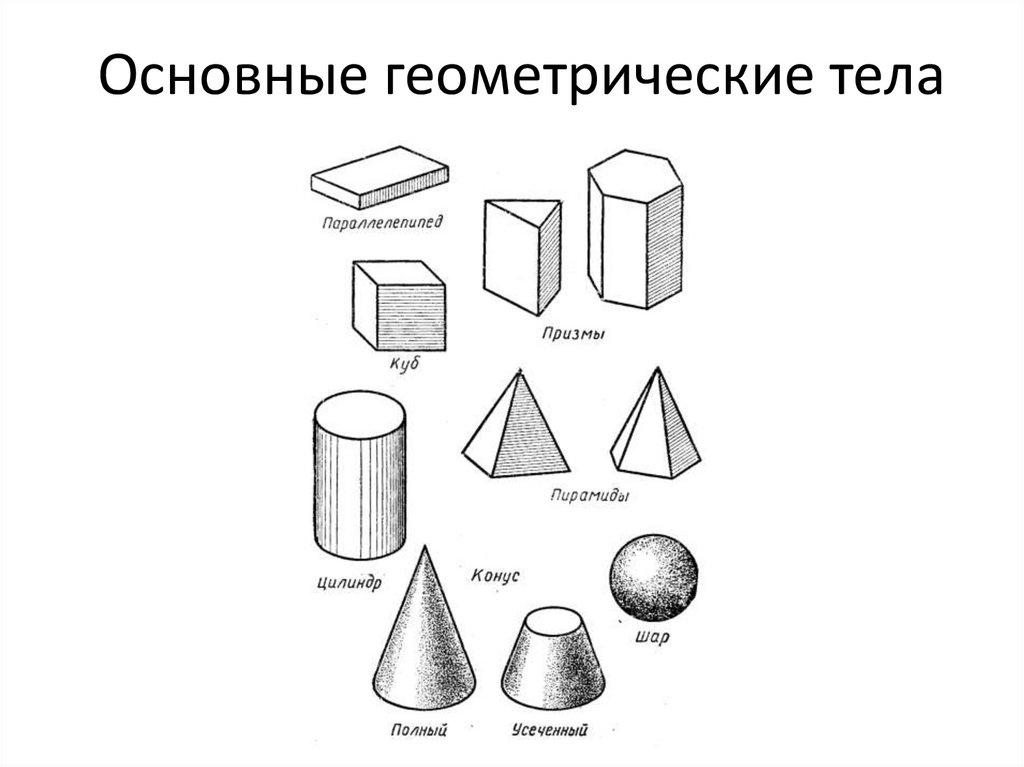 Эти элементы попарно соединены между собой.

Многоугольник

Вершинами многоугольников называют точки, соединяющие отрезки. А последние, в свою очередь, принято считать сторонами.

Объемные геометрические фигуры

• призма;
• сфера;
• конус;
• цилиндр;
• пирамида;

Эти тела имеют нечто общее. Все они ограничиваются замкнутой поверхностью, внутри которой находится множество точек.

Объемные тела изучают не только в геометрии, но и в кристаллографии.

Любопытные факты

Наверняка вам будет интересно ознакомиться с информацией, предоставленной ниже.

• Геометрия сформировалась как наука еще в давние века. Это явление принято связывать с развитием искусства и разнообразных ремесел. А названия геометрических фигур свидетельствуют об использовании принципов определения подобия и схожести.
• В переводе с древнегреческого термин «трапеция» обозначает столик для трапезы.
• Если вы возьмете различные фигуры, периметр которых будет одинаковым, то наибольшая площадь гарантированно будет у круга.
• В переводе с греческого языка термин «конус» обозначает сосновую шишку.
• Существует известная картина Каземира Малевича, которая начиная с прошлого века притягивает к себе взгляды многих живописцев. Работа «Черный квадрат» всегда была мистической и загадочной. Геометрическая фигура на белом полотне восхищает и поражает одновременно.

Существует большое количество геометрических фигур. Все они отличаются параметрами, а порой даже удивляют формами.

Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках. Но обучение будет проходить наиболее эффективно в том случае, если к распечатанному заданию вы добавите еще и различные образцы геометрических фигур. Для этой цели могут подойти такие предметы, как мячики, пирамидки, кубики, надутые воздушные шары (круглые и овальные), кружки для чая (стандартные, в форме цилиндра), апельсины, книги, клубки ниток, квадратные печенья и многое другое – все, что подскажет вам фантазия.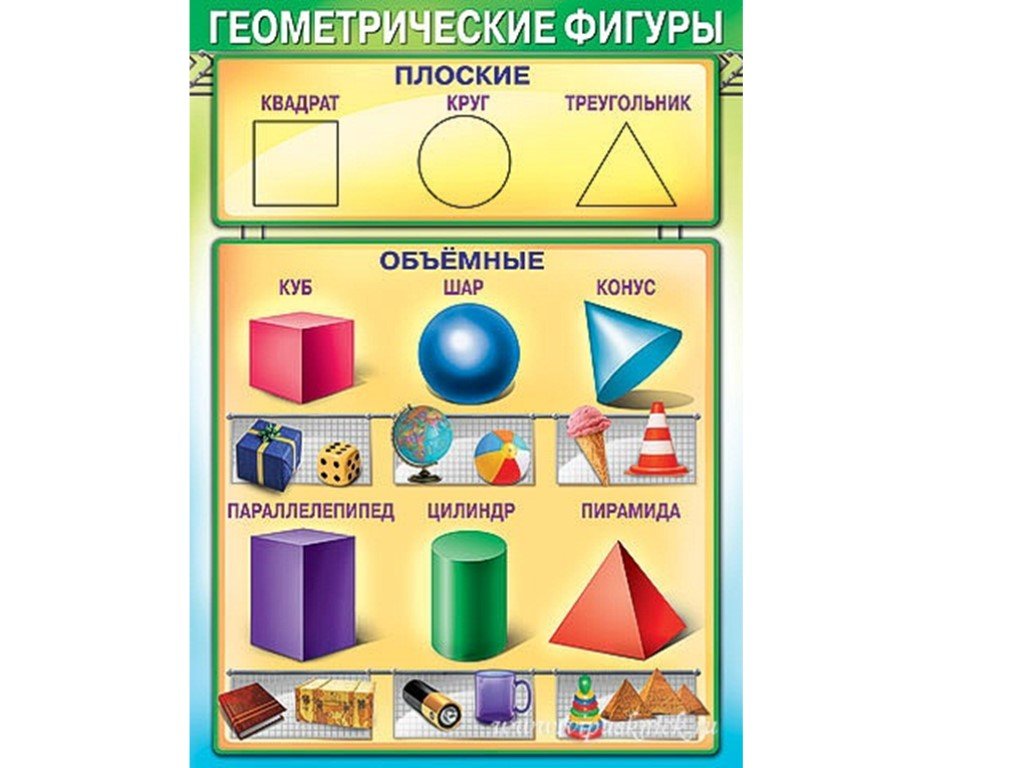

Все перечисленные предметы помогут ребенку понять, что значит объемная геометрическая фигура. Плоские фигуры можно подготовить, вырезав из бумаги нужные геометрические формы, предварительно раскрасив их в разные цвета.

Чем больше различных материалов вы подготовите для занятия, тем интереснее будет ребенку изучать новые для него понятия.

Также вам может понравиться наш онлайн тренажер по математике для 1 класса “Геометрические фигуры”:

Онлайн-тренажер по математике “Геометрические фигуры 1 класс” поможет первоклассникам потренироваться в умении различать основные геометрические фигуры: квадрат, круг, овал, прямоугольник и треугольник.

Геометрические фигуры и их названия – Проводим занятие с ребенком:

Чтобы легко и непринужденно ребенок смог запомнить геометрические фигуры и их названия, скачайте сначала картинку с заданием во вложениях внизу страницы, распечатайте на цветном принтере и положите на стол вместе с цветными карандашами. Также к этому времени у вас уже должны быть заготовлены различные предметы, которые мы перечисляли ранее.

• 1 этап.
  Сначала пусть ребенок выполнит задания на распечатанном листе – проговорит вслух названия фигур и раскрасит все картинки.
• 2 этап. Необходимо наглядно показать ребенку отличия объемных фигур от плоских. Для этого разложите все предметы-образцы (как объемные, так и вырезанные из бумаги) и отойдите с ребенком от стола на такое расстояние, с которого хорошо видны все объемные фигуры, но потерялись из виду все плоские образцы. Обратите внимание малыша на этот факт. Пусть он поэкспериментирует, подходя к столу то ближе, то дальше, рассказывая вам о своих наблюдениях.
• 3 этап. Дальше занятие нужно превратить в своеобразную игру. Попросите ребенка, чтобы он внимательно посмотрел вокруг себя и нашел предметы, которые имеют форму каких-либо геометрических фигур. Например, телевизор – прямоугольник, часы – круг и т.д. На каждой найденной фигуре – громко хлопайте в ладоши, чтобы добавить энтузиазма в игру.
• 4 этап. Проведите исследовательскую и наблюдательную работу с теми материалами-образцами, которые вы заготовили к занятию. Например, положите на стол книгу и плоский прямоугольник из бумаги. Предложите ребенку пощупать их, посмотреть на них с разных сторон и рассказать вам свои наблюдения. Таким же образом можно исследовать апельсин и бумажный круг, детскую пирамидку и бумажный треугольник, кубик и бумажный квадрат, воздушный шар овальной формы и овал, вырезанный из бумаги. Список предметов вы можете дополнить сами.
• 5 этап. Положите в непрозрачный пакет различные объемные образцы и попросите ребенка достать на ощупь квадратный предмет, затем круглый, затем прямоугольный и так далее.
• 6 этап. Разложите перед ребенком на столе несколько различных предметов из тех, которые участвуют в занятии. Затем пусть ребенок отвернется на несколько секунд, а вы спрячьте один из предметов. Повернувшись к столу ребенок должен назвать спрятанный предмет и его геометрическую форму.

Скачать геометрические фигуры и их названия – Бланк задания – вы можете во вложениях внизу страницы.

Названия геометрических фигур – Карточки для распечатки

Изучая с малышом геометрические фигуры, вы можете использовать во время занятий карточки для распечатки от Лисёнка Бибуши. Скачайте вложения, распечатайте на цветном принтере бланк с карточками, вырежьте каждую карточку по контуру – и приступайте к обучению. Карточки можно заламинировать, либо наклеить на более плотную бумагу, чтобы сохранить внешний вид картинок, ведь использоваться они будут неоднократно.

Первые шесть карточек дадут вам возможность изучить с ребенком такие фигуры: овал, круг, квадрат, ромб, прямоугольник и треугольник, под каждой фигурой в карточках можно прочесть ее название.

После того, как ребенок запомнил название определенной фигуры, попросите его выполнить следующее: обвести по контуру все имеющиеся на карточке образцы изучаемой фигуры, а затем раскрасить их в цвет основной фигуры, расположенной в верхнем левом углу.

Скачать названия геометрических фигур – Карточки для распечатки – вы можете во вложениях внизу страницы

С помощью следующих шести карточек ребенок сможет познакомиться с такими геометрическими фигурами: параллелограмм, трапеция, пятиугольник, шестиугольник, звезда и сердце. Как и в предыдущем материале под каждой фигурой можно найти ее название.

Чтобы разнообразить занятия с малышом, совмещайте обучение с рисованием – такой метод не даст ребенку переутомиться, и малыш с удовольствием будет продолжать учебу. Следите за тем, чтобы обводя фигуры по черточкам, ребенок не спешил и выполнял задание аккуратно, ведь подобные упражнения не только развивают мелкую моторику, они могут повлиять в дальнейшем на почерк малыша.

Скачать карточки для распечатки с изображением плоских геометрических фигур вы можете во вложениях

В процессе, того, как вы будете изучать с ребенком объемные геометрические фигуры и их названия, используя новые шесть карточек от Бибуши с изображениями куба, цилиндра, конуса, пирамиды, шара и полусферы, приобретите изучаемые фигуры в магазине, либо воспользуйтесь предметами, находящимися в доме, имеющими подобную форму.

Покажите малышу на примерах, как в жизни выглядят объемные фигуры, ребенок должен потрогать и поиграть с ними. Прежде всего, это необходимо для того, чтобы задействовать наглядно – действенное мышление малыша, с помощью которого ребенку проще познавать окружающий мир.

Скачать – Объемные геометрические фигуры и их названия – вы можете во вложениях внизу страницы

Также вам будут полезны и другие материалы по изучению геометрических фигур:

Веселые и красочные задания для детей “Рисунки из геометрических фигур” являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических форм:

Задания ознакомят ребенка с основными фигурами геометрии – кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.

Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги.

Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок.

Наложение фигур друг на друга – это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры.

Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.

Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.

В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии

Здесь мы подготовили для вас объемные геометрические фигуры из бумаги, которые нужно вырезать и склеить. Куб, пирамиды, ромб, конус, цилиндр, шестигранник, распечатать их на картоне (или цветной бумаге, а затем наклеить на картон), а затем дать ребенку для запоминания.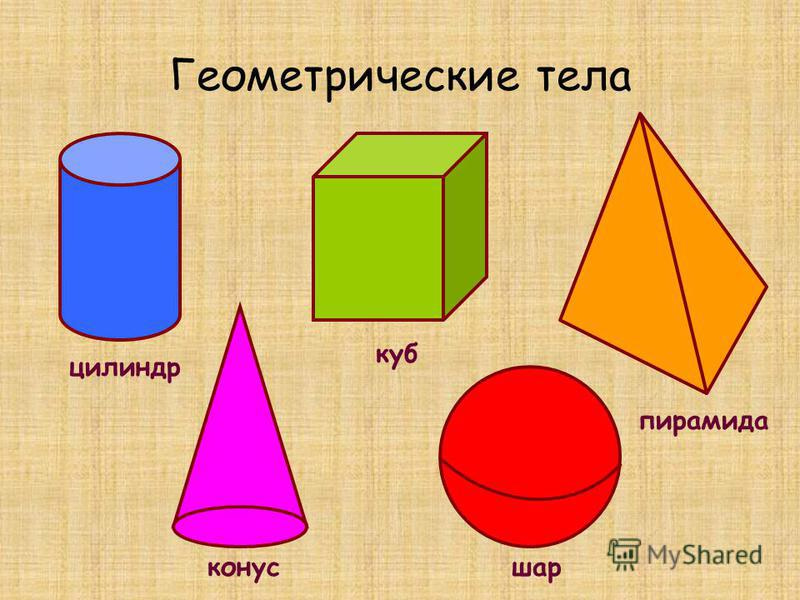

Здесь мы выложили для вас счет до 5 – картинки с математическими заданиями для малышей, благодаря которым ваши дети потренируют не только свои навыки счета, но и умение читать, писать, различать геометрические фигуры, рисовать и раскрашивать.

И еще можете поиграть в математические игры онлайн от лисенка Бибуши:

В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок. При этом необходимо руководствоваться признаками геометрических форм.

Геометрические объемные фигуры – это твердые тела, которые занимают ненулевой объем в евклидовом (трехмерном) пространстве. Эти фигуры изучает раздел математики, который носит название “пространственная геометрия”. Знания о свойствах объемных фигур применяются в инженерии и в науках о природе. Рассмотрим в статье вопрос, геометрические объемные фигуры и их названия.

Геометрические объемные тела

Поскольку эти тела имеют конечную размерность в трех пространственных направлениях, то для их описания в геометрии используют систему из трех координатных осей. Эти оси обладают следующими свойствами:

1. Они ортогональны друг другу, то есть перпендикулярны.
2. Эти оси нормализированы, то есть базисные вектора каждой оси имеют одинаковую длину.
3. Любая из осей координат – это результат векторного произведения двух других.

Говоря о геометрических объемных фигурах и их названиях, следует отметить, что все они принадлежат к одному из 2-х больших классов:

1. Класс полиэдров. Эти фигуры, исходя из названия класса, имеют прямые ребра и плоские грани. Грань – это плоскость, которая ограничивает фигуру. Место соединения двух граней называется ребром, а точка соединения трех граней – это вершина. К полиэдрам относятся геометрическая фигура куб, тетраэдры, призмы, пирамиды. Для этих фигур справедлива теорема Эйлера, которая устанавливает связь между числом сторон (С), ребер (Р) и вершин (В) для каждого полиэдра. Математически эта теорема записывается так: С + В = Р + 2.
2. Класс круглых тел или тел вращения. 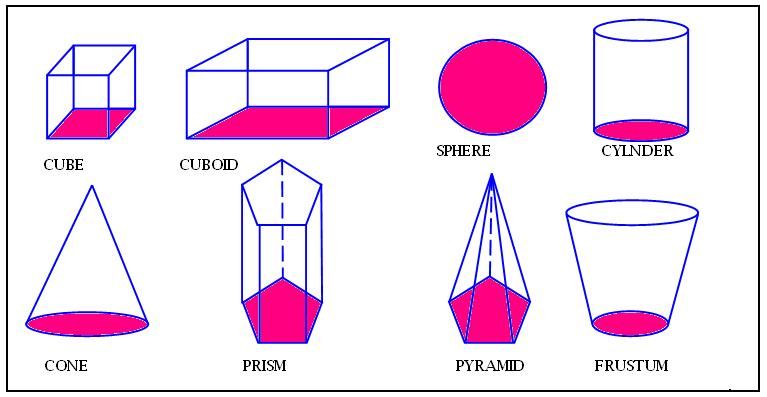Эти фигуры имеют хотя бы одну поверхность, образующую их, изогнутой формы. Например, шар, конус, цилиндр, тор.

Что касается свойств объемных фигур, то следует выделить два самых важных из них:

1. Наличие определенного объема, который фигура занимает в пространстве.
2. Наличие у каждой объемной фигуры площади поверхности.

Оба свойства для каждой фигуры описываются конкретными математическими формулами.

Рассмотрим ниже самые простые геометрические объемные фигуры и их названия: куб, пирамиду, призму, тетраэдр и шар.

Фигура куб: описание

Под геометрической фигурой куб понимают объемное тело, которое образовано 6-тью квадратными плоскостями или поверхностями. Также эту фигуру называют правильный гексаэдр, поскольку она имеет 6 сторон, или прямоугольный параллелепипед, так как он состоит из 3-х пар параллельных сторон, которые взаимно перпендикулярны друг другу. Называют куб и у которой основание является квадратом, а высота равна стороне основания.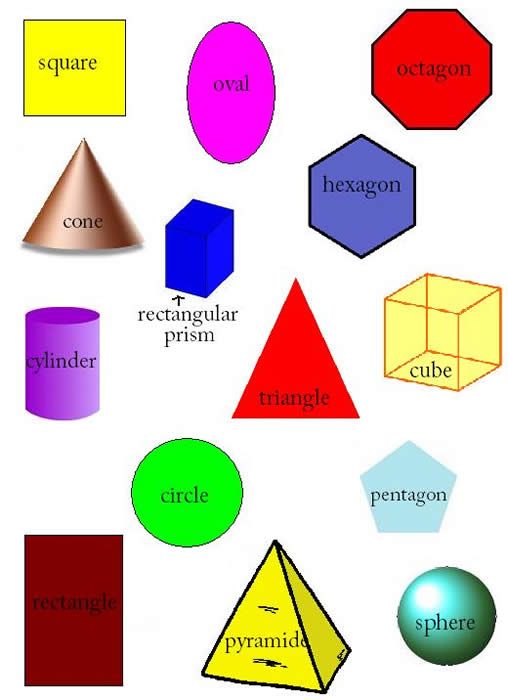

Поскольку куб является многогранником или полиэдром, то для него можно применить теорему Эйлера, чтобы определить число его ребер. Зная, что число сторон равно 6, а вершин у куба 8, число ребер равно: Р = С + В – 2 = 6 + 8 – 2 = 12.

Если обозначить буквой “a” длину стороны куба, тогда формулы для его объема и площади поверхности будут иметь вид: V = a 3 и S = 6*a 2 , соответственно.

Фигура пирамида

Пирамида – это полиэдр, который состоит из простого многогранника (основание пирамиды) и треугольников, которые соединяются с основанием и имеют одну общую вершину (вершина пирамиды). Треугольники называются боковыми гранями пирамиды.

Геометрические характеристики пирамиды зависят от того, какой многоугольник лежит в ее основании, а также от того, является ли пирамида прямой или косой. Под прямой пирамидой понимают такую пирамиду, для которой перпендикулярная основанию прямая, проведенная через вершину пирамиды, пересекает основание в ее геометрическом центре.

Одной из простых пирамид является четырехугольная прямая пирамида, в основании которой лежит квадрат со стороной “a”, высота этой пирамиды “h”. Для этой фигуры пирамиды объем и площадь поверхности будут равны: V = a 2 *h/3 и S = 2*a*√(h 2 +a 2 /4) + a 2 , соответственно. Применяя теорему Эйлера для нее, с учетом того, что число граней равно 5, и число вершин равно 5, получаем количество ребер: Р = 5 + 5 – 2 = 8.

Фигура тетраэдр: описание

Под геометрической фигурой тетраэдр понимают объемное тело, образованное 4-мя гранями. Исходя из свойств пространства, такие грани могут представлять только треугольники. Таким образом, тетраэдр является частным случаем пирамиды, у которой в основании лежит треугольник.

Если все 4-ре треугольника, образующие грани тетраэдра, являются равносторонними и равными между собой, то такой тетраэдр называется правильным. Этот тетраэдр имеет 4 грани и 4 вершины, число ребер составляет 4 + 4 – 2 = 6. Применяя стандартные формулы из плоской геометрии для рассматриваемой фигуры, получаем: V = a 3 * √2/12 и S = √3*a 2 , где a – длина стороны равностороннего треугольника.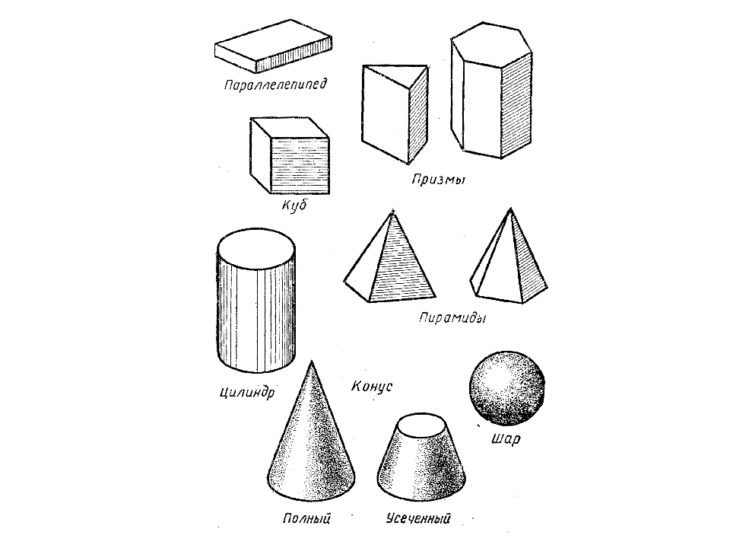

Интересно отметить, что в природе некоторые молекулы имеют форму правильного тетраэдра. Например, молекула метана CH 4 , в которой атомы водорода расположены в вершинах тетраэдра, и соединены с атомом углерода ковалентными химическими связями. Атом углерода находится в геометрическом центре тетраэдра.

Простая в изготовлении форма фигуры тетраэдр используется также в инженерии. Например, тетраэдрическую форму используют при изготовлении якорей для кораблей. Отметим, что космический зонд НАСА, Mars Pathfinder, который совершил посадку на поверхность Марса 4 июля 1997 года, также имел форму тетраэдра.

Фигура призма

Эту геометрическую фигуру можно получить, если взять два многогранника, расположить их параллельно друг другу в разных плоскостях пространства, и соединить их вершины соответствующим образом между собой. В итоге получится призма, два многогранника называются ее основаниями, а поверхности, соединяющие эти многогранники, будут иметь форму параллелограммов. Призма называется прямой, если ее боковые стороны (параллелограммы) являются прямоугольниками.

Призма – это полиэдр, поэтому для нее верна Например, если в основании призмы лежит шестиугольник, тогда, количество сторон у призмы равно 8, а количество вершин – 12. Число ребер будет равно: Р = 8 + 12 – 2 = 18. Для прямой призмы высотой h, в основании которой лежит правильный шестиугольник со стороной a, объем равен: V = a 2 *h*√3/4, площадь поверхности равна: S = 3*a*(a*√3 + 2*h).

Говоря о простых геометрических объемных фигурах и их названиях, следует упомянуть шар. Под объемным телом под названием шар понимают тело, которое ограничено сферой. В свою очередь, сфера – это совокупность точек пространства, равноудаленных от одной точки, которая называется центром сферы.

Поскольку шар относится к классу круглых тел, то для него не существует понятия о сторонах, ребрах и вершинах. сферы, ограничивающей шар, находится по формуле: S = 4*pi*r 2 , а объем шара можно вычислить по формуле: V = 4*pi*r 3 /3, где pi – число пи (3,14), r – радиус сферы (шара).

Фигура – это произвольное множество точек на плоскости. Точка, прямая, отрезок, луч, треугольник, круг, квадрат и так далее – всё это примеры геометрических фигур.

Точка – основное понятие геометрии, это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса.

Линия – это множество точек, последовательно расположенных друг за другом. У линии измеряют только длину. Ширины и толщины она не имеет.

Прямая линия – это линия, которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны.

Луч – это часть прямой линии, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону.

Отрезок – это часть прямой линии, ограниченная двумя точками. Отрезок имеет начало и конец, поэтому можно измерить его длину.

Кривая линия – это плавно изгибающаяся линия, которая определяется расположением составляющих её точек.

Ломаная линия – это фигура, которая состоит из отрезков, последовательно соединенных своими концами.

Вершины ломаной – это

1. точка, с которой начинается ломанная,
2. точки, в которых соединяются отрезки, образующие ломаную,
3. точка, которой заканчивается ломанная.

Звенья ломаной – это отрезки, из которых состоит ломаная. Количество звеньев ломаной всегда на 1 меньше, чем количество вершин ломаной.

Незамкнутая линия – это линия, концы которой не соединены вместе.

Замкнутая линия – это линия, концы которой соединены вместе.

Многоугольник – это замкнутая ломанная линия. Вершины ломаной называются вершинами многоугольника, а отрезки – сторонами многоугольника.

Объемные геометрические фигуры рисунок – 67 фото

Скетчинг геометрические фигуры

Натюрморт из геометрических фигур (куб, Призма)

Трехмерные геометрические фигуры

Объемные фигуры вектор

Понятие формы.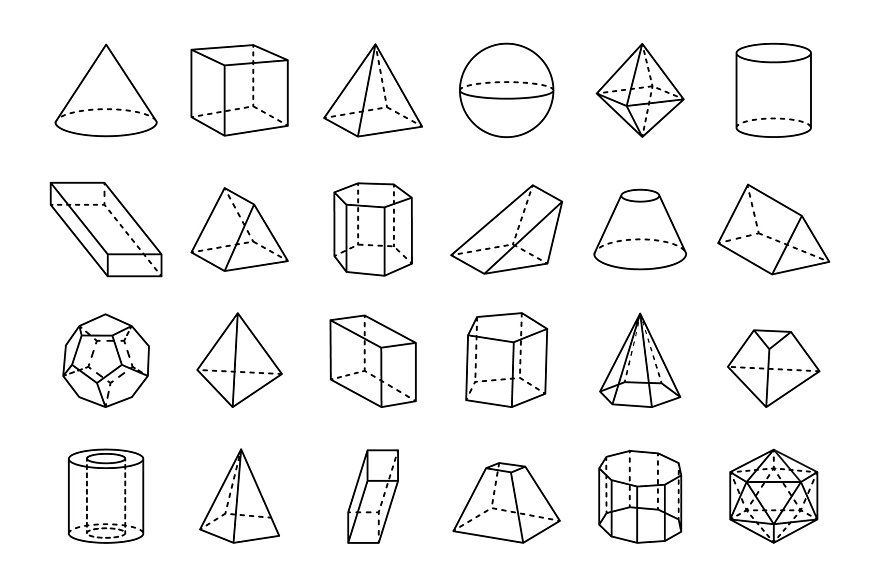 Геометрические тела: куб, шар, цилиндр, конус, Призма.

Объемные геометрические фигуры

Объемные геометрические фигуры Призма

Рисование сложных геометрических фигур

Андрей Андреев МАРХИ натюрморт

Биометрические фигуры

Объемные геометрические фигуры

Декор геометрические фигуры svg

Рисунок геометрических тел

Геометрические фигуры в изометрии

Геометрические фигуры объемные рисунок

Объемные геометрические фигуры

Освещение свет и тень изо 6 класс

Округлые геометрические фигуры

Рисование геометрических тел (Призма, пирамида, куб).

Объемные фигуры вектор

Трансформация простых геометрических форм

Штриховка геометрических фигур

Geometrické konstrukce Pro Pi

Геометрические фигуры для рисования

Объемные геометрические фигуры Призма

Рисование группы геометрических тел

Куб Призма пирамида конус цилиндр шар

Рисование объемных фигур

Нестандартные геометрические фигуры

Объемные фигуры вектор

3d фигуры

Геометрические фигуры конус и цилиндр

Пирамида Светотень

Геометрические фигуры для рисования

Геометрические фигурки 3d

Перспектива геометрических тел

Объемные фигуры карандашом

Фигуры объемные вектор карандаши

Композиция из объемных тел

Раскраска объемные геометрические фигуры

Объемные геометрические фигуры

Каркасное моделирование

Легкие развертки геометрических фигур

Светотень шар, конус, цилиндр, куб

Сложные геометрические фигуры

Композиция из геометрических тел

Круглые геометрические тела

Цилиндр Геометрическая фигура

Математика фигуры

Сложные геометрические фигуры

П образные геометрические фигуры

Объёмные геометрические фигуры и их названия для детей

Композиция из геометрических фигур

Объемные геометрические фигуры

3д геометрические фигуры для исследовательских работ по технологии

Невозможные фигуры Маурица Эшера

Геометрические фигуры объемные рисунок

Геометрические фигуры сложной формы

Врезки геометрических фигур

Точки соединения объёмные фигуры

Светотень геометрических фигур снизу

Геометрические фигуры Светотень

Геометрические фигуры карандашом для начинающих

Объёмные геометрические фигуры и их названия

Геометрические фигуры куб Призма

Геометрические фигуры дудл

Комментарии (0)

Написать

Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.

Список всех видов 3D-фигур на английском языке • 7ESL

Pin

Что такое трехмерные фигуры? Вы когда-нибудь задумывались, какое искусство без форм? Конечно, это то, что мы не можем понять. С искусством оно приходит с формами. Рисуем ли мы здания, природу, людей или другие предметы, формы всегда были и являются неотъемлемой частью искусства. Будь то квадрат, круг, треугольник или прямоугольник, каждое произведение искусства всегда будет иметь форму. Все эти формы считаются двумерными, но мы все знаем, что это нечто большее. Фигуры, имеющие длину, ширину и высоту, называются трехмерными фигурами.

Теперь, если ваш ребенок интересуется искусством и ищет способ научить его трехмерным формам, вы попали по адресу. Здесь мы дадим вам информацию о том, как вы можете объяснить, что такое трехмерная форма.

Содержание

3D-фигуры

Чтобы ответить на вопрос «Что такое 3D-фигуры?», 3D-фигуры — это трехмерные формы и объекты, которые отличаются от 2D-форм. Это фигуры, которые имеют высоту, ширину и длину. Он имеет толщину и глубину. Короче говоря, эти формы не плоские — это часть геометрических фигур, которые мы видим ежедневно.

Свойства 3D-фигур

Чтобы объяснить больше, 3D-фигуры обладают свойствами, которые отличают их от других фигур. Вы должны запомнить эти свойства, чтобы определить, является ли конкретная форма двухмерной или трехмерной. Ниже приведены следующие свойства.

• Лица

Каждая трехмерная фигура имеет лицо. Грани относятся к любой плоской поверхности или изогнутым поверхностям, которые можно увидеть в форме. Подумайте о коробке. Если вы посчитаете стороны коробки, вы увидите, что у нее шесть сторон. Эти стороны называются гранями.

• Края

Теперь, когда вы узнали, что такое лицо, давайте перейдем ко второму свойству — краю. Проще говоря, ребро — это место, где сходятся две грани. Просто посмотрите на коробку и попытайтесь найти ту часть, где сходятся лица.

• Вершины

Третье и последнее свойство трехмерной фигуры — это вершины. Это относится к заостренной части, где встречаются края. Часто ребра и вершины меняются местами. Представьте, что вы идете и ваш носок касается остроконечной части шкафа. Обычно мы говорим, что попали в край, но в геометрии это вершины.

Различные трехмерные фигуры

Теперь, когда вы узнали о различных свойствах трехмерных фигур, давайте рассмотрим их по отдельности.

1. Сфера — наиболее распространенный пример трехмерной формы. Вам может быть интересно, где находятся края сферы. Здесь ничего нет. Сфера имеет нулевые ребра и вершину, но имеет непрерывную грань, что позволяет ей быть трехмерной. Прекрасным примером этого является мяч.

2. Куб . Я знаю, что вы знакомы с кубиком Рубика. Это очень пример куба. У него 6 граней квадрата, 12 ребер и 8 вершин.

3. Пирамида . Да, знаменитая пирамида Египта считается трехмерной формой. У него 5 граней, 8 ребер и 5 вершин.

4. Цилиндр . представляет собой трехмерную форму с двумя плоскими поверхностями вверху и внизу и продолжающейся изогнутой поверхностью. У него 3 грани, 2 ребра и 0 вершин.

5. Конус . Представьте рожок мороженого. У него 2 грани, 1 ребро и 1 вершина. Вам может быть интересно, где лица на этой фигуре. Первая грань представляет собой круглую форму внизу. Вторая форма – треугольник, образующий конус.

6. Прямоугольный . Цилиндр имеет 3 стороны. Верхняя и нижняя формы считаются лицом, что делает их двумя. Третья грань — это изогнутое тело формы. У него есть 2 ребра, но они не пересекаются, поэтому у него нет вершин.

7. Тор . Это как пончик. 2 овальные фигуры соединены вместе и соединены отверстием в центре. Подобно окружности, он не имеет ребер и вершины, но имеет 1 поверхность.

Список 3D-фигур

Список общих 3D-фигур:

• Куб
• Прямоугольный
• Цилиндр
• Сфера
• Конус
• Пирамида
• Призма
• Тор

Список всех видов 3D-фигур:

• Куб
• Прямоугольный
• Цилиндр
• Полусфера (полусфера)
• Тетраэдр (Треугольная пирамида)
• Пятигранник
• Квадратная пирамида (Квадратная пирамида)
• Сфера
• Конус
• Многогранник
• Треугольная призма
• Пятиугольная призма
• Шестиугольная призма
• Семиугольная призма
• Восьмиугольная призма
• Неагональная призма
• Додекагональная призма
• Икосаэдр
• Эллипсоид
• Пирамида
• Шестигранник
• Семигранник
• Октаэдр
• Нонаэдр
• Додекаэдр
• Призма
• Тор

Факты о 3D-фигурах

Теперь, когда вы узнали об основах 3D-фигур, вот несколько интересных фактов, которые вы можете прочитать, чтобы пополнить свои знания.

• Дорожные конусы являются примерами конусов.
• Евклид — отец геометрии.
• Вершины — форма множественного числа вершины.
• Идеальным примером цилиндра является банка из-под газировки.
• Пространство, занимаемое трехмерной фигурой, называется объемом.
• Ромбико-ододекаэдр — самая большая трехмерная фигура в мире. У него есть грани из 20 треугольников, 30 квадратов, 12 пятиугольников, 60 вершин и 120 ребер.

Теперь, когда вы узнали, что такое трехмерные фигуры, вы наверняка сможете объяснить это своему ребенку, изучить эти фигуры и превратить их в великолепные изделия. Видите ли, эти формы можно найти вокруг нас. Возможно, раньше вы просто взаимодействовали как ни в чем не бывало, но теперь, когда вы этому научились, наверняка вы и ваш ребенок увидите мир по-другому, как никогда раньше.

3D-фигуры | Изображение

Штифт

Категории Визуальный словарь

Что такое 3D-фигуры? Объяснение для учителей, родителей и детей

Вот как помочь детям начальной и средней школы понять, что такое трехмерные фигуры, как идентифицировать и распознавать определенные трехмерные фигуры, а также как мы сравниваем и сопоставляем трехмерные фигуры, используя список свойств. .

Что такое трехмерные фигуры?

Трехмерные фигуры — это фигуры с тремя измерениями, такими как длина, ширина и высота. Примером трехмерной формы является призма или сфера. 3D-формы многомерны и их можно физически удерживать.

Что означает 3D?

3D в 3D-фигурах означает 3-мерный. Обычно мы говорим об измерениях как об измерениях в направлении. Примеры размеров включают длину, ширину или ширину, глубину и высоту.

Пример трехмерных фигур

Примеры трехмерных фигур окружают нас все время. Почти все, что мы видим и с чем взаимодействуем в повседневной жизни, имеет трехмерную форму, от кубиков Lego до подсолнухов. Однако детям достаточно знать названия и понимать свойства наиболее распространенных трехмерных фигур. Это контрастирует с 2D-формами, где дети должны знать как о правильных, так и о неправильных формах.

Какие трехмерные фигуры будут изучать дети?

В начальной школе ваш ребенок познакомится со следующими основными геометрическими фигурами: сферами, конусами, призмами, кубами и цилиндрами.

Стоит знать, что с геометрической точки зрения призмы включают в себя более твердые формы, чем вы обычно думаете о призмах. Например, знаете ли вы, что и куб, и прямоугольный параллелепипед с квадратным основанием и прямыми сторонами на самом деле считаются призмами?

Каковы свойства трехмерных фигур?

Свойства трехмерных фигур — это их грани, ребра и вершины, которые имеют особое значение в контексте школьных уроков математики.

Что такое лицо?

Лицо — это плоская поверхность трехмерного объекта. Например, призма с квадратным основанием имеет 5 граней. Сфера имеет 1 криволинейную поверхность, но не имеет грани.

Что такое ребро?

Ребро — это место, где встречаются два сегмента линии или грани. Цилиндр имеет 2 ребра.

Что такое вершины?

Вершины — это места, где встречаются две линии или ребра; в математике мы называем углы трехмерных фигур вершинами. Единственное число вершин на самом деле является вершиной, что может немного сбивать с толку. У конуса одна вершина, а у куба 4 вершины.

Изучение 3D-форм с помощью онлайн-вмешательств Third Space Learning

Названия 3D-форм

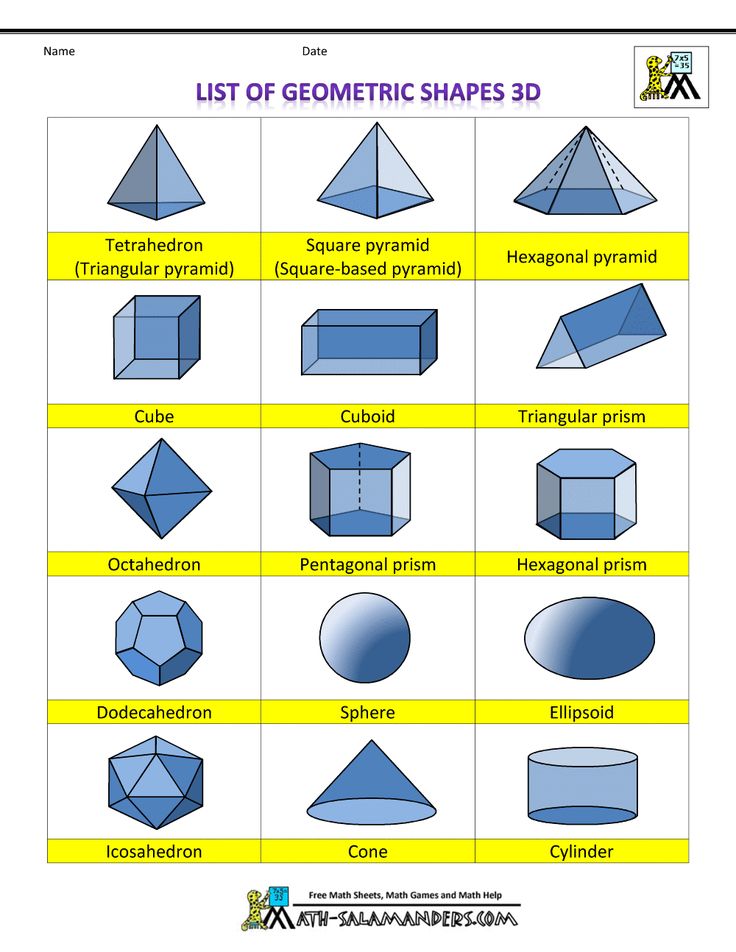
Вот названия 3D-форм:

• Сфера
• Полушарие
• Конус на основе треугольника или пирамиды
• Тетрагранник0024
• Cylinder
• Triangular prism
• Hexagonal prism
• Pentagonal prism
• Cube
• Cuboid

Properties of 3D shapes

As well as the names, children need to know the properties of 3D shapes as listed below и в таблице для печати.

• Сфера имеет 1 изогнутую поверхность.
• Полусфера имеет 1 грань, 1 изогнутую поверхность и 1 ребро.
• Конус имеет 1 грань, 1 изогнутую поверхность, 1 ребро и 1 вершину.
• Тетраэдр или пирамида с треугольным основанием имеет 4 грани, 6 ребер и 4 вершины.
• Пирамида с квадратным основанием имеет 5 граней, 8 ребер и 5 вершин.
• Цилиндр имеет 2 грани, 1 изогнутую поверхность и 2 ребра.

Призмы

• Треугольная призма имеет 5 граней, 9 ребер и 6 вершин.
• Куб имеет 6 граней, 12 ребер и 8 вершин.
• Кубоид имеет 6 граней, 12 ребер и 8 вершин.
• Пятиугольная призма имеет 7 граней, 15 ребер и 10 вершин.
• Шестиугольная призма имеет 8 граней, 18 ребер и 12 вершин.

Свойства трехмерных фигур – для печати

Подробнее: Двухмерные и трехмерные фигуры: свойства фигур

Когда дети узнают о трехмерных фигурах в школе?

Геометрия преподается в каждом классе начальной школы. Вот чему будут обучать 3D-фигуры, разделенные по классам:

3D-фигуры в детском саду

Детские сады должен уметь:

• Определять формы как двумерные (лежащие в плоскости, «плоские») или трехмерные («твердые»).
• Анализировать и сравнивать двух- и трехмерные формы разных размеров и ориентаций, используя неформальный язык для описания их сходств, различий, частей (например, количество сторон и вершин/”углов”) и других атрибутов (например, наличие стороны одинаковой длины).

Объемные фигуры в 1 классе

Первоклассники должны уметь:

• Составлять двухмерные фигуры (прямоугольники, квадраты, трапеции, треугольники, полукруги, четверть круга) или трехмерные фигуры (кубы, прямоугольные призмы, прямые круглые конусы и правильные круглые цилиндры) для создания составной формы и составления новых фигур из составной формы.

3D-фигуры во 2-м классе

Второклассники должны уметь:

• Распознавать и рисовать фигуры с заданными атрибутами, такими как заданное количество углов или заданное количество равных граней. Определите треугольники, четырехугольники, пятиугольники, шестиугольники и кубы.

In 3rd, 4th, and 5th grades, the standards focus on 2D shapes…

2D shapes in 3rd Grade

Third graders should be able to:

• Understand that shapes in разные категории (например, ромбы, прямоугольники и другие) могут иметь общие атрибуты (например, имеющие четыре стороны), и что общие атрибуты могут определять более крупную категорию (например, четырехугольники).
• Распознавать ромбы, прямоугольники и квадраты как примеры четырехугольников и рисовать примеры четырехугольников, не принадлежащих ни к одной из этих подкатегорий.

2D фигуры в 4 классе

Четвертоклассники должны уметь:

• Рисовать точки, прямые, отрезки прямых, лучи, углы (прямые, острые, тупые) и перпендикуляры . Определите их на двумерных фигурах.
• Классификация двухмерных фигур на основе наличия или отсутствия параллельных или перпендикулярных линий или углов заданного размера. Знать и определять прямоугольные треугольники.
• Распознавать линию симметрии двухмерной фигуры как линию, пересекающую фигуру, так что фигуру можно сложить по этой линии на соответствующие части. Определите линейно-симметричные фигуры и нарисуйте линии симметрии.

Двухмерные фигуры в 5-м классе

Пятиклассники должны уметь:

• Понимать, что атрибуты, принадлежащие к категории двумерных фигур, также принадлежат ко всем подкатегориям этой категории. Например, все прямоугольники имеют четыре прямых угла, а квадраты являются прямоугольниками, поэтому все квадраты имеют четыре прямых угла.
• Классифицировать двухмерные фигуры в иерархии на основе свойств.

Подробнее о 2D-фигурах можно узнать здесь .

Как трехмерные фигуры связаны с другими областями математики?

При работе с дробями детям часто приходится заштриховывать часть фигуры. Им придется связать свое понимание периметра, площади и объема с трехмерными формами.

Вопросы по 3D фигурам

1. Сколько вершин у куба?

(ответ: 8)

2. Сколько квадратов составляют развертку куба?

(ответ: 6)

3. Заполните таблицу.

(Ответ: Пирамида с треугольным основанием, 4 грани, 6 ребер / Сфера, 0 граней, 0 ребер / Треугольная призма, 5 граней, 9 ребер)

Хотите знать, как объяснить детям другие ключевые слова по математике ? Посмотрите наши Начальный математический словарь для детей. Почему бы не просмотреть другие наши блоги, посвященные 3D-формам:

• Что такое вершины, грани и ребра?
• Что такое 2D-фигуры?

Есть ли у вас ученики, которым нужна дополнительная помощь по математике?
Предоставьте учащимся четвертого и пятого классов больше возможностей для закрепления навыков обучения и практики с помощью персонализированного обучения элементарной математике с их собственным онлайн-репетитором по математике.