Не четные или нечетные как писать: Как пишется: нечетные или не четные?
Псевдокласс :nth-child | htmlbook.ru
| Internet Explorer | Chrome | Opera | Safari | Firefox | Android | iOS |
| 9.0+ | 1.0+ | 9.6+ | 3.1+ | 3.6+ | 2.1+ | 2.0+ |
Краткая информация
| Значение по умолчанию | Нет |
|---|---|
| Применяется | Ко всем элементам |
| Ссылка на спецификацию | http://www.w3.org/TR/css3-selectors/#nth-child-pseudo |
Версии CSS
| CSS 1 | CSS 2 | CSS 2.1 | CSS 3 |
|---|---|---|---|
Описание
Псевдокласс :nth-child используется для добавления стиля к элементам на основе нумерации в дереве элементов.
Синтаксис
элемент:nth-child(odd | even | <число> | <выражение>) {…}
Значения
- odd
- Все нечетные номера элементов.
- even
- Все четные номера элементов.
- число
- Порядковый номер дочернего элемента относительно своего родителя. Нумерация начинается с 1, это будет первый элемент в списке.
- выражение
- Задается в виде an+b, где a и b целые числа, а n — счетчик, который автоматически принимает значение 0, 1, 2…
Если a равно нулю, то оно не пишется и запись сокращается до b. Если b равно нулю, то оно также не указывается и выражение записывается в форме an. a и b могут быть отрицательными числами, в этом случае знак плюс меняется на минус, например: 5n-1.
За счет использования отрицательных значений a и b некоторые результаты могут также получиться отрицательными или равными нулю. Однако на элементы оказывают влияние только положительные значения из-за того, что нумерация элементов начинается с 1.
В табл. 1 приведены некоторые возможные выражения и ключевые слова, а также указано, какие номера элементов будут задействованы.
| Значение | Номера элементов | Описание |
|---|---|---|
| 1 | 1 | Первый элемент, является синонимом псевдокласса :first-child. |
| 5 | 5 | Пятый элемент. |
| 2n | 2, 4, 6, 8, 10 | Все четные элементы, аналог значения even. |
| 2n+1 | 1, 3, 5, 7, 9 | Все нечетные элементы, аналог значения odd. |
| 3n+2 | 2, 5, 8, 11, 14 | — |
| -n+3 | 3, 2, 1 | — |
| 5n-2 | 3, 8, 13, 18, 23 | — |
| even | 2, 4, 6, 8, 10 | Все четные элементы. |
| odd | 1, 3, 5, 7, 9 | Все нечетные элементы. |
Пример
HTML5CSS3IECrOpSaFx
<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title>nth-child</title>
<style>
table {
width: 100%; /* Ширина таблицы */
border-spacing: 0; /* Расстояние между ячейками */
}
tr:nth-child(2n) {
background: #f0f0f0; /* Цвет фона */
}
tr:nth-child(1) {
background: #666; /* Цвет фона */
color: #fff; /* Цвет текста */
}
</style>
</head>
<body>
<table border="1">
<tr>
<td> </td><td>2134</td><td>2135</td>
<td>2136</td><td>2137</td><td>2138</td>
</tr>
<tr>
<td>Нефть</td><td>16</td><td>34</td>
<td>62</td><td>74</td><td>57</td>
</tr>
<tr>
<td>Золото</td><td>4</td><td>69</td>
<td>72</td><td>56</td><td>47</td>
</tr>
<tr>
<td>Дерево</td><td>7</td><td>73</td>
<td>79</td><td>34</td><td>86</td>
</tr>
<tr>
<td>Камни</td><td>23</td><td>34</td>
<td>88</td><td>53</td><td>103</td>
</tr>
</table>
</body>
</html>В данном примере псевдокласс :nth-child используется для изменения стиля первой строки таблицы, а также для выделения цветом всех четных строк (рис.
1).
Рис. 1. Применение псевдокласса :nth-child к строкам таблицы
Псевдоклассы
CSS по теме
- Псевдокласс :nth-child
Статьи по теме
- Список с русскими буквами
Рецепты CSS
ЗАКОН НЕЧЕТНОСТИ ЧИСЛА БУКВ В РУССКИХ ПАЛИНДРОМАХ
Палиндромы (в переводе с греческого – бегущие назад), то есть слова и предложения, которые читаются одинаково как слева направо, так и справа налево, известны с античных времен. Они породили особый литературный жанр – палиндроматику. Ему отдали дань Гаврила Державин, Афанасий Фет, Валерий Брюсов и многие другие поэты и писатели. Сегодня этот жанр по-прежнему популярен (см. “Наука и жизнь” № 9, 1970 г.; №№ 2,1998г. 5,1998г..; № 2,2003г.). Но палиндромы – это не просто литературное развлечение. Предстоит еще понять законы их образования, способные привести к появлению новых идей в информационных технологиях.
Частотное распределение слов-палиндромов русского языка (синяя линия), иллюстрирующая “закон нечетности числа букв” n в словах-палиндромах.
N – относительная частота слов. Красным показана гистограмма обычных слов.
Основной список слов-палиндромов (включая предлоги, союзы, частицы, стандартные междометия, имена собственные с учетом падежей, глаголы с учетом спряжения и времен, а также некоторые распространенные сокращения; е≠ё).
‹
›
Открыть в полном размере
О палиндромах теперь знает едва ли не каждый читатель. Уже вышли десятки книг, целиком состоящие из палиндромных произведений. Многие тысячи строк-палиндромов “висят” в Интернете. Кажется, уже даже защищена докторская диссертация (А. Бубновым), посвященная палиндромам. И тем удивительнее, что в этой особой литературно-лингвистической форме вдруг открываются неожиданные свойства, достаточно простые для наблюдения, но пока незамеченные и потому неисследованные (это подтвердила координатор Справочного центра Института русского языка имени В. Виноградова кандидат филологических наук О. Грунченко). Итак, покажем, что для русских палиндромов выполняется “закон нечетности числа букв”, совершенно нехарактерный для обычных слов или фраз.
В качестве исходного материала рассмотрим Список слов-палиндромов , в котором собрана, по-видимому, подавляющая часть слов этого вида (включая производные формы), имеющихся в основном лексиконе русского языка, который насчитывает примерно 130 тысяч лексем. Источниками Списка послужили словарик из Антологии русского палиндрома [Антология , 2002, с.136] и коллекция автора. В Список из примерно 130 слов-палиндромов не вошли имена собственные, редко употребляемые в русском языке: географические названия (Яя, Анна и др.), иностранные фамилии и имена (Отто, Ала, Кук и т.п.), редко употребляемые сокращения и слова, где приравнены е и ё. В то же время в него включены примеры неологизмов, которые все чаще встречаются в палиндромных стихах и удачно отражают поэтические образы, например, девовед, икотопотоки, слова из молодежного жаргона (лабал, лажал), несколько распространенных сокращений (СОС, СЭС, РСФСР), известные имена и названия (Аза, Азиза, Асса), а также научно-технические термины (кек, тартрат).
Первый неожиданный результат был получен при частотном анализе распределения слов по числу букв. Почти все слова-палиндромы русского языка насчитывают нечетное число букв, от 1 до 11 (синие линии на гистограмме). Ничего подобного нет среди обычных, то есть несимметричных, слов (красные линии на гистограмме, демонстрирующие частотность слов, взятой из Частотного словаря русского языка, 1977, с.930). Гистограммы различаются настолько разительно, что нет смысла приводить математические выкладки по проверке статистической гипотезы о значимости указанного различия. Хотя сделать это несложно, и можно показать, что риск ошибки в сделанном выводе не превышает 0,01%.
Интереснее и сложнее вопрос о том, какому теоретическому закону распределения подчиняется объединение букв в симметричные слова. Как видно из колоколообразной сглаживающей кривой на графике из Частотного словаря, распределение обычных слов в основном словаре (не в текстах!) русского языка подчиняется нормальному (гауссовскому) закону распределения (см. “Наука и жизнь” № 2, 1995 г.). Математическое ожидание (среднее число) составляет приблизительно 9 букв. Между тем у слов-палиндромов оно равно 4,1 буквы, а среднее квадратичное отклонение (СКО) составляет 1,7 буквы. Эмпирический закон зафиксирован, но его математическое описание, моделирование или хотя бы аналитическая подгонка требуют специального исследования. Ведь этот закон явно не соответствует ни природе появления случайного события (сложение букв в слово-палиндром), ни внешнему подобию основным законам распределения, изучаемым в курсах математической статистики (равномерному, показательному, пуассоновскому, геометрическому и гипергеометрическому).
Простейшее лингвистическое (хотя и явно недостаточное) объяснение наблюдаемого “закона нечетности” можно предложить, рассмотрев противоположную (чисто умозрительную) гипотезу. Допустим, что в языке частотность симметричных слов с четным и нечетным числом букв была бы одного порядка. Тогда в словах с четным числом букв существовали бы десятки слов со сдвоенным центром в виде двух одинаковых гласных или же согласных. И действительно, таких слов немало: баллон, галлон, перрон, зуммер, триггер, выжжен, поддав, веер, леер, пиит и т. д. Только вот палиндромов среди них почти нет, кроме, пожалуй, слов массам и устаревшего итти, а также имен собственных Анна, Алла, АССА, Отто. Еще менее характерны сдвоенные гласные: с натяжкой можно привести единственный пример еле-еле, в котором центром служит дефис, а не двойная гласная.
Итак, “закон нечетности” распространяется исключительно на буквенно-симметричные словоформы, то есть на палиндромы! Однако, разумеется, это утверждение требует более строгой математико-лингвистической проверки путем подсчета слов со сдвоенным центром, имеющих как четное, так и нечетное число букв.
Замечательно, что действие “закона нечетности” распространяется не только на слова, но и на палиндромные фразы и более сложные тексты. Случайная выборка из 114 фраз у 33 авторов показала, что их доля с четным числом букв составляет 12,3%. У классика жанра Д. Авалиани она равна 13,5% в выборке из 200 фраз. Отсюда средняя доля центро-симметричных фраз, то есть фраз с центральной буквой, близка к 88% (тоже, кстати, цифровой палиндром!).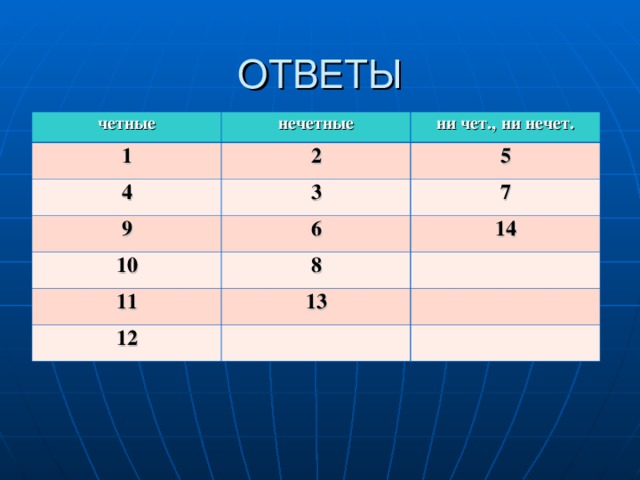
Отметим, что в число относительно редких четнобуквенных палиндромов входит класс “оборотней” – редкой разновидности палиндромов, обе половины которых имеют равное число букв и представляют собой законченные в смысловом отношении фразы, иногда совершенно несвязанные по смыслу. И это порой придает им неожиданную пикантность. Широко известен классический оборотень На Ритке снег. Генсек – тиран (С. Федин). Еще примеры: На вид Лавр опытен = Не ты порвал диван? / Лечу, сев на руле. – На в лоб! = Болван ел уран, вес учел (Б. Горобец).
Естественен вопрос: а для чего все это нужно? Законы словообразования (если они действительно законы, выраженные количественно) действуют специфично и объективно на данное множество элементов, помогают формировать ту научную базу данных, которая необходима для создания и совершенствования новых информационных технологий, в частности кодирования и декодирования сообщений, переводов, распознавания образов (слов, слогов) в сигнале на фоне шума.
И здесь нужны сведения о частотности слов в речи и литературе различных стилей. Эту работу еще предстоит выполнить.
Список новословий-палиндромов
Амфирифма
Сологолос
(В. Рыбинский)
Анархоохрана
Микрозорким
Маревоверам
Суперэпус
Синепенис
Трах-арт
Тревыверт
(В. Гершуни)
Лохохохол
(Джети
Автоботва
Аквалавка
Пракарп
Ретропортер
(Б. Гринберг)
Оленинело
(Ю. Телесин)
Девовед
Монгологном
Мордодром
(В. Хромов)
Икотопотоки
(Л. Адрианов)
Артсестра
Иноони
(Г. Лукомников)
Коненок
(К. Соприцкий)
Киторотик
(П. Нагорских)
Речевечер
(С. Красовицкий)
МакроЛоркам
МикроГорьким
Сотанатос
Солововолос
(С.
Федин)
Тревоговерт
(Д. Минский)
Китокотик
Лифонофил (лифон жарг.- лифчик)
Недороден
Ротомотор
(Б. Горобец)
Конещенок
Недеееден
(Б. Гольдштейн)
Молотолом (фольклор)
Четные и нечетные функции – определение, свойства, графики, примеры
В математике мы изучаем различные типы функций. Мы можем определить, является ли функция четной или нечетной, алгебраически или графически. Четные и нечетные функции можно проверить, подставив отрицательные входные данные (-x) вместо x в функцию f(x) и рассмотрев соответствующее выходное значение. Четные и нечетные функции классифицируются на основе их отношений симметрии. Четные и нечетные функции названы на основании того, что степенная функция f(x) = x n — четная функция, если n четное, и f(x) — нечетная функция, если n нечетное.
Давайте изучим другие четные и нечетные функции и поймем их свойства, графики и использование четных и нечетных функций в интегрировании.
Функция может быть четной или нечетной, или одновременно четной и нечетной, или ни четной, ни нечетной. Давайте рассмотрим различные примеры, чтобы понять концепцию.
| 1. | Что такое четные и нечетные функции? |
| 2. | Четные и нечетные функции в тригонометрии |
| 3. | Интегральные свойства четных и нечетных функций |
| 4. | График четных и нечетных функций |
| 5. | Свойства четных и нечетных функций |
| 6. | Часто задаваемые вопросы о четных и нечетных функциях |
Что такое четные и нечетные функции?
Обычно мы считаем вещественную функцию четной или нечетной. Чтобы определить, является ли функция четной или нечетной, мы подставляем -x вместо x в функцию f(x), то есть мы проверяем выходное значение f(-x), чтобы определить тип функции.
Четные и нечетные функции симметричны. Давайте сначала разберемся с их определениями.
Четные и нечетные функции Определение
- Четная функция — Для функции f(x) с действительным знаком, когда выходное значение f(-x) совпадает с f(x), для всех значений x в области f функция называется четной функцией. Четная функция должна содержать следующее уравнение: f(-x) = f(x) для всех значений x в D(f), где D(f) обозначает область определения функции f. Другими словами, мы можем сказать, что уравнение f (-x) – f (x) = 0 выполняется для четной функции для всех x. Рассмотрим пример, f(x) = x 2 .
f(-x) = (-x) 2 = x 2 для всех значений x, поскольку квадрат отрицательного числа равен квадрату положительного значения числа. Отсюда следует f(-x) = f(x) для всех x. Следовательно, f(x) = x 2 — четная функция. Точно так же такие функции, как x 4 , x 6 , x 8 и т. д., являются четными функциями. - Нечетная функция — Для функции f(x) с действительным знаком, когда выходное значение f(-x) совпадает с отрицательным значением f(x), для всех значений x в области определения f, функция называется нечетной. Нечетная функция должна содержать следующее уравнение: f(-x) = -f(x) для всех значений x в D(f), где D(f) обозначает область определения функции f. Другими словами, мы можем сказать, что уравнение f (-x) + f (x) = 0 выполняется для нечетной функции для всех x. Рассмотрим пример, f(x) = x 3 .
f(-x) = (-x) 3 = -(x 3 ) для всех значений x, поскольку куб отрицательного числа совпадает с отрицательным значением куба положительного значения числа . Отсюда следует f(-x) = -f(x) для всех x. Следовательно, f(x) = x 3 — нечетная функция. Точно так же такие функции, как x 5 , x 7 , x 9 и т. д., являются нечетными функциями. - И четные, и нечетные функции – Действительнозначная функция f(x) называется одновременно четной и нечетной, если она удовлетворяет условиям f(-x) = f(x) и f(-x) = -f (x) для всех значений x в области определения функции f(x). Существует только одна функция, которая одновременно является четной и нечетной, и это нулевая функция, f(x) = 0 для всех x. Мы знаем, что для нулевой функции f(-x) = -f(x) = f(x) = 0 для всех значений x. Следовательно, f(x) = 0 — четная и нечетная функция.
- Ни четная, ни нечетная функция — Говорят, что функция f(x) с действительным знаком не является ни четной, ни нечетной, если она не удовлетворяет f(-x) = f(x) и f(-x) = -f (x) хотя бы для одного значения x в области определения функции f(x). Давайте рассмотрим пример, чтобы лучше понять определение. Рассмотрим f(x) = 2x 5 + 3x 2 + 1, f(-x) = 2(-x) 5 + 3(-x) 2 + 1 = -2x 5 + 3x 2 + 1, что не равно ни f(x), ни -f(x). Следовательно, f(x) = 2x 5 + 3x 2 + 1 не является ни четной, ни нечетной функцией.
Существует только одна функция, которая одновременно является четной и нечетной, и это нулевая функция, f(x) = 0 для всех x. Мы знаем, что для нулевой функции f(-x) = -f(x) = f(x) = 0 для всех значений x. Следовательно, f(x) = 0 — четная и нечетная функция.Четные и нечетные функции в тригонометрии
В этом разделе мы разделим тригонометрические функции на четные и нечетные.
У нас есть шесть тригонометрических отношений (синус, косинус, тангенс, котангенс, косеканс и секанс). Эти тригонометрические отношения дают положительные значения в разных квадрантах для различных мер углов.
В первом квадранте (где все координаты x и y положительны) все шесть тригонометрических отношений имеют положительные значения. Во втором квадранте положительны только синус и косеканс. В третьем квадранте положительны только тангенс и котангенс. В четвертом квадранте положительны только косинус и секанс. На основании этих признаков мы разделим их на четные и нечетные функции.
Если тригонометрическое соотношение четное или нечетное, можно проверить через единичный круг. Угол, измеренный в направлении против часовой стрелки, является положительным углом, тогда как угол, измеренный в направлении по часовой стрелке, является отрицательным углом.
- sinθ = y, sin(-θ) = -y; Следовательно, sin(-θ) = -sinθ. Следовательно, sinθ — нечетная функция.
- cosθ = y, cos(-θ) = y; Следовательно, cos(-θ) = cosθ. Следовательно, cosθ — четная функция.
- тангенс θ = у, тангенс (-θ) = -у; Следовательно, tan(-θ) = -tanθ. Следовательно, tanθ — нечетная функция.
- cosecθ = y, cosec(-θ) = -y; Следовательно, cosec(-θ) = -cosecθ. Следовательно, cosecθ — нечетная функция.
- секθ = у, сек(-θ) = у; Следовательно, sec(-θ) = secθ. Следовательно, secθ — четная функция.
- кроватка θ = у, кроватка (-θ) = -у; Следовательно, cot(-θ) = -cotθ. Следовательно, cotθ — нечетная функция.
Следовательно, cosθ — четная функция.Интегральные свойства четных и нечетных функций
Интеграл функции дает площадь под кривой. Мы используем свойства четных и нечетных функций при решении определенных интегралов. Для этого нам нужно знать пределы интеграла и характер функции. Если функция четная или нечетная, а интервал равен [-a, a], мы можем применить следующие два правила: 9{а}\) f(x) dx = 0
График четных и нечетных функций
Теперь посмотрим, как графически ведут себя четные и нечетные функции.
График четной функции симметричен относительно оси Y . Другими словами, график четной функции остается прежним после отражения относительно оси у. Для любых двух противоположных входных значений x значение функции будет оставаться одинаковым на протяжении всей кривой.
Принимая во внимание, что график нечетной функции симметричен относительно начала координат . Другими словами, график нечетной функции находится на одном и том же расстоянии от начала координат, но в противоположных направлениях. Для любых двух противоположных входных значений x функция имеет противоположные значения y. Вот несколько примеров четных и нечетных функций.
Свойства четных и нечетных функций
- Сумма двух четных функций четна, а сумма двух нечетных функций нечетна.
- Разница между двумя четными функциями четна, а разница между двумя нечетными функциями нечетна.
- Сумма четной и нечетной функций не является ни четной, ни нечетной, если только одна из них не является нулевой функцией.
- Произведение двух четных функций является четным, и произведение двух нечетных функций также является четной функцией.
- Произведение четной и нечетной функций нечетно.
- Частное двух четных функций четно, и частное двух нечетных функций также является четной функцией.
- Частное четной и нечетной функций нечетно.
- Композиция двух четных функций четна, а композиция двух нечетных функций нечетна.
- Композиция четной и нечетной функций четна.
Важные замечания по четным и нечетным функциям
- Функция f(x) четна, если f(-x) = f(x), для всех значений x в D(f), и нечетна, если f (-x) = -f(x) для всех значений x.
- В тригонометрии cosθ и secθ — четные функции, а sinθ, cosecθ, tanθ, cotθ — нечетные функции.
- График четной функции симметричен относительно оси Y, а график нечетной функции симметричен относительно начала координат.
- f(x) = 0 — единственная функция, которая является четной и нечетной.
Темы, связанные с четными и нечетными функциями
- Функция четности
- Нечетная функция
- Типы функций
Часто задаваемые вопросы о четных и нечетных функциях
Что такое четные и нечетные функции в математике?
Функция f(x) является четной, если f(-x) = f(x), для всех значений x в D(f), и нечетной, если f(-x) = -f(x), для все значения х. График четной функции симметричен относительно оси y, а график нечетной функции симметричен относительно начала координат. Вещественная функция f(x) называется одновременно четной и нечетной, если она удовлетворяет f(-x) = f(x) и f(-x) = -f(x) для всех значений x в области функции f(x).
Как определить четные и нечетные функции алгебраически?
Чтобы проверить, является ли функция четной или нечетной алгебраически, мы проверяем, является ли f(-x) = f(x) или f(-x) = -f(x) для всех значений x соответственно. Если мы заменяем x на -x в функции и значение функции становится отрицательным, то функция называется нечетной функцией.
Если мы заменим x на -x в функции и значение функции не изменится, то функция будет известна даже как функция.
Если функция f четная, то какой тип симметрии имеет график f?
Четные и нечетные функции показывают разные типы симметрии. Даже функции имеют линейную симметрию. Линия симметрии является осью Y. Даже функции — это функции, в которых, когда мы заменяем x на -x, значение функции для этого конкретного x не меняется. График четной функции ведет себя одинаково для всех точек на оси X, которые находятся как слева от начала координат, так и справа от него.
Какие тригонометрические функции являются четными и нечетными функциями?
В тригонометрии cosθ и secθ — четные функции, а sinθ, cosecθ, tanθ, cotθ — нечетные функции. Различные тригонометрические отношения имеют положительные и отрицательные значения в разных квадрантах. Следовательно, используя единичный круг, мы можем видеть, что cosθ и secθ — четные функции, а остальные четыре тригонометрических отношения — нечетные.
Как определить графически четные и нечетные функции?
График четной функции симметричен относительно оси y. График нечетной функции симметричен относительно начала координат. График четной функции остается прежним после отражения относительно оси у. График нечетной функции находится на одинаковом расстоянии от начала координат, но в противоположных направлениях. Используя те же критерии, мы можем идентифицировать четные и нечетные функции графически.
Если f и g являются четными функциями, является ли f+g четной и нечетной функцией?
Если f и g — четные функции, то f + g — четная функция. Рассмотрим функцию h(x) = f(x) + g(x). Замените x на -x в h(x), h(-x) = f(-x) + g(-x) = f(x) + g(x) = h(x). Поскольку f(x) и g(x) четные, f(-x) = f(x) и g(-x) = g(x). Следовательно, f + g — четная функция. Это не четная и нечетная функция одновременно.
Как определить, является ли функция четной, нечетной или ни одной — Криста Кинг Математика
Что такое четные и нечетные функции?
Когда мы говорим о «четном, нечетном или ни одном», мы говорим о симметрии функции. Легче всего визуально увидеть четное, нечетное или ни то, ни другое, глядя на график. Иногда сложно или невозможно построить график функции, поэтому есть и алгебраический способ проверки.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Четные функции
Симметрично относительно оси ???y???
При подключении ???-x??? в функцию, она упростится, чтобы быть такой же, как исходная функция. Это означает, что не имеет значения, подключаете ли вы ???x??? или ???-x???, ваш вывод будет таким же. Итак,
???f(-x)=f(x)???
Ниже приведены четные и симметричные относительно оси ???y??? графики.
Нечетные функции
Симметричные относительно начала координат
При подключении ???-x??? в функцию, это упростит получение отрицательной исходной функции или исходной функции, умноженной на ???-1???. Это означает, что при подключении ???-x??? в функцию, вы получите тот же вывод, что и при подключении ???x???, за исключением того, что он будет отрицательным (или будет иметь противоположный знак, чем исходный вывод). Итак,
???f(-x)=-f(x)???
Ниже приведены нечетные и симметричные относительно начала координат графики. Обязательно визуально сравните квадранты, расположенные по диагонали друг от друга (квадранты 1 и 3 и квадранты 2 и 4).
Ни четная, ни нечетная
Несимметричная относительно оси ???y??? и несимметричная относительно начала координат
Функция не имеет симметрии. Вполне возможно, что график может быть симметричен относительно оси ???x???, но тогда он не пройдет тест вертикальной линии и, следовательно, не будет функцией.
Как определить, является ли функция четной, нечетной или ни одной из них 94???
Поскольку ???f(-x)=f(x)???, функция четная.