Названия геометрических тел в картинках: Картинки названия геометрических фигур (30 фото) • Прикольные картинки и позитив – Всё о детях – беременность, воспитание, уроки для детей

Содержание

Геометрические фигуры и их названия

Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках. Но обучение будет проходить наиболее эффективно в том случае, если к распечатанному заданию вы добавите еще и различные образцы геометрических фигур. Для этой цели могут подойти такие предметы, как мячики, пирамидки, кубики, надутые воздушные шары (круглые и овальные), кружки для чая (стандартные, в форме цилиндра), апельсины, книги, клубки ниток, квадратные печенья и многое другое – все, что подскажет вам фантазия.

Все перечисленные предметы помогут ребенку понять, что значит объемная геометрическая фигура. Плоские фигуры можно подготовить, вырезав из бумаги нужные геометрические формы, предварительно раскрасив их в разные цвета.

Чем больше различных материалов вы подготовите для занятия, тем интереснее будет ребенку изучать новые для него понятия.

Также вам может понравиться наш онлайн тренажер по математике для 1 класса “Геометрические фигуры”:

Геометрические фигуры 1 класс – Онлайн-тренажер

Онлайн-тренажер по математике “Геометрические фигуры 1 класс” поможет первоклассникам потренироваться в умении различать основные геометрические фигуры: квадрат, круг, овал, прямоугольник и треугольник.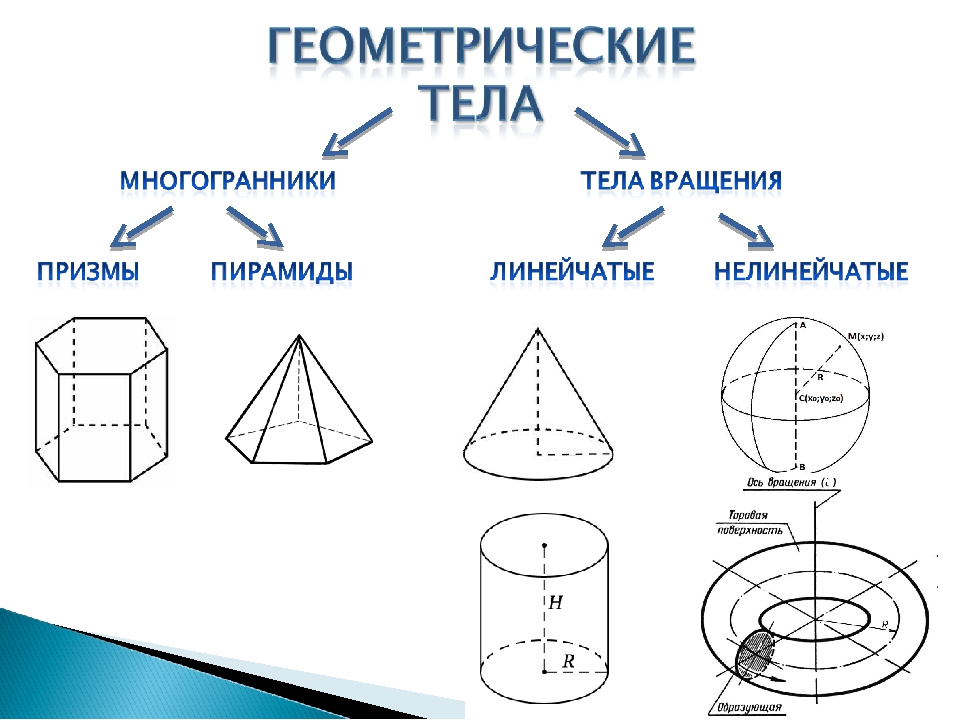

Геометрические фигуры и их названия – Проводим занятие с ребенком:

Чтобы легко и непринужденно ребенок смог запомнить геометрические фигуры и их названия, скачайте сначала картинку с заданием во вложениях внизу страницы, распечатайте на цветном принтере и положите на стол вместе с цветными карандашами. Также к этому времени у вас уже должны быть заготовлены различные предметы, которые мы перечисляли ранее.

1 этап. Сначала пусть ребенок выполнит задания на распечатанном листе – проговорит вслух названия фигур и раскрасит все картинки.
2 этап. Необходимо наглядно показать ребенку отличия объемных фигур от плоских. Для этого разложите все предметы-образцы (как объемные, так и вырезанные из бумаги) и отойдите с ребенком от стола на такое расстояние, с которого хорошо видны все объемные фигуры, но потерялись из виду все плоские образцы. Обратите внимание малыша на этот факт. Пусть он поэкспериментирует, подходя к столу то ближе, то дальше, рассказывая вам о своих наблюдениях.
3 этап. Дальше занятие нужно превратить в своеобразную игру. Попросите ребенка, чтобы он внимательно посмотрел вокруг себя и нашел предметы, которые имеют форму каких-либо геометрических фигур. Например, телевизор – прямоугольник, часы – круг и т.д. На каждой найденной фигуре – громко хлопайте в ладоши, чтобы добавить энтузиазма в игру.
4 этап. Проведите исследовательскую и наблюдательную работу с теми материалами-образцами, которые вы заготовили к занятию. Например, положите на стол книгу и плоский прямоугольник из бумаги. Предложите ребенку пощупать их, посмотреть на них с разных сторон и рассказать вам свои наблюдения. Таким же образом можно исследовать апельсин и бумажный круг, детскую пирамидку и бумажный треугольник, кубик и бумажный квадрат, воздушный шар овальной формы и овал, вырезанный из бумаги. Список предметов вы можете дополнить сами.

5 этап. Положите в непрозрачный пакет различные объемные образцы и попросите ребенка достать на ощупь квадратный предмет, затем круглый, затем прямоугольный и так далее.
6 этап. Разложите перед ребенком на столе несколько различных предметов из тех, которые участвуют в занятии. Затем пусть ребенок отвернется на несколько секунд, а вы спрячьте один из предметов. Повернувшись к столу ребенок должен назвать спрятанный предмет и его геометрическую форму.

Скачать геометрические фигуры и их названия – Бланк задания – вы можете во вложениях внизу страницы.

Названия геометрических фигур – Карточки для распечатки

Изучая с малышом геометрические фигуры, вы можете использовать во время занятий карточки для распечатки от Лисёнка Бибуши. Скачайте вложения, распечатайте на цветном принтере бланк с карточками, вырежьте каждую карточку по контуру – и приступайте к обучению. Карточки можно заламинировать, либо наклеить на более плотную бумагу, чтобы сохранить внешний вид картинок, ведь использоваться они будут неоднократно.

Первые шесть карточек дадут вам возможность изучить с ребенком такие фигуры: овал, круг, квадрат, ромб, прямоугольник и треугольник, под каждой фигурой в карточках можно прочесть ее название.

После того, как ребенок запомнил название определенной фигуры, попросите его выполнить следующее: обвести по контуру все имеющиеся на карточке образцы изучаемой фигуры, а затем раскрасить их в цвет основной фигуры, расположенной в верхнем левом углу.

Скачать названия геометрических фигур – Карточки для распечатки – вы можете во вложениях внизу страницы

Карточки для распечатки с изображением плоских геометрических фигур

С помощью следующих шести карточек ребенок сможет познакомиться с такими геометрическими фигурами: параллелограмм, трапеция, пятиугольник, шестиугольник, звезда и сердце. Как и в предыдущем материале под каждой фигурой можно найти ее название.

Чтобы разнообразить занятия с малышом, совмещайте обучение с рисованием – такой метод не даст ребенку переутомиться, и малыш с удовольствием будет продолжать учебу. Следите за тем, чтобы обводя фигуры по черточкам, ребенок не спешил и выполнял задание аккуратно, ведь подобные упражнения не только развивают мелкую моторику, они могут повлиять в дальнейшем на почерк малыша.

Скачать карточки для распечатки с изображением плоских геометрических фигур вы можете во вложениях

Объемные геометрические фигуры и их названия – скачать карточки

В процессе, того, как вы будете изучать с ребенком объемные геометрические фигуры и их названия, используя новые шесть карточек от Бибуши с изображениями куба, цилиндра, конуса, пирамиды, шара и полусферы, приобретите изучаемые фигуры в магазине, либо воспользуйтесь предметами, находящимися в доме, имеющими подобную форму.

Покажите малышу на примерах, как в жизни выглядят объемные фигуры, ребенок должен потрогать и поиграть с ними. Прежде всего, это необходимо для того, чтобы задействовать наглядно – действенное мышление малыша, с помощью которого ребенку проще познавать окружающий мир.

Скачать – Объемные геометрические фигуры и их названия – вы можете во вложениях внизу страницы

Также вам будут полезны и другие материалы по изучению геометрических фигур:

Рисунки из геометрических фигур – Задания в картинках и раскраски

Геометрические фигуры – Раскраска для дошкольников

Задания ознакомят ребенка с основными фигурами геометрии – кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.

Плоские геометрические фигуры – Обведи и дорисуй

Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги.

Найди формы геометрических фигур в картинках

Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок.

Наложение фигур друг на друга – Задание для детей

Наложение фигур друг на друга – это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры.

Свойства геометрических фигур для дошкольников

Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.

Счет геометрических фигур – Картинки с заданиями

Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.

Чертежи геометрических тел – Задание для детей

В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии

Геометрические фигуры из бумаги – Вырезаем и занимаемся

Здесь мы подготовили для вас объемные геометрические фигуры из бумаги, которые нужно вырезать и склеить. Куб, пирамиды, ромб, конус, цилиндр, шестигранник, распечатать их на картоне (или цветной бумаге, а затем наклеить на картон), а затем дать ребенку для запоминания.

Счет до 5 – Картинки с заданиями для малышей

Здесь мы выложили для вас счет до 5 – картинки с математическими заданиями для малышей, благодаря которым ваши дети потренируют не только свои навыки счета, но и умение читать, писать, различать геометрические фигуры, рисовать и раскрашивать.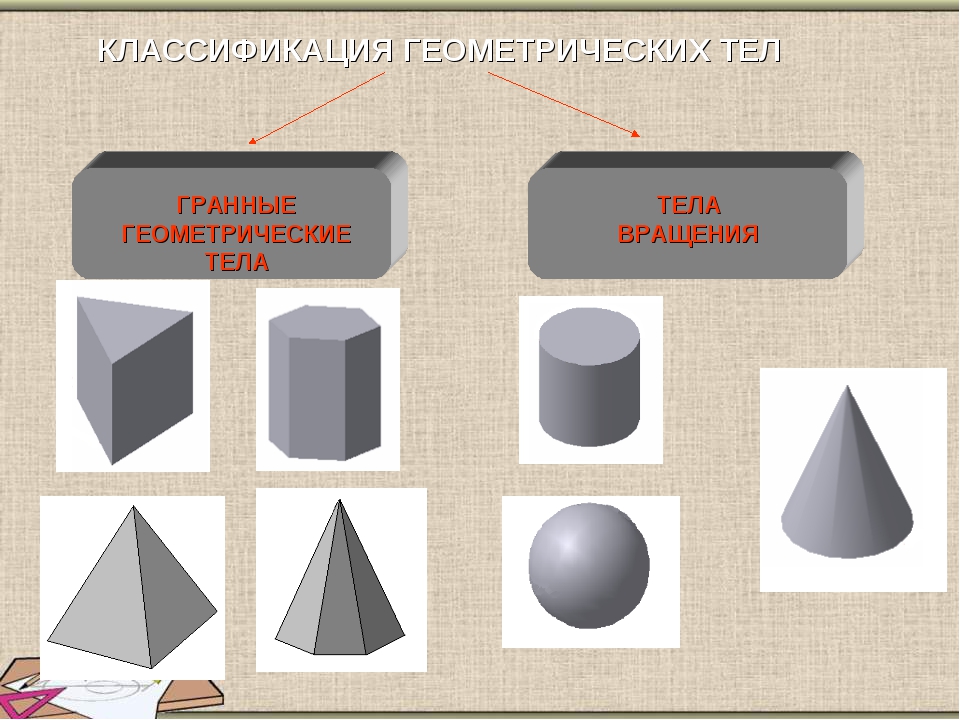

И еще можете поиграть в математические игры онлайн от лисенка Бибуши:

Игра “Что лишнее? – Геометрические формы”

В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок. При этом необходимо руководствоваться признаками геометрических форм.

MemorySecrets.ru

Наименование: Геометрические фигуры по-английски

Язык: английский

Транскрипция: есть

Количество карточек: 24 шт.

Примеры: нет

Небольшой набор слов на английском с транскрипцией на тему «геометрические фигуры». Данный набор слов используется не только для определения геометрических терминов, но и при описании формы различных предметов или описания движений. Например, описание траектории движения мыши при выделении рисунка, будет звучать примерно так: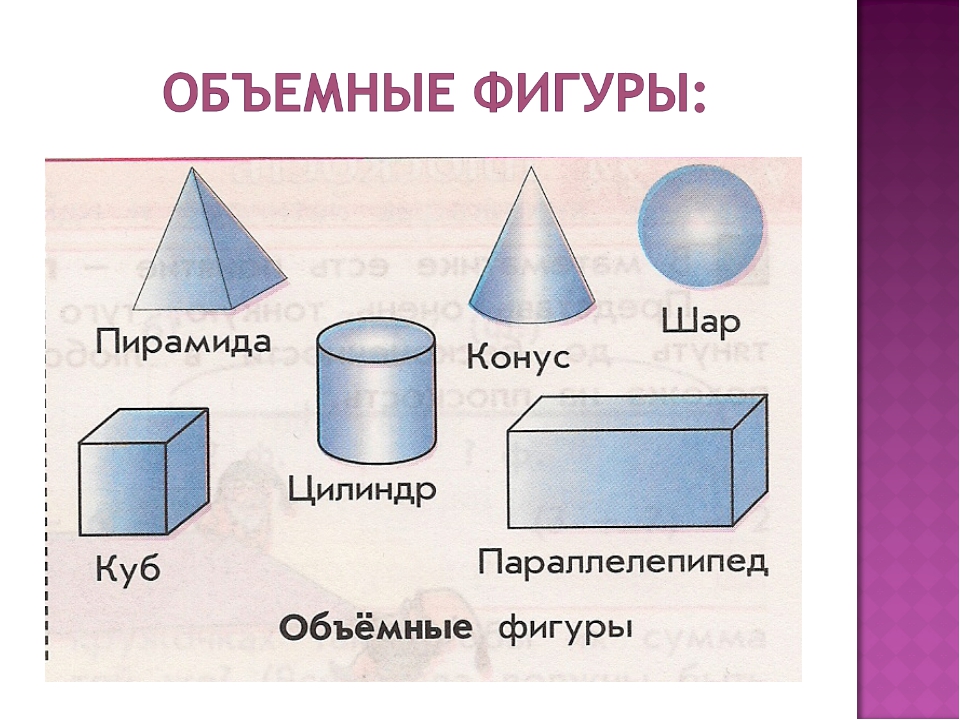

Select this tool and then use the mouse to frame the image with a rectangle.

Выучили все английские слова на тему «GEOMETRICAL SHAPES»? Проверьте свои знания с помощью кроссворда или карточек:

Скачать карточки для печати на принтер:

Английский в картинках

FlashCards

подробнее…

Английские слова с транскрипцией и переводом на тему «Геометрические фигуры»

sphere	[sfıə]	сфера
octagon	[‘ɔktəgən]	восьмиугольник
rhombus	[‘rɔmbəs]	ромб
rectangle	[‘rek,tæŋgl]	прямоугольник
parallelepiped	[,pærəle’lepıped]	параллелепипед
square	[skweə]	Квадрат
quadrilateral	[,kwɔdrı’lætərəl]	четырехугольник
cone	[kəun]	конус
hexagon	[‘heksəgən]	шестиугольник
cylinder	[‘sılındə]	цилиндр
hendecagon	[hen’dekəgən]	одиннадцатиугольник
pyramid	[‘pırəmıd]	пирамида
triangle	[‘traıæŋgl]	треугольник
helix	[‘hi:lıks]	спираль
trapezium	[trə’pi:zɪəm]	трапеция
hemisphere	[‘hemısfıə]	полушарие
parallelogram	[,pærə’leləugræm]	параллелограмм
heptagon	[‘heptəgən]	семиугольник
pentagon	[‘pentəgən]	пятиугольник
torus	[‘tɔ:rəs]	тор
octahedron	[‘ɔktə’hedrən]	октаэдр
dodecagon	[dəu’dekəgən]	двенадцатиугольник
decagon	[‘dekəgən]	десятиугольник
cube	[kju:b]	куб

Объёмные геометрические фигуры и их названия.

Геометрические фигуры. Играем в геометрическое лото

Геометрические фигуры представляют собой комплекс точек, линий, тел или поверхностей. Эти элементы могут располагаться как на плоскости, так и в пространстве, формируя конечное количество прямых.

Термин «фигура» подразумевает под собой несколько множеств точек. Они должны располагаться на одной или нескольких плоскостях и одновременно ограничиваться конкретным числом оконченных линий.

Основными геометрическими фигурами считаются точка и прямая. Они располагаются на плоскости. Кроме них, среди простых фигур выделяют луч, ломаную линию и отрезок.

Точка

Это одна из главных фигур геометрии. Она очень маленькая, но ее всегда используют для построения различных форм на плоскости. Точка – это основная фигура для абсолютно всех построений, даже самой высокой сложности. В геометрии ее принято обозначать буквой латинской алфавита, к примеру, A, B, K, L.

С точки зрения математики точка – это абстрактный пространственный объект, не обладающий такими характеристиками, как площадь, объем, но при этом остающийся фундаментальным понятием в геометрии. Этот нульмерный объект просто не имеет определения.

Прямая

Это фигура полностью размещается в одной плоскости. У прямой нет конкретного математического определения, так как она состоит из огромного количества точек, располагающихся на одной бесконечной линии, у которой нет предела и границ.

Существует еще и отрезок. Это тоже прямая, но она начинается и заканчивается с точки, а значит, имеет геометрические ограничения.

Также линия может превратиться в направленный луч. Такое происходит, когда прямая начинается с точки, но четкого окончания не имеет. Если же поставить точку посредине линии, то она разобьется на два луча (дополнительных), причем противоположно направленных друг к другу.

Несколько отрезков, которые последовательно соединяются друг с другом концами в общей точке и располагаются не на одной прямой, принято называть ломаной линией.

Угол

Геометрические фигуры, названия которых мы рассмотрели выше, считают ключевыми элементами, использующимися при построении более сложных моделей.

Угол – это конструкция, состоящая из вершины и двух лучей, которые выходят из нее. То есть стороны этой фигуры соединяются в одной точке.

Плоскость

Рассмотрим еще одно первичное понятие. Плоскость – это фигура, у которой нет ни конца, ни начала, равно как и прямой, и точки. Во время рассмотрения этого геометрического элемента во внимание берется лишь его часть, ограниченная контурами ломаной замкнутой линии.

Любую гладкую ограниченную поверхность можно считать плоскостью. Это может быть гладильная доска, лист бумаги или даже дверь.

Четырехугольники

Параллелограмм – это геометрическая фигура, противоположные стороны которой параллельны друг другу попарно. Среди частных видов этой конструкции выделяют ромб, прямоугольник и квадрат.

Прямоугольник – это параллелограмм, у которого все стороны соприкасаются под прямым углом.

Квадрат – это четырехугольник с равными сторонами и углами.

Ромб – это фигура, у которой все грани равны. При этом углы могут быть совершенно разными, но попарно. Каждый квадрат считается ромбом. Но в противоположном направлении это правило действует не всегда. Далеко не каждый ромб является квадратом.

Трапеция

Геометрические фигуры бывают совершенно разными и причудливыми. Каждая из них имеет своеобразную форму и свойства.

Трапеция – это фигура, которая чем-то схожа с четырехугольником. Она имеет две параллельные противоположные стороны и при этом считается криволинейной.

Круг

Эта геометрическая фигура подразумевает расположение на одной плоскости точек, равноудаленных от ее центра. При этом заданный ненулевой отрезок принято называть радиусом.

Треугольник

Это простая геометрическая фигура, которая очень часто встречается и изучается.

Треугольник считается подвидом многоугольника, расположенным на одной плоскости и ограниченным тремя гранями и тремя точками соприкосновения. Эти элементы попарно соединены между собой.

Многоугольник

Вершинами многоугольников называют точки, соединяющие отрезки. А последние, в свою очередь, принято считать сторонами.

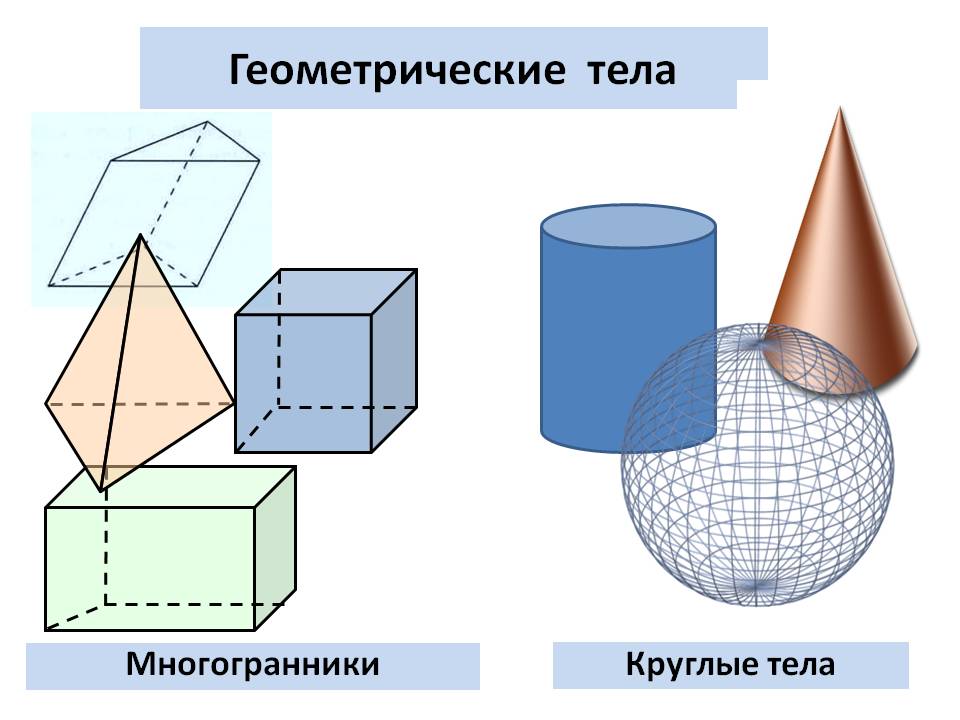
Объемные геометрические фигуры

призма;
сфера;
конус;
цилиндр;
пирамида;

Эти тела имеют нечто общее. Все они ограничиваются замкнутой поверхностью, внутри которой находится множество точек.

Объемные тела изучают не только в геометрии, но и в кристаллографии.

Любопытные факты

Наверняка вам будет интересно ознакомиться с информацией, предоставленной ниже.

Геометрия сформировалась как наука еще в давние века. Это явление принято связывать с развитием искусства и разнообразных ремесел. А названия геометрических фигур свидетельствуют об использовании принципов определения подобия и схожести.
В переводе с древнегреческого термин «трапеция» обозначает столик для трапезы.
Если вы возьмете различные фигуры, периметр которых будет одинаковым, то наибольшая площадь гарантированно будет у круга.
В переводе с греческого языка термин «конус» обозначает сосновую шишку.
Существует известная картина Каземира Малевича, которая начиная с прошлого века притягивает к себе взгляды многих живописцев. Работа «Черный квадрат» всегда была мистической и загадочной. Геометрическая фигура на белом полотне восхищает и поражает одновременно.

Существует большое количество геометрических фигур. Все они отличаются параметрами, а порой даже удивляют формами.

Чукур Людмила Васильевна
Геометрические фигуры. Особенности восприятия детьми формы предметов и геометрических фигур

«ГЕОМЕТРИЧЕСКАЯ ФИГУРА .

ОСОБЕННОСТИ ВОСПРИЯТИЯ ДЕТЬМИ

Подготовила : ст. воспитатель Чукур Л . В.

1. Понятие «геометрическая фигура » . Особенности развития представлений о форме предметов у детей дошкольного возраста

Одним из свойств окружающих предметов является их форма . Форма предметов получила обобщенное отражение в геометрических фигурах .

Фигура – латинское слово , означает «образ» , «вид» , «начертание» ; это часть плоскости, ограниченная замкнутой линией, или часть пространства, ограниченная замкнутой поверхностью. Этот термин вошел в общее употребление в XII в. До этого чаще употреблялось другое латинское слово – «форма » , также означающее «наружный вид» , «внешнее очертание предмета » .

Наблюдая за предметами окружающего мира , люди заметили, что есть некоторое общее свойство, позволяющее объединить предметы в одну группу . Это свойство было названо геометрической фигурой . Геометрическая фигура – это эталон для определения формы предмета , всякое непустое множество точек; обобщенное абстрактное понятие.

Само определение понятия геометрической фигуры дали древние греки . Они определили , что геометрической фигурой является внутренняя область, ограниченная замкнутой линией на плоскости. Активно это понятие применял в своей работе Евклид. Древние греки классифицировали все геометрические фигуры и дали им названия .

Упоминание о первых геометрических фигурах встречается и у древних египтян и древних шумеров.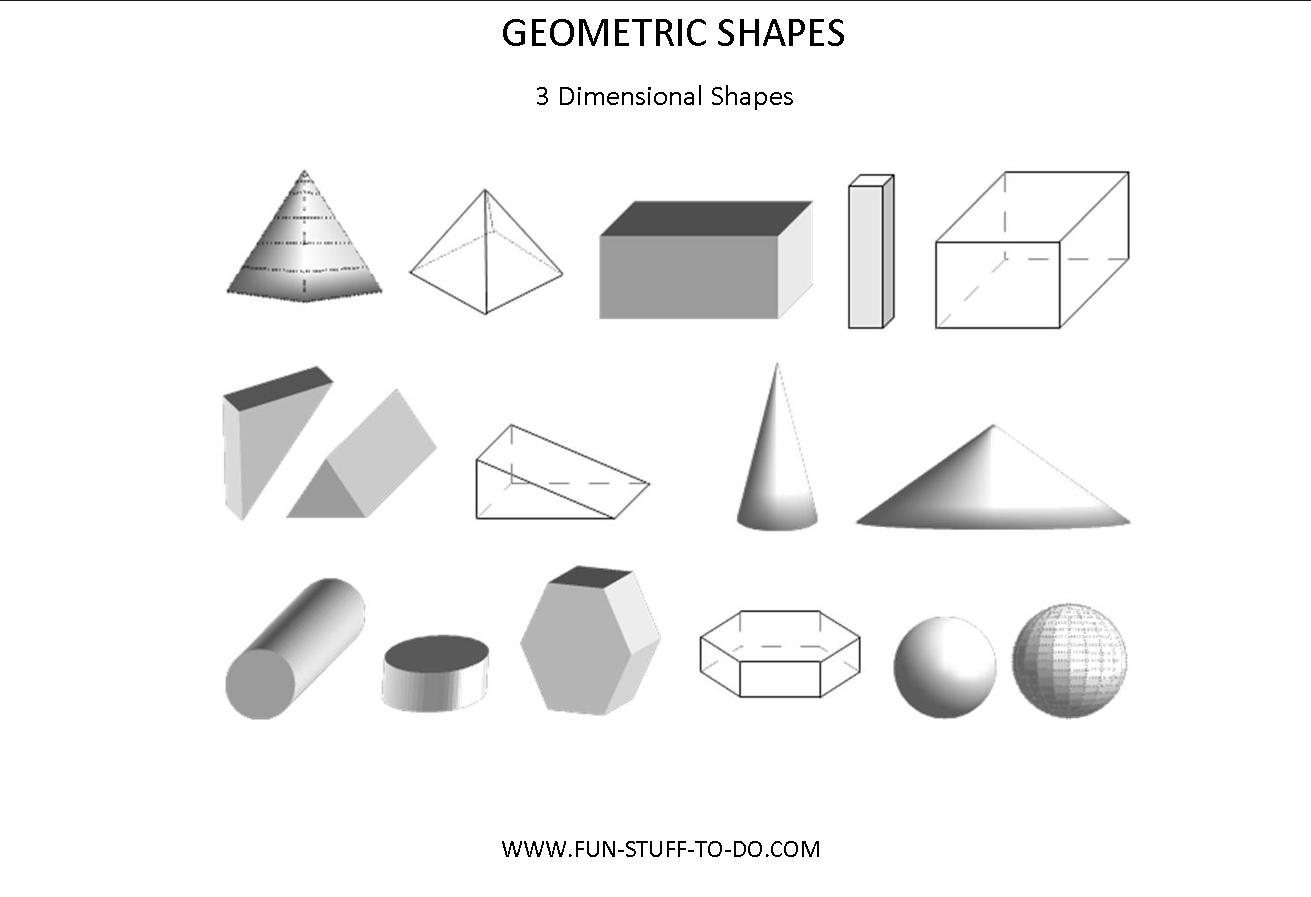 Учеными-археологами был найден папирусный свиток с геометрическими задачами , в которых упоминались геометрические фигуры . И каждая из них называлась каким-то определенным словом .

Таким образом, представление о геометрии и изучаемых этой наукой фигурах имели люди с давних времен, но название, «геометрическая фигура » и названия всем геометрическим фигурам дали древнегреческие ученые.

В наше время знакомство с геометрическими фигурами начинается с раннего детства и продолжается на всём пути обучения. Дошкольники, познавая окружающий мир, сталкиваются с разнообразием форм предметов , учатся называть и различать их, а затем знакомятся и со свойствами геометрических фигур .

Форма – это внешнее очертание предмета . Множество форм бесконечно .

Представления о форме предметов возникают у детей достаточно рано. В исследованиях Л. А. Венгера выясняется, возможно ли различение формы предметов детьми , у которых еще не сформировался акт хватания . В качестве индикатора он использовал ориентировочную реакцию ребенка в возрасте 3-4 месяцев.

Детям предъявлялись два объемных тела одинакового стального цвета и размера (призма и шар, одно из них подвешивалась над манежем, чтобы угасить ориентировочную реакцию; затем снова подвешивалась пара фигур . На одну из них (призма) реакция угашена, другая (шар) – новая. Малыши обращали взор на новую фигуру и фиксировали ее взглядом в течение более длительного времени, чем старую.

Л. А. Венгер заметил также, что что на геометрической фигуре с изменением пространственной ориентации возникает такое же зрительное сосредоточение, как и на новой геометрической фигуре .

Исследования М. Денисовой и Н. Фигурина показали , что грудной ребенок по форме на ощупь определяет бутылочку , соску, материнскую грудь. Зрительно дети начинают различать форму предметов с 5 месяцев . При этом индикатором различения являются движения рук, корпуса по направлению к экспериментальному объекту и схватывание его (при пищевом подкреплении) .

В других исследованиях выявлено, что, если предметы отличаются цветом , то ребенок 3-х лет выделяет их форму только в том случае , если предмет знаком ребенку из практического опыта (опыт манипуляций, действий) .

Это доказывает и тот факт, что ребенок одинаково узнает прямые и перевернутые изображения (может рассматривать и понимать знакомые картинки, держа книжку «вверх ногами» , предметы , окрашенные в несвойственные цвета (черное яблоко, но квадрат, повернутый на угол, т. е. в виде ромба, не узнает, так как исчезает непосредственное сходство формы предмета , которого нет в опыте.

2. Особенности восприятия детьми дошкольного возраста формы предметов и геометрических фигур

Одним из ведущих познавательных процессов детей дошкольного возраста является восприятие . Восприятие помогает отличить один предмет от другого , выделить какие-то предметы или явления из других похожих на него.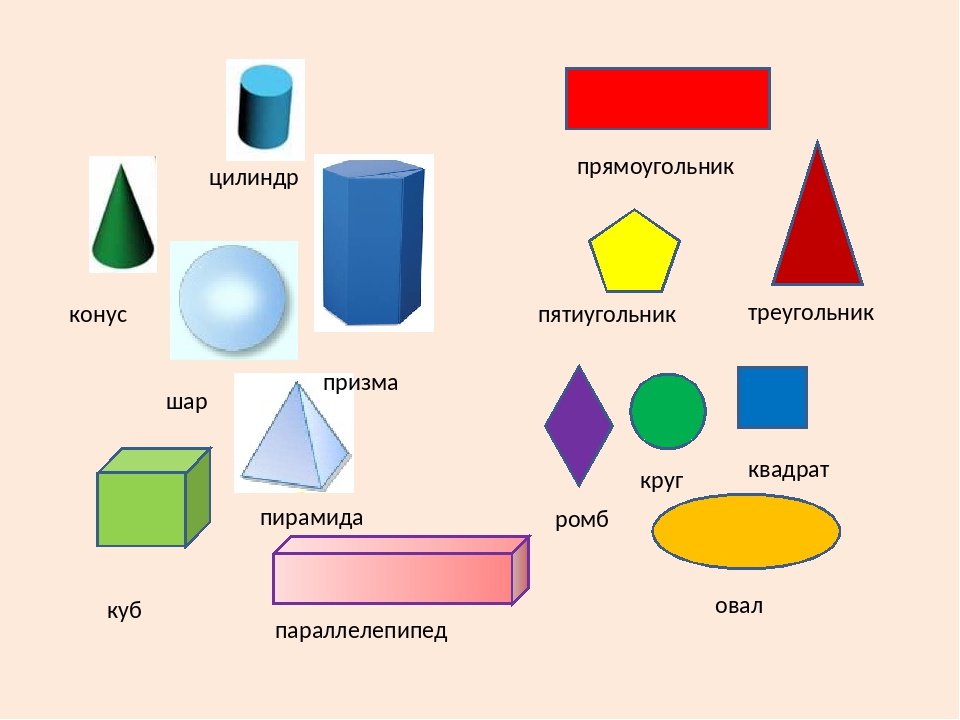

Первичное овладение формой предмета Форма предмета , как таковая, не предмета предшествовать практическим действиям. Действия детей с предметами на разных этапах различны.

Исследования психолога С. Н. Шабалина показывают, что геометрическая фигура воспринимается дошкольниками своеобразно. Если взрослый воспринимает ведро или стакан как предметы , имеющие цилиндрическую форму , то в его восприятие включается знание геометрических форм . У дошкольника происходит обратное явление.

В 3-4 года дети опредмечивают геометрические фигуры , так как они в их опыте представлена нераздельно с предметами , не абстрагированы. Геометрическая фигура воспринимается детьми как картинка , как некоторый предмет : квадрат – это платочек, кармашек; треугольник – крыша, круг – колесо, мячик, два круга рядом – очки, несколько кругов рядом – бусы и т. п.

В 4 года опредмечивание геометрической фигуры возникает только при столкновении ребенка с незнакомой фигурой : цилиндр – это ведро, стаканчик.

В 4-5 лет ребенок начинает сравнивать геометрическую фигуру с предметом : про квадрат говорит «это как платочек» .

В результате организованного обучения дети начинают выделять в окружающих предметах знакомую геометрическую фигуру , сравнивать предмет с фигурой (стаканчик как цилиндр, крыша как треугольник, учится давать правильное название геометрической фигуры и формы предмета , в их речи появляются слова «квадрат» , «круг» , «квадратный» , «круглый» и т. п.

Проблему знакомства детей с геометрическими фигурами и их свойствами следует рассматривать в двух аспектах :

В плане сенсорного восприятия форм геометрических фигур и использования их как эталонов в познании форм окружающих предметов ;

В смысле познания особенностей их структуры , свойств, основных свя-зей и закономерностей в их построении, т. е. собственно геометри-ческого материала .

Контур предмета это общее начало , которое является исходным как для зрительного, так и для осязательного восприятия .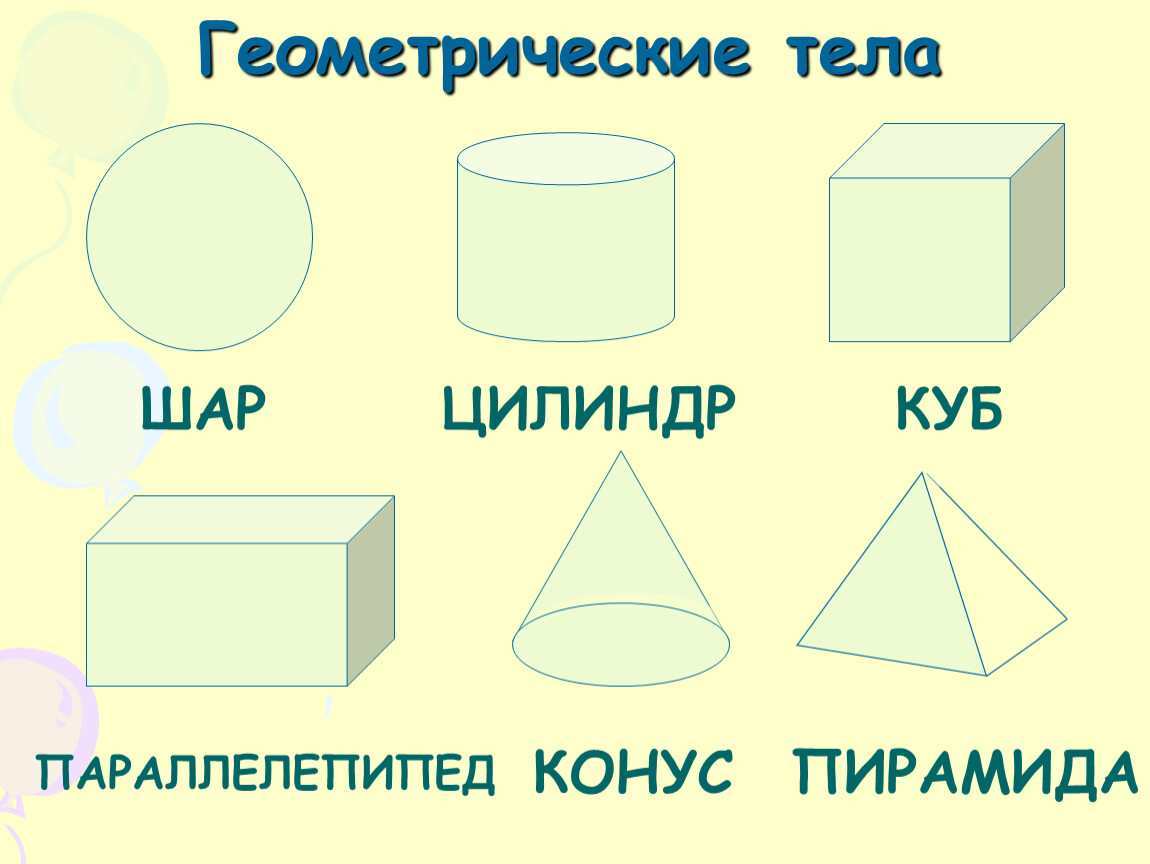 Однако вопрос о роли контура в восприятии формы и формировании целостного образа требует еще дальнейшей разработки.

Первичное овладение формой предмета осуществляется в действиях с ним. Форма предмета , как таковая, не воспринимается отдельно от предмета , она является его неотъемлемым признаком. Специфические зрительные реакции прослеживания контура предмета появляются в конце второго года жизни и начинают предшествовать практическим действиям.

Действия детей с предметами на разных этапах различны. Малыши стремятся, прежде всего, захватить предмет руками и начать манипулировать им. Дети 2,5 лет, прежде чем действовать, довольно подробно зрительно и осязательно – двигательно знакомятся с предметами . Значение практических действий остается главным. Отсюда следует вывод о необходимости руководить развитием перцептивных действий двухлетних детей. В зависимости от педагогического руководства характер перцептивных действий детей постепенно достигает познавательного уровня. Ребенка начинают интересовать различные признаки предмета , в том числе и форма . Однако он еще долго не может выделить и обобщить тот или иной признак, в том числе и форму разных предметов .

Сенсорное восприятие формы предмета должно быть направлено не только на то, чтобы видеть , узнавать формы , наряду с другими его признаками, но уметь, абстрагируя форму от вещи , видеть ее и в других вещах . Такому восприятию формы предметов и ее обобщению и способствует знание детьми эталонов – геометрических фигур . Поэтому задачей сенсорного развития является формирование у ребенка умений узнавать в соответствии с эталоном (той или иной геометрической фигурой ) форму разных предметов .

Экспериментальные данные Л. А. Венгера показали, что возможностью различать геометрические фигуры обладают дети 3-4 месяцев. Сосредоточение взгляда на новой фигуре – свидетельство этому.

Уже на втором году жизни дети свободно выбирают фигуру по образцу из таких пар : квадрат и полукруг, прямоугольник и треугольник. Но различать прямоугольник и квадрат, квадрат и треугольник дети могут лишь после 2,5 лет. Отбор же по образцу фигур более сложной формы доступен примерно на рубеже 4-5 лет, а воспроизведение сложной фигуры осуществляют дети пятого и шестого года жизни.

Под обучающим воздействием взрослых восприятие геометрических фигур постепенно перестраивается. Геометрические фигуры начинают восприниматься детьми как эталоны , с помощью которых познание структуры предмета , его формы и размера осуществляется не только в процессе восприятия той или иной формы зрением , но и путем активного осязания, ощупывания ее под контролем зрения и обозначения словом.

Совместная работа всех анализаторов способствует более точному восприятию формы предметов . Чтобы лучше познать предмет , дети стремятся коснуться его рукой, взять в руки, повернуть; причем рассматривание и ощупывание различны в зависимости от формы и конструкции познаваемого объекта. Поэтому основную роль в восприятии предмета и определении его формы имеет обследование , осуществляемое одновременно зрительным и двигательно-осязательным анализаторами с последующим обозначением словом. Однако у дошкольников наблюдается весьма низкий уровень обследования формы предметов ; чаще всего они ограничиваются беглым зрительным восприятием и поэтому не различают близкие по сходству фигуры (овал и круг, прямоугольник и квадрат, разные треугольники) .

В перцептивной деятельности детей осязательно-двигательные и зрительные приемы постепенно становятся основным способом рас-познавания формы . Обследование фигур не только обеспечивает целостное их восприятие , но и позволяет ощутить их особенности (характер, направления линий и их сочетания, образующиеся углы и вершины, ребенок учится чувственно выделять в любой фигуре образ в целом и его части. Это дает возможность в дальнейшем сосредоточить внимание ребенка на осмысленном анализе фигуры , сознательно выделяя в ней структурные элементы (стороны, углы, вершины) . Дети уже осознанно начинают понимать и такие свойства, как устойчивость, неустойчивость и др., понимать, как образуются вершины, углы и т. д. Сопоставляя объемные и плоские фигуры , дети находят уже общность между ними («У куба есть квадраты» , «У бруса – прямоугольники, у цилиндра – круги» и т. д.).

Сравнение фигуры с формой того или иного предмета помогает детям понять, что с геометрическими фигурами можно сравнивать разные предметы или их части . Так, постепенно геометрическая фигура становится эталоном определения формы предметов .

3. Особенности обследования и этапы обучения обследованию детьми дошкольного возраста формы предметов и геометрических фигур

Известно, что в основе познания всегда лежит сенсорное обследование, опосредованное мышлением и речью. В исследованиях Л. Венгера с детьми 2-3 лет индикатором зрительного различения формы предметов служили предметные действия ребенка .

По исследованиям С. Якобсон, В. Зинченко, А. Рузской дети 2-4 лет лучше узнавали предметы по форме , когда предлагалось сначала ощупать предмет , а потом найти такой же. Более низкие результаты наблюдались тогда, когда предмет воспринимался зрительно .

Исследования Т. Гиневской раскрывают особенности движений рук при обследовании предметов по форме . Детям завязывали глаза и предлагали ознакомиться с предметом путем осязания .

В 3-4 года – движения исполнительные (катают, стучат, возят) . Движения немногочисленны, внутри фигуры , иногда (однократно) по осевой линии, много ошибочных ответов, смешение разных фигур . В 4-5 лет – движения установочные (зажимают в руке) . Количество движений увеличивается в два раза; судя по траектории, ориентированы на размер и площадь; крупные, размашистые, обнаруживаются группы близко расположенных фиксаций, относящихся к наиболее характерным признакам фигуры ; дают более высокие результаты. В 5-6лет – движения обследовательские (прослеживание контура, проверка на упругость) . Появляются движения, прослеживающие контур, однако они охватывают наиболее характерную часть контура, другие части оказываются необследованными; движения внутри контура, количество то же, высокие результаты; как и в предыдущий период , наблюдается смешение близких фигур . В 6-7 лет – движения по контуру, пересечение поля фигуры , причем движения сосредотачиваются на наиболее информативных признаках , наблюдаются отличные результаты не только при узнавании, но и при воспроизведении .

Таким образом, для того, чтобы ребенок выделил существенные признаки геометрических фигур , необходимо их зрительное и двигательное обследование. Движения рук организовывают движения глаз и этому детей необходимо научить.

Этапы обучения обследованию

Задача первого этапа обучения детей 3-4 лет – это сенсорное восприятие формы предметов и геометрических фигур .

Второй этап обучения детей 5-6 лет должен быть посвящен формированию системных знаний о геометрических фигурах и развитию у них начальных приемов и способов «геометрического мышления » .

«Геометрическое мышление » вполне возможно развить еще в дошкольном возрасте. В развитии «геометрических знаний » у детей прослеживается несколько различных уровней.

Первый уровень характеризуется тем, что фигура воспринимается детьми как целое , ребенок еще не умеет выделять в ней отдельные элементы, не замечает сходства и различия между фигурами , каждую из них воспринимает обособленно .

На втором уровне ребенок уже выделяет элементы в фигуре и устанавливает отношения как между ними, так и между отдельными фигурами , однако еще не осознает общности между фигурами .

На третьем уровне ребенок в состоянии устанавливать связи между свойствами и структурой фигур , связи между самими свойствами. Переход от одного уровня к другому не является самопроизвольным, идущим параллельно биологическому развитию человека и зависящим от возраста. Он протекает под влиянием целенаправленного обучения, которое содействует ускорению перехода к более высокому уровню. Отсутствие же обучения тормозит развитие. Обучение поэтому следует организовывать так, чтобы в связи с усвоением знаний о геометрических фигурах у детей развивалось и элементарное геометрическое мышление .

Познание геометрических фигур , их свойств и отношений расширяет кругозор детей, позволяет им более точно и разносторонне воспринимать форму окружающих предметов , что положительно отражается на их продуктивной деятельности (например, рисовании, лепке) .

Большое значение в развитии геометрического мышления и про-странственных представлений имеют действия по преобразованию фигур (из двух треугольников составить квадрат или из пяти палочек сложить два треугольника).

Все эти разновидности упражнений развивают пространственные представления и начала геометрического мышления детей , формируют у них умения наблюдать, анализировать, обобщать, выделять главное, существенное и одновременно с этим воспитывают такие качества личности, как целенаправленность, настойчивость.

Итак, в дошкольном возрасте происходит овладение перцептивной и интеллектуальной систематизацией форм геометрических фигур . Перцептивная деятельность в познании фигур опережает развитие интеллектуальной систематизации.

Библиографический список

1. Белошистая А. В. Знакомство с геометрическими понятиями / А . Белошистая // Дошкольное воспитание . – 2008. – № 9. – с. 41- 51

2. Венгер Л. А. Воспитание сенсорной культуры ребенка / Л. А. Венгер Э. Г. Пилюгина, Н. Б. Венгер. – М. : Просвещение, 1988.- 144с.

3. Воспитание и обучение детей пятого года жизни : книга для воспитателя детского сада / (А. Н. Давидчук, Т. И. Осокина, Л. А. Парамонова и др.) ; под ред. В. В. Холмовской. – М. : Просвещение, 1986. – 144 с.

4. Габова М. А. Знакомство детей с геометрическими фигурами / М . А. Габова // Дошкольное воспитание . – 2002. – № 9. – с. 2- 17.

5. Дидактические игры и упражнения по сенсорному воспитанию дошкольников : (пособие для воспитателя детского сада / под ред. Л. А. Венгера). – М. : Просвещение, 1978. – 203 с.

6. Кербс Е. В. Математические досуги / Е. В. Кербс // Ребёнок в детском саду. – 2008. – № 3. – с. 21- 23.

7.Математика в детском саду : (пособие для воспитателя дет . сада / составитель Г. М. Лямина). – М. : Просвещение, 1977. – С. 224 – 228.

8. Метлина Л. С.Математика в детском саду : (пособие для воспитателя дет . сада) / Л. С. Метлина. – М. : Просвещение, 1994. – 256 с.

Точка

Прямая

Угол

Плоскость

Четырехугольники

Прямоугольник – это параллелограмм, у которого все стороны соприкасаются под прямым углом.

Квадрат – это четырехугольник с равными сторонами и углами.

Трапеция

Круг

Треугольник

Это простая геометрическая фигура, которая очень часто встречается и изучается.

Многоугольник

Объемные геометрические фигуры

призма;
сфера;
конус;
цилиндр;
пирамида;

Объемные тела изучают не только в геометрии, но и в кристаллографии.

Любопытные факты

Наверняка вам будет интересно ознакомиться с информацией, предоставленной ниже.

Геометрия сформировалась как наука еще в давние века. Это явление принято связывать с развитием искусства и разнообразных ремесел. А названия геометрических фигур свидетельствуют об использовании принципов определения подобия и схожести.
В переводе с древнегреческого термин «трапеция» обозначает столик для трапезы.
Если вы возьмете различные фигуры, периметр которых будет одинаковым, то наибольшая площадь гарантированно будет у круга.
В переводе с греческого языка термин «конус» обозначает сосновую шишку.
Существует известная картина Каземира Малевича, которая начиная с прошлого века притягивает к себе взгляды многих живописцев. Работа «Черный квадрат» всегда была мистической и загадочной. Геометрическая фигура на белом полотне восхищает и поражает одновременно.

Маленькие детки готовы учиться везде и всегда. Их юный мозг способен улавливать, анализировать и запоминать столько информации, сколько трудно даже взрослому человеку. То, чему родители должны научить малышей, имеет общепринятые возрастные рамки.

Основные геометрические фигуры и их названия дети должны узнать в возрасте от 3 до 5 лет.

Поскольку все дети разнообучаемы, то эти границы лишь условно приняты в нашей стране.

Геометрия – это наука о формах, размерах и расположении фигур в пространстве. Может создаться впечатление, что это сложно для малышей. Однако предметы изучения этой науки находятся повсюду вокруг нас. Вот почему иметь основные познания в этой области важно и для детей, и для старших.

Чтобы увлечь детей изучением геометрии, можно прибегнуть к веселым картинкам. Дополнительно хорошо бы иметь пособия, которые ребенок сможет потрогать, ощупать, обвести, раскрасить, узнать с закрытыми глазами. Основной принцип любых занятий с детьми – удержание их внимание и развития тяги к предмету с использованием игровых приемов и непринужденной веселой обстановки.

Сочетание нескольких средств восприятия сделает свое дело очень быстро. Воспользуйтесь нашей мини-методичкой, чтобы научить ребенка отличать геометрические фигуры, знать их названия.

Круг – самая первая из всех фигур. В природе вокруг нас многое имеет круглую форму: наша планета, солнце, луна, сердцевина цветка, многие фрукты и овощи, зрачки глаз. Объемный круг – это шар (мячик, клубок)

Начать изучение формы круга с ребенком лучше, рассматривая рисунки, а потом уже подкрепить теорию практикой, дав ребенку подержать что-нибудь круглое в руках.

Квадрат – это фигура, у которой все стороны имеют одинаковую высоту и ширину. Квадратные предметы – кубики, коробки, дом, окно, подушка, табурет и т. п.

Строить из квадратных кубиков всякие домики очень просто. Рисунок квадрата проще сделать на листочке в клетку.

Прямоугольник – родственник квадрата, который отличается тем, что имеет одинаковые противоположные стороны. Так же, как и у квадрата, у прямоугольника все равны 90 градусам.

Можно найти множество предметов, имеющих форму прямоугольника: шкафы, бытовая техника, двери, мебель.

В природе форму треугольника имеют горы и некоторые деревья. Из ближайшего окружения малышей можно привести в пример треугольную крышу дома, различные дорожные знаки.

В форме треугольника были построены некоторые древние сооружения, например храмы и пирамиды.

Овал – это круг, вытянутый с двух сторон. Формой овала обладают, например: яйцо, орехи, многие овощи и фрукты, человеческое лицо, галактики т. д.

Овал в объеме называется эллипсом. Даже Земля сплюснута с полюсов – эллипсовидная.

Ромб

Ромб – тот же квадрат, только вытянутый, т. е. имеет два тупых угла и пару острых.

Изучать ромб можно с помощью наглядных пособий – нарисованной картинки или объемного предмета.

Приемы запоминания

Геометрические фигуры по названиям запомнить несложно. В игру их изучение для детей можно превратить, применив следующие идеи:

Купите детскую книжку с картинками, в которой будут веселые и красочные рисунки фигур и их аналогии из окружающего мира.

Нарежьте из разноцветного картона побольше всяких фигурок, заламинируйте их скотчем и используйте как конструктор – очень много интересных сочетаний можно выложить, комбинируя разные фигурки.

Купите линейку с отверстиями в форме круга, квадрата, треугольника и других – для детей, которые уже дружат с карандашами, рисунки с помощью такой линейки – интереснейшее занятие.

Можно придумать много возможностей научить малышей знать названия геометрических фигур. Все способы хороши: рисунки, игрушки, наблюдения за окружающими предметами. Начните с малого, постепенно усложняя информацию и задания. Вы не ощутите, как пролетит время, а малыш обязательно порадует вас успехами в скором.

Геометрические объемные фигуры – это твердые тела, которые занимают ненулевой объем в евклидовом (трехмерном) пространстве. Эти фигуры изучает раздел математики, который носит название “пространственная геометрия”. Знания о свойствах объемных фигур применяются в инженерии и в науках о природе. Рассмотрим в статье вопрос, геометрические объемные фигуры и их названия.

Геометрические объемные тела

Поскольку эти тела имеют конечную размерность в трех пространственных направлениях, то для их описания в геометрии используют систему из трех координатных осей. Эти оси обладают следующими свойствами:

Они ортогональны друг другу, то есть перпендикулярны.
Эти оси нормализированы, то есть базисные вектора каждой оси имеют одинаковую длину.
Любая из осей координат – это результат векторного произведения двух других.

Говоря о геометрических объемных фигурах и их названиях, следует отметить, что все они принадлежат к одному из 2-х больших классов:

Класс полиэдров. Эти фигуры, исходя из названия класса, имеют прямые ребра и плоские грани. Грань – это плоскость, которая ограничивает фигуру. Место соединения двух граней называется ребром, а точка соединения трех граней – это вершина. К полиэдрам относятся геометрическая фигура куб, тетраэдры, призмы, пирамиды. Для этих фигур справедлива теорема Эйлера, которая устанавливает связь между числом сторон (С), ребер (Р) и вершин (В) для каждого полиэдра. Математически эта теорема записывается так: С + В = Р + 2.
Класс круглых тел или тел вращения. Эти фигуры имеют хотя бы одну поверхность, образующую их, изогнутой формы. Например, шар, конус, цилиндр, тор.

Что касается свойств объемных фигур, то следует выделить два самых важных из них:

Наличие определенного объема, который фигура занимает в пространстве.
Наличие у каждой объемной фигуры площади поверхности.

Оба свойства для каждой фигуры описываются конкретными математическими формулами.

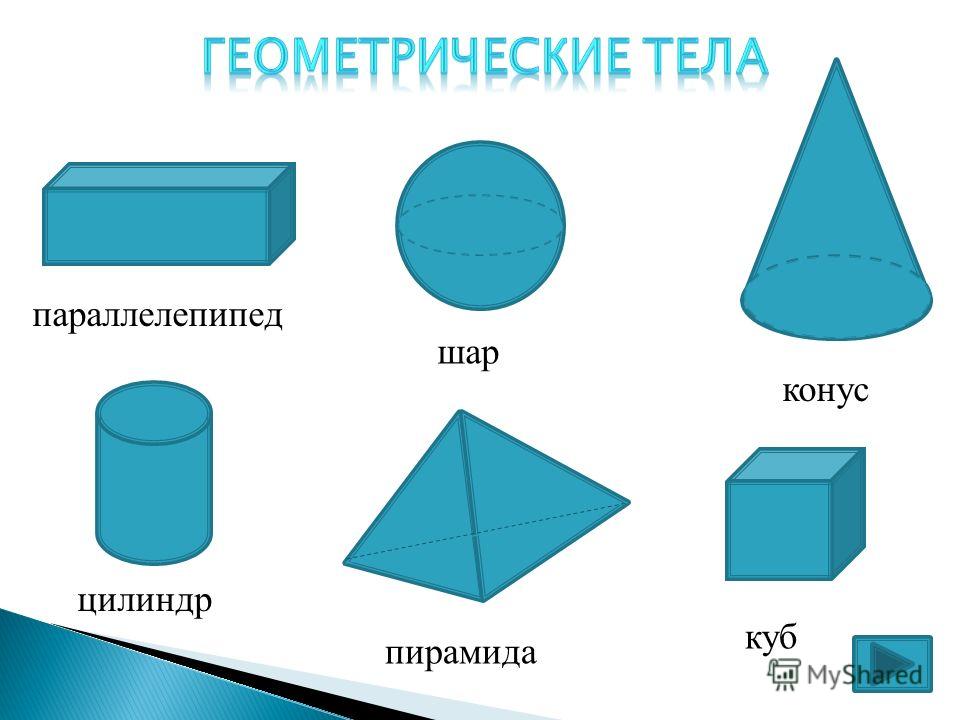
Рассмотрим ниже самые простые геометрические объемные фигуры и их названия: куб, пирамиду, призму, тетраэдр и шар.

Фигура куб: описание

Под геометрической фигурой куб понимают объемное тело, которое образовано 6-тью квадратными плоскостями или поверхностями. Также эту фигуру называют правильный гексаэдр, поскольку она имеет 6 сторон, или прямоугольный параллелепипед, так как он состоит из 3-х пар параллельных сторон, которые взаимно перпендикулярны друг другу. Называют куб и у которой основание является квадратом, а высота равна стороне основания.

Поскольку куб является многогранником или полиэдром, то для него можно применить теорему Эйлера, чтобы определить число его ребер. Зная, что число сторон равно 6, а вершин у куба 8, число ребер равно: Р = С + В – 2 = 6 + 8 – 2 = 12.

Если обозначить буквой “a” длину стороны куба, тогда формулы для его объема и площади поверхности будут иметь вид: V = a 3 и S = 6*a 2 , соответственно.

Фигура пирамида

Пирамида – это полиэдр, который состоит из простого многогранника (основание пирамиды) и треугольников, которые соединяются с основанием и имеют одну общую вершину (вершина пирамиды). Треугольники называются боковыми гранями пирамиды.

Геометрические характеристики пирамиды зависят от того, какой многоугольник лежит в ее основании, а также от того, является ли пирамида прямой или косой. Под прямой пирамидой понимают такую пирамиду, для которой перпендикулярная основанию прямая, проведенная через вершину пирамиды, пересекает основание в ее геометрическом центре.

Одной из простых пирамид является четырехугольная прямая пирамида, в основании которой лежит квадрат со стороной “a”, высота этой пирамиды “h”. Для этой фигуры пирамиды объем и площадь поверхности будут равны: V = a 2 *h/3 и S = 2*a*√(h 2 +a 2 /4) + a 2 , соответственно. Применяя теорему Эйлера для нее, с учетом того, что число граней равно 5, и число вершин равно 5, получаем количество ребер: Р = 5 + 5 – 2 = 8.

Фигура тетраэдр: описание

Под геометрической фигурой тетраэдр понимают объемное тело, образованное 4-мя гранями. Исходя из свойств пространства, такие грани могут представлять только треугольники. Таким образом, тетраэдр является частным случаем пирамиды, у которой в основании лежит треугольник.

Если все 4-ре треугольника, образующие грани тетраэдра, являются равносторонними и равными между собой, то такой тетраэдр называется правильным. Этот тетраэдр имеет 4 грани и 4 вершины, число ребер составляет 4 + 4 – 2 = 6. Применяя стандартные формулы из плоской геометрии для рассматриваемой фигуры, получаем: V = a 3 * √2/12 и S = √3*a 2 , где a – длина стороны равностороннего треугольника.

Интересно отметить, что в природе некоторые молекулы имеют форму правильного тетраэдра. Например, молекула метана CH 4 , в которой атомы водорода расположены в вершинах тетраэдра, и соединены с атомом углерода ковалентными химическими связями. Атом углерода находится в геометрическом центре тетраэдра.

Простая в изготовлении форма фигуры тетраэдр используется также в инженерии. Например, тетраэдрическую форму используют при изготовлении якорей для кораблей. Отметим, что космический зонд НАСА, Mars Pathfinder, который совершил посадку на поверхность Марса 4 июля 1997 года, также имел форму тетраэдра.

Фигура призма

Эту геометрическую фигуру можно получить, если взять два многогранника, расположить их параллельно друг другу в разных плоскостях пространства, и соединить их вершины соответствующим образом между собой. В итоге получится призма, два многогранника называются ее основаниями, а поверхности, соединяющие эти многогранники, будут иметь форму параллелограммов. Призма называется прямой, если ее боковые стороны (параллелограммы) являются прямоугольниками.

Призма – это полиэдр, поэтому для нее верна Например, если в основании призмы лежит шестиугольник, тогда, количество сторон у призмы равно 8, а количество вершин – 12. Число ребер будет равно: Р = 8 + 12 – 2 = 18. Для прямой призмы высотой h, в основании которой лежит правильный шестиугольник со стороной a, объем равен: V = a 2 *h*√3/4, площадь поверхности равна: S = 3*a*(a*√3 + 2*h).

Говоря о простых геометрических объемных фигурах и их названиях, следует упомянуть шар. Под объемным телом под названием шар понимают тело, которое ограничено сферой. В свою очередь, сфера – это совокупность точек пространства, равноудаленных от одной точки, которая называется центром сферы.

Поскольку шар относится к классу круглых тел, то для него не существует понятия о сторонах, ребрах и вершинах. сферы, ограничивающей шар, находится по формуле: S = 4*pi*r 2 , а объем шара можно вычислить по формуле: V = 4*pi*r 3 /3, где pi – число пи (3,14), r – радиус сферы (шара).

Урок 4. обозначение геометрических фигур буквами – Математика – 3 класс

Математика, 3 класс

Урок №4. Обозначение геометрических фигур буквами

Перечень вопросов, рассматриваемых в теме:

– Как обозначают геометрические фигуры?

– Как правильно прочитать обозначение угла?

Глоссарий по теме:

Для обозначения геометрических фигур пользуются буквами латинского алфавита. Используют для обозначения заглавные буквы. Отрезок обозначают буквами две точки. Чтобы назвать многоугольник, обозначают буквами его вершины. Угол обозначают тремя буквами.

Основная и дополнительная литература по теме урока:

1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 10.

2. М. И. Моро, С. И. Волкова. Для тех, кто любит математику 3 класс. Учебное пособие для общеобразовательных организаций. М.; Просвещение,2018. – с. 12.

Теоретический материал для самостоятельного изучения.

На этой весёлой картинке видим разные геометрические фигуры, которые ты хорошо знаешь. Назовём их:

Треугольник, круг, квадрат, овал, ромб, пятиугольник, шестиугольник, трапеция, прямоугольник.

На этом рисунке видим несколько прямоугольников. Они все одинаковые.

Попробуем назвать каждый. Не удается, прямоугольники все одинаковые и по цвету, и по размеру. Как быть?

А на этом рисунке много точек. Точка тоже геометрическая фигура. Как назвать каждую из них.

Раз, два, три, четыре, пять!

Вышли точки погулять.

Много их, посмотри: раз, два, три.

Как их нам различать?

Каждой имя надо дать.

Как у человека есть имя, так и у каждой фигуры должно быть своё имя.

Математики всего мира договорились обозначать геометрические фигуры заглавными буквами латинского алфавита. Точки на чертеже обозначают заглавными латинскими буквами: A, B, C, D, E, F и другими.

Чтобы назвать отрезок, обозначают буквами две точки – его концы. Например, отрезок AB, отрезок CD. В многоугольнике обозначают буквами его вершины и называют, например, так: квадрат ABCD, треугольник ABC

Угол обозначают тремя буквами. В середине названия всегда указывают букву, которой обозначена вершина угла.

Например, в треугольнике АВС угол с вершиной А – это угол ВАС или угол САВ

А С

Тренировочные задания.

1. Подчеркните правильное обозначение угла.

ВАС; АВС; САВ; СВА;

Правильный ответ:

ВАС; АВС; САВ; СВА;

2. Выберите фигуры, которые обозначены верно.

Правильный ответ:

Раскраска овал. Карточки домана бесплатно, картинки геометрические фигуры, карточки геометрические фигуры, изучаем геометрические фигуры. Геометрические фигуры – Раскраска с умом

Одновременно с изучением цветов, ребенку можно начать показывать карточки геометрические фигуры. На нашем сайте Вы сможете скачать их бесплатно.

Как изучить с ребенком фигуры по карточкам Домана.

1) Начинать нужно с простых фигур: круг, квадрат, треугольник, звезда, прямоугольник. По мере освоения материала, начинать изучать фигуры посложнее: овал, трапеция, параллелограмм и т.д.

2) Заниматься с ребенком по карточкам Домана нужно несколько раз в день. При демонстрации геометрической фигуры четко проговаривайте название фигуры. А если во время занятий вы будете еще пользоваться наглядными предметами, например, собирать вкладыши с фигурами или игрушку — сортер, то малыш очень быстро освоит материал.

3) Когда ребенок запомнит название фигур, можете переходить к более сложным заданиям: теперь показывая карточку говорите — это синий квадрат, у него 4 равные стороны. Задавайте ребенку вопросы, просите его самого описать, что он видит на карточке и т.д.

Такие занятия очень полезны для развития памяти и речи ребенка.

Занятия по карточкам Домана прекрасно развивают зрительную память, внимательность, речь ребенка. Это отличная зарядка для ума.

Вы можете скачать и распечатать бесплатно все

карточками Домана плоские геометрические фигуры

Кликните на карточку правой клавишей мышки, нажмите «Сохранить картинку как…» так вы сможете сохранить изображение на свой компьютер.

Как изготовить карточки Домана самостоятельно:

Распечатайте карточки на плотной бумаге или картоне по 2, 4 или 6 штук на 1 листе. Для проведения занятий по методике Домана карточки готовы, Вы их можете показывать малышу и называть название картинки.

Успехов и новых открытий Вашему малышу!

Развивающее видео для детей (малышей и дошкольников) выполненное по методике Домана «Вундеркинд с пеленок» – развивающие карточки, развивающие картинки на различные темы из части 1, части 2 методики Домана, которое можно смотреть бесплатно здесь или на нашем Канале Раннее развитие детей на youtube

Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей

Развивающие карточки геометрические фигуры по методике Глена Домана с картинками плоских геометрических фигур для детей

Еще наши карточки Домана по методике «Вундеркинд с пеленок»:

Карточки Домана Посуда
Карточки Домана Национальные блюда

Здесь вы можете скачать и распечатать задания в картинках по математике “Геометрические фигуры – Раскраска для дошкольников”. Что представляют собой эти задания? В первую очередь, это, конечно, ознакомление ребенка с основными фигурами науки геометрии – кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска. В первой раскраске ребенок будет по команде взрослого раскрашивать фигуры и таким образом запоминать их. А во второй – отыскивать среди множества картинок именно геометрические формы и сразу же раскрашивать свои находки.

1. Геометрические фигуры – Раскраска с умом – Условия заданий:

Выполнять задание – Геометрические фигуры “Раскраска с умом” – необходимо под руководством взрослых (родителей или педагогов), так как задание предназначено для детей от 3-4 лет. Для начала, скачайте бланк с заданием во вложениях внизу данной страницы, распечатайте его на черно-белом принтере и подготовьте цветные карандаши или фломастеры. Прочитайте малышу задания в указанном порядке.

В первом задании ребенок должен раскрасить в синий цвет все круги, а затем посчитать их количество.
Во втором задании нужно раскрасить все треугольники в оранжевый цвет и также посчитать их.
В третьем задании необходимо раскрашивать в красный цвет – квадраты, а в желтый – прямоугольники. После этого посчитать количество этих фигур и сравнить, чего больше, квадратов или прямоугольников.
В четвертом задании ребенку нужно раскрасить зеленым цветом все овалы. Пересчитать их после раскрашивания.

Требование взрослого раскрасить фигуру в определенный цвет подразумевает под собой, что ребенок должен уже различать цвета. Если же малыш еще не выучил названия основных цветов, то представленные задания помогут ему потренироваться в этом деле.

Скачать геометрические фигуры “Раскраска с умом” вы можете во вложениях внизу страницы.

2. Развивающее задание “Раскрась геометрические фигуры”

Здесь вы найдете интересное развивающее задание по поиску и раскрашиванию геометрических фигур среди множества различных картинок. Детям очень нравятся игры, в которых нужно что-нибудь искать. Поэтому изучение геометрических фигур с помощью подобных игр проходит очень легко и эффективно, так как ребенок даже не подозревает, что он учится, а не играет. К тому же, все дети, без исключения, обожают раскраски!

Как проводить занятие. Скачайте во вложениях бланк с заданием, распечатайте его и дайте ребенку. На отдельном листе бумаги нарисуйте четыре фигуры – круг, квадрат, ромб и треугольник. Подпишите их названия. Раскрасьте фигуры в разные цвета: круги – в синий цвет , квадраты – в зеленый , ромбы – в желтый , треугольники – в красный цвет . Затем отдайте лист ребенку, пояснив, что именно такие фигуры ему нужно найти среди всех изображений бланка-задания и раскрасить их именно в такие цвета, как на листе. Оставьте ребенка одного справляться с заданием. Через несколько минут поинтересуйтесь у него – много ли он нашел на картинке геометрических фигур?

Это задание можно выполнять повторно. Для этого нужно распечатать бланк заново, а на отдельном листе указанные фигуры раскрасить в другие цвета.

Чтобы усложнить задачу для ребенка, можно не использовать отдельный лист с раскрашенными фигурами, а сказать устно, какие фигуры нужно найти и в какой цвет раскрасить. Так у ребенка будет более активно работать память и внимание. Ведь ему придется во время выполнения задания держать эту информацию в голове, без визуальной подсказки.

Скачать развивающее задание “Раскрась геометрические фигуры” вы можете во вложениях внизу страницы.

Также вам будут полезны и другие материалы по изучению геометрических фигур:

Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках.

Дети любят раскрашивать и обводить, поэтому данные задания сделают ваши занятия по обучению счету максимально эффективными.

И еще можете поиграть в математические игры онлайн от лисенка Бибуши:

Веселые и красочные задания для детей “Рисунки из геометрических фигур” являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических форм: треугольника, круга, овала, квадрата, прямоугольника и трапеции. Все задания предназначены для самостоятельной работы ребенка под наблюдением взрослых. Родитель или педагог должны правильно объяснить ребенку, что он должен сделать в каждом задании.

Также вам может понравиться наш онлайн тренажер по математике для 1 класса “Геометрические фигуры”:

1. Рисунки из геометрических фигур – Условия к выполнению заданий:

Чтобы начать выполнять задания, скачайте во вложениях бланк, в котором вы найдете 2 типа заданий: рисунки из геометрических фигур для раскрашивания и задание для рисования фигур с помощью логического и образного мышления. Распечатайте скачанную страницу на цветном принтере и дайте ребенку вместе с цветными карандашами или фломастерами.

В первом задании малышу нужно мысленно соединить каждые две части представленных фигур в одну и нарисовать полученную геометрическую форму в соответствующей клетке. Объясните ребенку, что детали можно поворачивать в уме в разные стороны до тех пор, пока он не получит нужную комбинацию для составления фигуры. Например, два треугольника можно повернуть так, чтобы получился квадрат. После этого квадрат нужно нарисовать в клетке рядом с треугольником. По такому же принципу необходимо сделать и остальные рисунки.
Во втором задании дети должны правильно назвать фигуры из которых состоят нарисованные картинки. Затем эти картинки нужно раскрасить, используя цвета рядом с геометрическими фигурами. Каждую фигуру нужно раскрасить только в указанный цвет.

Чтобы придать занятию больше энергии и энтузиазма – можно объединить несколько детей в группу и предоставить им выполнение заданий на время. Тот ребенок, который первый выполнит все задания без ошибок, признается победителем. В качестве приза можно повесить его работу на стену достижений (такая стена обязательно должна присутствовать как дома, так и в детском саду).

Скачать задание “Рисунки из геометрических фигур” вы можете во вложениях внизу страницы.

2. Геометрические фигуры в рисунках – 3 задания-раскраски:

Следующее занятие также скрывает основные геометрические фигуры в рисунках. Ребенку нужно найти эти фигуры, назвать их, а затем раскрасить таким образом, чтобы каждой фигуре соответствовал определенный цвет (руководствуясь инструкцией на бланке с заданием).

Во втором задании нужно нарисовать на всех этажах любые геометрические фигуры, но при этом необходимо соблюдать условие: на каждом этаже фигуры должны находиться в разном порядке. В последствии можно это задание видоизменить. Для этого достаточно начертить на бумаге точно такой домик и попросить ребенка заполнить его фигурами так, чтобы в каждом подъезде не встречались одинаковые фигуры (подъезд – вертикальный ряд квадратов).

В третьем задании нужно, руководствуясь стрелками, нарисовать точно такие же геометрические фигуры внутри или снаружи данных фигур.

Не торопите ребенка и не подсказывайте ему, пока он сам вас об этом не попросит. Если у малыша что-то получилось неправильно – вы всегда можете распечатать еще один экземпляр учебного бланка с заданием.

Скачать задание “Геометрические фигуры в рисунках” вы можете во вложениях внизу страницы.

В этом занятии детям опять предстоит отыскать геометрические фигуры среди рисунков. После предыдущих занятий им будет уже легче ориентироваться в знакомых формах, так что, я думаю, оба задания не вызовут у них затруднений.

Второе задание также дает возможность малышу повторить математические знаки и усвоить счет до десяти, так как ему понадобится посчитать количество фигур и поставить знаки “больше” “меньше” между картинками.

Скачать раскраску “Смешные рисунки из фигур” вы можете во вложениях внизу страницы.

Также вам будут полезны и другие материалы по изучению геометрических фигур:

И еще можете поиграть в математические игры онлайн от лисенка Бибуши:

Геометрические – PeVuz.ru

Карточки геометрические фигуры скачать, развивающие карточки Домана «Вундеркинд с пеленок» — плоские геометрические фигуры

Svetlana

73 929 просмотров

(19 “понравилось”, Всего: 5,00 из 5)
Вам нужно зарегистрироваться, чтобы проать.

Как изучить с ребенком фигуры по карточкам Домана

Такие занятия очень полезны для развития памяти и речи ребенка.

Здесь вы можете скачать карточки Домана из серии «Плоские геометрические фигуры» Всего 16 штук, в их числе карточки: плоские геометрические фигуры, восьмиугольник, звезда, квадрат, кольцо, круг, овал, параллелограмм, полукруг, прямоугольник, прямоугольный треугольник, пятиугольник, ромб, трапеция, треугольник, шестиугольник.
Занятия по карточкам Домана прекрасно развивают зрительную память, внимательность, речь ребенка. Это отличная зарядка для ума.
Вы можете скачать и распечатать бесплатно все
карточками Домана плоские геометрические фигуры
Кликните на карточку правой клавишей мышки, нажмите «Сохранить картинку как…» так вы сможете сохранить изображение на свой компьютер.
Как изготовить карточки Домана самостоятельно:
Распечатайте карточки на плотной бумаге или картоне по 2, 4 или 6 штук на 1 листе. Для проведения занятий по методике Домана карточки готовы, Вы их можете показывать малышу и называть название картинки.
Успехов и новых открытий Вашему малышу!
Развивающее видео для детей (малышей и дошкольников) выполненное по методике Домана «Вундеркинд с пеленок» — развивающие карточки, развивающие картинки на различные темы из части 1, части 2 методики Домана, которое можно смотреть бесплатно здесь или на нашем Канале Раннее развитие детей на
Еще наши карточки Домана по методике «Вундеркинд с пеленок» :
Источник: https://Amelica.com/%D0%BA%D0%B0%D1%80%D1%82%D0%BE%D1%87%D0%BA%D0%B8-%D0%B3%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5-%D1%84%D0%B8%D0%B3%D1%83%D1%80%D1%8B/
Геометрические фигуры и их названия – Задания в картинках
Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках. Но обучение будет проходить наиболее эффективно в том случае, если к распечатанному заданию вы добавите еще и различные образцы геометрических фигур.
Для этой цели могут подойти такие предметы, как мячики, пирамидки, кубики, надутые воздушные шары (круглые и овальные), кружки для чая (стандартные, в форме цилиндра), апельсины, книги, клубки ниток, квадратные печенья и многое другое – все, что подскажет вам фантазия. Все перечисленные предметы помогут ребенку понять, что значит объемная геометрическая фигура.
Плоские фигуры можно подготовить, вырезав из бумаги нужные геометрические формы, предварительно раскрасив их в разные цвета.
Чем больше различных материалов вы подготовите для занятия, тем интереснее будет ребенку изучать новые для него понятия.
Геометрические фигуры и их названия – Проводим занятие с ребенком:
Чтобы легко и непринужденно ребенок смог запомнить геометрические фигуры и их названия, скачайте сначала картинку с заданием во вложениях внизу страницы, распечатайте на цветном принтере и положите на стол вместе с цветными карандашами. Также к этому времени у вас уже должны быть заготовлены различные предметы, которые мы перечисляли ранее.
1 этап. Сначала пусть ребенок выполнит задания на распечатанном листе – проговорит вслух названия фигур и раскрасит все картинки.
2 этап. Необходимо наглядно показать ребенку отличия объемных фигур от плоских. Для этого разложите все предметы-образцы (как объемные, так и вырезанные из бумаги) и отойдите с ребенком от стола на такое расстояние, с которого хорошо видны все объемные фигуры, но потерялись из виду все плоские образцы. Обратите внимание малыша на этот факт. Пусть он поэкспериментирует, подходя к столу то ближе, то дальше, рассказывая вам о своих наблюдениях.
3 этап. Дальше занятие нужно превратить в своеобразную игру. Попросите ребенка, чтобы он внимательно посмотрел вокруг себя и нашел предметы, которые имеют форму каких-либо геометрических фигур. Например, телевизор – прямоугольник, часы – круг и т.д. На каждой найденной фигуре – громко хлопайте в ладоши, чтобы добавить энтузиазма в игру.
4 этап. Проведите исследовательскую и наблюдательную работу с теми материалами-образцами, которые вы заготовили к занятию. Например, положите на стол книгу и плоский прямоугольник из бумаги. Предложите ребенку пощупать их, посмотреть на них с разных сторон и рассказать вам свои наблюдения. Таким же образом можно исследовать апельсин и бумажный круг, детскую пирамидку и бумажный треугольник, кубик и бумажный квадрат, воздушный шар овальной формы и овал, вырезанный из бумаги. Список предметов вы можете дополнить сами.
5 этап. Положите в непрозрачный пакет различные объемные образцы и попросите ребенка достать на ощупь квадратный предмет, затем круглый, затем прямоугольный и так далее.
6 этап. Разложите перед ребенком на столе несколько различных предметов из тех, которые участвуют в занятии. Затем пусть ребенок отвернется на несколько секунд, а вы спрячьте один из предметов. Повернувшись к столу ребенок должен назвать спрятанный предмет и его геометрическую форму.
Скачать геометрические фигуры и их названия – Бланк задания – вы можете во вложениях внизу страницы.
Названия геометрических фигур – Карточки для распечатки
Изучая с малышом геометрические фигуры, вы можете использовать во время занятий карточки для распечатки от Лисёнка Бибуши.
Скачайте вложения, распечатайте на цветном принтере бланк с карточками, вырежьте каждую карточку по контуру – и приступайте к обучению.
Карточки можно заламинировать, либо наклеить на более плотную бумагу, чтобы сохранить внешний вид картинок, ведь использоваться они будут неоднократно.
Первые шесть карточек дадут вам возможность изучить с ребенком такие фигуры: овал, круг, квадрат, ромб, прямоугольник и треугольник, под каждой фигурой в карточках можно прочесть ее название.
После того, как ребенок запомнил название определенной фигуры, попросите его выполнить следующее: обвести по контуру все имеющиеся на карточке образцы изучаемой фигуры, а затем раскрасить их в цвет основной фигуры, расположенной в верхнем левом углу.
Скачать названия геометрических фигур – Карточки для распечатки – вы можете во вложениях внизу страницы
Карточки для распечатки с изображением плоских геометрических фигур
С помощью следующих шести карточек ребенок сможет познакомиться с такими геометрическими фигурами: параллелограмм, трапеция, пятиугольник, шестиугольник, звезда и сердце. Как и в предыдущем материале под каждой фигурой можно найти ее название.
Чтобы разнообразить занятия с малышом, совмещайте обучение с рисованием – такой метод не даст ребенку переутомиться, и малыш с удовольствием будет продолжать учебу. Следите за тем, чтобы обводя фигуры по черточкам, ребенок не спешил и выполнял задание аккуратно, ведь подобные упражнения не только развивают мелкую моторику, они могут повлиять в дальнейшем на почерк малыша.
Скачать карточки для распечатки с изображением плоских геометрических фигур вы можете во вложениях
Объемные геометрические фигуры и их названия – скачать карточки
В процессе, того, как вы будете изучать с ребенком объемные геометрические фигуры и их названия, используя новые шесть карточек от Бибуши с изображениями куба, цилиндра, конуса, пирамиды, шара и полусферы, приобретите изучаемые фигуры в магазине, либо воспользуйтесь предметами, находящимися в доме, имеющими подобную форму.
Покажите малышу на примерах, как в жизни выглядят объемные фигуры, ребенок должен потрогать и поиграть с ними. Прежде всего, это необходимо для того, чтобы задействовать наглядно – действенное мышление малыша, с помощью которого ребенку проще познавать окружающий мир.
Скачать – Объемные геометрические фигуры и их названия – вы можете во вложениях внизу страницы
Также вам будут полезны и другие материалы по изучению геометрических фигур:
Рисунки из геометрических фигур – Задания в картинках и раскраски
Веселые и красочные задания для детей “Рисунки из геометрических фигур” являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических форм:
Геометрические фигуры – Раскраска для дошкольников
Задания ознакомят ребенка с основными фигурами геометрии – кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.
Плоские геометрические фигуры – Обведи и дорисуй
Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги.
Найди формы геометрических фигур в картинках
Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок.
Наложение фигур друг на друга – Задание для детей
Наложение фигур друг на друга – это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры.
Свойства геометрических фигур для дошкольников
Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.
Счет геометрических фигур – Картинки с заданиями
Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.
Чертежи геометрических тел – Задание для детей
В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии
Геометрические фигуры из бумаги – Вырезаем и занимаемся
Здесь мы подготовили для вас объемные геометрические фигуры из бумаги, которые нужно вырезать и склеить. Куб, пирамиды, ромб, конус, цилиндр, шестигранник, распечатать их на картоне (или цветной бумаге, а затем наклеить на картон), а затем дать ребенку для запоминания.
Счет до 5 – Картинки с заданиями для малышей
Здесь мы выложили для вас счет до 5 – картинки с математическими заданиями для малышей, благодаря которым ваши дети потренируют не только свои навыки счета, но и умение читать, писать, различать геометрические фигуры, рисовать и раскрашивать.
И еще можете поиграть в математические игры онлайн от лисенка Бибуши:
Игра “Что лишнее? – Геометрические формы”
В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок. При этом необходимо руководствоваться признаками геометрических форм.
Источник: https://bibusha.ru/geometricheskie-figury-i-ikh-nazvaniya-zadaniya-v-kartinkakh
Геометрические фигуры в интерьере: дизайнерские аксиомы
Узор из геометрических фигур – один из самых древних орнаментов, который используется в архитектуре, дизайне, мире моды. Этот декор особенно популярен в последние годы и стал неотъемлемой частью многих современных направлений.
Стильная геометрия
Окружить себя необычными и экстравагантными вещами решиться не каждый. На наш выбор влияет не только мода, но и собственное мировоззрение, привычки и окружающий мир. Способны ли вы украсить свой дом с помощью узора из геометрических фигур?
Яркое оформление интерьера с геометрическими мотивами уравновешивается базовым белым цветом
Такой орнамент – это возможность придать интерьеру броский и неординарный внешний вид. Но следует помнить о том, что если не рассчитать свои силы и заполнить всё вокруг одними лишь параллелепипедами и треугольниками, вы «убьёте» дизайн на корню, создав нечто безвкусное и нелогичное.
Интерьерные наклейки с геометрическими фигурами
Попробуем разобраться, чем привлекает рисунок из геометрических фигур? Почему нам так хочется использовать в своём интерьере разнообразные комбинации из треугольников, квадратов и ромбов? Ответ очевиден – лаконичность и правильность форм. Геометрические фигуры прекрасно подходят для разнообразных дизайнов, позволяя создавать идеальные интерьеры.
Геометрические орнаменты в оформлении интерьера спальни
Они способны дополнить скандинавский или минималистичный стиль, стать фокусной точкой в современном дизайне. Без обилия геометрических форм не обходятся неоклассические интерьеры, а фигуры ярких и кричащих цветов стали верными спутниками китча и поп-арта.
Оформление одной стены геометрическим узором
Геометрические фигуры в отделке
Геометрические фигуры способны создавать эффект динамики и движения в интерьере, задавать вектор для конкретного стиля. На это не влияет ни размер, ни форма комнаты, ведь даже в самом скромном по объёмам помещении можно расставить акцентные пятна.
Геометрические мотивы присутствуют в интерьере в отделке и предметах мебели
В зависимости от выбранного орнамента и вида геометрических фигур в интерьере создаётся определённый ритм (энергичный или размеренный). Этот нюанс необходимо учитывать при оформлении любого помещения.
Ковер с геометрическим орнаментом идеально сочетается с интерьером гостиной
Спокойный узор из крупных геометрических фигур лучше использовать в спальне, а динамичные рисунки с мелкими деталями – в гостиной и прихожей.
Декор гостиной с геометрическим орнаментом
Ультрасовременным трендом считается использование обоев и панелей с 3D рисунком из геометрических фигур. Подобные покрытия создают иллюзию выпуклых элементов.
Абстрактный 3D узор из квадратов создаёт иллюзию рельефа
Некоторые виды орнаментов можно комбинировать, выделяя один из них в доминирующий, а второй – во вспомогательный. Прекрасно сочетаются между собой различные виды полос, разных размеров квадраты, треугольники или всевозможные прямоугольники.
Интерьер с треугольниками в серых тонах
Интересно и неординарно смотрятся обои со сложными фигурами, которые созданы из простых геометрических элементов. Эффектного внешнего вида можно достичь и с помощью керамики. Неординарная плитка в форме геометрических фигур – популярный способ оформления кухни или ванной комнаты. Она придаёт помещению стильный и нарядный облик.
Оформление кухни плиткой в форме шестиугольников
Но не только комбинации форм и линий могут создавать разнообразие интерьерного оформления. Необычные цвета и их совмещение в разных фигурах даёт порой самый неожиданный результат. Выберите для оформления стен базовый цвет, который идеально сочетается с двумя другими выбранными оттенками. Это могут быть не только яркие комбинации, но и вариативные переходы между полутонами.
Виниловые наклейки в виде геометрических фигур в интерьере
На базовый цвет с помощью трафарета наносится орнамент из геометрических фигур, используя два дополнительных оттенка. Благодаря такому приёму в комнате создаётся объём и цветовой акцент. Подобным способом достаточно оформить одну стену или часть помещения, иначе вы рискуете перегрузить интерьер.
Оформление интерьера с использованием геометрического орнамента
Геометрические фигуры в интерьере
Если вам наскучило однообразие вашего интерьера, попробуйте оживить его с помощью мебели с выраженной геометрией.
Даже самые простые и лаконичные формы предметов способны преображаться интерьер своими четкими линиями.
Для того чтобы гармонично сочетать в помещении разные геометрические фигуры и принты, придерживайтесь общей цветовой гаммы. Оттенки мебельной обивки должны перекликаться с оттенками интерьера в целом.
Геометрическая мебель –актуальный тренд в дизайне интерьера
Одним из самых популярных геометрических узоров является «шеврон», который ещё называют узором «зигзаг». Без него не обходится ни один интерьер в стиле сканди. Мягкая мебель с таким орнаментом способна усиливать эффект движения и динамики. Стильно и необычно смотрится обивка «в горошек». Подобный узор прекрасно сочетается с предметами округлой формы.
Неординарные полки из геометрических фигур
В интерьерах в скандинавском стиле можно встретить не только мягкую мебель с геометрическими мотивами, но и корпусную мебель, выполненную в виде разнообразных фигур. Большой популярностью пользуются полки и консоли в форме шестиугольника, стеллажи, собранные из треугольных секций и идеально круглые зеркала.
Необычные зеркала в форме геометрических фигур
Геометрические фигуры можно обнаружить не только в предметах мебели, но и в светильниках. Осветительные приборы – самый доступный способ украсить ваш дом. Существует невероятное количество люстр с плафонами в виде геометрических фигур.
Особенно привлекательно смотрятся каркасные изделия сложных форм. Большое количество граней преломляет свет, создавая загадочные отблески в самых невероятных местах. Подобные концептуальные светильники будут уместны как в современных интерьерах, так и в интерьере в стиле ретро или поп-арт.
Геометрические мотивы в декоре
Декоративный текстиль и аксессуары позволяют преображать внешний вид интерьера, кардинально не изменяя его. Подобного рода предметы – это реальная возможность обновить дизайн без больших финансовых затрат.
Яркий декор с геометрическими мотивами
Оптические иллюзии, разнообразные узоры из прямых линий или зигзагов с успехом используются и сочетаются в предметах декора и текстильном оформлении.
Треугольные зеркала в качестве декора в интерьере домашнего офиса
Если вы хотите преобразить интерьер гостиной, оживить его и создать энергичную и весёлую атмосферу, то приобретите яркий ковёр с орнаментом из геометрических фигур. Скучный диван можно украсить декоративными подушками и уютным пледом с узором из квадратов, напоминающим шотландскую клетку.
Геометрические принты — отличительная особенность интерьера в стиле сканди
Если вам надоело старое постельное белье в цветочек, просто поменяйте его на комплект с геометрическими фигурами. Его можно дополнить схожими по стилю шторами с разнообразными узорами. Такой простой способ декорирования интерьера позволяет обновлять дизайн хоть каждый день!
Разноплановое оформление интерьера с помощью треугольников
Находясь в поиске аксессуаров, обратите своё внимание на необычные предметы, сделанные в форме объёмных геометрических фигур. Это могут быть разнообразные вазы, стаканчики под канцелярию или кухонные принадлежности, ёмкости для хранения.
Деревянный декор в форме геометрических фигур
Изысканно и утончённо смотрятся каркасные подсвечники и кашпо для цветов, выполненные из металла. Они могут иметь разнообразную форму, повторяющую очертания конкретной геометрической фигуры.
Изящные каркасные флорариумы в форме геометрических фигур
Привлекательность геометрических фигур заключена в их многогранности. Они способны создавать различные эффекты в зависимости от форм и размеров. Подключив фантазию и вдохновение, вы сможете с удовольствием сочетать геометрические фигуры в процессе оформления своего дома.
Источник: https://www.ivybush.ru/geometricheskie-figury-v-interere
Геометрические фигуры. Полные уроки — Гипермаркет знаний

Источник: http://edufuture.biz/index.php?title=%D0%93%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5_%D1%84%D0%B8%D0%B3%D1%83%D1%80%D1%8B._%D0%9F%D0%BE%D0%BB%D0%BD%D1%8B%D0%B5_%D1%83%D1%80%D0%BE%D0%BA%D0%B8

Геометрические термины на английском языке

В повседневной жизни мы постоянно используем слова, связанные с геометрией. Я имею в виду не термины вроде гипотенуза или биссектриса, а употребительные слова, например: круг, квадратный, длина, ширина, объем. Из этой подборки вы узнаете самые необходимые геометрические термины на английском языке и сможете повторить или выучить их с помощью озвученных карточек.

Статья по теме: “Математические действия на английском языке“.

Основные геометрические термины на английском языке

Когда я учился в школе, мы начинали знакомство с геометрией с таких элементарных понятий, как точка (point), прямая (straight line), отрезок (line segment), луч (ray), затем перешли к геометрическим фигурам (plane shapes) и геометрическим телам (solid shapes).

В списке и карточках ниже представлены эти и другие основные термины. Отмечу, что наиболее коварными являются два термина:

Angle – угол. Легко перепутать с corner. Но если corner – это угол в общем смысле, например, угол комнаты (corner of the room), то angle – это угол как геометрическое понятие (right angle – прямой угол).
Point – точка. В русском языке любая точка называется точкой: будто то точка в десятичной дроби или конце предложения. В английском несколько названий для разных точек: point, dot, period, full stop. Вот какая между ними разница:
Point – точка в геометрии, в десятичных дробях: 3.14 читается как three point one four.
Dot – точка в адресах веб-сайтов. Например, www.google.com читается как: double u double u double u google dot com. Кстати, забавно, что www – это сокращенно world wide web, но сокращенная форма при чтении намного длиннее полной.
Period (США) или full stop (Великобр.) – точка в конце предложения. Есть даже английское выражение “period” или “full stop” аналог русского «точка» в значении «разговор закончен, возражения не принимаются»: You are not going to the party. Period. – Ты не идешь на вечеринку. Точка.

Гипермаркет знаний>>Математика>>Математика 7 класс. Полные уроки>>Геометрия: Геометрические фигуры. Полные уроки

Что такое геометрическая фигура

Геометрические фигуры – это совокупность множества точек, линий, поверхностей или тел, которые расположены на поверхности, плоскости или пространстве и формирует конечное количество линий.

Термин «фигура» в какой-то степени формально применяется к множеству точек, но как правило фигурой принято называть такие множества, которые расположенные на плоскости и ограничиваются конечным числом линий.

Точка и прямая – это основные геометрические фигуры, расположенные на плоскости.

К самым простым геометрическим фигурам на плоскости принадлежат – отрезок, луч и ломаная линия.

Что такое геометрия

Геометрия – это такая математическая наука, которая занимается изучением свойств геометрических фигур. Если дословно перевести на русский язык термин «геометрия», то он обозначает «землемерие», так как в стародавние времена основной задачей геометрии, как науки, стало измерение расстояний и площадей на поверхности земли.

Практическое применение геометрии бесценно во все времена и независимо от профессии. Без знаний геометрии не может обойтись ни рабочий, ни инженер, ни архитектор и даже художник.

В геометрии есть такой раздел, который занимается изучением различных фигур на плоскости и называется планиметрия.

Вам уже известно, что фигурой называют произвольное множество точек, находящиеся на плоскости.
К геометрическим фигурам принадлежат: точка, прямая, отрезок, луч, треугольник, квадрат, круг и другие фигуры, которые изучает планиметрия.
Точка
Из выше изученного материала вам уже известно, что точка относится к главным геометрическим фигурам.
И хотя это самая малая геометрическая фигура, но она необходима для построения других фигур на плоскости, чертеже или изображении и является основой для всех остальных построений.
Ведь построение более сложноватых геометрических фигур складывается из множества точек, характерных для данной фигуры.
В геометрии точки обозначают прописными буквами латинского алфавита, например, такими, как: А, В, С, D ….
А теперь подведем итог, и так, с математической точки зрения, точка является таким абстрактным объектом в пространстве, который не имеет объема, площади, длины и других характеристик, но остается одним из фундаментальных понятий в математике. Точка – это такой нульмерный объект, которые не имеет определения. По определению Евклида, точкой называют то, что невозможно определить.
Прямая
Как и точка, прямая относится к фигурам на плоскости, которая не имеет определения, так как состоит из бесконечного множества точек, находящихся на одной линии, которая не имеет ни начала ни конца. Можно утверждать, что прямая линия бесконечна и не имеет предела.
Если же прямая начинается и заканчивается точкой, то она уже не является прямой и называется отрезком.
Но иногда прямая, с одной стороны имеет точку, а с другой нет. В таком случае прямая превращается в луч.
Если же взять прямую и на ее средине поставить точку, то она разобьет прямую на два противоположно направленных луча. Данные лучи являются дополнительными.
Если же перед вами несколько отрезков, соединенных между собой так, что конец первого отрезка становиться началом второго, а конец второго отрезка — началом третьего и т. д., и эти отрезки находятся не на одной прямой и при соединении имеют общую точку, то такая цепочка является ломаной линией.
Задание
• Какая ломаная линия называется незамкнутой?• Как обозначается прямая?• Как называется ломаная линия, у которой четыре замкнутых звена?• Какое название имеет ломаная линия с тремя замкнутыми звеньями?
Когда конец последнего отрезка ломаной совпадает с началом 1-го отрезка, то такую ломаную линию называют замкнутой. Примером замкнутой ломаной является любой многоугольник.
Плоскость
Как точка и прямая, так и плоскость является первичным понятием, не имеет определения и у нее нельзя увидеть ни начала, ни конца. Поэтому, при рассмотрении плоскости, мы рассматриваем только ту ее часть, которая ограничивается замкнутой ломаной линией. Таким образом, плоскостью можно считать любую гладкую поверхность. Этой поверхностью может быть лист бумаги или стола.
Угол
Фигура, которая имеет два луча и вершину, называется углом. Место соединения лучей, является вершиной этого угла, а его сторонами считаются лучи, которые этот угол образуют.
Задание:
1. Как в тексте обозначают угол?2. Какими единицами можно измерить угол?3. Какие бывают углы?
Параллелограмм
Параллелограмм – это четырехугольник, противолежащие стороны которого попарно параллельны.
Прямоугольник, квадрат и ромб являются частными случаями параллелограмма.
Параллелограмм, имеющий прямые углы равные 90 градусам, является прямоугольником.
Квадрат — это тот же параллелограмм, у него и углы и стороны равны.
Что до определения ромба, то это такая геометрическая фигура, все стороны которого равны.
Кроме того, следует знать, что любой квадрат является ромбом, но не каждый ромб может быть квадратом.
Трапеция
При рассмотрении такой геометрической фигуры, как трапеция, можно сказать, что в частности она, как и четырехугольник имеет одну пару параллельных противолежащих сторон и является криволинейной.
Окружность и круг
Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом.
Треугольник
Также к простым геометрическим фигурам принадлежит и уже изучаемый вами треугольник. Это один из видов многоугольников, у которого часть плоскости ограничена тремя точками и тремя отрезками, которые соединяют эти точки попарно. Любой треугольник имеет три вершины и три стороны.
Задание: Какой треугольник называют вырожденным?
Многоугольник
К многоугольникам относятся геометрические фигуры разных форм, у которых замкнутая ломаная линия.
В многоугольнике все точки, которые соединяют отрезки, являются его вершинами. А отрезки, из которых состоит многоугольник, являются его сторонами.
Интересные факты
• А известно ли вам, что возникновение геометрии уходит в глубину веков и связано с развитием различных ремесел, культуры, искусства и наблюдением за окружающим миром. Да и название геометрических фигур является тому подтверждением, так как их термины, возникли не просто так, а благодаря своей схожести и подобию.
• Ведь термин «трапеция» в переводе с древнегреческого языка от слова «трапезион» обозначает столик, трапеза и другие производные слова.
• «Конус» произошел от греческого слова «конос», что в переводе звучит, как сосновая шишка.
• «Линия» имеет латинские корни и происходит от слова «линум», в переводе это звучит, как льняная нить.
• А знаете ли вы, что если взять геометрические фигуры с одинаковым периметром, то среди них обладателем самой большой площади оказался круг.
• А вот одна из известных картин, созданная еще в начале прошлого века Малевичем, прославляет такую геометрическую фигуру, как квадрат. Черный квадрат на белом фоне является мистической загадкой для окружающих, притягивая к себе исследователей и восхищенные взгляды живописцев.
Предмети > Математика > Математика 7 класс

point	точка
line segment	отрезок
ray	луч
line	прямая
plane shape	геометрическая фигура
solid shape	геометрическое тело
volume	объем
area	площадь
perimeter	периметр
diagonal	диагональ
size	размер
side	сторона
angle	угол
lengh	длина
width	ширина
height	высота
depths	глубина
right angle	прямой угол
obtuse angle	тупой угол
acute angle	острый угол
vertical line	вертикальная линия
horizontal line	горизонтальная линия
curved line	кривая линия
broken line	ломаная линия
parallel lines	параллельные линии
perpendicular lines	перпендикулярные линии
radius	радиус
diameter	диаметр
base	основание
vertex	вершина
edge	ребро
convex	выпуклый
concave	вогнутый

Скачать PDF “Геометрические термины на английском”

Геометрические тела и фигуры

Напомню, геометрические фигуры двухмерные, а тела – объемные. Квадрат, треугольник – это фигуры, а куб, пирамида – тела. Некоторые трудности могут возникнуть с прилагательными, образованными от названий тел и фигур, потому что они образуются по-разному:

с помощью суффиксов: rectangle (прямоугольник) – rectangular (прямоугольный).
обозначаются другим словом: circle (круг) – round (круглый).
образуются без изменения слова: oval (овал) – oval (овальный).

От слова circle также образуется прилагательное circular – круглый, но оно обычно используется, когда речь идет о чем-то плоском и, как правило, идеально круглом.

Round может применяться к плоским и объемным предметам, это слово намного употребительнее в повседневной речи: round table – круглый стол, round building – круглое здание.

О шаровидных предметах тоже, скорее всего скажут, что они round (round ball – круглый мяч), хотя технически они spherical. Но по-русски мы тоже не называем мяч «сферическим».

К сожалению, в карточках Quizlet слово circumference (окружность) озвучено некачественно, правильный вариант можно прослушать с помощью онлайн-словаря “Лингво”: http://www.lingvo-online.ru/ru/Translate/ru-en/circumference.

circumference	окружность
square	квадрат
circle	круг
triangle	треугольник
rectangle	прямоугольник
rhombus	ромб
trapezium (US – trapezoid)	трапеция
oval	овал
cylinder	цилиндр
cube	куб
prism	призма
sphere	сфера
cone	конус
pyramid	пирамида
pentagon	пятиугольник
hexagon	шестиугольник
pentagram	пентаграмма
square (adjective)	квадратный
round	круглый
triangular	треугольный
rectangular	прямоугольный
oval (adjective)	овальный
cubic (-al) (adjective)	кубический
spherical	сферический

Скачать PDF “Геометрические тела и фигуры на английском”

Источник: https://langformula.ru/geometry-in-english/

Учим геометрические фигуры с малышами от 1 года | Скачать картинки

2015-03-24

В сегодняшней статье я хотела бы рассказать о том, как легко и увлекательно можно изучать геометрические фигуры с малышом, и зачем вообще в столь раннем возрасте грузить ребенка геометрией. Какие игры будут интересны малышу от 1 года, и какие материалы вам понадобятся для занятий – обо всем этом, читайте в статье. Кроме этого, здесь вы найдете несколько полезных материалов для скачивания.

Зачем изучать геометрические фигуры с малышом?
Геометрические формы встречаются нам повсюду, их можно разглядеть в большинстве окружающих нас предметов: мяч круглый, стол прямоугольный и т.д. Анализируя сходство окружающих предметов с геометрическими фигурами, ребенок замечательно тренирует ассоциативное и пространственное мышление.
Изучение геометрических фигур полезно для общего развития малыша, расширения его знаний об окружающем мире. Если знакомить ребенка с формами в раннем возрасте, в школе ему придется гораздо проще.
На умении отличать геометрические фигуры основано множество интересных развивающих игр. Это конструирование, игры с сортером, мозаикой, математическим планшетом, блоками Дьенеша и т.п. Поэтому изучение форм в столь раннем возрасте будет способствовать дальнейшему успешному развитию ребенка.
Итак, игры для изучения и закрепления знаний о геометрических фигурах:
1. Называем геометрические фигуры всегда и везде
Если во время игр или чтения книг вам встречается какая-либо фигура, обязательно обращайте на нее внимание малыша и называйте ее («Посмотри, мячик похож на круг, а кубик – на квадрат»).
Даже если вам кажется, что ребенок еще вряд ли запомнит названия фигур, все равно произносите их, и они обязательно отложатся у него в голове. Делать это можно уже до года.
Поначалу указывайте только на основные фигуры (квадрат, круг, треугольник), затем, когда поймете, что малыш их усвоил, начинайте изучать и другие фигуры.
2. Играем в геометрическое лото
При помощи лото можно изучать все, что угодно: цвета, геометрические фигуры, овощи, животных и т.д.
А геометрическое лото к тому же довольно легко сделать самостоятельно: на листе бумаги или картона рисуем или распечатываем два одинаковых набора фигур, один из которых разрезаем на карточки.
Все готово, можно играть. Наши шаблоны лото для изучения геометрических фигур можно СКАЧАТЬ ЗДЕСЬ.
Для первых занятий с малышом лучше использовать лото, где всего 3-4 фигуры. Когда малыш хорошо освоит такую игру, постепенно усложняйте поставленную задачу. Также полезно на первое время все фигуры на игровом поле сделать одного цвета и размера. В этом случае ребенок будет ориентироваться только на один признак – форму, другие же характеристики не будут ни отвлекать, ни подсказывать ему.
Накладывать на игровое поле можно как карточки с изображением фигур, так и объемные фигуры. Хорошо с этой целью подойдут блоки Дьенеша (Ozon, KoroBoom), фигурки от сортера, рамки-вкладыша.
Ну и самый нехлопотный вариант — это приобрести готовое лото с геометрическими фигурами.
3. Играем с сортером
Примерно в возрасте 1 года ребенок начинает замечать, что выбранную им фигурку сортера (Озон, Лабиринт, My-shop) можно протолкнуть далеко не в каждое отверстие.
Поэтому во время игры необходимо акцентировать на этом внимание: «Так, вот у нас круг – сюда он не подходит, сюда не подходит, а куда же подходит?». Поначалу повернуть фигуру под правильным углом малышу может быть тяжеловато, но это не страшно, это вопрос практики.
Главное, не забывайте вовремя увлекательного процесса «проталкивания» все время произносить названия фигур, и ребенок незаметно их все запомнит.
Важно! При выборе сортера обратите внимание на то, чтобы там были представлены все основные геометрические фигуры, а не только сердечки и полумесяцы.
4. Играем с рамкой-вкладышем
Понадобится такая рамка-вкладыш, на которой представлены все основные фигуры. По своей сути игра аналогична сортеру.
5. Сортируем геометрические фигуры
Процесс сортировки предметов стал интересовать мою дочь в возрасте 1 года 4 месяцев. Мы сортировали предметы по цветам, по размеру и, конечно же, по форме.
Думаю, эта игра очень нравилась Таисии, потому что мы часто привлекали в нее ее игрушечных друзей.
Стоило, например, куклу Машу позвать в игру, она тут же сообщала, что любит играть только с треугольниками, а мишка говорил, что ему нравятся только прямоугольники. Вот и приходилось нам тщательно отбирать фигуры, чтобы никого не обидеть:)
6. Рисуем
Во время совместного рисования с ребенком также не забывайте произносить названия форм. «Так, нарисуем квадрат, теперь треугольник – получился домик», «Нарисуем круг, овал, палочку, палочку – получился человечек».
Примерно с 1,5 лет малышу уже можно предлагать обводить фигуры по трафаретам. Первые трафареты с геометрическими фигурами вы можете сделать самостоятельно из плотного картона, т.к.
готовые трафареты, как правило, очень малы для самых первых опытов рисования.
Первые трафареты для Таисии я сделала из не очень удачного набора карточек (картинки были не очень, а вот картон отличный), четырех основных фигур нам хватило за глаза (размер наших трафаретов 8×8 см).
Года в 2 Таисия полюбила рисовать по небольшим трафаретам (еще вариант), а также в этом возрасте мы начали обводить с наружной стороны блоки Дьенеша, это было не менее интересно, хотя и потруднее.
7. Клеим
Использовать геометрические фигуры в занятиях по аппликации можно хоть с самого первого занятия. Когда малыш только знакомится с клеем (на мой взгляд, знакомство хорошо проходит в возрасте от 1 года 2-3 месяцев), ему больше интересен сам процесс приклеивания, нежели создание какой-то композиции.
Поэтому не стоит в первых аппликациях с малышом создавать сложные картины, начните просто с хаотичного приклеивания бумажек на листочек, а еще лучше с хаотичного приклеивания геометрических фигур! Пока малыш увлечено мажет фигурку клеем (с вашей помощью) и прикладывает ее на листочек, вы говорите ему, как она называется.
При такой игре все названия очень хорошо укладываются у малыша в голове, можно сказать, прочно «приклеиваются»
Когда у крохи уже будет получаться приклеивать элементы аппликации на заданные места (примерно с 1,5 лет), можно попробовать создать простую композицию.
Вы также можете в своих занятиях использовать различные готовые пособия, например:
Школа семи гномов 1+. Форма, цвет (Ozon, My-shop)
Развивающие наклейки для малышей. Форма (Ozon, My-shop)
Чудесные наклейки. Веселая геометрия (Ozon, My-shop)
8. Находим сходные по форме предметы
Для малышей чуть постарше (от 1 года 6–9 месяцев) очень полезно проводить аналогии между геометрическими фигурами и окружающими предметами. Во время чтения и игр, на прогулке обращайте внимание малыша на то, что тарелка – это круг, окно – прямоугольник, а песочница – квадрат и т.д. Таким образом, вы будете способствовать развитию пространственного и ассоциативного мышления ребенка.
Также можно выполнять задания на отыскание на картинке предметов, которые соответствуют заданной фигуре, например «Найди все круглые предметы». Несколько заданий можно СКАЧАТЬ ЗДЕСЬ.
Вот еще одна интересная игра на распознавание форм – «Найди похожую фигуру» (Лабиринт, My-shop). Несмотря на то, что возраст на ней указан 3-5 лет, она будет интересна ребенку 2-х лет и даже чуть раньше.
9. Учим формы по карточкам Домана
На самом деле, я считаю, что этот метод изучения форм самый эффективный. Если вы занимаетесь по карточкам Домана, ребенок очень быстро запомнит все фигуры, а вы потратите на это минимум усилий.
Однако нужно заметить, что для того, чтобы знания, полученные по карточкам Домана, отложились у малыша в голове, их нужно закреплять посредством других игр (см. выше). Иначе ребенок быстро забудет все, что вы ему показывали.
Поэтому я рекомендую начинать смотреть карточки Домана с геометрическими фигурами примерно в возрасте 1 года, так как в это время малышу становятся интересны сортеры, рамки-вкладыши, рисование, аппликация и т.п.
И, изучив формы по картинкам, он сможет использовать полученные знания в этих играх. Кстати, карточки “Геометрические фигуры” можно СКАЧАТЬ ЗДЕСЬ, а купить ЗДЕСЬ.
О нашем опыте изучения фигур по карточкам Домана можно почитать здесь.
10. Смотрим развивающие мультфильмы
Ну и, конечно, не помешает просмотр мультфильмов на тему «Геометрические фигуры», сейчас на просторах интернета их можно найти немало. Вот некоторые из них:
Вместо заключения
Очень часто процесс обучения ребенка геометрическим фигурам (да и не только фигурам) воспринимается родителями исключительно как постоянное экзаменирование ребенка, т.е.
они пару раз показывают ребенку, например, квадрат, а в дальнейшем же обучение сводится к вопросу «Скажи, какая это фигура?». Такой подход крайне неправильный.
Во-первых, потому что как и любой человек, ребенок не слишком любит, когда ему устраивают проверку знаний, и это только отбивает у него охоту заниматься. Во-вторых, прежде чем о чем-то спрашивать малыша, ему нужно очень много раз это объяснить и показать!
Поэтому постарайтесь сводить проверочные вопросы к минимуму. Просто повторяйте и повторяйте изучаемую информацию, будь то названия фигур или чего-то еще. Делайте это во время игр и бесед с малышом. А то, что ребенок все усвоил, вы вскоре и сами увидите без лишних проверок.
На этом у меня все, благодарю за внимание! Буду очень рада, если вы поделитесь с нами своими идеями игр для изучения фигур.
Искренне ваша, Яна Разначенко
Рекомендую также посмотреть статьи:
ГОТОВЫЙ ПЛАН ИГР И ЗАНЯТИЙ ДЛЯ ДЕТЕЙ ОТ 1 ГОДА ДО 1 ГОДА 3 МЕСЯЦЕВ
ПОДБОРКА КНИГ ДЛЯ ДЕТЕЙ 1-2 ЛЕТ
ПОДВИЖНЫЕ МУЗЫКАЛЬНЫЕ ИГРЫ ДЛЯ ДЕТЕЙ ОТ 1,5 ЛЕТ
Источник: https://jili-blog.ru/geometricheskie-figury-dlya-malyshej-ot-1-goda.html
Памятка Картотека дидактических игр по ФЭМП для детей старшего дошкольного возраста | Картотека по математике (старшая группа):
Муниципальное бюджетное дошкольное образовательное учреждение
детский сад № 57 «Дюймовочка»
Памятка
Картотека дидактических игр по ФЭМП
для детей старшего дошкольного возраста

Подготовила:
Н. С. Золотарёва,
воспитатель
г. Сургут, 2018 г.
Картотеки дидактических игр по ФЭМП для детей старшего дошкольного возраста
Карточка №1. «Геометрические фигуры»
Цель: ознакомление детей с основными геометрическими фигурами.
Материал: карточки с изображением домика, елочки, солнышка и т. д. из геометрических фигур.
Ход игры. После беседы по картинкам попросите ребенка показать (квадрат, треугольник, круг, прямоугольник, затем обвести карандашом фигуры, изображенные пунктирными линиями, после чего раскрасить картинку. В процессе работы чаще повторяйте с ребёнком слова: «Шарик круглый, окно квадратное»
Карточка №2. «Найди и назови фигуру»
Цель: упражнять детей в знании геометрических фигур.
Материал: карточки с изображением геометрических фигур.
Ход игры. Предложите ребенку сначала раскрасить фигуру в рамочке, а затем такую же, выделив ее из двух других. Попросите назвать те фигуры, которые он знает, и цвет, который он выбрал для раскрашивания.
Карточка №3. «Флажки и гирлянды»
Цель игры: развивать логическое мышление детей, упражнять в знании цветов и геометрических фигур.
Материал: карточки с изображением гирлянды из флажков и других геометрических фигур.
Ход игры. Предложите детям закрасить, каждую первую фигуру гирлянд и флажков, затем карандашом обвести фигуры, изображенные пунктиром, и раскрасить их в любой цвет. После чего попросите ребенка показать и назвать фигуры, а также сказать в какой цвет он их раскрасил.
Карточка №4. «Куриное семейство»
Цель игры: упражнять детей в узнавании и назывании геометрических фигур, развивать логическое мышление детей.
Материал: сюжетная картинка с изображением куриного семейства, карточка с изображением геометрических фигур.
Ход игры. Рассмотрите с ребенком сюжетную картинку (заранее раскрашенную). «Кто нарисован? Кто в семье папа, мама? Где детки? Сколько цыплят? Какого они цвета?» Затем предложите карточку с изображенными геометрическими фигурами и попросите отыскать в ней те фигуры, которые надо вырезать и приклеить к изображению курицы, петуха, цыплят. Помогите ребенку вырезать, а наклеит пусть он сам. По окончании работы порадуйтесь его успехам. Можно предложить ребенку показать на картинке самый большой круг, круг поменьше и самые маленькие кружочки. В конце игры уточните, какую геометрическую фигуру выполняли. Предложите найти предметы круглой формы в окружающем пространстве. Пусть ребенок начертит круги пальчиком на столе, на полу, в воздухе. Можно предложить нарисовать круги на бумаге.
Карточка №5. «Паруса»
Цель игры: познакомить детей с формой “треугольник”, развивать мышление.
Материал: сюжетная картинка с изображением лодочек из геометрических фигур, карточка с геометрическими фигурами.
Ход игры. Предложите детям рассказать о том, что нарисовано на картинке, затем обвести карандашом паруса. Спросите, на какую геометрическую фигуру они похожи, какие еще геометрические фигуры им известны. После этого дети отыскивают маленький треугольник, затем большой. Помогите им, если они затрудняются, раскрасить, вырезать и наклеить фигуры на изображение. В конце игры уточните, какую геометрическую фигуру вырезал. Предложите найти предметы треугольной формы в окружающем пространстве. Пусть ребенок начертит треугольники пальчиком на столе, на полу, в воздухе. Можно предложить нарисовать треугольник на бумаге.
Карточка №6. “Выкладывание картинок”
Цель игры: развитие логического мышления детей, закрепление знания геометрических фигур.
Материал: карточки-образцы с рисунками из геометрических фигур, пустые карточки, вырезанные геометрические фигуры разного цвета и размера.
Ход игры. Рассмотрите с детьми рисунки. Предложите отыскать на них знакомые геометрические фигуры. Вырежьте из цветной бумаги фигуры в двух экземплярах и из одного сделайте вместе с детьми аппликации. Второй комплект фигур предложите детям для выкладывания изображений. Не забудьте во время игры закрепить в памяти детей названия цветов. Для второго изображения вырезайте фигуры так, чтобы их форма была одинаковой, а цвет разный, чтобы ребенок отыскивал деталь и по форме, и по цвету.
Карточка №7. «Конструирование по схеме»
Цель игры: развитие логического мышления детей младшего дошкольного возраста.
Материал: карточки с контурными схемами, детали строителя.
Ход игры. Детям дают карточку с контурными схемами и предлагают выложить данные изображения из крупных деталей строительного набора на столе, используя данную карточку как образец. Чтобы усложнить детям задачу, предложите на несколько деталей больше, чем понадобится.
Карточка №8. “Конструируем из палочек”
Цель: закрепление знаний геометрических фигур, развитие логического мышления детей.
Материал: карточки с контурным изображением предметов, палочки разной длины.
Ход игры. Предложите детям палочки разной длины, попросите отобрать самые длинные, длинные и самые короткие. Выложите из палочек по предложению ребенка какую-нибудь фигурку. Затем дайте ребенку карточку, рассмотрите с ним контуры предметов, пусть он узнает их, назовет. Потом предложите выложить любую фигурку. В процессе работы закрепляйте названия знакомых геометрических фигур, которые будут возникать в процессе выкладывания. Попросите выложить палочками фигурки по собственному замыслу.
Карточка №9. «Найди фигуру»
Цель игры: ознакомление детей с названиями геометрических фигур, познакомить с конусом, цилиндром и призмой.
Материал: набор строительного конструктора, карточки с изображением геометрических фигур.
Ход игры. Попросите ребенка найти и принести кубик, кирпичик, затем длинную пластину (используется обычный строительный материал для конструирования). Покажите ребенку конус и предложите отыскать такую же деталь (потом цилиндр, затем призму). После этого дайте ребенку карточку и предложите найти эти детали.
Карточка №10. «Найди пару»
Цель игры: развитие логического мышления, упражнять в назывании цвета и названии геометрических фигур.
Материал: карточки с изображением геометрических фигур разделенные на 8 частей, не разрезанные карточки по числу играющих
Ход игры. Предложите ребенку поиграть в игру. (Одна из карт разрезается на восемь частей.) Наложить разрезанные карточки на целую карточки на карту, (фигуры, одинаковые по форме, но разные по цвету и размерам). Поднимайте ту или иную карточку и просите найти такую же деталь, но другого цвета или размера. При выполнении задания упражняйте детей в назывании цветов.
Карточка №11. «Построй по схеме»
Цель игры: учить детей выполнять элементарные постройки, ориентируясь на схемы.
Материал: схемы построек, строительный набор.
Ход игры. Вспомните с детьми строительные детали, которые они знают, продемонстрируйте им их свойства. Покажите карточку, спросите, что на ней изображено, предложите рассмотреть, и сказать, из каких деталей постройки. Попросите соорудить из строительных деталей такие же постройки. Важно, чтобы детали были изображены в натуральную величину.
Карточка №12. “Накладываем детали”
Цель игры: учить детей выкладывать изображения способом накладывания.
Материал: карточки с контурными рисунками, строительный набор или плоскостные геометрические фигуры.
Ход игры. Детей учат выкладывать изображения способом накладывания объемных деталей одной из граней на рисунок. Предложите детям карту и попросите создать красивые картинки (покажите на примере установки одной детали).
Карточка №13. «Выкладывание фигур»
Цель игры: упражнять детей в выкладывании изображений из геометрических фигур используя схемы.
Материал: карты-схемы изображений, строительный набор.
Ход игры. Детям предлагают схемы и геометрические фигуры для выкладывания изображений. После выполнения задания спрашивают: « Из каких фигур ты составил эту машину? Сколько всего фигур тебе потребовалось для этой ракеты? Сколько здесь одинаковых фигур?»
Карточка №14. «Найди лишнее»
Цель игры: развивать логическое мышление дошкольников.
Материал: карточки с изображением геометрических фигур.
Ход игры. На карте изображены ряды геометрических фигур. Детям предлагают рассмотреть их и определить, что на них лишнее, затем обосновать, почему.
Карточка №15. «На что похоже?»
Цель игры: развивать наглядно – образное мышление детей.
Материал: набор плоскостных геометрических фигур.
Ход игры. Воспитатель поочередно показывает вырезанные геометрические фигуры, называет их и просит сказать, на что они похожи. Например: шар – колобок, солнышко, лицо, воздушный шар и т. д.
Карточка №16. «Конструируем из палочек»
Цель игры: развитие логического умения детей.
Материал: палочки разной длины трех размеров, карточки с изображением простейших картинок.
Ход игры. Детям раздают палочки разной длины, предлагают разложить их по размеру на три части.
Затем дают картинки (реальные изображения предметов простой формы: флажок, машина, лодка с парусом, тачка, цветок, ваза и др.) и просят выложить изображение этих предметов палочками.
Карточка №17. «Сопоставь»
Цель игры: развитие логического мышления дошкольников.
Материал: рисунки с изображением геометрических фигур и реальных предметов, хорошо знакомых дошкольникам.
Ход игры. Детям предлагают два рисунка, на одном изображены геометрические тела (куб, цилиндр, шар, конус и др., на другом реальные предметы, хорошо знакомые дошкольникам, просят назвать, на какое геометрическое тело похож тот или иной предмет). Предложите ребятам поиграть в игру «На что похоже?» – отыскать в окружающем пространстве предметы, напоминающие знакомые им геометрические тела. Попросите детей показать и назвать круглые, квадратные, фигуры на одном и другом рисунке.
Карточка №18. «Вспомни, на что похоже?»
Цель игры: упражнять детей в назывании геометрических фигур.
Материал: карточки с изображением геометрических фигур.
Ход игры. Детям предлагают карточки с изображением строительных деталей. Воспитатель просит назвать деталь и вспомнить предметы, имеющие с ней сходство, обосновать при этом, почему он эти предметы указывает.
Карточка №19. «Посчитай и сконструируй»
Цель игры: Развитие логического мышления дошкольников.
Материал: карточки с изображением роботов из геометрических фигур, строительные наборы или плоскостные геометрические фигуры.
Ход игры. Детям показывают рисунок с изображением роботов из геометрических фигур. Воспитатель предлагает сосчитать, роботов человечков, спрашивает, сколько роботов-собачек. Просит выбрать любого робота, рассказать, из каких фигур он составлен, сколько на него пошло одинаковых фигур-деталей. Затем детям дают геометрические фигуры и просят выложить из них понравившиеся изображения.
Карточка №20. «Обустрой комнату»
Цель игры: развитие логического мышления дошкольников.
Материал: лист бумаги (35* 45см), строительный набор, плоскостные геометрические фигуры.
Ход игры. Воспитатель предлагает детям лист бумаги (З5*45 см) и говорит, что это пол кукольной комнаты, просит обстроить его кирпичиками (стены комнаты, оставив промежутки для окна и двери). После того как дети сделают это, вынимает лист и кладет его рядом с построенной комнатой. Затем достает геометрические фигуры и предлагает разложить их на бумаге, подбирая похожие по форме на предметы мебели (квадрат – табуретка, прямоугольник – кровать и т. д.). Воспитатель рассматривает с дошкольниками получившуюся схему и просит расставить по ней «мебель» в комнате, обстроенной кирпичиками. По окончании работы дети сравнивают изображение с постройкой.
Карточка №21. «Соотношение геометрических тел и фигур»
Цель игры: учить детей соотносить изображения геометрических фигур и строительные детали конструктора.
Материал: Карточки с изображением геометрических фигур, строительный набор.
Ход игры. Дошкольникам предлагают рассмотреть изображения геометрических тел, а затем геометрические фигуры, изображенные ниже. Воспитатель просит отыскать строительные детали, изображенные на карточке, и показать те стороны, которые имеют форму геометрических фигур, изображенных под карточкой. Задание усложняется, если детям предложить соотнести геометрические фигуры и тела, не используя строительные детали.
Карточка №22. «Накладываем детали»
Цель игры: развитие логического мышления дошкольников.
Материал: карточки схемы, строительные детали.
Ход игры. Дошкольникам дают две карточки: на одной в виде схемы изображены различные теремки, на другой – строительные детали, которые следует отобрать для решения данной задачи.
Цель задания: уложить детали в контуре так, чтобы они соприкасались с поверхностью листа одной из граней. В процессе решения задания воспитатель уточняет, какие детали использует ребенок, какого цвета, какая форма граней у той или иной детали, сколько граней у детали, сколько деталей пошло на сборку изображения.
Карточка №23 «Назови форму предмета»
Цели: закреплять умение зрительно соотносить форму предмета с эталоном.
Ход игры: дети делятся на две команды. Одна команда называет предметы прямоугольной формы, а другая квадратной. За каждый названный предмет дети получают фишку. В конце игры выясняется, сколько фишек заработала каждая команда.
Карточка №24 «Назови величину»
Цели: формировать у детей дифференцированное восприятие качеств величины.
Ход игры: дети стоят вокруг стола. На столе разложены картинки с изображением предметов разной величины по кругу. Например: карандаш длинный и короткий. В середине круга лежит стрелка. Дети ее раскручивают и говорят слова: «Стрелка, стрелка покружись, всем картинкам покажись. Покажи нам поскорее, какая из них тебе милее. Дети берут картинку, на которую указывает стрелка, и называют величину предметов.
Карточка №25. «Кто больше запомнит».
Цели: закреплять у детей умение зрительно узнавать в окружающем пространстве цвет, форму, величину предметов, развивать зрительное внимание, память.
Ход игры: В игре принимают участие несколько детей. Им предлагается в течение нескольких минут увидеть вокруг себя как можно больше предметов одного и того же цвета, величины, формы. По сигналу один ребенок начинает называть, а другой дополняет.
Карточка №26. «Коробочки».
Цели: развивать умение зрительно соотносить предметы по цвету, развивать цветоразличение, внимание.
Ход игры: Играет 5-6 человек. На подносе лежат мелкие игрушки четырех основных цветов. Педагог показывает 4 коробочки. На дне каждой есть кружок определенного цвета (из 4х). Идя по кругу, педагог открывает одну из коробочек. Дети должны взять с подноса и положить в эту коробочку игрушку такого же цвета, какого цвета кружок в коробочке. Слова: «На донышке в коробочке огонек горит, какие брать игрушки. Он нам говорит. Смотри не перепутай, внимательно следи, что такого цвета, в коробочку клади.
Карточка №27. «Подбери предмет по цвету»
Цели: закреплять умение соотносить цвет, как основной признак с цветностью предметов, развивать зрительное внимание, память, ориентировку в пространстве.
Ход игры: Дети стоят в кругу. В середине стоит стол. На нем лежит карта с кружками разного цвета. (в зависимости от возраста). В середине карты – стрелка. Карта круглая. Дети по очереди поворачивают стрелку, приговаривая слова «Стрелка, стрелка покружись, всем кружочкам покажись. И какой тебе милее, укажи нам поскорее! Стоп!» На какой цветной кружок укажет стрелка, такого цвета предмет на картинке надо положить рядом с кружком. Карточки с контурами и силуэтами предметов лежат на другом столе. Например: стрелка остановилась на бордовом кружке. Рядом с этим кружком нужно положить силуэт или контур свеклы. Стрелку крутят все по очереди. Усложнение: можно подбирать к цветному кружку несколько силуэтов или контуров предметов данного цвета.
Карточка №28. «Разложи, как я скажу»
Цель: развивать зрительную память, дифференцировку плоских геометрических фигур, зрительное внимание, ориентировку в микропространстве.
Ход игры: Перед детьми лежат разные геометрические фигуры. Педагог убеждается, что дети знают их названия. Затем педагог предлагает детям выложить эти фигуры в определенном порядке. Порядок может быть самый разный: слева направо, сверху вниз, по образцу, по памяти, в определенной последовательности, по счету (выложить так, чтобы второй была трапеция, четвертым- ромб и т. д.).
Карточка №29. «Что в левой, что в правой руке?».
Цель: закреплять ориентировку по направлениям, на листе бумаги, зрительное внимание, зрительная память.
Ход игры: Педагог показывает детям две картинки, одинаковые по сюжету, но разные по расположению предметов. Дети должны назвать расположение предметов на обеих картинках. Например: на картинке справа солнце находится в левом верхнем углу, а на картинке слева – оно в правом верхнем углу. Картинки можно сделать по любой теме. Чем старше дети, тем больше предметов может быть на картинках и больше отличий.
Карточка №30. «Раз, два, три, как ты шёл, назови?».
Цель: развитие ориентировки в микропространстве, по направлениям (право, лево, верх, низ).
Ход игры: Детям показывают лабиринт. Нужно помочь зайке пройти к зайчихе. Чтобы помочь, надо провести пальчиком по лабиринту и сказать слова: «С лабиринтом я играю, по дорожке пробегаю. Пальчик мой идет, идет, но куда он приведет? Раз, два, три – как ты шел, назови». Ребенок рассказывает, как сначала пальчик шел вправо, потом вверх, потом налево и т. д. Усложнение: лабиринт перекрещивается лабиринтом другого цвета. Можно усложнить направления.
Карточка №31. «Двенадцать месяцев».
Цель: развивать ориентировку во времени (названиях месяцев, временах года), слуховое внимание.
Ход игры: педагог раскладывает на столе карточки с цифрами от 1 до 12 и перемешивает их. Играющие берут карточки и выстраивают по порядку в соответствии с цифрой, указанной на карточке. Они превратились в 12 месяцев. Педагог задает вопросы: «Первый месяц – как тебя зовут?». «Двенадцатый месяц – как тебя зовут?» «Шестой месяц. А тебя как зовут?» и т. д. Можно сделать подсказку – на обратной стороне написать первую букву месяца.
Список геометрических фигур с изображениями
Вы знаете все эти формы? Давай выясним!
Список геометрических фигур
сердце
квадрат
прямоугольник
круг
звезда
полумесяц
пирог
крест
куб
цилиндр
овал
овал
овал
овал
семиугольник
шестиугольник
воздушный змей
нонагон
восьмиугольник
пятиугольник
параллелограмм
многоугольник
четырехлистник
ромб
9000 9000 9000 9000 9000 9000 трапеция 9000 7000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 7000 9000 9000
сфера
треугольник
клин
Изображения фигур
Сердце
геометрическая форма сердца
Квадратная геометрическая форма
Прямоугольник
прямоугольная геометрическая форма
Круговая круглая геометрическая форма
Геометрическая форма звезды
Геометрическая форма полумесяца
Геометрическая форма Пипи
Геометрическая форма крест-накрест
Геометрическая форма куба
Геометрическая форма цилиндра-цилиндра
Овальная геометрическая форма
Эллипс-эллипс геометрическая форма
9000 форма 9000 шестиугольник
9000 геометрическая форма
Шестиугольник, геометрическая форма
Геометрическая форма Kitekite
Геометрическая форма неугольника
Геометрическая форма восьмиугольника, геометрическая форма
Геометрическая форма пятиугольника
Параллелограмма, параллелограмма
Форма параллелограмма
ПолукругПолукруг геометрическая форма
Трапеция, трапеция, геометрическая форма
Форма Archarch 900 03
Форма конуса
Пирамида Форма пирамиды
Форма кольца
Форма сферы
Форма треугольника
Форма клина
Видео геометрических фигур с американским произношением
<strong></h3><p> <iframe loading="lazy" title="Learn Shapes in 6 minutes / Geometric Shapes for Kids and their Parents / Whiteboard Animation" data-ezsrc="https://www.youtube.com/embed/6ffzBCZqFR0?feature=oembed&enablejsapi=1" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen=""/> 9 с вашими друзьями!
Прочтите:
Названия частей человеческого тела на английском 💪🙎‍♀️🦶🏃‍♀️👀
Простые против сложных и составных объектов [ГРАММАТИКА]
24 Синонима к мягкому: мягкий, нежный, толерантный, …
Автомобильная промышленность [Урок английского]
Довольно тихо ✅ Разница между тихим и спокойным
Английский язык для продавцов ›› Английский договор купли-продажи
15 самых популярных цветов: роза, лилия, маргаритка,…
Vicious Определение, порочный круг и косвенная ответственность
🎲 У меня никогда не было вопросов 👉 для детей 👉 Смешно 👉 Грязно
36 наиболее распространенных словосочетаний с Keep
Разница между IN, ON и AT
Список омонимов и омографы: слова, которые являются Написано одинаково
Все против.Все 🙂🙃 Разница между всеми и всеми
64 Классные комнаты и школьные объекты
31 Типы домов ›› Типы домов, такие как квартира, коттедж, квартира, хижина, иглу…
25 классных фраз на английском языке для учителей и учеников
Имена геометрических фигур, геометрические фигуры и изображения
Имена геометрических фигур, геометрические фигуры и изображения

Геометрические фигуры
В математике 6 геометрических фигур.У каждой геометрической формы есть свои правила и углы. Сегодня мы расскажем вам об этих геометрических фигурах и их свойствах.
Что это за шесть основных геометрических фигур?
Круг – один из них. Круги составляются путем вычисления их окружностей по линии, проведенной от их центра к краю. Это должно быть одинаковое расстояние от каждой точки центрального круга.

Треугольник : Треугольники могут быть разных типов, но всегда имеют 3 угла и стороны.Сумма углов треугольников всегда должна быть равна 180 градусам. Стороны треугольников не всегда равны, и треугольники делятся на три части по сторонам.
Равносторонний треугольник : В этом типе треугольника все стороны треугольника равны друг другу. Каждый угол в этом треугольнике должен составлять 60 градусов.
Равнобедренный треугольник : В треугольнике этого типа только две стороны равны по длине. Третья сторона имеет другую длину.
Масштабный треугольник : В треугольнике этого типа нет сторон равной длины.
Треугольники также делятся на три в соответствии с их углами.
Прямой треугольник : Наибольший угол в этом треугольнике – прямой. Прямой угол – 90 градусов.
Острый треугольник : Этот треугольник является самым большим из трех углов. Узкие углы менее 90 градусов.

Тупой треугольник : Самый большой угол этого треугольника называется тупым углом.Широкие углы больше 90 градусов, т.е. перпендикулярны.
Прямоугольник : Прямоугольник – это геометрическая фигура, в которой длины противоположных сторон равны друг другу. Углы внутри всегда равны 90 градусам и равны между собой.
Ромб : он состоит из 4 прямых линий, но не каждый угол равен 90 градусам. Длины четырех сторон равны друг другу.
Квадрат : четыре стороны равны, каждый угол равен 90 градусам.Он похож на ромб тем, что все стороны равны друг другу. Независимо от их размера, все квадраты параллельны друг другу.
Трапеция : Трапеция имеет 4 стороны, но, как следует из названия, не все стороны равны. Только 2 противоположные стороны параллельны друг другу.
Параллелограмм : Параллелограмм означает, что противоположные стороны параллельны друг другу. Некоторые параллелограммы также имеют линии симметрии.
Воздушный змей : Имеет две равные стороны.Эти края примыкают друг к другу.
Трапеция : Эта форма, называемая в Великобритании трапецией, представляет собой четырехугольник, у которого нет равных или параллельных сторон.
Геометрические формы, такие как Пентагон, Шестиугольник, Гептагон, Октагон, Нонагон, Десятиугольник, также имеют определенный порядок. Кроме того, геометрические формы делятся на две: вогнутые и выпуклые.
Геометрические формы на этом не заканчиваются. Но это основные геометрические формы, у которых есть правила и которые мы называем гладкими.Внутренние углы, длины сторон и параллельность у всех различаются.
Фигур и их названия, определение и примеры с изображениями
Фигуры и их названия, определение и примеры с изображениями

Имена фигур на английском языке
Очень важно, в чем сходство или различие форм угловой зоны и щита корзины. В то время как в футболе есть отверстие в форме угловой зоны, форма баскетбольного щита полностью закрыта.Отсюда можно сказать, что фигуры могут быть открытыми или закрытыми. Мы подробно рассмотрим « имен форм », приведя примеры форм для этих ситуаций ниже. Замкнутые формы, созданные с помощью прямых и изогнутых линий, являются геометрическими фигурами.
Вот названия линий на английском языке

У некоторых геометрических фигур есть особые названия. Треугольник, квадрат, прямоугольник и круг – самые известные геометрические фигуры. Давайте подробнее рассмотрим названия фигур на английском языке :
Треугольник
Треугольник – это замкнутая геометрическая фигура, образованная соединением трех прямых линий.Многие формы, с которыми мы сталкиваемся, обычно имеют треугольную форму. Треугольник имеет три угла и три ребра. Закрашенное состояние треугольника – это треугольная область. Треугольная зона состоит из внутренней зоны треугольника и самого себя.
Учитель объяснил информацию о треугольнике на нашем первом уроке, но наши одноклассники не поняли.
Квадрат
Квадрат – это замкнутая геометрическая фигура, образованная соединением четырех линий одинаковой длины.У квадрата четыре угла и четыре края. Все его стороны одинаковой длины. Полная версия квадрата находится в области квадрата. Квадратная область состоит из внутренней области квадрата и самого себя.
Они сделали наш дом большой площадью.
Прямоугольник
Прямоугольник представляет собой замкнутую геометрическую фигуру, образованную соединением четырех линий одинаковой длины. Прямоугольник имеет четыре угла и четыре края. Длины противоположных кромок равны. Внутренняя часть прямоугольника заполнена прямоугольной областью.Прямоугольная область состоит из внутренней части прямоугольника и самого себя.
Многие ученики не могут составлять прямоугольные вопросы на уроках геометрии.
Круг
Вы можете видеть множество круговых и круговых моделей вокруг себя. Круг баскетбольного щита имеет форму круга из монеты. Круг и круг не имеют краев и углов. Это самая важная особенность, которая отличает круг и круг от других геометрических фигур.
Баскетбольные тигли обычно изготавливаются по кругу.
Куб
Это геометрический объект, все стороны которого составляют квадрат. Куб со всеми одинаковыми гранями – это особая призма. Все стороны куба равны. Каждая из областей квадрата здесь – это одна сторона куба. У куба 12 сторон, 8 углов и 6 поверхностей. Форма куба может иметь множество различных расширений. В его расширении есть 6 четырехугольных областей. В лекциях обычно объясняются четыре различных аспекта куба.
У моего брата Марри было много трудностей, потому что он не мог нарисовать куб.
Прямоугольная призма
Это геометрический объект со всеми сторонами в форме прямоугольной области. Прямоугольная призма образуется путем объединения двух из трех различных прямоугольных областей. Противоположные грани прямоугольной призмы идентичны. Детали призмы из прямоугольников бывают разной длины, ширины, длины и высоты. Детали, отмеченные оранжевым цветом, – это высота призмы.Прямоугольная призма имеет 12 сторон, 8 углов и 6 поверхностей.
Футбольное поле в школьном саду спроектировали в виде прямоугольной призмы.
Квадратная призма
Это призма, состоящая из верхней и нижней поверхностей квадратных областей и сторон прямоугольных областей. Многие коробки из-под молока и сока вокруг нас имеют форму квадратной призмы. Края темно-синего цвета – это высота призмы. Оранжевые края – это базовые края призмы.В призмах высота – это края, которые соединяют верхнюю и нижнюю подошвы с их точным значением. Квадратная призма имеет 12 сторон, 8 углов и 6 поверхностей.
Пакет для молока в форме квадратной призмы стал незаменимым помощником в наших ремесленных работах.
Треугольная призма
Это призма, верхняя и нижняя поверхности которой состоят из прямоугольных областей, а боковые грани. В отличие от других призм, треугольная призма имеет 6 углов, 9 делений и 5 поверхностей.
По мнению многих специалистов, египетские пирамиды выполнены в виде треугольной призмы.
Цилиндр
Это геометрический объект, у которого верхняя и нижняя поверхности равноудалены, а стороны изогнуты. В отверстии цилиндра есть два одинаковых круга и прямоугольная область. Валик не имеет раздельного и углового.
Ему никогда не нравились предметы, которые были цилиндрами.
Сфера
Это геометрический объект, не имеющий отверстия, разделения и угла.Мяч и мяч – это сферические модели. Есть кусочек круга и круг у отверстия конуса.
Мир не совсем шар или овал.
Конус
Конус не имеет углов и деталей. Новогодние шапки конусообразные.
Мой дедушка на Новый год купил вместе с ним много шляп и фишек в форме конусов.
Равносторонний треугольник
Это треугольник с равной длиной сторон. Их внутренние углы также составляют 60 градусов каждый.Пониженная высота также является биссектрисой, краем угла и центральной стойкой края.
Томас согласился с частным учителем выучить урок равностороннего треугольника.
Ромб
Ромб – это квадрат с четырьмя сторонами равной длины. Плитка ромб видна на игральных картах, таблетки этой формы – ромбовидные, игровое поле этой формы для бейсбола называется ромбами. Каждый ромб – это параллельный край, а прямой угол – это квадрат.
Для нас проще всего было нарисовать ромб.
Многоугольник
Замкнутые фигуры, образованные отрезками линий, которые объединяют любые три нелинейные бесконечные точки два на два в плоскость. Многоугольники, созданные путем соединения бесконечных точек, называются ngenes. Его называют треугольником, прямоугольником. У многоугольников столько углов, сколько ребер.
Многоугольник – очень сложный для понимания предмет.
Трапеция
В школах многие вопросы не задают по таким предметам геометрии, как трапеция, площадь и периметр трапеции, трапеция и трапеция.В общем, мы уже знаем, что есть небольшое количество вопросов по всем предметам урока геометрии. Невозможно предсказать, какой заголовок возникнет из-за проблем с геометрией. Поэтому нам нужно знать трапеции и связанные с ними подзаголовки.
Я не мог понять проблему трапеции, описанную в прошлом уроке.
Шестигранник
Шестиугольник – это многоугольник с шестью ребрами и шестью углами. Его еще называют гладким шестиугольником, если его края и внутренние углы равны.Каждый внутренний угол гладкого шестиугольника составляет 120 °. Поскольку он состоит из шести шестиугольных треугольников, его площадь и периметр легко найти.
Историческое здание шестиугольной конструкции.
восьмиугольник
Восьмиугольник – это многоугольник с восемью сторонами и 20 диагоналями. Сумма внутренних углов: градусы. Внутренний угол становится градусом. Сумма внешних углов: градусы. Внешний угол становится градусом.
После восьмиугольного многоквартирного дома, который я видел раньше, меня не удивляет другое здание.
Овальный
Овал – это замкнутая кривая на плоскости, очень похожая на очертание яйца. Термин не очень конкретный, но в некоторых регионах дается более точное определение, которое может включать одну или две оси симметрии. В обычном английском этот термин используется в более широком смысле. Например, его можно использовать как любую форму, напоминающую яйцо.
Яйцо овальной формы меня очень радует. Потому что продукты овальной формы усиливают аппетит.
Параллелограмм
Параллелограмм представляет собой четырехугольный прямоугольник с равными сторонами, равный 360 градусам. Их противоположные края параллельны и равны по длине.
Нарисовать форму параллелограмма очень просто.
различных имен форм (с полезным списком и типами) • 7ESL
Вы ищете разные названия фигур на английском языке? Здесь вы найдете список фигур с разными типами и полезные примеры предложений.Если вы работаете в бизнесе, который требует использования математики, например, тогда очень важно знать английские названия фигур.
Однако это может быть не единственной причиной, по которой вам нужно узнать эту информацию. Принимая участие в повседневных беседах, вам нужно будет выучить названия форм, чтобы что-то описать или уметь понимать, о чем кто-то говорит, например, если человек говорит вам о «квадратной тарелке». Здесь вы можете выучить названия фигур и еще больше расширить свой словарный запас.
Формы
Что такое формы?
Фигуры – это геометрические фигуры или узор, в который попадает контур. Формы часто рисуются (тушью, карандашом или цифровым способом), но они встречаются и в жизни. Часто люди представляют 2D (двумерные или плоские) изображения, когда слышат слово «формы», поэтому большинство объектов, перечисленных в этом уроке, будут двухмерными, но некоторые также будут трехмерными.
Различные типы фигур
Существует много-много различных типов фигур, и практически у всех есть названия.В следующем списке представлены более распространенные формы, с которыми вы, скорее всего, столкнетесь, или что вам нужно будет узнать их имя.
Названия форм с изображениями
Штифт
Двумерные (плоские) формы
Круг: Круг имеет одинаковую круглую форму. Изобразите крышку банки, плоскую, сверху. Это круг. Колеса у машины тоже круглые. То же самое с отверстиями в большинстве линованных бумаг и блокнотов.
Овал: Овал – это, по сути, немного сплющенный круг.Чашечки накладных наушников обычно называют овальными. Таков профиль яйца. Некоторые проводят различие между кругами, сжатыми посередине, и кругами, сжатыми вверху, причем первые называются эллипсами, но при обычном использовании оба они рассматриваются как овалы.
Прямоугольник: Прямоугольник – это фигура с четырьмя сторонами, состоящая из двух наборов параллельных линий с четырьмя прямыми углами (углы 90 градусов; изобразите заглавную L). Не имеет значения, имеют ли стороны одинаковые длины.Представьте себе простой лист бумаги для печати. Это прямоугольник, у которого один набор сторон (обычно верхняя и нижняя) короче, чем другой набор сторон (обычно левая и правая).
Квадрат: Квадрат – это очень специфический тип прямоугольника с четырьмя равными сторонами. Некоторые коробки имеют квадратную форму. Бумага для оригами квадратная.
Треугольник: Треугольник – это фигура с тремя прямыми сторонами. Эти стороны могут быть любой длины, с любым углом наклона, если три стороны соединены своими концами.Многие предупреждающие знаки имеют треугольную форму. Кусочек круглой пиццы в основном имеет треугольную форму (корочка слишком округлая, чтобы быть идеальной).
Пентагон: Пятиугольник – это фигура с пятью сторонами. Базовый чертеж дома с двумя линиями крыши, линией для каждой стороны и линией для дна, как правило, представляет собой пятиугольник.
Фигуры с большим количеством сторон обычно называют в зависимости от того, сколько у них сторон. Шестигранник имеет шесть сторон, семиугольник – семь, а восьмиугольник – восемь.
Трехмерные фигуры
Трехмерные формы – это формы, которые не просто лежат на бумаге, но также занимают место по вертикали. Лишь немногие из них действительно часто называются.
Сфера: Сфера – это трехмерный круг, похожий на шар.
Куб: Куб – это трехмерный квадрат, похожий на коробку.
Пирамида: Пирамида – это трехмерный треугольник. Гигантские сооружения в Египте – пирамиды, как и Луксор в Лас-Вегасе.
Имена форм
Очень важно пополнять словарный запас на любом языке.Чем больше слов вы знаете и понимаете, тем лучше вы сможете общаться. Даже если вы нечасто используете эти слова, их понимание позволит вам продолжить разговор, даже если он выходит за пределы вашей зоны комфорта. Этот урок специально посвящен различным типам фигур.
Список фигур
Нонагон
Восьмиугольник
семиугольник
Шестиугольник
Треугольник
Чешуйчатый треугольник
Правый треугольник
Параллелограмм
Ромб
Площадь
Пентагон
Круг
Овал
Сердце
Крест
Стрелка
Куб
Цилиндр
Звезда
Полумесяц
Различные имена форм с изображениями и примерами
Nonagon
Студент-математик измерил каждую сторону nonagon , пока не получил измерения для всех девяти ребер.
Штифт
восьмиугольник
Форма сечения – четверть восьмиугольника .
Штифт
Гептагон
Пагода имеет основание из семиугольника .
Штифт
Шестигранник
Шестигранник – шестигранная фигура.
Штифт
Треугольник
Сумма всех углов треугольника равна 180 градусам.
Штифт
Чешуйчатый треугольник
Разносторонний треугольник – это треугольник с тремя неравными сторонами.
Штифт
Правый треугольник
Гипотенуза – это самая длинная сторона прямоугольного треугольника .
Штифт
Параллелограмм
Это противоположные стороны параллелограмма .
Штифт
Ромб
Ромб – это простой четырехугольник, все четыре стороны которого имеют одинаковую длину.
Штифт
Квадрат
Внутренние углы квадрата являются прямыми углами или углами в 90 градусов.
Штифт
Пентагон
Нарисуйте пятиугольник , правильную пятиугольную фигуру.
Штифт
Круг
Ученики сидят в круге на полу.
Штифт
Овальный
Земля имеет форму овала .
Штифт
Сердце
Бассейн имел форму сердца .
Штифт
Крест
Крест – символ христианства.
Штифт
Стрелка
Прям летела стрела .
Штифт
Куб
Коробка куб -образная.
Штифт
Цилиндр
Цилиндр поворачивается на 180 градусов.
Штифт
Звезда
Она разрезает эту бумагу на звездочки -образной формы.
Штифт
Полумесяц
У него нож в форме полумесяца –.
Штифт
Фигуры | Картинка
Учите различные формы с изображениями, чтобы улучшить и расширить свой словарный запас, особенно форм и цветов словарных слов на английском языке.
PinShapes: разные имена фигур (с полезным списком и типами)
Имена фигур Видео
Фигуры встречаются повсюду, поэтому ссылки на них часто встречаются.Надеюсь, после этого урока вы будете готовы работать с формами!

Список геометрических фигур и их имен
Одним из свойств объектов, изучаемых геометрией, является их форма . Геометрические фигуры и их названия ниже дают вам общее представление о том, что вы найдете в любом данном классе геометрии. Интуитивно можно представить себе форму как набор линий, ограничивающих пространство. Согласно этому интуитивному пониманию, форма объекта – это внешняя форма или внешний вид объекта в пространстве, который может быть представлен набором линий, ориентированных определенным образом.
В более математических терминах форму объекта можно рассматривать как математическое описание, которое остается, когда информация о местоположении, масштабе, ориентации и свойствах материала объекта абстрагируется. Вот некоторые простые формы:
Квадраты
Круги
Кубики
Конусы
Шестиугольники
Декаэдры
Формы изучались людьми с давних времен.Древние египтяне понимали уникальные свойства различных форм и использовали это понимание в своих монументальных сооружениях, таких как пирамиды, а греки считали абстрактные геометрические формы одними из самых фундаментальных составляющих существования; совершенные идеализации своих несовершенных материальных аналогов. Исаак Ньютон обращался в первую очередь к геометрическим законам и формам для построения своей системы механики, а величайшая работа Эйнштейна заключалась в описании крупномасштабной геометрической формы Вселенной.Формы – одна из первых вещей, которую человеческие младенцы учатся распознавать, и, по мнению многих философов и ученых на протяжении всей истории, изучение формы и геометрии в более широком смысле является одним из немногих случаев, когда человеческий разум может напрямую контактировать с конечным реальность.
Свойства геометрических фигур
Существует много разных форм, но все формы имеют несколько общих свойств. Во-первых, все формы как минимум двумерны. Такие вещи, как одномерные линии или нулевые точки, не имеют площади и не считаются формами.Во-вторых, все формы размера N состоят из элементов размеров N – 1. Например, двумерный квадрат состоит из одномерных линий. Точно так же 3-мерный куб состоит из 2-х мерных квадратов, 4-мерный гиперкуб состоит из 3-х мерных кубов и т. Д. Конструкция фигур дает им уникальную иерархию, в которой определенные фигуры имеют аналоги в разных измерениях. Сфера – это трехмерный аналог двумерного круга, а тетраэдр – трехмерный аналог двумерного треугольника.
«Прямой угол – одна из основных фигур в мире». – Клас Ольденбург
Наконец, для любой заданной формы существует по крайней мере одно (во многих случаях более одного) математическое представление этой формы в терминах алгебраической функции, связывающей по крайней мере два значения упорядоченной пары на координатной плоскости. . Например, уравнение, определяющее круг: (x – h) ² + (y – k) ² = r ², где (h, k) представляет собой центральную точку круга, а r представляет радиус круга.Математический аппарат алгебры позволяет нам закодировать свойства геометрического объекта в одно математическое выражение, что значительно упрощает анализ.
Фигуры часто подразделяются на категории в зависимости от их размеров, количества сторон и того, построены ли они из прямых или изогнутых линий. Двухмерная фигура, состоящая из прямых линий, называется многоугольником . Многоугольники можно разделить по количеству сторон. Поскольку фигура должна охватывать пространство, минимально возможный многоугольник в евклидовой геометрии – это треугольник с 3 сторонами.Некоторые системы геометрии допускают односторонние или двусторонние формы, но не традиционную евклидову геометрию. Трехмерная фигура, состоящая из прямых линий и плоских двумерных поверхностей, называется многогранниками . , как и многоугольники, многогранники делятся на количество граней. Выпуклые формы, образованные из изогнутых линий, обычно называются эллипсоидами , но есть много других форм, которые явно не попадают ни в одну категорию.
Список геометрических форм и имен
Многоугольники
Моногон – 1 сторона (вырожденная в евклидовой геометрии)
Дигон – 2 стороны (вырожденная в евклидовой геометрии)
Треугольник – 3 стороны
Равносторонний треугольник – 3 равные стороны
Равнобедренный треугольник – 2 равных стороны
Чешуйчатый треугольник – нет равных сторон
Четырехугольник – 4 стороны
Прямоугольник – 4 стороны и 4 прямых угла
Трапеция
Ромб
Пятиугольник Шестигранник – 6 сторон
Шестиугольник – 7 сторон
Восьмиугольник – 8 сторон
Неугольник – 9 сторон
Десятиугольник – 10 сторон
Додекагон – 12 сторон
Икосагон – 20 сторон
Различные многоугольники в форме звезды
Пентаграмма – 5 баллов
Гексаграмма – 6 сторон
Гептаграмма – 7 баллов
Многогранники
90 007 Правильные многогранники – трехмерная фигура, состоящая из того же правильного многоугольника
Тетраэдр – 4 грани
Куб – 6 граней
Октоэдр – 8 граней
Додекаэдр – 12 граней
Икосаэдр – 20 граней
5 «Говорят, что форма пирамиды таит в себе все секреты и удивительные свойства.Одно из них – чувство удивления ». – Вера Назарян
Однородные многогранники – трехмерная фигура, состоящая из комбинации как минимум двух различных правильных многоугольников
В отличие от правильных многоугольников, которых практически бесконечное количество, существует только 5 возможных правильных многогранников.
Изогнутые формы
Двумерные изогнутые формы
Окружность – все точки на одинаковом расстоянии от центральной точки в двухмерном пространстве
Эллипс – сумма расстояний до двух фокусных точек одинакова по всей кривой
Парабола – зеркально-симметричная плоская кривая (u-образная)
траектория наземных снарядов
Кольцевое пространство – область, ограниченная двумя концентрическими окружностями
Линза – множество, образованное двумя выпуклыми кривыми
многоугольников Рело
Луна – выпуклых -вогнутая область, ограниченная двумя кривыми (форма «полумесяца»)
3-D изогнутые формы
Конусы
Цилиндры
Сфера – все точки, равноудаленные от центральной точки в трехмерном пространстве.
Эллипсоид – трехмерный аналог двумерного эллипса (форма «яйца»)
Тор – трехмерный аналог двумерного кольца (форма «бублика»)
Геометрические формы более высоких измерений
До сих пор мы рассматривали формы только в двух или трех измерениях. Эти формы составляют подавляющее большинство форм, с которыми человек может столкнуться в повседневной жизни. Существует целый каталог экзотических форм, которые существуют в более высоких измерениях, чем обычные 3 измерения нашего повседневного опыта.
Например, тессеракт, также называемый гиперкубом, является 4-мерным аналогом куба. Это правильный четырехмерный многогранник, как куб – правильный трехмерный многогранник. Подобно тому, как куб состоит из 6 квадратных граней, тессеракт состоит из 8 кубических ячеек. Помимо тессеракта, существует еще 5 других регулярных 4-D многогранников, таких как 5-элементный пентахорон или 600-элементный (!) Тетраэдр гексакозихорон-тетраэдр. Теоретически этот метод геометрической абстракции может расширять до бесконечности , что приводит к постоянно расширяющейся восходящей иерархии многомерных форм.
Кроме того, введение неевклидовой геометрии позволяет создавать странные аналоги форм, найденных в евклидовой геометрии, которые имеют другие свойства. Например, неевклидов треугольник имеет внутренние углы, которые в сумме могут быть больше или меньше 180 °, в зависимости от конкретной используемой неевклидовой геометрии.
Была ли эта статья полезной?
😊 ☹️ Приятно слышать! Хотите больше научных тенденций? Подпишитесь на нашу рассылку новостей науки! Нам очень жаль это слышать! Мы любим отзывы 🙂 и хотим, чтобы вы внесли свой вклад в то, как сделать Science Trends еще лучше.
Что такое формы? [Определение, факты и пример]
Учитесь с помощью полной программы обучения математике K-5
Что такое фигуры?
В геометрии форма может быть определена как форма объекта или его контур, внешняя граница или внешняя поверхность.
Все, что мы видим в окружающем мире, имеет форму. Мы можем найти различные основные формы, такие как двумерный квадрат, прямоугольник и овал или трехмерную прямоугольную призму, цилиндр и сферу в объектах, которые мы видим вокруг.Эти геометрические формы появляются в объектах, которые мы видим как кредитные карты, банкноты и монеты, кольца на пальцах, фоторамки, доски для дартса, хижины, окна, волшебные палочки, высокие здания, цветочные горшки, игрушечные поезда и воздушные шары.
Различные типы фигур
Фигуры можно разделить на открытые и закрытые.
Замкнутые геометрические фигуры можно разделить на две большие категории, а именно двухмерные и трехмерные формы.
Вот список двухмерных или двумерных фигур с их названиями и изображениями:
Двумерные геометрические формы
Вот список трехмерных или трехмерных фигур с их названиями и изображениями:
Трехмерные геометрические фигуры
Цвет, общий размер и ориентация, называемые не определяющими атрибутами двухмерной или трехмерной формы, никоим образом не определяют и не влияют на форму.Эти атрибуты могут изменяться без какого-либо влияния на форму.
С другой стороны, определение таких атрибутов, как количество сторон (параллельных или непараллельных, прямых или изогнутых), вершин, ребер и граней формы, является ли форма открытой или закрытой, а также угловые меры определяют форму. двухмерного или трехмерного объекта. Любое изменение этих определяющих атрибутов изменит форму.
Интересные факты
Все трехмерные формы состоят из двухмерных форм.
Давайте споем!
Накидка волшебника.
Портьерная занавеска.
Кислый виноград.
Лента электрика.
И непослушный детеныш обезьяны.
Что в них общего?
Все они имеют форму.
Давайте сделаем это!
Вместо того, чтобы раздавать листы-раскраски по математике своим дошкольникам и детям, поиграйте с ними в игру «покажи мне».Вы можете попросить их показать вам повседневные предметы, которые имеют двухмерную или трехмерную форму, которую вы назвали. Или вы также можете показать им разные объекты и попросить их определить двухмерную или трехмерную форму, которую они видят в них.
Вы также можете дать своим детям пластилин и спички для создания двумерных или трехмерных фигур. Смоделируйте это для них.
Сопутствующая математическая лексика
Название геометрических фигур – многоугольники, многогранники
Поиск инструмента
Название геометрических фигур
Инструмент для поиска названия геометрических фигур.Многоугольники – это геометрические фигуры в плоскости 2D, а многогранники – это геометрические фигуры в пространстве 3D
Результаты
Название геометрических фигур – dCode
Тег (ы): Geometry
Поделиться
dCode и другие
dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !
Рекламные объявления
Ответы на вопросы (FAQ)
Как называется многоугольник с…?
Укажите dCode количество сторон и он найдет имя.
Пример: 6: HEXAGON
12: DODECAGON
В более общем смысле, многоугольников записываются с префиксом, указывающим их количество сторон, и суффиксом -угольник .
Вот список в виде таблицы всех различных правильных геометрических форм двухмерной плоскости (таблица имен n-сторонних многоугольников ):
Как называется многогранник с…?
Укажите количество граней, и он найдет имя трехмерной геометрической фигуры.
Пример: 6: HEXAHEDRON
Пример: 12: DODECAHEDRON
Вот таблица всех правильных геометрических форм / многогранников трехмерного пространства (таблица названий n-гранных многогранников ):
Как выучить геометрические фигуры?
Некоторые ресурсы для детей отлично подходят для изучения фигур и других геометрических фигур, например здесь (ссылка)
Какие многоугольники обладают осевой симметрией?
Все правильные многоугольники имеют по крайней мере одну осевую симметрию.
Правильный многоугольник с таким количеством осей симметрии, сколько у него сторон.
Оси симметрии проходят через центр многоугольника и центр каждой стороны или каждой вершины / угла.
Какие многоугольники имеют центральную симметрию?
Все правильные многоугольники с четным номером стороны имеют центральную симметрию (центр многоугольника ). Многоугольники с нечетным числом сторон не имеют центральной симметрии.
Что такое многогранник?
Многогранник – это обобщение многоугольника / многогранника на все измерения.
Задайте новый вопрос
Исходный код
dCode сохраняет за собой право собственности на исходный код онлайн-инструмента «Имя геометрических фигур». За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / бесплатно), любого алгоритма, апплета или фрагмента «Имя геометрических фигур» (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любой другой » Имя функции геометрических фигур (вычислить, преобразовать, решить, расшифровать / зашифровать, расшифровать / зашифровать, декодировать / закодировать, перевести), написанное на любом информационном языке (Python, Java, PHP, C #, Javascript, Matlab и т. Д.)), и никакая загрузка данных, скрипт, копипаст или доступ к API для «Имя геометрических фигур» не будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.
Нужна помощь?
Пожалуйста, посетите наше сообщество dCode Discord для получения помощи!
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!
Вопросы / Комментарии
Сводка
Похожие страницы
Поддержка
Форум / Справка
Ключевые слова
многоугольник, многогранники, многогранник, геометрия, евклидово, форма, префикс, геометрический, сторона, грань, форма, 2d, 3d, имя, список
Ссылки

Источник: https: // www.dcode.fr/geometric-shapes
© 2021 dCode – Идеальный «инструментарий» для решения любых игр / загадок / геокэшинга / CTF. .