Название геометрических форм: Картинки названия геометрических фигур (100 фото) • Прикольные картинки и позитив

Названия геометрических фигур . Математика для мам и пап: Домашка без мучений

Правильные геометрические фигуры – треугольники, квадраты, пятиугольники и т. д. – фигурируют в математике со времен древних греков. Этим объясняются их названия (по крайней мере, варианты названий), семь из которых происходят непосредственно от греческих названий чисел:

Однако – наверное для того, чтобы всех нас запутать, – название правильной четырехсторонней фигуры, четырехугольника, пришло из латыни (quadratus), тогда как 9– и 11-угольники встречаются так редко, что трудно найти человека, который знал бы, как они называются (на случай, если вас это интересует, скажем, что эти названия соответственно «нонагон» и «гендекагон»).

Числа в названиях действительно указывают на количество сторон в многоугольнике, а вот «гон» – часть названия, которая произошла от греческого gonu, означающего колено; это слово начали применять в отношении углов, поскольку колено человека тоже образует угол. Фигура называется

правильной, если все ее стороны одинаковой длины, а все углы равны, так что вот это, к примеру, правильный шестиугольник:

С другой стороны, эти два шестиугольника не являются правильными (по крайней мере в строго математическом смысле этого слова):

Фигуры с большим числом сторон, как правило, называют просто многоугольниками, или полигонами, используя приставку поли-, что означает «много».

Игра: «Я вижу… шестиугольник»

Интересные геометрические фигуры можно найти везде: в доме, на улицах, в путешествиях. Некоторые фигуры по-настоящему вездесущи. Оглянитесь вокруг – и в любом помещении вы, вероятно, без труда отыщете несколько прямоугольников и пару окружностей. С остальными фигурами сложнее. Можно превратить поиск интересных фигур в игру «Я вижу…» и давать за разные фигуры разное количество очков. Во время поездки на машине попросите детей обращать внимание на:

• Дорожные знаки и крыши, которое чаще всего треугольные.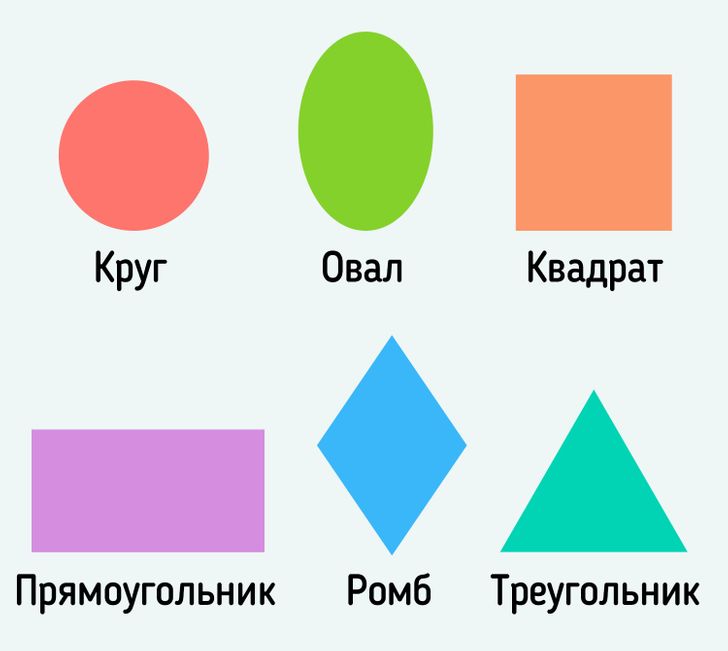

(Вообще треугольники довольно-таки трудно найти в помещениях. В качестве примеров можно привести угловые лестницы.) Стоимость: 1 очко.

• Очень небольшое число предметов или зданий имеет форму пятиугольника (знаменитый американский Пентагон – редкий пример). Можно, однако, отыскать пятиугольники в предметах, если знаешь, на что обращать внимание. На большинстве футбольных мячей пятиугольники имеются (см. «Футбольный мяч и шестиугольники» в этой главе). Разрежьте яблоко поперек – и увидите пять ячеек с семечками, образующих правильный пятиугольник. Разрежьте поперек неочищенный банан – и увидите, что в сечении он образует пятистороннюю фигуру со слегка скругленными сторонами, по существу, пятиугольник. Возьмите узкую полоску бумаги, завяжите ее в узел и осторожно расплющите. Из узла получится правильный пятиугольник (посмотрите через него на свет, чтобы разглядеть получше).

Стоимость: 5 очков.

• Пчелиные соты состоят из правильных шестиугольников, но вряд ли вы каждый день изучаете внутреннее устройство пчелиных сот.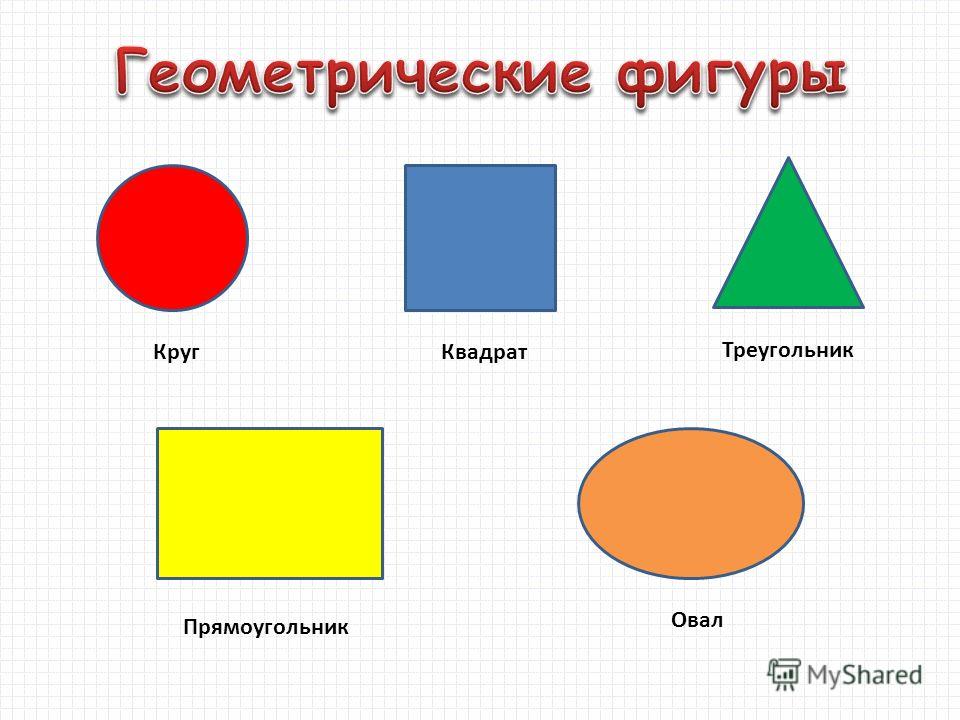 Если взять игральный кубик и наклонить его так, чтобы один из углов указывал прямо на вас, то очертания кубика образуют шестиугольник. Шестиугольники имеются на большинстве футбольных мячей, а у многих стаканов для воды на кухне и в ресторанах шестиугольные донышки. Большинство карандашей представляет собой шестиугольные призмы – как и современные упаковки некоторых мелких конфет-драже. Стоимость: 4 очка.

• Единственными семиугольниками, которые вы встретите в обычной жизни, окажутся, скорее всего, английские монеты по 20 и 50 пенсов, представляющие собой сглаженные семиугольники. (Монеты с нечетным числом сторон имеют постоянный диаметр и потому годятся для использования в автоматах, поскольку машина может распознать края монеты, какой бы стороной она ни легла.)

Стоимость: 10 баллов.

Ширина 50-пенсовой монеты остается одной и той же, какой стороной ни поверни.

• Обычный дорожный знак «СТОП» представляет собой восьмиугольник. Кроме того, восьмиугольники в сочетании с квадратами были популярным элементом дизайна викторианских каминов и выложенных плиткой дорожек, так что в Британии их иногда можно обнаружить на полу какого-нибудь учреждения (или даже жилого дома, если он достаточно стар). Эстрада, на которой играет местный любительский оркестр, скорее всего, имеет восьмиугольную форму (в принципе она может оказаться шестиугольной, но такие увидишь редко. В церквях, да и в других важных зданиях, нередко имеются пространства восьмиугольной формы – такие строения легко возводить, потому что восьмиугольник – это просто квадрат со срезанными углами. Дома стоит обратить внимание на форму всевозможных косметических тюбиков и коробочек; вероятно, среди этих предметов найдется что-нибудь восьмиугольное.

Стоимость: 5 баллов.

• Фигуры, у которых сторон больше восьми, встречают чрезвычайно редко. Может быть, вам удастся обнаружить их в граненом стакане или в форме какого-нибудь здания, а иногда также в иностранных монетах: канадская монета номиналом в доллар, известная как «луни», – редкий пример гендекагона (это, если вы помните, 11-угольник), а австралийские 50 центов и старый британский (еще до введения десятичной денежной системы) трехпенсовик – додекагоны (12-угольники).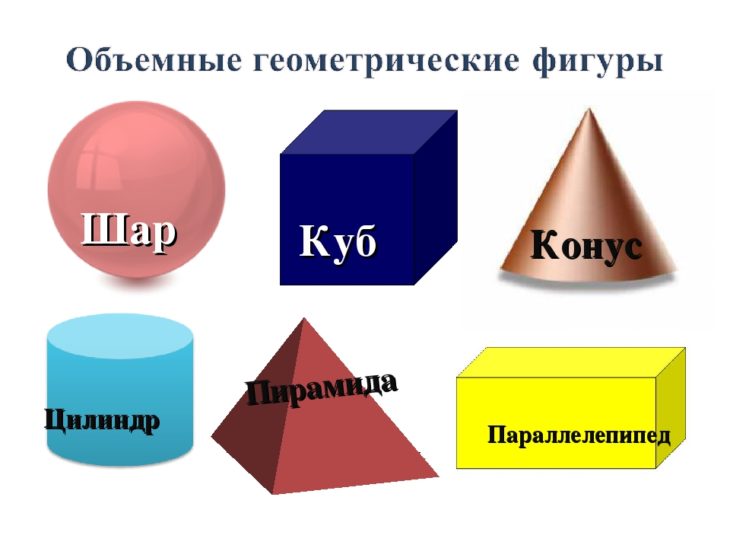 А на ярмарочной площади мы обнаружили настоящий 16-угольник в основании карусели. Одна из причин редкой встречаемости этих геометрических фигур заключается в том, что их форма настолько приближается к окружности, что проще сделать вещь круглой, чем устраивать канитель с многочисленными прямыми сторонами.

Стоимость: 20 баллов.

Плоские и объемные геометрические фигуры. Геометрические фигуры

Фигура – это произвольное множество точек на плоскости. Точка, прямая, отрезок, луч, треугольник, круг, квадрат и так далее – всё это примеры геометрических фигур.

Точка – основное понятие геометрии, это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса.

Линия – это множество точек, последовательно расположенных друг за другом. У линии измеряют только длину. Ширины и толщины она не имеет.

Прямая линия – это линия, которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны.

Луч – это часть прямой линии, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону.

Отрезок

– это часть прямой линии, ограниченная двумя точками. Отрезок имеет начало и конец, поэтому можно измерить его длину.

Кривая линия – это плавно изгибающаяся линия, которая определяется расположением составляющих её точек.

Ломаная линия – это фигура, которая состоит из отрезков, последовательно соединенных своими концами.

Вершины ломаной – это

1. точка, с которой начинается ломанная,
2. точки, в которых соединяются отрезки, образующие ломаную,
3. точка, которой заканчивается ломанная.

Звенья ломаной – это отрезки, из которых состоит ломаная. Количество звеньев ломаной всегда на 1 меньше, чем количество вершин ломаной.

Незамкнутая линия – это линия, концы которой не соединены вместе.

Замкнутая линия – это линия, концы которой соединены вместе.

Многоугольник – это замкнутая ломанная линия. Вершины ломаной называются вершинами многоугольника, а отрезки – сторонами многоугольника.

Геометрия – это раздел математики, в котором изучаются формы и их свойства.

Геометрия, которая изучается в школе, называется евклидовой, по имени древнегреческого учёного Евклида (III век до н. э.).

Изучение геометрии начинается с планиметрии. Планиметрия – это раздел геометрии, в котором изучаются фигуры, все части которых находятся в одной плоскости.

Геометрические фигуры

В окружающем нас мире существует множество материальных предметов разных форм и размеров: жилые дома, детали машин, книги, украшения, игрушки и т. д.

В геометрии вместо слова предмет говорят геометрическая фигура. Геометрическая фигура (или кратко: фигура ) – это мысленный образ реального предмета, в котором сохраняются только форма и размеры, и только они принимаются во внимание.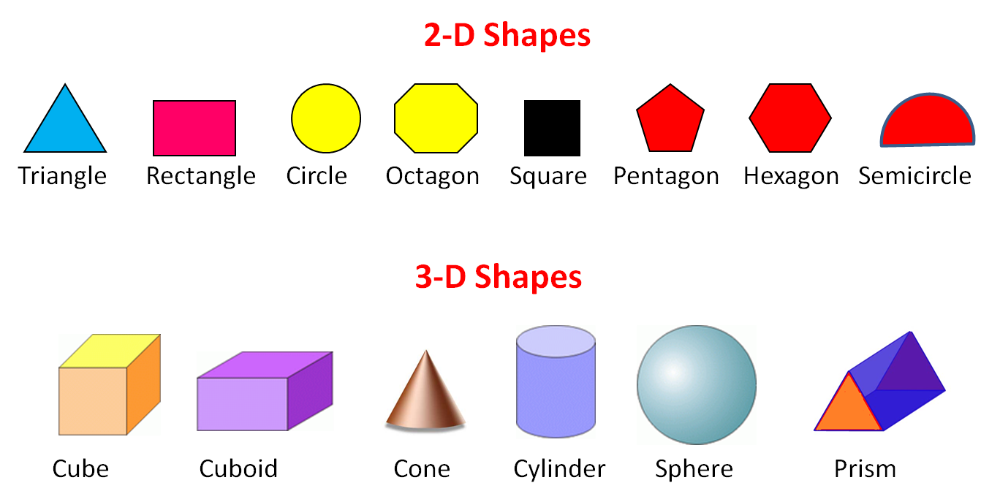

Геометрические фигуры разделяют на плоские и пространственные . В планиметрии рассматриваются только плоские фигуры. Плоской геометрической фигурой называется такая, все точки которой лежат на одной плоскости. Представление о такой фигуре даёт любой рисунок, сделанный на листе бумаги.

Геометрические фигуры бывают весьма разнообразны, например, треугольник, квадрат, окружность и др.:

Часть любой геометрической фигуры (кроме точки), также является геометрической фигурой. Объединение нескольких геометрических фигур, тоже будет являться геометрической фигурой. На рисунке ниже левая фигура состоит из квадрата и четырёх треугольников, а правая фигура состоит из окружности и частей окружности.

В сегодняшней статье я хотела бы рассказать о том, как легко и увлекательно можно изучать геометрические фигуры с малышом, и зачем вообще в столь раннем возрасте грузить ребенка геометрией. Какие игры будут интересны малышу от 1 года, и какие материалы вам понадобятся для занятий – обо всем этом, читайте в статье.

Кроме этого, здесь вы найдете несколько полезных материалов для скачивания.

Зачем изучать геометрические фигуры с малышом?

Геометрические формы встречаются нам повсюду, их можно разглядеть в большинстве окружающих нас предметов: мяч круглый, стол прямоугольный и т.д. Анализируя сходство окружающих предметов с геометрическими фигурами, ребенок замечательно тренирует ассоциативное и пространственное мышление.

1. Изучение геометрических фигур полезно для общего развития малыша, расширения его знаний об окружающем мире. Если знакомить ребенка с формами в раннем возрасте, в школе ему придется гораздо проще.

На умении отличать геометрические фигуры основано множество интересных развивающих игр. Это конструирование, игры с , мозаикой, математическим планшетом, и т.п. Поэтому изучение форм в столь раннем возрасте будет способствовать дальнейшему успешному развитию ребенка.

Итак, игры для изучения и закрепления знаний о геометрических фигурах :

1. Называем геометрические фигуры всегда и везде

Если во время игр или чтения книг вам встречается какая-либо фигура, обязательно обращайте на нее внимание малыша и называйте ее («Посмотри, мячик похож на круг, а кубик – на квадрат»). Даже если вам кажется, что ребенок еще вряд ли запомнит названия фигур, все равно произносите их, и они обязательно отложатся у него в голове. Делать это можно уже до года. Поначалу указывайте только на основные фигуры (квадрат, круг, треугольник), затем, когда поймете, что малыш их усвоил, начинайте изучать и другие фигуры.

2. Играем в геометрическое лото

Для первых занятий с малышом лучше использовать лото, где всего 3-4 фигуры. Когда малыш хорошо освоит такую игру, постепенно усложняйте поставленную задачу. Также полезно на первое время все фигуры на игровом поле сделать одного цвета и размера. В этом случае ребенок будет ориентироваться только на один признак – форму, другие же характеристики не будут ни отвлекать, ни подсказывать ему.

Накладывать на игровое поле можно как карточки с изображением фигур, так и объемные фигуры. Хорошо с этой целью подойдут блоки Дьенеша (Ozon , KoroBoom ), фигурки от сортера, рамки-вкладыша.

Ну и самый нехлопотный вариант — это приобрести готовое лото с геометрическими фигурами .

3. Играем с сортером

Примерно в возрасте 1 года ребенок начинает замечать, что выбранную им фигурку сортера (Озон , Лабиринт , My-shop ) можно протолкнуть далеко не в каждое отверстие. Поэтому во время игры необходимо акцентировать на этом внимание: «Так, вот у нас круг – сюда он не подходит, сюда не подходит, а куда же подходит?». Поначалу повернуть фигуру под правильным углом малышу может быть тяжеловато, но это не страшно, это вопрос практики. Главное, не забывайте вовремя увлекательного процесса «проталкивания» все время произносить названия фигур, и ребенок незаметно их все запомнит.

Важно! При выборе сортера обратите внимание на то, чтобы там были представлены все основные геометрические фигуры, а не только сердечки и полумесяцы.

4. Играем с рамкой-вкладышем

Понадобится такая рамка-вкладыш , на которой представлены все основные фигуры. По своей сути игра аналогична сортеру.

Вот еще одна интересная игра на распознавание форм – «» (Лабиринт , My-shop ). Несмотря на то, что возраст на ней указан 3-5 лет, она будет интересна ребенку 2-х лет и даже чуть раньше.

9. Учим формы по карточкам Домана

На самом деле, я считаю, что этот метод изучения форм самый эффективный. Если вы занимаетесь по , ребенок очень быстро запомнит все фигуры, а вы потратите на это минимум усилий. Однако нужно заметить, что для того, чтобы знания, полученные по карточкам Домана, отложились у малыша в голове, их нужно закреплять посредством других игр (см. выше). Иначе ребенок быстро забудет все, что вы ему показывали. Поэтому я рекомендую начинать смотреть карточки Домана с геометрическими фигурами примерно в возрасте 1 года, так как в это время малышу становятся интересны сортеры, рамки-вкладыши, рисование, аппликация и т. п. И, изучив формы по картинкам, он сможет использовать полученные знания в этих играх. Кстати, карточки “Геометрические фигуры” можно , а купить ЗДЕСЬ .

О нашем опыте изучения фигур по карточкам Домана можно почитать .

10. Смотрим развивающие мультфильмы

Ну и, конечно, не помешает просмотр мультфильмов на тему «Геометрические фигуры», сейчас на просторах интернета их можно найти немало. Вот некоторые из них:

Вместо заключения

Очень часто процесс обучения ребенка геометрическим фигурам (да и не только фигурам) воспринимается родителями исключительно как постоянное экзаменирование ребенка, т.е. они пару раз показывают ребенку, например, квадрат, а в дальнейшем же обучение сводится к вопросу «Скажи, какая это фигура?». Такой подход крайне неправильный. Во-первых, потому что как и любой человек, ребенок не слишком любит, когда ему устраивают проверку знаний, и это только отбивает у него охоту заниматься. Во-вторых, прежде чем о чем-то спрашивать малыша, ему нужно очень много раз это объяснить и показать!

Поэтому постарайтесь сводить проверочные вопросы к минимуму. Просто повторяйте и повторяйте изучаемую информацию, будь то названия фигур или чего-то еще. Делайте это во время игр и бесед с малышом. А то, что ребенок все усвоил, вы вскоре и сами увидите без лишних проверок.

Цели урока :

• Познавательная : создать условия для ознакомления с понятиями плоские и объёмные геометрические фигуры, расширить представление о видах объёмных фигур, научить определять вид фигуры, сравнивать фигуры.
• Коммуникативная : создать условия для формирования умения работать в парах, группах; воспитание доброжелательного отношения друг к другу; воспитывать у учащихся взаимопомощь, взаимовыручку.
• Регулятивная : создать условия для формирования планировать учебную задачу, выстраивать последовательность необходимых операций, корректировать свою деятельность.
• Личностная : создать условия для развития вычислительных навыков, логического мышления, интереса к математике, формирования познавательных интересов, интеллектуальных способностей учащихся, самостоятельность в приобретении новых знаний и практических умений.

Планируемые результаты:

личностные:

• формирование познавательных интересов, интеллектуальных способностей учащихся; формирование ценностных отношений друг к другу;
  самостоятельность в приобретении новых знаний и практических умений;
• формирование умений воспринимать, перерабатывать полученную информацию, выделять основное содержание.

метапредметные:

• овладение навыками самостоятельного приобретения новых знаний;
• организация учебной деятельности, планирования;
• развитие теоретического мышления на основе формирования умений устанавливать факты.

предметные:

• усвоить понятия плоские и объёмные фигуры, научиться сравнивать фигуры, находить плоские и объёмные фигуры в окружающей действительности, научиться работать с развёрткой.

УУД общенаучные :

• поиск и выделение необходимой информации;
• применение методов информационного поиска, осознанное и произвольное построение речевого высказывания в устной форме.

УУД личностные :

• оценивать свои и чужие поступки;
• проявление доверия, внимательности, доброжелательности;
• умение работать в паре;
• выражать положительное отношение к процессу познания.

Оборудование : учебник, интерактивная доска, смайлики, модели фигур, развёртки фигур, светофоры индивидуальные, прямоугольники -средства обратной связи, Толковый словарь.

Тип урока : изучение нового материала.

Методы : словесные, исследовательские, наглядные, практические.

Формы работы : фронтальная, групповая, парная, индивидуальная.

1. Организация начала урока.

Утром солнышко взошло.
Новый день нам принесло.
Сильными и добрыми
Новый день встречаем мы.
Вот мои руки, я раскрываю
Их навстречу солнцу.
Вот мои ноги, они твердо
Стоят на земле и ведут
Меня верной дорогой.
Вот моя душа, я раскрываю
Её навстречу людям.
Наступи, новый день!
Здравствуй, новый день!

2. Актуализация знаний.

Создадим хорошее настроение. Улыбнитесь мне и друг другу, садитесь!

Чтобы дойти до цели, надо прежде всего идти.

Перед вами высказывание, прочитайте. Что означает это высказывание?

(Чтобы чего-то добиться, нужно что-то делать)

И действительно, ребята, попадающим в цель может стать только тот, кто настраивает себя на собранность и организованность своих действий. И вот я надеюсь, что мы с вами на уроке достигнем своей цели.

Начнем наш путь к достижению цели сегодняшнего урока.

3. Подготовительная работа.

Посмотрите на экран. Что вы видите? (Геометрические фигуры)

Назовите эти фигуры.

Какое задание, вы можете предложить своим одноклассникам? (разделите фигуры на группы)

У вас на партах лежат карточки с этими фигурами. Выполните это задание в парах.

По какому признаку вы разделили эти фигуры?

• Плоские и объемные фигуры
• По основаниям объемных фигур

С какими фигурами мы уже работали? Что учились находить у них? Какие фигуры встречаются нам на геометрии впервые?

Какая же тема нашего урока? (Учитель добавляет слова на доске: объёмные, на доске появляется тема урока: Объёмные геометрические фигуры. )

Чему мы должны научиться на уроке?

4. «Открытие» нового знания в практической исследовательской работе.

(Учитель показывает куб и квадрат.)

Чем они похожи?

Можно ли сказать, что это одно и тоже?

Чем же отличается куб от квадрата?

Давайте проведём опыт. (Ученики получают индивидуальные фигуры – куб и квадрат.)

Попробуем приложить квадрат к плоской поверхности порты. Что видим? Он весь (целиком) лёг на поверхность парты? Вплотную?

! Как назовём фигуру, которую можно целиком расположить на одной плоской поверхности? (Плоской фигурой.)

Можно ли куб полностью (весь) прижать к парте? Проверим.

Можно ли назвать куб плоской фигурой? Почему? Есть ли пространство между рукой и партой?

! Значит, что мы можем сказать о кубе? (Занимает определённое пространство, является объёмной фигурой.)

ВЫВОДЫ: Чем же отличаются плоские и объёмные фигуры? (Учитель вывешивает на доске выводы. )

• Можно целиком расположить на одной плоской поверхности.

ОБЪЁМНЫЕ

• занимают определённое пространство,
• возвышаются над плоской поверхностью.

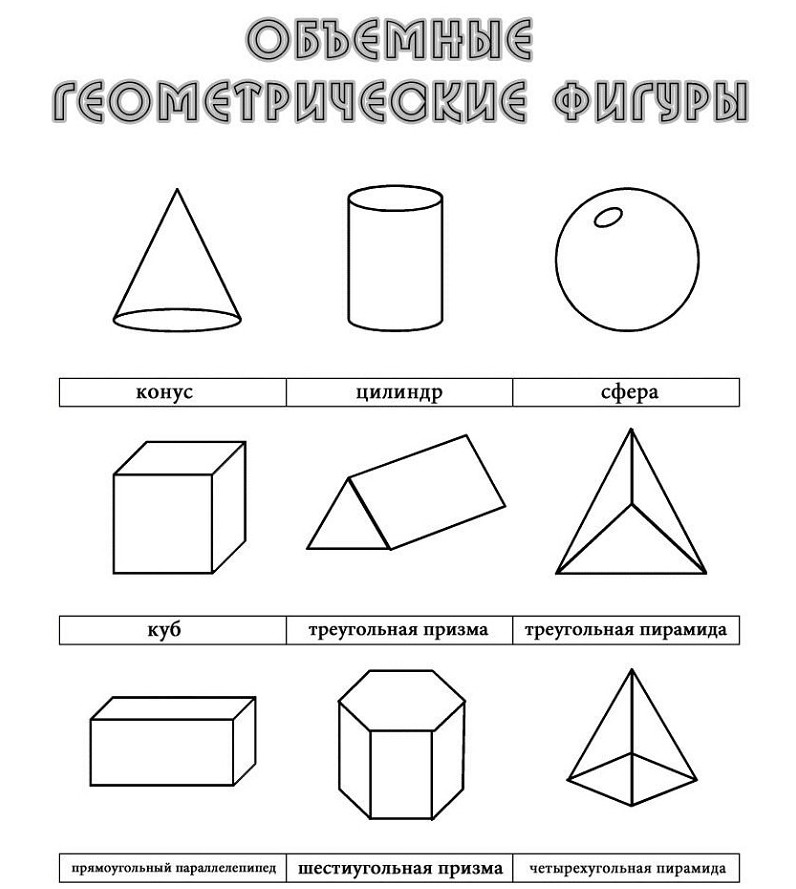
Объёмные фигуры: пирамида, куб, цилиндр, конус, шар, параллелепипед.

4. Открытие новых знаний.

1. Назовите фигуры, изображенные на рисунке.

Какую форму имеют основания этих фигур?

Какие еще формы можно увидеть на поверхности куба и призмы?

2. Фигуры и линии на поверхности объемных фигур имеют свои названия.

Предложите свои названия.

Боковые стороны, образующие плоскую фигуру называются гранями. А боковые линии – рёбра. Углы многоугольников – вершины. Это элементы объемных фигур.

Ребята, а как вы думаете, как называются такие объемные фигуры, у которых много граней? Многогранники.

Работа с тетрадями: чтение нового материала

Соотнесение реальных объектов и объёмных тел.

А теперь подберите для каждого предмета ту объёмную фигуру, на которую он похож.

Коробка – параллелепипед.

• Яблоко – шар.
• Пирамидка – пирамида.
• Банка – цилиндр.
• Горшок из-под цветка – конус.
• Колпачок – конус.
• Ваза – цилиндр.
• Мяч – шар.

5. Физминутка.

1. Представьте себе большой шар, погладьте его со всех сторон. Он большой, гладкий.

(Ученики «обхватывают» руками и гладят воображаемый шар.)

А теперь представьте себе конус, дотроньтесь до его вершины. Конус растёт вверх, вот он уже выше вас. Допрыгните до его вершины.

Представьте, что вы внутри цилиндра, похлопайте по его верхнему основанию, потопайте по нижнему, а теперь руками по боковой поверхности.

Цилиндр стал маленькой подарочной коробочкой. Представьте, что вы сюрприз, который находится в этой коробочке. Я нажимаю кнопку и… сюрприз выскакивает из коробочки!

6. Групповая работа :

(Каждая группа получает одну из фигур: куб, пирамиду, параллелепипед.Полученную фигуру дети изучают, выводы записывают в подготовленную учителем карточку . )
Группа 1. (Для изучения параллелепипеда)

Группа 2. (Для изучения пирамиды)

Группа 3. (Для изучения куба)

7. Решение кроссворда

8. Итог урока. Рефлексия деятельности.

Решение кроссворда в презентации

Что нового вы для себя сегодня открыли?

Все геометрические фигуры можно разделить на объёмные и плоские.

А я узнал названия объёмных фигур

Геометрические фигуры представляют собой комплекс точек, линий, тел или поверхностей. Эти элементы могут располагаться как на плоскости, так и в пространстве, формируя конечное количество прямых.

Термин «фигура» подразумевает под собой несколько множеств точек. Они должны располагаться на одной или нескольких плоскостях и одновременно ограничиваться конкретным числом оконченных линий.

Основными геометрическими фигурами считаются точка и прямая. Они располагаются на плоскости. Кроме них, среди простых фигур выделяют луч, ломаную линию и отрезок.

Точка

Это одна из главных фигур геометрии. Она очень маленькая, но ее всегда используют для построения различных форм на плоскости. Точка – это основная фигура для абсолютно всех построений, даже самой высокой сложности. В геометрии ее принято обозначать буквой латинской алфавита, к примеру, A, B, K, L.

С точки зрения математики точка – это абстрактный пространственный объект, не обладающий такими характеристиками, как площадь, объем, но при этом остающийся фундаментальным понятием в геометрии. Этот нульмерный объект просто не имеет определения.

Прямая

Это фигура полностью размещается в одной плоскости. У прямой нет конкретного математического определения, так как она состоит из огромного количества точек, располагающихся на одной бесконечной линии, у которой нет предела и границ.

Существует еще и отрезок. Это тоже прямая, но она начинается и заканчивается с точки, а значит, имеет геометрические ограничения.

Также линия может превратиться в направленный луч. Такое происходит, когда прямая начинается с точки, но четкого окончания не имеет. Если же поставить точку посредине линии, то она разобьется на два луча (дополнительных), причем противоположно направленных друг к другу.

Несколько отрезков, которые последовательно соединяются друг с другом концами в общей точке и располагаются не на одной прямой, принято называть ломаной линией.

Угол

Геометрические фигуры, названия которых мы рассмотрели выше, считают ключевыми элементами, использующимися при построении более сложных моделей.

Угол – это конструкция, состоящая из вершины и двух лучей, которые выходят из нее. То есть стороны этой фигуры соединяются в одной точке.

Плоскость

Рассмотрим еще одно первичное понятие. Плоскость – это фигура, у которой нет ни конца, ни начала, равно как и прямой, и точки. Во время рассмотрения этого геометрического элемента во внимание берется лишь его часть, ограниченная контурами ломаной замкнутой линии.

Любую гладкую ограниченную поверхность можно считать плоскостью. Это может быть гладильная доска, лист бумаги или даже дверь.

Четырехугольники

Параллелограмм – это геометрическая фигура, противоположные стороны которой параллельны друг другу попарно. Среди частных видов этой конструкции выделяют ромб, прямоугольник и квадрат.

Прямоугольник – это параллелограмм, у которого все стороны соприкасаются под прямым углом.

Квадрат – это четырехугольник с равными сторонами и углами.

Ромб – это фигура, у которой все грани равны. При этом углы могут быть совершенно разными, но попарно. Каждый квадрат считается ромбом. Но в противоположном направлении это правило действует не всегда. Далеко не каждый ромб является квадратом.

Трапеция

Геометрические фигуры бывают совершенно разными и причудливыми. Каждая из них имеет своеобразную форму и свойства.

Трапеция – это фигура, которая чем-то схожа с четырехугольником. Она имеет две параллельные противоположные стороны и при этом считается криволинейной.

Круг

Эта геометрическая фигура подразумевает расположение на одной плоскости точек, равноудаленных от ее центра. При этом заданный ненулевой отрезок принято называть радиусом.

Треугольник

Это простая геометрическая фигура, которая очень часто встречается и изучается.

Треугольник считается подвидом многоугольника, расположенным на одной плоскости и ограниченным тремя гранями и тремя точками соприкосновения. Эти элементы попарно соединены между собой.

Многоугольник

Вершинами многоугольников называют точки, соединяющие отрезки. А последние, в свою очередь, принято считать сторонами.

Объемные геометрические фигуры

• призма;
• сфера;
• конус;
• цилиндр;
• пирамида;

Эти тела имеют нечто общее. Все они ограничиваются замкнутой поверхностью, внутри которой находится множество точек.

Объемные тела изучают не только в геометрии, но и в кристаллографии.

Любопытные факты

Наверняка вам будет интересно ознакомиться с информацией, предоставленной ниже.

• Геометрия сформировалась как наука еще в давние века. Это явление принято связывать с развитием искусства и разнообразных ремесел. А названия геометрических фигур свидетельствуют об использовании принципов определения подобия и схожести.
• В переводе с древнегреческого термин «трапеция» обозначает столик для трапезы.
• Если вы возьмете различные фигуры, периметр которых будет одинаковым, то наибольшая площадь гарантированно будет у круга.
• В переводе с греческого языка термин «конус» обозначает сосновую шишку.
• Существует известная картина Каземира Малевича, которая начиная с прошлого века притягивает к себе взгляды многих живописцев. Работа «Черный квадрат» всегда была мистической и загадочной. Геометрическая фигура на белом полотне восхищает и поражает одновременно.

Существует большое количество геометрических фигур. Все они отличаются параметрами, а порой даже удивляют формами.

Изучение геометрических фигур на английском языке

Названия геометрических фигур на английском языке для малышей

Небольшой набор слов на английском с транскрипцией на тему «геометрические фигуры». Данный набор слов используется не только для определения геометрических терминов, но и при описании формы различных предметов или описания движений. Например, описание траектории движения мыши при выделении рисунка, будет звучать примерно так: Select this tool and then use the mouse to frame the image with a rectangle.

Большинство детей знают имена основных двумерных форм, когда идут в школу. Квадраты, треугольники, круги, овалы легко нарисовать и распознать. Когда дети становятся старше, они могут различить больше отличий между формами и могут изучить точный перевод для самых разнообразных геометрических объектов и форм, с которыми сталкиваются в жизни. Ниже представлен список общих и более редких геометрических фигур, таких как куб, конус, цилиндр, сфера и многих других.

Геометрические фигуры на английском языке

• sphere[sfıə] — сфера
• octagon[‘ɔktəgən] — восьмиугольник
• rhombus[‘rɔmbəs] — ромб
• rectangle[‘rek, tæŋgl] — прямоугольник
• parallelepiped[, pærəle’lepıped] — параллелепипед
• square[skweə] — Квадрат
• quadrilateral[, kwɔdrı’lætərəl] — четырехугольник
• cone[kəun] — конус
• hexagon[‘heksəgən] — шестиугольник
• cylinder [‘sılındə] — цилиндр
• hendecagon[hen’dekəgən] — одиннадцатиугольник
• pyramid[‘pırəmıd] — пирамида
• triangle[‘traıæŋgl] — треугольник
• helix[‘hi:lıks] — спираль
• trapezium[trə’pi:zɪəm] — трапеция
• hemisphere[‘hemısfıə] — полушарие
• parallelogram[, pærə’leləugræm] — параллелограмм
• heptagon[‘heptəgən] — семиугольник
• pentagon[‘pentəgən] — пятиугольник
• torus[‘tɔ:rəs] — тор
• octahedron[‘ɔktə’hedrən] — октаэдр
• dodecagon[dəu’dekəgən] — двенадцатиугольник
• decagon[‘dekəgən] — десятиугольник
• cube[kju:b] — куб

Песенка для освоения геометрических фигур на английском языке

I have two sweets in my bag

White triangle and a yellow square

I have two sweets in my bag

White triangle and a yellow square

I have two sweets in my hand

I have two sweets in my bag

Yellow circle and an orange square

I have two sweets in my bag

Yellow circle and an orange square

I have two sweets in my mouth

Геометрические фигуры на английском языке для детей Видео

Английский язык для детей в игровой форме. Геометрические фигуры

Геометрические фигуры — это одна из первых тем для изучения английского языка с малышами. Английский для детей лучше всего изучать в игровой форме, и, так как, тема «геометрические фигуры» для этого хорошо подходит, изучение геометрии деткам очень нравится 🙂

Изучению геометрии у нас посвящена целая рубрика, поэтому следите за обновлениями — статьи будут добавляться.

В этой же статье, я поделюсь одним, чрезвычайно интересным и увлекательным творческим проектом, под названием «Пластилиновая геометрия», в котором мы начнем изучать геометрические фигуры на английском языке.

Введение материала

Послушайте песенку и изучите геометрические фигуры.

Создание проекта

Нарисуйте различные формы на листе бумаги и подпишите их.

Список слов с русифицированной транскрипцией:

• Circle [сёкл] круг
• Square [скwээ] квадрат
• Rectangle [рэктэньгл] прямоугольник
• Ova [оувл] овал
• Triangle [трайэньгл] треугольник
• Diamond [дайэмэнд] ромб
• Star [ста:] звезда

Покажите ребёнку, как делать фигуры, сделав первую фигуру самостоятельно. Сначала скатайте шарики и разложите по углам.

Теперь возьмите зубочистки и сделайте стороны фигуры.

Лучше начинать с квадрата или равностороннего треугольника, потому что все стороны у этих фигур равны и вы будете использовать целые зубочистки.

Когда же дойдёт очередь до фигур с разными сторонами (ромб, прямоугольник), не спешите показывать ребенку, как именно можно сделать такие фигуры. Дайте малышу время подумать: пусть он сам догадается, что зубочистку необходимо сломать, предварительно измерив сторону.

Несмотря на то, что мы изучаем английский язык с нашими детьми в игровой форме, нет никакой необходимости лишать малыша его суверенных прав на раннее развитие — пусть подумает. Пусть ощутит сладкую радость победы, если сможет догадаться 🙂

Теперь спросите ребёнка, как можно сделать круг и овал. Есть ли прямые стороны у этих фигур? И, понадобятся ли, в этом случае, зубочистки?

На фото вы видите два варианта, но на самом деле их очень много. Подождите, пока ребёнок предложит свой вариант, а потом предложите свой… Молодым — везде у нас дорога… Помните о его суверенных правах!

Совет:

Когда вы будете лепить фигуры, проговаривайте их название по-английски. Поместите фигуры на несколько дней на видное место, время от времени подходите к ним, и повторяйте их названия.

Дополнительные идеи:

Если вы изучали тему «Эмоции и Чувства», то самое время закрепить знания. Как говорится, «Повторение – мать учения».

Нарисуйте на фигурах забавные рожицы, отражающие различные чувства и назовите их. Например:

«a sad oval» — грустный овал

«a happy square» — счастливый квадрат

«a sleepy diamond» — сонный ромб

Полный список слов на тему «Эмоции и чувства» находится здесь

Изучаем Геометрические фигуры на английском языке

Геометрические фигуры – еще одна из популярных тем в занятиях с малышами.

В данной статье я поделюсь планом тематического урока по теме

“Геометрические фигуры на английском языке”

Итак, какие же фигуры на английском языке мы сегодня выучим?

triangle (треугольник), square (квадрат), circle (круг), rectangle (прямоугольник), diamond (ромб), star (звезда), etc.

Вырежьте из картона данные геометрические фигуры и продемонстрируйте их ребенку по очереди, четко произнося их названия на английском языке. Вам поможет вот такое стихотворение из школы Кулен (Cullen’s ABCs)

I’m a baby triangle – three sides have I!
I’m mama circle – round like a pie!
I’m papa square – my sides are four!
I’m an uncle rectangle – shaped like a door!

2. Закрепление материала.

Спрячьте ваши картонные фигуры в разных местах в комнате и даже у себя в одежде.

Вытаскивайте эти фигуры из самых неожиданных мест.

Строя самые невероятные рожицы, задавайте ребенку вопросы на английском языке :

— Is it a triangle or a square?
— Is it a circle or a star?
Пусть он отвечает.

Можно угаданные фигуры прикреплять на заготовленном листе бумаге или ватмане в таком порядке, чтобы получился какой-то рисунок (аппликация). Например, из квадрата и треугольника можно сделать дом, а из прямоугольника и ромба – дерево, из круга солнце и т. д.

В конце спросите ребенка, что он видит на картинке:

— What is in the picture?
— A house, a tree and a sun!

3. Использование материала.

Игра “сортер” (рамки и вкладыши).

Если у вас нет готового сортера или рамок, их можно быстро изготовить самим.

На листе бумаги или картона по трафарету нарисуйте фигуры. Аккуратно вырежете фигуры так, чтобы картон не повредился. Получилась рамка и вкладыш.

Теперь ребенок должен правильно разложить вырезанные фигурки в рамки, при этом называя геометрические фигуры на английском языке.

4. Аппликация “что какой формы?”

Старое доброе занятие еще из детского сада.

Вы спрашиваете, какой формы у нас тот или иной предмет, а потом вырезаете его и наклеиваете на бумагу.

Либо же наоборот.

Вы спрашиваете, что бывает круглым , квадратным, прямоугольным и так далее, а ребенок отвечает:

— What is round?
— The ball is round
— What shape is the cat’s ear?
— It is triangular

Здесь вам понадобятся следующие прилагательные, характеризующие геометрические фигуры на английском языке:

Circle – round
Oval-oval
Triangle – triangular
Rectangle – rectangular
Square-square
Star – star-shaped
Diamond – diamond-shaped

А еще можно найти формы с помощью вот такой песенки:

Shapes are everywhere you look,
Everywhere you look there are shapes.
Shapes are found in everything,
Everything is made out of shapes.

Common! Let’s find shapes!

I see a circle! I see a square!
I see a triangle up there! X2
Common kids!
Let’s draw shapes in the air.
Square! Triangle! Circle! (рисуем фигуры в воздухе)
Faster!

Ну и напоследок еще песенка для освоения геометрических фигур на английском языке

I have two sweets in my bag
White triangle and a yellow square
I have two sweets in my bag
White triangle and a yellow square
I have two sweets in my hand
Mmmm

I have two sweets in my bag
Yellow circle and an orange square
I have two sweets in my bag
Yellow circle and an orange square
I have two sweets in my mouth
Mmmm

По словам песенки видно, что в них можно менять цвета и форму конфет.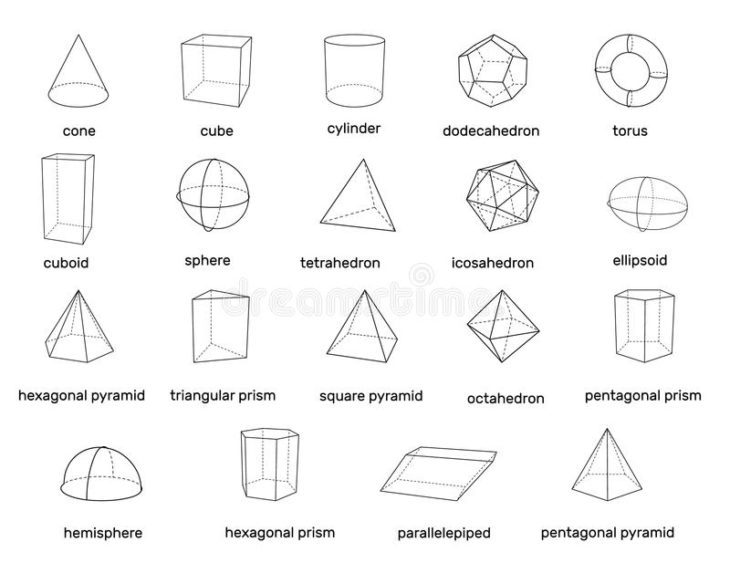

Заготовьте несколько видов конфет разной формы и цвета и смело встраивайте в песню. При этом перекладывайте их из сумки в руку из руки в рот. И не забывайте мычать от наслаждения. Ммм

Вот так играя можно выучить с малышами геометрические фигуры на английском языке.
Вкусных вам игр!

Источники: http://englishfull.ru/deti/geometricheskie-figury.html, http://anglijskij-dlja-detej.ru/temy/geometricheskie-figury/anglijskij-yazyk-dlya-detej-v-igrovoj-forme-geometricheskie-figury, http://blog.bilingual-child.ru/izuchaem-geometricheskie-figury-na-anglijskom-yazyke/

Список, определение, типы геометрических фигур

Содержание

Математические геометрические фигуры — это математические фигуры, представляющие формы повседневных предметов. Геометрия форм — это изучение объектов с границами, углами и поверхностями. Изучаются как двумерные, так и трехмерные формы.

Точно так же формы классифицируются в соответствии с их регулярностью или однородностью. Правильная форма обычно симметрична, например, квадрат или круг. Асимметричные формы – это неправильные формы. Их также называют органическими формами или формами произвольной формы. Деревья, например, имеют неправильную форму.

Двумерные фигуры в планиметрии — это плоские формы и замкнутые фигуры, такие как круги, квадраты, прямоугольники, ромбы и т. д. Трехмерные фигуры в объемной геометрии — это куб, прямоугольный параллелепипед, конус, сфера и цилиндр. Некоторые из этих форм знакомы нам в повседневной жизни. Например, книги имеют прямоугольную форму, очки — цилиндрическую, дорожные конусы — коническую и т. д. В этой статье вы узнаете о различных геометрических фигурах и их определениях.

Геометрические фигуры: определение

Объекты могут быть представлены геометрическими фигурами, которые являются геометрическими фигурами. Трехмерные формы бывают иногда двухмерными, а иногда двумерными. Двумерные фигуры лежат только на осях x и y, а трехмерные фигуры лежат на осях x, y и z.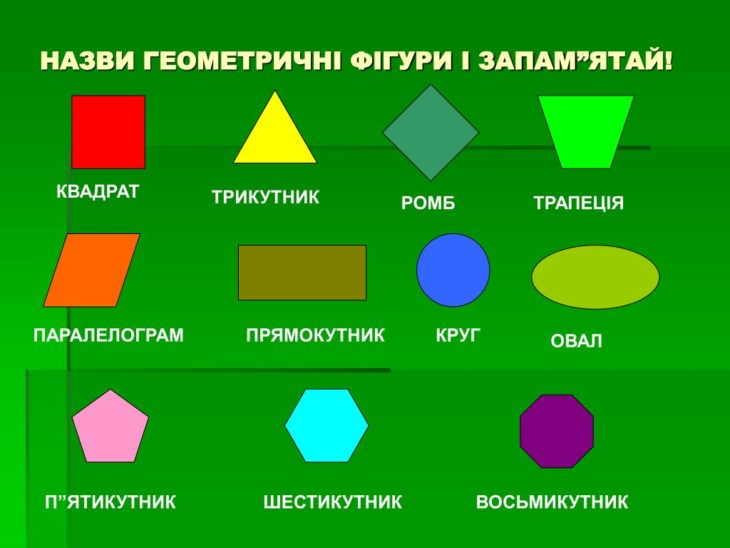 Это высота объекта по оси Z. В геометрии определяются различные формы. Мы уже обсуждали это во введении.

Геометрические фигуры

Любую из этих фигур можно нарисовать или создать, начав с линии, сегмента линии или кривой. Мы можем создавать различные типы фигур и форм, располагая эти линии по-разному, например, треугольник, фигуру, состоящую из соединенных сегментов трех линий, пятиугольник, состоящий из пяти линий, и так далее. Но не все фигуры являются полными фигурами.

Типы геометрических фигур

Открытой геометрической формой считается объект или форма, оба конца которой не соединены. Объекты или фигуры, соединенные с обоих концов, определяются как замкнутые геометрические фигуры. Замкнутые геометрические фигуры бывают двух типов:

1. Геометрические фигуры в двух измерениях: Это двумерные фигуры только с осями x и y. Это плоские двухмерные структуры. Примеры включают треугольники, квадраты, прямоугольники и т. д.
2. Трехмерные геометрические фигуры: Это трехмерные фигуры, имеющие оси x, y и z. Это высота объекта по оси Z. Это твердые трехмерные конструкции. Например, это могут быть кубики или параллелепипеды.

Чтобы нарисовать любую из этих фигур, мы должны начать с линии, кривой или отрезка. Таким образом, исходя из количества и расположения линий, мы можем составлять различные фигуры и фигуры, например, соединяя отрезки из четырех линий, получается прямоугольник. При соединении трехлинейных отрезков получается треугольник и т. д.

Список двухмерных геометрических фигур

• Треугольник
• Круг
• Полукруг
• Квадрат
• Прямоугольник
• Параллелограмм
• Ромб
• Трапеция
• Воздушный змей
• Многоугольники (пятиугольник, шестиугольник, восьмиугольник, нонагон, десятиугольник и т. д.)

Двухмерные геометрические фигуры

Давайте рассмотрим пять основных двухмерных геометрических фигур.

Треугольник: Треугольник — это замкнутая двумерная геометрическая фигура с тремя сторонами. Например, кусок пиццы в форме начос.

Квадрат: Квадрат — это двумерная геометрическая фигура с четырьмя равными сторонами. Например, формы шахматной доски и карромной доски.

Прямоугольник: Прямоугольник — это четырехсторонняя двумерная геометрическая фигура, у которой противоположные стороны равны по длине. Экраны компьютеров являются примерами прямоугольников.

Окружность: Окружность – это замкнутая двумерная геометрическая фигура, имеющая круглую форму. Круги не имеют углов или линий. Например, основа для пиццы, колесо.

Овал: Овал похож на круг, но имеет слегка вытянутую форму. Овал не имеет прямых линий и углов. Например, число ноль (0).

Список трехмерных геометрических фигур

• Сфера
• Куб
• Прямоугольный
• Конус
• Цилиндр

Трехмерные геометрические фигуры

Давайте узнаем о шести основных трехмерных геометрических фигурах.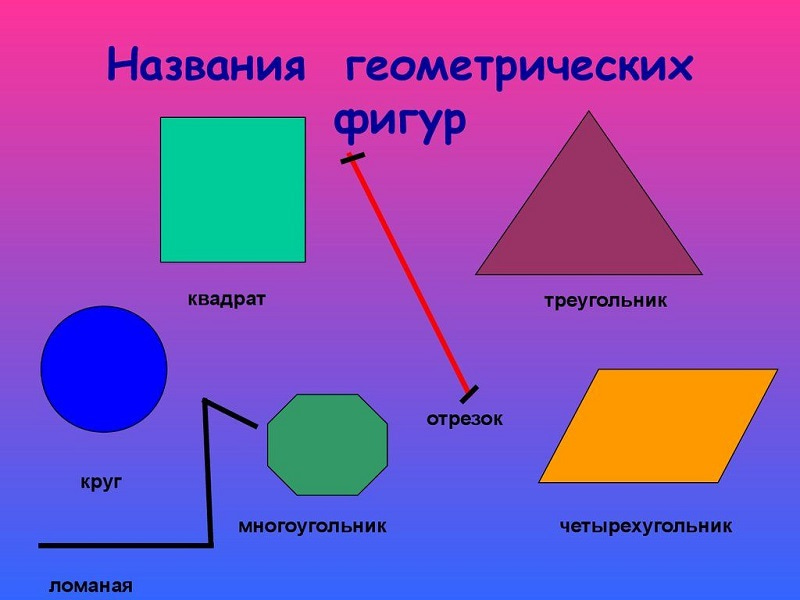

Куб: Куб — это трехмерная геометрическая фигура, состоящая из шести квадратов с равными сторонами. Например, игральные кости Людо, кубик Рубика

.

Кубоид: Прямоугольник — это трехмерная геометрическая фигура, состоящая из шести прямоугольников. Например, книга, коробка

Цилиндр: В качестве геометрической формы цилиндр имеет два одинаковых круглых плоских конца, которые являются твердыми в трех измерениях. Например, банка прохладительного напитка или лапша для бассейна.

Сфера: Сфера — это твердая трехмерная геометрическая фигура, похожая на шар. Например, футбол, баскетбол и т. д.

Полушарие: Полушарие — это геометрическая фигура, которая составляет половину сферы. Например, тарелки для супа.

Конус: Конусы представляют собой геометрические трехмерные фигуры, которые имеют плоское круглое основание и закругленную вершину, называемую вершиной. Например, рожки от мороженого и клоунские шляпы.

Примеры двухмерных геометрических фигур в повседневной жизни

Двумерные фигуры — это плоские фигуры с шириной и высотой, но без глубины. Прямоугольная форма, квадрат, треугольник или круг — это тип двумерной геометрической формы. Ознакомьтесь со списком различных 2D-геометрических фигур, а также описаниями и примерами того, как их обнаружить.

Все это плоские формы без глубины. Поэтому можно еще определить форму этих предметов по картинке. Это не относится к трехмерным формам.

Примеры кругов

Окружность — это закругленная форма с одинаковым радиусом от фиксированной точки в центре. Некоторые примеры реальных кругов:

• Пироги с пиццей
• Файлы cookie
• Колеса велосипеда
• Циферблаты
• Обеденные тарелки

Квадрат Примеры

Четыре равные прямые стороны с четырьмя прямыми углами образуют квадрат.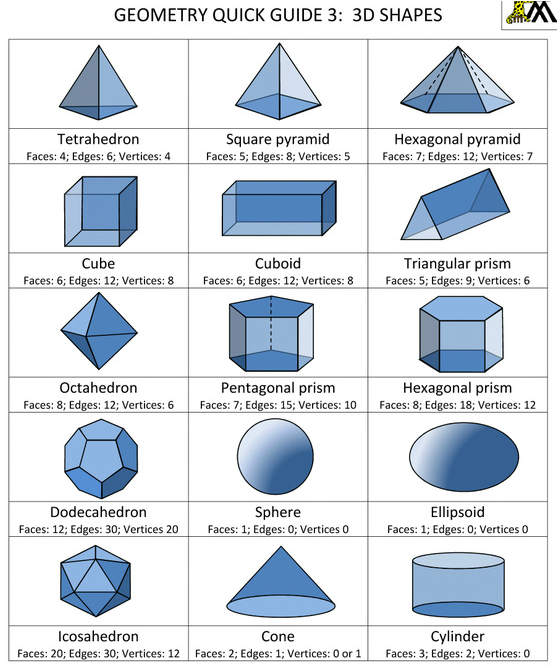 Некоторые реальные примеры квадратов:

• Квадратные резиновые штампы
• Квадратная плитка на полу
• Квадратные бумажные салфетки
• Шахматные доски
• Клавиши виртуальной клавиатуры

Примеры треугольников

Треугольник – это трехсторонняя фигура с прямыми сторонами. Существует много различных видов треугольников, в зависимости от их угла. Вот несколько примеров треугольников в реальной жизни:

• Ломтики пиццы
• Нарезанный по диагонали сэндвич
• Чипсы из лепешек
• Лодка плывет
• Знак «уступи дорогу» говорит водителям уступить дорогу

Примеры прямоугольников

Прямоугольники имеют четыре прямые стороны с четырьмя прямыми углами, как и квадраты. Однако две стороны короче других. Посмотрите примеры вроде этих:

• Обложки книг глав
• Смартфоны
• Рамки для картин
• Долларовая банкнота
• Сэндвичи с мороженым

Пентагон Примеры

Пятиугольник равной длины — пятиугольник. Четырехугольники имеют четыре стороны, и они более распространены, чем восьмиугольники, но все же встречаются в природе. Примеры пятиугольников включают:

• Здание Пентагона
• Футбольные мячи с черными секциями
• Бейсбольная тарелка
• Дорожные знаки перехода

Примеры шестигранников

Шестиугольники образуются путем добавления одной стороны к пятиугольнику. У них шесть прямых сторон одинаковой длины. Взгляните на эти примеры:

• Кристаллы льда
• Снежинки
• Ячейки улья
• Контур металлической гайки
• Белые секции на футбольных мячах

Примеры восьмиугольников

Форма восьмиугольника состоит из восьми прямых сторон, как правило, одинаковой длины. У вас больше шансов найти их в повседневной жизни, чем вы думаете. Вот несколько примеров:

• Знаки остановки
• Открытые зонтики
• Кольцо UFC
• Покерные столы

Примеры трапеций

Трапеция – это четырехсторонняя фигура, у которой только одна пара параллельных сторон. Вы можете найти трапеции в следующих примерах:

• Фермы на мостах
• Некоторые стороны сумки
• Недоеденный кусок пиццы
• Музыкальные цимбалы

Примеры трехмерных геометрических фигур

Трехмерная фигура имеет длину, ширину и толщину, в отличие от двумерных фигур. Формы в трех измерениях включают пирамиды, сферы и кубы. Взгляните на эти повседневные трехмерные геометрические фигуры.

Конечно, некоторые из этих форм взаимозаменяемы. Конечно, есть круглые сумки и другие типы сумок, которые не обязательно являются параллелограммами. Есть также много других двухмерных и трехмерных геометрических фигур, не включенных в этот список.

Примеры сфер

Сфера — твердая фигура круглой формы. Кроме того, каждая точка на сфере равноудалена от радиуса в центре. Они обладают объемом, но не глубиной, в отличие от кругов. Вот несколько примеров:

• Баскетбольные мячи
• Планеты
• Апельсины
• Мрамор
• Теннисные мячи

Примеры кубов

Все шесть граней куба являются квадратами. Они создают глубину, когда расположены в виде трехмерного куба, также называемого квадратной призмой. Куб может включать в себя следующее:

• Шестигранный кубик
• Кубики сахара
• Квадратные строительные блоки
• Кубики Рубикса
• Квадратные упаковочные коробки

Примеры конусов

Основание конуса сужается к одной точке. Конус можно найти во многих повседневных предметах, таких как:

• Дорожные конусы
• Вафельные рожки для мороженого
• Праздничные шляпы
• Рождественские елки
• Воронки

Примеры цилиндров

Цилиндры представляют собой объемные фигуры с параллельными сторонами и круглым поперечным сечением. Их можно найти в реальных жизненных ситуациях, подобных этим:

• Тубы из картона для бумажных полотенец
• Трубы прямые
• Бокалы для питья
• Тубы для гигиенической помады
• Банки

Примеры эллипсоидов

Сплющенный с обеих сторон эллипсоид не является идеально круглым. Сфероид, также известный как эллипсоид, создает овальную форму в 3D. Примеры эллипсоидов включают:

• Мячи
• Яйца
• Некоторые спутники Сатурна (Мимас, Энцелад, Тефия)

Примеры прямоугольных призм

Абстрактный объект, состоящий из двух противоположностей одинаковой формы и соединенных параллельными прямыми сторонами, представляет собой прямоугольную призму. Эти призмы имеют четыре прямоугольника и два квадрата. Прямоугольные призмы встречаются в следующих примерах:

• Масляные палочки
• Кирпичи
• Камеры
• Коробки для хлопьев
• Прямоугольные упаковочные коробки

Треугольная призма

Треугольные призмы напоминают прямоугольные призмы, за исключением того, что их квадратные грани представляют собой треугольники, что делает их трехсторонними призмами. Реальные примеры треугольных призм включают:

• Палатки
• Дольки арбуза
• Сырные дольки
• Кусочки торта

Примеры пирамид

Пирамида — это трехмерная фигура, стороны которой сходятся в одной точке и которая имеет одну плоскую сторону. Возможна любая трехсторонняя форма, включая треугольники (треугольные пирамиды), квадраты (квадратные пирамиды) и пятиугольники (пятиугольные пирамиды). Некоторые примеры:

• Великая пирамида Гизы
• Крыша дома
• Некоторые отдельно стоящие терки для сыра
• Стеклянная пирамида Лурв

Часто задаваемые вопросы

Каковы примеры геометрических фигур?

К геометрическим фигурам относятся квадраты, прямоугольники, треугольники, круги, овалы, пятиугольники и т. д.

Что такое геометрическая фигура?

Математические фигуры — это геометрические фигуры. Они регулярны и совершенны. Точки, линии и углы составляют математическую фигуру. Идеальный круг является исключением из этого правила, поскольку он не имеет прямых линий или точек. К другим геометрическим формам относятся квадраты, прямоугольники, треугольники, параллелограммы, шестиугольники и т. д.

Сколько существует типов геометрических фигур?

Существует два типа геометрических фигур: двухмерные (2D) и трехмерные (3D). Первый можно нарисовать, обращаясь к осям X и Y, а последний также включает ось Z. 2D-формы и фигуры в основном состоят из точек и соединительных линий.

Какие 5 основных форм?

К основным формам относятся квадрат, прямоугольник, круг, овал, треугольник и ромб, которые чаще всего встречаются вашему ребенку.

Каковы основные геометрические понятия?

• Точки, линии, плоскости и углы
• Доказательство
• Перпендикулярно и параллельно
• Треугольники
• Подобие
• Прямоугольные треугольники и тригонометрия
• Четырехугольники
• Преобразования

Как называются 2 типа фигур?

Геометрические фигуры и фигуры произвольной формы — это два типа фигур. Геометрические фигуры — это точные формы, которые можно описать математическими формулами. К геометрическим формам относятся круги, квадраты, треугольники, овалы, прямоугольники, восьмиугольники, параллелограммы, трапеции, пятиугольники и шестиугольники.

Список геометрических фигур с названиями и чертежами

Плоские геометрические фигуры — это пространства, ограниченные плоскими поверхностями. Эти элементы состоят из прямых и изогнутых линий, соединенных, например, кругом, квадратом или треугольником. Многоугольники — это те типы геометрических фигур, которые ограничены прямыми линиями.

Напротив, сплошные фигуры представляют собой фигуры, представленные в трехмерном пространстве. Эти трехмерные фигуры занимают объем в пространстве. Примером сплошной формы является куб, который представляет собой фигуру с 12 ребрами, восемью вершинами и шестью гранями.

Раздел математики, изучающий геометрические фигуры, называется геометрия.

Таблица названий геометрических фигур

Вот основной список 2D фигур с их названиями, чертеж и краткое описание основных названных правильных геометрических фигур: Круг состоит из одного кругового сегмента. Это круговой сектор, в котором концы соединены. Кроме того, все точки на этой кривой линии находятся на одинаковом расстоянии от центральной точки.

Эллипс

Эллипс представляет собой геометрическую фигуру, образованную изогнутой линией с центрами, называемыми фокусами. Основная характеристика эллипса состоит в том, что сумма расстояния от точки до одного из фокусов с расстоянием от этой же точки до другого из фокусов всегда постоянна.

Треугольник

Треугольник — это простейший многоугольник, который можно представить. Он состоит из трех сторон, трех вершин и трех углов.

В зависимости от углов треугольники бывают трех типов: равнобедренные, равнобедренные и разносторонние.

• Равносторонний треугольник: У него три равные стороны.

• Равнобедренный треугольник: У него только две равные стороны.

• Разносторонний треугольник: Три стороны треугольника различны.

Эта форма очаровательна, потому что все многоугольники можно разбить на треугольники. Поскольку вычислить площадь треугольника несложно, это интересный способ вычисления площади любого многоугольника.

Квадрат

Квадрат представляет собой четырехугольник, образованный четырьмя сторонами равной длины и равными внутренними углами (90 градусов).

Прямоугольник

Прямоугольник представляет собой геометрическую фигуру, образованную четырьмя ребрами. Стороны равны два на два: стороны одинаковой длины параллельны. Как и у квадрата, угол, образованный соприкасающимися сторонами, равен 9.0 градусов.

Алмаз

Ромб – это четырехугольник, у которого все четыре стороны равны, а углы равны два на два.

Ромб

Ромбовидный четырехугольник с двумя парами равных сторон. Его углы также попарно равны.

Трапеция

Трапеция – это многоугольник, четыре стороны которого параллельны двум противоположным сторонам.

Трапеция

Трапеция – это четырехугольник, у которого ни одна из противоположных сторон не параллельна.

Пятиугольник

Пятиугольник — это многоугольник с пятью углами. Правильный пятиугольник – это пятиугольник, у которого все стороны и углы равны.

Шестиугольник

Пятиугольник — это многоугольник с шестью сторонами, углами и вершинами.

Что такое изогнутые формы?

Изогнутые геометрические фигуры — это фигуры, которые можно изобразить на плоской поверхности, хотя бы одна из сторон которой представляет собой кривую линию.

Изогнутые формы — это круг и эллипс в списке фигур выше. В обоих случаях мы имеем дело с замкнутыми кривыми линиями.

Что такое многоугольник?

В геометрии многоугольники представляют собой двумерные геометрические фигуры, состоящие из конечной последовательности последовательных прямых отрезков, охватывающих область на плоскости. Эти отрезки называются сторонами, а точки пересечения — вершинами. Многоугольник является двумерным случаем многогранника.

Сегменты называются ребрами или сторонами, а концы сторон называются вершинами или углами многоугольника.

Многоугольник является пересеченным, если пересекаются хотя бы две непоследовательные стороны, и простым, если пересечение двух сторон пусто или сводится к вершине для двух последовательных сторон. Сумма углов простого многоугольника (выпуклого или нет) зависит только от количества его вершин.

В случае простых многоугольников многоугольник и его внутреннюю часть часто путают, называя поверхность, ограниченную замкнутой многоугольной линией, многоугольником.

Что такое четырехугольники?

Четырехугольник — плоская фигура, многоугольник с четырьмя углами и четырьмя сторонами. Сумма углов каждого четырехугольника равна 360°.

В приведенном выше списке геометрических фигур квадрат, прямоугольник, ромб, ромбоид, трапеция и трапеция являются примерами четырехугольников.

Что такое параллелограммы?

Частным случаем четырехугольников являются параллелограммы: Параллелограмм представляет собой плоскую фигуру, образованную пересечением двух пар параллельных прямых. Противоположные стороны этих геометрических фигур параллельны два на два; то есть два ребра параллельны, а два других также параллельны друг другу. Из приведенного выше списка квадрат, ромб, прямоугольник и ромбоид являются примерами параллелограммов.

Двухмерные геометрические фигуры | Типы, свойства, примеры

Что такое двумерная геометрическая фигура?

Форма, имеющая длину и ширину, но не имеющая глубины. Называется двумерной формой. Короче говоря, все двумерные формы плоские и не могут удерживаться физически. Геометрические фигуры — это математические модели объектов реального мира со схожими геометрическими свойствами.

На изображении ниже показаны некоторые двумерные фигуры, которые мы используем в геометрии.

Какие существуют типы двухмерных геометрических фигур?

Мы можем классифицировать двумерную фигуру в зависимости от количества сторон, того, как она сформирована, а также по ее длине и ширине.

Окружность

Окружность — это замкнутая 2D-форма, точки которой всегда находятся на одинаковом расстоянии от центральной точки. Круг состоит из изогнутой линии. Следовательно, у него нет ни сторон, ни ребер.

Студенты иногда путают круг с многоугольником. Однако круг не является многоугольником и не будет многоугольником, поскольку круг образован одной изогнутой линией, а не отрезками прямых. Таким образом, он не соответствует критериям полигона.

Многоугольник

Многоугольник — это замкнутая плоская фигура на плоскости с прямыми сторонами. Он состоит из отрезков, каждый из которых пересекается ровно с двумя другими отрезками. Многоугольники именуются и определяются по количеству сторон, например, треугольники, четырехугольники, пятиугольники, шестиугольники и т. д.

Как мы можем классифицировать двумерную геометрическую фигуру?

Мы можем классифицировать 2D-форму как правильную и неправильную форму. При классификации 2D-формы нам необходимо учитывать меру длин каждой стороны и ее внутренних углов.

Правильные формы

Если все стороны 2D-объекта имеют одинаковую длину и все внутренние углы одинаковы, он называется правильным.

Неправильные формы

Если все стороны 2D-объекта имеют разную длину и все углы разной величины, объект считается неправильным.

На изображении ниже показано, чем правильная 2D-форма отличается от неправильной 2D-формы.

Каковы свойства двумерных геометрических фигур?

Двухмерные фигуры нельзя удерживать физически, но их можно нарисовать на листе бумаги. Мы можем видеть вокруг себя разные объекты, напоминающие круг, треугольник, квадрат, прямоугольник и т. д. Давайте углубимся в различение характеристик и свойств двухмерной геометрической фигуры.

Круг

Круг не имеет длины и ширины. Однако мы по-прежнему рассматриваем его как двумерную форму, потому что она не имеет глубины.

Мы можем сказать, что двумерная фигура является кругом, если это замкнутая, полностью закругленная форма.

Частями круга являются центральная точка, радиус, диаметр и длина окружности.

• Центральная точка — это точка, расположенная в центре окружности.
• Расстояние вокруг окружности можно определить как ее длину окружности . Предположим, что нить длиной 15 см согнута в виде круга. Длина окружности равна длине проволоки, которая в данном случае равна 15 см.
• Радиус — это расстояние от центра круга до любой точки окружности.
• Диаметр окружности — это самый длинный возможный отрезок, который можно нарисовать в окружности. Это отрезок, проходящий через окружность через ее центр. Мера диаметра в два раза больше меры радиуса.
• Все окружности имеют угол в 360 градусов.

Многоугольник

Свойства и виды многоугольников различаются в зависимости от количества их сторон. Некоторые распространенные типы многоугольников: треугольник, квадрат, прямоугольник, пятиугольник, шестиугольник и т. д. Давайте рассмотрим некоторые из многоугольников и определим их характеристики.

Треугольник

Треугольник — это замкнутая двумерная фигура с тремя прямыми сторонами. Треугольник образуется при пересечении трех прямых. Каждый треугольник имеет три стороны, три вершины и три угла.

Любой трехсторонний многоугольник называется треугольником. Название частей треугольника различается в зависимости от того, какой у вас треугольник. В общем случае мы называем их сторонами и вершинами.

• Стороны треугольника — это расстояние отрезка прямой от одной вершины до другой.
• Вершина — это точка, где сходятся две стороны.
• Сумма трех внутренних углов любого треугольника равна 180°.

Треугольники можно классифицировать двумя способами – по углам и сторонам. На изображении ниже показаны некоторые образцы треугольников.

• Равносторонний треугольник — это треугольник, у которого все стороны и все углы равны. Следовательно, мера трех внутренних углов равна 60°.
• Прямоугольный треугольник — это треугольник, в котором один угол равен 90°.
• Разносторонний треугольник — это треугольник, у которого все три стороны имеют разную меру. Так как все стороны имеют разную длину, то и меры трех углов также различны.

Четырехугольники

Четырехугольник — это многоугольник, у которого ровно четыре стороны. Сумма внутренних углов четырехугольника равна 360°. Существуют различные виды четырехугольников, такие как квадрат, прямоугольник, ромб и воздушный змей. Четырехугольники можно классифицировать по их сторонам, углам, диагоналям и вершинам.

Квадрат – это двухмерный четырехугольник, все стороны которого равны по длине, а каждый угол прямой.

• Все четыре стороны квадрата равны.
• Противоположные стороны квадрата параллельны.
• Все внутренние углы квадрата равны и равны 90°.

Прямоугольник – это двумерный четырехугольник, у которого противоположные стороны параллельны и равны.

• Все внутренние углы прямоугольника равны ровно 90°.
• Противоположные стороны равны.
• Противоположные стороны параллельны друг другу.

На изображении ниже показано больше образцов четырехугольника.

• Параллелограмм – это четырехугольник, у которого обе пары противоположных сторон параллельны и равны. Частными случаями параллелограмма являются квадрат, прямоугольник, ромб и ромбоид.
• Трапеция — это четырехугольник геометрической формы, имеющий только одну пару параллельных сторон. Параллельные стороны трапеции называются основаниями, а две другие стороны – катетами.
• Ромб – это четырехугольник, четыре стороны которого равны по размеру, а две противоположные стороны параллельны друг другу. Внутренний угол ромба не равен 90°.
• Воздушный змей — это четырехугольник, две пары смежных сторон которого равны.

Пятиугольник

Пятиугольник — это двумерный замкнутый многоугольник с пятью сторонами и пятью внутренними углами. Сумма внутренних углов любого пятиугольника равна 540°. Пятиугольники могут быть классифицированы как правильные пятиугольники или неправильные пятиугольники.

Правильный пятиугольник – пятиугольник, у которого все стороны и внутренние углы равны.

• Все стороны правильного пятиугольника равны по длине.
• Все внутренние углы правильного пятиугольника равны 108°.
• Все внешние углы правильного пятиугольника равны 72°.

Неправильный пятиугольник – это двумерный пятиугольник, у которого все стороны и углы разной величины.

• Все пять сторон неправильного пятиугольника имеют разную длину.
• Все пять внутренних углов не равны.

Пятиугольники также можно классифицировать в зависимости от того, направлены вершины наружу или внутрь. Давайте посмотрим на изображение выпуклого и вогнутого пятиугольника.

• Выпуклый пятиугольник — это пятиугольник, у которого все пять вершин направлены наружу.
• Пятиугольник называется вогнутым пятиугольником, если хотя бы одна его вершина направлена ​​внутрь.

В таблице ниже показано больше видов правильных и неправильных многоугольников.

NAME	NUMBER OF SIDES
Hexagon	6	The sum of all interior angles of a hexagon is 720°. Правильный шестиугольник – это шестиугольник, у которого все стороны и внутренние углы равны. Размер каждого внутреннего угла правильного шестиугольника равен 120°. С другой стороны, неправильный шестиугольник не имеет равных сторон и углов.
Семиугольник	7	Сумма всех внутренних углов семиугольника равна 900°. Говорят, что это правильный семиугольник, если все семь сторон и семь углов равны. Неправильный шестиугольник не имеет равных сторон и углов.
Восьмиугольник	8	Восьмиугольник — это восьмиугольник, сумма всех внутренних углов которого равна 1080°. В правильном восьмиугольнике все стороны равны, а каждый внутренний угол равен 135°. Если стороны и мера угла восьмиугольника не равны, он называется неправильным восьмиугольником.
Нонагон	9	Многоугольник — это 9-сторонний многоугольник, сумма внутренних углов которого равна 1260°. Если все стороны и внутренние углы девятиугольника равны, то это правильный девятиугольник. Размер каждого внутреннего угла правильного девятиугольника равен 140°. Если стороны и внутренние углы не равны, то это неправильный девятиугольник.
Десятиугольник	10	Десятиугольник — это 10-сторонний многоугольник, сумма всех внутренних углов которого равна 1440°. В правильном десятиугольнике все стороны равны, а размер каждого внутреннего угла равен 144°. Между тем, неправильный десятиугольник — это 10-сторонний многоугольник, у которого нет равных сторон и внутренних углов.

Каковы реальные образцы двумерных геометрических фигур?

Двухмерные геометрические фигуры используются для моделирования объектов реального мира. Студенты иногда рассматривают лист бумаги или пластика как двумерную форму, когда это не так. Несмотря на то, что толщина листа бумаги тонкая, это трехмерный объект.

Давайте рассмотрим несколько примеров двухмерной формы в реальных объектах.

двумерная геометрическая форма	Объект реального мира
Круг	Некоторые объекты реального мира, которые выглядят как круг, — это обручи, колеса, кольца, вентиляторы, часы и т. д. Кроме того, всякий раз, когда мы рисуем солнце или планета, мы также используем круг для ее представления.
Треугольник	Треугольник почти везде можно увидеть, например, на дорожном знаке, чипсах для начо, вешалке и гроте парусника (флаге). Есть также инструмент, названный треугольником, потому что он напоминает треугольник. Более того, треугольники иногда используются при создании пирамид, мостов и зданий.
Квадрат	Некоторые объекты реального мира, напоминающие квадрат, — это шахматные доски, ломтик сыра и бутерброд.
Прямоугольник	Подобно треугольнику, многие вещи вокруг нас напоминают прямоугольник. Большинство столешниц созданы в форме прямоугольника. Некоторыми другими примерами прямоугольника являются экраны ноутбуков, книги, листа бумаги. Даже стены, двери и окна в нашем доме напоминают прямоугольник.

В чем разница между 2D-формой и 3D-объектом?

Как следует из названия, 2D- и 3D-формы различаются по количеству измерений, которые они имеют. Двумерная форма имеет размеры длины и ширины, а трехмерная — это твердая форма, имеющая размеры длины, ширины и глубины (или высоты).

Давайте посмотрим на таблицу ниже, чтобы сравнить характеристики 2D и 3D формы.

	Двумерная форма	Трехмерная форма
Определение	Двумерная форма — это плоская форма, имеющая только два измерения — длину и ширину. Двумерную форму нельзя удерживать физически.	Трехмерная фигура — это объемная фигура, имеющая три измерения: длину, ширину и глубину (высоту).
Размеры	длина x ширина	длина x ширина x высота
Математические оси	оси x и y	оси x, y и z
	Мы можем вычислить только площадь и периметр 2D-фигуры.	Для любого трехмерного объекта мы можем вычислить площадь поверхности, боковую площадь, площадь поперечного сечения и объем.
Примеры	Круг, треугольник, квадрат, прямоугольник, параллелограмм, трапеция, пятиугольник, шестиугольник, семиугольник и т. д.	Сфера, треугольная призма, куб, прямоугольная призма, пирамида, цилиндр, конус и т. д.

Какое значение имеют двумерные геометрические фигуры?

Помимо обучения нашего ребенка рисованию кругов, треугольников или квадратов на листе бумаги, большинство детей играли с игрушками различной формы. В раннем возрасте дети уже воспринимают различные формы, даже если не знают их названий. Конкретным качествам каждой формы, таким как количество сторон или размеры углов, учат, когда они достигают начальной школы.

В дошкольном возрасте дети много практикуются с фигурами, что помогает им укрепить свое понимание и представление о двухмерных фигурах.