Название геометрических фигур всех: Основные геометрические фигуры 🟢🟨🔺 и их названия
Какие геометрические фигуры. Геометрические фигуры для детей
Геометрия – точная математическая наука, которая занимается изучением пространственных и других подобных отношений и форм. Но ее часто называют «сухой», поскольку она не способна описать форму многих природных объектов, ведь облака – это не сферы, горы – не конусы, а молнии распространяются не по прямым линиям. Многие объекты в природе отличаются сложностью форм в сравнении со стандартной геометрией.
Тем не менее, существует ряд удивительных фигур, которые обычно не изучаются на школьных уроках геометрии, но именно они окружают человека в реальном мире: в природе и архитектуре, головоломках, компьютерных играх и т. д.
Главное свойство этой сложной геометрической фигуры – самоподобие, то есть она состоит из нескольких частей, каждая из которых подобна целому объекту. Именно это свойство отличает фракталы от объектов классической (или, как говорят, евклидовой) геометрии.
При этом сам термин «фрактал» не является математическим и не имеет однозначного определения, поэтому может применяться к объектам, которые являются самоподобными или приближенно самоподобными.
Фрактальные формы как нельзя лучше подходят для описания реального мира и часто встречаются среди природных объектов: снежинок, листьев растений, системы кровеносных сосудов человека и животных.
Это одна из самых необыкновенных трехмерных фигур в геометрии, которую легко сделать в домашних условиях. Для этого достаточно взять бумажную полоску, ширина которой в 5-6 раз меньше ее длины, и, перекрутив один из концов на 180°, склеить их между собой.
Если все сделано правильно, то можно проверить самостоятельно ее удивительные свойства:
- Наличие только одной стороны (без разделения на внутреннюю и внешнюю). Это легко проверить, если попробовать закрасить карандашом одну из ее сторон. Независимо от того, в каком месте и направлении будет начато закрашивание, в результате вся лента будет закрашена одним цветом.
- Непрерывность: если вести ручкой линию вдоль всей поверхности, ее конец соединится с начальной точкой без пересечения границ поверхности.
- Двухмерность (связность): при разрезании ленты Мебиуса вдоль она остается цельной, просто получаются новые фигуры (к примеру, при разрезании надвое получится одно кольцо большего размера).
- Отсутствие ориентированности. Путешествие по такой ленте Мебиуса всегда будет бесконечным, оно приведет к начальной точке пути, только в зеркальном отображении.
Лента Мебиуса широко используется в промышленности и науке (в ленточных конвейерах, матричных принтерах, механизмах для заточки и пр.). Кроме этого существует научная гипотеза, по которой сама Вселенная также представляет собой ленту Мебиуса невероятных размеров.
Полимино
Названия полимино зависят от количества квадратов, из которых они сформированы:
- мономино – 1;
- домино – 2;
- тримино – 3;
- тетрамино – 4 и т. д.
При этом для каждой разновидности существует разное количество типов фигур: у домино 1 тип, у тримино – 3 типа, у гексамино (из 6 квадратов) – 35 типов.
Число различный вариаций зависит от количества используемых квадратов, но при этом еще никому из ученых не удалось найти удивительную формулу, которая будет выражать эту зависимость. Из деталей полимино можно выкладывать как геометрические фигуры, так и изображения людей, животных, предметов. Несмотря на то, что это будут схематичные силуэты, основные признаки и формы предметов делают их вполне узнаваемыми.
Полиамонд
Наряду с полимино, существует еще одна удивительная геометрическая фигура, используемая для составления других фигур – полиамонд. Он представляет собой многоугольник, сформированный из нескольких равносторонних треугольников равного размера.
Название придумал математик Т. О’Бейрн на основании одного из названий ромба в английском языке – диамонд, который можно составить из 2-х равносторонних треугольников. По аналогии, фигуру из 3-х равносторонних треугольников О’Бейрн назвал триамондом, из 4-х – тетриамондом и т. д.
Главным вопросом их существования остается вопрос о возможном количестве полиамондов, которые можно составить из определенного количества треугольников.
Применение полиамондов в реальной жизни также аналогично использованию полимино. Это могут быть разного рода головоломки и логические задачи.
Треугольник Рело
Как ни удивительно звучит, но с помощью дрели можно просверлить квадратное отверстие, а помогает в этом треугольник Рело. Он представляет собой область, образованную посредством пересечения 3 равных окружностей, центры которых являются вершинами правильного треугольника, а радиусы равны его стороне.
Сам треугольник Рело назван по фамилии немецкого ученого-инженера, который первым наиболее детально исследовал его особенности и использовал для своих механизмов на рубеже XIX-XX в. в., хотя его удивительные свойства были известны еще Леонардо да Винчи. Кто бы ни был его первооткрывателем, в современном мире эта фигура нашла широкое применение в виде:
- сверла Уаттса, которое позволяет сверлить отверстия практически идеальной квадратной формы, только с чуть закругленными краями;
- медиатора, необходимого для игры на музыкальных щипковых инструментах;
- кулачковых механизмов, используемых для создания зигзагообразных швов в швейных машинах, а также немецких часах;
- стрельчатых арок, характерных для готического стиля в архитектуре.
Отдельного внимания заслуживают так называемые невозможные фигуры – удивительные оптические иллюзии, которые на первый взгляд кажутся проекцией трехмерного объекта, но при ближайшем рассмотрении становятся заметны необычные соединения элементов. Наиболее популярными из их числа являются:
Трибар, созданный отцом и сыном Лайонелом и Роджером Пенроузами, который представляет собой изображение равностороннего треугольника, но имеет странные закономерности. Стороны, образующие верхнюю часть треугольника кажутся перпендикулярными, но правая и левая грани в нижней части также кажутся перпендикулярными. Если рассматривать каждую часть этого треугольника по отдельности, еще можно признать их существование, но в действительности такая фигура существовать не может, поскольку при ее создании были неправильно соединены правильные элементы.
Бесконечная лестница, авторство которой также принадлежит отцу и сыну Пенроузам, поэтому ее часто называют по их имени – «лестницей Пенроуза», а также «Вечной лестницей».
На первый взгляд, она выглядит как обычная, ведущая вверх или вниз лестница, но при этом человек, шагающий по ней будет непрерывно подниматься (против часовой стрелки) или опускаться (по часовой стрелке). Если визуально путешествовать по такой лестнице, то по окончании «путешествия» взгляд останавливается в точке начала пути. Если бы такая лестница существовала в действительности, по ней пришлось бы подниматься и спускаться бесконечное число раз, что можно сравнить с бесконечным сизифовым трудом.
Невозможный трезубец – удивительный объект, глядя на который невозможно определить, где начинается средний зубец. Он также основан на принципе неправильных соединений, которые могут существовать только в двухмерном, но не трехмерном пространстве. Рассматривая части трезубца по отдельности, с одной стороны видны 3 круглых зуба, с другой стороны – 2 прямоугольных.
Таким образом, части фигуры вступают в своеобразный конфликт: во-первых, происходит смена переднего и заднего плана, во-вторых круглые зубцы в нижней части трансформируются в плоские в верхней.
Тема урока
Геометрические фигуры
Что такое геометрическая фигура
Геометрические фигуры – это совокупность множества точек, линий, поверхностей или тел, которые расположены на поверхности, плоскости или пространстве и формирует конечное количество линий.
Термин «фигура» в какой-то степени формально применяется к множеству точек, но как правило фигурой принято называть такие множества, которые расположенные на плоскости и ограничиваются конечным числом линий.
Точка и прямая – это основные геометрические фигуры, расположенные на плоскости.
К самым простым геометрическим фигурам на плоскости принадлежат – отрезок, луч и ломаная линия.
Что такое геометрия
Геометрия – это такая математическая наука, которая занимается изучением свойств геометрических фигур. Если дословно перевести на русский язык термин «геометрия», то он обозначает «землемерие», так как в стародавние времена основной задачей геометрии, как науки, стало измерение расстояний и площадей на поверхности земли.
Практическое применение геометрии бесценно во все времена и независимо от профессии. Без знаний геометрии не может обойтись ни рабочий, ни инженер, ни архитектор и даже художник.
В геометрии есть такой раздел, который занимается изучением различных фигур на плоскости и называется планиметрия.
Вам уже известно, что фигурой называют произвольное множество точек, находящиеся на плоскости.
К геометрическим фигурам принадлежат: точка, прямая, отрезок, луч, треугольник, квадрат, круг и другие фигуры, которые изучает планиметрия.
Точка
Из выше изученного материала вам уже известно, что точка относится к главным геометрическим фигурам. И хотя это самая малая геометрическая фигура, но она необходима для построения других фигур на плоскости, чертеже или изображении и является основой для всех остальных построений. Ведь построение более сложноватых геометрических фигур складывается из множества точек, характерных для данной фигуры.
В геометрии точки обозначают прописными буквами латинского алфавита, например, такими, как: А, В, С, D ….
А теперь подведем итог, и так, с математической точки зрения, точка является таким абстрактным объектом в пространстве, который не имеет объема, площади, длины и других характеристик, но остается одним из фундаментальных понятий в математике. Точка – это такой нульмерный объект, которые не имеет определения. По определению Евклида, точкой называют то, что невозможно определить.
Прямая
Как и точка, прямая относится к фигурам на плоскости, которая не имеет определения, так как состоит из бесконечного множества точек, находящихся на одной линии, которая не имеет ни начала ни конца. Можно утверждать, что прямая линия бесконечна и не имеет предела.
Если же прямая начинается и заканчивается точкой, то она уже не является прямой и называется отрезком.
Но иногда прямая, с одной стороны имеет точку, а с другой нет. В таком случае прямая превращается в луч.
Если же взять прямую и на ее средине поставить точку, то она разобьет прямую на два противоположно направленных луча.
Данные лучи являются дополнительными.
Если же перед вами несколько отрезков, соединенных между собой так, что конец первого отрезка становиться началом второго, а конец второго отрезка – началом третьего и т. д., и эти отрезки находятся не на одной прямой и при соединении имеют общую точку, то такая цепочка является ломаной линией.
Задание
Какая ломаная линия называется незамкнутой?
Как обозначается прямая?
Как называется ломаная линия, у которой четыре замкнутых звена?
Какое название имеет ломаная линия с тремя замкнутыми звеньями?
Когда конец последнего отрезка ломаной совпадает с началом 1-го отрезка, то такую ломаную линию называют замкнутой. Примером замкнутой ломаной является любой многоугольник.
Плоскость
Как точка и прямая, так и плоскость является первичным понятием, не имеет определения и у нее нельзя увидеть ни начала, ни конца. Поэтому, при рассмотрении плоскости, мы рассматриваем только ту ее часть, которая ограничивается замкнутой ломаной линией.
Таким образом, плоскостью можно считать любую гладкую поверхность. Этой поверхностью может быть лист бумаги или стола.
Угол
Фигура, которая имеет два луча и вершину, называется углом. Место соединения лучей, является вершиной этого угла, а его сторонами считаются лучи, которые этот угол образуют.
Задание:
1. Как в тексте обозначают угол?
2. Какими единицами можно измерить угол?
3. Какие бывают углы?
Параллелограмм
Параллелограмм – это четырехугольник, противолежащие стороны которого попарно параллельны.
Прямоугольник, квадрат и ромб являются частными случаями параллелограмма.
Параллелограмм, имеющий прямые углы равные 90 градусам, является прямоугольником.
Квадрат – это тот же параллелограмм, у него и углы и стороны равны.
Что до определения ромба, то это такая геометрическая фигура, все стороны которого равны.
Кроме того, следует знать, что любой квадрат является ромбом, но не каждый ромб может быть квадратом.
Трапеция
При рассмотрении такой геометрической фигуры, как трапеция, можно сказать, что в частности она, как и четырехугольник имеет одну пару параллельных противолежащих сторон и является криволинейной.
Окружность и круг
Окружность – геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом.
Треугольник
Также к простым геометрическим фигурам принадлежит и уже изучаемый вами треугольник. Это один из видов многоугольников, у которого часть плоскости ограничена тремя точками и тремя отрезками, которые соединяют эти точки попарно. Любой треугольник имеет три вершины и три стороны.
Задание: Какой треугольник называют вырожденным?
Многоугольник
К многоугольникам относятся геометрические фигуры разных форм, у которых замкнутая ломаная линия.
В многоугольнике все точки, которые соединяют отрезки, являются его вершинами.
А отрезки, из которых состоит многоугольник, являются его сторонами.
А известно ли вам, что возникновение геометрии уходит в глубину веков и связано с развитием различных ремесел, культуры, искусства и наблюдением за окружающим миром. Да и название геометрических фигур является тому подтверждением, так как их термины, возникли не просто так, а благодаря своей схожести и подобию.
Ведь термин «трапеция» в переводе с древнегреческого языка от слова «трапезион» обозначает столик, трапеза и другие производные слова.
«Конус» произошел от греческого слова «конос», что в переводе звучит, как сосновая шишка.
«Линия» имеет латинские корни и происходит от слова «линум», в переводе это звучит, как льняная нить.
А знаете ли вы, что если взять геометрические фигуры с одинаковым периметром, то среди них обладателем самой большой площади оказался круг.
Геометрические фигуры – это замкнутые множества точек на плоскости или в пространстве, которые ограничены конечным числом линий.
Они могут быть линейными (1D), плоскими (2D) или пространственными (3D).
Любое тело, имеющее форму, представляет собой совокупность геометрических фигур.
Любую фигуру можно описать математической формулой различной степени сложности. Начиная от простого математического выражения до суммы рядов математических выражений.
Основными математическими параметрами геометрических фигур являются радиусы, длины сторон или граней и углы между ними.
Ниже представлены основные геометрические фигуры, наиболее часто используемые в прикладных расчетах, формулы и ссылки на расчетные программы.
Линейные геометрические фигуры
1. Точка
Точка – это базовый объект измерения. Основной и единственной математической характеристикой точки является её координата.
2. Линия
Линия – это тонкий пространственный объект имеющий конечную длину и представляющий собой цепь связанных друг с другом точек. Основной математической характеристикой линии является длина.
Луч – это тонкий пространственный объект имеющий бесконечную длину и представляющий собой цепь связанных друг с другом точек. Основными математическими характеристиками луча являются координата его начала и направление.
Плоские геометрические фигуры
1. Круг
Круг – это геометрическое место точек на плоскости, расстояние от которых до его центра, не превышает заданного числа, называемого радиусом этого круга. Основной математической характеристикой круга является радиус.
2. Квадрат
Квадрат – это четырёхугольник, у которого все углы и все стороны равны. Основной математической характеристикой квадрата является длина его стороны.
3. Прямоугольник
Прямоугольник – это четырехугольник, у которого все углы равны 90 градусам (прямые). Основными математичскими характеристиками прямоугольника являются длины его сторон.
4. Треугольник
Треугольник – это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки (вершины треугольника), не лежащие на одной прямой.
Основными математическими характеристиками треугольника являются длины сторон и высота.
5. Трапеция
Трапеция – это четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Основными математическими характеристиками трапеции являются длины сторон и высота.
6. Параллелограмм
Параллелограмм – это четырёхугольник, у которого противоположные стороны параллельны. Основными математическими характеристиками параллелограмма являются длины его сторон и высота.
Ромб – это четырехугольник, у которого все стороны, а углы его вершин не равны 90 градусам. Основными математическими характеристиками ромба являются длина его стороны и высота.
8. Эллипс
Эллипс – это замкнутая кривая на плоскости, которая может быть представлена как ортогональная проекция сечения окружности цилиндра на плоскость. Основными математическими характеристиками окружности являются длина его полуосей.
Объемные геометрические фигуры
1.
Шар
Шар – это геометрическое тело, представляющее собой совокупность всех точек пространства, находящихся от его центра на заданном расстоянии. Основной математической характеристикой шара является его радиус.
Сфера – это оболочка геометрического тела, представляющее собой совокупность всех точек пространства, находящихся от его центра на заданном расстоянии. Основной математической характеристикой сферы является её радиус.
Куб – это геометрическое тело, представляющее собой правильный многогранник, каждая грань которого представляет собой квадрат. Основной математической характеристикой куба является длина его ребра.
4. Параллелепипед
Параллелепипед – это геометрическое тело, представляющее собой многогранник, у которого шесть граней и каждая из них прямоугольник. Основными математическими характеристиками параллелепипеда являются длины его ребер.
5. Призма
Призма – это многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани параллелограммами, имеющими общие стороны с этими многоугольниками.
Основными математическими характеристиками призмы являются площадь основания и высота.
Конус – это геометрическая фигура, полученная объединением всех лучей, исходящих из одной вершины конуса и проходящих через плоскую поверхность. Основными математическими характеристиками конуса являются радиус основания и высота.
7. Пирамида
Пирамида – это многогранник, основанием которого является произвольный многоугольник, а боковые грани являются треугольниками, имеющие общую вершину. Основными математическими характеристиками пирамиды являются площадь основания и высота.
8. Цилиндр
Цилиндр – это геометрическая фигура, ограниченная цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. Основными математическими характеристиками цилиндра являются радиус основания и высота.
Быстро выполнить эти простейшие математические операции можно с помощью наших онлайн программ. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлены все геометрические фигуры, которые наиболее часто встречаются в геометрии для представления объекта или его части на плоскости или в пространстве.
Существует бесконечное множество форм. Формой называют внешнее очертание предмета.
Изучение форм можно начинать с самого раннего детства, обращая внимание своего ребенка на окружающий нас мир, который состоит из фигур (тарелка – круглая, телевизор – прямоугольный).
Уже с двух лет малыш должен знать три простые фигуры – круг, квадрат, треугольник. Сначала он их должен просто показывать, когда вы это просите. А в три года уже называть их самостоятельно и отличать круг от овала, квадрат от прямоугольника.
Чем больше упражнений на закрепление форм будет выполнено ребенком, тем больше новых фигур он запомнит.
Будущий первоклашка должен знать все простые геометрические фигуры и уметь составлять из них аппликации.
Что мы называем геометрической фигурой?
Геометрическая фигура – это эталон, с помощью которого можно определить форму предмета или его частей.
Фигуры разделяют на две группы: плоские фигуры, объемные фигуры.
Плоскими фигурами мы назовем те фигуры, которые расположены в одной плоскости. К ним относятся круг, овал, треугольник, четырёхугольник (прямоугольник, квадрат, трапеция, ромб, параллелограмм) и всевозможные многоугольники.
К объемным фигурам относят: сфера, куб, цилиндр, конус, пирамида. Это те фигуры, которые имеют высоту, ширину и глубину.
Следуйте двум простым советам при объяснении геометрических фигур:
- Терпение. То, что нам, взрослым, кажется простым и логичным ребенку покажется просто непонятным.
- Попробуйте рисовать фигуры вместе с ребенком.
- Игра. Начинайте изучать фигуры в игровой форме. Хорошие упражнения для закрепления и изучения плоских форм – аппликации из геометрических фигур. Для объемных – можно использовать готовые покупные игры, а также выбирать аппликации, где можно вырезать и склеивать объемную форму.
Геометрические фигуры представляют собой комплекс точек, линий, тел или поверхностей.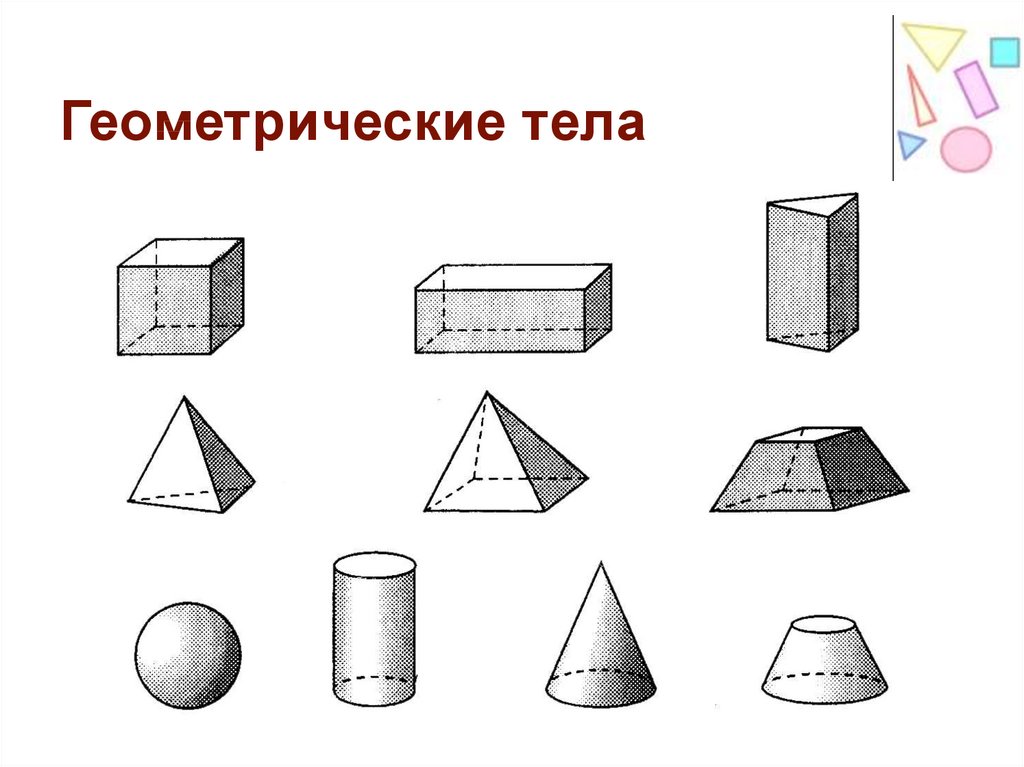
Эти элементы могут располагаться как на плоскости, так и в пространстве, формируя конечное количество прямых.
Термин «фигура» подразумевает под собой несколько множеств точек. Они должны располагаться на одной или нескольких плоскостях и одновременно ограничиваться конкретным числом оконченных линий.
Основными геометрическими фигурами считаются точка и прямая. Они располагаются на плоскости. Кроме них, среди простых фигур выделяют луч, ломаную линию и отрезок.
Точка
Это одна из главных фигур геометрии. Она очень маленькая, но ее всегда используют для построения различных форм на плоскости. Точка – это основная фигура для абсолютно всех построений, даже самой высокой сложности. В геометрии ее принято обозначать буквой латинской алфавита, к примеру, A, B, K, L.
С точки зрения математики точка – это абстрактный пространственный объект, не обладающий такими характеристиками, как площадь, объем, но при этом остающийся фундаментальным понятием в геометрии. Этот нульмерный объект просто не имеет определения.
Прямая
Это фигура полностью размещается в одной плоскости. У прямой нет конкретного математического определения, так как она состоит из огромного количества точек, располагающихся на одной бесконечной линии, у которой нет предела и границ.
Существует еще и отрезок. Это тоже прямая, но она начинается и заканчивается с точки, а значит, имеет геометрические ограничения.
Также линия может превратиться в направленный луч. Такое происходит, когда прямая начинается с точки, но четкого окончания не имеет. Если же поставить точку посредине линии, то она разобьется на два луча (дополнительных), причем противоположно направленных друг к другу.
Несколько отрезков, которые последовательно соединяются друг с другом концами в общей точке и располагаются не на одной прямой, принято называть ломаной линией.
Угол
Геометрические фигуры, названия которых мы рассмотрели выше, считают ключевыми элементами, использующимися при построении более сложных моделей.
Угол – это конструкция, состоящая из вершины и двух лучей, которые выходят из нее.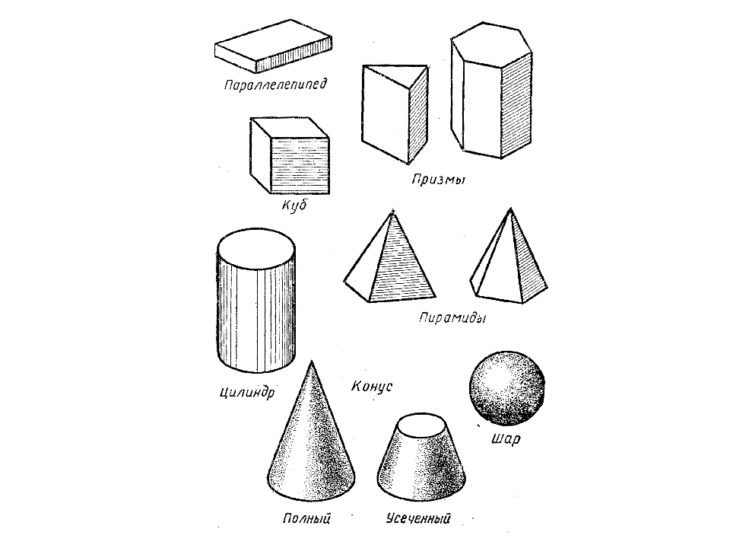
То есть стороны этой фигуры соединяются в одной точке.
Плоскость
Рассмотрим еще одно первичное понятие. Плоскость – это фигура, у которой нет ни конца, ни начала, равно как и прямой, и точки. Во время рассмотрения этого геометрического элемента во внимание берется лишь его часть, ограниченная контурами ломаной замкнутой линии.
Любую гладкую ограниченную поверхность можно считать плоскостью. Это может быть гладильная доска, лист бумаги или даже дверь.
Четырехугольники
Параллелограмм – это геометрическая фигура, противоположные стороны которой параллельны друг другу попарно. Среди частных видов этой конструкции выделяют ромб, прямоугольник и квадрат.
Прямоугольник – это параллелограмм, у которого все стороны соприкасаются под прямым углом.
Квадрат – это четырехугольник с равными сторонами и углами.
Ромб – это фигура, у которой все грани равны. При этом углы могут быть совершенно разными, но попарно. Каждый квадрат считается ромбом.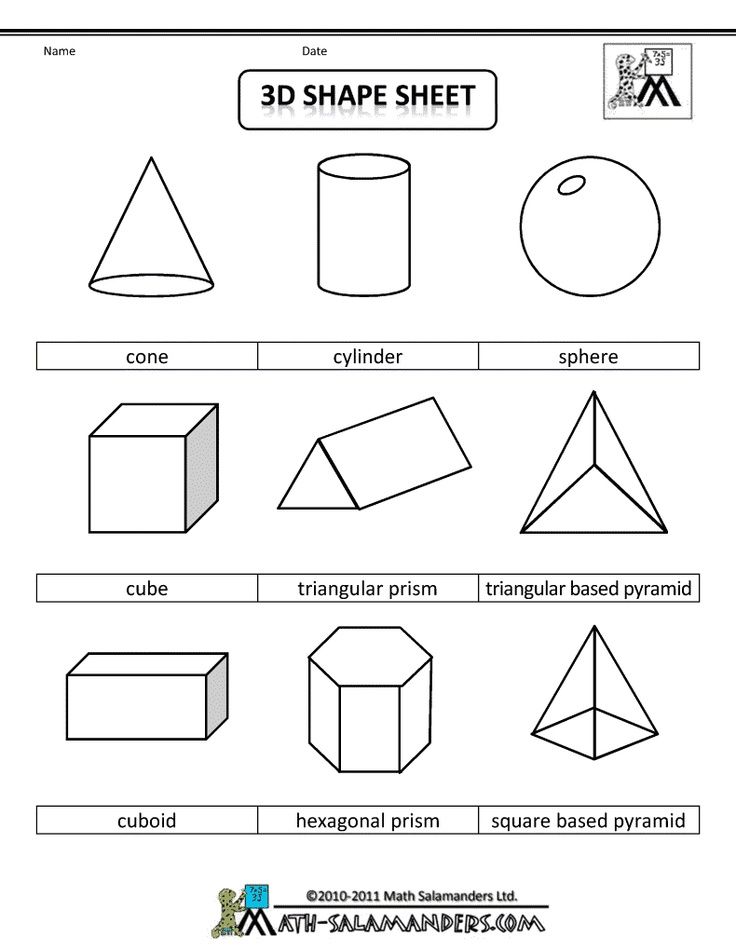
Но в противоположном направлении это правило действует не всегда. Далеко не каждый ромб является квадратом.
Трапеция
Геометрические фигуры бывают совершенно разными и причудливыми. Каждая из них имеет своеобразную форму и свойства.
Трапеция – это фигура, которая чем-то схожа с четырехугольником. Она имеет две параллельные противоположные стороны и при этом считается криволинейной.
Круг
Эта геометрическая фигура подразумевает расположение на одной плоскости точек, равноудаленных от ее центра. При этом заданный ненулевой отрезок принято называть радиусом.
Треугольник
Это простая геометрическая фигура, которая очень часто встречается и изучается.
Треугольник считается подвидом многоугольника, расположенным на одной плоскости и ограниченным тремя гранями и тремя точками соприкосновения. Эти элементы попарно соединены между собой.
Многоугольник
Вершинами многоугольников называют точки, соединяющие отрезки. А последние, в свою очередь, принято считать сторонами.
Объемные геометрические фигуры
- призма;
- сфера;
- конус;
- цилиндр;
- пирамида;
Эти тела имеют нечто общее. Все они ограничиваются замкнутой поверхностью, внутри которой находится множество точек.
Объемные тела изучают не только в геометрии, но и в кристаллографии.
Любопытные факты
Наверняка вам будет интересно ознакомиться с информацией, предоставленной ниже.
- Геометрия сформировалась как наука еще в давние века. Это явление принято связывать с развитием искусства и разнообразных ремесел. А названия геометрических фигур свидетельствуют об использовании принципов определения подобия и схожести.
- В переводе с древнегреческого термин «трапеция» обозначает столик для трапезы.
- Если вы возьмете различные фигуры, периметр которых будет одинаковым, то наибольшая площадь гарантированно будет у круга.
- В переводе с греческого языка термин «конус» обозначает сосновую шишку.
- Существует известная картина Каземира Малевича, которая начиная с прошлого века притягивает к себе взгляды многих живописцев. Работа «Черный квадрат» всегда была мистической и загадочной. Геометрическая фигура на белом полотне восхищает и поражает одновременно.
Работа «Черный квадрат» всегда была мистической и загадочной. Геометрическая фигура на белом полотне восхищает и поражает одновременно.Существует большое количество геометрических фигур. Все они отличаются параметрами, а порой даже удивляют формами.
Фигуры на английском для детей. Английский язык для детей в игровой форме. Геометрические фигуры. Английские названия геометрических фигур в пространстве
Геометрические фигуры — это одна из первых тем для изучения английского языка с малышами. Английский для детей лучше всего изучать в игровой форме, и, так как, тема «геометрические фигуры» для этого хорошо подходит, изучение геометрии деткам очень нравится 🙂
Изучению геометрии у нас посвящена целая рубрика, поэтому следите за обновлениями — статьи будут добавляться.
В этой же статье, я поделюсь одним, чрезвычайно интересным и увлекательным творческим проектом, под названием «Пластилиновая геометрия», в котором мы начнем изучать геометрические фигуры на английском языке.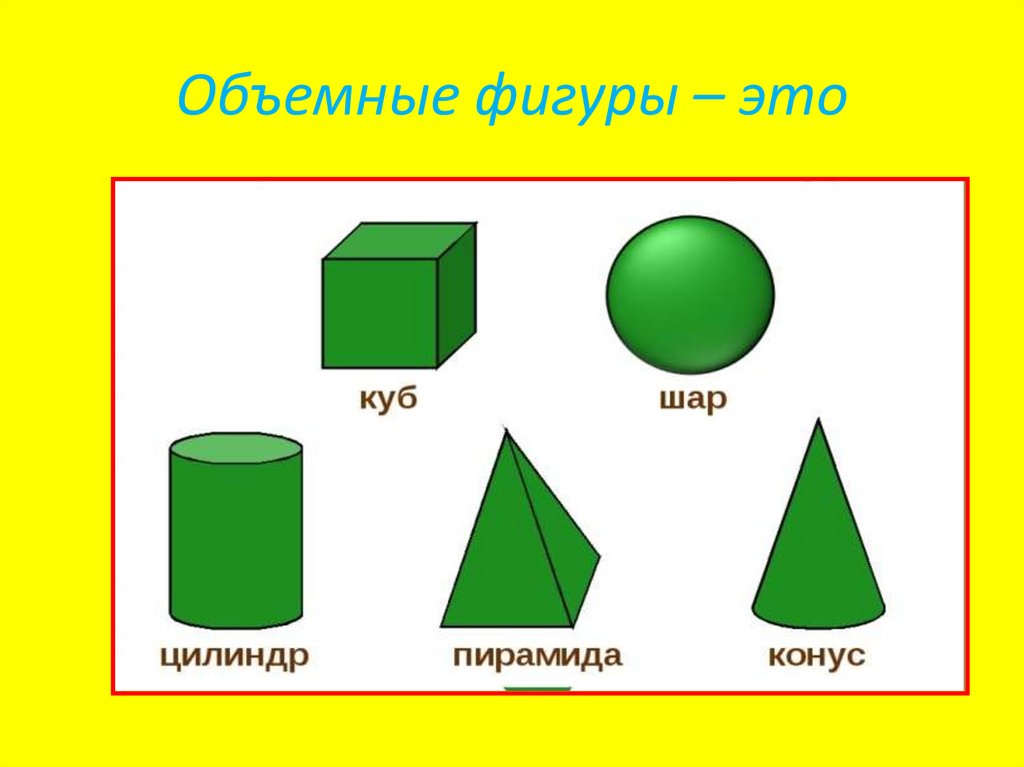
Введение материала
Послушайте песенку и изучите геометрические фигуры.
Создание проекта
Вам понадобятся:
- Пластилин
- Зубочистки
- Лист бумаги и карандаши
Нарисуйте различные формы на листе бумаги и подпишите их.
Список слов с русифицированной транскрипцией:
- Circle [сё кл] круг
- Square [скwэ э] квадрат
- Rectangle [рэ ктэньгл] прямоугольник
- Ova [о увл] овал
- Triangle [тра йэньгл] треугольник
- Diamond [да йэмэнд] ромб
- Star [ста:] звезда
Покажите ребёнку, как делать фигуры, сделав первую фигуру самостоятельно. Сначала скатайте шарики и разложите по углам.
Теперь возьмите зубочистки и сделайте стороны фигуры.
Лучше начинать с квадрата или равностороннего треугольника, потому что все стороны у этих фигур равны и вы будете использовать целые зубочистки.
Когда же дойдёт очередь до фигур с разными сторонами (ромб, прямоугольник), не спешите показывать ребенку, как именно можно сделать такие фигуры. Дайте малышу время подумать: пусть он сам догадается, что зубочистку необходимо сломать, предварительно измерив сторону.
Несмотря на то, что мы изучаем английский язык с нашими детьми в игровой форме, нет никакой необходимости лишать малыша его суверенных прав на раннее развитие — пусть подумает. Пусть ощутит сладкую радость победы, если сможет догадаться 🙂
Теперь спросите ребёнка, как можно сделать круг и овал. Есть ли прямые стороны у этих фигур? И, понадобятся ли, в этом случае, зубочистки?
На фото вы видите два варианта, но на самом деле их очень много. Подождите, пока ребёнок предложит свой вариант, а потом предложите свой… Молодым — везде у нас дорога… Помните о его суверенных правах!
Совет:
Когда вы будете лепить фигуры, проговаривайте их название по-английски.
Поместите фигуры на несколько дней на видное место, время от времени подходите к ним, и повторяйте их названия.
Учим названия геометрических фигур на английском языке. По-английски геометрические фигуры — 🔊 geometrical shapes ([ʤɪəˈmetrɪkl ʃeɪps]).
Английские названия геометрических фигур на плоскости
Представленные ниже геометрические термины определены на плоскости. Обобщенное их название: 🔊 geometric shapes on a plane.
| Транскрипция | Перевод | |
|---|---|---|
| 🔊 Point | Точка | |
| 🔊 Straight line | Прямая | |
| 🔊 Intersecting lines | [ɪntəˈsektɪŋ laɪnz] | Пересекающиеся прямые |
| 🔊 Parallel lines | [ˈpærəlel laɪnz] | Параллельные прямые |
| 🔊 Perpendicular lines | Перпендикулярные прямые | |
| 🔊 Triangle | [ˈtraɪæŋgl] | Треугольник |
| 🔊 Isosceles triangle | Равнобедренный треугольник | |
| 🔊 Equilateral triangle | [ˈiːkwɪˈlætərəl ˈtraɪæŋgl] | Равносторонний треугольник |
| 🔊 Right angle triangle | Прямоугольный треугольник | |
| 🔊 The altitude of a triangle | [ðiː ˈæltɪtjuːd ɔv ə ˈtraɪæŋgl] | Высота треугольника |
| 🔊 Bisector of a triangle | Биссектриса треугольника | |
| 🔊 Median of a triangle | [‘miːdɪən ɔv ə ˈtraɪæŋgl] | Медиана треугольника |
| 🔊 Quadrangle | [ˈkwɔdræŋgl] | Четырехугольник |
| 🔊 Diagonal | Диагональ | |
| 🔊 Square | Квадрат | |
| 🔊 Pentagon | [ˈpentəgən] | Пятиугольник |
| 🔊 Hexagon | [ˈheksəgən] | Шестиугольник |
| 🔊 Octagon | [ˈɔktəgən] | Восьмиугольник |
| 🔊 Decagon | [‘dekəgən] | Десятиугольник |
| 🔊 Vertex | [‘vɜːteks] | Вершина |
| 🔊 Side | Сторона | |
| 🔊 Ellipse | [ɪ’lɪps] | Эллипс |
| 🔊 Hyperbole | Гипербола | |
| 🔊 Parabola | Парабола |
Английские названия геометрических фигур в пространстве
Есть ряд геометрических терминов, которые определены в пространстве.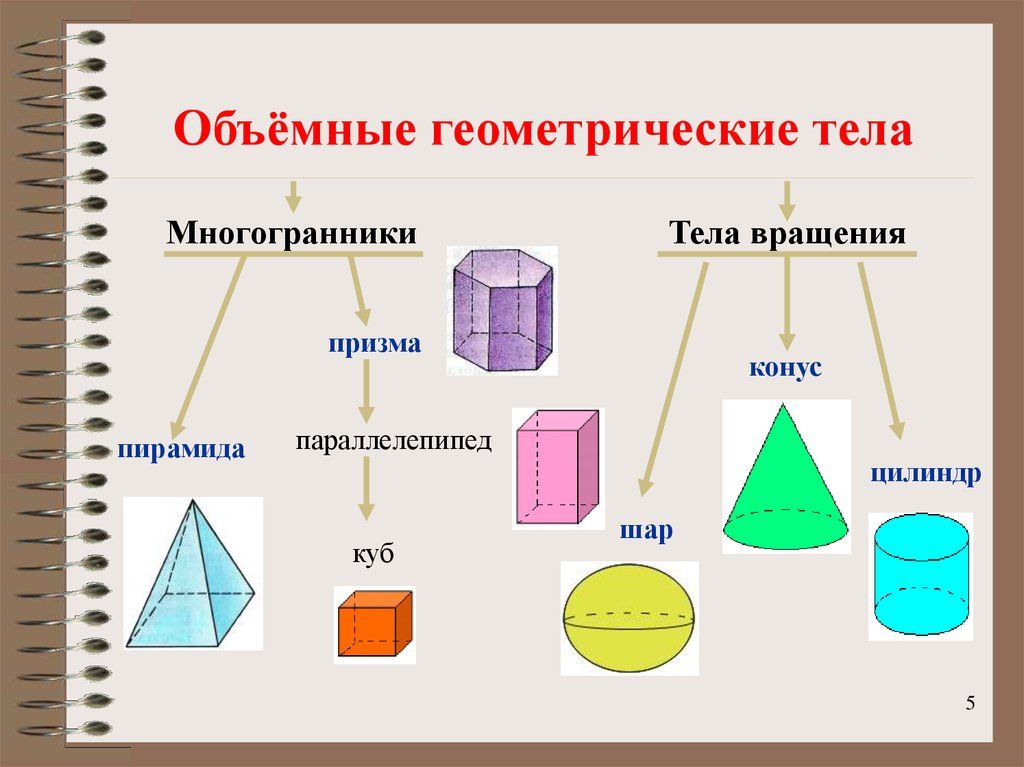
Обобщенно: 🔊
geometric shapes in space.
| Название геометрической фигуры (Произношение) | Транскрипция | Перевод |
|---|---|---|
| 🔊 Edge | Ребро | |
| 🔊 Face | Грань | |
| 🔊 Plane | Плоскость | |
| 🔊 Hyperplane | Гиперплоскость | |
| 🔊 Collinear lines | Коллинеарные прямые | |
| 🔊 Coplanar lines | Компланарные прямые | |
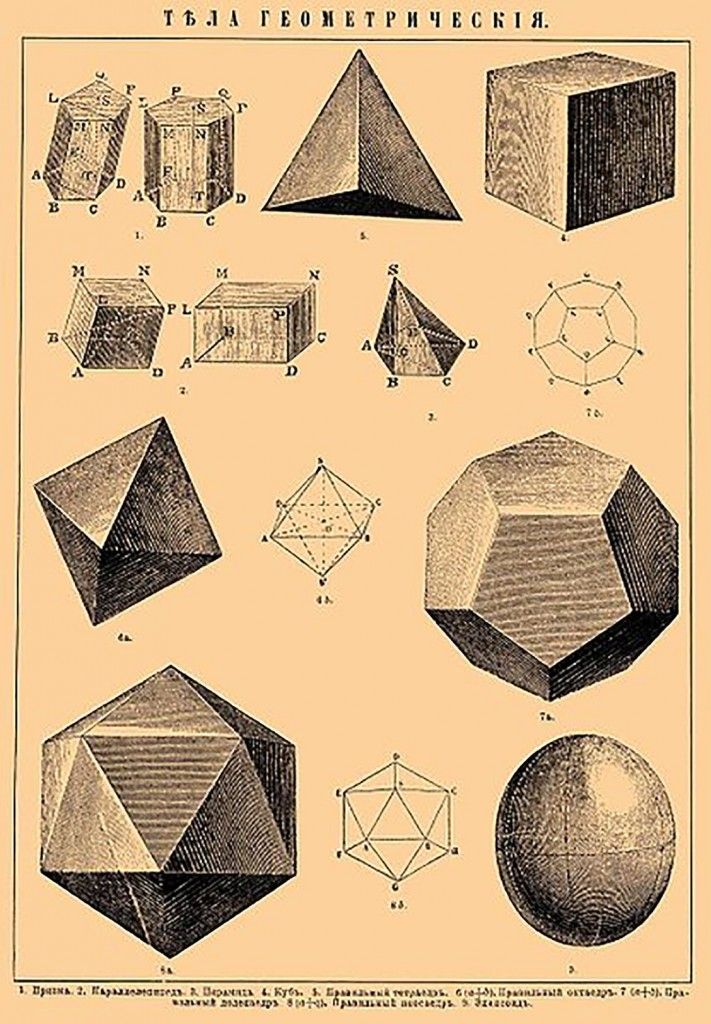
| 🔊 Polyhedron | [ˌpɔlɪ’hiːdr(ə)n] | Многогранник |
| 🔊 Tetrahedron | [ˌtetrə’hiːdr(ə)n] | Тетраэдр |
| 🔊 Cube | Куб | |
| 🔊 Pentahedron | [ˌpentə’hiːdrən] | Пятигранник |
| 🔊 Hexahedron | [ˌheksə’hiːdrən] | Шестигранник |
| 🔊 Octahedron | [‘ɔktə’hiːdr(ə)n] | Восьмигранник (Октаэдр) |
| 🔊 Decahedron | [ˌdekə’hiːdr(ə)n] | Десятигранник (Декаэдр) |
| 🔊 Dodecahedron | [ˌdəudekə’hiːdr(ə)n] | Двенадцатигранник (Додекаэдр) |
| 🔊 Icosahedron | [ɪkəˈsɑːdrən] | Двадцатигранник (Икосаэдр) |
| 🔊 Regular polyhedron | [ˈregjʊlə ˌpɔlɪ’hiːdr(ə)n] | Правильный многоугольник |
| 🔊 N-dimensional simplex | [ən-dɪˈmenʃənl ˈsɪmpleks] | N-мерный симплекс |
| 🔊 N-dimensional octahedron | [ən-dɪˈmenʃənl ‘ɔktə’hiːdr(ə)n] | N-мерный октаэдр (Гипероктаэдр) |
| 🔊 N-dimensional cube | [ən-dɪˈmenʃənl kjuːb] | N-мерный куб (Гиперкуб) |
| 🔊 Sphere | Сфера |
- Еще несколько полезных статей
Статья предлагает вам методический и наглядный материал к уроку английского языка «Геометрические фигуры».
Необходимые английские слова по теме «Геометрические фигуры» для начинающих, детей: список с транскрипцией и переводом
Одна из основных тем в изучении английского языка – это «геометрические фигуры». Казалось бы, совершенно бессмысленная тема, которая не должна пригодиться в повседневной жизни, но нет!
Названия геометрических фигур могут пригодиться в случае:
- Описания внешности человека
- Описания внешних признаков зданий, природных мест
- Описании игрушек и предметов
- В кулинарии (круглая тарелка, квадратная форма и т.д.)
- В творчестве и науке
На самом деле, формы и фигуры присутствуют практически везде: дома, на улице, даже в описании ситуаций (например, хожу по кругу, любовный треугольник). Лексика эта сложна для изучения и порой бывает скучна, но при правильном подходе и выборе методик преподавания (насыщение уроков наглядностями и видео) вполне реально заинтересовать ребенка и помочь ему запомнить важные слова.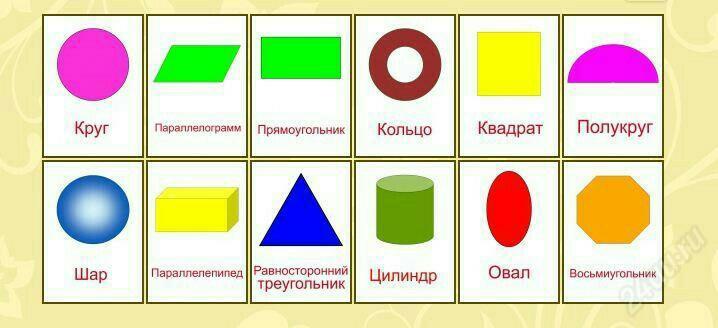
Вокабуляр:
Упражнения и задания на английском языке для детей по теме «Геометрические фигуры»
Важную роль на уроках английского (особенно в данной тематике) играют упражнения, как устные, так и письменные. Ученику важно видеть перед собой изображения геометрических фигур и различать их, сравнивая, обозначая или выделяя.
Задания:
- Простое задание для младшего класса. В нем необходимо назвать каждую геометрическую фигуру, раскрасить ее и правильно назвать.
- Для выполнения этого задания следует заранее подготовить цветную бумагу или уже вырезанные разные геометрические фигуры. Задание предполагает создание картинок-аппликаций, но укладывая каждую фигурку, следует называть ее форму.
- Задание № 3: Простое письменное задание, которое предполагает, что ученик перечислит все геометрические фигуры, которые находятся в одном помещении с ним (прямоугольник – окно, квадрат – стол, круг – подушка).
Диалог на английском языке для детей по теме «Геометрические фигуры» с переводом
Важная форма работы на уроках английского – практика устной разговорной речи. Для этого вам пригодится такое задание, как составление и разыгрывание диалога. Данная тематика не предполагает, что диалог будет только лишь на «геометрическую» тематику, ведь брать можно любую тему, главное, чтобы вы там использовали 2-5 слов «фигуры и формы».
Диалоги:
Фразы на английском языке для детей по теме «Геометрические фигуры» с переводом
Придумать предложения и построить диалоги вам помогут не только слова, но также и словосочетания в теме «Фигуры и формы».
Фразы на английском:
| English | Перевод |
| Geometric Figures | Геометрические фигуры |
| Shapes | Фигуры и формы |
| Right Angle | Прямой угол |
| Equilateral | Равносторонний |
| V oluminous bodies | Объемные тела |
| Straight line | Прямая линия |
| Curved line | Кривая линия |
| Line segment | Отрезок |
| To measure | Измерять |
| Calculate | Вычислять |
| Line | Мерить линейкой |
| Side | Сторона |
| Diameter | Диаметр |
| Flat figure | Плоская фигура |
Песенки и стихи для детей на английском языке по теме «Геометрические фигуры» с переводом
Даже такую сложную тему по английскому, как «Фигуры и формы» можно сделать интересной и веселой, разбавив ее песнями и стихами.
Карточки на английском языке по теме «Геометрические фигуры» с переводом
Наглядности и тематические карточки к уроку «Геометрические фигуры» очень важны, так как играют значительную роль – знакомят детей с основными формами.
Варианты карточек:
Игры на английском языке по теме «Геометрические фигуры»
Даже в такой урок, как «Геометрические формы» на английском можно ввести игровой момент, который не только развлечет ребенка, но и заинтересует его.
Для игры подготовьте:
- Лист белой бумаги (лучше всего ватман А6)
- Пластилин или пластилиновое тесто
- Упаковка зубочисток или спичек
- Цветные фломастеры
Как играть:
- Объясните ребенку, что с помощью этих материалов нужно сделать геометрические фигуры на плоскости.
- Каждая сторона – это зубочистка, а крепятся они с помощью пластилина.
- По мере создания фигур, каждую следует правильно называть по-английски.
- Чтобы игра стала более насыщенной и подарила приятные эмоции, попросите ребенка нарисовать эмоции к полученным фигуркам.
Этапы работы:
Загадки на английском языке по теме «Геометрические фигуры» с переводом
Еще один игровой момент на уроке – это загадки. Чтобы ученики с большим азартом занимались их разгадкой, попробуйте как-то их за это поощрить (баллы к оценке, наклейки, бонусы).
Советы для самостоятельного изучения темы на английском языке «Геометрические фигуры» для детей и родителей
Советы:
- Перед тем, как начинать учить ребенка английским словам (названиям фигур), следует проверить, насколько хорошо он знает сами геометрические фигуры (попросите его озвучить их на родном языке).
- Сделайте яркие наглядности с геометрическими фигурами и каждую выделите отдельным цветом (чтобы четко и сразу их различать визуально).
- Хорошо иметь кроме наглядностей-распечаток или картинок также объемные фигуры, чтобы ребенок мог их пощупать и рассмотреть со всех сторон.
- Если ребенок плохо запоминает слова, можно найти более созвучное слово,чтобы вызвать у него ассоциации (например: circle – это круг, похоже на русское слово «циркуль», а циркуль что рисует: круг).
- За весь урок вы должны повторить названия форм и новую лексику множество раз. Если повторять очень часто, а к тому же дополнять жестами (хлопками, топтанием или танцем), запоминание будет более эффективным.
- Поможет также метод «визуализации». Для этого после того, как произнесете слово, нарисуйте геометрическую фигуру в воздухе.
Видео: «Геометрические фигуры на английском»
В повседневной жизни мы постоянно используем слова, связанные с геометрией. Я имею в виду не термины вроде гипотенуза или биссектриса , а употребительные слова, например: круг, квадратный, длина, ширина, объем. Из этой подборки вы узнаете самые необходимые геометрические термины на английском языке и сможете повторить или выучить их с помощью озвученных карточек.
Основные геометрические термины на английском языке
Когда я учился в школе, мы начинали знакомство с геометрией с таких элементарных понятий, как точка (point) , прямая (straight line) , отрезок (line segment) , луч (ray) , затем перешли к геометрическим фигурам (plane shapes) и геометрическим телам (solid shapes) .
В списке и карточках ниже представлены эти и другие основные термины. Отмечу, что наиболее коварными являются два термина:
- Angle – угол. Легко перепутать с corner . Но если corner – это угол в общем смысле, например, угол комнаты (corner of the room), то angle – это угол как геометрическое понятие (right angle – прямой угол).
- Point – точка. В русском языке любая точка называется точкой: будто то точка в десятичной дроби или конце предложения. В английском несколько названий для разных точек: point, dot, period, full stop . Вот какая между ними разница:
- Point – точка в геометрии, в : 3.14 читается как three point one four .
- Dot – точка в адресах веб-сайтов. Например, www.google.com читается как: double u double u double u google dot com . Кстати, забавно, что www – это сокращенно world wide web, но сокращенная форма при чтении намного длиннее полной.
- Period (США) или full stop (Великобр.) – точка в конце предложения. Есть даже английское выражение “period” или “full stop” аналог русского «точка» в значении «разговор закончен, возражения не принимаются»: You are not going to the party. Period. – Ты не идешь на вечеринку. Точка.
| point | точка |
| line segment | отрезок |
| ray | луч |
| line | прямая |
| plane shape | геометрическая фигура |
| solid shape | геометрическое тело |
| volume | объем |
| area | площадь |
| perimeter | периметр |
| diagonal | диагональ |
| size | размер |
| side | сторона |
| angle | угол |
| lengh | длина |
| width | ширина |
| height | высота |
| depths | глубина |
| right angle | прямой угол |
| obtuse angle | тупой угол |
| acute angle | острый угол |
| vertical line | вертикальная линия |
| horizontal line | горизонтальная линия |
| curved line | кривая линия |
| broken line | ломаная линия |
| parallel lines | параллельные линии |
| perpendicular lines | перпендикулярные линии |
| radius | радиус |
| diameter | диаметр |
| base | основание |
| vertex | вершина |
| edge | ребро |
| convex | выпуклый |
| concave | вогнутый |
Геометрические тела и фигуры
Напомню, геометрические фигуры двухмерные, а тела – объемные. Квадрат, треугольник – это фигуры, а куб, пирамида – тела. Некоторые трудности могут возникнуть с прилагательными, образованными от названий тел и фигур, потому что они по-разному:
- с помощью суффиксов: rectangle (прямоугольник) – rectangular (прямоугольный).
- обозначаются другим словом: circle (круг) – round (круглый).
- образуются без изменения слова: oval (овал) – oval (овальный).
От слова circle также образуется прилагательное circular – круглый, но оно обычно используется, когда речь идет о чем-то плоском и, как правило, идеально круглом. Round может применяться к плоским и объемным предметам, это слово намного употребительнее в повседневной речи: round table – круглый стол, round building – круглое здание. О шаровидных предметах тоже, скорее всего скажут, что они round (round ball – круглый мяч), хотя технически они spherical . Но по-русски мы тоже не называем мяч «сферическим».
| circumference | окружность |
| square | квадрат |
| circle | круг |
| triangle | треугольник |
| rectangle | прямоугольник |
| rhombus | ромб |
| trapezium (US – trapezoid) | трапеция |
| oval | овал |
| cylinder | цилиндр |
| cube | куб |
| prism | призма |
| sphere | сфера |
| cone | конус |
| pyramid | пирамида |
| pentagon | пятиугольник |
| hexagon | шестиугольник |
| pentagram | пентаграмма |
| square (adjective) | квадратный |
| round | круглый |
| triangular | треугольный |
| rectangular | прямоугольный |
| oval (adjective) | овальный |
| cubic (-al) (adjective) | кубический |
| spherical | сферический |
названий фигур: 30 популярных названий фигур с изображением ESL