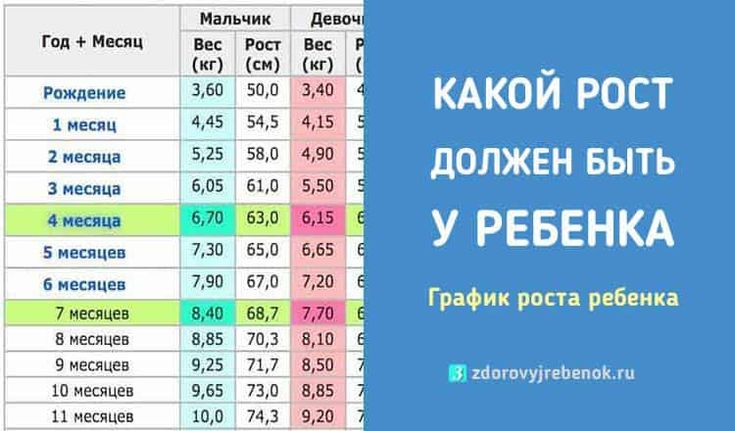
Найти средний рост мальчиков класса если результаты измерения их роста: Средний рост мальчиков в классе равен 160 см.На сколько процентов рост вани выше среднего если…
Рост. Вес. Три соседа / Хабр
В поиске интересного и простого ДатаСета я набрёл этого красавца.
Об этом красавце
В нём есть данные о росте и весе 10 000 мужчин и женщин. Никакого описания. Ничего «лишнего». Только рост, вес и метка пола. Эта таинственная простота мне понравилась.
Что ж, начнём!
Что мне было интересно?
- В каком диапазоне вес и рост у большинства мужчин и женщин?
- Какие они — «средний» мужчина и «средняя» женщина?
- Сможет ли простенькая модель машинного обучения «KNN» по этим данным угадать вес по росту?
Погнали!
Первый взгляд
Для начала подгрузим нужные модули
# Для работы с табличными данными import pandas as pd # Для моих любимых графиков import matplotlib.pyplot as plt %matplotlib inline # Модель машинного обучения «К ближайших соседей» from sklearn.neighbors import KNeighborsRegressor # Для разбивки данных на тренировочный и тестовый наборы from sklearn.model_selection import train_test_split
Когда библиотеки встали ровно — пришло время загрузить сам ДатаСет и посмотреть на первые 10 элементов. Это нужно, чтобы наше нутро было спокойно, что мы всё загрузили правильно.
Кстати, не пугайтесь, что рост и вес отличаются от привычных нам. Это из-за другой системы измерений:
data = pd.read_csv('weight-height.csv')
data.head(10)| Gender | Height | Weight | |
|---|---|---|---|
| 0 | Male | 74 | 242 |
| 1 | Male | 69 | 162 |
| 2 | Male | 74 | 213 |
| 3 | Male | 72 | 220 |
| 4 | Male | 70 | 206 |
| 5 | Male | 68 | 152 |
| 6 | Male | 69 | 184 |
| 7 | Male | 68 | 168 |
| 8 | Male | 67 | 176 |
| 9 | Male | 63 | 156 |
Хорошо! Мы видим, что первые десять записей — «мужчины».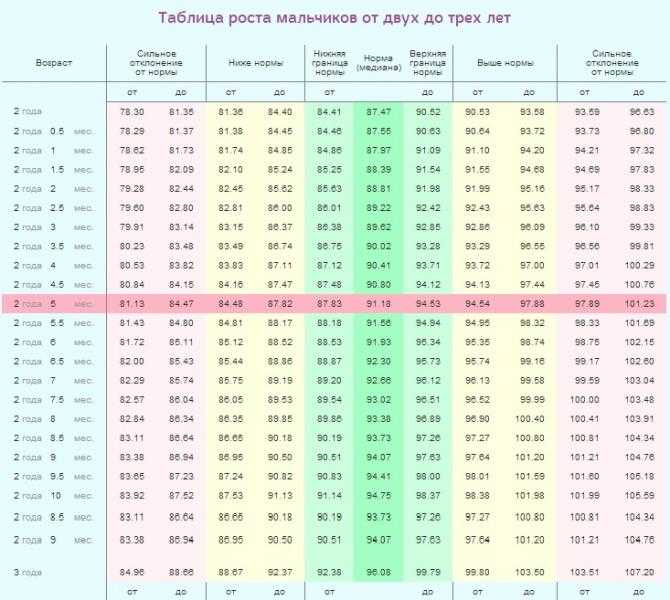 Мы видим их рост (height) и вес (weight). Данные подгрузились хорошо.
Мы видим их рост (height) и вес (weight). Данные подгрузились хорошо.
Теперь можно посмотреть на количество строк в наборе.
data.shape >> (10000, 3)
Десять тысяч строк / записей. И у каждой по три параметра. То, что нужно!
Пришло время исправить систему измерений. Теперь тут сантиметры и килограммы.
data['Height'] *= 2.54 data['Weight'] /= 2.205 # И проверим результат data.head(10)
| Gender | Height | Weight | |
|---|---|---|---|
| 0 | Male | 188 | 110 |
| 1 | Male | 175 | 74 |
| 2 | Male | 188 | 96 |
| 3 | Male | 182 | 100 |
| 4 | Male | 177 | 94 |
| 5 | Male | 171 | 69 |
| 6 | Male | 175 | 83 |
| 7 | Male | 174 | 76 |
| 8 | Male | 170 | 80 |
| 9 | Male | 161 | 71 |
Вот теперь стало привычнее.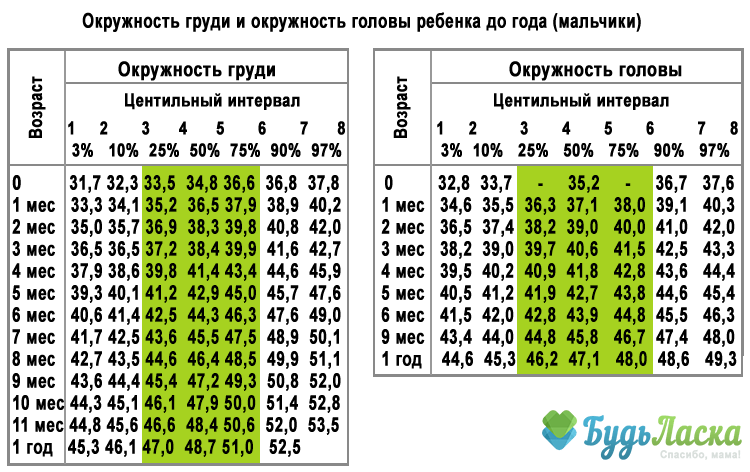 И первая же запись нам говорит о мужчине с ростом ~190см и весом ~110кг. Большой человек. Назовём его Боб.
И первая же запись нам говорит о мужчине с ростом ~190см и весом ~110кг. Большой человек. Назовём его Боб.
Но как понять: это много или мало по сравнению с остальными? Возможно ли, что мы все плюс-минус Бобы? Это немного позже.
А сейчас узнаем, насколько симметрично в этом наборе данных сочетаются два гендера?
data['Gender'].value_counts() >> Male 5000 Female 5000 Name: Gender, dtype: int64
Идеально поровну. И это хорошо, ведь если бы было: 9999 мужчин и 1 женщина, то не осталось бы смысла делать вид, что этот ДатаСет одинакого хорошо раскрывает оба пола. В нашем случае — всё ок!
Разделяй и изучай!
Сейчас интуиция подсказывает, что будет правильно разделить два пола и исследовать отдельно. Ведь в жизни мы часто видим, что мужчины и женщины имеют плюс-минус разные рост и вес
# Мужчины data_male = data[data['Gender'] == 'Male'].copy() # Женщины data_female = data[data['Gender'] == 'Female'].copy()
Давайте взглянем на небольшую описательную статистику, которую нам предлагает модуль 
Мужчины:
data_male.describe()
| Height | Weight | |
|---|---|---|
| count | 5000 | 5000 |
| mean | 175 | 85 |
| std | 7 | 9 |
| min | 148 | 51 |
| 25% | 171 | 79 |
| 50% | 175 | 85 |
| 75% | 180 | 91 |
| max | 201 | 122 |
Женщины:
data_female.describe()
| Height | Weight | |
|---|---|---|
| count | 5000 | 5000 |
| mean | 162 | 62 |
| std | 7 | 9 |
| min | 138 | 29 |
| 25% | 157 | 56 |
| 50% | 162 | 62 |
| 75% | 167 | 67 |
| max | 186 | 92 |
Небольшой ликбез по инфе выше
Простым языком:
Описательная статистика — это набор чисел / характеристик для описания. Пожалуй, это самый простой для понимания вид статистики.
Пожалуй, это самый простой для понимания вид статистики.
Представьте, что вы описываете параметры мяча. Он может быть:
- большой / маленький
- гладкий / шершавый
- синий / красный
- прыгучий / и не очень.
С сильным упрощением можно сказать, что этим и занимается описательная статистика. Но делает это не с мячиками, а с данными.
А вот параметры из таблицы выше:
- count — Количество экземпляров.
- mean — Среднее или сумма всех значений, делённая на их количество.
- std — Стандартное отклонение или корень из дисперсии. Показывает разброс величин относительно среднего.
- min — Минимальное значение или минимум.
- 25% — Первый квартиль. Показывает значение, меньше которого находится 25% записей.
- 50% — Второй квартиль или медиана.
 Показывает значение, выше и ниже которого одинаковое количество записей.
Показывает значение, выше и ниже которого одинаковое количество записей. - 75% — Третий квартиль. По анологии с первым квартилем, но ниже 75% записей.
- max — Максимальное значение или максимум.
Среднее значение очень чувствительно к выбросам! Если четыре человека получают зарплату 10 000 ₽, а пятый — 460 000 ₽. То среднее будет — 100 000 ₽. А медиана останется прежней — 10 000 ₽.
Это не значит, что среднее — это плохой показатель. К нему нужно относиться внимательнее.
Кстати, с медианой тоже есть загвоздка.
Если количество измерений нечётное. То медиана — это значение посередине, если поставить данные «по росту».
А если чётное, то медиана — это среднее между двумя «самыми центральными».
Если в наборе данных только целые числа, а медиана получилась дробной — не удивляйтесь. Скорее всего количество измерений чётно.
Пример:
Сын принёс отметки со школы.
Пять оценок → нечётное количество
Сроим по росту: 1, 2, 3, 4, 5
Берём центральное — 3
Медианная оценка — 3
На следующий день сын принёс со школы новые оценки: 4, 2, 3, 5
Четыре оценки → нечётное количество
Строим по росту: 2, 3, 4, 5
Берём центральные: 3, 4
Находим их среднее: 3.5
Медиана — 3.5
Вывод: Молодец сына 🙂
Видим, что у мужчин среднее и медиана: 175см и 85кг. А у женщин: 162см и 62кг. Это говорит нам, что сильных выбросов нет. Либо они симметричны в обе стороны от медианы. Что бывает очень редко.
Но у обоих полов есть небольшие отклонения среднего от медианы. Но они несущественны и их видно только на сотых долях. Идём дальше!
Гистограма
Это график, который строит значения от минимума до максимума в порядке роста, и показывает количество отдельных экземпляров.
fig, axes = plt.subplots(2,2, figsize=(20,10)) plt.subplots_adjust(wspace=0, hspace=0) axes[0,0].hist(data_male['Height'], label='Male Height', bins=100, color='red') axes[0,1].hist(data_male['Weight'], label='Male Weight', bins=100, color='red', alpha=0.4) axes[1,0].hist(data_female['Height'], label='Female Height', bins=100, color='blue') axes[1,1].hist(data_female['Weight'], label='Female Weight', bins=100, color='blue', alpha=0.4) axes[0,0].legend(loc=2, fontsize=20) axes[0,1].legend(loc=2, fontsize=20) axes[1,0].legend(loc=2, fontsize=20) axes[1,1].legend(loc=2, fontsize=20) plt.savefig('plt_histogram.png') plt.show()
Данные распределяются колоколообразно. Очень похоже на нормальное распределение.
Помимо статистических тестов на нормальность распределения есть визуальный тест. Если распределение по виду и логике похоже на нормальное — можно считать с долей допущений, что мы имеем дело именно с ним.
Можно было бы сделать статистический тест на нормальность и определить p-value, но не умею это выходит за рамки статьи.
Учимся работать ручками
Pandas за нас может посчитать многое. Но нужно хотя бы раз посчитать некоторые статистики самому. Сейчас покажу, как скалькулировать стандартное отклонение.
Сделаем это на примере мужчин и характеристике — рост.
Среднее
Формула:
, где
- М — среднее значение
- N — количество экземпляров
- ni — отдельный экземпляр
Код:
mean = data_male['Height'].mean()
print('mean:\t{:.2f}'.format(mean))
>> mean: 175.33Средний рост — 175см
Квадрат отклонения от среднего
, где
- di — отдельное отклонение
- ni — отдельный экземпляр
- M — среднее
Код:
data_male['Height_d'] = (data_male['Height'] - mean) ** 2 data_male['Height_d'].head(10) >> 0 149.927893 1 0.385495 2 166.739089 3 47.193692 4 4.721246 5 20.288347 6 0.375539 7 2.964214 8 25.997623 9 200.149603 Name: Height_d, dtype: float64
Дисперсия
Формула:
, где
- D — значение дисперсии
- di — отдельное отклонение
- N — количество экземпляров
Код:
disp = data_male['Height_d'].mean()
print('disp:\t{:.2f}'.format(disp))
>> disp: 52.89Дисперсия — 53
Стандартное отклонение
Формула:
, где
- std — значение стандартного отклонения
- D — значение дисперсии
Код:
std = disp ** 0.5
print('std:\t{:.2f}'.format(std))
>> std: 7.27Стандартное отклонение — 7
Доверительные интервалы
Сейчас мы узнаем, в каких диапазонах роста и веса находятся 68%, 95% и 99.7% мужчин и женщин.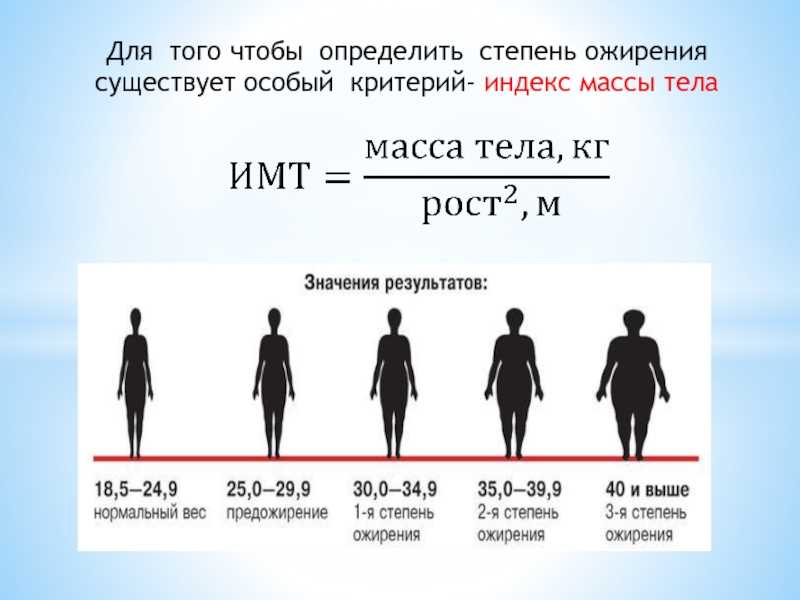
Это не так сложно — нужно прибавлять и отнимать стандартное отклонение от среднего. Выглядит это так:
- 68% — плюс-минус одно стандартное отклонение
- 95% — плюс-минус два стандартных отклонения
- 99.7% — плюс-минус три стандартных отклонения
Напишем вспомогательную функцию, которая будет считать это:
def get_stats(series, title='noname'):
# выводим название характеристики
print('= {} =\n'.format(title.upper()))
# получаем описательную статистику от pandas
descr = series.describe()
# выводим среднее
mean = descr['mean']
print('= Mean:\t{:.0f}'.format(mean))
# выводим стандартное отклонение
std = descr['std']
print('= Std:\t{:.0f}'.format(std))
# разделитель для красоты
print('\n= = = =\n')
# считаем интвервалы
## 68%
devi_1 = [mean - std, mean + std]
## 95%
devi_2 = [mean - 2 * std, mean + 2 * std]
## 99. 7%
devi_3 = [mean - 3 * std, mean + 3 * std]
# выводим результат
print('= 68% is from\t\t{:.0f} to {:.0f}'.format(devi_1[0], devi_1[1]))
print('= 95% is from\t\t{:.0f} to {:.0f}'.format(devi_2[0], devi_2[1]))
print('= 99.7% is from\t\t{:.0f} to {:.0f}'.format(devi_3[0], devi_3[1]))
7%
devi_3 = [mean - 3 * std, mean + 3 * std]
# выводим результат
print('= 68% is from\t\t{:.0f} to {:.0f}'.format(devi_1[0], devi_1[1]))
print('= 95% is from\t\t{:.0f} to {:.0f}'.format(devi_2[0], devi_2[1]))
print('= 99.7% is from\t\t{:.0f} to {:.0f}'.format(devi_3[0], devi_3[1]))Ну и применяем её к данным:
Мужчины | Рост
get_stats(data_male['Height'], title='Male Height') >> = MALE HEIGHT = = Mean: 175 = Std: 7 = = = = = 68% is from 168 to 183 = 95% is from 161 to 190 = 99.7% is from 154 to 197
Мужчины | Вес
get_stats(data_male['Height'], title='Male Height') >> = MALE WEIGHT = = Mean: 85 = Std: 9 = = = = = 68% is from 76 to 94 = 95% is from 67 to 103 = 99.7% is from 58 to 112
Женщины | Рост
get_stats(data_male['Height'], title='Male Height') >> = FEMALE HEIGHT = = Mean: 162 = Std: 7 = = = = = 68% is from 155 to 169 = 95% is from 148 to 176 = 99.7% is from 141 to 182
Женщины | Вес
get_stats(data_male['Height'], title='Male Height') >> = FEMALE WEIGHT = = Mean: 62 = Std: 9 = = = = = 68% is from 53 to 70 = 95% is from 44 to 79 = 99.7% is from 36 to 87
Отсюда выводы:
- Большинство мужчин: 154см–197см и 58кг–112кг.
- Большинство женщин: 141см–182см и 36кг–87кг.
Теперь осталось только применить машинное обучение к этому набору и попробовать предстазать вес по росту.
Ближайшие соседи
Алгоритм «К ближайших соседей» прост. Он существует для задач классификаций — отличить котика от собачки — и для задач регрессии — угадать вес по росту. Это то, что нам нужно!
Для регрессии он использует такой алгоритм:
- Запоминает все точки данных
- При появлении новой точки — ищет К её ближайших соседей (число К задаёт пользователь)
- Усредняет результат
- Выдаёт ответ
Для начала нужно разделить набор данных на обучающую и тестовую части и опробовать алгоритм
Экспериментируем на мужчинах
X_train, X_test, y_train, y_test = train_test_split(data_male['Height'], data_male['Weight'])
Разделили, настало время пробовать.
# Три соседа knr3 = KNeighborsRegressor(n_neighbors=3) knr3.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr3.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.8298400793623182 # Пять соседей knr5 = KNeighborsRegressor(n_neighbors=5) knr5.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr5.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.7958051642678619 # Семь соседей knr7 = KNeighborsRegressor(n_neighbors=7) knr7.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr7.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.7769249318420969
Не будем далеко ходить и остановимся на трёх соседях. Но вопрос: сможет ли такая модель угадать мой вес?
knr3.predict([[180]])[0, 0] >> 88.67596236265881
88кг — это очень близко. В эту секунду мой вес — 89.8кг
График предсказаний для мужчин
Время построить мою любимую часть науки — графики.
array_male = []
# доверительный интервал 99.7%
xaxis = range(154, 198)
for h in xaxis:
ans = knr3.predict([[h]])
array_male.append(ans[0, 0])
plt.figure(figsize=(20,10))
plt.plot(xaxis, array_male, 'r-', linewidth=4)
plt.title('Male heght-weight dependence', fontsize=30)
plt.xlabel('Height', fontsize=30)
plt.ylabel('Weight', fontsize=30)
plt.grid()
plt.savefig('plt_knn_male.png')
plt.show()Модель и график предсказаний для женщин
X_train, X_test, y_train, y_test = train_test_split(data_female['Height'], data_female['Weight']) knr3 = KNeighborsRegressor(n_neighbors=3) knr3.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr3.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.8135681584074799
array_female = []
# доверительный интервал 99.7%
xaxis = range(141, 183)
for h in xaxis:
ans = knr3.predict([[h]])
array_female.append(ans[0, 0])
plt.figure(figsize=(20,10))
plt.plot(xaxis, array_female, 'b-', linewidth=4)
plt. title('Female heght-weight dependence', fontsize=30)
plt.xlabel('Height', fontsize=30)
plt.ylabel('Weight', fontsize=30)
plt.grid()
plt.savefig('plt_knn_female.png')
plt.show()
title('Female heght-weight dependence', fontsize=30)
plt.xlabel('Height', fontsize=30)
plt.ylabel('Weight', fontsize=30)
plt.grid()
plt.savefig('plt_knn_female.png')
plt.show()Ну и конечно интересно, как выглядят эти графики вместе:
# объединение интервалов мужчин и женщин
xaxis = range(154, 183)
plt.figure(figsize=(20,10))
plt.plot(xaxis, array_male[:-15], 'r-', linewidth=4)
plt.plot(xaxis, array_female[13:], 'b-', linewidth=4)
plt.title('Together heght-weight dependence', fontsize=30)
plt.xlabel('Height', fontsize=30)
plt.ylabel('Weight', fontsize=30)
plt.grid()
plt.savefig('plt_knn_together.png')
plt.show()Ответы на вопросы
— В каком диапазоне вес и рост у большинства мужчин и женщин?
99.7% мужчин: от 154см до 197см и от 58кг до 112кг.
А 99.7% женщин: от 141см до 182см и от 36кг до 87кг.
— Какие они — «средний» мужчина и «средняя» женщина?
Средний мужчина — 175см и 85кг.
А средняя женщина — 162см и 62кг.
— Сможет ли простенькая модель машинного обучения «KNN» по этим данным угадать вес по росту?
Да, модель предсказала 88кг, а у меня 89.8кг.
Все, что сделал, собрал тут
- Нет описания ДатаСета. Вероятно, возраст и другие факторы у людей различались. Поэтому на веру принимать его нельзя, а ради эксперимента — пожалуйста.
- По-хорошему — нужно было сделать тест на нормальность распределения
Эпилог
Ставь лайк, если попал в 99.7% интервал
Как рассчитать ИМТ с учетом роста в метрах? – Обзоры Вики
Формула ИМТ: вес в килограммах разделенный на рост в метрах в квадрате. Если рост был измерен в сантиметрах, разделите его на 100, чтобы преобразовать его в метры. При использовании английских единиц измерения фунты следует разделить на квадратные дюймы. Затем это следует умножить на 703, чтобы преобразовать из фунтов / дюймов.2 до кг / м2.
Точно так же, каков ИМТ роста 5.7? Например, если вы весите 160 фунтов и имеете рост 5 футов 7 дюймов, ваш ИМТ равен 25.
Как рассчитать ИМТ с учетом роста и веса? Формула: вес (фунты) / [рост (дюймы)]2 х 703
Затем рассчитайте ИМТ по деление веса в фунтах (фунтах) на рост в дюймах (дюймах) в квадрате и умножение на коэффициент преобразования 703
Что такое м2 в высоту? Основная формула вес деленный на рост в квадратеили кг/м2. Вы просто берете свой рост в метрах и возводите его в квадрат, что означает, что вы берете количество метров, умноженное на само себя.
Во-вторых, как рассчитать формулу ИМТ? Индекс массы тела — это простой расчет с использованием роста и веса человека. Формула ИМТ = кг / м2 где кг – это вес человека в килограммах, а м2 их высота в метрах в квадрате.
Как шаг за шагом рассчитать ИМТ?
Выполните следующие действия, чтобы рассчитать свой ИМТ:
- Преобразуйте свой вес из фунтов в килограммы.
 Ваш вес (в фунтах) ÷ 2.2 = ваш вес (в килограммах). …
Ваш вес (в фунтах) ÷ 2.2 = ваш вес (в килограммах). … - Преобразуйте свой рост из дюймов в метры. Ваш рост (в дюймах) ÷ 39.37 = ваш рост (в метрах). …
- Рассчитайте свой индекс массы тела.
тогда как рассчитать ИМТ с учетом роста и стопы? Например, если ваш вес составляет 60 кг, а рост — 5 футов 3 дюйма, ваш ИМТ будет рассчитываться следующим образом: 60 / 2.61 (1.6 * 1.6) (5 футов 3 дюйма примерно 1.6 метра). Это дает нам значение ИМТ 22.9. Почему расчет ИМТ важен для вашего здоровья?
Как я могу рассчитать свой рост? Человек ростом 5 футов 6 дюймов имеет рост 66 дюймов. Один дюйм равен 2.54 сантиметра (см). Итак, чтобы сделать преобразование, просто умножьте свой рост в дюймах на 2.54, чтобы получите свой рост в сантиметрах. В этом случае рост человека 5 футов 6 дюймов в метрической системе составляет 167.64 см (66 x 2.54).
Какой самый быстрый способ рассчитать ИМТ?
Чтобы рассчитать свой ИМТ, разделите свой вес в фунтах на свой рост в дюймах в квадрате, затем умножьте результаты на коэффициент преобразования 703. Для человека ростом 5 футов 5 дюймов (65 дюймов) и весом 150 фунтов расчет будет выглядеть следующим образом: [150 ÷ (65)2] х 703 = 24.96.
Для человека ростом 5 футов 5 дюймов (65 дюймов) и весом 150 фунтов расчет будет выглядеть следующим образом: [150 ÷ (65)2] х 703 = 24.96.
Как рассчитать ИМТ без калькулятора? Как рассчитать индекс массы тела
- Умножьте свой рост в дюймах на свой рост в дюймах.
- Разделите свой вес на число, которое вы получили на шаге 1.
- Умножьте число, которое вы получили на шаге 2, на 705. Результат – ваш ИМТ.
Как рассчитать свой ИМТ класса 10?
Формула ИМТ = кг/м2 где кг — вес человека в килограммах, а м2 — его рост в метрах в квадрате. ИМТ 25.0 и выше свидетельствует об избыточном весе, в то время как нормальный диапазон составляет от 18.5 до 24.9.
Как рассчитывается ИМТ в Индии? ИМТ или индекс массы тела — это мера того, сколько массы тела имеет человек в зависимости от его веса и роста. Чтобы рассчитать свой ИМТ, просто разделите свой вес в килограммах на свой рост в квадрате в метрах.
Какой у меня ИМТ, если я вешу 220?
Масса тела (фунты)
| BMI | 36 | 46 |
|---|---|---|
| 58 | 172 | 220 |
| 59 | 178 | 227 |
| 60 | 184 | 235 |
Какой рост у 14-летнего ребенка?
Для американских мужчин от 20 лет средний рост с поправкой на возраст составляет 69. 1 см, или чуть более 175.4 футов 5 дюймов.
1 см, или чуть более 175.4 футов 5 дюймов.
…
Рост по возрасту.
| Age (years) | 50-й процентиль роста для мальчиков (дюймы и сантиметры) |
|---|---|
| 13 | 61.4 дюйма (156 см) |
| 14 | 64.6 дюйма ( 164 см) |
| 15 | 66.9 дюйма (170 см) |
| 16 | 68.3 дюйма (173.5 см) |
Какой у меня будет рост в 14 лет? Какой средний рост в 14 лет? Средний рост для 14-летнего мальчик 162.4 см (5 футов 3), а для девочек – 159.8 см (5 футов 2). Ожидайте большой разброс в росте в этом возрасте, однако у некоторых людей половая зрелость завершится, а у некоторых еще не началось.
Сколько см в 5 5 фута? 5’5 = 165.1 см
Преобразуйте 5 футов 5 в сантиметры.
Является ли калькулятор ИМТ точным?
ИМТ не является точным показателем здоровья потому что он не учитывает процентное содержание жира в организме или его распределение. … Измерения, которые более точны, чем ИМТ, при прогнозировании результатов для здоровья, включают артериальное давление, окружность талии и уровни холестерина.
… Измерения, которые более точны, чем ИМТ, при прогнозировании результатов для здоровья, включают артериальное давление, окружность талии и уровни холестерина.
Что такое нормальный ИМТ? ИМТ – это вес человека в килограммах, деленный на квадрат роста в метрах. … Если ваш ИМТ меньше 18.5, он попадает в диапазон недостаточного веса. Если ваш ИМТ 18.5 – 24.9, он попадает в диапазон нормального или здорового веса. Если ваш ИМТ составляет от 25.0 до 29.9, он попадает в диапазон избыточного веса.
Как рассчитать ИМТ для женщины?
Калькулятор ИМТ для женщин
Чтобы рассчитать свой ИМТ, используйте этот калькулятор ИМТ для взрослых. Вы также можете использовать эти формулы для расчета ИМТ: единицы США. (Вес в фунтах ÷ рост2 в дюймах) x 703 = ИМТ (Например: 150 фунтов ÷ 65 дюймов2 х 703 = 26.6)
Какой ИМТ для 10 класса? ИМТ означает Индекс массы тела. Объяснение: ИМТ используется для определения веса человека по отношению к его росту, что в результате показывает, имеет ли человек недостаточный вес, нормальный вес, избыточный вес или ожирение.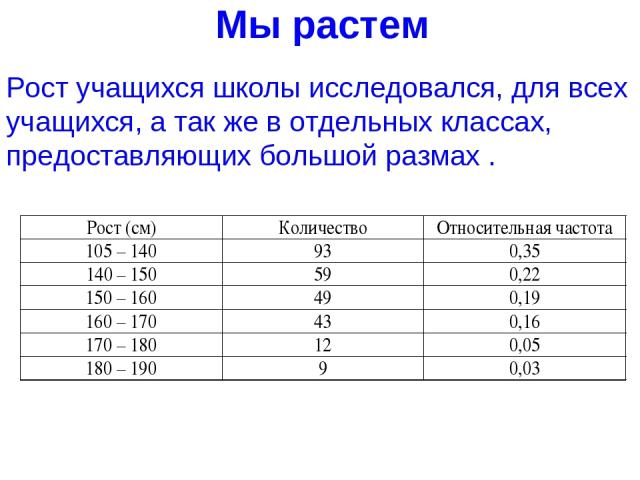
Что такое ИМТ, как он рассчитывается Класс 11?
Формула – ИМТ = (Вес в килограммах), разделенный на (Рост в метрах в квадрате) Нормальный показатель ИМТ — это тот, который находится между 18.5 и 24.9. Это указывает на то, что человек находится в пределах нормального диапазона веса для своего роста.
Что такое вес по отношению к росту в кг?
| Таблица соотношения веса и роста взрослых | ||
|---|---|---|
| 5 футов 5 дюймов (165 см) | 113/138 фунта (51.2 / 62.6 кг) | 122/150 фунтов (55.3 / 68 кг) |
| 5 футов 6 дюймов (168 см) | 117/143 фунтов (53 / 64.8 кг) | 128/156 фунтов (58 / 70.7 кг) |
| 5 футов 7 дюймов (170 см) | 122/149 фунтов (55.3 / 67.6 кг) | 133/163 фунтов (60.3 / 73.9 кг) |
| 5 футов 8 дюймов (173 см) | 126/154 фунтов (57.1 / 69.8 кг) | 139/169 фунтов (63 / 76.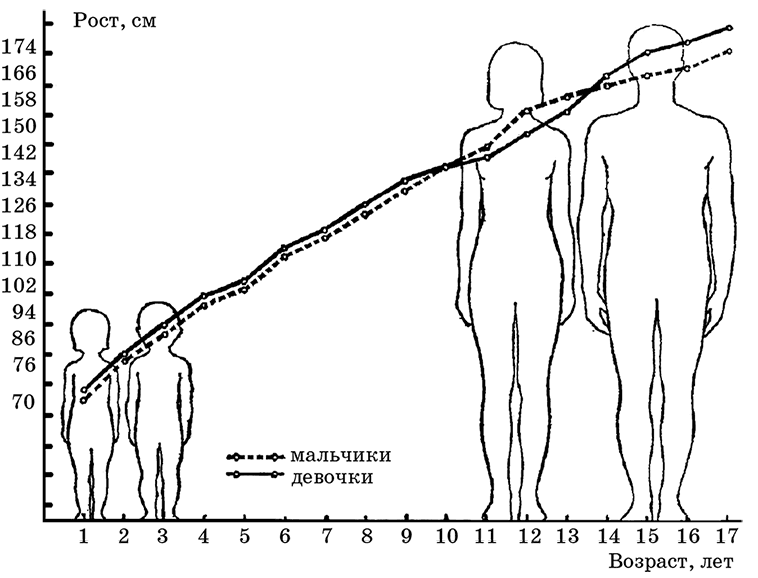 6 кг) 6 кг) |
• 22 января 2022 г.
Что такое женский ИМТ?
Индекс массы тела (ИМТ) – это оценка того, насколько умеренная масса тела человека зависит от его роста и веса. Врачи считают здоровый ИМТ для женщин 18.5-24.9. ИМТ 30 или выше может указывать на ожирение. Измерения ИМТ могут помочь понять, есть ли у него избыточный или недостаточный вес.
Какой у меня ИМТ, если я вешу 120? При расчете в фунтах и дюймах, если человек весит 120 фунтов, а его рост составляет 5 футов 6 дюймов (66 дюймов), ИМТ рассчитывается как 703 х 120/(66)2 = 19.3 кг/м2, что означает, что ИМТ человека составляет 19.3 кг / м2, и считается, что он имеет здоровый вес.
Какой хороший вес для 5 5?
Таблица идеального веса
| M | F | |
|---|---|---|
| 5 ′ 4 ″ | 117 – 143 lbs. | 108 – 132 lbs. |
| 5 ′ 5 ″ | 122 – 150 lbs . | 113 – 138 lbs. |
| 5 ′ 6 ″ | 128 – 156 lbs. | 117 – 143 lbs. |
| 5 ′ 7 ″ | 133 – 163 lbs. | 122 – 149 lbs. |
210 – это нормальный вес?
Нормальный или здоровый вес обозначается ИМТ от 18.5 до 24.9, избыточный вес составляет от 25 до 29.9, а ожирение – от 30 и выше. Согласно расчетам ИМТ, для большинства людей ростом менее 6 футов 4 дюймов вес более 200 фунтов относит их к категории «полных» или «страдающих ожирением».
Справка по статистике точки доступа
Студенты, нуждающиеся в помощи AP Statistics, получат большую пользу от нашей интерактивной программы.
Мы разбираем все ключевые элементы, чтобы вы могли получить адекватную помощь по статистике AP.
Имея под рукой обязательные концепции обучения и актуальные практические вопросы, вы мгновенно получите множество подсказок по статистике AP.
Получите помощь сегодня с нашей обширной коллекцией важной статистической информации AP.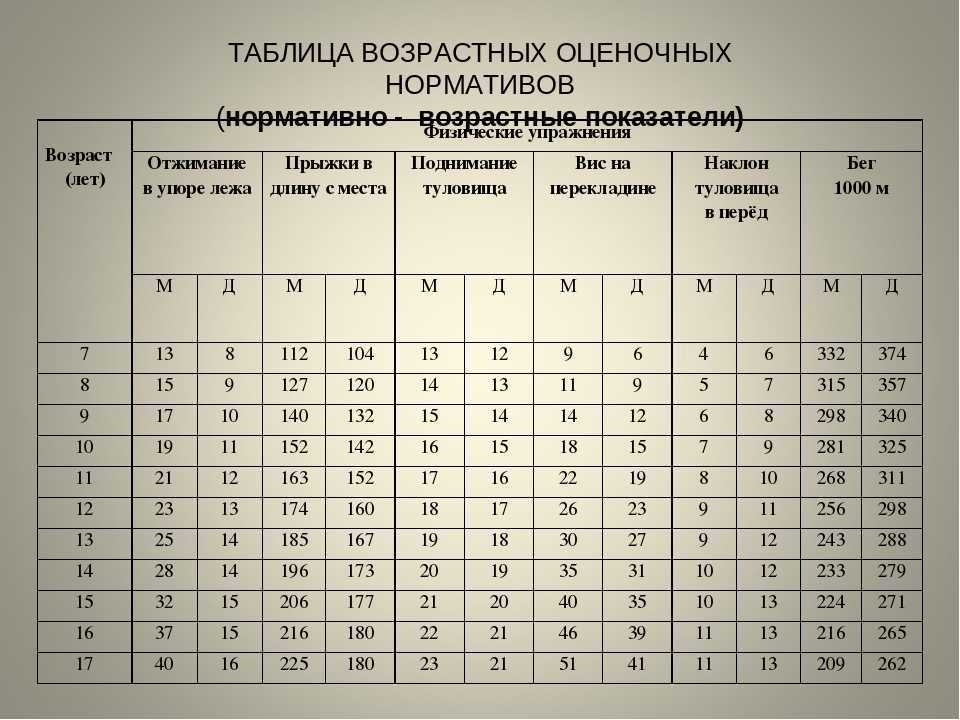
Если вы поступаете на курсы AP Statistics в старших классах, вы можете использовать некоторые дополнительные учебные инструменты, чтобы ваши оценки оставались на уровне, необходимом для получения кредита колледжа. Инструменты обучения Varsity Tutors предлагают множество вариантов, которые помогут вам не сбиться с пути и избавиться от путаницы и беспокойства, которые могут возникнуть у вас. Интерактивная учебная программа AP Statistics Learn by Concept позволяет легко изучать статистические концепции. Эти бесплатные учебные материалы дадут вам возможность углубиться во все конкретные темы, которые рассматриваются на курсах и экзаменах AP Statistics. Вы можете начать с самого начала и пройти через интерактивную программу, чтобы выяснить, на какие темы вам нужно уделить больше времени, а какие у вас есть. Если вы уже знаете, какие концепции вам нужно больше практиковать, вы можете выбрать эти конкретные области и проверить свои способности. Независимо от того, на каком этапе обучения вы находитесь, примеры вопросов AP Statistics будут вам полезны. Нужны ли вам лучшие преподаватели статистики в Буффало, преподаватели статистики в Кливленде или лучшие преподаватели статистики в Хьюстоне, работа с профессионалом может вывести ваше обучение на новый уровень.
Нужны ли вам лучшие преподаватели статистики в Буффало, преподаватели статистики в Кливленде или лучшие преподаватели статистики в Хьюстоне, работа с профессионалом может вывести ваше обучение на новый уровень.
Программа AP Statistics Learn by Concept разделена на три раздела: данные, логические выводы и статистические закономерности и случайные явления. Раздел данных охватывает двумерные данные, информацию о сборе данных, такую как проведение выборочных обследований и экспериментов, графические данные и одномерные данные. В разделе вывода рассматриваются доверительные интервалы, оценка и значимость. В разделе статистических закономерностей и случайных явлений исследуются комбинации независимых случайных величин, нормальное распределение, вероятность и выборочные распределения. Вы сможете исследовать свои знания в остаточных графиках, выборке, экспериментах, процентилях, гипотезах, вероятности и многом другом. Varsity Tutors предлагает такие ресурсы, как бесплатные практические тесты по статистике AP, которые помогут вам в самостоятельном обучении.
Каждый раздел, на который вы нажимаете, дает пример вопроса с возможными ответами на выбор. Выбрав ответ, вы можете прокрутить вниз и увидеть правильный ответ с подробным объяснением того, как решить проблему. Эти примеры вопросов AP Statistics позволяют вам лучше понять, насколько хорошо вы понимаете каждую концепцию. Если вы не уверены в ответе на один из вопросов, не переживайте. Подробное объяснение каждой проблемы поможет вам изучить концепцию. Каждый вопрос AP Statistics был создан профессионалом, а ответы объясняются в простой для понимания форме, что дает вам уверенность в том, что вы изучаете каждую концепцию наиболее эффективным образом. В дополнение к разделу справки по статистике AP и обучению по статистике AP вы также можете рассмотреть некоторые из наших карточек со статистикой AP.
Интерактивная программа AP Statistics Learn by Concept не предназначена для использования в одиночку. Инструменты обучения Varsity Tutors также предлагают вам практические тесты AP Statistics, которые помогут вам ознакомиться с концепцией, по которой вы будете тестироваться.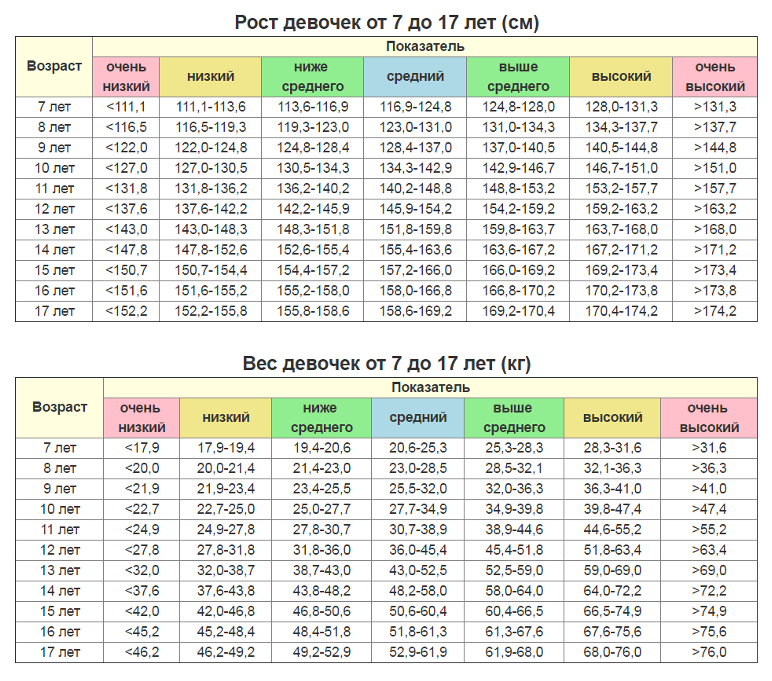 Практические тесты помогут вам перейти к конкретным областям, над которыми вам нужно поработать. Карточки позволяют изучать концепции статистики и могут быть настроены в соответствии с вашими потребностями. «Вопрос дня» позволяет вам решать разные вопросы каждый день и смотреть, как вы продвигаетесь в учебе. Интерактивная учебная программа AP Statistics в сочетании с другими средствами обучения поможет вам создать эффективный учебный план для изучения наиболее важных концепций AP Statistics.
Практические тесты помогут вам перейти к конкретным областям, над которыми вам нужно поработать. Карточки позволяют изучать концепции статистики и могут быть настроены в соответствии с вашими потребностями. «Вопрос дня» позволяет вам решать разные вопросы каждый день и смотреть, как вы продвигаетесь в учебе. Интерактивная учебная программа AP Statistics в сочетании с другими средствами обучения поможет вам создать эффективный учебный план для изучения наиболее важных концепций AP Statistics.
Статистика точки доступа
Данные
Двумерные данные
Как создать остаточные участки
Как делать логарифмические преобразования
Как найти корреляцию
Как найти линейность
Как найти выбросы
Как найти линию регрессии методом наименьших квадратов
Сбор данных
Перепись и исследования
Как провести перепись
Как провести обсервационное исследование
Как провести выборочное обследование
Как определить набор образцов
Как определить обследуемую совокупность
Как сделать случайный выбор для опроса
Как сделать кластерную выборку
Как сделать простую случайную выборку
Как проводить стратифицированную случайную выборку
Как определить источники систематической ошибки в опросе
Как провести эксперимент
Как проводить эксперименты с подобранными парами
Как определить контрольные группы в эксперименте
Как определить экспериментальные единицы
Как делать случайные назначения в эксперименте
Как проводить слепые эксперименты
Как определить смешанные факторы в эксперименте
Как выявить источники смещения в эксперименте
Как выявить эффект плацебо в эксперименте
Графические данные
Как интерпретировать точечные диаграммы
Как интерпретировать гистограммы
Как интерпретировать исходные диаграммы
Одномерные данные
Наборы данных и Z-показатели
Как найти описательные данные из z-показателя
Как найти z-значения для набора данных
Одномерные дескрипторы данных
Как найти межквартильный диапазон для набора данных
Как найти среднее значение для набора данных
Как найти медиану для набора данных
Как найти процентили для набора данных
Как найти квартили для набора данных
Как найти диапазон для набора данных
Как найти стандартное отклонение для набора данных
Как использовать ящичные диаграммы для суммирования набора данных
Вывод
Оценка
Доверительные интервалы
Уверенность и пропорция
Как найти доверительные интервалы для разницы между двумя пропорциями
Как найти доверительные интервалы для пропорции
Доверительные интервалы и среднее значение
Как найти доверительные интервалы для разницы между парными средними
Как найти доверительные интервалы для разницы между непарными средними
Как найти доверительные интервалы для среднего
Доверительные интервалы и регрессия
Как найти доверительные интервалы
Как найти доверительные интервалы для наклона линии регрессии методом наименьших квадратов
Оценки
Как оценить пределы погрешности
Как оценить параметры популяции
Как найти точечные оценщики
Как определить изменчивость оценок
Значение
Определение ошибок
Как определить ошибку типа I
Как определить ошибку типа II
Пропорции больших образцов
Как проводить тесты значимости для больших выборок различий между двумя пропорциями
Среднее значение и линейная регрессия
Как проводить тесты на значимость разницы между двумя средними значениями
Как проводить тесты значимости для среднего
Как проверить значимость наклона линии регрессии методом наименьших квадратов
Логика значимости и установление гипотез
Как проводить односторонние тесты значимости
Как проводить двусторонние тесты значимости
Как установить нулевую гипотезу
Как установить альтернативную гипотезу
Как найти p-значения
Статистические закономерности и случайные явления
Независимая комбинация случайных величин
Зависимость и Независимость
Как идентифицировать зависимые переменные
Как определить независимые переменные
Меры независимых случайных величин
Как найти среднее значение суммы независимых случайных величин
Как найти стандартное отклонение суммы независимых случайных величин
Нормальное распределение
Как определить характеристики нормального распределения
Как пользоваться таблицами нормального распределения
Вероятность
Независимые и зависимые события
Как применять условную вероятность
Как идентифицировать независимые события
Случайные величины
Как выполнить линейное преобразование случайной величины
Как найти среднее значение случайной величины
Как найти распределения вероятностей для дискретных случайных величин
Как найти стандартное отклонение случайной величины
Как имитировать случайное поведение
Правила вероятности
Как использовать правило сложения
Как использовать правило умножения
Распределение образцов
Меры распределения
Как найти распределение хи-квадрат
Как найти t-распределение
Свойства распределений одной выборки
Как найти выборочное распределение выборочного среднего
Как найти выборочное распределение доли выборки
Как использовать центральную предельную теорему
Если вам нужна помощь в подготовке к экзамену AP Statistics, ознакомьтесь с бесплатными ресурсами, предоставляемыми Varsity Tutors, чтобы получить представление о многочисленных способах обучения. Вы можете начать с прохождения бесплатного диагностического теста AP Statistics, чтобы понять, какие концепции вы хорошо знаете, а какие вам еще предстоит изучить. После этого вы можете пройти бесплатные практические тесты AP Statistics, чтобы сосредоточиться на изучении тем, которые вы понимаете хуже всего. Если у вас нет времени пройти весь практический тест AP Statistics, вы можете использовать бесплатные карточки AP Statistics Flashcard от Varsity Tutors, чтобы учиться в течение более коротких периодов времени. Кроме того, не забудьте проверить вопрос дня по статистике AP для ежедневной практики.
Вы можете начать с прохождения бесплатного диагностического теста AP Statistics, чтобы понять, какие концепции вы хорошо знаете, а какие вам еще предстоит изучить. После этого вы можете пройти бесплатные практические тесты AP Statistics, чтобы сосредоточиться на изучении тем, которые вы понимаете хуже всего. Если у вас нет времени пройти весь практический тест AP Statistics, вы можете использовать бесплатные карточки AP Statistics Flashcard от Varsity Tutors, чтобы учиться в течение более коротких периодов времени. Кроме того, не забудьте проверить вопрос дня по статистике AP для ежедневной практики.
Математическая задача: Средний рост – вопрос № 7898, статистика
Средний рост всех учеников 162 см. Рост классного руководителя 178 см. Средний рост всех (учителя и всех учеников) 163 см. Подсчитайте количество учеников в классе.
Правильный ответ:
n = 15Пошаговое объяснение:
n·162 + 178 = 163·(n+1)
n = 15
n = 0 4 n = 15
Наш простой калькулятор уравнений вычисляет это.
Нашли ошибку или неточность? Не стесняйтесь
пишите нам. Спасибо!
Советы по использованию связанных онлайн-калькуляторов
Нужна помощь в вычислении среднего арифметического?
Ищете статистический калькулятор?
У вас есть линейное уравнение или система уравнений и вы ищете ее решение? Или у вас есть квадратное уравнение?
Вы хотите преобразовать единицы длины?
Для решения этой математической задачи вам необходимо знать следующие знания:
- statistics
- mean
- algebra
- equation
- expression of a variable from the formula
Units of physical quantities:
- length
Grade of the word problem:
- Практика для 13-летних
- Практика для 14-летних
Мы рекомендуем вам посмотреть это обучающее видео по этой математической задаче: видео1
- Соответствующий 33321
При измерении 63 учеников были получены следующие данные о росте и соответствующем количестве учеников: 2,167см-3 6,172см-7,173см-9,174см -5,175см-2,177см-1,178см-4,179см-2,181см-1, - Средний рост
В классе 34 ученика. Средний рост учеников 165 см. Каков будет средний рост учеников в классе, когда двое учеников ростом 176 см и 170 см перейдут из этой школы/класса? Средний рост в метрах всех учеников i
Средний рост учеников 165 см. Каков будет средний рост учеников в классе, когда двое учеников ростом 176 см и 170 см перейдут из этой школы/класса? Средний рост в метрах всех учеников i - Измерение 5443
При последнем измерении 4 одноклассника были ростом 164 см, 168 см, 172 см и 176 см, а 5-й одноклассник был на 5 см ниже среднего роста первых четырех. Каков был средний рост пятерых одноклассников в см? - Рассчитать 63894
В 8А классе средний рост 12 девочек 156 см, а средний рост 14 мальчиков 172 см. Рассчитайте среднее количество учеников в 8А. - Тест по математике
Студенты написали тест по математике. Среднее количество баллов, полученное ими, составило 64. Другой студент написал этот тест на 80 баллов. Если бы учитель добавил свой результат к первоначальным, общее среднее значение всех учеников было бы 65. Сколько учеников исходно - Средний рост
Девочек в классе вдвое больше, чем мальчиков. Средний рост девочек 177 см, мальчиков 186 см. Каков средний рост учеников этого класса?
Каков средний рост учеников этого класса? - Дирекция 3845
В школе обучалось 560 учеников. Они наградили 8% всех мальчиков и 10% всех девочек за отличные результаты. В дирекции заявили, что учителя наградили 9% всех учеников. Сколько мальчиков и сколько девочек посещало школу? - Оценка 34581
Всего в классе 26 учеников. При оценке контрольной работы учитель сказал: «4 ученика получили номер один, а это 16%. «Все ли ученики написали контрольную работу? - Математики 11761
Пять лучших математиков в классе воспользовались помощью учителя для расчета среднего балла за работу. Они продиктовали следующие результаты: Миша: «У меня получилось 3,30». Даша: «Это странно, потому что получилось именно 3,45». Яна: «Ты, наверное, 9».0016 - Стандартное отклонение
Рассчитать стандартное отклонение для файла: 63,65,68,69,69,72,75,76,77,79,79,80,82,83,84,88,90 - Салями
Мы есть шесть видов салями из десяти кусочков и один вид салями из четырех кусочков.
 model_selection import train_test_split
model_selection import train_test_split