Найдите закономерность: Найди закономерность, продолжи ряд – задания для детей
Найди закономерность и продолжи ряд
опубликовано Pixel
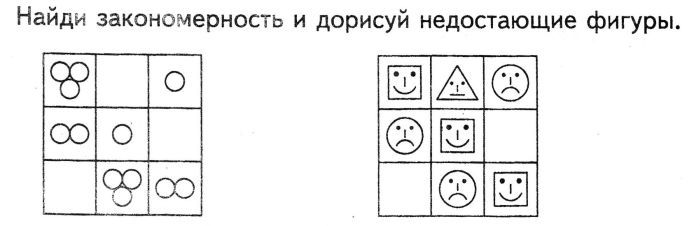
Найди закономерность в изображенных в таблице фигурах и скажи, какая фигура должна быть расположена последней.
Подпишитесь на новости в VKонтакте, Одноклассниках и Telegram
Понравилось?
52 Баллов
Да Нет
excoтест
Не пропустите
Тест: ваш IQ выше чем у 99%, если эти логические задания покажутся вам простыми
Уверены, что у вас все в полном порядке с логикой? А что если это только иллюзия и с логикой у вас все совсем не так […] Больше
Большинство людей недостаточно умны, чтобы пройти этот тест на логику.
 А у вас получится?
А у вас получится?Высокий показатель IQ не является гарантией того, что человек достигнет счастья, будет здравомыслящим или обретет духовное совершенство. Низкий показатель IQ не значит, что человек будет […] Больше
Тест на логику: Сможешь найти лишнее слово?
Тест: Выше ли ваш логический IQ, чем у остальных?
Как думаете: выше ли ваш логический IQ, чем у большинства людей? Проверьте свои догадки и способность решать логические задачи с помощью этого интересного теста. Удачи! Больше
Только люди с высоким IQ идеально справляются с этим тестом на логику
На первый взгляд это испытание не выглядит таким уж сложным. Однако, как показывает практика, дать 100% правильных ответов могут только люди с IQ не ниже […] Больше
Необычный тест на логику: только гении пройдут без ошибок
Прохождение тестов на логику может принести множество пользы для развития ума и мышления.
 Такие тесты помогают тренировать мозг, улучшать концентрацию, развивать логическое и абстрактное мышление, […] Больше
Такие тесты помогают тренировать мозг, улучшать концентрацию, развивать логическое и абстрактное мышление, […] БольшеТест на гениальность. Только творческие натуры могут пройти этот IQ-тест
Всем нам приятно думать, что мы гениальны, если понимаем хотя бы в одной определенной области. Хочешь узнать, есть ли в тебе что-то исключительное, что выделяет […] Больше
Сможете ли вы пройти логический школьный тест 1926 года?
Это вы сейчас можете считать себя источником мудрости и знаний. А как бы вы учились в далеком 1926 году? Говорят, что в те времена уже […] Больше
Тест: Найдите пропавшее число в последовательности
За всё время существования такой оценки, как IQ, было выяснено немало фактов и обнаружено огромное количество закономерностей, связанных с главным показателем интеллектуального развития. Известно, например, […] Больше
Тест на сообразительность: 12 вопросов для самых головастых логиков
На чьем вы уровне? Узнаем в тесте.
 или поделиться: Подпишитесь на новости в VKонтакте, Одноклассниках и Telegram Больше
или поделиться: Подпишитесь на новости в VKонтакте, Одноклассниках и Telegram Больше
Занятие 15 Закономерности в буквах и словах
1. Игра на внимание «Цепочка» (3 мин)
Правила игры: учитель называет ряд слов: «Апельсин – носорог – гном – мороженое – енот…» – и предлагает детям обнаружить закономерность построения ряда (каждое последующее слово начинается на последнюю букву предыдущего) и продолжить его дальше.
Игра может проходить в быстром темпе на выбывание.
2. Упражнение «Алфавит» (5–7 мин)
На доске записаны буквенные ряды. Нужно установить закономерность и продолжить ряд: назвать две следующие буквы.
Примеры рядов букв:
В конце работы – анализ: на какие две группы можно разбить эти ряды.
Например:
1. Ряды, в которых требуется только знание последовательности букв по алфавиту.
2. Ряды, для составления которых требуется не только знание алфавита, но и дополнительные знания (например, о гласных и согласных, о звонких и глухих звуках и т.
3. Работа в группах «Продолжи ряд» (7–8 мин)
Каждая группа получает одинаковые ряды слов, в которых нужно найти закономерность построения ряда и дописать следующее слово.
Примеры рядов слов:
1. Молоко – колесо – сода —…
2. Дом – дочь – доска —…
3. Арбуз – бочка – ветер —…
4. Позвонил – поговорил – поранился —…
5. Киев – Воронеж – Жлобин —…
6. Антилопа – актриса – аптека – …
Ответы и комментарии к ним:
1. Закономерность: две последние буквы каждого предыдущего слова и две первые буквы последующего слова – одинаковые. Значит, нужно написать любое слово, начинающееся на «да»: дамба, далеко и т. д.
2. Закономерность: слова начинаются на «до», каждое последующее слово длиннее на одну букву. Значит, нужно написать любое слово из 6 букв, начинающееся на «до»: дорога, домино и т. д.
3. Закономерность: слова из 5 букв, начинающиеся на буквы, следующие по алфавиту. Значит, нужно написать любое слово из 5 букв, начинающееся на «г»: город, гений и т. д.
д.
4. Закономерность: глаголы из 9 букв с приставкой «по». Значит, нужно написать любой глагол из 9 букв с приставкой «по»: поздравил, посмотрел и т. д.
5. Закономерность: города, каждый последующий начинается на последнюю букву предыдущего. Значит, нужно написать любой город, начинающийся на Н: Новгород, Нью-Йорк и т. д.
6. Закономерность: все слова начинаются на А и заканчиваются на А, количество букв уменьшается (8, 7, 6). Значит, нужно написать слово из 5 букв, которое начинается и заканчивается на букву А. Например, афиша, акула.
В конце – обсуждение результатов всех групп и составление краткой инструкции, на что нужно обращать внимание при выполнении подобных заданий.
Например: сравнить все слова в ряду: какие буквы повторяются, как изменяется количество букв в словах, принадлежность к части речи, значение слов и т. д.4. Домашнее задание (3 мин)
Придумать как можно больше рядов слов, построенных по разным правилам.
Проверка выполнения этого домашнего задания проводится на уроке русского языка.
5. Упражнение «Проверь себя» (7–8 мин)
– Бывают такие буквенные закономерности, когда нужно расшифровать слово, изображённое условными значками. Например, даны слова: пуля, дядя, арка, торт (Учитель записывает слова на доске).
Какое из этих слов зашифровано следующим образом «+ *! *»? («Шифр» записывается на доске.)
– … (дядя, т. к. в слове вторая и четвертая буквы одинаковые)
– А это какое слово: «X # = У»? (Запись на доске.)
– … (Пуля, так как все буквы в слове разные).
На доске открывается несколько рядов слов, нужно выбрать и записать то слово, которое соответствует условным значкам. Возможен вариант выполнения задания, когда все ряды предъявляются не одновременно, а поочередно, по мере их выполнения и проверки.
Примеры рядов закономерностей:
* Х: * стук, кино, крик, няня;
! * = # обед, тара, соус, рама;
?:? = мука, обои, град, лапа;
+? *? лицо, река, желе, окно;
Х = Х О + старт, сосна, ребро, ответ;
* +?? + маска, касса, сумка, лассо;
0 = * Х = слово, олово, казак, шапка, жажда;
= * Х = * тайна, каска, жажда, ванна.
6. Задание на смекалку (7–8 мин)
На доске написаны буквенные ряды, представляющие собой не механическое чередование букв алфавита в каком-либо порядке, а первые буквы определённых устойчивых последовательностей. Нужно обнаружить эту последовательность и продолжить ряд.
Примеры рядов:
7. Игра «Да-нетка» (5–6 мин)
– Три месяца узник находился в старом и мрачном подвале. В качестве пищи ему давали только с ухой хлеб и воду. Когда его освободили, в его темнице, в углу, оказалось много костей. Откуда они взялись?
(Это были рыбьи кости из ухи.)
Комментарий к ответу: при восприятии задания на слух предлог + существительное «с ухой» сливаются в прилагательное «сухой», которое воспринимается как определение к слову «хлеб». И в таком случае действительно непонятно, откуда появились кости, если были только хлеб и вода.
8. Подведение итогов занятия.
Решение задач: поиск закономерности (2–8 классы)
Что это такое?
Поиск закономерности — это стратегия, в которой учащиеся ищут закономерности в данных, чтобы решить проблему. Учащиеся ищут повторяющиеся элементы или числа или серию повторяющихся событий. Следующую задачу можно решить, найдя закономерность:
Учащиеся ищут повторяющиеся элементы или числа или серию повторяющихся событий. Следующую задачу можно решить, найдя закономерность:
В старшей школе 1000 учеников, 1000 шкафчиков. Первый ученик открывает все 1000 шкафчиков; затем второй студент закрывает шкафчики 2, 4, 6, 8, 10 и так далее до шкафчика 1000; третий ученик меняет состояние (открывает закрытые шкафчики, закрывает открытые шкафчики) шкафчиков 3, 6, 9, 12, 15 и так далее; четвертый ученик меняет состояние шкафчиков 4, 8, 12, 16 и так далее. Так продолжается до тех пор, пока каждый ученик не сделает свой ход. Сколько шкафчиков будет открыто в конце?
Чтобы найти ответ, перейдите по ссылке: Задача о шкафчике от докторов математики
Почему это важно?
Шаблоны часто вводятся учащимся без контекста словесной задачи, как в следующем примере: «Найдите шаблон в этой последовательности, объясните, как он работает, и используйте этот шаблон для предсказания следующих четырех чисел. 7, 10, 13 , 16, 19, __, __, __, __.”
7, 10, 13 , 16, 19, __, __, __, __.”
Младшие школьники часто обнаруживают и продолжают использовать шаблоны, в которых используются геометрические фигуры. Например, желтый круг, красный квадрат, зеленый треугольник, желтый круг, красный квадрат, зеленый треугольник и так далее.
Обнаружение закономерностей может помочь учащимся изучить факты умножения, когда они заметят, что 4 x 7 равно 7 x 4 и что все числа в столбце десятков заканчиваются на 0.
Стратегию «Найти закономерность» можно использовать для решения многие математические задачи и могут использоваться в сочетании со многими другими стратегиями, включая составление таблицы, составление списка или упрощение задачи.
Как это сделать?
Предложите учащимся задачу, которая требует от них найти шаблон для решения задачи. Например:
Если построить четырехгранную пирамиду из баскетбольных мячей и не считать дно стороной, сколько шаров будет в шестислойной пирамиде?
Использование совместных учебных групп для поиска решений проблем помогает учащимся формулировать свои мысли, проводить мозговой штурм, обсуждать варианты и обосновывать свою позицию.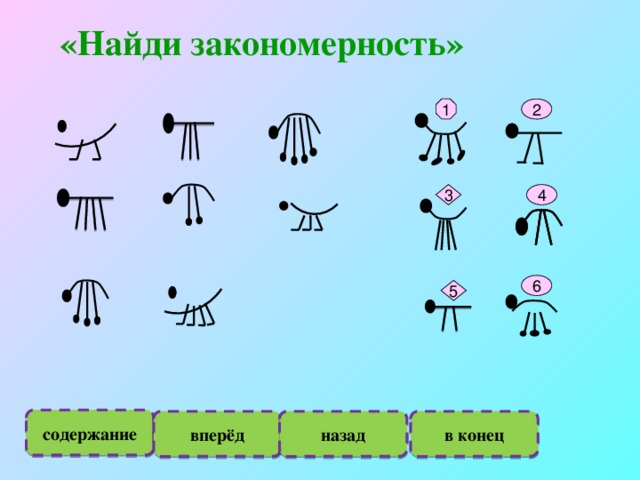 Найдя решение, каждая группа может представить его классу, объяснив, как они пришли к своему решению и почему они считают его правильным. Или учащиеся могут объяснить свои решения в письменной форме, а учитель может показать решения. Затем учащиеся могут ходить по комнате, чтобы прочитать решение каждой группы.
Найдя решение, каждая группа может представить его классу, объяснив, как они пришли к своему решению и почему они считают его правильным. Или учащиеся могут объяснить свои решения в письменной форме, а учитель может показать решения. Затем учащиеся могут ходить по комнате, чтобы прочитать решение каждой группы.
Понять проблему
Продемонстрировать, что первым шагом к решению проблемы является понимание ее. Это включает в себя определение ключевых фрагментов информации, необходимой для поиска ответа. Это может потребовать, чтобы учащиеся прочитали задачу несколько раз или изложили ее своими словами.
Иногда проблему можно решить, просто распознав шаблон, но чаще для поиска решения необходимо расширить шаблон. Составление числовой таблицы может помочь вам более четко увидеть закономерности.
В этой задаче учащиеся понимают:
На верхнем ярусе будет один баскетбольный мяч. Мне нужно найти, сколько шаров будет в каждом ярусе пирамиды, с первого по шестой.
 Мне нужно найти, сколько баскетбольных мячей будет во всей пирамиде.
Мне нужно найти, сколько баскетбольных мячей будет во всей пирамиде.Выберите стратегию
Чтобы успешно использовать эту стратегию, вы должны быть уверены, что модель действительно продолжится. Попросите учащихся объяснить, почему они считают, что эта закономерность предсказуема, а не основана на вероятности. Задачи, которые проще всего решить путем нахождения закономерности, включают те, которые просят учащихся расширить последовательность чисел или сделать прогноз на основе данных. В этой задаче учащиеся также могут составить таблицу или нарисовать картинку, чтобы организовать и представить свое мышление.
Найти закономерность — это подходящая стратегия для решения проблемы. Это закономерность, которая предсказуема и будет продолжаться.
Решить задачу
Начните с верхнего слоя или одного баскетбольного мяча. Определите, сколько шаров должно быть под этим шаром, чтобы получился следующий слой пирамиды.
 При необходимости используйте манипуляторы. Учащиеся могут использовать любые манипуляции, от монет до кубиков и мячей для гольфа. Студенты также могут рисовать картинки, чтобы помочь им решить проблему.
При необходимости используйте манипуляторы. Учащиеся могут использовать любые манипуляции, от монет до кубиков и мячей для гольфа. Студенты также могут рисовать картинки, чтобы помочь им решить проблему.Вы можете предложить группам использовать разные манипуляции, а затем сравнить их решения, чтобы определить, повлиял ли тип манипуляции на решение. Если учащиеся моложе, начните с трех слоев и обсудите их ответы на эту более простую задачу. Затем переходите к другим уровням, когда учащиеся понимают, как решить проблему.
Слой Шары добавлены Шары в этом слое 1 (top) 1 1 2 3 4 (1 + 3 = 4) 3 5 9 (4 + 5 = 9) 4 7 16 (9 + 7 = 16) 5 9 25 (16 + 9 = 25) 69 99999966996699669666669666666666666666666666666666666666666666666666666666666666. = 36)
= 36)Если это помогает визуализировать пирамиду, используйте манипуляции для создания третьего слоя. Запишите число и найдите закономерность. Второй слой добавляет 3 баскетбольных мяча, а следующий добавляет 5 баскетбольных мячей. Каждый раз, когда вы добавляете новый слой, количество баскетбольных мячей, необходимых для создания этого слоя, увеличивается на 2.
- 1
- 1 + 3 = 4
- 4 + 5 = 9
- 9 + 7 = 16
- 16 + 9 = 25
- 25 + 11 = 36
Продолжайте, пока не будут записаны шесть слоев. Как только шаблон найден, учащимся может не понадобиться использовать манипулятивные приемы.
Затем добавьте баскетбольные мячи, из которых сделаны все шесть слоев. Ответ: 91 шар. Посмотрите на список, чтобы увидеть, есть ли другой шаблон. Количество шаров, используемых на каждом уровне, равно квадрату номера слоя. Таким образом, в 10-м слое будет 10 х 10 = 100 шаров.
Проверить
Прочтите задачу еще раз, чтобы убедиться, что ответ на вопрос дан.

Да, я нашел общее количество баскетбольных мячей в шестислойной пирамиде.
Проверьте правильность математических расчетов.
1 + 4 + 9 + 16 + 25 + 36 = 91
Определите, была ли выбрана наилучшая стратегия для этой задачи, или был ли другой способ решения проблемы.
Нахождение закономерности было хорошим способом решить эту проблему, поскольку закономерность была предсказуема.
Объяснить
Учащиеся должны объяснить свой ответ и то, как они его нашли. Студентам важно говорить или писать о своем мышлении. Продемонстрируйте, как написать абзац, описывающий шаги, предпринятые учащимися, и то, как они принимали решения на протяжении всего процесса.
Сначала я начал с первого слоя. Я использовал блоки, чтобы построить пирамиду, и составил список блоков, которые я использовал. Затем я создал таблицу для записи количества шаров в каждом слое.
Layer Balls Added Balls in This Layer 1 (top) 1 1 2 3 4 (1 + 3 = 4) 3 5 9 (4 + 5 = 9) 4 7 16 (9 + 7 = 16) 66666666666669 6666666666666669 66666666669 66666669 6666666666.  (16 + 9 = 25)
(16 + 9 = 25)6 11 36 (25 + 11 = 36) Я сделала четыре слоя и выпилила выкройку. Я видел, что для каждого слоя количество использованных шаров равно количеству слоя, умноженному на него самого. Я закончил узор без блоков, перемножив количество шаров, которые должны быть в слоях 5 и 6.
Затем я сложил все шарики в каждом слое.
1 + 4 + 9 + 16 + 25 + 36 = 91Всего у меня 91 баскетбольный мяч.
Управляемая практика
Предложите учащимся решить следующую задачу, используя стратегию «Найти закономерность».
Женщина пытается сократить количество банок газировки, которые она выпивает каждую неделю. Она планирует, что через несколько недель выпьет только одну банку газировки. Если она начнет с 25 банок в первую неделю, 21 банки во вторую неделю, 17 банок в третью неделю, 13 банок в четвертую неделю и продолжит в том же духе, сколько недель потребуется ей, чтобы достичь своей цели?
Пусть учащиеся поработают в парах, группах или индивидуально, чтобы решить эту задачу.
 Они должны уметь рассказать или написать о том, как они нашли ответ, и обосновать свои рассуждения.
Они должны уметь рассказать или написать о том, как они нашли ответ, и обосновать свои рассуждения.
Как можно расширить эту стратегию?
Математические задачи могут быть простыми, для их решения требуется несколько критериев, или они могут быть многомерными, требующими диаграмм или таблиц для организации мышления учащихся и записи шаблонов. При использовании шаблонов учащимся важно выяснить, сохранится ли шаблон предсказуемо. Попросите учащихся определить, есть ли причина для сохранения шаблона, и убедитесь, что учащиеся используют логику при поиске шаблонов для решения проблем.
Например, если в воскресенье идет дождь, в понедельник идет снег, во вторник идет дождь, а в среду идет снег, будет ли дождь в четверг?
Другой пример: если Лорен выиграла первую и третью партию в шахматы, а Уолтер выиграл вторую и четвертую партию, кто выиграет пятую партию?
Другой пример: если растение выросло на 13 сантиметров за первую неделю и на 10 сантиметров за вторую неделю, на сколько сантиметров оно вырастет за третью неделю?
Поскольку это вопросы о вероятности или природе, убедитесь, что учащиеся понимают, почему шаблоны нельзя использовать для поиска этих ответов.
 А у вас получится?
А у вас получится?