На какие непересекающиеся подмножества можно разбить множество фигур: Разбить на подмножества..Математический язык. Математические выражения.ГДЗ.Математика 5 класс.Дорофеев Г.В.Глава 1.Параграф 1.Задание 22

Разбить на подмножества..Математический язык. Математические выражения.ГДЗ.Математика 5 класс.Дорофеев Г.В.Глава 1.Параграф 1.Задание 22

Разбить на подмножества..Математический язык. Математические выражения.ГДЗ.Математика 5 класс.Дорофеев Г.В.Глава 1.Параграф 1.Задание 22 – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания “Останкино”?

Не знаю как сделать, поможете ?

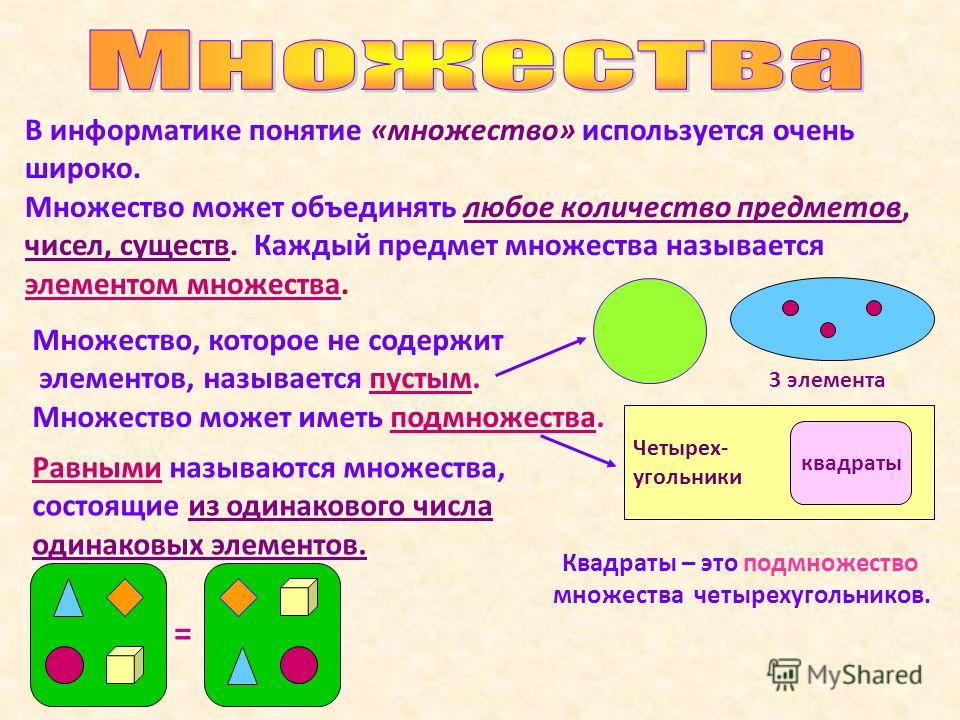
На какие непересекающиеся подмножества (части) можно разбить множество фигур на рисунке? Приведи три примера. Какому признаку разбиения соответствуют записанные рядом с рисунком равенства? Какие свойства сложения и вычитания выражают данные равенства?
 
3  + 4 = 7
4 + 3 = 7
7-3 = 4
7-4 = 3
 

ответы

Я знаю, вот так:
Множество фигур на рисунке можно разбить на 3 подмножества:
1)  по форме; 2) по размеру; 3) по цвету
Записанные равенства соответствуют признаку разбиения по форме.
 

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

3 класс

Репетитор

Химия

Алгебра

похожие вопросы 5

Координатная прямая. Математика 5 класс.Зубарева И.И.Параграф 10, задание 191

Укажите начало отсчёта и координаты точек А, В, С, (Подробнее… )

ГДЗЗубарева И.И.Математика5 класс

Помогите установить соответствие между неравенствами. Математика базовый уровень ЕГЭ – 2017. Вар.№1. Зад.№17. Под руководством Ященко И.В.

   Здравствуйте! Помогите установить соответствие между неравенствами и их решениями: (Подробнее…)

ЕГЭЭкзаменыМатематикаЯщенко И.В.

Помогите выбрать утверждения. Математика базовый уровень ЕГЭ – 2017. Вар.№1. Зад.№18. Под руководством Ященко И.В.

   Здравствуйте! Перед волейбольным турниром измерили рост игроков волейбольной команды города N. Оказалось, что рост каждого из (Подробнее…)

ЕГЭЭкзаменыМатематикаЯщенко И.В.

Вырежи из бумаги № 694 ГДЗ Математика 6 класс Дорофеев Г.В. Часть3.

Вырежи из бумаги 20 одинаковых произвольных треугольников и составь
из них паркет. Всегда ли это можно сделать? Почему?

ГДЗМатематика6 классДорофеев Г. В.

11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.

11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

5. Разбиение множества на классы

Можно говорить о разбиении данного множества на попарно непересекающиеся подмножества или классы тогда, когда одновременно выполняются следующие условия:

1. Все подмножества, образующие разбиение, не пусты.

2. Любые два таких подмножества не пересекаются.

1. Объединение всех подмножеств есть данное множество. Условие 1 иногда опускают.

Символическая запись этого определения следующая.

Пусть дано множество А и совокупность его подмножеств: А₁, А₂, .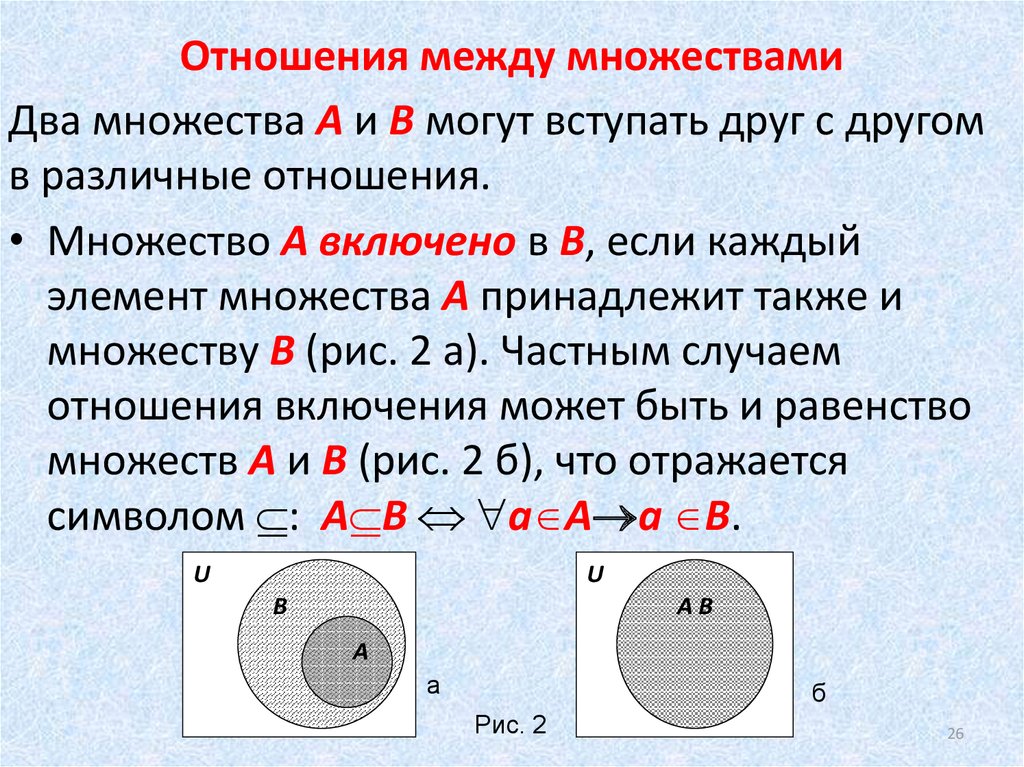 .., А_п (где А_i  А, i = 1, 2,…, n).

Совокупность подмножеств А₁, А₂, …, А_п называется разбиением множества А на классы, а сами подмножества – классами, если выполняются условия:

1. А

   i , i = 1, 2,…, n.

2. A_iA_j = , i, j = 1, 2, …,n; i  j.

3. A₁A₂…A_n = A

Рассмотрим задачи, связанные с оценкой правильности разбиения множества на классы и с самостоятельным разбиением множества на классы при использовании двух свойств.

Задача 7

Учащийся из множества четырехугольников выделил подмножества трапеций, параллелограммов и прямоугольников. Произошло ли разбиение множества на классы?

Решение.

Пусть А – множество четырехугольников. А₁ – множество трапеций А₂ – множество параллелограммов, А₃ – множество прямоугольников.

Разбиение множества А на классы произойдет, если будут выполнены условия (1, 2, 3).

Проверим выполнимость условий: А_i  А, где i = 1, 2, 3.

1. А_i , где i = 1, 2, 3, т.к. каждое множество содержит хотя бы по oдной фигуре.

2. А₁ А₂ = ; А₁ А₃ = ; А₂ А₃, т.

к. А₃  А₂ и А₂ А₃=А₃.

Второе условие не выполняется, значит разбиения множества на классы не произошло.

Задача 8

На какие классы разбивается множество натуральных чисел, если использовать такие свойства: «делится на 2» и «быть однозначным»?

Решение.

Обозначим через А множество четных натуральных чисел, В – множество однозначных чисел, N – множество натуральных чисел. Заметим, то А  В  , т.к. некоторые четные числа являются однозначными, а некоторые однозначные числа – четными. Далее с помощью кругов Эйлера изобразим множества А, В, N и выделим классы разбиения. Из рисунка видим, что их 4. Охарактеризуем каждый из них.

I – множество четных однозначных натуральных чисел.

II – множество четных неоднозначных натуральных чисел.

III – множество нечетных однозначных натуральных чисел.

IV – множество нечетных неоднозначных натуральных чисел.

Упражнения

93. Из множества Р = {1, 2, 3, 4, 5, 6, 7, 8, 9} выделили подмножества А, В и С. Выясните, в каком случае произошло разбиение множества Р на классы:

а) А = {1, 3, 5}, В = {2, 4, 6, 8}, С = {7, 9};

б) А = {5}, В = {3, 4, 8, 9}, С = {1, 6};

в) А = {1, 3, 5), В = {2, 4, 6, 8}, С = {5, 7, 9};

г) А = {1, 3}, В = {4, 6, 8}, С = {5, 6, 9}.

94. Множество А состоит из 3, 4, 5, 6, 7, 8, 9; множество В – его подмножество, состоящее из чисел, которые делятся на 3; множество С – подмножество, состоящее из чисел, которые при делении на 3 дают в остатке 1; множество D – подмножество, состоящее из чисел, которые при делении на 3 дают в остатке 2. Можно ли утверждать, что множество А разбивается в этом случае на попарно непересекающиеся подмножества В, С и D? Произошло ли разбиение множества на классы, если да, то сколько классов?

95. На координатной прямой выделены два множества: (–;2)и (2; +). Можно ли утверждать, что множество действительных чисел разбито на два класса? Можно ли разбить множество точек координатной прямой на 3 класса? на 4 класса? Ответ проиллюстрируйте на примере.

96. Выясните, в каких случаях классификация выполнена верно:

а) треугольники делятся на прямоугольные, тупоугольные и равнобедренные;

б) углы классифицируются на острые, прямые и развернутые;

в) целые числа можно разбить на натуральные числа, число 0 и отрицательные целые числа;

г) глаголы русского языка делятся на глаголы настоящего, прошедшего и будущего времени;

д) члены предложения бывают главные и второстепенные.

97. Из множества Т треугольников выделили два подмножества: X – подмножество прямоугольных треугольников и

Y – подмножество равнобедренных треугольников. Постройте для данных множеств круги Эйлера; установите, на сколько непересекающихся областей разбился круг, изображающий множество Т, и все множества, изображенные этими областями, задайте описанием характеристического свойства. При помощи скольких свойств произведено разбиение множества треугольников на классы?

98. Разбейте множество четырехугольников на классы: а) по какому-либо одному свойству; б) по двум свойствам. Укажите эти свойства, для каждого случая постройте круги Эйлера, установите число непересекающихся областей и выясните, какие множества изображаются этими областями.

99. Множества Р ромбов, Т треугольников и К многоугольников, имеющих угол 30°, являются подмножествами множества М многоугольников. Постройте круги Эйлера для данных множеств, установите, на сколько непересекающихся областей разбился круг, изображающий множество М, и для всех множеств, изображенных этими областями, укажите характеристическое свойство.

100. Из множества треугольников выделены подмножества прямоугольных, равнобедренных и тупоугольных треугольников. Произошло ли разбиение множества на классы?

101. Произведите разбиение на классы множества целых чисел, используя свойства «быть кратным 4» и «быть кратным 5».

102. Укажите классы разбиения множества треугольников, которые получаются при рассмотрении таких свойств, как «иметь хотя две равные стороны» и «иметь прямой угол».

103. Из множества четырехугольников выделили следующие подмножества: а) прямоугольников, не являющихся ромбами; б) ромбов не являющихся прямоугольниками; в) квадратов; г) четырехугольников, не являющихся ни ромбами, ни прямоугольника. Произошло ли разбиение множества на классы?

104. Истинно ли высказывание: «Параллелограммы делятся на прямоугольники, ромбы и квадраты»? Почему?

105. На множестве геометрических фигур плоскости выделены множества фигур, имеющих: а) центр симметрии; б) ось симметрии; в) не имеющих ни центра, ни оси симметрии. Можно ли считать, что произошло разбиение множества на классы?

106. Произведите разбиение множества целых чисел на классы используя такие свойства: «быть однозначным числом» и «быть двузначным числом».

107. Укажите, какие классы разбиения получаются при рассмотрении на множестве треугольников таких свойств: «иметь тупой угол» и «все углы острые».

108. Произошло ли разбиение множества натуральных чисел на классы, если из него выделены подмножества чисел, делящихся на три чисел, которые при делении на 3 дают остаток 1?

109. Установите, правильны ли следующие классификации:

а) натуральные числа делятся на однозначные, двузначные и трехзначные;

б) параллелограммы могут быть прямоугольниками, квадратами и ромбами;

в) треугольники бывают равносторонними и неравносторонними;

г) четырехугольники делятся на параллелограммы и трапеции.

110. Из множества N выделили два подмножества: А – подмножество натуральных чисел, кратных 3, и В – подмножество натуральных чисел, кратных 4. Постройте круги Эйлера для множеств N, А и В; установите, на сколько попарно непересекающихся множеств произошло разбиение множества N; укажите характеристические свойства этих множеств.

111. Из множества параллелограммов выделили подмножество прямоугольников и подмножество квадратов. Постройте круги Эйлера для данных множеств. Можно ли утверждать в данном случае, что множество параллелограммов разбито на 3 попарно непересекающихся подмножества: квадраты; прямоугольники, не являющиеся квадратами; параллелограммы, не являющиеся прямоугольниками?

абстрактная алгебра – Общие вопросы о классах эквивалентности и разбиениях

Идея первого из них такова: для данного разбиения $\Delta$ $X$ это разбиение индуцирует отношение эквивалентности на $X$.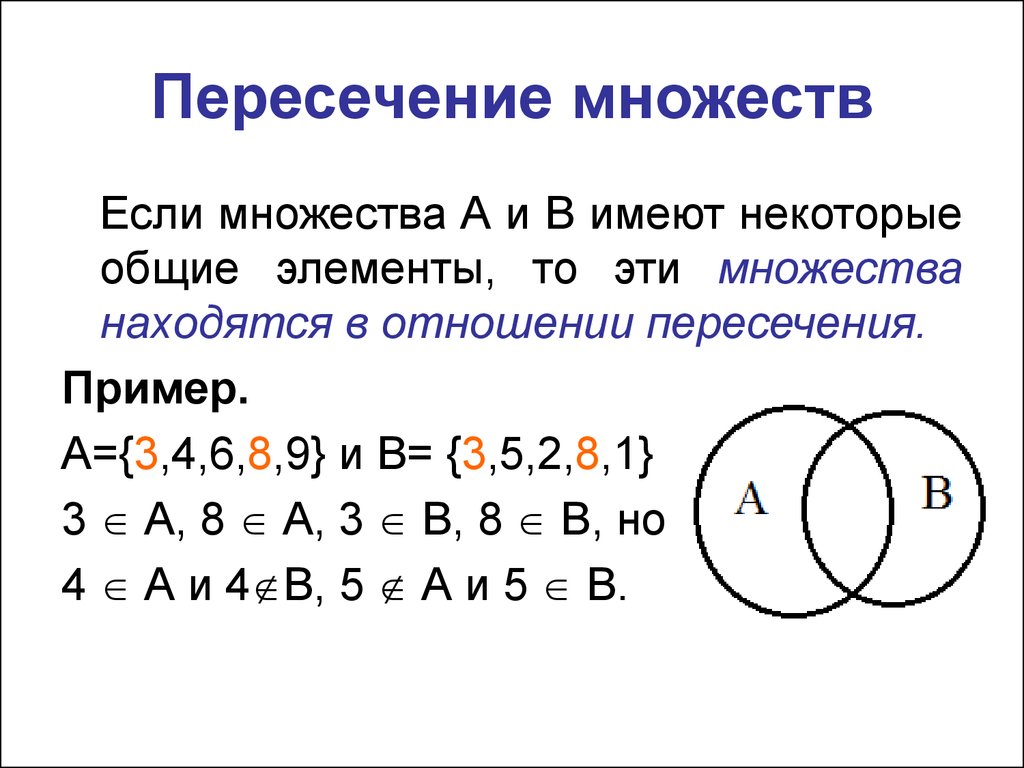 А именно, мы говорим, что $x$ и $y$ находятся в отношении , если они принадлежат одному и тому же множеству раздела . Вы можете проверить, что это действительно отношение эквивалентности. Потому что

$(1)$ $x$ всегда находится в том же множестве, что и $x$.

$(2)$ Если $x$ находится в том же множестве, что и $y$, то $y$ находится в том же множестве, что и $x$.

$(3)$ Если $x$ находится в том же множестве, что и $y$, и $y$ находится в asme-наборе как $z$, то $x$ находится в asme-наборе как $z$.

Для данного отношения $\sim $ на множестве $X$ мы называем его отношением эквивалентности, если оно обладает следующими тремя свойствами:

$(1)$ Рефлексивность $x\sim x$. То есть каждый элемент находится в отношении к самому себе.

$(2)$ Симметрия Если $x\sim y$, то $y\sim x$. То есть, если $x$ находится в отношении к $y$, то $y$ находится в отношении к $x$.

$(3)$ Транзитивность Если $x\sim y$ и $y\sim z$, то $x\sim z$. То есть, если $x$ находится в связи с $y$ и $y$ находится в связи с $z$, то $x$ находится в связи с $z$.

Можно проверить, что отношение делимости является транзитивным и рефлексивным. Вы проверяете, что отношение включения также транзитивно и рефлексивно, но не симметрично. Можно проверить, что сравнение $\mod{}$ числа $n$ является отношением эквивалентности, а значит, и обычным равенством чисел.

Учитывая отношение $\sim$ на множестве $X$ и элемент $X$, мы определяем класс эквивалентности $[[x]]$ множества $x$ как все элементы в $X$, которые стоят по отношению к $x$. То есть

$$[[x]]=\{a\in X:a\sim x\}$$

Вы можете проверить классы эквивалентности:

$(1)$ Непусто : Для каждый $x$, $x\in [[x]]$.

$(2)$ Либо не пересекается, либо равно : Если в $[[x]]\cap[[y]]$ есть один элемент $p$, то $p\sim y$ и $p \сим х$. Рефлексивность означает $y\sim p$ и $p\sim x$, поэтому транзитивность означает $y\sim x$.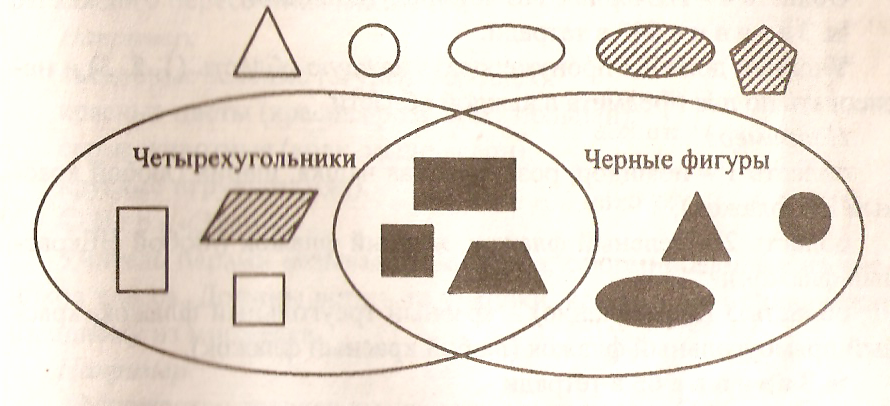 Рефлексивность снова дает $y\sim x$. Таким образом, всякий раз, когда $a\in [[x]]$, $a\sim x$ и $x\sim y$, откуда $a\sim y$. Аналогично всякий раз, когда $b\in [[y]]$, $b\sim y$ и $y\sim x$, откуда $b\sim x$. Это означает $[[x]]=[[y]]$.

Это означает, что они являются разделом $X$. Таким образом, любое разбиение индуцирует отношение эквивалентности и наоборот.

Что касается первого, что вы говорите: если под уникальным вы подразумеваете $x\sim y\iff x=y$, то у вас есть отношение эквивалентности равенства, которое просто индуцирует разбиение $X$ на одиночные элементы его элементы.

В последнем вопросе вы говорите об эквивалентности на разделенных подмножествах . Я предполагаю, что вы имеете в виду отношение эквивалентности, но что вы подразумеваете под «на разделенных подмножествах»?

Относительно части “Разбиение действительных чисел на подмножества с равным количеством знаков после запятой”. Вспомним, что существуют рациональные числа с неконечным десятичным представлением, и любое иррациональное число будет иметь бесконечное десятичное расширение.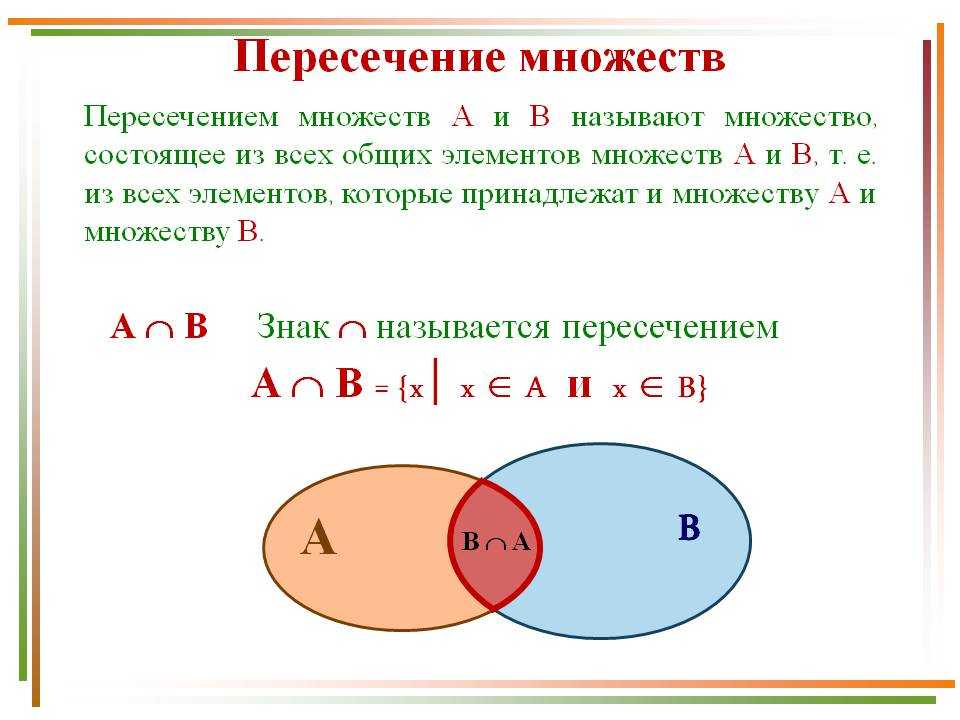 {-1}=0.\hat 3$. В противном случае, если число иррациональное, оно переходит в $\mathbb I$, множество иррациональных чисел.

реальный анализ – Любое открытое подмножество $\Bbb R$ является счетным объединением непересекающихся открытых интервалов

Это доказательство является расширенной версией хорошего доказательства, предложенного Stromael и лучше всего подходит для начинающих, которые хотят понять каждую деталь (та, которая для любого состоявшегося математика логически кажется тривиальной) доказательства.

$ \textbf{Доказательство:} $

Пусть $U \subseteq \mathbb{R}$ открыто, и пусть $x \in U$. Тогда либо $x$ рационально, либо $x$ иррационально.

Предположим, что $x$ рационально, тогда определите

\begin{align} I_x = \bigcup\limits_{\substack{I\text{открытый интервал} \\ x~\in~I~\subseteq~U} } I,\end{align}

Утверждение : $I_x$ — это интервал, $I_x$ открыт и $ I_x \subseteq U $

Определение: Интервал — это подмножество $ I \subseteq \mathbb{ R}$ такое, что для всех $ a

Теперь рассмотрим любой $ a

Обозначим через $I_a$ такой интервал, что $x\inI_a$ и $a\inI_a$. Другими словами, $I_a$ — это один из интервалов из объединения $I_x$, содержащих $a$. Таким же образом пусть $I_b$ будет интервалом таким, что $x\inI_b$ и $b\inI_b$.

1. $c=x$: Если $c=x$, то по построению $I_x$, $c\in I_x$

2. $ c

3. $ c > x $: Если $ c>x $, то либо $ a Поскольку $x\inI_b$, то поскольку $I_b$ является интервалом $c\inI_b$ и, следовательно, $c\inI_x$. Что касается второго случая, обратите внимание, что поскольку $ x \in I_b$ мы имеем $ a \in I_b $. Но тогда, поскольку $ I_b $ является интервалом, мы имеем $ c \in I_b $ и, следовательно, $ c \in I_x$. Отсюда мы сделали вывод, что $ c \in I_x $.

Это доказывает, что $ I_x $ является интервалом.

$ I_x $ открыто, потому что это объединение открытых множеств.

$ I_x \subseteq U $ по построению.

Предположим, что $x$ иррационально, тогда в силу открытости $U$ существует $\varepsilon > 0$ такое, что $(x – \varepsilon, x + \varepsilon) \subseteq U$, и по свойству действительных чисел что для любого иррационального числа существует последовательность рациональных единиц, сходящаяся к этому иррациональному числу, существует рациональное $y \in (x – \varepsilon, x + \varepsilon) $. Тогда по построению $ (x – \varepsilon, x + \varepsilon) \subseteq I_y $.