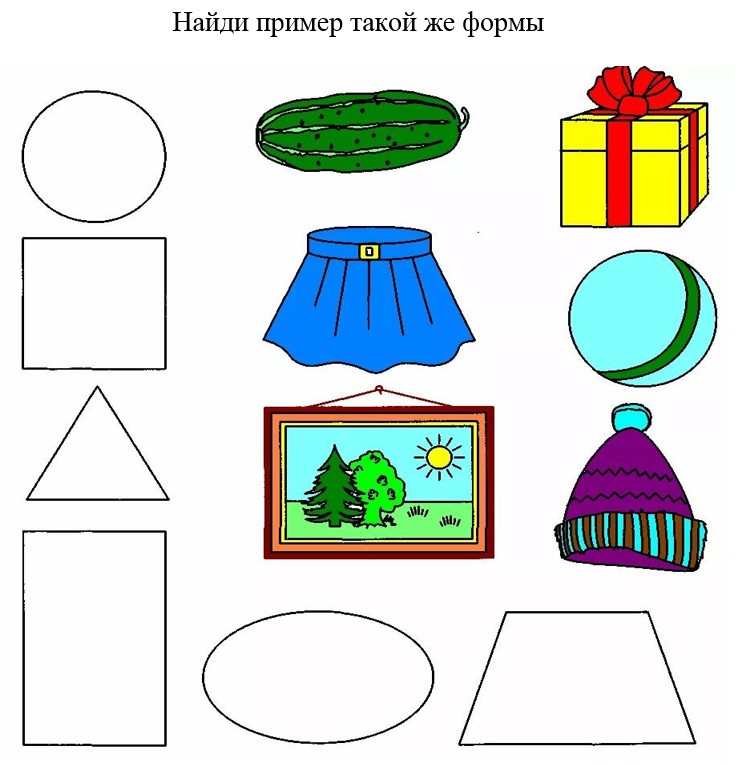
На что похож квадрат для детей картинки: Геометрические фигуры и предметы, похожие на них. | Учебно-методический материал по математике (средняя группа) по теме:

Составить рисунок из геометрических фигур. Картинки животных из геометрических фигур

Этот проективный психогеометрический онлайн тест создан на основе модификации психоаналитиком А.Ф. Ермошиным идеографического теста Либиных. Тест базируется на комбинации трех принципов психографического анализа личности:

• предпочтения семантики основных геометрических форм
• конструктивные рисунки
• психографическое изображение фигуры человека

Пройдя тест, Вы узнаете тип Вашей личности и его описание, а также экспертную оценку, отношения с противоположным полом, свой общепсихологический статус и самоописание людей с таким же типом психики как у Вас (возможно, и Вы говорите что-то подобное).

Инструкция к тесту
Из геометрических фигур – треугольника, квадрата, круга – требуется составить рисунок человека. При этом, во-первых, нужно использовать ровно десять фигур, а, во-вторых, каждая геометрическая фигура (треугольник, квадрат, круг) должна использоваться хотя бы один раз.

Фигуры можно масштабировать, вращать, накладывать друг на друга. Особой аккуратности и художественной достоверности не требуется. Рисуйте так, как Вам подсказывает Ваша фантазия. Когда все десять фигур будут использованы, появится кнопка «Результат теста».

Управление фигурами
перетаскивание: клик на элементе + перемещение мыши
масштаб: указатель мыши над фигурой + колесико мыши
масштаб по ширине: клавиша «W» + колесико мыши
масштаб по высоте: клавиша «H» + колесико мыши
вращение: клавиша «R» + колесико мыши
добавить фигуру: перетащите фигуру в рабочую область (прямоугольник бледно-желтого цвета)
удалить фигуру: перетащите фигуру за пределы рабочей области

14.11.2016 119092 +928

Пройти бесплатные психологические тесты—–

Умеете ли вы составлять животных из геометрических фигур?

Никогда не пробовали?

Тогда стоит посмотреть картинки на сайте, где из геометрических фигур сложены разнообразные животные.

Предложите эти рисунки своим детям: наверняка они оценят их оригинальность.

Вполне понятно, что встает вопрос: одно дело художники, но зачем детям такое видение мира?

Конечно, картинки с животными из геометрических фигур не ставят целью навязать малышу неординарное видение мира. Однако почему бы ни показать, что и такая трактовка всего, что нас окружает, возможна.

По картинкам можно интересно и увлекательно изучать названия геометрических фигур. От простого показа и повторения ребенок быстро устает и начинает отказываться от занятий, даже если их проводит мама в домашних условиях. Другое дело, если фигуры необходимо отыскать в животных. Тут просыпается неподдельное любопытство.

Когда вы полностью изучите с ребенком названия фигур и их внешний вид, попросите ребенка проявить свое видение мира. Пусть для примера будет взято животное или любой предмет.

Спросите: на какую геометрическую фигуру он похож.

Такие упражнения:

1. — развивают наблюдательность;
2. — совершенствуют логическое и пространственное мышление;
3. — способствуют видению скрытого за внешней оболочкой предмета.

Малыш учится видеть и наблюдать то, что не могут или не умеют видеть другие . Это ли не воспитание художника и творческой личности?

А можно поиграть в обратную игру. Представьте, что вы художники-абстракционисты. Пусть один из вас нарисует что-нибудь, состоящее из геометрических фигур, а другой попытается отгадать, что нарисовано. Живописцы постмодернизма часто зашифровывали свои рисунки на полотне, заполненной квадратами, прямоугольниками, трапециями… такие же головоломки предлагали ранее детские журналы.

Вы и сами можете создать такую головоломку: нужно лишь немного фантазии и взгляд на мир сквозь призму геометрии.

Примеры страниц тетради с аппликациями для детей от 1 года до 3 лет.

Выявление индивидуально-типологических различий.

Инструкция к тесту

«Вам нужно нарисовать фигуру человека, составленную из 10 элементов, среди которых могут быть треугольники, круги, квадраты. Вы можете увеличивать или уменьшать эти элементы (геометрические фигуры) в размерах, накладывать друг на друга по мере надобности. Важно, чтобы все эти три элемента в изображении человека присутствовали, а сумма общего количества использованных фигур была равна десяти. Если при рисовании вы использовали большее количество фигур, то нужно зачеркнуть лишнее, если же вами использовано фигур меньше, чем десять, необходимо дорисовать недостающие. Выполните рисунок по данной инструкции».

Материал : испытуемым предлагается три листа бумаги размером 10×10 см, каждый лист нумеруется и подписывается. На листе № 1 выполняется первый пробный рисунок; далее, соответственно, на листе № 2 – второй, на листе № 3 – третий. После выполнения трех рисунков данные обрабатываются. При нарушении инструкции материал не обрабатывается.

Обработка результатов теста

Обработка данных производится следующим образом: подсчитывается количество затраченных в изображении человечка треугольников, кругов и квадратов (по каждому рисунку отдельно), и результат записывается в виде трехзначных чисел, где

• сотни обозначают количество треугольников ,
• десятки – количество кругов ,
• единицы -количество квадратов .

Эти трехзначные цифры составляют так называемую «формулу рисунка», по которой происходит отнесение рисующих к соответствующим типам и подтипам, которые представлены в таблице.

Интерпретация результатов теста

Интерпретация теста основана на том, что геометрические фигуры, используемые в рисунках, различаются по семантике. Треугольник обычно относят к «острой», «наступательной» фигуре, связанной с мужским началом. Круг – фигура обтекаемая, более созвучна с сочувствием, мягкостью, округлостью, женственностью. Из элементов квадратной формы строить что-либо легче, чем из других, поэтому квадрат , прямоугольник интерпретируются как специфически техническая конструктивная фигура, «технический модуль».

Типы личности

I тип – «руководитель ». Обычно это люди, имеющие склонность к руководящей и организаторской деятельности. Ориентированы на социально-значимые нормы поведения, могут обладать даром хороших рассказчиков, основывающимся на высоком уровне речевого развития.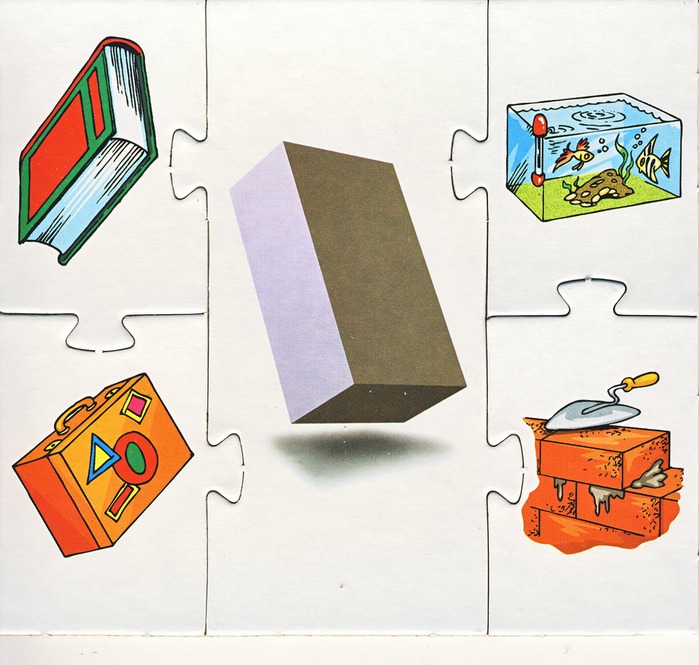 Обладают хорошей адаптацией в социальной сфере, доминирование над другими удерживают в определенных границах.

Формулы рисунков : 901, 910, 802, 811, 820, 703, 712, 721, 730, 604, 613, 622, 631, 640.

• Наиболее жестко доминирование над другими выражено у подтипов 901, 910, 802, 811, 820;
• ситуативно -у 703, 712, 721, 730;
• при воздействии речью на людей – вербальный руководитель или «преподавательский подтип» – 604, 613, 622, 631, 640.

Нужно помнить, что проявление данных качеств зависит от уровня психического развития. При высоком уровне развития индивидуальные черты развиты, реализуемы, достаточно хорошо осознаются. При низком уровне развития могут не выявляться в профессиональной деятельности, а присутствовать ситуативно, хуже, если неадекватно ситуациям. Это относится ко всем характеристикам.

II тип – «ответственный исполнитель » обладает многими чертами типа «руководитель», однако в принятии ответственных решений часто присутствуют колебания.

Данный тип людей более ориентирован на «умение делать дело», высокий профессионализм, обладает высоким чувством ответственности и требовательности к себе и другим, высоко ценит правоту, т.е. характеризуется повышенной чувствительностью к правдивости. Часто они страдают соматическими заболеваниями нервного происхождения как следствие перенапряжения.

Формулы рисунков : 505, 514, 523, 532, 541, 550.

III тип – «тревожно-мнительный » -характеризуется разнообразием способностей и одаренности – от тонких ручных навыков до литературной одаренности. Обычно людям данного типа тесно в рамках одной профессии, они могут поменять ее на совершенно противоположную и неожиданную, иметь также хобби, которое по сути является второй профессией. Физически не переносят беспорядок и грязь. Обычно конфликтуют из-за этого с другими людьми. Отличаются повышенной ранимостью и часто сомневаются в себе. Нуждаются в мягком подбадривании.

Формулы рисунков : 406, 415, 424, 433, 442, 451, 460.

• 415 – «поэтический подтип» – обычно лица, имеющие такую формулу рисунка, обладают поэтической одаренностью;
• 424 – подтип людей, узнаваемых по фразе: «Как это можно плохо работать? Я себе не представляю, как это можно плохо работать». Люди такого типа отличаются особой тщательностью в работе.

IV тип – «ученый ». Эти люди легко абстрагируются от реальности, обладают «концептуальным умом», отличаются способностью разрабатывать «на все» свои теории. Обычно обладают душевным равновесием и рационально продумывают свое поведение.

Формулы рисунков : 307, 316, 325, 334, 343, 352, 361, 370.

• 316 характеризуется способностями создавать теории, по преимуществу глобальные, или осуществлять большую и сложную координационную работу;
• 325 – подтип, характеризующийся большой увлеченностью познания жизни, здоровья, биологическими дисциплинами, медициной.

Представители данного типа часто встречаются среди лиц, занимающихся синтетическими видами искусства: кино, цирк, театрально-зрелищная режиссура, мультипликация и т. д.

V тип – «интуитивный ». Люди этого типа обладают сильной чувствительностью нервной системы, высокой ее истощаемостью.

Легче работают на переключаемости от одной деятельности к другой, обычно выступают «адвокатами меньшинства», за которым стоят новые возможности. Обладают повышенной чувствительностью к новизне. Альтруистичны, часто проявляют заботу о других, обладают хорошими ручными навыками и образным воображением, что дает возможность заниматься техническими видами творчества.

Обычно вырабатывают свои нормы морали, обладают внутренним самоконтролем, т.е. предпочитают самоконтроль, отрицательно реагируя на посягательства, касающиеся их свободы.

Формулы рисунков : 208, 217, 226, 235, 244, 253, 262, 271, 280.

• 235 – часто встречается среди профессиональных психологов или лиц с повышенным интересом к психологии людей;
• 244 – обладает способностью литературного творчества,
• 217 – обладает способностью к изобретательской деятельности;
• 226 – большая потребность в новизне, обычно ставит очень высокие критерии достижений для себя.

VI тип – «изобретатель, конструктор, художник ». Часто встречается среди лиц с «технической жилкой». Это люди, обладающие богатым воображением, пространственным видением, часто занимаются различными видами технического, художественного и интеллектуального творчества. Чаще интравертированы, так же, как интуитивный тип, живут собственными моральными нормами, не приемлют никаких воздействий со стороны, кроме само контроля.

Эмоциональны, одержимы собственными оригинальными идеями.

Формулы рисунков : 109, 118, 127, 136, 145, 019, 028, 037, 046.

• 019 – встречается среди лиц, хорошо владеющих аудиторией;
• 118 – тип с наиболее сильно выраженными конструктивными возможностями и способностью к изобретениям.

VII тип – «эмотивный ». Обладают повышенным сопереживанием по отношению к другим людям, тяжело переживают жестокие кадры фильма, могут надолго быть выбитыми из колеи и быть потрясенными от жестоких событий. Боли и заботы других людей находят у них участие, сопереживание и сочувствие, на которое они тратят много собственной энергии, в результате становится затруднительной реализация их собственных способностей.

Формулы рисунков : 550, 451, 460, 352, 361, 370, 253, 262, 271, 280, 154, 163, 172, 181, 190, 055, 064, 073, 082, 091.

VIII тип – «нечувствительный к переживаниям других ». Обладает противоположной тенденцией эмотивному типу. Обычно не чувствует переживаний других людей или относится к ним с невниманием и даже усиливает давление на людей.

Если это хороший специалист, то он может заставить других делать то, что он считает нужным. Иногда для него характерна «черствость», которая возникает ситуативно, когда в силу каких-либо причин человек замыкается в кругу собственных проблем.

Формулы рисунков : 901, 802, 703, 604, 505, 406, 307, 208, 109.

Когда понадобится: для выявления типов личностей: руководитель, исполнитель, ученый, изобретатель и т. п.

ТЕСТ
«Конструктивный рисунок человека из геометрических фигур»

Инструкция

Нарисуйте, пожалуйста, фигуру человека, составленную из 10 элементов, среди которых могут быть треугольники, круги, квадраты. Вы можете увеличивать или уменьшать эти элементы (геометрические фигуры) в размерах, накладывать друг на друга по мере надобности.

Важно, чтобы все эти три элемента в изображении человека присутствовали, а сумма общего количества использованных фигур была равна 10. Если при рисовании вы использовали большее количество фигур, то нужно зачеркнуть лишние, если же вами использовано фигур меньше чем 10, необходимо дорисовать недостающие.

Ключ к тесту «Конструктивный рисунок человека из геометрических фигур»

Описание

Тест «Конструктивный рисунок человека из геометрических фигур» предназначен для выявления индивидуально-типологических различий.

Сотруднику предлагают три листа бумаги размером 10 × 10 см. Каждый лист нумеруется и подписывается. На первом листе выполняется первый пробный рисунок, далее, соответственно, на листе втором – второй, на листе третьем – третий.

Сотруднику необходимо на каждом листе нарисовать фигуру человека, составленную из 10 элементов, среди которых могут быть треугольники, круги, квадраты. Сотрудник может увеличивать или уменьшать эти элементы (геометрические фигуры) в размерах, накладывать друг на друга по мере надобности. Важно, чтобы все эти три элемента в изображении человека присутствовали, а сумма общего количества использованных фигур была равна 10.

Если при рисовании сотрудник использовал большее количество фигур, то ему необходимо зачеркнуть лишние, если же использовал фигур меньше чем 10, ему необходимо дорисовать недостающие.

При нарушении инструкции данные не обрабатываются.

Пример рисунков, сделанных тремя оцениваемыми

Обработка результата

Подсчитайте количество затраченных в изображении человечка треугольников, кругов и квадратов (по каждому рисунку отдельно). Запишите результат в виде трехзначных чисел, где:

• сотни обозначают количество треугольников;
• десятки – количество кругов;
• единицы – количество квадратов.

Эти трехзначные цифры составляют так называемую формулу рисунка, по которой происходит отнесение рисующих к соответствующим типам и подтипам.

Интерпретация результата

Собственные эмпирические исследования, в которых получено и проанализировано более 2000 рисунков, показали, что соотношение различных элементов в конструктивных рисунках не случайно. Анализ позволяет выделить восемь основных типов, которым соответствуют определенные типологические характеристики.

Интерпретация теста основана на том, что геометрические фигуры, использованные в рисунках, различаются по семантике:

• треугольник обычно относят к острой, наступательной фигуре, связанной с мужским началом;
• круг – фигура обтекаемая, более созвучна с сочувствием, мягкостью, округлостью, женственностью;
• квадрат, прямоугольник интерпретируются как специфически техническая конструктивная фигура, технический модуль.

Типология, основанная на предпочтении геометрических фигур, позволяет сформировать своего рода систему индивидуально-типологических различий.

Типы

I тип – руководитель

Формулы рисунков: 901, 910, 802, 811, 820, 703, 712, 721, 730, 604, 613, 622, 631, 640. Наиболее жестко доминирование над другими выражено у подтипов 901, 910, 802, 811, 820; ситуативно – у 703, 712, 721, 730; при воздействии речью на людей – вербальный руководитель или преподавательский подтип – 604, 613, 622, 631, 640.

Обычно это люди, имеющие склонность к руководящей и организаторской деятельности, ориентированные на социально значимые нормы поведения, могут обладать даром хороших рассказчиков, основывающимся на высоком уровне речевого развития. Обладают хорошей адаптацией в социальной сфере, доминирование над другими удерживают в определенных границах.

Нужно помнить, что проявление данных качеств зависит от уровня психического развития. При высоком уровне развития индивидуальные черты развития реализуемы, достаточно хорошо осознаются.

При низком уровне они могут не выявляться в профессиональной деятельности, а присутствовать ситуативно, хуже, если неадекватно ситуациям. Это относится ко всем характеристикам.

II тип – ответственный исполнитель

Формулы рисунков: 505, 514, 523, 532, 541, 550.

Данный тип людей обладает многими чертами типа «руководитель», являясь расположенным к нему, однако в принятии ответственных решений часто присутствуют колебания. Такой человек ориентирован на умение делать дело, высокий профессионализм, обладает высоким чувством ответственности и требовательности к себе и другим, высоко ценит правоту, то есть характеризуется повышенной чувствительностью к правдивости. Часто он страдает соматическими заболеваниями нервного происхождения вследствие перенапряжения.

III тип – тревожно-мнительный

Формулы рисунков: 406, 415, 424, 433, 442, 451, 460.

Данный тип людей характеризуется разнообразием способностей и одаренности – от тонких ручных навыков до литературной одаренности. Обычно этим людям тесно в рамках одной профессии, они могут поменять ее на совершенно противоположную и неожиданную, иметь также хобби, которое по сути является второй профессией. Физически не переносят беспорядка и грязи. Обычно конфликтуют из-за этого с другими людьми. Отличаются повышенной ранимостью и часто сомневаются в себе. Нуждаются в подбадривании.

Кроме этого, 415 – «поэтический подтип» – обычно лица, имеющие такую формулу рисунка, обладают поэтической одаренностью; 424 – подтип людей, узнаваемых по фразе «Как это можно плохо работать? Я себе не представляю, как это можно плохо работать». Люди такого типа отличаются особой тщательностью в работе.

IV тип – ученый

Формулы рисунков: 307, 316, 325, 334, 343, 352, 361, 370.

Эти люди легко абстрагируются от реальности, обладают концептуальным умом, отличаются способностью разрабатывать все свои теории. Обычно обладают душевным равновесием и рационально продумывают свое поведение.

Подтип 316 характеризуется способностью создавать теории, по преимуществу глобальные, или осуществлять большую и сложную координационную работу.

325 – подтип, характеризующийся большой увлеченностью познания жизни, здоровья, биологическими дисциплинами, медициной. Представители этого типа часто встречаются среди лиц, занимающихся синтетическими видами искусства: кино, цирк, театрально-зрелищная режиссура, мультипликация и т. д.

V тип – интуитивный

Формулы рисунков: 208, 217, 226, 235, 244, 253, 262, 271, 280.

Люди этого типа обладают сильной чувствительностью нервной системы, ее высокой истощаемостью. Легче работают на переключаемости от одной деятельности к другой, обычно выступают адвокатами меньшинства. Обладают повышенной чувствительностью к новизне. Альтруистичны, часто проявляют заботу о других, обладают хорошими ручными навыками и образным воображением, что дает им возможность заниматься техническими видами творчества. Обычно вырабатывают свои нормы морали, обладают внутренним самоконтролем, то есть предпочитают самоконтроль, отрицательно реагируя на посягательства, касающиеся их свободы.

235 – часто встречается среди профессиональных психологов или лиц с повышенным интересом к психологии;

244 – обладает способностью к литературному творчеству;

217 – обладает способностью к изобретательской деятельности;

226 – имеет большую потребность в новизне, обычно ставит очень высокие критерии достижений для себя.

VI тип – изобретатель, конструктор, художник

Формулы рисунков: 109, 118, 127, 136, 145, 019, 028, 037, 046.

Часто встречается среди лиц с технической жилкой. Это люди, обладающие богатым воображением, пространственным видением, часто занимаются различными видами технического, художественного и интеллектуального творчества. Чаще интровертированы, так же как интуитивный тип, живут собственными моральными нормами, не приемлют никаких воздействий со стороны, кроме самоконтроля. Эмоциональны, одержимы собственными оригинальными идеями.

Также выделяют особенности следующих подтипов:

019 – встречается среди лиц, хорошо владеющих аудиторией;

118 – тип с наиболее сильно выраженными конструктивными возможностями и способностью к изобретениям.

VII тип – эмотивный

Формулы рисунков: 550, 451, 460, 352, 361, 370, 253, 262, 271, 280, 154, 163, 172, 181, 190, 055, 064, 073, 082, 091.

Обладают повышенным сопереживанием по отношению к другим, тяжело переживают жестокие кадры фильма, могут надолго быть выбитыми из колеи и быть потрясенными от жестоких событий. Боли и заботы других людей находят в них участие, сопереживание и сочувствие, на которое они тратят много собственной энергии, в результате становится затруднительной реализация их собственных способностей.

VIII тип – противоположность эмотивного

Формулы рисунков: 901, 802, 703, 604, 505, 406, 307, 208, 109.

Данный тип людей обладает противоположной тенденцией эмотивному типу. Обычно не чувствует переживаний других людей, или относится к ним с невниманием, или даже усиливает давление на людей. Если это хороший специалист, то он может заставить других делать то, что он считает нужным. Иногда для него характерна черствость, которая возникает ситуативно, когда в силу каких-либо причин человек замыкается в кругу собственных проблем.

Загадки про квадрат для детей: короткие, с ответами

Главная » Загадки про школу

На чтение 4 мин. Просмотров 1.5k.

Где может попасться такая геометрическая фигура, как квадрат? В принципе, абсолютно везде в повседневной жизни. Если хорошенько подумать, то на Гладстон попадается достаточно часто: строительные конструкции, элементы одежды.

Ознакомившись с нашими загадками про квадрат для детей можно неплохо расширить собственный кругозор и узнать о том, какие роли ещё может встретиться данный объект. Не просто отличный способ весело провести время с ребёнком, но ещё и достаточно поучительный.

ЧИТАЙТЕ ТАКЖЕ: Загадки про горох.

У меня угла четыре
И четыре стороны.
Все они между собою
Одинаково равны.

Квадрат.

Четыре палочки сложили
И фигуру получили.
Он давно знаком со мной,
Каждый угол в нем — прямой.
Все четыре стороны
Одинаковой длины.
Вам его представить рад,
А зовут его — …

Квадрат.

Тень от кубика упала
Вниз, на ламинат.
Эта тень нарисовала
На полу …

Квадрат.

Не овал я и не круг,
Треугольнику я друг,
Прямоугольнику я брат,
Ведь зовут меня…

Квадрат.

Четырёхугольник я.
У сторон – одна длина.
Все углы мои прямые.
Догадайся, кто же я?

Квадрат.

Из него мы строим дом
И окошко в доме том
За него в обед садимся
В час досуга веселимся
Ему каждый в доме рад
И зовут его — …

Квадрат.

ИНТЕРЕСНО: Загадки про подсолнух.

Фигура в геометрии мила,
Внутри четыре прямых угла,
Четыре линии в фигурной окантовке,
Равны в размерах, сопрягаясь ловко!

Квадрат.

Его стороны равны,
Углом соединены.
Это ромба старший брат.
А зовут его …

Квадрат.

Четыре угла и четыре сторонки,
Похожи точно родные сестренки.

Квадрат.

В ворота его не закатишь, как мяч,
И он за тобою не пустится вскачь.
Фигура знакома для многих ребят.
Его вы узнали? Ведь это …

Квадрат.

Он давно знакомый мой,
Каждый угол в нем прямой,
Все четыре стороны
Одинаковой длины.
Вам его представить рад.
А зовут его…

Квадрат.

Кубик в краску окуни,
Приложи и подними.
Если ты уже так сделал –
Отпечатались они.

Квадраты.

РЕКОМЕНДУЕМ: Загадки про петрушку.

Красив и строг: ведь у него
Равны все стороны его.
Сложен словно на парад.
Что же это? Да…

Квадрат.

Если стороны равны
И углы его прямы,
А сторон, углов четыре,
Что с тобой мы начертили?

Квадрат.

Если шесть мы их возьмём,
Сможем куб собрать.
Только помни: надо шесть,
А совсем не пять.

Квадрат.

Смотреть на ту фигуру радостно,
Углы в три сотни с лишним градусов,
Все стороны всегда, к примеру,
Изумительно равных размеров!

Квадрат.

Я фигура – хоть куда,
Очень ровная всегда,
Все углы во мне равны
И четыре стороны.
Кубик – мой любимый брат,
Потому что я…

Квадрат.

Знаем точно мы с тобой:
Угол у него прямой,
Есть четыре стороны,
Меж собой они равны.
Что же значит этот факт?
Что перед тобой …

Квадрат.

Оцените автора

20 уникальных занятий и поделок с квадратами для детей разного возраста

Изучение основных форм начинается в раннем возрасте, и четырехсторонняя форма квадрата обычно знакомится с ним первой. Умение распознавать эти четыре равные стороны и четыре равных угловых угла сослужит ребенку хорошую службу. Как только они узнают форму и ее название, они смогут указать ее в реальном мире. Поощряйте это признание и укрепляйте принципы формы, участвуя в некоторых из наших забавных поделок и занятий с вашим ребенком.

1. Квадратный бумажный пингвин

Сделайте этих очаровательных бумажных пингвинов. Вырежьте большие черные квадраты и маленькие оранжевые и белые квадраты. Затем позвольте своим ученикам построить своих пингвинов, размещая квадраты под разными углами. Дайте им клей-карандаш и дайте им приклеить его к синему арктическому фону.

Подробнее: Принцесса для печати

2. Квадратная штамповка

Получайте удовольствие от штамповки форм! Поиск форм может быть забавным, и обычно вы можете штамповать множество вещей, которые можно найти на кухне или дома. Разрезание губок на квадраты может позволить вашему ребенку накладывать слои и экспериментировать с краской, создавая фигуры поверх других фигур.

Узнать больше: Powerful Mothering

3. Lego

Не ищите ничего, кроме своей корзины Lego, чтобы найти множество форм и других вариантов четырехсторонних фигурок. Игра с лего — отличная двигательная активность, поскольку она позволяет детям использовать зрительно-моторную координацию для сборки. Работая с различными формами, они могут узнать, из чего состоит трехмерный квадрат, если его собрать.

Узнать больше: Play Dough to Plato

4. Квадратные монстры

Это занятие с милыми формами монстров позволяет учащимся раскрыть свой творческий потенциал, исследуя различные формы тела. Большинство детей назовут их монстрами, но другие могут считать их инопланетянами. Дайте им другие формы, чтобы добавить больше основных форм, или придерживайтесь квадратов для забавных поделок.

Узнайте больше: All Kids Network

5. Созвездия

Эти созвездия красивой формы используют основные линии и круглые формы звезд для формирования астрологических изображений, наблюдаемых на протяжении миллионов лет. Основная квадратная форма заключается во многих этих формах, и учащимся будет интересно создавать свои собственные созвездия с линиями и точками. Добавьте фонарик для имитации солнца!

Узнать больше: 123Homeschool 4 Me

6. Marshmallow Engineering

Дети сходят с ума от этой игры STEM, в которой скромный квадрат используется для создания огромных конструкций. Вы можете использовать маленькие зефирки с зубочистками или получить еще больше съедобного удовольствия с крендельками на палочках и большими зефирами s’more. Посмотрите, кто может построить их выше всех, и расскажите о важности фундамента.

Узнать больше: Филиал музея

7. Выравнивание зубочистки

Подойдут любые прямые формы, но дети в восторге от зубочисток. Попробуйте купить цветные и позвольте детям делать коврики, формировать картинки и изучать поделки в форме дома. Посмотрите, могут ли они использовать другие формы для создания квадратов, чтобы развивать свое пространственное мышление и логические навыки.

Узнать больше: Числовая дислексия

8. Кубик Рубика

Вы когда-нибудь собирали кубик Рубика? Большинство малышей никогда раньше не видели это кубическое чудо, и им будет интересно узнать, как играть с ним и решать его. Они будут очарованы цветовыми узорами и увидят, куда их заведут их логические способности; проверка их способности думать на несколько ходов вперед.

Узнать больше: Кубик Рубика

9. Кости

Кости могут дополнить любую учебную программу, и дети любят играть с ними во время настольных игр. Пусть дети бросают кости и работают с числами и счетными формами. Вы также можете сложить кубики, использовать их, чтобы попрактиковаться в математических фактах по мере того, как числа разворачиваются, и обсудить вероятность. Этот 3D-куб дает потенциал.

Узнать больше: Шаг за шагом

10. Квадратное мороженое

Квадратная форма доставляет большое удовольствие летом, когда вы делаете эскимо из бумаги. Возьмите несколько палочек для эскимо и создайте квадратное мороженое. Поэкспериментируйте с теорией цвета, смешивайте различные узоры и формы или попробуйте штамповать или рисовать на них. Приклейте палочки сзади!

Узнайте больше: мазок клея поможет

11. Создание квадратов

Дети могут манипулировать множеством предметов, чтобы создавать и строить фигуры. Используйте палочки от эскимо, ватные палочки, крендели с солью, лакрицу или любую прямую форму, чтобы построить свои собственные квадраты. Дети могут обсудить необходимость равных сторон, чтобы сделать идеальный квадрат, и, возможно, даже съесть результат!

Узнать больше: Мама двух шикарных Lil Divas

12. Играть в классики

Возьмите мел на тротуаре или используйте клейкую ленту на полу, чтобы создать типичную сетку. Покажите детям, как бросать камень, а затем прыгать, прыгать и прыгать по фигурам. Покажите им, как простой квадрат может разделить другой, чтобы получить более сложную форму, например кирпичи.

Узнать больше: Готово к празднику

13. Квадратные десерты

Рисовые угощения Krispie, желейные желе, печенье… что угодно. Есть тонны квадратных десертов, чтобы насладиться. Устройте квадратную вечеринку с друзьями в качестве веселого занятия по распознаванию форм. Используйте квадратные салфетки, ешьте квадратные угощения и сидите на квадратном одеяле. Пусть дети помогут вам приготовить угощения и подготовиться к вечеринке.

Узнать больше: Educatall

14. Календари своими руками

Дети любят узнавать дни недели, так что используйте эту возможность с собственным календарем. Они могут создать новый в начале каждого месяца с множеством забавных печатных материалов, доступных в Интернете. Помогите им вычеркнуть каждый день и обсудить шаблон сетки; анализируя, как квадраты представляют дни.

Подробнее: Рабочие листы для суперучителей

15. Кубики сахара

Большинство сегодняшних детей никогда раньше не видели кубики сахара, но их очень весело лепить. Практикуйте числовые навыки, складывая несколько башен; сравнивая размер по мере того, как вы добавляете все больше и больше кубиков. Это также отличный способ преподавать единицу площади на уроке математики.

Узнать больше: Domino Sugar

16. Крестики-нолики

Эта классическая игра обязательно станет хитом в вашем классе. Покажите им, как рисовать сетку, и они скоро станут экспертами. Вы даже можете увидеть буквы в этой форме хэштега и обсудить хэштег с точки зрения символов. Затем покажите им крестики и нолики, и вперед.

Узнать больше: CBC Kids

17. Стикеры для рисования

Стикеры для заметок доставят вам массу удовольствия. Дайте детям разнообразные цветные стикеры и посмотрите, насколько креативно они могут работать с искусством, которое они создают. Это действие можно повторять снова и снова с классической съемной палкой. Можно даже разветвиться и обсудить кубизм!

Узнать больше: Сборник игр для дошкольников

18. Искусство Кандинского

Василий Кандинский известен своим творческим подходом к формированию фигур, что дает вашим учащимся возможность по-настоящему исследовать пространственные отношения с помощью этой простой художественной деятельности. Узнайте, как фигуры вписываются друг в друга, и экспериментируйте с цветом, как это делал он. Или используйте подход смешанной техники для большей универсальности.

Узнать больше: EduArt 4 Kids

19. Художественные проекты на деревянном квадрате

С деревянным квадратом можно сделать многое. Варианты безграничны: от подвесного мобильного искусства «сделай сам» до мозаичных и гипсовых презентаций! Исследуйте искусство с помощью квадратов, пробуя различные способы объединения квадратов и создания чего-то совершенно нового. Квадраты нужны не только для строительства, но и для милых поделок!

Узнать больше: Oriental Trading

20. Одеяло из бумаги

Один из замечательных способов продемонстрировать свои творческие способности — создать лоскутное одеяло. Дайте детям квадрат и позвольте им украсить его по-своему. Тематические дизайны или используйте их как возможность поэкспериментировать с новой художественной техникой. Затем соедините их все вместе и стабилизируйте спину.

Узнайте больше: Художники помогают детям

Похожие сообщения:

Что такое Square? Определение, свойства, формы, примеры, факты

Квадрат – Введение

Взгляните на изображения, приведенные ниже.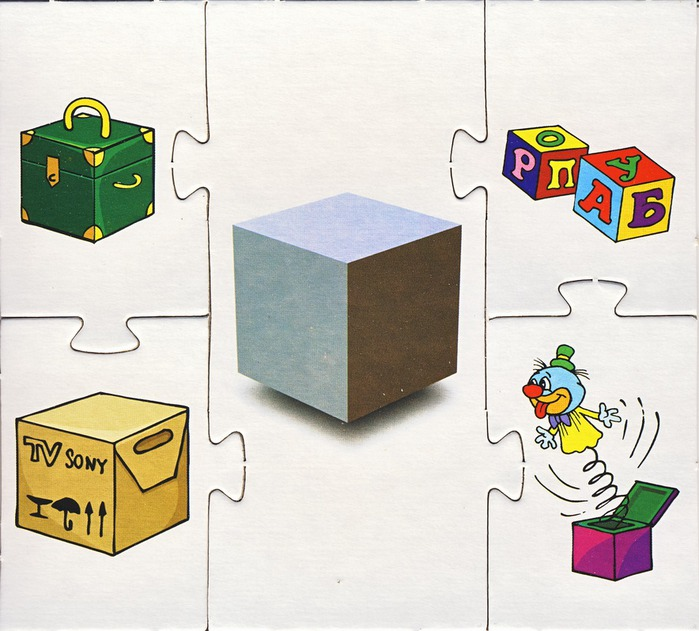 В повседневной жизни вы могли сталкиваться с такими предметами, как фоторамка или крафт-бумага. Сможете ли вы определить, что в них общего?

Все они имеют квадратную форму.

Родственные игры

Определение квадрата в математике

Квадрат – это правильный многоугольник, имеющий четыре равные стороны и равные углы, каждая из которых равна 90°.

Связанные рабочие листы

Что такое квадрат в математике?

Квадрат представляет собой двумерную замкнутую фигуру с 4 равными сторонами и 4 вершинами. Его противоположные стороны параллельны друг другу. Мы также можем думать о квадрате как о прямоугольнике с одинаковой длиной и шириной.

Оглядевшись, можно найти много вещей, напоминающих квадратную форму. Типичные примеры этой формы включают шахматную доску, крафт-бумагу, ломтик хлеба, фоторамку, коробку для пиццы, настенные часы и т. д.

Свойства квадрата

• У квадрата 4 стороны и 4 вершины.
• Его стороны равны по длине.
• Все внутренние углы равны и прямые, что означает, что каждый угол равен 90°.
• Сумма всех внутренних углов равна 360°.
• Две его диагонали пересекают друг друга под прямым углом.

Площадь и периметр квадрата

Площадь представляет собой пространство, занимаемое формой или фигурой, тогда как периметр представляет собой длину внешней границы фигуры. Давайте обсудим формулу нахождения площади и периметра квадрата.

Площадь

Площадь двумерной фигуры определяется как количество пространства, занимаемого фигурой, если мы будем держать ее на плоском столе. 92$ и т. д.

Периметр

Периметр двумерной формы определяется как общая длина ее границы.

Периметр квадрата со стороной, равной единицам s, определяется по формуле:

Периметр $= \text{side} + \text{side} + \text{side} + \text{side} = 4$ $\text{x}$ $\text{s}$

Периметр выражается в линейных единицах, таких как см, дюймы, м и т. д.

Решаемые примеры на площади

Пример 1: сторона квадратной бумаги составляет 12 футов. Найдите площадь бумаги. 92 = 12 х 12 = 144 $ кв. фут

Пример 2. Если периметр квадрата равен 68 см, какова мера его стороны?

Решение :

Мы знаем, что периметр квадрата равен 4 сторонам.

Дан периметр 68см.

Следовательно, 4 x сторона $= 68$ 

Значит, сторона $= \frac{68}{4} = 17$ см

Пример 3. Каков периметр квадрата со стороной 15 метров?

Решение: Мы знаем, что периметр квадрата равен 4 x s, где s представляет собой длину каждой стороны.

Дана сторона s $= 15$ метров.

Следовательно, периметр $= 4 \times 15 = 60$ метров.

Практические задачи на квадрате

1

Если сторона квадратной шахматной доски имеет длину 20 см, найдите периметр доски.

80 см

170 см

200 см

150 см

Правильный ответ: 80 см
Мы знаем, что периметр квадрата равен 4 x s,
, где s представляет собой длину каждой стороны.