Минус на минус плюс математика примеры: Сложение и вычитание отрицательных и положительных чисел. Решение примеров.
Сложение и вычитание отрицательных и положительных чисел. Решение примеров.
- Альфашкола
- Статьи
- Сложение и вычитание отрицательных чисел
Существуют разные типы чисел – четные числа, нечетные числа, простые числа, составные числа. Также на основе знака числа могут быть двух видов – положительные числа и отрицательные числа. Эти числа могут быть представлены на числовой линией. Среднее число в этой строке равно нулю. С левой стороны от нуля находятся отрицательные числа, а с правой стороны – положительные.
Ноль – это нейтральный элемент относительно сложения целых чисел. В основном в этой статье мы будем изучать операции сложения и вычитания с отрицательными числами.
Существуют определенные правила для знаков при сложении и вычитании:
- Для того чтобы сложить два отрицательных числа, надо сложить два числа и поставить знак минус.
\((-2)+(-3)=-5\)
- Если первое число положительное, а второе отрицательное, смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа:
\((-8)+4=4-8=-4\)
\(9+(-4)=9-4=5\)
Для каждого числа кроме \(0\) существует противоположный элемент, при сумме с ним образуется ноль:
\(-9+9=0\) \(7,1+(-7,1)=0\)
- При вычитания двух чисел, в которых оба отрицательные, следует знать правило: минус на минус дает плюс. То есть, если стоят рядом два минуса, в сумме получается плюс.
\((-7)-(-6)=(-7)+6=(-1)\)
- Если первое число положительное, а второе отрицательное, вычитаем по тому же принципу, что и складываем: смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа.
\(7-9=-2\) так как \(9>7\)
- Также не стоит забывать минус на минус дает плюс:
\(7-(-9)=7+9=16\)
Задача 1. Вычислите:
- \(4+(-5)\)
- \(-36+15\)
- \((-17)+(-45)\)
- \(-9+(-1)\)
Решение:
- \(4+(-5)=4-5=-1\)
- \(-36+15=-21\)
- \((-17)+(-45)\) \(=-17-45=-62\)
- \(-9+(-1)=-9-1=-10\)
Задача 2. Вычислите:
- \(3-(-6)\)
- \(-16-35\)
- \(-27-(-5)\)
- \(-94-(-61)\)
Решение:
- \(3-(-6)=3+6=9\)
- \(-16-35=-51\)
- \(-27-(-5)=-27+5=-22\)
- \(-94-(-61)=-94+61=-33\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы “Альфа”. Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку “Записаться” принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Даниил Владимирович Савельев
Репетитор по математике
Стаж (лет)
Образование:
Пензенский Государственный Педагогический Университет им.
Белинского
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Адель Василевич Халиков
Репетитор по математике
Стаж (лет)
Образование:
Казанский федеральный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Анна Александровна Ваструхина
Репетитор по математике
Стаж (лет)
Образование:
Краснодарский государственный университет культуры и искусств
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Предметы
- Математика
- Репетитор по физике
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по английскому языку
- Репетитор по обществознанию
- Репетитор по истории России
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
Специализации
- Подготовка к ЕГЭ по математике (базовый уровень)
- Подготовка к ОГЭ по математике
- Репетитор по алгебре
- Репетитор по химии для подготовки к ЕГЭ
- Репетитор для подготовки к ЕГЭ по физике
- Репетитор для подготовки к сочинению ЕГЭ по русскому
- Репетитор по грамматике русского языка
- ВПР по физике
- Репетитор по географии для подготовки к ОГЭ
- Программирование Pascal
Похожие статьи
- Медиана треугольника
- Как заинтересовать детей учить математику?
- Площадь сектора окружности
- ИВТ (Информатика и Вычислительная Техника): МФТИ
- Иррациональные уравнения: примеры с решениями
- Задачи на координатной решетке. Задание №3 из ЕГЭ прошлых лет
- Что ваша ступня может рассказать о вашей личности?
- Зачем кормить птиц зимой и как правильно это делать
Задание №3 из ЕГЭ прошлых летНажимая кнопку “Записаться” принимаю условия Пользовательского соглашения и Политики конфиденциальности
Текст с ошибкой:
Расскажите, что не так
Плюс минус
Плюс минусПлюс и минус – это признаки положительных и отрицательных чисел в математике. Какой результат получается при умножении и делении положительных и отрицательных чисел? Эта простая таблица наглядно показывает результаты умножения и деления двух чисел с разными знаками.
Приведенные в таблице результаты применимы как при умножении и делении целых чисел, так и при умножении и делении дробей.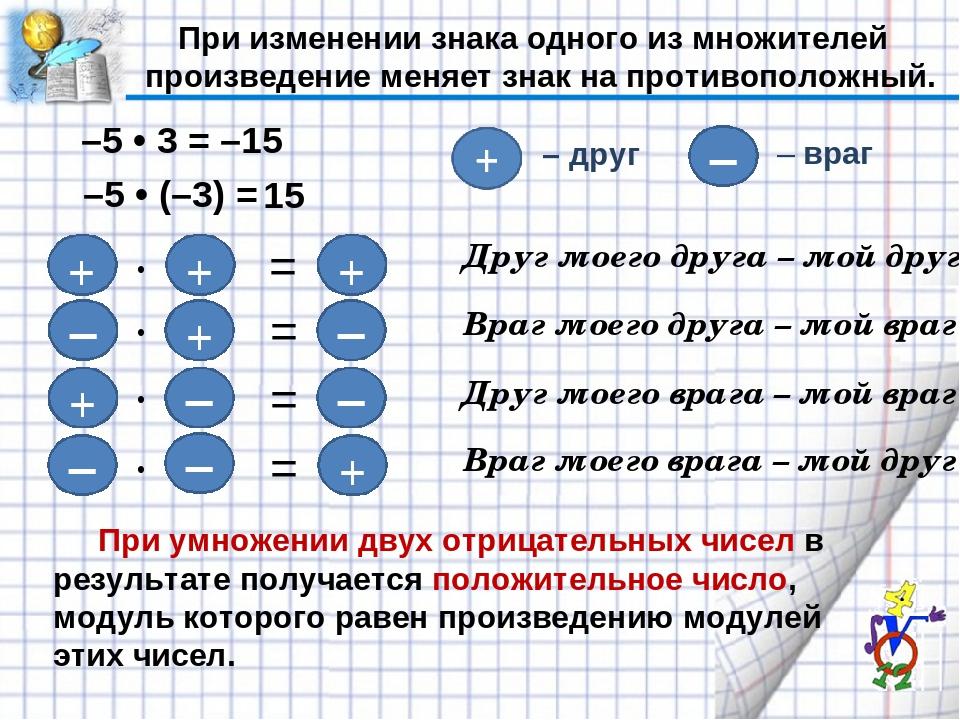
Для определения числовых значений результата умножения или деления воспользуйтесь таблицами умножения и деления, которые можно скачать бесплатно.
При умножении или делении двух положительных чисел в результате получается положительное число. Плюс умноженный на плюс дает плюс, плюс деленный на плюс будет плюс. Это правило математики. Произведение двух положительных чисел – число положительное, частное двух положительных чисел – положительное число.
В математике умножение или деление положительного числа на отрицательное дает в результате отрицательное число. Плюс умноженный на минус дает минус. Плюс деленный на минус будет минус. Если положительную дробь умножить или разделить на отрицательную дробь получится отрицательное число. Это число может быть целым или дробным. Произведение положительного числа на отрицательное – число отрицательное, частное положительного числа на отрицательное число – отрицательное число. Если числитель дроби положительный, а знаменатель отрицательный – дробь (или целое число) будет отрицательной.
При делении или умножении отрицательного числа на положительное в результате получается отрицательное число. Минус умноженный на плюс будет минус. Минус деленный на плюс в математике будет минус. Когда числитель дроби отрицательный, а знаменатель положительный – дробь (или целое число) будет отрицательной. Если отрицательную дробь умножить или разделить на положительную дробь получится отрицательное число. Это число может быть целым или дробным, что определяется другими правилами математики. Произведение отрицательного числа на положительное – число отрицательное, частное отрицательного числа на положительное число – отрицательное число.
Когда умножаются или делятся два отрицательных числа, результатом будет положительное число. Минус умноженный на минус дает плюс, минус деленный на минус будет плюс. Произведение двух отрицательного чисел – положительное число, частное двух отрицательного чисел – число положительное. При делении или умножении двух отрицательных чисел получается положительное число.
Правила знаков в математике распространяются как на целые, так и на дробные числа. При делении двух отрицательных дробей результат будет положительным. При умножении двух отрицательных дробей результат так же будет положительным, то есть со знаком плюс.
ВОПРОС – ОТВЕТ
“Кто ввел знаки сложения и вычитания в математику?” – первое употребление слов plus (больше) и minus (меньше) как обозначения действия сложения было найдено историком математики Энестремом в итальянской алгебре четырнадцатого века. Вначале действия сложения и вычитания обозначали перввыми буквами слов “p” и “m”. Современные знаки плюс “+” и минус “-” появились в Германии в последнее десятилетие пятнадцатого века в книге Видмана, которая была руководством по счету для купцов (“Behende und ubsche Rechenung auf allen Kaufmannschaft”, 1498). Существует предположение, что знаки плюс “+” и минус “-” появились из торговой практики: проданные меры вина отмечались на бочке черточкой “-“, а при восстановлении запаса их перечеркивали, откуда получился знак “+”.
Здесь я хочу особо подчеркнуть, что знаком “минус” отмечалась не мера (бочка) с “отрицательным” вином, а пустая мера (бочка), что гораздо больше соответствует понятию “ноль”. Когда вам математики будут рассказывать об отрицательных числах, всегда помните о пустой бочке, которая по воле математиков превратилась в бочку со знаком “минус”.
“Минус 6 делить на минус 3 как быть?” – сперва отбрасываем знаки минус и делим просто 6 (шесть) на 3 (три) при помощи таблицы деления и получаем в результате 2 (два). Потом по табличке вверху странички делим минус на минус и получаем плюс. Теперь прилепливаем полученный плюс к ранее полученной двойке
(-6) : (-3) = +2
Впрочем, знак “+” перед числами писать не принято, поэтому красивее и правильнее будет так:
(-6) : (-3) = 2
“Если число со знаком минус спереди умножаем на такое же число?” – решение смотри выше.
13 ноября 2009 года – 22 сентября 2019 года.
© 2006 – 2021 Николай Хижняк. Все права защищены.
положительных и отрицательных чисел | SkillsYouNeed
Стандартные числа, большие нуля, описываются как «положительные» числа. Мы не ставим перед ними знак плюс (+), потому что нам это не нужно, так как общее понимание таково, что числа без знака положительны.
Числа меньше нуля называются «отрицательными». Перед ними стоит знак минус (-), указывающий, что они меньше нуля (например, -10 или ‘ минус 10 ‘).
Визуализация отрицательных и положительных чисел
Вероятно, самый простой способ визуализировать отрицательные и положительные числа — использовать числовую прямую, инструмент, с которым вы, возможно, хорошо знакомы, особенно если ваши дети учатся в начальной школе.
Это выглядит примерно так:
Числовая линия может помочь вам визуализировать как положительные, так и отрицательные числа, а также операции (сложение и вычитание), которые вы можете с ними выполнять.
Когда вам нужно вычислить сложение или вычитание, вы начинаете с первого числа и перемещаете второе число разрядов вправо (для сложения) или влево (для вычитания).
Эта числовая линия является упрощенной версией, но вы можете нарисовать их, включив в них все числа, если хотите. Большим преимуществом числовой линии является то, что ее очень легко нарисовать самому себе на обратной стороне конверта или на клочке бумаги, а также очень сложно ошибиться в расчетах. Пока вы внимательно подсчитываете количество мест, которые вы перемещаете, вы получите правильный ответ.
Вычитание отрицательных чисел
Если вы вычитаете отрицательное число, два отрицательных числа объединяются, чтобы получить положительное.
−10−(−10) не равно −20. Вместо этого вы можете думать об этом как о повороте одного из отрицательных знаков вертикально, чтобы пересечь другой и сделать плюс. Тогда сумма будет равна −10+10 = 0.
Краткое примечание о скобках
Для ясности: вы никогда не будете писать два отрицательных знака рядом без скобок.
Таким образом, если вас попросят вычесть отрицательное число, оно всегда будет заключено в скобки, чтобы вы могли видеть, что использование двух отрицательных знаков было преднамеренным.
-10–10 неверно (и сбивает с толку)
-10-(-10) правильно (и более ясно)
Умножение и деление с положительными и отрицательными числами
положительные и отрицательные числа, вы можете упростить процесс, сначала игнорируя знаки (+/-) и просто умножая или разделяя числа, как если бы они оба были положительными. Получив числовой ответ, вы можете применить очень простое правило для определения знака ответа:
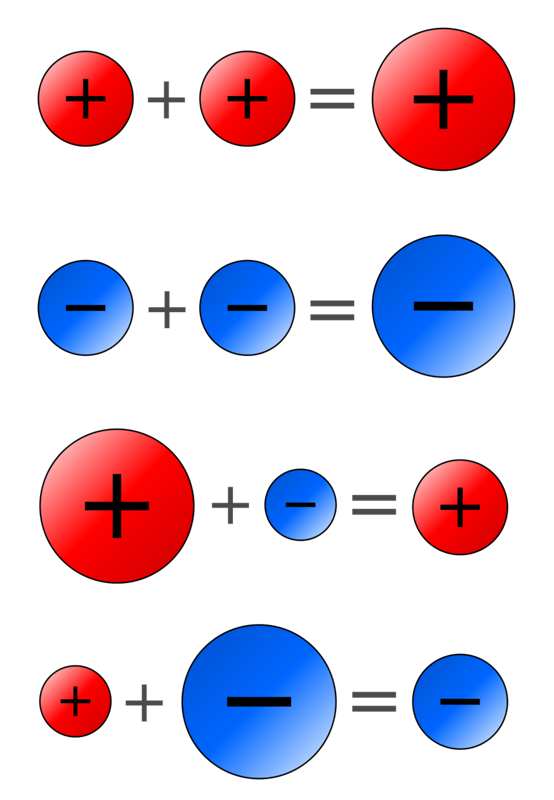
- Когда знаки двух чисел совпадают с , ответ будет положительным .
- Когда знаки двух чисел отличаются , ответ будет отрицательным .
Итак:
(положительное число) × (положительное число) = положительное число
(отрицательное число) × (отрицательное число) = положительное число
Но:
× (положительное число) число) = отрицательное число
В качестве побочного вопроса, это каким-то образом объясняет, почему вы не можете получить квадратный корень из отрицательного числа (подробнее об этом читайте на нашей странице Специальные числа и концепции ).
Квадратный корень — это число, которое нужно умножить само на себя, чтобы получить число. Нельзя умножать число само на себя, чтобы получить отрицательное число. Чтобы получить отрицательное число, вам нужно одно отрицательное и одно положительное число.
Правило работает так же, когда у вас есть более двух чисел для умножения или деления. Четное количество отрицательных чисел даст положительный ответ. Нечетное количество отрицательных чисел даст отрицательный ответ.
Почему умножение двух отрицательных чисел дает положительный ответ?
Тот факт, что отрицательное число, умноженное на другое отрицательное число, дает положительный результат, часто сбивает с толку и кажется нелогичным.
Чтобы объяснить, почему это так, вернитесь к числовым линиям, использованным ранее в этой статье, поскольку они помогают объяснить это визуально.
- Во-первых, представьте, что вы стоите на числовой прямой в нулевой точке и смотрите в положительном направлении, то есть в сторону 1, 2 и так далее. Вы делаете два шага вперед, останавливаетесь, затем делаете еще два шага. Вы прошли 2 × 2 шага = 4 шага.
Следовательно, положительный × положительный = положительный - Теперь вернитесь к нулю и повернитесь лицом в отрицательном направлении, то есть к −1, −2 и т. д. Сделайте два шага вперед, затем еще два. Теперь вы стоите на −4. Вы переместились на 2 × -2 шага = -4 шага.
Отсюда минус × плюс = минус
Вы делаете два шага вперед, останавливаетесь, затем делаете еще два шага. Вы прошли 2 × 2 шага = 4 шага. В обоих этих примерах вы двигались вперед (т. е. в том направлении, в котором вы смотрели), положительное движение.
- Снова вернитесь к нулю, но на этот раз вы пойдете назад (негативное движение). Снова повернитесь лицом в положительном направлении и сделайте два шага назад. Теперь вы стоите на −2. Положительное (направление, в котором вы смотрите) и отрицательное (направление, в котором вы движетесь) приводят к отрицательному движению.
Отсюда положительный × отрицательный = отрицательный - Наконец, снова вернитесь к нулю, повернитесь лицом в отрицательном направлении. Теперь сделайте два шага назад , а затем еще два назад. Вы стоите на +4. Повернувшись лицом в отрицательном направлении и пройдя назад ( два отрицания ), вы достигли положительного результата.
Отсюда минус × минус = плюс
Теперь сделайте два шага назад , а затем еще два назад. Вы стоите на +4. Повернувшись лицом в отрицательном направлении и пройдя назад ( два отрицания ), вы достигли положительного результата. - Два отрицательных числа компенсируют друг друга. Вы можете увидеть это в речи:
- «Просто сделай это!» позитивное побуждение к действию.
- «Не делай этого!» просит кого-то не делать что-то. Это минус.
- «Не делай этого» означает «пожалуйста, сделай это». Два отрицания компенсируются и дают положительный результат как в математике, так и в речи.
- Знаки складываются физически. Когда у вас есть два отрицательных знака, один переворачивается, и они складываются вместе, чтобы получить положительный. Если у вас есть положительный и отрицательный, остается одна черточка, и ответ отрицательный. Это простая и наглядная памятка, несмотря на то, что она не обязательно удовлетворит тех, кто хочет понять правило.
Заключение
Отрицательные знаки могут показаться немного пугающими, но правила их использования просты и понятны. Помните об этом, и у вас не будет проблем.
Основные правила для положительных и отрицательных чисел
ОПИСАНИЕ
правила сложения и вычитания двух положительных и отрицательных чисел0003
РАЗРЕШЕНИЕ
Принадлежит YourDictionary, Copyright YourDictionary
Числа больше нуля называются положительными числами, а числа меньше нуля — отрицательными числами. Это означает, что они падают по обе стороны от числовой прямой. Однако то, что они находятся на одной линии, не означает, что они следуют одним и тем же правилам! Продолжайте читать список основных правил использования положительных и отрицательных чисел в математике.
При использовании положительных и отрицательных чисел используются правила для чисел со знаком (числа с положительными или отрицательными знаками перед ними).
Эти шаги, также известные как операции над числами со знаком, помогут вам избежать путаницы и решить математические задачи как можно быстрее и правильнее.
Следуйте этим правилам, чтобы определить лучший способ сложения, вычитания, умножения и деления положительных и отрицательных чисел. Помните, что если нет знака + или -, число положительное.
Реклама
Дополнение: одинаковые знаки, сложите числа
Когда вы складываете два числа вместе, и они имеют одинаковый знак (два положительных или два отрицательных числа), сложите числа и сохраните знак. Например:
- 1 + 1 = 2
- 51 + 32 = 83
- -14 + (-6) = -20
- -196 + (-71) = -267
Обратите внимание, что уравнения с двумя положительными числами имеют положительные суммы, а уравнения с двумя отрицательными числами имеют отрицательные суммы. Если вы используете числовую прямую для решения задачи, добавление двух положительных чисел приведет к положительной стороне, а добавление двух отрицательных чисел приведет к отрицательной стороне.
Сложение: разные знаки, вычитание чисел
Если вы складываете вместе положительные и отрицательные числа, вычтите меньшее число из большего и используйте знак из большего числа. Например:
- 6 + (-5) = 1
- -17 + 22 = 5
- -100 + 54 = -45
- 299 + (-1) = 298
Как видите, сложение чисел с разными знаки на самом деле являются формой вычитания. При использовании числовой прямой ваша сумма будет ближе к нулю.
Advertisement
Вычитание: Переключиться на сложение
Вычитание положительных и отрицательных чисел означает, что вы складываете противоположные числа или добавите обратное. Замените знак вычитания на сложение, а следующий за ним знак измените на противоположный. Затем следуйте инструкциям по добавлению. Например:
- -3 – (+5) становится -3 + (-5) = -8
- 9 – (-7) становится 9 + (+7) = 16
- -14 – (+8) становится -14 + (-8) = -22
- 25 – (-90) становится 25 + (+90) = 115
Хороший совет: всякий раз, когда вы видите знак минус и знак минус вместе, например, в 9 – (-7), немедленно сделайте их положительными знаками.
Отрицательные знаки компенсируют друг друга, и уравнение становится задачей на сложение.
Умножение и деление: одинаковый знак, положительный результат
Кажется, что умножение и деление сложнее, чем сложение и вычитание, но на самом деле они намного проще. Правило умножения положительных и отрицательных чисел с одинаковым знаком (два положительных или два отрицательных) состоит в том, что произведение всегда будет положительным. Например:
- 8 х 4 = 32
- (-8) х (-4) = 32
- 10 х 9 = 90
- (-10) х (-9) = 90
То же правило претендует на разделение. При делении числа на другое число с тем же знаком частное (ответ) положительно. Например:
- 12 ÷ 6 = 2
- -12 ÷ (-6) = 2
- 100 ÷ 5 = 20
- -100 ÷ (-5) = 20
числа всегда равны положительному числу? Подобно вычитанию отрицательных чисел, эти операции превращают отрицательные числа в противоположные (обратные).
По сути, вы вычитаете отрицательное число несколько раз — и, как показано выше, вычитание отрицательных чисел приводит к положительному уравнению.
Реклама
Описание
Правила для умножения и деления двух чисел положительные и отрицательные
Источник
Созданы Karina goto For yourdictionary
. С собственно Yourmictionary
.
.
..9003. Умножение и деление: противоположный знак, отрицательный результатПри умножении положительного и отрицательного числа произведение всегда будет отрицательным. Неважно, в каком порядке стоят знаки. Например:
- 6 x (-7) = -42
- -7 x 6 = -42
- 12 x (-11) = -132
- -11 x 12 = -132
Во всех этих случаях вам сначала нужно умножить или разделить числа. Затем решите, является ли произведение или частное положительным (два положительных или два отрицательных в уравнении) или отрицательным (один положительный и один отрицательный в уравнении).
