Методы запоминания таблицы умножения для детей: 6 ✔️ Способов быстро и легко выучить таблицу умножения

Учим таблицу умножения эффективно и без стресса

Как правильно начать знакомство с таблицей умножения?

Несмотря на то, что в разных образовательных учреждениях педагоги составляют отличные по структуре и наполненности учебные планы на год, в подавляющем большинстве случаев ученики начинают знакомство с таблицей умножения во втором классе. Причем учителя просят родителей начинать учить с детьми таблицу умножения заранее. Согласитесь, заставить дочь или сына зубрить непонятные формулы во время летних каникул — задачка не из легких. Но смысл в том, чтобы не заставить, а заинтересовать будущего второклашку в изучении пресловутой таблицы. 

Сделать это лучше, учитывая основные каналы восприятия информации ребенком. Всего их четыре — аудиальный, визуальный, кинестетический, дискретный. Последний появился не так давно и определяет довольно небольшую группу людей, легко запоминающих новый материал с помощью создания логических цепочек. Остальные три психотипа легко распознать при помощи специальных тестов из интернета. Визуалы быстрее схватывают учебный материал через наглядные пособия, таблицы, рисунки. Аудиалы запомнят материал легко, если будут регулярно повторять таблицу умножения вслух или про себя. Кинестетики используют мышечную память, процесс запоминания у них проходит дольше, зато информация остается в памяти навсегда. 

Самые интересные способы запоминания таблицы умножения для детей

Современный подход педагогов и родителей к изучению новых тем в корне отличается от прошлых нудных школьных программ. К тому же существует огромное количество дополнительных возможностей для интересного изучения школьных предметов. Тем не менее есть дети, для которых необходимость запоминания непонятных пока для них примеров становится настоящим стрессом. Помочь им можно, сохраняя позитивный настрой и заинтересованность в конечном результате. 

Среди наиболее эффективных способов изучения можно отметить следующие:

• Таблица Пифагора — в отличие от привычной всем схемы, которую часто печатают на обратной стороне тетради, такая структура намного меньше по объему. Для сравнения — в традиционной таблице умножения ребенку нужно выучить 100 примеров, тогда как в таблице Пифагора всего 36. Важно показать сыну или дочери основные закономерности — повторяющиеся примеры и особенности умножения на единицу и 10.
• Игровые карточки — в продаже есть готовые наборы, но лучше сделать их совместно с ребенком. Так он будет вовлечен в процесс с самого начала и сможет самостоятельно выбрать размер, цвет и форму учебного пособия. Также есть различные варианты исполнения карточек. Можно на лицевой стороне написать действие умножения, а на обратной — правильный ответ. Или же сделать часть карточек с примерами, другую — с ответами.
• Настольные игры — сюда же относятся многочисленные приложения в мобильных телефонах. В игровой форме новый материал запоминается легко и незаметно. Предложенные создателями правила игры можно менять и дополнять для поддержания стимула у ребенка. Устраивайте веселые соревнования между членами семьи, и вы не заметите, как школьник сможет усвоить математическую таблицу.
• Метод «От простого к сложному» — поможет быстрее запомнить примеры из таблицы умножения. В этом случае лучше начать с наиболее простых примеров умножения на один и десять. Затем перейти к таблице умножения на два и пять. Вычисления на девять можно попробовать запомнить необычным способом вычисления на пальцах. Остальные примеры легко запомнить, подключая такие методы, как рифмы или плакаты.

Некоторые родители используют готовые математические тренажеры. Они объединяют примеры в блоки. Каждый последующий блок сложнее предыдущего. По мере изучения блоки можно менять местами, тем самым способствуя запоминанию таблицы умножения вразброс. 

Польза изучения таблицы умножения

Правильная мотивация поможет школьнику быстрее усвоить материал. Важно объяснить ребенку, что в старших классах без знаний таблицы умножения ему будет трудно понимать новые темы. После окончания младшей школы детей тестируют, проверяя усвоенный материал. А по окончанию учебы все школьники в обязательном порядке сдают ЕГЭ.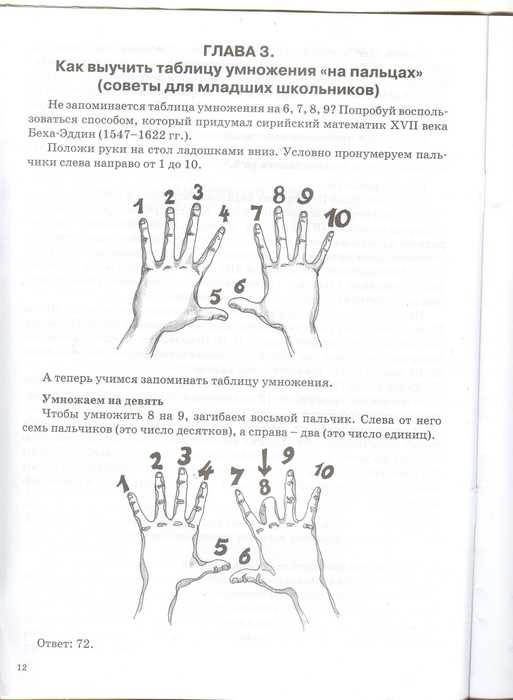 По его итогам высшие учебные заведения принимают решение о зачислении студента. Все эти этапы школьной жизни ребенку предстоит пройти не только с учителями, а и родителями. От них зависит, как школьник будет воспринимать учебу. Вовремя выученная таблица умножения в последующем поможет:

• понять принцип деления;
• извлекать корни;
• возводить число в степень;
• быстро решать задачи и примеры в несколько действий.

Таблица умножения помогает ребенку понять связь между числами. Если подойти к процессу изучения примеров творчески, он станет начальным этапом интересного погружения школьника в мир точных наук.

Родителям на заметку

Начальная школа готовит ребенка к более сложным программам, на этом этапе важно выбрать правильную стратегию. Родители в первую очередь обязаны мотивировать сына или дочь к изучению предмета. Для этого нужно использовать все доступные материалы. Главное не перегружать и не давить, подавать информацию небольшими объемами. После того как школьник выучил примеры по порядку, начинайте спрашивать таблицу вразброс. Постепенно сокращайте время, отведенное для ответа. Важно держать ровный эмоциональный фон, ни в коем случае не сравнивайте ребенка с другими детьми. Хвалите сына или дочь за достижения, обязательно применяйте полученные знания на практике. Если вы практикуете хоумскулинг, обращайте внимание на круг общения школьника, чтобы исключить кибербуллинг. Учеба может быть интересной, в ваших силах показать это своему ребенку.

Беседа для родителей «Способы эффективного запоминания таблицы умножения» | Материал:

Беседа для родителей

«Способы эффективного запоминания таблицы умножения»

Родителям в какой – то момент приходится столкнуться с одной очень непростой проблемой: как помочь ребёнку выучить таблицу умножения. Существует множество различных способов, помогающих детям запомнить таблицу Пифагора.

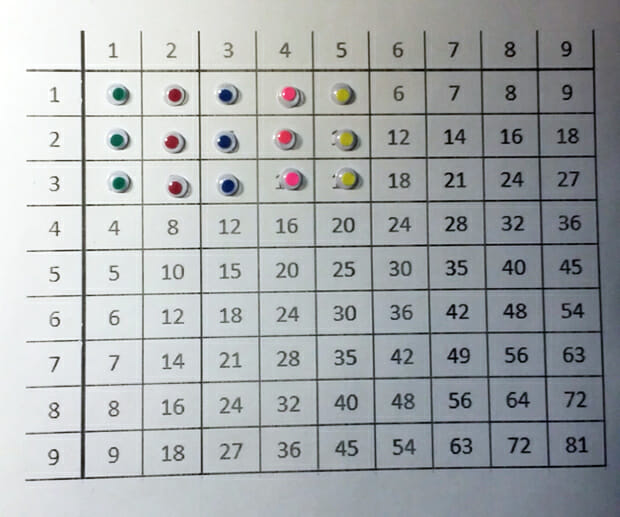
Необходимо объяснить, как устроена сама таблица умножения, что число из левого столбика умножается на число из верхней строчки, а на пересечении строки и столбца, в которых находятся эти числа, и следует искать ответ, то есть их произведение.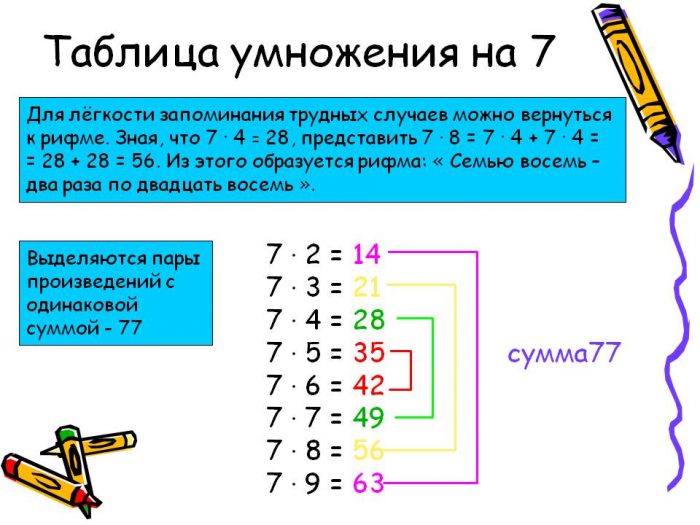 Например, пятью восемь равно сорок (5×8=40).

В процессе изучения таблицы умножения должен обязательно присутствовать элемент игры, он необходим для детей! Обучение с привлечением игровых приемов заставит ребенка вникнуть в задание, по-настоящему заинтересоваться предметом умножения и забыть о трудностях. Одно из правил запоминания гласит: интересное запоминается лучше и быстрее. Если вы сможете пробудить интерес ребенка к умножению, вы уже сделаете половину дела! Одной из игр изучения таблицы умножения, является игра в карточки. Необходимо распечатать уже готовые карточки с примерами и ответами. Суть этой игровой таблицы умножения заключается в том, что ребенок в случайном порядке вытягивает карточку из стопки и видит на каждой карточке пример умножения без ответа (например, 7×7=? или 3×8=?). Если он дает правильный ответ, то карточка «выходит из игры», а если ответ неверен, то карточка возвращается в самый низ стопки, и может быть вытянута снова. Игра продолжается до тех пор, пока не закончатся все карточки, то есть пока ребенок не даст правильный ответ на все примеры. Когда карточек остается мало, как правило, это трудные примеры, которые ребенок уже пытался решить, то путем повторения они достаточно легко запоминаются, особенно когда в процессе игры у ребенка появляется азарт. Эту игру иногда называют «тренажер таблицы умножения». Весь игровой процесс можно проводить этапами, в зависимости от выученного материала. Например, можно начать свой домашний урок с карточек «таблица умножение на 2», а потом разбавлять их новыми выученными примерами. Карточки для запоминания таблицы умножения являются наиболее простым и эффективным способом для её заучивания.

Выучить любое произведение из таблицы Пифагора будет проще, если продемонстрировать его на практике. Например, у мальчиков можно спросить, сколько всего нужно колес для 5 автомобилей (5×4=20). А таблица умножения для девочек может иметь примеры в стиле, сколько нужно резинок, чтобы заплести по две косички трем куклам (2×3=6).

Если вы только начали изучать с ребёнком таблицу умножения, то можно сразу объясните ребенку наиболее простые примеры из таблицы, которые он сможет решить без каких-либо проблем:

А) Умножение на 1 всегда дает то же самое число, которое мы умножали на 1. Например, 1*1=1, 2*1=2, 3*1=3, и даже миллион на 1 равняется миллион.

Б) Умножение на 10, это то же самое, что просто приписать нолик к числу. Сколько будет 2*10? Правильно, 2 с ноликом, то есть 20.

Выучив таблицу умножения на 1 и на 10, ребенок должен понять, что он теперь знает все крайние столбцы и строки таблицы.

В) Таблицу умножения на 2 дети запоминают довольно легко. Умножение на 2 равнозначно простому сложению двух одинаковых чисел.

Г) Таблица умножения на 5 обычно дается просто. Интуитивно ребенку становится понятно, что все значения этого умножения расположены через 5 друг от друга и заканчиваются либо на 5, либо на 0. Все четные числа, умноженные на 5, всегда оканчиваются на ноль, а нечетные – оканчиваются на 5.

После того, как ваш ребенок освоил самые простые значения таблицы умножения, можно приступать к более сложным множителям. Тут важно использовать приёмы эффективного запоминания: ассоциации, повторение, дробление на части, проверочные задачки.

1. Приём последовательного сложения. В первую очередь следует разъяснить ученику суть действия умножения: что 2 умножить на 3 означает сложить 3 раза число 2, то есть 2+2+2. Ребенок должен хорошо это осознавать, чтобы в дальнейшем избежать многих трудностей и непонимания в изучении таблицы умножения. Приём последовательного сложения одинаковых слагаемых является основным приёмом получения результатов табличного умножения и удобен даже при вычислениях табличных случаев умножения чисел 7, 8, 9, при небольших значениях второго множителя. 9Х2=9+9
2. Перемена множителей (приём взаимосвязанной пары: 2х6, 6х2, 12:2, 12:6). При хорошем понимании правила перестановки множителей ребёнок заучивает в два раза меньше случаев табличного умножения, чем содержит полная таблица. Ребенку нужно объяснить и показать, почему вторая строка и второй столбец таблицы Пифагора содержат одни и те же числа, ровно, как и 3-я строка и 3-й столбец. Противоположное умножению действие – деление, как в сложении – вычитание. 12:2=6, 12:6=2
3. Квадраты чисел. Квадратом числа называется его произведение на самого себя. В таблице умножения есть всего 10 квадратов, которые нужно запомнить. Квадраты до примера «шесть на шесть тридцать шесть» обычно запоминаются на ура, и следующие 3 квадрата обычно тоже не вызывают особых трудностей. А 10 на 10 – будет сто.
4. Приём счёта двойками, тройками, пятёрками (2, 4, 6, ….20), (3, 6, 9…30), (5, 10, 15, 20….50) При хорошем усвоении таких способов счёта ребёнку будет легко освоить таблицы умножения чисел 2, 3, 5. Знание этого базового объема табличных случаев поможет ребёнку при освоении более сложных случаев.
5. Приём прибавления слагаемого к предыдущему результату (вычитания из предыдущего результата) Данный приём используется в том случае, если ребёнок смог выучить хотя бы несколько случаев из каждой таблицы. Это могут быть 3 – 4 первых самых лёгких случая или 2 – 3 наиболее запоминающихся случая. Например, случай 6х7 является одним из наиболее плохо запоминающимся. В то же время случаи 6х6 и 6х8 наиболее легко запоминаются из этой таблицы. Запомнив результат 6х6=36, ребёнок может использовать приём прибавления 6 к предыдущему результату для получения значения случая 6х7, 36+7=42. Запомнив случай 6х8, ребёнок использует приём вычитания 6 из его результата 48-6=42
6. Приём запоминания последовательности случаев с ориентиром на возрастание одного множителя. Обратите внимание детей, что в таблице есть закономерность: при увеличении одного из множителей увеличивается и результат. Напишите на листочке таблицу умножения на 6: 1х6=6, 2х6=12, 3х6=18, ?х6=24 Сможет ли ребёнок вставить следующее число? Дальше можно усложнить: пропустить сразу несколько множителей: 1х6, 2х6, ?х6, 4х6, ?х6…
7. Приём чтения записей действия умножения. Для осознанного применения этого приёма необходимо хорошее понимание смысла действия умножения и смысла каждого множителя в записи действия умножения. Сколько есть способов, чтобы прочитать запись 6х7? (шестью семь, взяли семь раз по шесть, сумма семи шестёрок, шесть увеличили в семь раз, произведение шести и семи…)

Таким образом, всего за несколько уроков вся таблица умножения может быть легко и быстро

Хитрости для изучения таблиц умножения и методов запоминания

Uncategorized > Хитрости для изучения таблицы умножения и техники запоминания

Опубликовано 7 июля 2020 г.

Автор: Сидк Ахмад

Итак, теперь, когда наши дети знают сложение и вычитание, дело доходит до хитрого понятия умножения. Нас, взрослых, это может не заинтересовать. Однако в детстве эта концепция может сбивать с толку. Мы должны сделать эту концепцию легкой и удобоваримой для наших детей. Вот почему сегодня мы в Holiday Educationist собрали 5 хитростей для изучения таблицы умножения и методов запоминания. Вы будете поражены, увидев, какое влияние это небольшое усилие может оставить на способности вашего ребенка к обучению.

1. Свяжите умножение со сложением.

Не начинать с запоминания. Дети часто борются за то, чтобы сохранить реальность в первой попытке, и это может вызвать страх перед таблицей умножения. Самый простой подход к обучению умножению — понять идею о его связи со сложением — занятием, с которым ваши дети уже должны быть в порядке.

Пошаговые инструкции по умножению.

Прежде чем продолжить, убедитесь, что ваши дети усвоили принцип умножения: это всего лишь перефразированное сложение. Используйте соответствующие модели, подобные приведенной выше, чтобы контекстуализировать эту реальность. Это поможет в разработке моделей, чтобы дублеры могли представить себе мысль:

2 x 2 эквивалентно 2 + 2

или, с другой стороны,

3 x 4 эквивалентно 4 + 4 + 4

2. Начнем с произведения нуля и единицы

2 объясните своим детям, что прибавление нуля к числу не влияет на его характер:

n + 0 = n

Затем объясните, что при умножении любое число, увеличенное на ноль, также равно нулю:

n x 0 = 0

Предложите детям найти экземпляры нулевого свойства в комнате. Например, учебный зал с 25 сиденьями, на каждом из которых не сидит кошка, означает, что в учебном зале нет кошек. В качестве альтернативы, одним из забавных случаев приятной математической игры является вовлечение ваших детей в рассмотрение забавных случаев этого свойства, подобного 0 x один миллион = 0 … или … 0 x бутерброд с ветчиной = 0,

Увеличение на единицу: Свойство индивидуальности

Проще говоря, свойство индивидуальности выражает результат данного числа, а единица есть само это число:

n x 1 = n.

Почти так же, как и с нулевым свойством, научите своих детей увеличивать число на один результат в аналогичном значении. Чтобы обосновать свойство в подлинной обстановке, предложите своим детям рассмотреть примеры свойств личности в классе. Например, одна группа из восьми рабочих областей — это восемь рабочих областей. Единственная строка в расписании, показывающая семь дней, — это семь дней

3. Выучить таблицу умножения, начиная с «простых» чисел

В настоящее время это идеальная возможность совершить, возможно, величайший скачок: пройти таблицу умножения.

Покажите диаграмму или слайд с таблицей дублирования 12 x 12. Если хотите, учите этому детей, умножая увеличенный контур. В случае, если схема 12 х 12 кажется чрезмерно подавляющей, повторите аналогичную процедуру с графиком увеличения 10 х 10. Покажите детям, как использовать схему и находить предметы, следуя и координируя положение чисел, используя вертикаль и даже томагавки.

Теперь поговорим о некоторых примерах, которые вы найдете в плане. Предлагайте детям намеки или указания. Например, обратите внимание, что каждая таблица из десяти заканчивается нулем, а каждая таблица из пяти замыканий — нулем или пятью.

Спросите детей, какие реалии наименее требовательны. Например, единицы и десятки простые. Поскольку вы изучили «простые» реалии умножения — и то, что делает их простыми — избавьтесь от них на диаграмме. Дети, как правило, соглашаются, что двойки, пятерки и одиннадцать тоже простые. Продолжайте скрещивать числа с «простыми» числами.

4. Покажите, как свойство коммутативности упрощает задачу

Как и сложение, умножение является коммутативным, что означает, что запрос множителей не меняет элемент (соответствующий ответ). Как бы, два числа можно увеличить в любом запросе, и пункт будет равноценным. Например, повторение 8 х 2 даст вам такую ​​же реакцию, как и увеличение 2 х 8. Когда вы правильно объясните это, это зарядит энергией ваших детей.

Покажите своим детям, что каждый ответ повторяется, так что им просто нужно выучить половину остальных таблиц. Например, объясните, что обучение 3 x 6 эквивалентно обучению 6 x 3!

Если дублеры только что набрали реальные группы от 0 до 3, то они также знают четыре числа от 4 до 10.

Чтобы дополнительно усилить свойство коммутативности, вы также можете использовать визуальную модель, подобную приведенной выше, и показать, как организованы желтые квадраты.

Спросите своих детей: «Разве эти два плана игры не эквивалентны, хотя и являются разными формами друг друга? Если мы проверим общее количество единиц, скажут ли они, что они эквивалентны?»

Помощь дублерам в освоении этого свойства является ключевой частью обучения умножению. Чтобы заставить детей делать это без чьей-либо помощи и учиться через прямое понимание, пусть ваш класс создаст модели, представляющие эту мысль, и продемонстрирует, что a x b приводит к тому же результату, что и b x a.

5. Разделите запоминание на простые продвижения

Теперь ваши дети готовы начать запоминать увеличенную таблицу. Учитывая все обстоятельства, они только начали действовать как таковые. Знайте, что обычно детям не очевидно, почему они должны учить умножение наизусть. Расскажите о важности понимания важности умножения и того, как его можно использовать в обычных обстоятельствах.

Методы запоминания.

Хотя существует множество способов сохранить диаграмму умножения, рассмотрите приведенные выше модели — «простые» числа — в качестве подходящего начального этапа. Приступая к выполнению упражнения, подумайте о том, чтобы придерживаться этих приемов для изучения методов запоминания таблицы умножения.

Расширьте возможности детей и дайте им время для устной репетиции или записи в виде печатной копии.

Представляйте новые таблицы прибавок индивидуально, шаг за шагом, постепенно открывая идею для дальнейшего развития шагов умножения на 2, 3, 4 и т. д. Дайте детям время отрепетировать таблицы прибавок. Откройте для себя ритм, который превосходно работает в вашей классной комнате.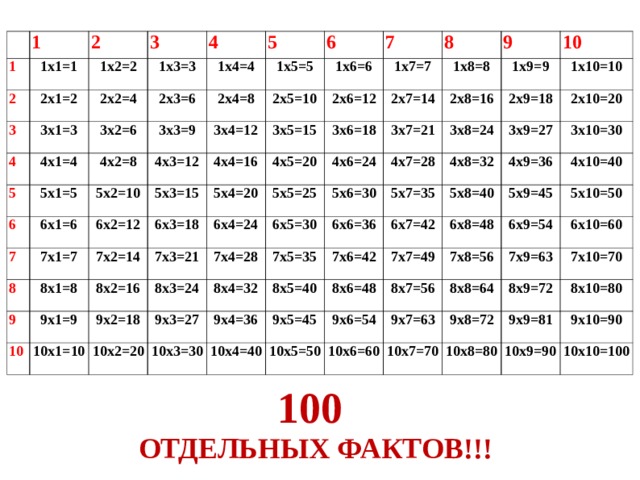 Если хотите, используйте взаимное обучение для детей, которые борются.

Запомнить таблицы в ключевом запросе. Когда ваши дети наберут 0-3, продолжайте до 4-7, а затем 8-10. В зависимости от вашего желания, вы также можете покрыть 11 и 12. Считая все дополнительные проблемы с тестами чем-то дополнительным, вы сможете оценивать детей с высокими достижениями. Несколько педагогов включат несколько более сложных вопросов для вознаграждения или признания детей с высокими достижениями. Чтобы облегчить запоминание, держите наглядные материалы рядом с собой в учебном зале. Независимо от того, как часто вы распространяете умножение, постоянно разумно иметь физическую таблицу умножения, доступную в вашем учебном зале.

Маленький подарок.

Пока вы этим занимаетесь. Использование обучающих приложений помогает детям понять и усвоить концепцию в удобной для детей форме. Вот почему приложения в основном определяются с игровым интерфейсом. Доступно бесплатно для IOS и Android.

 

 

Рекомендуется для возрастных групп

12 лет

---

23 года

---

3-6 лет (детский сад)

---

Сидк Ахмад

MD-блогер о здоровье.

Детское образование и психологическое развитие Энтузиаст

На миссии вырезать детей с лучшими личностями, восприимчивым умом и самыми сильными механизмами выживания.

Приемы для изучения таблицы умножения

Начнем с принципа таблицы умножения ноль (0)

Вау, очень просто.

Любое число, умноженное на 0 , дает 0 .

Каждый раз, когда вы находите 0 в своем вопросе на умножение, ответ на этот вопрос автоматически равен 0 .

Пример : 4 x 0 = 0; 0 x 8 = 0

Принцип x1 самый лучший и простой.

На самом деле не требует никакой техники.
Любое число, умноженное на 1, является просто тем же самым числом.

Пример : 3 x 1= 3; 1 х 1 = 1; 9 х 1 = 9; 1 х 12 = 12,

Вы знаете четные числа? Да, тогда ты попал.

лучший метод для умножения на 2 это просто для того, чтобы пропустить счет в 2 с

:
2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24.

Здесь вы заметите, что все ваши ответы являются четными числами.

Пример : 2 x 1 = 2; 2 х 2 = 4; 3 х 2 = 6; 2 x 4 = 8

Тем не менее, еще один трюк здесь может заключаться в том, чтобы ДОБАВИТЬ число , что должно быть , умноженное на 2 , к самому этому числу.

Это означает, что вы должны просто найти двойное число, чтобы умножить его на 2 .

Пример : 2 x 3 = (3 + 3) = 6; 8 х 2 = (8 + 8) = 16; 5 х 2 = (5 + 5) = 10

• x2 Викторина

  Открыть

• x2 Оценка

  Открыть

• x2 Рабочие листы

  Открыть

Самый быстрый и простой способ для ребенка узнать умножение на 3 — просто применить метод счета с пропусками .

Сначала мы пропустим счет за 3 секунды.

Поехали:

3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36 .

Теперь решите 3 x 4. Эй, это просто.

Просто вернитесь к линии подсчета пропусков. Начните считать с 1 ^st позиция , которая равна 3 , до 4 ^th позиция .
Вы обнаружите, что 4 ^й позиция имеет номер 12 .

Следовательно, 3 x 4 = 12

Однако еще один совет в таблице 3 умножить — умножить данное число на 2. метод.

Пример : 3 x 4 = (4 x 2) + 4 = 8 + 4 = 12     ИЛИ     4 + 4 + 4 = 8 + 4 = 12

• x3 Викторина

  Открыть

• x3 Оценка

  Открыть

• x3 Рабочие листы

  Открыть

Простой. Дети, способные к сложению, могут использовать этот трюк при умножении числа на 4.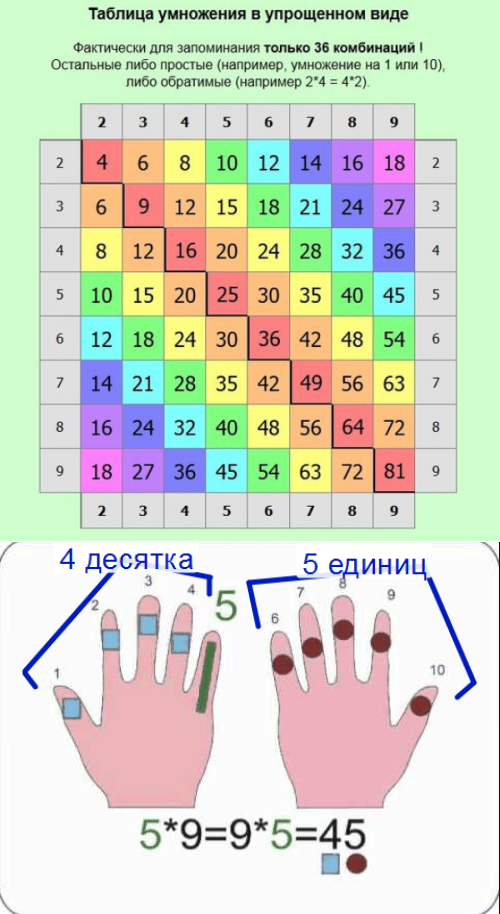

Это потому, что умножение на 4 эквивалентно умножению этого числа на 2, два раза .

Когда это будет сделано, вы, тем не менее, сложите два результата.

Пример : 6 х 4 = (6 х 2) + (6 х 2) 12 + 12 = 24

• x4 Викторина

  Открыть

• x4 Оценка

  Открыть

• x4 Рабочие листы

  Открыть

Умножение на 5 очень легко освоить.
В начале вы даже можете попробовать пропустить счет вслух в 5 секунд.

Попробуем: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60 .

Если вы внимательно посмотрите на серию чисел выше, вы поймете, что каждое число заканчивается либо на 5, либо на 0.

Хорошо. Это означает, что четное число, умноженное на 5, дает результат, оканчивающийся на 0 , а нечетное число, умноженное на 5, дает результат, оканчивающийся на 5 .

Пример : 3 х 5 = 15; 6 х 5 = 30

• x5 Викторина

  Открыть

• x5 Оценка

  Открыть

• x5 Рабочие листы

  Открыть

Этот принцип очень легко понять.
Все мы знаем, что половина 6 равна 3 верно.

Хорошо. Учитывая, что вы решаете 8 x 6 , первое, что нужно сделать, это просто умножить данное число (8) на 3 ; Однако
повторите это упражнение дважды, получив два результата.

Наконец-то ты добавить два результата .

Пример : 8 х 6 = (8 х 3) + (8 х 3) = 24 + 24 = 48

Кроме того, мы никогда не забываем наш метод подсчета пропусков, который в 6 секундах дает: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72 .

Как указывалось ранее, при заданном 8 x 6 , например, простой счет от 1 ^st

позиции до 8 ^th точки .

Вы заметите 8 ^й позиция это номер 48 .

• x6 Викторина

  Открыть

• x6 Оценка

  Открыть

• x6 Рабочие листы

  Открыть

Освоив таблицу умножения с 0 до 6 , вы автоматически становитесь экспертом.

От x8 до x12 больше не будет проблемой, но его будет легко запомнить.

Здесь мы просто используем метод подсчета пропусков

Таким образом, в 7s; 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 71, 84 .

Учитывая 7 x 8 , как обычно, начните отсчет с 1 ^st позиции что 7 , до 8 ^-й .

Подсчитав, вы понимаете, что на 8-й позиции стоит число 56. Следовательно,

7 x 8 = 56

• x7 Викторина

  Открыть

• x7 Оценка

  Открыть

• x7 Рабочие листы

  Открыть

До сих пор мы заметили, что умножение четных чисел, таких как 4 , 6 и 8 , имеет уникальный принцип.

Итак, никакого стресса.
Теперь этот уникальный принцип заключается в использовании половины нашего четного числа для упражнения.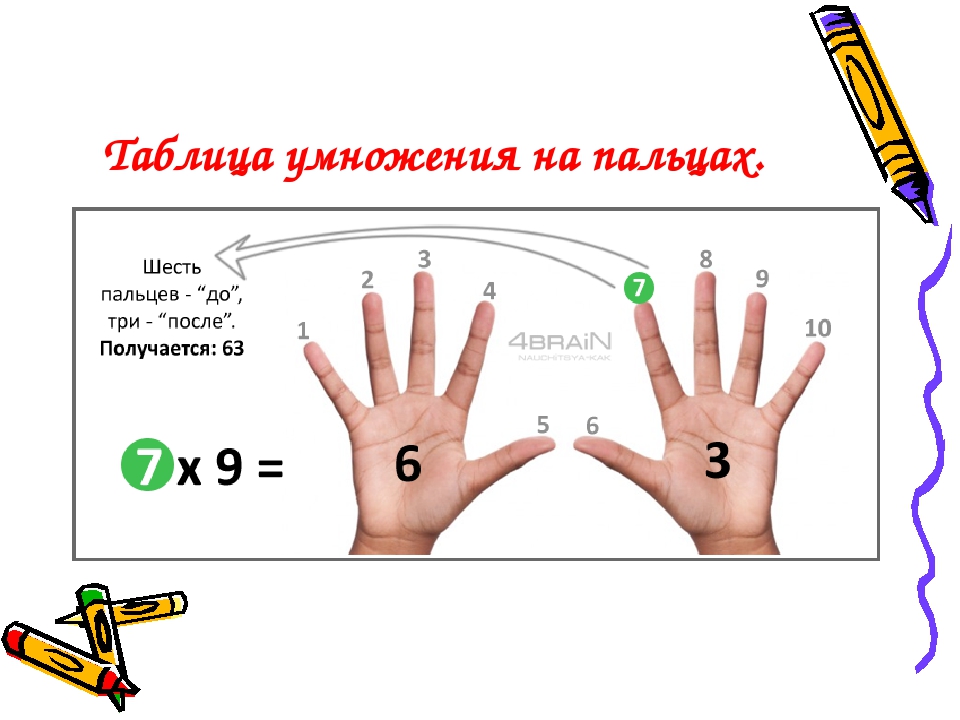

Теперь с таблицей 8 раз половина 8 равна 4 .

Идеально. Поэтому, учитывая задачу 6 x 8 , мы просто умножаем данное число (6) на 9.0019 4 .

Как обычно, упражнение проводится дважды.
Получив два результата, вы теперь добавляете (два результата).

Пример : 6 х 8 = (6 х 4) + (6 х 4) = 24 + 24 = 48

• x8 Викторина

  Открыть

• x8 Оценка

  Открыть

• x8 Рабочие листы

  Открыть

Умножение на 9 — одна из самых простых для запоминания таблиц умножения.

Вот оно.
Учитывая проблему 9 x 4 , мы можем решить ее, выполнив следующие действия:

Первое, что нужно сделать, это добавить a 0 после числа, которое нужно умножить на 9 .
Если вы сделаете это, ваш результат будет 40 .

Далее, вычесть это число (его значение) из полученного результата (40 – 4) = 36 .

9 x 4 = 36

Пример :Пример: 9 x 9 = 90 – 9 = 81; 7 х 9 = 70 – 7 = 63

• x9 Викторина

  Открыть

• x9 Оценка

  Открыть

• x9 Рабочие листы

  Открыть

Умножение на десятки — лучшая и простейшая таблица умножения на сегодняшний день.

Вам не нужно дважды думать. Просто добавьте a 0 к числу, которое вы хотите умножить на 10 .

Это твой ответ.
Вы обнаружите, что в вашем результате была лишняя цифра.

Пример : 3 x 10 = 30 12 x 10 = 120

• x10 Викторина

  Открыть

• x10 Оценка

  Открыть

• x10 Рабочие листы

  Открыть

До сих пор вы заметили, что любое число, умноженное на 11, означает запись этого числа дважды или добавить ту же цифру рядом с существующей.

Эй, будь осторожен! Это правило применяется только от 11 x 1 до 11 x 9 .

Пример 1 : 6 x 11= 66; 7 х 11 = 77;

Для номера 10 просто добавьте 0 в конце 11 . Итак, 11 х 10 = 110

Здесь мы имеем частный случай для чисел до десяти ( 11 х 11 и более). Есть простая формула ее решения. давайте попробуем 11 х 12 ;

Пример 2 : 11 x 12 = (11 x 10) + (11 x 2) = 110 + 22 = 132

• x11 Викторина

  Открыть

• x11 Оценка

  Открыть

• x11 Рабочие листы

  Открыть

Есть небольшой практический тест, который нужно применить при умножении числа на 12.

Это очень просто. Это выглядит следующим образом: n x 12 = (n x 10) + (n x 2) [ здесь n число ]

Пример : пусть n равно 3.