Методы изучения таблицы умножения: 6 ✔️ Способов быстро и легко выучить таблицу умножения

Исследовательская работа “Способы изучения таблицы умножения на пальцах”

МБОУ АЗЕВСКАЯ ООШ  

АГРЫЗСКОГО МУНИЦИПАЛЬНОГО РАЙОНА РЕСПУБЛИКИ ТАТАРСТАН

III научно-практическая конференция

младших школьников «Первые шаги»

СПОСОБЫ ИЗУЧЕНИЯ ТАБЛИЦЫ УМНОЖЕНИЯ НА ПАЛЬЦАХ

(математическое направление)

Работу выполнила:

Широких Светлана,

ученица 3 класса

Научный руководитель:

Мордвинова С.Н.

Содержание

Введение

1.  Что известно о таблице умножения

2. Таблицы умножения на пальцах (способы)

3. Практическое исследование

3.1 Результаты анкетирования

3.2 Результат письменной проверки  знаний таблицы умножения

4. Вывод

Введение

             Всем детям приходится в школе знакомиться с таблицей умножения. И некоторым очень  трудно её  понять и выучить. Мне стало интересно, кто придумал эту таблицу? Тогда стала думать, а как легче её запомнить? Существуют ли какие-нибудь способы умножения?

Я предположила, что мы не всё знаем о таблице умножения, может быть, существуют простые способы запоминания таблицы умножения, например,  на пальцах. В своей работе я постараюсь доказать это и  получить  ответы на интересующие меня  вопросы.

Цель работы:  изучить способы  изучения (запоминания) таблицы умножения на пальцах.

Задачи исследования:

1. Изучить литературу по теме.

2. Провести анкетирование моих одноклассников по теме: «Как ты запоминал таблицу умножения».

3. Провести  письменную проверку знания таблицы умножения  у учащихся 3  класса до знакомства со способами запоминания таблицы умножения на пальцах.

4. Познакомить одноклассников со способами запоминания таблицы умножения на пальцах

5. Провести  письменную проверку знания таблицы умножения  у учащихся 3  класса после знакомства со способами запоминания таблицы умножения на пальцах.

Методы, приёмы, используемые  в работе: изучение литературы, анализ, наблюдение, анкетирование, вычислительный срез.

Гипотеза. Существуют способы запоминания таблицы умножения на пальцах, которые не являются общеизвестными.

1. Что известно о таблице умножения?

Составителем таблицы называют древнегреческого математика Пифагора.

Пифагор, прежде всего – это мудрец и философ. Точной даты рождения Пифагора не знает никто, но исторические исследователи датируют это событие приблизительно 580 годом до нашей эры.

        Будущий математик и философ уже в детстве проявлял большую способность к наукам.  Он с ранних лет стремится узнать, как можно больше. У опытных наставников Пифагор изучал геометрию и астрономию, музыку и живопись. Особенное внимание он уделял числам и их свойствам, стремясь познать смысл и природу вещей.

         Число для Пифагора было и материей, и формой всего мира, поэтому естественные явления объяснялись с помощью чисел.   Утверждение «Всё есть число, числа правят миром!» принадлежит самому Пифагору. Пифагор придавал числам мистические свойства, считал, что числа правят миром. Философ считал и саму таблицу умножения отображением вселенной, где угадывается за закономерностью чисел ровный строй планет и скоплений звезд, где угадывается гармония космоса и слышится божественная музыка.

        Изначально  Пифагором таблица заполнялась не теми цифрами, которые мы привыкли видеть, а греческими числами ионийской нумерации         

α β γ δ ε  ζ ξ  η θ  ι   – Цифры греческой ионийской нумерации.

1 2 3 4 5 6 7 8 9 10  – цифры,  которыми мы сегодня привыкли пользоваться.

        Таблица умножения скрывает в себе много замечательных математических закономерностей, поиск которых способен превратиться в увлекательное занятие, сулящее немало сюрпризов. Что представляет собой таблица Пифагора? По горизонтали и по вертикали расположены числа натурального ряда; на пересечении столбцов и строк стоят их произведения. Диагональ таблицы образуют квадраты чисел. Таблицу можно продолжать вправо и вниз до бесконечности  (таблица I).

Таблица I

∑	1	2	3	4	5	6	7	8	9
1	1	2	3	4	5	6	7	8	9
2	2	4	6	8	10	12	14	16	18
3	3	6	9	12	15	18	21	24	27
4	4	8	12	16	20	24	28	32	35
5	5	10	15	20	25	30	35	40	45
6	6	12	18	24	30	36	42	48	54
7	7	14	21	28	35	42	49	56	63
8	8	16	24	32	40	48	56	64	72
9	9	18	27	36	45	54	63	72	81

В российских школах значения традиционно доходят до 10×10.

В Великобритании до 12×12, что связано в том числе с единицами английской системой мер длины

2. Способы запоминания таблицы умножения на пальцах

Прием пальцевого счета при получении значений табличного умножения малоизвестен, хотя является одним из древнейших вычислительных приемов. Многие учителя не признают приемов пальцевого счета при изучении табличного сложения и табличного умножения, придерживаясь мнения, что их результаты необходимо учить наизусть. На самом деле многие дети не могут твердо освоить весь объем таблицы умножения именно по причине неумения использовать приемы, помогающие ее освоению. Выучить всю таблицу наизусть могут не все дети. Среди школьников средних и даже старших классов имеется достаточное количество детей, плохо знающих таблицу умножения. Актуальность: Для детей младшего школьного возраста прием пальцевого счета при освоении таблицы умножения  может быть рекомендован как вспомогательный. Для того чтобы его эффективно использовать, следует знать результаты табличного умножения в пределах таблицы умножения числа 4.

1. Способ.

Например, нужно умножить 6 на 7. Зажимаем пальцы на обеих руках в кулак, а затем на каждой руке отгибаем столько пальцев, насколько каждый множитель больше, чем  пять.

На двух руках отогнуто три пальца – это число десятков в искомом числе. На одной руке остались прижатыми к ладони три пальца, на другой – четыре пальца эти числа перемножаем 3 * 4 = 12 и прибавляем к числу имеющихся десятков. 30 + 12 = 42. Ответ: 6 * 7 = 42.

Еще один пример: необходимо умножить 8 на 9.

Отгибаем на одной руке три пальца, а на другой руке

– четыре пальца (на столько каждый множитель больше, чем пять). Отогнуто 7 пальцев – это десятки в искомом числе.

Перемножаем число загнутых пальцев обеих рук: 2 * 1 = 2.

Прибавляем это количество к числу десятков 70 + 2 = 72.

Таким образом, 9 * 8 = 72.

2 Способ

Этот способ похож на первый, только намного проще. Не надо высчитывать насколько число больше пяти. Надо просто загнуть пальцы при счете после 5. Например, умножим 7 на 8. Ладошки открытые.

Считаем слева направо 1,2,3,4,5 пальцы на одной руке закончились, переходим на вторую руку и пальцы начинаем загибать  – 6,7. Загнули 2 пальца.

 Теперь считаем справа налево 1,2,3,4,5, переходим на другую руку 6,7,8. Загибаем 3 пальца.

Загнутые пальцы это десятки т.е. 50. А единицы надо перемножить 3 умножить на 2 равно 6. Значит ответ 50+6=56

  3 Способ

Нужно запомнить соответствия: мизинцы это 6, безымянный палец это 7, средний – 8, указательный 9, большой – 10. Например, нужно умножить 7 на 8. Соединяем пальцы, как показано на рисунке.

Каждый палец снизу, вместе с соединенными, это десятки, т.е. 50. А верхние это единицы, которые нужно перемножить, т.е. 3 умножить на 2 равно 6. Значит 56. 

4.Способ

Умножение на 5.  Каждый палец это 5. Например, нужно умножить 7 на 5. Загибаем 3 пальца справа. Считаем 5+5+5+5+5+5+5=35 или считаем по два пальца – десятками 10+10+10+5=35

5 Способ.

Умножение на 9 с помощью пальцев.

Я  была удивлена изобретательностью этого способа умножения. Всё очень просто и интересно. Совсем не нужно запоминать таблицу умножения на девять!
        И калькулятор  не потребуется – нам помогут  пальцы рук. Посмотрим на раскрытые ладони. Перед нами десять пальцев. Теперь загибаем первый палец слева. Осталось девять пальцев. Мы умножили девять на один. Теперь попробуем умножить на 2: раскрываем ладони и загибаем второй палец слева. С одной стороны от загнутого остался один палец, а с другой – восемь. Один, восемь – получилось 18!Умножим 9 на 7? Загибаем седьмой по счету палец. Слева остается шесть, а справа три – 63!

3.  Практическое исследование.

3.1. Результаты анкетирования.

 Чтобы выяснить, какой способ выбрали мои одноклассники для заучивания таблицы, мы провели анкетирование учеников 3 класса (6 человека) по теме «Знаешь ли ты таблицу умножения?»

Результаты анкетирования:

1. Знаешь ли ты таблицу умножения? (да -4 человека, нет- 2 человека)

2. Испытывал ли ты сложности при запоминании таблицы умножения? (испытывали трудности -4 человек, не испытывали – 2 человека).

3. Каким способом ты учил таблицу умножения?

4. Таблицу умножения, на какое число выучить сложнее?

Выводы:

1.²⁄ ³ моих одноклассников знают таблицу умножения.

2. .²⁄ ³моих одноклассников испытывали сложности при её запоминании.

3. Самый распространенный способ запоминания:

– зрительный -3 человека,

– рисованием – 1 человек,

– записывали – 1 человек,

– на слух – 1 человек.

4. Сложнее всего было выучить таблицу на 9.

3.2 Результаты письменной проверки знания таблицы умножения до знакомства со способами запоминания на пальцах:

 Выполнили верно – 2 человека.

Допустили ошибки:

1) На знание таблицы умножения на 4, на 5 – 0 человек,

2) На знание таблицы умножения на  6 – 2  человека.

3) На знание таблицы умножения на  7 –  3 человека.

4) На знание таблицы умножения на  8 – 2 человека.

5) На знание таблицы умножения на  9 – 4 человека.

Таким образом, можно сделать вывод, что больше всего ошибок мои одноклассники делают, выполняя задания с таблицей на 9.

Таблицу умножения мы прошли совсем недавно, но некоторые ребята, до сих пор не могут ее запомнить. Поэтому я решила познакомить своих одноклассников со способами запоминания таблицы умножения с помощью пальцев и еще раз провести проверку.

3.3 Результаты письменной проверки знания таблицы умножения после знакомства со способами запоминания на пальцах:

Выполнили верно – 4 человека. Допустили ошибки:

1) На знание таблицы умножения на 4, на 5 – 0 человек,

2) На знание таблицы умножения на  6 – 1  человека.

3) На знание таблицы умножения на  7 –  1 человека.

4) На знание таблицы умножения на  8 – 1 человека.

5) На знание таблицы умножения на  9 – 2 человека.

4. Выводы.

1.Моё предположение подтвердилось: мы не всё знаем о таблице умножения.

2. Оказывается, в школьном курсе математики рассматривается лишь незначительная часть имеющихся сведений о табличном умножении на пальцах.

3. Существуют  различные способы запоминания таблицы умножения на пальцах.

     С цифрами связан каждый день нашей жизни, и познавать новое это очень интересно и увлекательно.

4. При изучении новых способов умножения меня удивляли необычные и простые  правила, которые можно применять при умножении чисел.        

ДЛЯ  КАЖДОГО  ЧЕЛОВЕКА НАЙДЕТСЯ  СВОЙ  СПОСОБ ЗАПОМИНАНИЯ  ТАБЛИЦЫ УМНОЖЕНИЯ,  А  МОЖЕТ БЫТЬ ДАЖЕ  И  НЕСКОЛЬКО, КОТОРЫЕ  ПОЗВОЛЯТ  В НЕПРИНУЖДЕННОЙ  ФОРМЕ,  ВЕСЕЛО  И  ИНТЕРЕСНО,  БЕЗ  ЗУБРЕЖКИ,  ЗАПОМНИТЬ ЕЁ   РЕЗУЛЬТАТЫ.

Занимательная таблица умножения – презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Муниципальное бюджетное
общеобразовательное учреждение
«Средняя общеобразовательная школа №5»
г. Ижевска
Исследовательская работа
На тему:
Занимательная таблица умножения
Выполнил:
Ученик 2 «Г» класса МБОУ СОШ №5
Янситов Артём

Руководитель:
Бехтерева Кристина Петровна
Цель работы:
облегчить изучение
таблицы умножения
для одноклассников
Задачи исследования:
Подготовить материал по истории появления
таблицы умножения.
Оценить роль таблицы умножения в жизни
человека.
Найти и изучить различные способы
изучения таблицы умножения.
Предложить одноклассникам выявленные
способы запоминания таблицы и провести
исследование эффективности найденных
методов.
Подвести итог проделанной работы
Гипотеза:
используя различные
методы выучить
таблицу умножения
быстро и увлекательно
Объект исследования –
таблица умножения.
Предмет исследования
– методы изучения
таблицы умножения.
Методы исследования:
Изучение материалов по
выбранной теме
Практическое исследование
разных способов
заучивания таблицы и их
эффективности
Анкетирование
Практическая значимость
работы заключается в том, чтобы
помочь своим одноклассникам
выучить таблицу умножения
увлекательно и легко
База исследования:
Муниципальное Бюджетное
Общеобразовательное Учреждение “МБОУ
СОШ №5″.
Таблички,
найденные при
археологических
раскопках

9. Таблица умножения в жизни человека

10. Результат заучивания таблицы умножения

100
90
80
70
60
50
40
30
20
10
0
знают
не знают

11. Таблица Пифагора

12.

Методы изучения таблицы умноженияКарточки – один из способов изучения

13. Умножение на 6,7,8,9 и10

Расположить пальцы друг против друга и пронумеровать от 6 до 10
Соприкаснуть пальцы , которые соответствуют перемножаемым числам.
Соприкасающиеся пальцы и расположенные ниже составляют десятки
Посчитать пальцы на левой и правой руке, расположенные выше
соприкасающихся, и перемножить их
Сложить получившиеся два числа

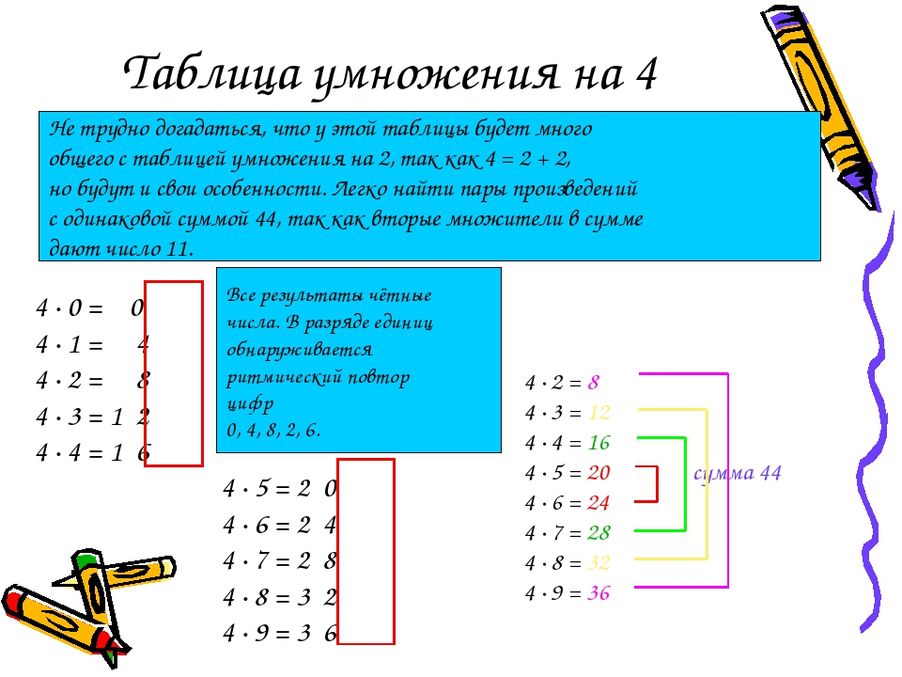
18. Умножение чисел от 5 до 10

Сжатый кулак равен 5, каждый отогнутый палец добавляет 1.
Отогнутые пальцы – это десятки, загнутые пальцы единицы.
Перемножаем единицы одной руки на единицы другой и складываем с десятками.
Пример на рисунке: 6 х 7 = (3х10)+(4 х 3) = 30 + 12 = 42.

19. Умножение на 9

Пронумеровать пальцы рук от 1 до 10
Загнуть палец, соответствующий числу, умножаемому на 9
Пальцы слева от загнутого десятки, а справа единицы.
Пример: 9 х 2 = 1 х 10 + 8 = 18

23. Результаты изучения таблицы умножения с помощью предложенных методов

100
90
80
70
60
50
40
30
20
10
0
знают
не знают
По полученным результатам можно сделать
вывод, что с применением различных
приемов, изучение таблицы умножения
было более увлекательным и интересным.
Процесс превращался в веселую игру,
таблица училась легче и быстрее.

English     Русский Правила

Дискалькулия и запоминание таблиц умножения — Обнаружение дискалькулии

«Как я могу помочь учащимся запомнить свои таблицы умножения?» Это распространенный вопрос родителей и учителей относительно учащихся с дискалькулией (также и учащихся с дислексией).

Что, если это лучший ответ? «Не требуйте от них заучивания таблицы умножения».

Это может быть неожиданным предложением. Тем более, что традиционно от школьников всего мира требуется заучивать таблицу умножения. Его часто рассматривают как средство измерения математических способностей или интеллектуальных способностей учащегося. Это ошибка дискалькуликов.

Эксперты по дискалькулии постоянно подчеркивают, что учащимся с дискалькулией не рекомендуется заучивать таблицу умножения.

Почему людям с дискалькулией не рекомендуется запоминать?

Дискалькулия чрезвычайно ограничивает память, доступную для восприятия чисел и вычисления чисел. Из-за этого требования к памяти должны быть снижены, чтобы система памяти меньше нагружалась и могла быть зарезервирована для нескольких важных элементов, часто называемых «ключевыми фактами». Запоминание 144 фактов умножения — слишком большая нагрузка на систему памяти дискалькулика.

Для дискалькулического ученика запоминание таблицы умножения автоматически не коррелирует с пониманием концепции умножения.

Эти реалии не означают, что учащиеся с дискалькулией не могут научиться умножать или что они не смогут запомнить какие-либо факты умножения. Но адаптируя методы обучения к более эффективным способам, ведущим к реальному пониманию, учащиеся с дискалькулитом могут успешно прийти к пониманию процесса умножения — без механического запоминания. Для этого особенно важно учить для понимания .

Вот несколько идей об эффективных методах, с помощью которых дискалькулистических учащихся могут успешно выучить умножение.

Процесс обучения начинается с твердого понимания учащимся нескольких ранее изученных понятий: удвоение, деление пополам, подсчет шагов, компоненты, соединение, разделение, размещение значения и умножение/деление на 10. Эти предварительные навыки помогут учащемуся понять умножение с большим успехом.

Эксперты по дискалькулии рекомендуют учащимся начинать с изучения таблиц 2x, 5x и 10x. Это позволяет учащемуся полностью понять и запомнить только несколько ключевых фактов. Поскольку нагрузка на память снижается, учащиеся могут вспомнить их с большей достоверностью. Затем учащиеся учатся тому, как использовать эти три ключевых кратных вместе с разумом и логикой, чтобы вывести остальные факты умножения.

Этот метод позволяет учащимся соединиться и развить ранее полученные навыки. Например, таблицу 2x можно воспринимать как «удвоение» числа — важный предварительный навык. Таблицу 5x можно воспринимать как «уменьшение вдвое» таблицы 10x — еще один важный предварительный навык для дискалькуликов, который нужно освоить перед умножением.

«Лучший способ изучить факты таблицы умножения — это использовать мультисенсорный подход, который делает связи между фактами явными, а также предоставляет множество возможностей для проверки фактов. Научить учащихся понимать понятие умножения путем рассуждений. Они используют навыки подсчета шагов и свое знание числовых закономерностей, чтобы рассматривать умножение как структурированное повторение количества. Если ученики знают ключевые факты о 10 x N и 5 x N для каждой таблицы умножения и понимают структуру умножения, они могут быстро вывести другие факты». – Джейн Эмерсон и Патрисия Бэбти, 9 лет.0036 Решение проблемы дискалькулии , с. 148

Если вы хотите узнать больше об обучении умножению учащихся с дискалькулией или о других методах обучения, наиболее подходящих для дискалькулии, ознакомьтесь с приведенными ниже ресурсами.

Мини-семинар для преподавателей — адаптировано из моего родительского класса, предназначено только для преподавателей для дискалькулии.

Список для чтения для родителей – бесплатная загрузка моих любимых книг, включая примечания о том, почему я рекомендую каждую из них.

Обнаружение дискалькулии — моя книга, опубликованная в феврале 2022 г.

Ежемесячный субботний информационный бюллетень — информирование о дискалькулии, обучение и поддержка на ваш почтовый ящик каждый месяц. Зарегистрируйтесь в этой форме ниже. Конфиденциальность соблюдается, никакого спама, отписаться в любое время.

Горячие клавиши для таблицы умножения

В этом разделе вы узнаете горячие клавиши, которые будут полезны для простого выполнения таблицы умножения.

Чтобы понять сочетания клавиш, вы должны запомнить следующее умножение.

Однозначное число x Однозначное число

Пример:

6 x 7 = 42

8 x 9 = 72

4 x 9 = 36

И нам трудно запомнить два ответа для

2

9 число цифр x однозначное число

и

двузначное число x двузначное число

Здесь мы дали ярлыки, чтобы найти ответ для приведенных выше умножений, которые входят в таблицу умножения.

Двузначное число x Однозначное число

Этот метод объясняется для 1 в десятом разряде двузначного числа (Таблица умножения).

Шаги, которые необходимо выполнить, чтобы понять приведенный выше ярлык:

Шаг 1:

Сначала возьмите однозначное число и умножьте его на 10. :

Умножьте однозначную и единичную цифру двузначного числа.

(7 x 2 = 14  в приведенном выше примере)

Шаг 3 :

Добавьте значение шага 1 и значение шага 2.

(70 + 14 = 84 в приведенном выше примере)

Попробуйте сами:

14 x 8 = ?

19 х 8 = ?

7 х 18 = ?

Таким образом можно многое попробовать.

Двузначное число x Двузначное число

Этот метод объясняется для 1 в десятках обоих двузначных чисел (Таблица умножения).

Метод 1 :

Метод 2:

Шаги, которые необходимо выполнить, чтобы понять оба метода:

Шаг 1:

Добавьте одно из двухзначных чисел и цифру на место другого числа. Умножьте результат на 10.

(17 + 2 = 19 —-> 19 x 10 = 190)

или

(12 + 7 = 19 —-> 19 x 10 = 190)

Шаг 2:

Умножьте цифры вместо одного из обоих чисел.

Шаг 3 :

Сложите результаты шагов 1 и 2, вы получите ответ.

Попробуйте сами:

17 x 18 = ?

18 х 19 = ?

15 х 19 = ?

Таким способом можно многое попробовать.

Осторожно!

Чтобы использовать эти ярлыки, вы должны иметь большую практику. В противном случае описанные выше сочетания клавиш не будут работать должным образом, и вы не сможете получить правильный ответ. Поэтому, пожалуйста, попрактикуйтесь с этими сочетаниями клавиш, используя разные номера.

Примечание:

Ярлыки, описанные выше, будут работать только для 1 в десятках двузначных чисел, а не для любого числа.

Решенные проблемы

Оцените следующие продукты.

Задача 1 :

8 x 12

Решение :

8 x 10 = 80 —-A

8 x 2 = 16 —-B

Добавьте A и B.

800016

= 96

Следовательно,

8 x 12 = 96

Задача 2 :

9 x 16

Решение:

9 x 10 = 90 —-A

9 x 6 = 54 —-B

Сложите A и B.

90 + 54 = 144

Следовательно,

9 x 11 = 144

Задача 3:

6 x 18

Решение:

6 x 10 = 60 —-A

6 x 8 = 48 —-B

Сложите A и B.

25

5 60 + 48 = 108

Следовательно,

6 x 18 = 108

Задача 4:

17 x 4

Решение:

4 x 10 = 40 —-A

4 x 7 = 28 —-B

Сложите A и B.

40 + 28 = 68

Следовательно,

17 x 4 = 68

Решение 5 : 00002 9

:

7 x 10 = 70 —-A

7 x 9 = 63 —-B

Добавьте A и B.

70 + 63 = 133

Следовательно,

19 x 7 = 133

Задача 6 :

16 x 6

Решение :

6 x 10 = 60 —-A

6 x 6 = 36 —-B

Добавить A и B.

60 + 36 = 96

Следовательно,

16 x 6 = 96

Проблема 7:

14 x 12

Решение:

14 + 2 = 16 —— > 16 x 10 = 160 —-A

4 x 2 = 8 —-B

Добавьте A и B.

160 + 8 = 168

Следовательно,

14 x 12 = 168

2 Задача 8:

15 x 13

Решение:

15 + 3 = 18 —-> 18 x 10 = 180 —-A

5 x 3 = 15 —-B

Добавить A и B.

180 + 15 = 195

Следовательно,

15 x 13 = 195

Проблема 9:

19 x 16

Решение:

19 + 6 = 25 — -> 25 x 10 = 250 —-A

9 x 6 = 54 —-B

Добавьте A и B.

250 + 54 = 304

Следовательно,

19 x 16 = 304

Задача 10 :

12 x 19

Решение :

12 + 9 = 21 —-> 21 x 10 = 210 —- A

2 x 9 = 18 —- B

Добавить A и B.

210 + 18 = 228

Следовательно,

12 x 19 = 228

Задача 11:

15 x 18

Решение :

15 + 8 = 23 —-> 23 x 10 = 230 —-A

5 x 8 = 40 —-B

Добавьте A и B.