Методика математического развития: Теоретические основы и методика математического развития дошкольников – Всё о детях – беременность, воспитание, уроки для детей

Методика математического развития (экзамен) – Шпаргалка по Методике математического развития

Шпаргалка по Методике математического развития

Скачать все файлы (4262 kb.)

Доступные файлы (1):

n1.doc

4262kb.

15.02.2014 20:00

скачать

1 2 3 4 5 6 7 8 9 … 20

Методика математического развития (экзамен)

1. Основные математические понятия: множество, число, цифра, натуральный ряд чисел, система счисления, счетная, вычислительная, измерительная деятельность, величина, форма, геометрическая фигура, время, пространство.
Методика ФЭМП в системе пед.наук призвана оказать помощь в подготовке детей дошкольного возраста к восприятию и усвоению математики – одного из важнейших предметов в школе и всестороннего развития ребёнка.
Методика ФЭМП имеет специфическую, чисто математическую терминологию.
Это:

– множество;

– число;

– счётная и вычислительная деятельность;

– величина;

– геометрические фигуры;

– время;

– пространство.
МНОЖЕСТВО — это совокупность объектов, которые рассматриваются как единое целое. Мир, в котором живет человек, представлен разнообразными множествами: множество звезд на небе, растений, животных вокруг него, множество разных звуков, частей собственного тела.

Множества состоят из элементов. Элементами множества называют объекты, составляющие множества. Это могут быть реальные предметы (вещи, игрушки, рисунки), а также звуки, движения, числа и др.

Элементами множества могут быть не только отдельные объекты, но и их совокупности. Например, при счете парами, тройками, десятками. В этих случаях элементами множества выступает не один предмет, а два, три, десять – совокупность.
Таким образом, множества рассматривают как набор, совокупность, собрание каких-либо предметов и объектов, объединённых общим, для всех характерным свойством.
Всякое свойство можно рассматривать как принадлежность некоторым предметам.

Например, свойством быть красным обладают некоторые цветы, ягоды, автомашины и другие предметы. Свойством быть круглым обладают луна, мяч, колеса велосипедов и автомашин, детали различных машин и станков и др.

Таким образом, с каждым свойством связывается множество (предметов), обладающих этим свойством. Говорят также, что множество характеризуется данным свойством — или множество задано указанием характеристического свойства.
Под характеристическим свойством множества подразумеваются такое свойство, которым обладают все объекты, принадлежащие данному множеству (элементы этого множества), и не обладает ни один предмет, который не принадлежит ему, т.е. этот предмет не является его элементом.
Если некоторое множество А задано указанием характеристического свойства Р, то это записывается следующим образом:
А = {х | Р(х)}
и читается так: «А – множество всех х таких, что х обладает свойством Р», или, короче, «А – множество всех х, обладающих свойством Р». Когда говорят: «множество всех предметов, обладающих свойством Р», имеются в виду те и только те предметы, которые обладают этим свойством.

Таким образом, если множество А задано характеристическим свойством Р, то это означает, что оно состоит из всех предметов, обладающих этим свойством, и только из них. Если какой-нибудь а обладает свойством Р, то он принадлежит множеству А, и, наоборот, если предмет а принадлежит множеству А, то он обладает свойством Р.
Некоторым свойством может обладать бесконечное множество предметов, другим — лишь конечное множество. Поэтому множества подразделяются на конечные и бесконечные.
Конечное множество может быть задано непосредственным перечислением всех его элементов в произвольном порядке. Например, множество детей данной группы, живущих на Садовой улице, может быть задано описанием с помощью характеристического свойства: {х | х – живет на Садовой улице) или перечислением всех его элементов в произвольном порядке: {Лена, Саша, Витя, Ира, Коля}.
Вполне понятно, что бесконечное множество нельзя задать перечислением всех его элементов.

Математика в большей мере имеет дело с бесконечными множествами (числа, точки, фигуры и другие объекты), но основные математические идеи и логические структуры могут быть смоделированы на конечных множествах.

Естественно, что в предматематической подготовке обычно имеют дело с конечными множествами.
СЧЕТ – первая и основная математическая деятельность, основанная на поэлементном сравнении конечных множеств.

ЧИСЛО – это общая неизменная категория множества, которая является показателем мощности множества. Это лишь звуковое обозначение.
Теоретические основы формирования элементарных математических представлений у дошкольников включают детальное изучение лишь системы натуральных чисел. Поэтому, говоря «числа», мы имеем в виду натуральные числа.
ЦИФРЫ — система знаков (“буквы”) для записи чисел (“слов”) (числовые знаки). Слово “цифра” без уточнения обычно означает один из следующих десяти знаков: 0 1 2 3 4 5 6 7 8 9 (т.н. “арабские цифры”). Сочетания этих цифр порождают дву-(и более) значные числа.
Число имеет 2 значения: количественное и порядковое.
При количественном значении нас интересует количество элементов во множестве. Мы используем вопрос СКОЛЬКО? и счёт начинаем с количественного числительного ОДИН.
При порядковом значении числа нас интересует место числа среди других или порядковый номер элемента во множестве. Используется вопрос КОТОРЫЙ ПО СЧЁТУ? и задаётся направление счёту. Используются порядковые числительные, счёт начинается со слова ПЕРВЫЙ.
Когда мы говорим о количестве, не имеет значения направление счёта, предмет, с которого начали счёт. Итоговое число не меняется. При порядковом счёте – итоговое число может меняться.
СЧЁТНАЯ ДЕЯТЕЛЬНОСТЬ рассматривается как деятельность с конкретными элементами множества, при которых устанавливается взаимосвязь между предметами и числительными. Изучение числительных и множеств предметов ведёт к усвоению счётной деятельности.
ВЫЧИСЛИТЕЛЬНАЯ ДЕЯТЕЛЬНОСТЬ – это деятельность с абстрактными числами, осуществляемая посредством сложения и вычитания. Простое называние числительных не будет называться счётной деятельностью. Система вычислительных действий формируется на основе количественных знаний.
ВЕЛИЧИНА – это качество и свойство предмета, с помощью которого мы сравниваем предметы друг с другом и устанавливаем количественную характеристику сравниваемых предметов.

Понятие величина в математике рассматривается как основное.
Прямого ответа на вопрос “что такое величина?” нет, так как общее понятие величины является непосредственным обобщением более конкретных понятий: длины, площади, объёма, массы, скорости и т.д.
Величина предмета — это его относительная характеристика, подчеркивающая протяженность отдельных частей и определяющая его место среди однородных. Величина является свойством предмета, воспринимаемым различными анализаторами: зрительным, тактильным и двигательным. При этом чаше всего величина предмета воспринимается одновременно несколькими анализаторами: зрительно-двигательным, тактильно-двигательным и т.д.
Величина предмета, т.е. размер предмета, определяется только на основе сравнения. Нельзя сказать, большой это или маленький предмет, его только можно сравнить с другим.

Восприятие величины зависит от расстояния, с которого предмет воспринимается, а также от величины предмета, с которым он сравнивается. Чем дальше предмет от того, кто его воспринимает, тем он кажется меньшим, и наоборот, чем ближе – тем кажется большим.

Характеристика величины предмета зависит также от расположения его в пространстве. Один и тот же предмет может характеризоваться то как высокий (низкий), то как длинный (короткий). Это зависит от того, в горизонтальном или вертикальном положении он находится. Так, например на рисунке предметы расположены в вертикальном положении и характеризуются как высокий и низкий, а на другом рисунке (в горизонтальном положении) эти же самые предметы характеризуются как длинный и короткий.

Величина предмета всегда относительна, она зависит от того, с каким предметом он сравнивается. Сравнивая предмет с меньшим, мы характеризуем его как больший, а сравнивая этот же самый предмет с большим, называем его меньшим.

Итак, величина конкретного предмета характеризуется такими особенностями: сравнимость, изменчивость и относительность.

1) сравнимость, осуществляемая:

– наложением,

– приложением,

– измерением с помощью условной мерки,

– сравнением на глаз.

2) относительность – зависит от предмета, с которым мы сравниваем, от расстояния, на которое мы сравниваем, от расположения в пространстве.

3) изменчивость. Величина тесно связана с размером. А размер является свойством изменчивости величины. Каждый предмет имеет своё родовое предназначение. Он может изменять свои размеры, не меняя своей сущности.
ГЕОМЕТРИЧЕСКАЯ ФИГУРА – абстрактное понятие, с помощью которого мы все окружающие нас предметы олицетворяем в форме.

Геометрическая фигура – это наличие точек на плоскости, ограниченное пространством.
Фигуры бывают плоские (круг, квадрат, треугольник, многоугольник…) и пространственные (шар, куб, параллелепипед, конус…), которые ещё называют геометрическими телами.
ГЕОМЕТРИЧЕСКОЕ ТЕЛО – это замкнутая часть пространства, ограниченная плоскими и кривыми поверхностями.
Если поверхность, ограничивающая тело, состоит их плоскостей, то тело называют многогранником. Эти плоскости пересекаются по прямым, которые называются рёбрами, и образуют грани тела. Каждая из граней есть многоугольник, стороны которого являются рёбрами многогранника; вершины этого многоугольника называются вершинами многогранника.
Некоторые многогранники с определённым числом граней имеют особые названия: четырёхгранник – тетраэдр, шестигранник – эксаэдр, восьмигранник – октаэдр, двенадцатигранник – додекаэдр, двадцатигранник – икосаэдр.
Что же такое геометрическая ФОРМА?

ФОРМА – это очертание, наружный вид предмета.

Форма (лат. forma – форма, внешний вид) – взаимное расположение границ (контуров) предмета, объекта, а так же взаимное расположение точек линии.
ВРЕМЯ – это философское понятие, которое характеризуется сменой событий и явлений и длительностью их бытия.
Время имеет свойства:

– текучесть (время не остановить)

– необратимость и неповторимость

– длительность.
ПРОСТРАНСТВО – это такое качество, с помощью которого устанавливаются отношения типа окрестностей и расстояния.

Ориентировка в пространстве предполагает ориентировку на себе, от себя, от других объектов, ориентировку на плоскости и ориентировку на местности.
2. Предмет и задачи курса “Методика математического развития и обучения математики”. Связь методики математического развития с другими науками.
Методика формирования элементарных математических представлений в системе педагогических наук призвана оказать помощь в подготовке детей дошкольного возраста к восприятию и усвоению математики — одного из важнейших учебных предметов в школе, способствовать воспитанию всесторонне развитой личности.
Выделившись из дошкольной педагогики, методика формирования элементарных математических представлений стала самостоятельной научной и учебной областью.
Предметом ее исследования является изучение основных закономерностей процесса формирования элементарных математических представлений у дошкольников в условиях общественного воспитания.
Круг задач, решаемых методикой, достаточно обширен:

– научное обоснование программных требований к уровню развития количественных, пространственных, временных и других математических представлений детей в каждой возрастной группе;

– определение содержания фактического материала для подготовки ребенка в детском саду к усвоению математики в школе;

– совершенствование материала по формированию математических представлений в программе детского сада;

– разработка и внедрение в практику эффективных дидактических средств, методов и разнообразных форм организации процесса развития элементарных математических представлений;

– реализация преемственности в формировании основных математических представлений в детском саду и соответствующих понятий в школе;

– разработка содержания подготовки высококвалифицированных кадров, способных осуществлять педагогическую и методическую работу по формированию и развитию математических представлений у детей во всех звеньях системы дошкольного воспитания;

– разработка на научной основе методических рекомендаций родителям по развитию математических представлений у детей в условиях семьи.
Общая задача методики — исследование и разработка практических основ процесса формирования элементарных математических представлений у детей дошкольного возраста. Она решается с позиций марксистско-ленинской теории, которая, выработает единый взгляд на мир, открыв законы развития природы, общество, личности, служит методологической, мировоззренческой основой собой науки.
Формирование элементарных математических представлений — это целенаправленный и организованный процесс передачи и усвоения знаний, приемов и способов умственной деятельности, предусмотренных программными требованиями Основная его цель — не только подготовка к успешному овладению математикой в школе, но и всестороннее развитие детей.
Методика формирования элементарных математических представлений у детей в детском саду связана со многими науками, и прежде всего с теми, предметом изучения которых являются разные стороны личности и деятельности ребенка-дошкольника, процесс но воспитания и обучения.

Наиболее тесная связь существует у нее с дошкольной педагогикой. Методика формирования элементарных математических представлений опирается на разрабатываемые дошкольной педагогикой и дидактикой задачи обучения и умственного воспитания подрастающего поколения: принципы, условия, пути, содержание, средства, методы, формы организации и т. д. Связь эта по своему характеру взаимная: исследование и разработка проблем формирования элементарных математических представлений у детей в свою очередь совершенствовать педагогическую теорию, обогащая ее новым фактическим материалом.
Многосторонние контакты существуют между частными методиками, изучающими конкретные закономерности процесса воспитания и обучения маленьких детей: методикой формирования элементарных математических представлений, развития речи, теорией и методикой физического воспитания и др.
Подготовка детей к усвоению математики в школе не может осуществляться успешно без связи с методикой начального обучения математике и теми аспектами самой математики, которые являются теоретической основой обучения дошкольников и младших школьников.

Опора на эти науки позволяет, во-первых, определить объем и содержание знаний, которые должны быть освоены детьми в детском саду, и служить фундаментом математического образования; во-вторых, использовать методы и средства обучения, в полной мере отвечающие возрастным особенностям дошкольников, требованиям принципа преемственности.

Обучение должно строиться с учетом закономерностей развития познавательной деятельности, личности ребенка, что является предметом изучения психологических наук. Восприятие, представление, мышление, речь не только функционируют, но и интенсивно развиваются в процессе обучения.

Психологические особенности и закономерности восприятия ребенком множества предметов, числа, пространства, времени служат основой при разработке методики формирования элементарных математических представлений. Психология определяет возрастные возможности детей в усвоении знаний и навыков, которые не являются чем-то застывшим и меняются в зависимости от типа обучения.
Рациональное построение процесса обучения связано с созданием оптимальных условий на основе анатомо-физиологических особенностей маленьких детей. Закономерности протекания физиологических процессов у дошкольников служат основой для определения длительности занятий по формированию элементарных математических представлений для каждой возрастной группы детского сада, обусловливают саму их структуру, сочетание и чередование различных методов и средств обучения, разных по характеру видов деятельности (включение физкультминуток, дозирование учебно-познавательных задач и т. д.).
Связь с различными науками создает теоретическую базу методики формирования математических представлений у детей в детском саду.

3. Этапы развития методики математического развития: эмпирический, классический, современный.
Вопросы математического развития детей дошкольного возраста своими корнями уходят в классическую и народную педагогику. Различные считалки, пословицы, поговорки, загадки, потешки были хорошим материалом в обучении детей счету, позволяли сформировать у ребенка понятия о числах, форме, величине, пространстве.

В ходе их освоения дети не только овладевали пересчетом предметов, но и умением воспринимать и осознавать изменения, происходящие в окружающей их действительности: природные, цветовые, пространственные и временные; количественные, изменения по форме, размеру, расположению, пропорциям. Это обеспечивало естественное развитие у детей некоторых представлений, смекалки и сообразительности.
Первая печатная учебная книжка И.Федорова «Букварь» (1574 г.) включала мысли о необходимости обучения детей счету в процессе различных упражнений.
В XIII—XIX вв. вопросы содержания и методов обучения математике детей дошкольного возраста и формирования у них представлений о размере, измерении, о времени и пространстве можно найти в педагогических трудах Я.А. Коменского, М.Г. Песталоцци, К.Д. Ушинского, Л.Н. Толстого и других.
Взгляды педагогов XIII—XIX вв. на содержание и методы развития у детей математических представлений – это первый этап развития методики — эмпирический.
Педагоги той эпохи под влиянием требований развивающейся практики пришли к выводу о необходимости подготовки детей к усвоению математики в школе. Ими высказывались определенные предложения о содержании и методах обучения детей, в основном в условиях семьи. Надо сказать, что специальных пособий по подготовке детей к школе они не разрабатывали, а основные свои идеи включали в книги по воспитанию и обучению.

Так, Чешский мыслитель-гуманист и педагог Я.А. Коменский (1592—1670) в книге «Материнская школа» (1632) рекомендует еще до школы обучать ребенка счету в пределах двадцати, умению различать числа больше-меньшие, четные-нечетные, сравнивать предметы по величине, узнавать и называть некоторые геометрические фигуры, пользоваться в практической деятельности единицами измерения: дюйм, пядь, шаг, фунт и др.

И. Г. Песталоцци (1746—1827), швейцарский педагог-демократ, указывал на недостатки существующих в то время методов обучения, в основе которых лежит зубрежка, и рекомендовал учить детей счету конкретных предметов, пониманию действий над числами, умению определять время. Предложенные им методы обучения предпо переход от простых элементов к более сложным, широкое использование наглядности, облегчающей усвоение детьми чисел. Идеи И. Г. Песталоцци послужили в дальнейшем (середина XIX в.) основой реформы в области обучения математике в школе.
Передовые идеи в обучении детей арифметике до школы высказывал русский педагог-демократ, основоположник научной педагогики в России К. Д. Ушинский (1824—1871). Он считал важным научить ребенка считать отдельные предметы и их группы, выполнять действия сложения и вычитания, формировать понятие о десятке как единице счета. Однако все это было лишь пожеланиями, не имеющими никакого научного обоснования.
Писатель и педагог Л. Н. Толстой издал в 1872 году «Азбуку», одна из частей которой называлась «Счет». Критикуя существующие методы обучения, Л.Н. Толстой предлагал учить детей счету «вперед» и «назад» в пределах сотни и нумерации, основываясь при этом на детском практическом опыте, приобретенном в игре.

Методы развития у детей представлений о числе и форме нашли свое отражение и дальнейшее развитие в системах сенсорного воспитания немецкого педагога Ф. Фребеля (1782—1852), итальянского педагога Марии Монтессори (1870—1952) и др.
В классических системах сенсорного обучения Ф. Фребеля (1782-1852) и М. Монтессори (1870—1952) представлена методика ознакомления детей с геометрическими фигурами, величинами, измерением и счетом, составлением рядов предметов по размеру, весу и т. д.
Ф. Фребель видел задачи обучения счету в усвоении детьми дошкольного возраста ряда чисел. Им созданы знаменитые «Дары» — специальное пособие для развития конструктивных навыков в единстве с познанием чисел, форм, размеров, пространственных отношений. Ф. Фребель был убежден в том, что развитие в дошкольном возрасте «пространственного» воображения и мышления создает условия для перехода к усвоению геометрии в школе. Созданные Ф. Фребелем «дары» и в настоящее время используются в качестве дидактического материала для ознакомления детей с числом, формой, величиной и пространственными отношениями.
М. Монтессори, опираясь на идеи саморазвития и самообучения, признавала необходимым создание специальной среды для освоения чисел, форм, величин, а также письменной и устной нумерации.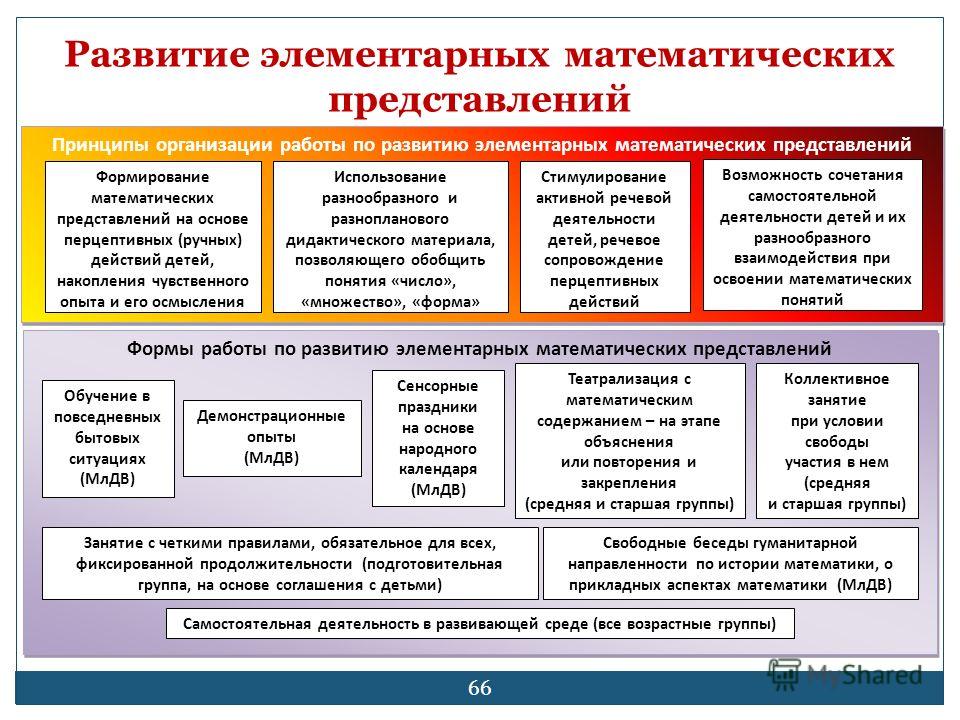 Она предлагала использовать для этого специальный материал: счетные ящики, связки цветных бус, нанизанных десятками, счеты, монеты и многое другое.

Наиболее результативно педагогическая деятельность М. Монтессори протекала в первой половине XX в. Использование в обучении и воспитании ребенка материалов по развитию у детей математических представлении строилось на определенном стиле взаимодействия взрослого с ребенком; необходимости наблюдения за поведением детей в условии специально созданной среды; организации совместной с ребенком свободной работы и др. Система М. Монтессори предусматривает развитие у ребенка сенсомоторной сферы и в дальнейшем — интеллекта. Особо выделяемый по своей значимости «золотой» математический материал сначала осваивается ребенком как набор бус в разной количественности, затем — в символах (цифрах), после этого — как средство освоения умений сравнивать числа. Таким образом, десятичная система счисления представляется ребенку зримо и осязаемо, что ведет к успешному овладению арифметикой.
Обширно представлен в системе М. Монтессори раздел «Логика и счет»: изучение фигур, размеров, способов измерения, проекции, моделирования множеств. Наиболее интересны следующие пособия: «Фигуры из гвоздиков», «Математическое солнце», «Сложи узор», «Объедини множества».
В целом обучение математике по системе М. Монтессори начиналось с сенсорного впечатления, затем осуществлялся переход к пониманию символа (т. е. от конкретного — к абстрактному), что делало математику привлекательной и доступной даже для 3—4-летних детей.
Итак, передовые педагоги прошлого, русские и зарубежные, признавали роль и необходимость первичных математических знаний в развитии и воспитании детей до школы, выделяли при этом счет в качестве средства умственного развития и настоятельно рекомендовали обучать детей ему как можно раньше, примерно с трех лет. Обучение понималось ими как «упражняемость» в выполнении практических, игровых действий с применением наглядного материала, использование накопленного детьми опыта в различении чисел, времени, пространства, мер в разнообразных детских деятельностях.

Особое значение вопросы методики математического развития приобретают в педагогической литературе начальной школы на рубеже XIX–XX ст. Авторами методических рекомендаций тогда были передовые учителя и методисты. Опыт практических работников не всегда был научно обоснованным, зато был проверен на практике. Со временем он усовершенствовался, сильнее и полнее в нем выявилась прогрессивная педагогическая мысль.
В конце XIX – в начале XX столетия у методистов возникла потребность в разработке научного фундамента методики арифметики. Значительный вклад в разработку методики сделали передовые русские учителя и методисты П.С. Гурьев, А.И. Гольденберг, Д.Ф. Егоров, В.А. Евтушевский, Д.Д. Галанин и другие.
Становление методики развития элементарных математических представлений в XIX — начале XX вв. происходило также под непосредственным воздействием идей реформирования школьных методов обучения арифметике. Особо выделились два направления: с одним из них связан так называемый метод изучения чисел, или монографический метод, а с другим — метод изучения действий, который назвали вычислительным.

Согласно методу изучения чисел, в разработке немецкого методиста А.В. Грубе преподавание арифметики осуществлялось «от числа к числу». Каждое из чисел, якобы доступное «непосредственному созерцанию», сравнивалось с каждым из предыдущих чисел путем установления между ними разностного и кратного отношения. Действия как бы сами вытекали из знания наизусть состава чисел. Монографический метод получил определение метода, описывающего число.

В процессе изучения каждого числа материалом для счета служили пальцы рук, штрихи на доске или в тетради, палочки. Например, при изучении числа 6 предлагалось разложить палочки по одной. Задавались вопросы: «Из какого количества палочек составилось число?», «Отсчитайте по одной палочке, чтобы получилось шесть и т.д. После каждой группы таких упражнений действия записывались в виде таблицы, результаты которой заучивались наизусть, с тем чтобы в дальнейшем производить арифметические действия по памяти, не прибегая к вычислениям.

В 70-х гг. XIX в. стали появляться противники монографического метода. Недовольство методом нарастало, и в 80—90-х гг. русские математики выступили с его резкой критикой, противопоставляя ему метод изучения действий, или, иначе, вычислительный метод.. Метод изучения действий (вычислительный) — предполагал обучение детей вычислениям и пониманию смысла арифметических действий. Обучение при этом строилось по десятичным концентрам. В пределах каждого концентра изучались не отдельные числа, а счет и действия с числами.

Оба метода (и монографический, и вычислительный) сыграли положительную роль в дальнейшем развитии методики, которая вобрала в себя приемы, упражнения, дидактические средства одного и другого методов.
В конце ХIХ — начале XX вв. были широко распространены идеи обучения математике без принуждения и дидактичности, забавно, но без излишней занимательности. Математики, психологи, педагоги разрабатывали математические игры и развлечения, составляли сборники задач на смекалку, преобразование фигур, решение головоломок (В. А. Латышев, Н. Н. Аменицкий, И. П. Сахаров, А. П. Доморяд, В. Арене и др.).
Авторы стремились придать четкую логику построения, необычность задачам-шуткам, арифметическим ребусам, задачам-головоломкам, задачам на деление целого на части и т. д. В ходе решения таких задач развиваются способность к правильному мышлению, логичность и последовательность мысли, острый ум и смекалка. Задачи на сообразительность, сметливость учат детей применять имеющиеся у них знания к различным случаям жизни, приучают к самоконтролю, а главное — способствуют выработке у детей умений самостоятельно искать путь решения.
Ряд книг был издан специально с целью развития способностей детей, в частности «Забавная арифметика» Н. Н. Аменицкого и И. П. Сахарова. В ней предлагалось живое и забавное решение различных практических задач и вопросов, что стимулировало проявления детской самодеятельности.
Широко применялись в обучении и развитии детей математические игры, в ходе которых был необходим подробный и четкий анализ игровых действий, возможность проявить смекалку в ходе поисков, самостоятельность. Значение математических игр рассматривалось авторами с позиций развития у детей интереса к изучению математики, становления умственных способностей, смекалки и сообразительности, находчивости, волевых черт характера, а также приучения детей к умственному труду.

1 2 3 4 5 6 7 8 9 … 20

2. Предмет и задачи курса “Методика математического развития и обучения математики”. Связь методики математического развития с другими науками.

Методика формирования элементарных математических представлений в системе педагогических наук призвана оказать помощь в подготовке детей дошкольного возраста к восприятию и усвоению математики — одного из важнейших учебных предметов в школе, способствовать воспитанию всесторонне развитой личности.

Выделившись из дошкольной педагогики, методика формирования элементарных математических представлений стала самостоятельной научной и учебной областью.

Предметом ее исследования является изучение основных закономерностей процесса формирования элементарных математических представлений у дошкольников в условиях общественного воспитания.

Круг задач, решаемых методикой, достаточно обширен:

– совершенствование материала по формированию математических представлений в программе детского сада;

– разработка на научной основе методических рекомендаций родителям по развитию математических представлений у детей в условиях семьи.

Общая задача методики — исследование и разработка практических основ процесса формирования элементарных математических представлений у детей дошкольного возраста. Она решается с позиций марксистско-ленинской теории, которая, выработает единый взгляд на мир, открыв законы развития природы, общество, личности, служит методологической, мировоззренческой основой собой науки.

Формирование элементарных математических представлений — это целенаправленный и организованный процесс передачи и усвоения знаний, приемов и способов умственной деятельности, предусмотренных программными требованиями Основная его цель — не только подготовка к успешному овладению математикой в школе, но и всестороннее развитие детей.

Методика формирования элементарных математических представлений у детей в детском саду связана со многими науками, и прежде всего с теми, предметом изучения которых являются разные стороны личности и деятельности ребенка-дошкольника, процесс но воспитания и обучения.

Многосторонние контакты существуют между частными методиками, изучающими конкретные закономерности процесса воспитания и обучения маленьких детей: методикой формирования элементарных математических представлений, развития речи, теорией и методикой физического воспитания и др.

Подготовка детей к усвоению математики в школе не может осуществляться успешно без связи с методикой начального обучения математике и теми аспектами самой математики, которые являются теоретической основой обучения дошкольников и младших школьников.

Рациональное построение процесса обучения связано с созданием оптимальных условий на основе анатомо-физиологических особенностей маленьких детей. Закономерности протекания физиологических процессов у дошкольников служат основой для определения длительности занятий по формированию элементарных математических представлений для каждой возрастной группы детского сада, обусловливают саму их структуру, сочетание и чередование различных методов и средств обучения, разных по характеру видов деятельности (включение физкультминуток, дозирование учебно-познавательных задач и т. д.).

Связь с различными науками создает теоретическую базу методики формирования математических представлений у детей в детском саду.

Важность методологии для облегчения изучения математики

Американский математик Пол Локхарт утверждает, что Математика является « искусством объяснения ». Цитата, которая попадает прямо в голову: как

Наука она имеет огромное значение, потому что ее можно использовать для описания множества реальных явлений и для того, чтобы помочь нам понять мир вокруг нас.

Следовательно, в идеале люди должны познакомиться с миром чисел и в раннем возрасте научиться использовать их для решения задач .

Вооружившись пониманием основных понятий математики, дети учатся описывать и анализировать величины, открывать пространство и формы, устанавливать отношения между объектами и т. д. Другими словами, они приобретают навыки и компетенции , которые помогают им, с этого момента на, чтобы лучше знать и понимать реальность и реагировать на нее в соответствии со своими потребностями.

Вот почему первый контакт ребенка с математикой представляет собой решающий момент , который может отметить его последующие отношения с математикой.

Инновация в обучении для «дружественного» математического подхода к решению задач

Именно здесь методологический подход приобретает жизненно важное значение. Обучение математике по учебной программе должно находиться под сильным влиянием последних технологических инноваций и новые педагогические стратегии , чтобы юные ученики могли извлечь выгоду из программы, адаптированной к их потребностям, и сразу же получить ключи для интерпретации своей среды и выполнения решения задач с числовой точки зрения.

И, в соответствии с этим, новые методы, выбранные и разработанные для преподавания этого предмета , уделяют меньше внимания вычислениям , в то же время отдавая приоритет индивидуальному контенту и использованию эффективных механизмов для закрепления наиболее важных концептуальных аспектов.

Таким образом, наиболее новаторские подходы предлагают методы «простой математики» , где манипулирование объектами и выполнение простых упражнений являются путями, с помощью которых дети могут достичь четырех четких целей:

Решение проблем
Способность рассуждать, делать выводы и спорить
Способность соединять идеи и/или концепции
Способность передавать и представлять математическую информацию по любому каналу

Обучение математике с помощью видеоигр возможно

Одной из первых форм манипулятивного обучения, появившихся в Испании, является «Метод ABN (алгоритмы, основанные на числах)» . Он был разработан

Хайме Мартинесом Монтеро , чтобы облегчить изучение традиционной математики благодаря использованию операций, полностью понятных ученику. Как? Проще говоря, путем преобразования количества в реальность, которой можно манипулировать: чечевица, шарики, зубочистки или каучуки. Таким образом, через визуализация и манипулирование , учащиеся намного легче усваивают математическую концепцию каждой фигуры , из-за пределов мира чисел, в дополнение к обучению установлению ассоциаций.

Однако в ProFuturo мы пошли немного дальше, разработав еще более своеобразную и инновационную методологию изучения математики. Благодаря сотрудничеству Fundación Telefónica Perú и Pontificia Universidad Católica of Perú , мы продвигали проект «Матемагический оракул» в качестве дидактического и игрового подхода обучения к этой отрасли знаний.

Результатом этой работы стало создание компьютерными программистами и преподавателями из вышеупомянутого университета новаторского приложения в Латинской Америке . Это приложение специально предназначено для учащихся в возрасте от 10 до 14 , чтобы с помощью подхода, основанного на упражнениях и играх, они могли изучать математику в веселой и увлекательной обстановке. В основном потому, что видеоигра мотивирует учеников , предлагая им постоянные испытания и постоянные ситуации проб и ошибок в интересном повествовательном контексте, сочетающем историю и магию.

На самом деле не случайно персонажи, которых ученики могут встретить в своих приключениях в приложении, вдохновлены великими всемирно известными математиками, такими как Гипатия Александрийская, Лю Хуэй, Леонардо Фибоначчи или Алан Тьюринг . И вот, ведомые таким образом, дети и юноши приближаются к развивать свои математические навыки со страстью и амбициями и получать удовольствие от решения задач, которые в другом контексте могут показаться им неудобными и скучными.

« Решение задач в мире чисел», доступный ресурс, облегчающий математику

И это еще не все, потому что через наш каталог ресурсов мы также предоставляем учителям учебный модуль «Решение задач в мире чисел». Потому что это должно стать отправной точкой для обучения Математика , он предлагает ряд настраиваемых задач для учеников, которые дают им возможность решать задачи, связанные с рассуждениями, дедукцией или анализом .

Для правильного использования детям (в возрасте от 6 до 8 лет) не нужно быть уже знакомым с этой дисциплиной . Потому что на самом деле этот модуль представляет собой некоторую «простую математику», предлагая учителям необходимые инструменты, чтобы помочь ученикам разобраться с наиболее важными понятиями. Так что, как только они закончат, они понимают культурную и социальную полезность чисел, знают, как использовать их в простых задачах (упорядочение, сравнение или идентификация) и учатся интерпретировать, организовывать и представлять их в различных контекстах.

Методика математического развития (экзамен) – Шпаргалка по Методике математического развития

2. Предмет и задачи курса “Методика математического развития и обучения математики”. Связь методики математического развития с другими науками.

Важность методологии для облегчения изучения математики

Добавить комментарий Отменить ответ