Методика и теория математического развития: Теория и методика математического развития детей дошкольного возраста – Всё о детях – беременность, воспитание, уроки для детей

Содержание

Читать онлайн «Теория и методика развития математических представлений у дошкольников», Л. И. Павлова – Литрес

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего образования

«Московский педагогический государственный университет»

Рецензенты:

Т. Н. Доронова, кандидат педагогических наук, старший научный сотрудник, заведующая отделом дошкольного образования ФГАУ «ФИРО»

Т. И. Ерофеева, кандидат педагогических наук, профессор кафедры дошкольной педагогики МПГУ

Пояснительная записка

Учебная дисциплина «Теория и методика развития математических представлений у детей дошкольного возраста» занимает одно из важных мест в профессиональной подготовке педагогов для системы дошкольного образования.

Пособие составлено в соответствии с новыми Федеральными государственными образовательными стандартами высшего образования РФ. Содержание материалов пособия опирается на рабочую программу учебной дисциплины, современные нормативные документы высшего и дошкольного образования, на исследования в области методических и психолого-педагогических наук.

В ходе изучения учебной дисциплины предусматривается усвоение студентами теоретических и дидактических основ развития у детей математических представлений. Студенты анализируют вопросы становления методики обучения детей математике, современные проблемы и концепции математического образования дошкольников. Знакомятся с содержанием, формами и методами формирования математических знаний, дидактическими средствами обучения. В процессе изучения дисциплины предполагается самостоятельная деятельность студентов, в ходе которой они изучают и анализируют научно-методическую литературу, пишут рефераты, конспекты занятий, упражняются в разработке дидактических игр и упражнений, выполняют творческие задания, разрабатывают диагностические методики, готовят консультации для воспитателей и родителей. Для самостоятельной подготовки к контрольным мероприятиям предложен перечень примерных вопросов к зачету и экзамену, проверочные тестовые задания. Представлена тематика рефератов, курсовых, выпускных квалификационных работ.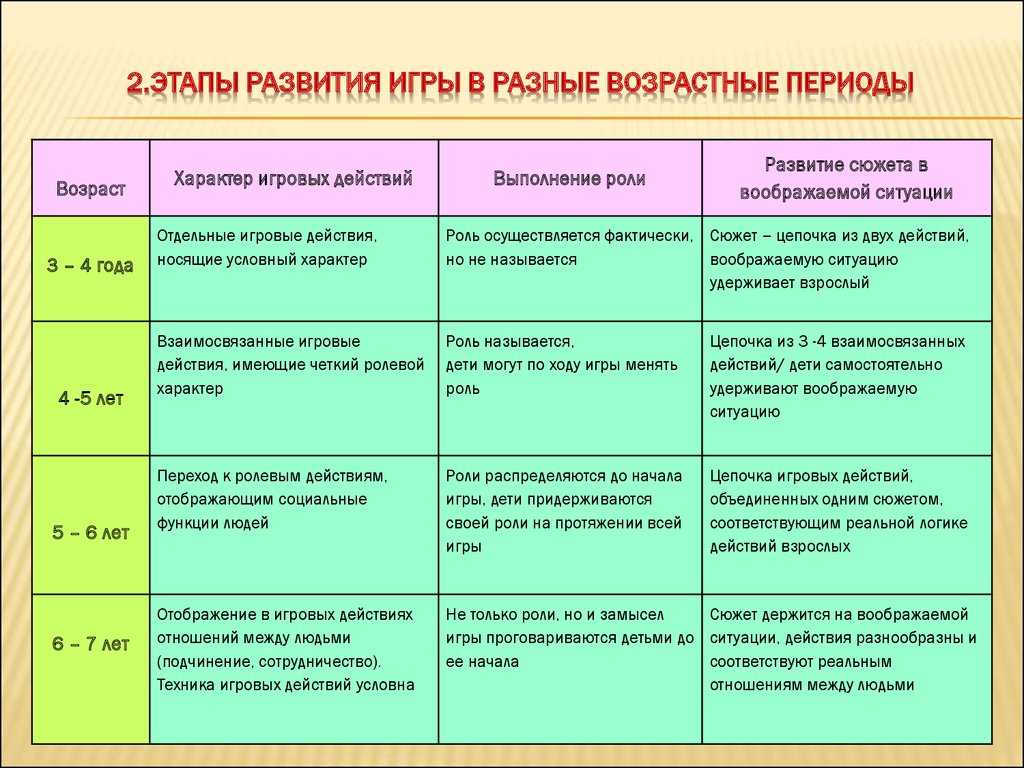 Даны рекомендации к их написанию с примерными планами и списками литературы. Выполнение практических заданий должно показать уровень понимания и осмысления изученного материала.

Часть I

Содержание практических занятий

Раздел 1

Теоретические и дидактические основы дисциплины «Теория и методика развития математических представлений у детей дошкольного возраста»

Тема 1

Основные математические понятия дисциплины

Вопросы для обсуждения

1. Характеристика понятия «множество».

2. Понятие о числе, его виды и функции.

3. Натуральное число, натуральный ряд чисел и его свойства.

4. Сущность счета и вычислительной деятельности.

Методические указания к изучению темы

Понятия «множество», «число», «счет» являются центральными при обучении дошкольников математике. Эти знания составят теоретическую основу для осмысления содержания и методики развития исходного математического понятия у детей.

При изучении темы рассматриваются основные положения Г. Кантора о множестве. Изучаются основные понятия теории множеств: множество, элемент множества, подмножество, пустое множество, характеристическое свойство или условие задания множества. Рассматриваются основные виды и операции над множествами и др. Затем необходимо остановиться на основном способе сравнения множеств – установлении взаимно однозначного соответствия, понятии эквивалентности. С позиции теоретико-множественного подхода необходимо дать определение натурального числа. Анализируется роль теории множеств для понимания того, как дети осваивают представление о числе и счете. Анализируется аксиоматическое определение системы натуральных чисел. Для этого необходимо изучить систему аксиом для определения натурального числа Дж. Пеано.

При подготовке к третьему вопросу следует знать, что натуральное число имеет несколько функций, и с некоторыми из них дети знакомятся уже в дошкольном возрасте.

Рассматривается вопрос о сущности счета и вычислительной деятельности, уточняются их отличительные особенности.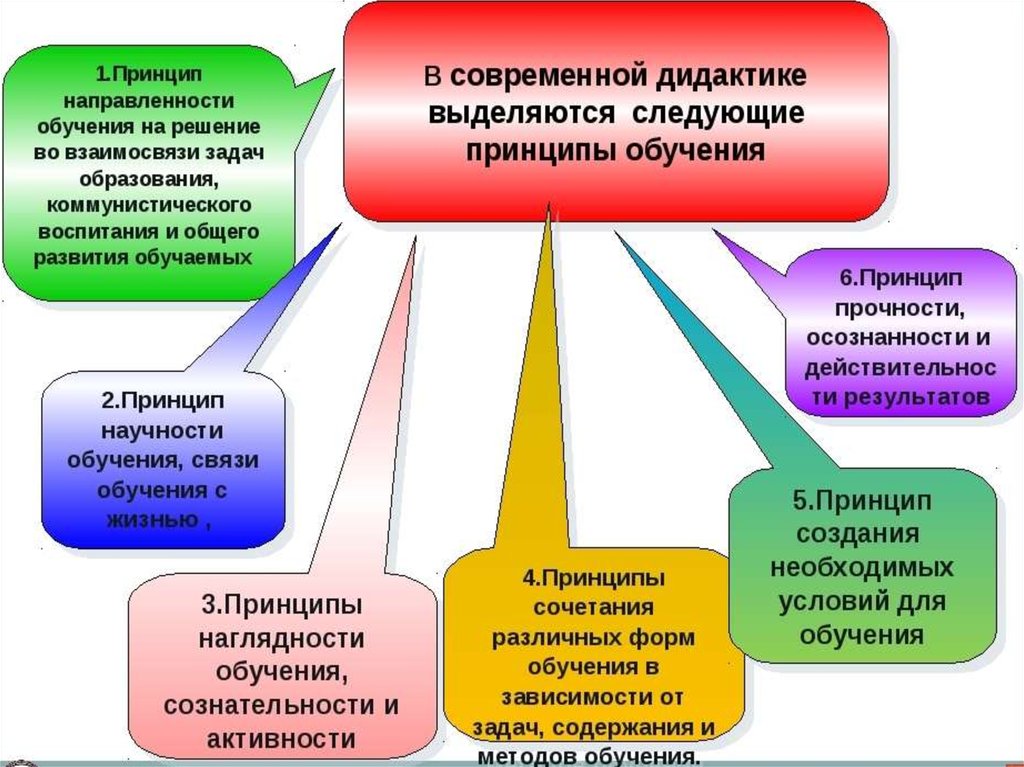

Задания для самостоятельной работы

1. Приведите по 1 примеру к каждой операции над множествами, зарисовав их кругами Эйлера – Венна.

2. Приведите примеры, как дети используют в жизненных ситуациях для определения равенства предметов свойства симметричности и транзитивности эквивалентных множеств.

3. Приведите по 2 примера множеств, которые тождественны и которые эквивалентны, но не тождественны.

4. Приведите по 2 примера дискретных, бесконечных, непрерывных, конечных множеств.

Основная литература

1. Верещагин Н. К., Шенъ А. Лекции по математической логике и теории алгоритмов. Ч. 1. Начало теории множеств. – 4-е изд., доп. – М.: МЦНМО, 2012. – 112 с.

2. Энциклопедия «Кругосвет». – www.krugosvet.ru (Теория множеств).

Дополнительная литература

1. Виленкин Н. Я. Рассказы о множествах. – М., 2005.

2. Кожухов И. Б., Прокофьев А. А. Справочник по математике. – М. , 1999. – С. 5–8, 16–24, 30–54.

3. Попов Ю. П., Пухначев Ю. В. Математика без формул. Кн. 1. -М.: КомКнига, 2010. -232 с.

4. Попов Ю. П., Пухначев Ю. В. Математика без формул. Кн. 2. -М.: Либроком, 2011. -242 с.

5. Рыбников К. К. Введение в дискретную математику и теорию решения экстремальных задач на конечных множествах: Учебное пособие. – М.: Гелиос АРВ, 2010. – 320 с.

6. Стойлова Л. П., Фрейлах Н. И. Теоретические основы формирования элементарных математических представлений у дошкольников. – М., 1997.

7. Шпорер 3. Ох, эта математика! – М.: Педагогика, 1985.

8. Энциклопедия для детей. Математика. Т. 11 / Под ред. М. Д. Аксенова. – М.: Аванта+, 2000.

Тема 2

Развитие математических понятий в истории человечества

Вопросы для обсуждения

1. Этапы развития представлений о числе и счете в истории человечества.

2. История возникновения систем счисления и видов письменной нумерации. Характеристика десятичной системы счисления.

3. Этапы развития системы измерения протяженности предметов, массы и объема веществ.

4. Генезис геометрических представлений в истории человечества.

5. История мер времени.

Методические указания к изучению темы

Практическое занятие посвящено изучению истории возникновения и развития основных понятий математики.

Числа возникли из потребности счета и измерения и претерпели длительный путь исторического развития. Зная пути развития в человеческом обществе деятельности счета и измерения, можно яснее представить значение тех знаний, которые предстоит освоить детям. Анализируя данный исторический материал, следует выделить этапы развития понятия числа и счета в истории человечества.

Разбирая вопрос о письменной нумерации, следует дать характеристику различным видам записи чисел (иероглифы, клинопись, алфавитные системы записи чисел, римские и арабские цифры), показать сущность позиционной (аддитивной) и непозиционной (мультипликативной) систем счисления, познакомиться с правилами перевода из одной системы счисления в другую. Необходимо определить преимущества и отличительные черты позиционной десятичной системы счисления, понятия разряда, класса, отношений между ними.

Изучая историю понятия числа, необходимо рассмотреть действия над числами. Кроме того, необходимо уяснить сущность счетной и вычислительной деятельности.

В процессе изучения этой темы необходимо рассмотреть роль вычислительных приборов (абак, счеты, арифмометр, ЭВМ, персональный компьютер) в развитии как самой математики, так и методики обучения математике.

Основные единицы измерения в процессе развития человеческой цивилизации прошли сложный эволюционный путь. При его рассмотрении необходимо ориентироваться на основные системы единиц измерения величин (русскую, английскую и метрическую) и самостоятельно выделить стадии в истории развития единиц измерения протяженностей, массы и объема веществ в истории человечества.

Необходимо рассмотреть основные геометрические понятия в истории человечества, историю происхождения названий геометрических фигур. Вклад известных математиков в развитие геометрической науки.

Задания для самостоятельной работы

1. Приведите примеры того, как считали наши предки, находясь на этапах попарного счета и счета числами-качествами совокупностей.

2. Наименование какой цифры дало название всем остальным цифрам в русском языке и почему?

3. Переведите число 149 в следующие виды письменной нумерации: римскую, вавилонскую, племени майя.

4. Составьте кроссворд на тему: развитие понятий о геометрических фигурах и форме предметов в истории человечества (не менее 10 слов).

5. Кто был выше Дюймовочка или Мальчик-с-пальчик? Обоснуйте ответ.

6. Какой год в нашей стране был самым коротким и почему?

7. Какого размера был Конек-Горбунок в метрической системе измерения?

Основная литература

1. Просветов Г. И. История математики. – М.: Альфа-Пресс, 2017.

2. Манкевич Р. История математики. – М.: Ломоносовъ, 2011. -256 с.

3. Николаева Е. А. История математики от древнейших времен до XVIII века: учебное пособие / Е. А. Николаева. – Кемерово: Кемеровский государственный университет, 2012. – 112 с.

Дополнительная литература

1. Бурау И. Я. Загадки мира цифр и чисел. – Донецк, 1996. – 448 с.

2. Виленкин Н. Я. За страницами учебника математики. – М., 2008.

3. Выготский Л. С., Лурия А. Р. Числовые операции примитивного человека // Этюды по истории поведения. – М., 1993. – С. 108–118.

4. Рыбников К. А. Возникновение и развитие математической науки. – М., 1987. – С. 5–13.

5. Свечников А. Путешествие в историю математики, или как люди учились считать. – М., 1995.

6. Энциклопедия для детей. Математика. Т. 11 / Под ред. М. Д. Аксенова. – М.: Аванта+, 2000.

Теория и методика математического развития дошкольников

Содержание

Почему это так важно?
Какие навыки должны быть сформированы у ребенка к концу дошкольного периода?
Необходимые условия проведения математических занятий с ребенком
Особенности формирования математических представлений в зависимости от возраста
Какие методы лучше всего использовать для развития математических представлений дошкольника?
Структура математического занятия для дошкольника

Дошкольный возраст – это время, когда познавательное, нравственное, физическое развитие ребенка происходит особенно интенсивно. В частности, именно до 5-6 лет ребенок приобретает более половины суммарных навыков мышления, которые пригодятся ему в будущем. Именно поэтому ему необходимо уделять особое внимание. В частности именно в этом возрасте у ребенка должны отложиться первые математические навыки. Рассмотрим теоретические основы математического развития детей младшего и старшего дошкольного возраста.

Занятие по математике в детсаду, старшая группа

Почему это так важно?

Математика является одним из наиболее значимых, предметов. Однако именно он зачастую вызывает у учащихся немалые трудности
Изучение этого предмета благотворно сказывается на познавательных способностях ребенка (мышлении, памяти, речи)
Математические навыки совершенствуют эмоционально-волевую сферу, формируют настойчивость и целеустремленность
Совершенствуется основы воображения ребенка

Роль математики в жизни

Какие навыки должны быть сформированы у ребенка к концу дошкольного периода?

К окончанию дошкольного периода ребенок должен обладать следующими математическими умениями и навыками:

Способность к сравнению величин по базовым признакам; сформированность представлений о понятиях «больше-меньше», «выше-ниже» и т. д.
Способность к группировке предметов по их базовым свойствам (основы – величина, цвет, назначение, материал, форма)
Способность к сопоставлению части-целого; умение собирать картинку не менее чем из 12-24 фрагментов

Сформированные навыки счета и умение производить математические операции с числами в пределах десяти
Сформированность у детей количественных и качественных представлений предмета

Суть математического развития

Необходимые условия проведения математических занятий с ребенком

На чем строится теория и методика математического развития для дошкольников? Для того чтобы занятия были по-настоящему интересны для ребенка, а информация усваивалась им быстрее и легче, их необходимо строить с учетом следующих рекомендаций:

Использование наглядного дидактического материала, подобранного с учетом возрастных и других индивидуальных особенностей ребенка
Наличие у занятия четкого сюжета, согласно которого будет происходить его развитие
Подбор задач в строгом соответствии с возрастными особенностями ребёнка, уровнем его интеллектуального развития
Использование разнообразных методов и форм для создания основы работы (к ним можно отнести решение логических задач, дидактические игры, работа с раздаточным материалом и т.
д.)
Многозадачность (направленность на развитие пространственных, временных, количественных представлений)
Использование игровой формы ведения занятий
Акцент на формировании игровой мотивации; элементы сюрпризов и внезапности
Помощь ребенку не только в освоении определенной системы знаний и навыков, но также развитие у него навыков самостоятельной познавательной активности, независимости суждений и т.д.
Формирование оптимальной развивающей среды для развития у ребенка базовых познавательных процессов
Научение детей восприятию количественных и качественных особенностей предмеов, формирование соответствующих представлений

Задачи развития математических способностей

Особенности формирования математических представлений в зависимости от возраста

Учитывая то, что дошкольный возраст условно подразделяется на три основных периода, цели, задачи, а также методы и формы математического воспитания детей также будут различаться.

Младший дошкольный период. В это время необходимые математические навыки и представления только начинают развиваться. Поэтому ребенку необходимо дать представление о базовых операциях. Лучшими играми на развитие навыков мышления – детская мозаика (от 5 фрагментов), сложение геометрических фигур (от 4 деталей). Особого внимания к себе требует методика развития количественных и качественных представлений у дошкольников.

Средний дошкольный период. Происходит активное развитие знаково-символической функции сознания. Ребенка уже можно приучать к счету и самым простым математическим операциям. Закладываются основы логического мышления. К числу наиболее предпочтительных игр относятся: «Нелепицы», «Сосчитай предметы, «Найди пару», «Математическое лото», «Домино фигур». Для развития аналитико-синтетических способностей ребенка ему можно предложить игры наподобие танграма, где ему нужно будет составить из отдельных частей геометрическую фигуру, силуэт животного и т.д.

Индивидуальное занятие на определение уровня математического развития

В старшем дошкольном возрасте для детей все более заметную и значимую роль начинает играть самостоятельность ребенка, его способность к самоорганизации. Все более значимую роль приобретает логическое мышление.

Ребёнок начинает пробовать составлять рассказы по картинкам, составлять логические ряды, соблюдая правильную последовательность элементов.

Математические тесты для малышей 3-4 лет

Какие методы лучше всего использовать для развития математических представлений дошкольника?

Наглядный метод играет наиболее важную роль в обучении детей математике, особенно – если речь идет о младшем дошкольном периоде.

Методы развития математических знаний

Различают следующие разновидности наглядного метода обучения:

Работа с раздаточным, либо демонстрационным материалом. Использование бессюжетного или сюжетного метода (за основу можно взять сюжет любой знакомой ребенку сказки, где фигурировали бы счет или числа)
Объемный или плоскостной. Занятия с использованием специальных счетных материалов (например, детских счет, палочек, кубиков и т.д.)
Самодельный, либо фабричный.

Раздаточный материал для математических занятий

Для того чтобы эффективнее использовать наглядный материал, необходимо строить развивающие занятия с учетом следующих закономерностей:

Изучение каждой новой темы должно начинаться с более объемного наглядного материала.
Это упростит его восприятие ребенком
По мере взросления ребенка необходимо сделать так, чтобы доля объемного и сюжетного наглядного материала понижалась, а доля плоского и бессюжетного возрастала
Желательно использовать несколько типов наглядного материала для решения одной программной задачи
Очень желательно заранее ознакомить ребенка с новым для него для него материалом

Отдельно стоит рассмотреть требования, предъявляемые к наглядным пособиям.

Дидактический материал для занятий

Как мы уже указали выше, он может быть как готовым заводским, так и сделанным руками родителей. Тем не менее важно, чтобы он соответствовал следующему:

Гигиеничность. Игрушки должны быть сделаны из экологически чистых, безопасных материалов и иметь все необходимые сертификаты
Эстетичность. Привлекательный материал скорее привлечет внимание ребенка
Реальность, позволяющая ребенку воспринимать изучаемый материал без искажений

Прочность и надежность
Разнообразие и достаточное количество для возможности использовать вариативные техники
Принцип логического построения, объединяющего основы материала
Однородность

Игровой уголок с дидактическим материалов

Существенным плюсом практического метода обучения является то, что он в наиболее полной степени объясняет ребенку то, зачем он изучает тот или иной материал. И как именно полученные знания смогут пригодиться ему в будущем?

Активное применение на практике разнообразного дидактического материала
Выполнение разнообразных как умственных, так и практических действий
Развитие навыка прогнозирования результата действий с дидактическим материалом различного вида
Не только привитие ребенку математических навыков, но и подробное разъяснение их роли в жизни ребенка (в игровой деятельности, в быту и т.д.)

Словесный метод обучения строится на непосредственном взаимодействии ребенка с родителем, либо воспитателем.

Именно поэтому основные требования, предъявляемые к этому методу, будут направлены на речь участников процесса

Речь родителя, либо воспитателя, должна быть:

Грамотной
Четкой
Эмоциональной и живой
Доступной
Доброжелательной
Умеренно громкой

Развитие речи на занятиях по математике

Темп речь, ее интонацию и другие особенности необходимо корректировать в зависимости от индивидуально-возрастных особенностей ребенка.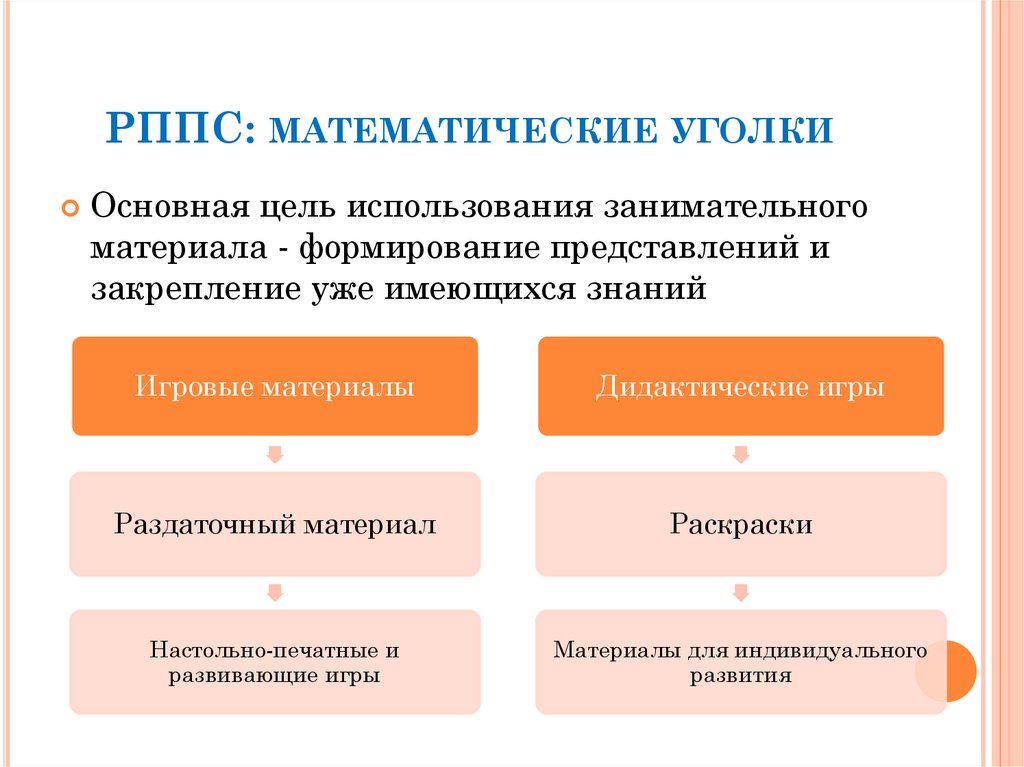 Например, ребенок младшего дошкольного возраста намного лучше воспринимает довольно медленную речь; несформированные процессы памяти требуют многократных повторений.

Развитие логики и пространственного мышления в игровой форме

Разговаривая с ребенком более старшего возраста, можно несколько ускорить темп речи, а также активнее использовать проблемные ситуации.

Определенные требования предъявляются также и к речи детей. Она должна быть:

Грамотная
Содержать необходимую математическую терминологию и основы математики по возрасту
Разборчивая и понятная
Ребенок должен говорить полными распространенными предложениями с правильным грамматическим строем
Иметь достаточную громкость

Структура математического занятия для дошкольника

Правильная структура занятия является еще одним важным условием, на котором строится методика математического развития детей дошкольников.

Используемые игры на занятиях по математике

Вводная часть.
Логическая разминка. Включает в себя наиболее простые задания для детей, которые должны «разогреть» ум ребенка, заинтересовав его и подготовив к занятию
Основная часть занятия, в ходе которой происходит изучение нового материала для формирования математических представлений, либо закрепление уже изученного. Упражнения можно подбирать при помощи специальной методической литературы (хорошим примером может стать книга, которую составила Щербакова Е.И. «Теория и методика математического развития для дошкольников»).
3Пальчиковая гимнастика. Переключает внимание ребенка, служит предупреждением переутомления. Для этих же целей можно использовать физминутку (если занятие было связано преимущественно с интеллектуальной деятельностью), артикуляционную гимнастику или упражнения для глаз (если у ребенка было активное занятие с использованием подвижных игр).
Повторение пройденного материала.

Рисование, шнуровка, либо игры, направленные на развитие мелкой моторики.

Изучение формы и размера на занятиях физкультуры

Развитые математические навыки у детей дошкольного возраста позволит ему не только успешно приступить к школьному обучению, но и сформировать у себя такие качества, как усидчивость, внимание, целеустремленность.

Роль теории в математическом образовании и исследованиях

Артиг, М. и Перрин-Глориан, М.Дж.: 1991, «Дидактические инженерные исследования и разработки: некоторые теоретические проблемы, связанные с этой двойственностью», Для изучения математики 11(1),13–17.
Google Scholar
Bachelard, D.: 1938 (переиздано в 1983 г.), La Formation de l’Esprit Scientifique
, Presse Universitaire de France, Paris.
Google Scholar
Бахтин, М. : (1986a), «Выдержки из «Заметок» (1970–1971)», в Г. С. Морсоне (ред.) Бахтин: Очерки и диалоги о его работе , The University of Chicago Press, Чикаго.
Google Scholar
Бахтин М.: (1986б). «Отрывки из «Проблемы речевых жанров»», в Г. С. Морсон (ред.) Бахтин: очерки и диалоги о его творчестве , Издательство Чикагского университета, Чикаго.
Google Scholar
Балачев, Н.: 1990, «На пути к проблеме исследований в области преподавания математики», Journal for Research in Mathematics Education 21 ( 4 ), 258–272.
Перекрёстная ссылка Google Scholar
Барон-Кук, С.: 1995, Слепота разума , MIT Press, Кембридж, Бостон
Google Scholar
Бауэрсфельд, Х.: 1990, «Теория деятельности и радикальный конструктивизм: что у них общего?» в Ф. Штайере (ред.) Экологическое понимание , Ежегодная конференция Американского общества кибернетики, Осло.
Google Scholar
Бауэрсфельд, Х.: 1991, «Структурирование структур», Л. Штеффе (ред.) Конструктивизм и образование , Лоуренс Эрлбаум, Хиллсдейл, Нью-Джерси.
Google Scholar
Бауэрсфельд, Х.: 1992, «Интеграция теорий для математического образования», Для изучения математики 12(2), 19–28.
Google Scholar
Bennett, J.: 1993, Элементарная систематика: инструмент для понимания целого , Bennett Books, Santa Fe.
Google Scholar
Бишоп, А.: 1992, «Международные перспективы исследований в области математического образования», в Д. Гроувсе, (ред.) Справочник по исследованиям в области преподавания и обучения математике , MacMillan, Оксфорд, 710–723.
Google Scholar
Боэро, П.: 1990, «О долгосрочном развитии некоторых общих навыков решения проблем: продольное сравнительное исследование», в книге Г. Букера, П. Кобба и Т.Н. Мендикути (ред.) Труды четырнадцатой конференции PME , Международная группа психологии математического образования, Мексика, том. 2, 169–176.
Google Scholar
Бруссо, Г.: 1981, «Проблемы дидактики Десимо», Recherches en Didactique des Mathématiques 2(1), 37–125.
Google Scholar
Бруссо, Г.: 1984, «Решающая роль дидактического контракта в анализе и построении ситуаций в преподавании и изучении математики», в HG Steiner (ред.) Теория математического образования , Статья 54, Институт математики Университета Билефельда.
Google Scholar
Браун С. , Коллинз А. и Дугуид П.: 1989, «Ситуативное познание и культура обучения», Исследователь в области образования 18(1), 32–41.
Перекрёстная ссылка Google Scholar
Брунер, Дж.: 1986, Актуальные умы, возможные миры , Издательство Гарвардского университета, Кембридж.
Google Scholar
Карпентер, Т. и Феннема, Э.: 1992, «Когнитивно управляемое обучение: опираясь на знания учащихся и учителей», в В. Секаде (ред.) Реформа учебной программы: пример математического образования в США .
Google Scholar
Каррахер Т., Каррахер Д. и Шлиманн А.: 1985, «Математика на улицах и в школах», British Journal of Developmental Psychology 3, 21–29.
Перекрёстная ссылка Google Scholar
Карр, В.: 1986, «Теории теории и практики», Journal of Philosophy of Education 20(2), 177–186.
Перекрёстная ссылка Google Scholar
Кобб, П.: 1990, «Конструктивистский взгляд на обработку информации: теории математической деятельности», Международный журнал исследований в области образования 14, 67–92.
Перекрёстная ссылка Google Scholar
Кобб, П.: 1995, «Культурные инструменты и математическое обучение: тематическое исследование», Journal for Research in Mathematics Education 26(4), 362–385.
Перекрёстная ссылка Google Scholar
Коэн, Л.: 1976, Образовательные исследования в классах и школах: Руководство по материалам и методам , Harper & Row, Лондон.
Google Scholar
Конфри, Дж.: 1995, «Теория интеллектуального развития» (в трех частях), Для изучения математики 15(1), стр. 2–8,
Google Scholar
Конфри, Дж. : 1995, «Теория интеллектуального развития» (в трех частях), Для изучения математики 15(2), стр. 38–47,
Google Scholar
Конфри, Дж.: 1995, «Теория интеллектуального развития» (в трех частях), Для изучения математики 15 (3), стр. 36–47.
Google Scholar
Давыдов В.: 1990, Советское математическое образование: виды обобщения в обучении , т. 1, с. 2, Национальный совет учителей математики, Рестон, Вирджиния.
Google Scholar
Давуд, Дж. (пер.): 1956, Коран , Penguin Classics, Harmondsworth.
Google Scholar
Дональдсон, М.: 1978, Children’s Minds , Нортон, Нью-Йорк.
Google Scholar
Дуади Р. и Мерсье А.: 1992 (ред.), Исследования в области дидактики математики , La Pensée Sauvage, Гренобль.
Google Scholar
Эльбез, Ф.: 1983, Мышление учителей: исследование практических знаний , Николс, Нью-Йорк.
Google Scholar
Франкенштейн, М.: 1989, Повторное изучение математики: другой третий R — радикальная математика , Free Association Press, Лондон.
Google Scholar
Фройденталь, Х.: 1971, «Геометрия между дьяволом и глубоким синим морем», Образовательные исследования по математике 5,413–435.
Перекрёстная ссылка Google Scholar
Freudenthal, H.: 1991, Revisiting Mathematics Education , Kluwer, Dordrecht.
Google Scholar
Gattegno, C: 1970, Чем мы обязаны детям: подчинение преподавания обучению , Рутледж и Кеган Пол, Лондон.
Google Scholar
Goodman, N.: 1978, Ways of World Making , Harvester press, Hassocks.
Google Scholar
Гравемейер, К.: 1994, «Развитие образования и исследования развития в области математического образования», Journal for Research in Mathematics Education 25(5), 443–471.
Перекрёстная ссылка Google Scholar
Грей, Э. и Талл, Д.: 1994, «Двойственность, двусмысленность и гибкость: «Процептуальный взгляд на простую арифметику», Journal for Research in Mathematics Education 25(2), 116–140.
Перекрёстная ссылка Google Scholar
Гамильтон, Э. и Кэрнс, Х. (ред.): (1961, переиздано в 1985 г.) Платон: Сборник диалогов , Серия Боллинген LXXI, Princeton University Press, Принстон.
Google Scholar
Hanson, N. : 1958, Patterns of Discovery , Cambridge University Press, Кембридж, Великобритания.
Google Scholar
Харт, К.: 1993, «Уверенность в успехе», в I. Hirabayashi, N. Nohda, K. Shigematsu and Fou-Lai Liu (ред.) Proceedings of the Seventeen International PME Conference , vol. 1, Цукуба, Ибараки, Япония, 1–17.
Google Scholar
Холквист, М. (изд.): 1981, Диалогическое воображение , University of Texas Press, Остин.
Google Scholar
Howie, G.: 1969, St. Augustine on Education , Henry Regnery Co., Чикаго.
Google Scholar
Хоусон, Г., Кейтель, К. и Килпатрик, Дж.: 1981, Разработка учебных программ по математике , Издательство Кембриджского университета, Кембридж, Великобритания.
Перекрёстная ссылка Google Scholar
Джейнс, Дж. : 1976, Происхождение сознания в распаде двухпалатного разума , Университет Торонто, Торонто.
Google Scholar
Килпатрик, Дж.: 1981, «Исследования математического обучения и мышления в Соединенных Штатах», Proceedings of PME I , vol. 2, 18–29.
Google Scholar
Kitcher, P.: 1984, The Nature of Mathematical Knowledge , Oxford University Press, Оксфорд.
Google Scholar
Кернер, К.: 1992, «Гипотеза Сепира-Уорфа: от Лейбница до Люси», Journal of Linguistic Anthropology 2(2).
Google Scholar
Kuhn, T.: 1970, Структура научных революций , Чикагский университет, Чикаго.
Google Scholar
Laborde, C: 1989a, «Смелость и разум: французские исследования в области математического образования», Для изучения математики 9 (3), 31–36.
Google Scholar
Laborde, C: 1989b, «Hardiesse et Raison des Recherches Françaises en Didactique des Mathématiques», в G. Vergnaud, J. Rogalski and M. Artigue (eds.) Actes de la 13e Conférence Internationale PME , vol. 1,46–61.
Google Scholar
Лакан, Дж.: 1977, «Зеркальная сцена», в А. Шеридане (перевод), Écrits: A Selection , Тависток, Лондон.
Google Scholar
Лакатос, И.: 1976, Доказательства и опровержения , Издательство Кембриджского университета, Кембридж.
Перекрёстная ссылка Google Scholar
Lave, J.: 1988, Познание на практике: разум, математика и культура в повседневной жизни , издательство Кембриджского университета, Бостон.
Перекрёстная ссылка Google Scholar
Линкольн Ю. и Губа Э.: 1985, Naturalistic Inquiry , Sage, Beverly Hills.
Google Scholar
Lyotard, J.-F.: 1984, Состояние постмодерна: отчет о знаниях, теории и истории литературы V10, издательство Манчестерского университета, Манчестер.
Google Scholar
Lyotard, J.-F.: 1991, Phenomenology , (пер. Б. Бикли), State University of New York Press, Олбани.
Google Scholar
Лиотар, Ж.-Ф.: 1992. «Из состояния постмодерна: отчет о знаниях», в Д. Ингрэме и Дж. Ингрэме (ред.) Критическая теория: основные материалы , Paragon House, Нью-Йорк.
Google Scholar
Лиотар, Ж.-Ф.: 1994, «Бюрократия: сопротивление, свидетельствование, письмо», L’Esprit Creative 34(1), 101–108.
Google Scholar
Мартон Ф. : 1981, «Феноменография: описание представлений об окружающем нас мире», Instructional Science 10, 177–200.
Перекрёстная ссылка Google Scholar
Мартон, Ф.: 1988, «Феноменография: исследовательский подход к изучению различных представлений о реальности», в Дж. Шерман и Н. Уэбб (ред.) Качественные исследования в образовании: фокус и методы , Falmer Press , Лондон, 141–161.
Google Scholar
Мейсон, Дж. и Дэвис, Дж.: 1989, «Заметки о радикальной конструктивистской эпистеметологии в применении к дидактическим ситуациям», Журнал структурного обучения 10, 157–176.
Google Scholar
Мейсон, Дж.: 1979, «Какой носитель, какое сообщение?» Визуальное образование , февраль 1979 г., стр. 29–33.
Google Scholar
Мейсон, Дж. : 1994, «Исследования изнутри в математическом образовании: определение отношения «я-ты», в Дж. П. да Понте и Дж. Ф. Матос (ред.) Труды восемнадцатой конференции по психологии математики Образование , том. 1, PME, Лиссабон, 176–190.
Google Scholar
Мейсон, Дж.: 1996, Личный запрос: переход от озабоченности к исследованиям , Открытый университет, Милтон Кейнс.
Google Scholar
Мейсон, Дж.: в печати, «Исследования изнутри в математическом образовании», в А. Серпинска и Дж. Килпатрик (ред.) Исследование ICMI: что такое исследования в области математического образования и каковы их результаты? Клювер, Дордрехт.
Google Scholar
Матурана, Х. и Варела, Ф.: 1988, Древо познания: биологические корни человеческого понимания , Шамбала, Бостон.
Google Scholar
Меллин-Олсен, С. : 1987, Политика математического образования , Рейдель, Дордрехт.
Google Scholar
Мюхойслер, П. и Харри, Р.: 1990, Местоимения и люди: лингвистическое построение личной идентичности , Бэзил Блэквелл, Оксфорд.
Google Scholar
Нагель, Э.: 1961, Структура науки , Рутледж и Кеган Пол, Лондон.
Google Scholar
Нуньес, Т.: 1992, «Этноматематика и повседневное познание», в Д. Гроувсе (ред.) Справочник по исследованиям в области преподавания и обучения математике , Макмиллан, Нью-Йорк, 557–574.
Google Scholar
Ортон, Р.: 1988, «Две теории« теории »в математическом образовании: использование Куна и Лакатоша для изучения четырех фундаментальных вопросов», Для изучения математики 8 (2), 36–43.
Google Scholar
Открытый университет: 1980, PME233 Математика в учебном плане , Открытый университет, Милтон Кейнс.
Google Scholar
Перри, В.: 1968, Формы интеллектуального и этического развития в студенческие годы: Схема , Холт, Райнхарт и Уинстон, Нью-Йорк.
Google Scholar
Ромберг, Т.: 1983, «К «нормальной науке» в некоторых исследованиях в области математического образования», Zentralblatt fur Didaktik der Mathematik 15(8), 89–92.
Google Scholar
Ройс, Дж.: 1978, «Как мы можем лучше всего продвигать построение теории в психологии?» Canadian Psychological Review 19(4), 259–276.
Перекрёстная ссылка Google Scholar
Salomon, G.: 1979, Interaction of Media, Cognition and Learning , Jossey-Bass, London.
Google Scholar
Шеффер, JD: 1990, Senus Communis: Vico, Rhetoric and the Limits of Relativism , Duke University Press, Лондон.
Google Scholar
Шенфельд, А., Смит, Дж. и Аркави, А.: 1993, «Микрогенетический анализ развития понимания сложной предметной области одним учащимся», в Р. Глейзере (ред.) Достижения в педагогической психологии , том. 4, Лоуренс Эрлбаум, Хиллсдейл, Нью-Джерси.
Google Scholar
Шваб, Дж.: 1962, «Преподавание науки как исследование», в Дж. Швабе и П. Брандвейне (ред.) Преподавание науки , издательство Гарвардского университета, Кембридж.
Google Scholar
Сфард, А.: 1991, «О двойственной природе математических понятий: размышления о процессах и объектах как о разных сторонах одной медали», Образовательные исследования по математике 22, 1–36.
Перекрёстная ссылка Google Scholar
Саймон, М.: 1995, «Реконструкция математической педагогики с конструктивистской точки зрения», Journal for Research in Mathematics Education 26(2), 114–145.
Перекрёстная ссылка Google Scholar
Скемп, Р.: 1983, «Международная группа по психологии математического образования: прошлое, настоящее и будущее», Zentralblatt fur Didaktik der Mathematik 15, 112–117.
Google Scholar
Столлингс, В.: 1995, «Исповедь исследователя количественных исследований в области образования, пытающегося преподавать качественные исследования», Исследователь в области образования 24 (3), 31–32.
Google Scholar
Стеффе, Л. и Кобб, П.: 1983, Построение арифметических значений и стратегий , Springer-Verlag, Нью-Йорк.
Google Scholar
Стейнбринг, Х.: 1989, «Рутина и смысл в классе математики», Для изучения математики 9(1), 24–33.
Google Scholar
Штайнер, Г. Г.: 1985, «Теория математического образования (TME): введение», Для изучения математики 5 (2), 11–17.
Google Scholar
Тахта, Д.: 1991, «Три яблока упали с неба в…, в… Размышления об одном дне… », IF 2, Центр математического образования, Открытый университет, Милтон-Кейнс , 25–30.
Google Scholar
Торн, Р.: 1973, «Современная математика: существует ли она?» в Г. Хоусон (ред.) Развитие математического образования , Cambridge University Press, Кембридж.
Google Scholar
Тодоров, Т.: 1984, Михаил Бахтин: Диалогический принцип (пер. В. Годзич), University of Minnesota Press, Миннеаполис.
Google Scholar
Усискин, З.: 1982, Уровни Ван Хиле и достижения в геометрии средней школы , Чикагский университет, Чикаго.
Google Scholar
Варела Ф., Томпсон Э. и Рош Э.: 1991, Воплощенный разум: когнитивная наука и человеческий опыт , MIT Press, Кембридж.
Google Scholar
Vergnaud, G.: 1981, Quelques Orientations Théoriques et Méthodlogiques des Recherches Françaises en Didactique des Mathématiques, in Actes du Vième Colloque de PME, Grenoble, Edition IMAG, vol. 2, 7–17.
Google Scholar
Vergnaud, G.: 1990, «La Théorie des Champs Conceptuels», Recherches en Didactique des Mathématiques 10 (2–3), 133–170.
Google Scholar
Vico, Великобритания: 1744, Principi di Scienza Nuova , переиздано как Bergin & Fisch (пер.) 1961, Anchor Books, Garden City.
Google Scholar
фон Глазерсфельд, Э. : 1984, «Введение в радикальный конструктивизм», в П. Вацлавике (ред.), Изобретенная реальность , Нортон, Лондон, 17–40.
Google Scholar
фон Глазерсфельд, Э.: 1995, Радикальный конструктивизм , Falmer Press, Лондон.
Перекрёстная ссылка Google Scholar
Выготский Л.: 1978, Психика в обществе: развитие высших психических процессов , издательство Гарвардского университета, Лондон.
Google Scholar
Watzlawick P.: 1984, Выдуманная реальность: откуда мы знаем то, во что верим, что знаем? – Вклад в конструктивизм , Нортон, Лондон.
Google Scholar
Вейвуд, А.: 1993, «В поисках подходящего объекта исследования в области образования: размышления о трех презентациях», Журнал исследований в области математического образования 2(5), 83–89.
Перекрёстная ссылка Google Scholar
Wertsch, J.: 1985, Культура, коммуникация и познание: взгляды Выготского , Cambridge University Press, Кембридж, Великобритания.
Google Scholar
Винникот, Д.: 1971, Игра и реальность , Тависток, Лондон
Google Scholar
Вудроу, Д.: 1995, «В поисках множественных верований в теории обучения: разочарование из-за одной веры», Chreods 9, 10–14.
Google Scholar

Ссылки на скачивание

Изучение и адаптация теории реалистической математики образование

Баккер А. и Гравемейер К. (2003). Планирование обучения статистике через решение задач. В R. Charles & H. L. Schoen (Eds.), Преподавание математики посредством решения задач: 6–12 классы (стр. 105–117). Рестон, Вирджиния: Национальный совет учителей математики.

Баккер А. и Гравемейер К. (2004 г.). Учимся рассуждать о распределении. В D. Ben-Zvi & J. Garfield (Eds.), Проблема развития статистической грамотности, рассуждений и мышления (стр. 147–168). Дордрехт, Нидерланды: Kluwer.

Болл, Д. Л. (1993). С прицелом на математический горизонт : дилеммы преподавания математики в начальной школе. 9Журнал начальной школы 0827 , 93 (4), 373-397.

Болл, Д. Л., и Коэн, Д. (1996). Реформа по книге: какова или может быть роль учебных материалов в обучении учителей и педагогической реформе ? Исследователь в области образования , 25 (9), 6–8, 14.

Болл, Д. Л., и Коэн, Д. (1999). Развитие практики, развитие практиков: к практической теории профессионального образования. В Г. Сайкс и Л. Дарлинг-Хаммонд (ред.), Преподавание как учебная профессия : Справочник по политике и практике (стр. 3–32). Сан-Франциско : Джосси-Басс.

Билер, Р. (1993). Программные средства и математическое образование : пример статистики. В книге К. Кейтеля и К. Рутвена (редакторы), Обучение на компьютерах: математическое образование и технологии (стр. 68–100). Берлин : Springer.

Блюменфельд П., Фишман Б. Дж., Крайчик Дж., Маркс Р. В. и Солоуэй Э. (2000). Создание полезных инноваций в системной реформе: расширение масштабов проектной науки с внедренными технологиями в городских школах. Педагог-психолог , 35 (3), 149–164.

Браун, К. А., Штейн, М. К., и Форман, Э. А. (1996). Помощь учителям и ученикам в реформировании кабинета математики. Образовательные исследования по математике , 31 , 63-93.

Кларк, К. М. (1988). Задавать правильные вопросы о подготовке учителей: материалы исследований мышления учителей. Исследователь в области образования , 17 (2), 5-12.

Клемент Дж. и Браун Д. Э. (1989). Преодоление заблуждений с помощью рассуждений по аналогии : абстрактный перенос против построения объяснительной модели. Педагогическая наука , 18 , 327-361.

Кобб, П. (1999). Индивидуальное и коллективное математическое обучение : случай статистического анализа данных. Математическое мышление и обучение , 1 , 5-44.

Кобб, П. (2002). Рассуждение с инструментами и надписями. Journal of the Learning Sciences , 11 , 187-216.

Кобб П. и Макклейн К. (2004 г.). Предлагаемые принципы разработки для преподавания и изучения элементарной статистики. В D. Ben-Zvi & J. Garfield (Eds.), Проблема развития статистической грамотности, рассуждений и мышления (стр. 375-396). Дордрехт, Нидерланды: Kluwer.

Кобб П., Макклейн К. и Гравемейер К. (2003 г.). Изучение статистической ковариации. Познание и обучение , 21 , 1-78.

Кобб П. и Стеффе Л. П. (1983). Конструктивист-исследователь как педагог и создатель моделей. Journal for Research in Mathematics Education , 14 , 83–94.

Кобб П., Стефан М., Макклейн К. и Гравемейер К. (2001). Участие в классных математических занятиях. Journal of the Learning Sciences , 10 , 113-164.

Кобб П. и Якель Э. (1996 г.). Конструктивистские, эмерджентные и социокультурные перспективы в контексте исследований в области развития. Педагог-психолог , 31 , 175-190.

Коул, М. (1996). Культурная психология . Кембридж, Массачусетс: Belknap Press of Harvard University Press.

Конфри, Дж., Белл, К., и Каррехо, Д. (2001 г., апрель). Системный перекрестный огонь: что показывают исследования внедрения городской реформы в математике . Документ, представленный на Документ, представленный на ежегодном собрании Американской ассоциации исследований в области образования, Сиэтл.

Давыдов В. В. (1988). Проблемы развивающего обучения (Часть I). Советское образование , 30 (8), 6-97.

Давыдов В. В. (1995). Влияние Л. С. Выготского на теорию, исследования и практику образования. Исследователь в области образования , 24 (3).

Давыдов В. В., Радзиховский Л. А. (1985). Теория Выгецкого и деятельностный подход в психологии. В J. V. Wertsch (Ed.), 90 827 Культура, коммуникация и познание : точки зрения Выготского (стр. 35–65). Нью-Йорк: Издательство Кембриджского университета.

де Абреу, Г. (2000). Отношения между макро- и микросоциокультурными контекстами : последствия для изучения взаимодействий в классе математики. Образовательные исследования по математике , 41 , 1-29.

де Серто, М. (1984). Практика повседневной жизни . Беркли : University of California Press.

деЛанж Дж., ван Реувейк М. , Беррилл Г. и Ромберг Т. А. (1993). Изучение и тестирование математики в контексте. Дело : визуализация данных 90 828 . Мэдисон, Висконсин: Университет Висконсина, Национальный центр исследований в области образования в области математических наук.

Дьюи, Дж. (1951/1981). Опыт и природа : повторное знакомство. В Дж. А. Бойдстоне (ред.), Джон Дьюи: более поздние работы 1925-1953 (том 1, стр. 361-364). Карбондейл, Иллинойс: Издательство Университета Южного Иллинойса.

Дойз, В., и Магни, Г. (1979). Индивидуальные и коллективные конфликты центраций в познавательном развитии. Европейский журнал психологии , 9 , 105-108.

Дерфлер, В. (2000). Средство для смысла. В P. Cobb, E. Yackel & K. McClain (Eds.), Символизация и общение на уроках математики: точки зрения на дискурс, инструменты и учебный дизайн (стр. 99–132). Махва, Нью-Джерси: Эрлбаум.

Эмирбайер М. и Мише А. (1998). Что такое агентство? Американский журнал социологии , 103 , 962-1023.

Фейман-Немсер, С., и Ремиллард, Дж. (1996). Перспективы обучения преподаванию. В F. Murray (Ed.), The Teacher Educator’s Handbook (стр. 63–91). Сан-Франциско : Джосси-Басс.

Франке, М. Л., Карпентер, Т. П., Леви, Л., и Феннема, Э. (2001). Захват генеративных изменений учителей: последующее исследование профессионального развития учителей в области математики. Американский журнал исследований в области образования , 38 , 653-689.

Фройденталь, Х. (1971). Геометрия между дьяволом и морскими глубинами. Образовательные исследования по математике , 3 , 413-435.

Фройденталь, Х. (1973). Математика как учебное задание . Дордрехт, Нидерланды : Reidel.

Гаморан, А., Андерсон, К. В., Кирос, П. А., Секада, В. Г., Уильямс, Т., и Эшман, С. (2003). Преобразование преподавания математики и естественных наук: как школы и школьные округа могут поддержать изменения . Нью-Йорк: Издательство педагогического колледжа.

Гаморан, А., Секада, В. Г., и Марретт, К. Б. (2000). Организационный контекст преподавания и обучения: изменение теоретических взглядов. В MT Hallinan (Ed.), Справочник по социологии образования (стр. 37-63). Нью-Йорк: Kluwer Academic/Plenum Publishers.

Гравемейер, К. (1990). Контекстные задачи и реалистичное обучение математике. К. Гравемейер, М. ван ден Хеувел и Л. Стрифленд (ред.), Контексты, бесплатные постановки, тесты и геометрия в реалистичном математическом образовании (стр. 10–32). Утрехт, Нидерланды: Исследовательская группа OW & OC.

Гравемейер, К. (1994). Развитие реалистичного математического образования . Утрехт, Нидерланды: CD-ß Press.

Гравемейер, К. (1999). Как возникающие модели могут способствовать формированию формальной математики. Математическое мышление и обучение , 1 , 155-177.

Гравемейер, К. , Кобб, П., Бауэрс, Дж. С., и Уайтнак, Дж. В. (2000). Символизация, моделирование и учебный дизайн. В P. Cobb, E. Yackel & K. McClain (Eds.), Символизация и общение на уроках математики: точки зрения на дискурс, инструменты и учебный дизайн (стр. 225–274). Махва, Нью-Джерси: Эрлбаум.

Хэнкок, К., Капут, Дж. Дж., и Голдсмит, Л. Т. (1992). Аутентичный запрос с данными : критические препятствия для внедрения в классе. Педагог-психолог , 27 , 337-364.

Холланд, Д., Скиннер, Д., Лашикотт, В., младший, и Кейн, К. (1998). Идентичность в культурных мирах . Кембридж, Массачусетс: Издательство Гарвардского университета.

Конольд, К., и Хиггинс, Т. (2002). Работа с данными: основные моменты, связанные с исследованиями. В S. J. Russell, D. Schifter & V. Bastable (Eds.), Развитие математических идей : сбор, представление и анализ данных . Парсиппани, Нью-Джерси: публикации Дейла Сеймура.

Конольд, К. , Поллацек, А., Велл, А., и Ганьон, А. (1997). Анализ данных студентов: исследование критических барьеров. В J. B. Garfield & G. Burrill (Eds.), Исследование роли технологий в статистике преподавания и обучения: материалы конференции круглого стола Международной ассоциации статистического образования 1996 г. (стр. 151-167). Ворбург, Нидерланды: Международный статистический институт.

Ламперт, М. (2001). Проблемы обучения и проблемы обучения . Нью-Хейвен, Коннектикут: Йельский университет.

Латур, Б. (1987). Наука в действии . Кембридж: Издательство Гарвардского университета.

Лав, Дж., и Венгер, Э. (1991). Обучение в помещении: законное периферийное участие . Нью-Йорк: Издательство Кембриджского университета.

Лерер, Р., и Ромберг, Т. (1996). Изучение детского моделирования данных. Познание и обучение , 14 , 69-108.

Леш Р. и Дорр Х. М. (2000). Символизация, общение и математизация : ключевые компоненты моделей и моделирования. В P. Cobb, E. Yackel & K. McClain (Eds.), Символизация и общение на уроках математики: точки зрения на дискурс, инструменты и учебный дизайн (стр. 364-381). Махва, Нью-Джерси: Эрлбаум.

Масингила, Дж. (1994). Математическая практика по укладке ковров. Антропология и образование Ежеквартальный выпуск , 25 , 430-462.

Макклейн, К. (2002). Понимание учителя и учащихся : роль инструментов и надписей в поддержке эффективного общения. Journal of the Learning Sciences , 11 , 217-249.

Макклейн, К., Кобб, П., и Гравемейер, К. (2000). Поддержка способов рассуждений учащихся о данных. В М. Берке (ред.), Изучение математики для нового века (Ежегодник Национального совета учителей математики, 2001 г.) (стр. 174–187). Рестон, Вирджиния: Национальный совет учителей математики.

МакГата, М. , Кобб, П., и Макклейн, К. (2002). Анализ первоначального статистического понимания учащихся: разработка предполагаемой траектории обучения. Журнал математического поведения , 16 , 339-355.

Нельсон, Британская Колумбия (1999). Получение новых знаний путем размышлений : как администраторы могут узнать то, что им нужно знать о реформе математического образования . Кембридж, Массачусетс: Центр развития образования.

Носс Р., Поцци С. и Хойлс К. (1999). Прикосновение к эпистемологии : значения среднего и вариации в сестринской практике. Образовательные исследования по математике , 40 (1), 25-51.

Нуньес, Т., Шлиман, А. Д., и Каррахер, Д. В. (1993). Уличная математика и школьная математика . Кембридж: Издательство Кембриджского университета.

Пири, С., и Кирен, Т. Э. (1994). Рост математического понимания: как мы можем его охарактеризовать и как мы можем его представить? Образовательные исследования по математике , 26 , 61-86.

Прават, Р. С. (1995). Неверное прочтение Дьюи: реформа, проекты и языковая игра. Исследователь в области образования , 24 (7), 13-22.

Пресмег, Северная Каролина (1997). Рассуждения с помощью метафор и метонимий в обучении математике. In LD English (Ed.), Математическое рассуждение : аналогии, метафоры и образы . Хиллсдейл, Нью-Джерси: Эрлбаум.

Рот, В. М. (1997). Где находится контекст в контекстуальных текстовых задачах ? Математические практики и продукты в ответах учащихся 8 класса на сюжетные задачи. Познание и обучение , 14 , 487-527.

Роуэн, Б. (1990). Обязательство и контроль : альтернативные стратегии организационного дизайна школ. В C. Cazden (Ed.), Review of Educational Research (том 16, стр. 353–389). Вашингтон, округ Колумбия: Американские исследования в области образования.

Саксен, Великобритания (1994). Изучение когнитивного развития в социокультурном контексте: разработка практического подхода. Разум, культура и деятельность , 1 , 135-157.

Шифтер, Д. (1995). Меняющиеся представления учителей о природе математики : реализация в классе. В Б. Нельсон (ред.), Исследование и развитие обучения: проблемы трансформации преподавания математики (стр. 17-25). Ньютон, Массачусетс: Центр развития преподавания, Центр развития образования.

Сенгер, Э. (1999). Рефлексивная реформа в математике : рекурсивный характер смены учителя. Образовательные исследования по математике , 37 , 199-201.

Сфард, А. (1991). О двойственной природе математических представлений: размышления о процессах и объектах как о разных сторонах одной медали. Образовательные исследования по математике , 22 , 1-36.

Сфард, А. (1994 г., сентябрь). Развитие концепции развития концепции : от взгляда Бога к тому, что можно увидеть мысленным взором . Доклад, представленный на Симпозиуме по тенденциям и перспективам математического образования, Клагенфарт, Австрия.

Скемп, Р. (1976). Реляционное понимание и инструментальное понимание. Учитель арифметики , 77 , 20-26.

Смит, Дж. П. (1996). Эффективность и преподавание математики путем рассказывания : вызов реформе. Журнал исследований в области математического образования , 27 , 387-402.

Штеффе, Л. П. (1983). Методология обучающего эксперимента в конструктивистской исследовательской программе. В М. Цвенг, Т. Грин, Дж. Килпатрик, Х. Поллак и М. Суйдам (ред.), Материалы Четвертого Международного конгресса по математическому образованию (стр. 469-471). Бостон : Биркхаузер.

Стеффе, Л. П., и Кирен, Т. Е. (1994). Радикальный конструктивизм и математическое образование. Журнал исследований в области математического образования , 25 , 711-733.

Стеффе, Л. П., и Томпсон, П. В. (2000). Методология обучающего эксперимента : основные принципы и основные элементы. В A. Kelly & R. Lesh (Eds.), Справочник по дизайну исследований в области математики и естественных наук (стр. 267–307). Махва, Нью-Джерси: Эрлбаум.

Штейн, М. К., и Браун, К. А. (1997). Обучение учителей в социальном контексте: интеграция совместных и институциональных процессов с изучением смены учителей. В книге Э. Феннема и Б. Скотта Нельсона (ред.), учителей математики в переходный период (стр. 155–192). Махва, Нью-Джерси: Эрлбаум.

Стиглер, Дж. В., и Хиберт, Дж. (1999). Пробел в обучении . Нью-Йорк: Свободная пресса.

Стрифленд, Л. (1991). Дроби в реалистическом математическом образовании. Парадигма исследования развития . Дордрехт, Нидерланды: Kluwer.

Тарп, Р. Г., и Галлимор, Р. (1988). Пробуждение разума к жизни . Нью-Йорк: Издательство Кембриджского университета.

Томпсон, А. Г., Филипп, Р. А., Томпсон, П. В., и Бойд, Б. А. (1994). Расчетно-концептуальные ориентиры в обучении математике. В Ежегоднике Национального совета учителей математики за 1994 г. (стр. 79).-92). Рестон, Вирджиния: Национальный совет учителей математики.

Томпсон, А. Г., и Томпсон, П. В. (1996). Говоря о ставках концептуально, часть II: математические знания для обучения. Журнал исследований в области математического образования , 27 , 2–24.

Томпсон, П. В. (1992). Обозначения, принципы и ограничения : вклад в эффективное использование конкретных манипуляций в элементарной математике. Журнал исследований в области математического образования , 23 , 123-147.

Томпсон, П. В., и Салдана, Л. А. (2000). Эпистемологический анализ математических идей: методология исследования. В М. Фернандес (ред.), Труды двадцать второго ежегодного собрания Североамериканского отделения Международной группы психологии математического образования (том 2, стр. 403-407). Колумбус, Огайо: Информационный центр ERIC по науке, математике и экологическому образованию.

Трефферс, А. (1987). Три измерения : модель описания цели и теории в обучении математике – проект Wiskobas . Дордрехт, Нидерланды : Reidel.

ван дер Веер, Р., и Валсинер, Дж. (1991). Понимание Выготского: поиски синтеза . Кембридж, Массачусетс: Блэквелл.

ван Орс, Б. (1996). Изучение математики как осмысленная деятельность. В книге П. Нешера, Л. П. Стеффе, П. Кобба, Г. А. Голдина и Б. Грира (ред.), Теории математического обучения (стр. 9).1-114). Хиллсдейл, Нью-Джерси: Эрлбаум.

Варенн, Х., и Макдермотт, Р. (1998). Успешный провал: школы, которые строит Америка . Боулдер, Колорадо: Westview.

Выготский Л. С. (1987). Мышление и речь. В R. W. Rieber & A. S. Carton (Eds.), 90 827 Собрание сочинений Выготского, L. S. (vol.1): Проблемы общей психологии 90 828 . Нью-Йорк: Пленум.

Верч, Дж. В. (1998). Разум как действие . Нью-Йорк: Издательство Оксфордского университета.