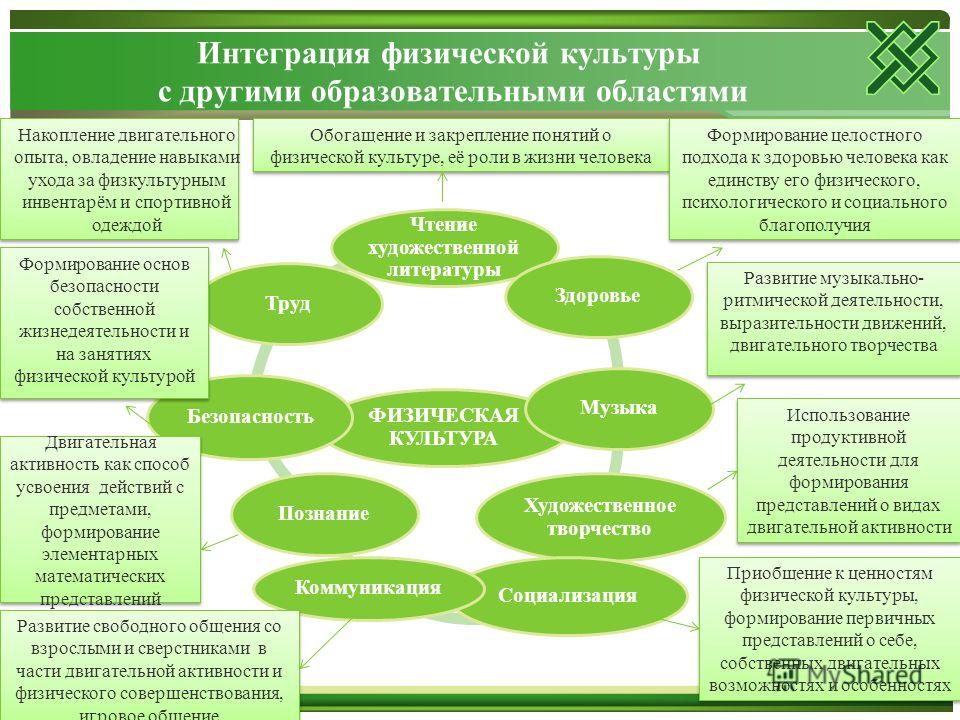
Методика формирования математических представлений включает в себя: Методика формирования элементарных математических представлений

Формирование элементарных математических представлений у детей дошкольного возраста

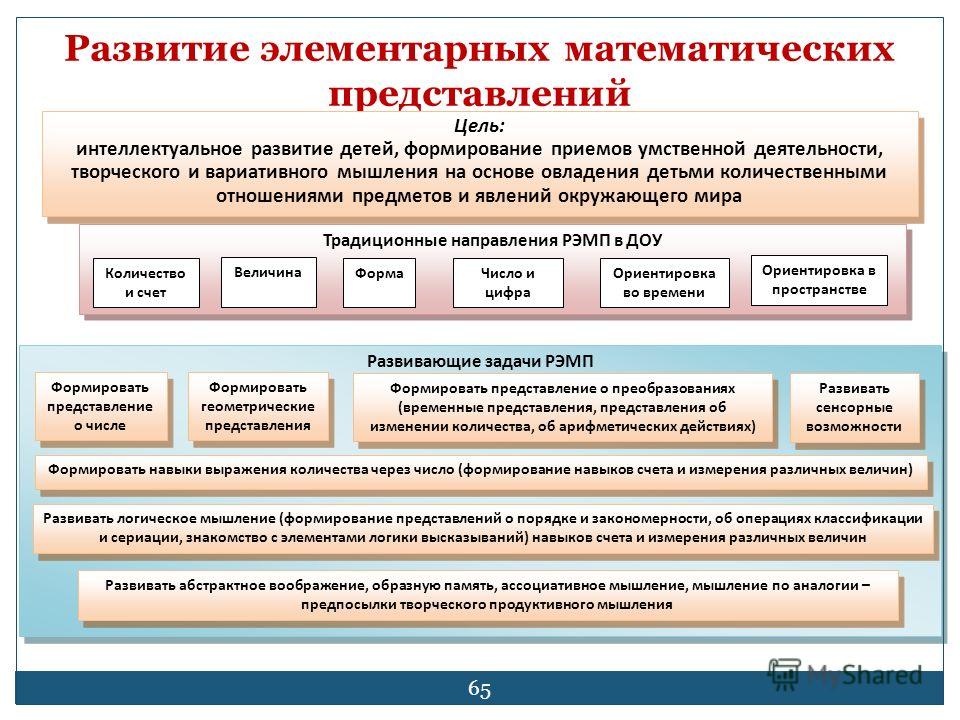
Одной из наиболее важных и актуальных задач подготовки детей к школе является формирование у них элементарных математических представлений, умений и навыков, а также развитие логического мышления и познавательных способностей.

Математическое развитие дошкольников определяется качественными изменениями в формах познавательной активности ребенка, которые происходят в итоге формирования элементарных математических представлений и связанных с ними логических операций.

При систематическом обучении математике дошкольники осваивают специальную терминологию: названия чисел, геометрических фигур (круг, квадрат, треугольник, ромб и др.), элементы фигур (сторона, вершина, основание) и т. п.

Большое внимание в математической подготовке детей дошкольного возраста уделяется операциям с наглядно представленными множествами, проведению измерений с помощью условных мерок, развитию представлений о геометрических фигурах, о времени, формированию понимания пространственных отношений.

Происходит также обучение дошкольников счету, развитие представлений о количестве и числе в пределах первого десятка.

Такой комплекс задач включен в программу математического развития, обеспечивает более глубокое понимание детьми дошкольного возраста количественных и других отношений и закладывает основы дальнейшего совершенствования математического мышления. Одновременно все это способствует умственному развитию дошкольников и успешной подготовке их к обучению в школе.

Целенаправленный и организованный процесс передачи и усвоения знаний, приемов и способов умственной деятельности, предусмотренных программными требованиями, является составляющей формирования элементарных математических представлений. Формирование элементарных математических представлений ставит своей целью не только подготовку к успешному овладению математикой в школе, но и всестороннее развитие детей.

В организованной образовательной деятельности по формированию элементарных математических представлений воспитатели используют разнообразные методы такие, как: указание и объяснение, образец, вопросы детям, ответы детей, подвижные игры, беседа, дидактические игры и упражнения, рассказ, показ реальных предметов, картин, описание и др.

В течение всего учебного года дети упражняются в счете. С большим интересом дети выполняют задания в дидактических играх: «Что изменилось?», «Найди ошибку», «Чудесный мешочек», «Считай дальше», «Считай – не ошибись», «Кто быстрее назовет», «Сколько», «Поймай мяч» и др.

Одна из главных задач в формировании элементарных математических представлений у детей дошкольного возраста – осуществить математическую подготовку детей и вывести развитие их мышления на уровень, достаточный для успешного усвоения математики в школе. Комплексное использование всех методов и приемов, а также форм обучения способствуют ее успешному решению. Возраст детей и индивидуальные особенности каждого ребенка необходимо учитывать при организации и проведении занятий по формированию элементарных математических представлений.

К общедидактическим принципам, составляющим основу методики обучения математике, относятся:

• систематичность;
• последовательность;
• постепенность;
• индивидуальный подход;
• научность;
• доступность;
• непрерывное повторение материала.

Программы обучения и воспитания в ДОО и в начальной школе по математике имеют преемственную связь. К отставанию по математике в школе может привести то, что ребенок плохо усвоил какое-либо правило или понятие в детском саду. Поэтому задача воспитателя – включить дошкольников в активное и систематическое усвоение программного материала. Для этого он должен хорошо знать индивидуальные особенности каждого ребенка, уровень их математического развития и степень понимания ими нового материала, а также их мотивацию.

Учет индивидуальных особенностей детей при проведении образовательной деятельности по формированию элементарных математических представлений позволяет не только помочь детям в усвоении программного материала, но и развить их интерес к этим занятиям, а также обеспечить активное участие всех детей в общей работе. Это способствует развитию внимания и умственных способностей дошкольников, предупреждает интеллектуальную пассивность у отдельных детей, воспитывает целеустремленность, настойчивость и другие волевые качества.

Воспитатель должен стараться развить у детей дошкольного возраста способности к проведению счетных операций, научить их применять полученные ранее знания, творчески подходить к решению предложенных заданий. В организации образовательной деятельности по формированию элементарных математических представлений все эти вопросы воспитатель решает с учетом индивидуальных особенностей дошкольников.

Образовательную деятельность у детей дошкольного возраста по формированию элементарных математических представлений воспитатель осуществляет на занятиях и вне их 1-2 раза в неделю. Как правило, несколько занятия объединяются одной темой. Каждое занятие обязательно должно содержать физкультурную минутку для снятия умственного и физического напряжения, протяженностью 1-3 минуты. Такие перерывы включают в себя динамические упражнения с речевым сопровождением или пальчиковую гимнастику, или упражнения на релаксацию, или упражнения для глаз. На каждом занятии дошкольники выполняют различные виды деятельности с целью закрепления у них математических знаний.

Таким образом, при планировании организованной образовательной деятельности по формированию элементарных математических представлений, воспитатель должен учитывать возрастные и индивидуальные особенности дошкольников, преемственность образовательных программ, степень усвоения программного материала детьми, а также сочетать различные виды детской деятельности, методы, приемы и формы ее организации.

Методика формирования элементарных математических представлений у детей дошкольного возраста

Методика формирования элементарных математических представлений у детей дошкольного возраста

20.10.2014 22:31

Турбина Ольга Ивановна Воспитатель логопедической группы МБДОУ детский сад комбинированного вида №5 «Родничок», г.Луховицы Первоначальные математические знания ребенок приобретает уже враннем возрасте. Знакомство с математикой дает первое интуитивное ощущение, что мир не есть хаос, но скорее некая тонкая архитектура, которая имеет канон своего создания, и человек способенприкоснуться к этому канону. Математика дает возможность увидеть, что порядок и определенность, симметрия и пропорциональность есть как в природе, так и в истинном искусстве. «Природа формулирует свои законы языком математики». Эти слова принадлежат Г.Галилею. Познакомить детей с простейшими законами математики, дать им элементарные математические представления, дать понять, что мир упорядочен и потому постижим, а следовательно, предсказуем для человека – вот основные цели занятий математикой. Чем же мы, воспитатели дошкольных учреждений, должны руководствоваться, что знать, о чем помнить, чему следовать, формируя детей элементарные математические представления? Прежде всего, по какой бы программе мы не работали, мы должны четко представлять ее содержание. Любая программа по ФЭМП включает следующие разделы: «Количество и счет», «Величина». «Форма», «Ориентировка во времени», «Ориентировка в пространстве». Программа младшей группы ограничена дочисловым периодом обучения и включает в себя разделы: «Количество», «Форма», «Величина». Исходными принципами построения всех разделов программы являются системность и последовательность, которые позволяют обеспечить определенный уровень как общего развития ребенка, его познавательных интересов и творческих способностей, так и математического развития, а оно в свою очередь предполагает усвоение ребенком ряда представлений, понятий, отношений, закономерностей (количество, число, порядок, равенство – неравенство, целое – часть, величина – мера и др.) Кроме того, программа построена с учетом возрастных особенностей детей и с постепенным усложнением учебных задач, чаще всего вытекающих одна из другой. Следует обратить особое внимание на заключительную часть-«К концу года дети должны уметь», что позволит нам понять, какими знаниями должен овладеть ребенок к концу учебного года, поможет также при составлении и проведении мониторинга по ознакомлению детей с элементарными математическими представлениями. Большое значение последнего заключается и в том, что он помогает нам увидеть четкую картину усвоения определенных знаний каждым ребенком в отдельности и проследить динамику роста. Не факт, что хорошо изучив программу и зная задачи, поставленные перед нами, мы сможем методически правильно передать элементарные математические знания детям. В этом нам поможет книга «Методические рекомендации к Программе воспитания и обучения в детском саду», которая раскрывает особенности работы с детьми по реализации поставленных в ней воспитательно-образовательных задач и которая должна стать нашей настольной книгой. Методические рекомендации подготовлены с учетом материалов научных исследований, выполненных в разное время под руководством Венгера, Запорожца, Леушиной, Метлиной, Тарунтаевой и др. Современные составители «Методических рекомендаций», как и выше названные авторы, ратуют за то, чтобы обучение детей носило наглядно-действенный характер, то есть, чтобы дети усваивали знания не только на основе восприятия действий воспитателя и его пояснений, но и посредством самостоятельных действий с дидактическим материалом. Поэтому они нацеливают нас, прежде всего, на создание благоприятных условий для успешного развития элементарных математических представлений. В группах нашего детского сада такие условия имеются. В математических уголках есть достаточно богатый базовый набор различных пособий. Это раздаточный и демонстрационный материал, математические таблицы, дидактические игры, вызывающие интерес дошкольников к математике, развивающие их способности, мышление. В нашей группе много игр, соответствующих разному возрастному уровню: «Найди Пару», «Найди свой домик», «Разложи по форме», «Найди такие же фигуры», «Домино фигур», «Цветовое лото», «Найди отличия», «Разрезные картинки», «Чудесный мешочек», «Танграм», «Волшебные палочки» и многие другие. Есть математическая игротека с заданиями для детей по всем разделам программы. Целесообразно использовать такие дидактические игры и упражнения для закрепления изученного материала, как в свободное время, так и на занятиях. Занятия являются основной формой работы по формированию математических представлений. Именно на занятиях мы решаем большую часть программных задач, формируем в определенной последовательности представления, вырабатываем необходимые умения и навыки. В «Методических рекомендациях» мы найдем четкие указания о продолжительности занятий в каждой возрастной группе. Можем воспользоваться примерным распределением программного материала на весь учебный год, что значительно облегчает процесс тематического планирования. Здесь же есть сноска: последовательность ознакомления с некоторыми темами может определяться воспитателем произвольно и варьироваться по его усмотрению. Далее, что немаловажно, мы получаем сведения о структуре занятия. Уясняем, что структура занятая определяется объемом, содержанием, сочетанием программных задач, уровнем усвоения соответствующих знаний, возрастными особенностями детей. Изучение нового материала включает такие виды работ: показ и объяснение, демонстрацию образца, выявление свойств и связей математических объектов. На первом занятии изучению нового отводится большая часть времени, на последующем занятии изучение нового занимает половину лимита времени, вторую половину отводят повторению пройденного. В течение года необходимо время от времени возвращаться к повторению уже изученного материала. Одним из главных условий успешности обучения детей элементарным математическим представлениям является знание методики и владение ею. Математика – наука точная, с определенными законами и многочисленными терминами. И потому она требует от нас, воспитателей, использования четких, традиционно устоявшихся методов и приемов, независимо от того, по какой программе мы работаем. Методика работы с детьми каждой возрастной группы широко представлена в «Методических рекомендациях». Есть много методических пособий, но чаще всего мы используем методику Метлиной, которая подкупает нас своей последовательностью, системностью, четкой конкретикой, разнообразием приемов и методов при решении каждой программной задачи. Ценно в методике Метлиной и то, что у нее стройная и последовательно выстроенная система вопросов, адресованная детям. Вопросы лаконичны, математически грамотны и конкретны. Рассмотрим методику на примере обучения детей составу числа из единиц. В старшей группе мы знакомим детей с составом из единиц чисел первого пятка. Показ состава числа из единиц осуществляем на конкретном материале. Причем, на первом этапе знакомства с составом числа из единиц, как советует Метлина, мы подбираем объемные группы предметов, в которых каждый предмет отличается от других (1 матрешка. 1 пирамидка…). Далее используем предметы одного вида, но отличающихся друг от друга либо окраской, либо размером, либо формой (наборы разноцветных флажков, набора матрешек, елочек разной высоты и т.п.). Позднее – предметы, объединенные одним родовым понятием (комплекты посуды, мебели, овощей) На завершающем этапе используем плоскостные изображения предметов или предметные картинки. Понять состав числа из единиц помогут четко сформулированные конкретные вопросы: Сколько всего игрушек? Что ты можешь сказать об игрушках, какие они? Сколько пирамидок? Мячей? По сколько каждого из них? (По сколько разных игрушек?) Как получилось 5 игрушек? Длясообщения знаний и осознания количественного, значения числа задаем детям вопросы: Сколько разных игрушек вы возьмете, если я назову число 4? Сколько раз вы подпрыгните, если я назову число 1? И предлагаем выполнить эти действия и движения. Для закрепления знаний о составе числа используем словесные и дидактические игры. («Назови 4 предмета», «Кто быстрее назовет 5 головных уборов?», «Выложи квадрат из палочек разного цвета» …) Закреплению изученного материала содействуют наши узкие специалисты, которые включают методическое содержание в контекст традиционных видов деятельности: рисование, аппликация, движения под музыку Для индивидуальной работы мы используем ситуации одевания, прогулки, приготовление к обеду, подготовку к занятиям и т.д. – словом, всевозможные ситуации повседневной жизни ребенка. Большим подспорьем для нас стали и индивидуальные рабочие тетради по математике. Работу с детьми подготовительной группы начинаем с повторения учебного материала, изученного в старшей группе, а затем переходим к знакомству с составом числа из единиц второго пятка. Кроме выше названных приемов используем новые, усложненные; зарисовка определенного числа разных предметов или геометрических фигур, распределение предметов по группам по одному из признаков, выделение каждой группы как единицы счета и определение общего количества групп. Шестилетним детям можно одновременно назвать два числа и дать задание составить сразу две группы предметов: на верхней полоске составить группу из 3 разных геометрических фигур, на нижней – из 4. При этом обратить внимание не только на количественный состав, но и на отношения между числами (на сколько одно число больше или меньше другого). Постепенно дети начинают понимать, что каждое число содержит определенное количество единиц и могут отвечать на более сложные вопросы: «Сколько предметов вы возьмете, если я назову число 7? Почему?», «Как составлено число 7?», «Сколько единиц содержится в числе 7?» Такую скрупулезность, в какой-то мере даже педантичность, а также обращение к разнообразным, правильным методическим приемам мы должны использовать при решении любой программной задачи. Но точность и строгость математики как науки никак не должны выливаться в сухость ее преподавания детям. Вот почему приветствуется игровая форма обучения, которая способствует развитию интереса детей к математике, более эмоциональному восприятию скупых математических законов и качественному усвоению этих законов. Теги: дети дошкольный возраст математические представления методика

Эффективное преподавание математики. Практика 3: Использование и соединение математических представлений

Перейти к основному содержанию

Вы здесь

Домашняя страница

Меню поддержки обучения

• Лучшая первая инструкция по математике
• Эффективная практика преподавания математики NCTM
• Практика преподавания математики на основе долевого участия
• Планирование урока для обучения и размышлений
• Научно-практические руководства для преподавания математики
• Поддержка учащихся, испытывающих затруднения в изучении математики
• Подготовка к математике на 2020-2021 год

---

Использование и соединение математических представлений

Большая часть внимания NCTM к практике использования и соединения математических представлений сосредоточена на том, чтобы помочь учащимся установить связи между контекстуальными, визуальными, вербальными, физическими и символическими формами представления. Видя и представляя математику в различных формах, учащиеся могут лучше связать математические идеи и понять их смысл, а также предлагают возможности для понимания и общения для всех учащихся, особенно для тех, у кого могут возникнуть трудности из-за трудностей в обучении или из-за языка, используемого в классе. не является их родным языком. Также важна возможность гибкого перемещения между различными представлениями. Качественная учебная программа должна предоставлять учащимся целенаправленные и регулярные возможности для перемещения между представлениями. Некоторые из этих действий можно считать частью математического моделирования, например, принятие контекстуальных форм и создание графика, таблицы или уравнения, но движение в другом направлении, например, начало с таблицы или графика и предположение о возможных деталях модели. контекст — одинаково важны.

• Посмотреть все 8 эффективных методик преподавания математики

---

Практика в действии

Одним из способов, которым NCTM (2014, стр.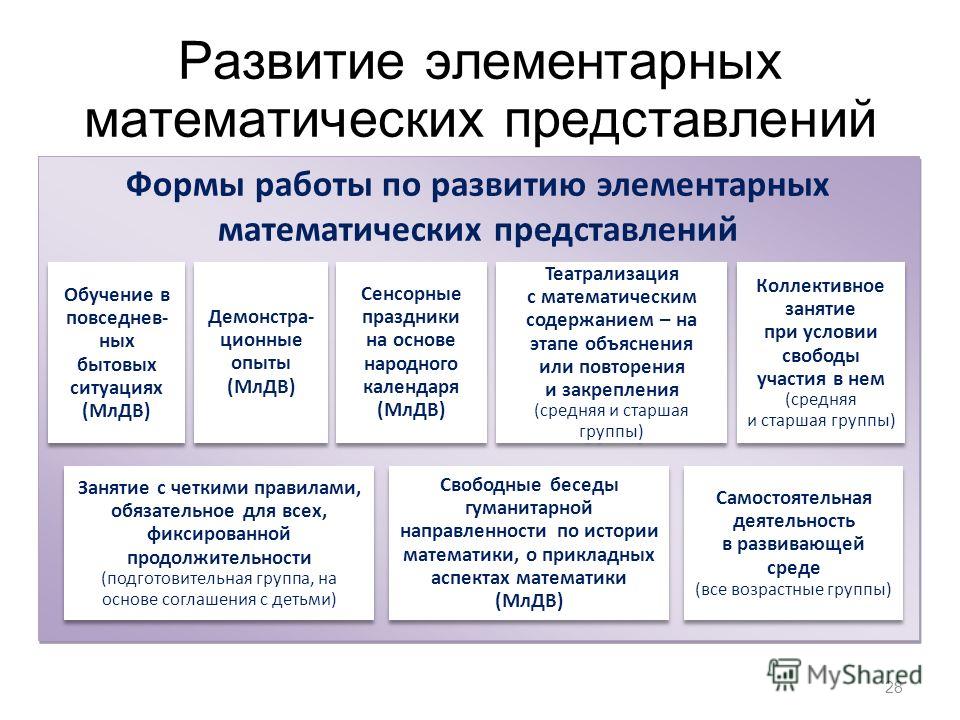 29) обобщает практику использования и соединения математических представлений , является описание набора действий, ожидаемых от учителей и учащихся, которые указывают на участие в этом обучении. упражняться.

Внимание! Не переоценивайте собственное понимание, основанное на этих кратких описаниях педагогической практики. Профессиональные преподаватели должны более глубоко изучить ресурсы NCTM, присоединиться к исследовательским группам и профессиональным сетям, а также стремиться к профессиональному развитию и обучению, чтобы обеспечить качественное участие в практике.

Чем занимаются учителя?

• Выбор заданий, позволяющих учащимся решить, какие представления использовать для понимания задач.
• Выделение значительного учебного времени учащимся для использования, обсуждения и установления связей между представлениями.
• Знакомство с формами представления, которые могут быть полезны учащимся.
• Попросить учащихся сделать математические рисунки или использовать другие визуальные средства для объяснения и обоснования своих рассуждений.
• Сосредоточение внимания учащихся на структуре или существенных чертах математических идей, появляющихся вне зависимости от их представления.
• Разработка способов выявления и оценки способностей учащихся осмысленно использовать представления для решения задач.

Чем занимаются студенты?

• Использование нескольких форм представления для понимания математики.
• Описание и обоснование своего математического понимания и рассуждений с помощью рисунков, диаграмм и других представлений.
• Выбор того, какие формы представлений использовать в качестве инструментов для решения проблем.
• Наброски диаграмм для понимания проблемных ситуаций.
• Контекстуализировать математические идеи, связывая их с реальными ситуациями.
• Рассмотрение преимуществ или целесообразности использования различных представлений при решении задач.

---

Ресурсы

• Принципы действий: обеспечение математического успеха для всех (NCTM, 2014, стр. 24-29).)
• Принятие мер: внедрение эффективных методов преподавания математики в K-классе 5 (NCTM, 2017, стр. 119-143)
• Принятие мер: внедрение эффективных методов преподавания математики в 6–8 классах (NCTM, 2017, стр. 99–121)
• Принятие мер: внедрение эффективных методов преподавания математики в 9–12 классах (NCTM, 2017, стр. 99–123)
• Улучшение практики в классе с помощью исследований, лежащих в основе принципов действий (NCTM, 2017, стр. 27-36)

Почему они важны и как их эффективно использовать

Toggle Nav

При рассмотрении вопроса о преподавании и изучении математики и регулярном планировании таких возможностей обучения, независимо от того, является ли обучение очным, гибридным или онлайновым, решения, связанные с ролью представлений как неотъемлемого компонента ваших уроков математики, самое важное. Рассмотрим следующее утверждение о важности представлений как математического процесса из «Принципов и стандартов школьной математики» (NCTM, 2000).

Представления следует рассматривать как важные элементы в поддержке понимания учащимися математических понятий и отношений; в передаче математических подходов, аргументов и понимания себе и другим; в распознавании связей между родственными математическими понятиями; и в применении математики к реальным проблемным ситуациям посредством моделирования. (стр. 67)

Существует ряд представлений, с которыми ваши ученики должны регулярно сталкиваться, занимаясь изучаемой ими математикой. На рисунке 1 представлена ​​модель, которая представляет типы представлений, с которыми сталкиваются учащиеся, и их возможные связи друг с другом (Леш, Пост и Бер 19).87).

Рисунок 1

По мере того, как учащиеся начинают заниматься математикой, знания математики, которые они изучают, улучшаются благодаря опыту с различными представлениями. Основное внимание здесь уделяется признанию важности конкретных учебных соображений при планировании и использовании репрезентаций.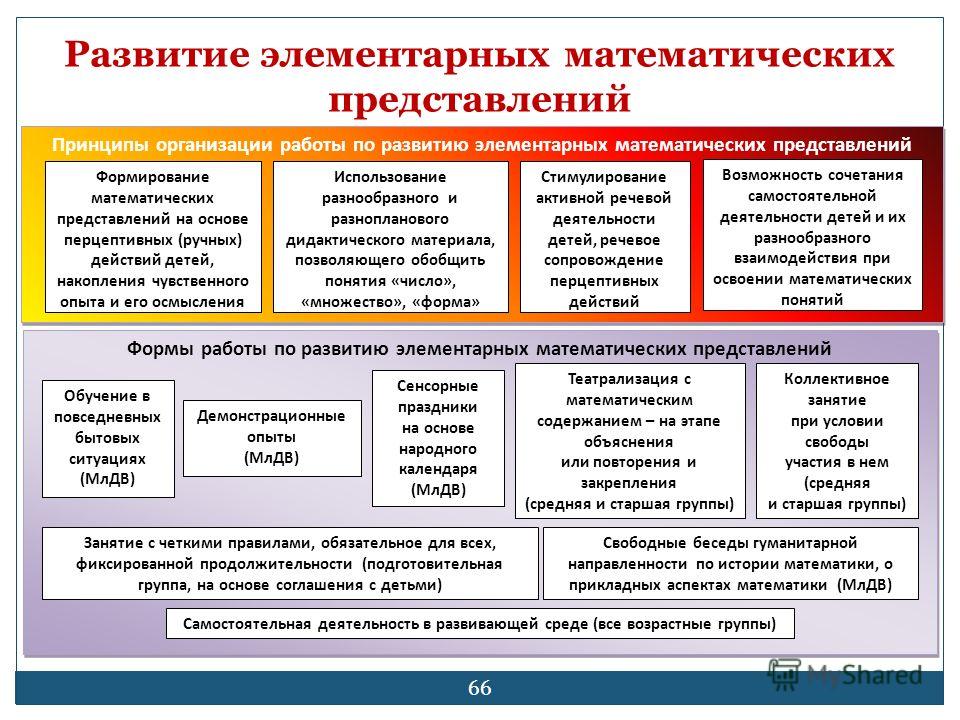 Выбор, который вы делаете в отношении использования учащимися типов представлений, должен учитывать следующее:

• Доступ: Будут ли ваши ученики иметь доступ к представлениям, которые вы ожидаете от них использовать? В условиях очного или гибридного класса вы можете попросить своих учеников хранить определенные практические манипулятивные материалы (например, блоки с основанием 10 или блоки шаблонов) на своих партах или поблизости от того места, где вы предполагаете их использовать *. Для решения многих математических задач вы можете предложить своим учащимся работать в парах или тройках, таким образом совместно используя практические манипулятивные материалы или создавая групповой рисунок или письменный ответ на математическую задачу. В онлайн-учебной среде ваши ученики могут создавать общие визуальные представления, используя домашние наборы для манипулирования, онлайн-манипуляторы или совместные доски.
• Опыт: Насколько комфортно ваши ученики используют те или иные представления? Использовали ли они числовые ряды различными способами для представления и сравнения целых чисел и дробей (например, незамкнутые числовые ряды, двойные числовые ряды, вертикальные числовые ряды)? Понимают ли они, как блоки с основанием десять можно использовать для представления целых чисел, а также десятичных сумм? Используют ли они блоки шаблонов для сравнения, сложения и вычитания дробей? Важно признать, что «новички» и ранние пользователи манипулятивных материалов (например, практическое использование блоков с основанием десяти, стержней Кюизенера, блоков узоров, цветных плиток), числовых линий, 10 рамок, 100 диаграмм и т. д. часто являются, по понятным причинам оспаривается намерением и фактическим использованием таких представлений. Дайте вашим учащимся время ознакомиться с характеристиками и ожиданиями представлений, которые они будут использовать. Такой опыт необходим учащимся, поскольку они учатся использовать репрезентации надлежащим образом, с комфортом и уверенностью. Мы, взрослые, иногда забываем, что репрезентативные модели могут восприниматься нашими учениками не так, как мы могли бы ожидать.0012
• Связи: Когда ваши ученики занимаются математикой, они естественным образом связывают одни представления с другими. Возможно, вы не рассматривали такие связи напрямую, так как ожидали вовлечения учащихся в урок. Например, вы можете запланировать, чтобы пары учащихся использовали цветные плитки или рисунки для представления периметров прямоугольных областей площадью 24 квадратных дюйма, предлагая парам учащихся отметить периметры каждого из прямоугольников и обсудить свои решения. Можно, конечно, предположить, что это занятие может вовлечь ваших учеников во все типы представлений, изображенных на рисунке 1 (выше), ясно демонстрируя, что математические идеи улучшаются за счет множественных представлений.
• Оценка и обратная связь: Поскольку установление связей между математическими представлениями может углубить понимание учащимися концепций и процедур, часто выступая связующим звеном или связующим звеном с процессом решения задач, очень важно регулярно контролировать такие действия учащихся. Использование методов формирующего оценивания в классе будет направлять ваше внимание к использованию репрезентаций, поскольку вы, например, наблюдаете, как учащиеся вовлечены в использование определенных практических манипулятивных материалов, а затем подключаются к визуальным (рисунок), символическим (уравнение) , так и вербальные (дискуссионные) представления. Постоянное использование формативного оценивания также дает возможность давать обратную связь вашим учащимся относительно их понимания и следующих шагов, а также запрашивать отзывы учащихся относительно их восприятия того, что они понимают, а также их собственную оценку своих учебных потребностей.

В заключение, когда вы регулярно планируете уроки математики, которые действительно сосредоточены на том, чтобы ваши ученики выполняли изучаемую ими математику, рассмотрите типы представлений (например, манипулятивные материалы, рисунки, уравнения, обсуждения), которые вы предполагаете использовать в качестве более чем важных элементов обучения. такие планы. Думайте о таких возможностях для привлечения ваших учеников как о порталах для доступа и углубления понимания и связанных с этим побочных продуктов уверенности и удовольствия от математики.

*hand2mind — отличный, пользующийся уважением источник манипулятивных материалов и связанных с ними практических действий, связанных с манипулятивными материалами.

 

Ссылки

Леш Р., Пост Т. и Бер М. (1987). Представления и переводы среди представлений в изучении математики и решении задач. В К. Жанвье (ред.), Проблемы представления в преподавании и изучении математики (стр.