Мерка в математике это: Урок математики на тему ” Мерка. Единичный отрезок” (1 класс)

Урок математики на тему ” Мерка. Единичный отрезок” (1 класс)

Урок математики в 1 классе

Тема: Мерка. Единичный отрезок.

Цель: формирование умений сравнивать при помощи единичного отрезка

Задачи:

– сформировать представление о мерке и единичном отрезке.

– развивать мыслительные операции, вычислительный навык, коммуникативные универсальные учебные действия (в т.ч. диалог ученик – ученики), умение ставить вопросы и находить на них ответы, обогащать и усложнять словарный состав, учить самооцениванию;

-воспитывать познавательный интерес к предмету, коммуникативную культуру, учить взаимодействию.

Оборудование:

«Моя математика» (Т.Е.Демидова, С.А.Козлова, А.П. Тонких), 1 класс, рабочая тетрадь, раздаточный материал (мерки разной длины, карандаши), числовой веер, опорные сигналы на доске, презентация, электронная физминутка «Коробка с карандашами»

Этапы урока

Ход урока

Примечание

1. Орг. момент

Друзья мои, я очень рада войти в приветливый ваш класс.

И для меня уже награда – вниманье ваших умных глаз.

Я знаю, каждый в классе гений, но без труда талант не впрок.

От вас ответы, взгляды, мненья, мы вместе проведём урок

– Сегодня, мы продолжаем изучать такой интересный предмет, как математика.

Что я вижу? Вижу стол.

Странно, он и пуст и гол.

Не оборудован урок – это главный мне упрек.

Удивлены моим видом? Представляю, как вы еще больше удивитесь, если узнаете, что школа по- гречески значит « досуг»., т е отдых.

Не правда ли странно: школа – и вдруг досуг?

Дело в том, что греки под досугом подразумевали не безделье, а свободные беседы мудрецов – философов со своими учениками о разных науках. И от учеников требовалось внимание, старание, догадка наблюдательность.

Пусть поработает ваша догадка.

Ответьте на загадки из багажа знаний

Учитель выносит коробку с надписью «Багаж знаний»

2. Актуализа-ция знаний

1. Сколько было моркови?

Сколько моркови съел зайчик?

2. Четыре спелых груши

На веточке качалось.

Две груши снял Павлуша,

А сколько груш осталось?

– Что надо найти часть или целое?

– Как найти целое? часть?

3. Ёжик по лесу шёл,
На обед грибы нашёл:

Два – под берёзой,
Один – у осины.
Сколько их будет
В плетёной корзине?

4. Подарил утятам ёжик

Восемь кожаных сапожек.

Кто ответит из ребят,

Сколько было всех утят?

– Ребята, посмотрите на доску. Что вы видите? Кто может предложить задание по этому ряду карточек? Кому из ребят его выполнить? (___________, поставь карточки по порядку)

-О чём теперь можно спросить?

Придумайте задание со словами «наибольшее число», «наименьшее число».

Со словами «стоит за», «перед», «между». (Какое число…)

На улице, где я живу дома стоят тоже в ряд , но вот номера домов расположены следующим образом…

Назови их (на доске карточки с точками) (номер 3..5, 7)

Найди закономерность. (Каждое число больше предыдущего на два)

– Назови и покажи номер дома, который стоит слева от дома №3, 1

– Номер дома – справа от дома №7, 9

Вы сейчас провели маленькое исследование, составили ряд, соблюдая закономерность

– А знаете ли вы, кто такой исследователь? (человек, изучающий какое либо явление или предмет)

– Сегодня, вы – исследователи. (наденьте бейджики) Чтобы быть лучшим, необходимо быть очень вдумчивым, внимательным и наблюдательным.

– Перед началом исследования проведём разминку

Я люблю очень рисовать. В магазине я купила карандаши для себя и для своей дочки. Какой карандаш достанется дочке ? А мне? Короткий, длинный

Как узнать, какой карандаш длиннее, а какой короче?

(Приложить друг к другу так, чтобы один из концов совпал (ученики показывает с места)

Слайды

Числовой веер

Учитель достает из коробки карточки с ответами, а ребята вешают на доску

1, 2, 4, 3

1, 2, 3, 4

Фиксация на доске:

Сравнить

1) наложением

Физминут-ка

Разминку мы провели.

Но исследователи должны быть не только смекалистыми, но и очень зоркими. Для этого потренируем наши глазки.

– Одинакова ли длина карандашей в коробке?

Электронная физминутка «Коробка с карандашами»

3. Открытие нового знания и формулирование темы урока.

Подводящий диалог.

Проблемная ситуация

Поиск решения проблемы

Поблемная ситуация (столкнуть мнения учеников с помощью практического задания.)

Подводящий к теме диалог

Историчес-кая справка

В нашем дальнейшем исследовании участвуют помощники Катя, Петя и Вова, они приготовили задание № 1 на стр. 50 учебника. Начинаем исследование

– Как сравнить длины отрезков, изображенных на рисунке? Тоже наложить их друг на друга? Нет. Сделать этого нельзя. Они нарисованы

-Какой отрезок самый короткий? Самый длинный? 5>4.

34

-Что помогло сравнить отрезки

Вывод: можем сравнить наложением, подсчитать количество клеток

Исследование продолжается

Работа в паре

-У вас на партах лежат карточки с геометрическими фигурами?

– Какими?

– Как сравнить по длине данные отрезки?

? Не знаем

Можем проверить наложением? По клеткам? – Значит цель нашего урока? (Узнать, как сравнить отрезки)

-Исследуем проблему.

– У вас есть зелёная полоска.

– Можем ли сравнить длину отрезков при помощи данной полоски?

– Эта полоска, при помощи которой мы будем сравнивать длины отрезков, называется МЕРКА.

От слова мерить.

Словарь Д.Н.Ушакова

Мерка – предмет определённой длины, служащей мерой для измерения чего-нибудь.

Меркою из бумаги сапожники измеряют размер ноги. Мерка из верёвки заменяет складной метр.

– Как сравним отрезки? С помощью мерки?

– Как надо укладывать мерку? Последовательно, друг за другом

Показать наглядно на бумажных моделях

– Равны ли данные отрезки?

– Как вы это доказали?

Работа в группах

Герои из мультфильма «38 попугаев» измеряли длину удава. Поможем им. Разделимся на группы: попугайчики, слонята, мартышки

Покажите ваши работы, поднимите вверх.

– Сколько мерок входит в длину удава у I группы, II группы, III группы? (удав одинаковой длины во всех группах)

– Почему результаты разные? (возникло противоречие)

– Вы смогли выполнить задание? Нет?

– В чем затруднение? (измерительном приборе)

– Чем это задание не похоже на предыдущие?(разные мерки)

– Можно ли сравнивать отрезки, измеренные разными мерками? нет

– Какими должны быть мерки? одинаковыми

– А вот как называются одинаковые мерки. Мы с вами прочитаем в учебнике.

– Верный ли вывод мы сделали о том, что мерки для сравнения длин должны быть одинаковыми?(да)

– Как называются такие мерки Единичный отрезок

– Исследовали ли мы ещё один способ сравнения длин отрезков? (да)

– Можем снять эту карточку – ? Не знаем

ТЕМА нашего урока?

В древности использовались для измерения длин те измерительные приборы, которые всегда были при себе. Одним из самых распространенных единиц длины был локоть, т.е. расстояние от локтя до конца среднего пальца (

размер локтя колебался в пределах от 38 см до 46 см). Локтями купцы измеряли продаваемые ткани, наматывая их на руку, высоту дерева, срубленного на постройку дома и т.д. Сохранилась поговорка: «Сам с ноготок, а борода с локоток»

– Почему в наше время мы не пользуемся этой меркой? (результаты разные, есть современные мерки)

Работа с учебником

Нет. Сделать этого нельзя. Они нарисованы

5>4. 34

клетка

Фиксация на доске:

2) по клеткам

На доске вопрос

Можно линейкой – это инструмент для измерения длины. Но есть ещё один способ точно сравнить длину отрезков и без использования линейки

Слайды

При помощи мерки

Фиксация на доске:

3) меркой

С. 51 – правило

На доске е_______

На доске

Мерка. Единичный отрезок

Слайды

5.Первич-ное закрепле-ние

– Нам при выполнении следующей работы понадобиться современная мерка.

Выполним упр. 5 на стр. 51из учебника.

Прочитайте задание.

-Какой отрезок самый длинный (тот в котором поместилось 3 одинаковых мерки)

-Какой отрезок самый короткий (который имеет длину в 1мерку)

Вывод

Закончи предложение. Если отрезки измерены одинаковыми мерками, то чем больше… (число мерок, тем больше отрезок)

-Это вывод вам понадобиться для выполнения самостоятельной работы

Работа с учебником

Слайд

4.Самостоятельная работа и самооценка

В тетрадях с. 25 №2 самостоятельная работа с последующей проверкой на доске.

Самооценка по алгоритму(спросить 1 или 2 человек)

1 шаг. Что нужно было сделать в этом задании ?

2 шаг. Удалось получить результат?

3 шаг. Справился полностью правильно или с незначительной ошибкой (какой, в чем)?

4 шаг. Справился полностью самостоятельно или с небольшой помощью (кто помогал, в чем)?

Слайды с проверкой и алгоритмом

5. Рефлексия

– Чему учились на уроке? (сравнивать отрезки)

– Как сравнить по длине отрезки? (по клеткам, меркой)

– Как можно по-другому назвать одну и туже мерку? (единичный отрезок)

Оцените свое эмоциональное
состояние на уроке в дневнике, при помощи кружков разного цвета.

– Хотели бы вы еще когда-нибудь провести исследование? А нужно ли проводить такие исследования? (можно узнать много интересного).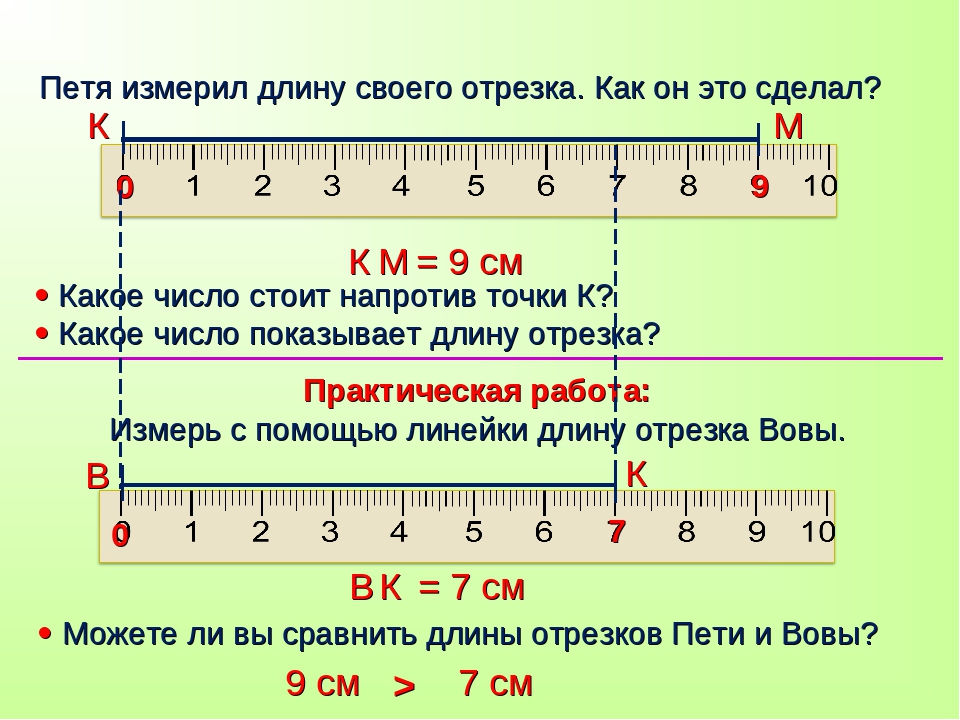 Урок подошёл к концу, но главные ваши исследования ещё впереди.

– И последнее задание из «Багажа знаний»

Поднимите ту мерку, которая соответствовала вашим знаниям в начале урока, а теперь, которая соответствует полученным знаниям на уроке. Положите её в наш багаж знаний и возьмите конверт с пожеланиями «Для маленьких исследователей» Пожелания читаются вслух.

Спасибо за урок!

что и как измеряли на Руси

Здравствуйте, дорогие ребята! И вам, уважаемые родители, большой привет!

Всем вам из математики известны меры длины. В наш век больших технологий мы без труда вычисляем метры и километры, пользуемся линейкой и меряем расстояния. Заведённые не только в России, но и по всему миру единые единицы измерения позволяют нам говорить на одном математическом языке.

А знаете ли вы, чем измерялась длина у наших предков, ведь никаких расчерченных линеек тогда не было! Кому-нибудь говорят о чём-то такие слова, дошедшие до нас издалека, как сажень, пядь или вершок? Сколько это верста или аршин? Старинные меры длины – вот чем мы сегодня займёмся.

Чем меряли на Руси?

В стародревние времена на Руси для измерения длины использовали человека, вернее, его части тела – руки, ладони, ступни. Вот некоторые самые древнейшие методы измерения, которыми пользовались тысячи лет назад.

Локоть

Его, начиная с 11 века, отмеряли по руке от кончика среднего пальца до локтевого сустава, и по разным дошедшим до нас источникам показатель составлял около 45-47 сантиметров. В используемый у древних людей локоть входило шесть ладоней, а в ладонь – четыре пальца.

«Но ведь люди-то разные!» — скажете вы, и будете правы. Пришлось придумать единый образец в виде условной палочки, чтобы пользоваться не индивидуальным, а «общим» локтем. Такая мера длины широко применялась купцами-торговцами, чтобы отмерять сукно и полотно.

Это интересно! Про не очень умных людей говорят: «Нос с локоть, а ума с ноготь».  И вправду, так бывает, человек суёт свой длинный нос, куда не надо.

Пядь

Вы сможете представить, сколько это, если вытянете в стороны большой и указательный пальцы. Померяйте между ними расстояние, оно должно получиться 17,78-19 сантиметров.

Большая пядь получится между большим и средним пальцем (22-23 сантиметра), а также пядь «с кутыркой» — с добавкой, когда присчитывается плюсом ещё два сустава указательного пальца (27-30 сантиметров).

Это интересно! Раньше пядями меряли иконы, в быту это была мерка для толщины снега. Про очень умных говорят: «Семи пядей во лбу», как бы считая, что большой лоб пропорционален большому уму. Поговорка эта буквально восприниматься не должна, иначе только представьте, что лоб умника должен быть высотой 1,26 метра!

Сажень

Это была одна из самых используемых мерок длины на Руси. Происходит она от глагола «сягать», то есть насколько можно дотянуться рукой. Сначала это было расстояние между двумя вытянутыми на ширине плеч руками от большого пальца одной до большого пальца другой (152 сантиметра).

Потом появилась великая косая сажень, измеряемая по диагонали от развёрнутой в сторону левой ноги до пальцев поднятой вверх правой руки (248 сантиметров). Мерка между широко расставленными вразмах мужскими руками, исчисленная по кончикам пальцев, именовалась маховой саженью (176 сантиметров).

Это интересно! В строительстве и при межевании земельных участков применяли саженные верёвки. Если про вас скажут «Косая сажень в плечах», то вам есть, чем гордиться, ведь эта поговорка характеризует широкоплечего богатыря.

Верста

Применяемая на Руси мера, которой отчитывали путь. Раньше её звали «поприще». Обозначало первоначально она расстояние от поворота пахотного плуга до следующего поворота. Что примечательно, в разное время в версту вкладывали разную длину, так как была путевая верста, измеряющая расстояние, и межевая, измеряющая землю.

Так, в 15 веке в версте было 750 саженей, в 1649 году при царе Алексее Михайловиче межевая величина включала 1000 саженей, а при Петре I сохранилась лишь путевая, которая охватывала только 500 (1070 метров), окончательно вытеснив межевую мерку.

Это интересно! Верстой именовали не только расстояние, так называли ещё высокие столбы, стоящие вдоль дорог. Знаете ли вы, почему высоких людей иногда называют «верстой коломенской»? Вдоль главной дороги из Москвы в село Коломенское, где располагался летний дом царя Алексея Михайловича, поставили огромные столбы, которых её не было нигде в России. Так и прилипло выражение к тем, у кого небывало высокий рост.

Шаг

Зачастую расстояние меряли шагами, средняя длина которого 71 сантиметр. Во время дуэлей это было самым распространённым мерилом.

Это интересно! На расстоянии 10 шагов Дантес стрелял в Александра Пушкина в 1837 году в Санкт-Петербурге.

Аршин

Мера длины появилась под необходимостью торговать с Востоком, и пришла они вместе с иностранными купцами. В переводе на сантиметры это 71,12, и ранее аршин был привязан к длине человеческой руки.

Чтобы никто никого при торговле не обманывал, в Москве была изготовлена деревянная линейка, с которой сделали копии и распространили по всей России. Концы казённого аршина были окованы железом и отмечены государственной печатью, чтобы мерку нельзя было укоротить. Аршин вытеснил из системы мерок такие длины, как локоть и пядь.

Это интересно! Как вы думаете, что означает пословица «Как аршин проглотил»? Так говорят о том, кто неестественно прямо ходит, словно «по струнке», как будто у него внутри деревянная линейка.

Вершок

Эта мера длины появляется вместе с аршином в 17 веке и составляет длину главной фаланги указательного пальца руки, приблизительно 4,45 сантиметра. Обычно вершком измеряли человеческий рост или высоту животных.

Это интересно! Как вы думаете, правильно ли говорят «От горшка два вершка, а уже указчик»? Давайте посчитаем: два вершка – это всеголишь около 9 сантиметров (4,45*2). Разве бывают такие люди? Ошибка?! Абсолютно нет. Дело в том, что раньше рост человека меряли, начиная с двух аршинов, так как чуть больше 142 сантиметров было обязательным для взрослого человека. Вот к этой базе и прибавляли потом вершки. Так что от горшка в два вершка – это 151 сантиметр!

Линия

Малюсенькая длина, равная ширине пшеничного зёрнышка, составляет 2,54 миллиметра.

Раньше она применялась, чтобы померять горлышко у стеклянной лампы. Была она и единицей измерения калибра огнестрельного оружия.

Это интересно! Знаете ли вы, почему винтовка названа трёхлинейной? Думаю, догадались правильно:  калибр этого оружия составляет три величины мерки под названием «линия» — 3*2,54мм.

К XIII веку существовало около 400 всяких мерок у разных стран, что осложняло торговлю между ними. В 1835 году Россия соотнесла свои мерки с английскими, после чего к нам пришли дюймы и футы, вытеснив сажени и аршины. В 1918 году за основу единицы длины был положен метр.

Вот такие были раньше мерки. Теперь, встретив где-нибудь в литературном произведении слова «верста», «аршин» и «сажень», вы без труда сможете объяснить, что это, как меряется и сколько составляет. Ну а за научный проект по данной теме, вы без труда получите пятерку и удивите друзей-одноклассников новой информацией.

Успехов в учебе!

Евгения Климкович.

Знакомство с различными единицами измерения длины. Мерка длины сантиметр. 1-й класс

Предмет: математика.

Класс: 1.

Автор учебника: И.И.Аргинская, Е.П. Бененсон, Л.С.Итина, С.Н.Кормишина.

Тема урока: “Знакомство с различными единицами измерения длины. Мерка длины “сантиметр”.

Цель: познакомить с историей измерения и разными мерами длины.

Задачи.

Образовательные:

– рассмотреть первую общепринятую единицу измерения длины – сантиметр, познакомить с использованием сантиметра для измерения длины и высоты объектов, учить читать таблицу, столбчатую диаграмму.

Развивающие:

– развивать речь, познавательные способности, логическое мышление.

Воспитательные:

– прививать интерес к математике;

– прививать культуру учебного труда.

Планируемые результаты (универсальные учебные действия)

Личностные универсальные учебные действия

– проявлять интерес к учебному материалу, в частности, к изучению математики;

– осознавать свою гражданскую идентичность на основе исторического математического содержания.

Регулятивные универсальные учебные действия

– принимать и сохранять учебную задачу, соответствующую этапу обучения;

– понимать выделенные учителем ориентиры действия в учебном материале;

– в сотрудничестве с учителем, классом находить несколько вариантов решения учебной задачи.

Познавательные универсальные учебные действия

– самостоятельно осуществлять поиск необходимой информации при работе с учебником;

– под руководством учителя осуществлять действие подведения под понятие “выражение”;

– проводить анализ предлагаемых рисунков (с целью выделения предметов определённой формы, сравнение количества предметов).

Коммуникативные универсальные учебные действия

– принимать участие в работе парами и группами;

– допускать существование различных точек зрения;

– корректно формулировать и отстаивать свою точку зрения;

– использовать в общении правила вежливости.

Планируемые предметные результаты

Овладение понятием “меры длины”.

Знакомство с историей измерения и разными мерами длины.

Овладение умениями анализировать данные таблицы и выбирать нужные для решения задач.

Решение задач на разностное сравнение на основе правила сравнения двух чисел

Проведение качественного и количественного, явного и неявного сравнения.

Тип урока: урок изучения нового материала

Методы:проблемный, словесный, наглядный, частично-поисковый.

Форма организации познавательной деятельности: фронтальная, групповая, работа в паре.

Средства обучения:учебник “Математика,1 класс” часть 2, И.И.Аргинская, Е.П.Бененсон, Л.С.Итина, С.Н.Кормишина, мультимедиа проектор, экран, компьютер, презентация, индивидуальный раздаточный материал (полоски, мерки).

Ход урока

1. Организационный момент

– Здравствуйте, ребята!

– Сегодня у нас необычный урок математики. И начнем мы его с игры. Будьте внимательны. Если вы согласны, отвечайте хором – “да”, если не согласны – “нет”.

– Мы друг друга понимаем?
Хором: Да, да, да!
– Хорошо всегда считаем?
Хором: Да, да, да!
– А задачи мы решаем?
Хором: Да, да, да!
– На уроке засыпаем?
Хором: Нет!
Игры, шутки, всё для вас!
Пожелаем всем удачи – 
За работу, в добрый час.

– А вот девиз нашего урока. Прочитаем его хором! (Слайд 4). Презентация

– Мы дружные!

– Мы умные!

– Мы внимательные!

– Мы старательные!

– Мы в первом классе учимся!

– Всё у нас получится!

3. Актуализация знаний

–А вот и первое задание. Найдите лишнее. (Слайд 5-7)

–Определите, какая фигура лишняя. (Отрезок) (Слайд 8)

– Объясните, почему.

–Что же такое отрезок? (Это часть прямой, ограниченная с двух концов)

4. Создание проблемной ситуации

– Попробуйте выполнить следующее задание.

– Перед вами лист бумаги, на котором начерчен отрезок. Измерьте длину отрезка с помощью мерки.

– Что значит измерить длину?

– Поменяйтесь с соседом по парте мерками, еще раз измерьте длину отрезка.

– Что заметили? (Мерки разные, поэтому и разные результаты измерений)

5. Построение проекта выхода из затруднения

– С такой же проблемой столкнулись и герои известного мультфильма “38 попугаев”.

– Внимание на экран. (Показ отрывка из мультфильма)

– Будьте внимательны, потому что после просмотра мы с вами должны будем сделать ещё один вывод.

– Почему длина удава получилась разной? (Измеряли разными предметами)

– Какой выход можете предложить? (Мерки должны быть одинаковыми…)

– Какую же задачу мы поставим сегодня на уроке? (Познакомиться с общепринятой мерой измерения длины)

6. “Открытие” нового знания и первичное закрепление

– Как вы думаете, почему герои фильма измеряли рост удава в попугаях, мартышках, слонах? А удобно ли это – измерять длину предметов в слонах? А в чём же удобно измерять длину предмета? (В метрах, сантиметрах)

– А давайте узнаем, как люди измеряли длину раньше и как измеряют сейчас. Рассмотрите рисунки учебника на страницах 24 и 25.

Работа с учебником.

– Для чего необходимо измерять длину?

– Нужно ли вам это умение?

– Что вам знакомо на этих рисунках?

– Познакомимся с историческими мерками. Просмотрите материал. Что вам более всего знакомо? В России в старину для измерения длины использовали локоть, сажень, пядь, вершок, ладонь. А в других странах использовали величины ярд, дюйм, фут. (Слайд 13)

– Одной из самых распространенных единиц длины был ЛОКОТЬ. (Слайд 14)

– Покажите эту мерку – локоть.

– Локтями купцы измеряли продаваемые ткани, наматывая на руку. При помощи локтя можно измерить длину ткани или нити. (Учитель измеряет длину нити, затем предлагает измерить ученику)

– Что заметили? (Результат измерений разный)

– Наряду с локтем была распространена другая мера длины ПЯДЬ. 

– Было даже такое выражение, “семь пядей во лбу” (Учитель показывает меру длины на лбу и предлагает показать детям).

– Как вы думаете, про какого человека можно сказать, что у него “семь пядей во лбу” (так говорили про очень умного человека).

– А также существовали и другие меры длины: САЖЕНЬ, КОСАЯ САЖЕНЬ. (Слайд 15)

– Покажите, как можно изобразить сажень.

– Было такое выражение “Косая сажень в плечах”. Про какого человека так могли сказать? (Сильного, здорового, человека крепкого телосложения)

– Также были такие меры длины как ВЕРСТА, АРШИН, ВЕРШОК. (Слайд 16)

– Наверное, вам знакомо такое выражение “От горшка два вершка” . Что оно обозначает? (Очень маленький). Вспомните сказку про Мальчика – с – Пальчик. Какого же он был роста? (Вершок)

– Посмотрите на иллюстрацию учебника и постарайтесь объяснить, почему Дюймовочку так звали. (Слайд 17)

– Постарайтесь объяснить, что такое ярд? Фут? (Слайд)

– Определите длину колонны. (7 футов)

Практическая работа.

– Попробуем измерить длину парты разными старинными мерками.

1 группа – Измеряет длину парты в ладонях

2 группа – Измеряет длину парты в локтях

3 группа – Измеряет длину парты пядью

Отчёт групп о результатах работы.

– Зависит ли результат от мерки ?

– Теперь вы сами убедились, какая получается путаница, неразбериха, когда люди пользуются разными мерками. Поэтому в настоящее время используются более точные мерки. Это общие для всех стран единицы измерения.

– Какими инструментами для измерения длины пользуются в настоящее время?

– А как называется единица измерения, с которой мы с вами сегодня знакомимся, вы узнаете из учебника (стр. 26)

– Прочитайте, как же называется одна из единиц измерения длины? (Сантиметр)

–Определите тему нашего урока.

–Посмотрите на отрезок АК. О таком отрезке говорят, что его длина

1 сантиметр

Слово сантиметр после числа пишут кратко см(Слайд)

Работа с учебником.

– Сколько отрезков длиной 1 см поместилось в отрезке АМ?

– Чему равна длина отрезка АМ?

– Запишите длину отрезка АМ в сантиметрах.

7. Закрепление изученного материала.

Задание № 63

– Посмотрите, ребята, в этом задании герои сказок изображены рядом со шкалой, которая позволяет определить их рост. Посмотрите внимательно на этот рисунок и определите рост сказочных героев.

– Проверьте правильность данных в таблице.

– На сколько сантиметров нужно вырасти Дюймовочке, чтобы стать такого же роста, как Мальчик- с- Пальчик? (6-3=3)

А такого же роста, как Крошечка –Хаврошечка? (8-3=5)

Физминутка.

8. Закрепление ранее пройденного материала

Задание 64. Работа в парах

– Расположите карточки с цифрами под рисунками так. Чтобы можно было понять, что было сначала, а что потом.

– Предметы какой формы нужны, чтобы сделать снеговика?

Задание 65. Работа в тетради

– Чем похожи снеговики?

– Чем различаются?

Задание 66. Самостоятельная работа в тетрадях

8-3=5		9- 4=5		6+2=8
4-4=0		4+ 1=5		3+5=8

Задание 67

– Сколько пушистых одуванчиков на верхнем рисунке?

– Сколько облетевших одуванчиков?

– На сколько пушистых одуванчиков больше, чем облетевших?

– Запишите выражение и его значениею

– Сколько облетевших одуванчиков на нижнем рисунке?

– Сколько пушистых одуванчиков?

– На сколько пушистых одуванчиков меньше, чем облетевших?

– Как узнать, на сколько одно число больше или меньше другого?

Вывод: Чтобы узнать на сколько одно число больше или меньше другого, нужно из большего числа вычесть меньшее.

9. Итог урока

– С какими мерами длины мы познакомились на уроке?

– Где вам пригодятся полученные знания?

10. Рефлексия

– Продолжите: Я узнал…

Мне было легко…

Мне было трудно…

Мне понравилось…

– Скажите, кому было трудно на уроке?

– Мы изучили еще слишком мало, чтобы сразу было легко и понятно. На следующем уроке мы продолжим работу, которую сегодня начали.

– Ребята, посмотрите, на смайлики. Если вы довольны своей работой и вам понравился урок ,прикрепите магнитик на улыбающегося смайлика. А если испытывали затруднения, прикрепите магнитик к грустному смайлику.

(Дети подходят и прикрепляют магнитики)

– Молодцы, ребята! Всем спасибо за работу и активность. На этом наш урок окончен.

Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/96512-znakomstvo-s-razlichnymi-edinicami-izmerenija

Измерение величин, меры, единицы измерения

Величина — это то, что можно измерить. Такие понятия, как длина, площадь, объём, масса, время, скорость и т. д. называют величинами. Величина является результатом измерения, она определяется числом, выраженным в определённых единицах. Единицы, в которых измеряется величина, называют единицами измерения.

Для обозначения величины пишут число, а рядом название единицы, в которой она измерялась. Например,  5 см,  10 кг,  12 км,  5 мин.  Каждая величина имеет бесчисленное множество значений, например длина может быть равна:  1 см,  2 см,  3 см  и т. д.

Одна и та же величина может быть выражена в разных единицах, например килограмм, грамм и тонна — это единицы измерения веса. Одна и та же величина в разных единицах выражается разными числами. Например:

5 см = 50 мм (длина),

1 ч = 60 мин (время),

2 кг = 2000 г (вес).

Измерить величину — значит узнать, сколько раз в ней содержится другая величина того же рода, принятая за единицу измерения.

Например, мы хотим узнать точную длину какой-нибудь комнаты. Значит нам нужно измерить эту длину при помощи другой длины, которая нам хорошо известна, например при помощи метра. Для этого откладываем метр по длине комнаты столько раз, сколько можно. Если он уложится по длине комнаты ровно  7  раз, то длина её равна  7  метрам.

В результате измерения величины получается или именованное число, например  12  метров, или несколько именованных чисел, например  5  метров  7  сантиметров, совокупность которых называется составным именованным числом.

Меры

В каждом государстве правительство установило определённые единицы измерения для различных величин. Точно рассчитанная единица измерения, принятая в качестве образца, называется эталоном или образцовой единицей. Сделаны образцовые единицы метра, килограмма, сантиметра и т. п., по которым изготавливают единицы для обиходного употребления. Единицы, вошедшие в употребление и утверждённые государством, называются мерами.

Меры называются однородными, если они служат для измерения величин одного рода. Так, грамм и килограмм — меры однородные, так как они служат для измерения веса.

Единицы измерения

Ниже представлены единицы измерения различных величин, которые часто встречаются в задачах по математике:

Меры веса/массы:

• 1 тонна = 10 центнеров;
• 1 центнер = 100 килограмм;
• 1 килограмм = 1000 грамм;
• 1 грамм = 1000 миллиграмм.

Меры длины:

• 1 километр = 1000 метров;
• 1 метр = 10 дециметров;
• 1 дециметр = 10 сантиметров;
• 1 сантиметр = 10 миллиметров.

Меры площади (квадратные меры):

• 1 кв. километр = 100 гектарам;
• 1 гектар = 10000 кв. метрам;
• 1 кв. метр = 10000 кв. сантиметров;
• 1 кв. сантиметр = 100 кв. миллиметрам.

Меры объёма (кубические меры):

• 1 куб. метр = 1000 куб. дециметров;
• 1 куб. дециметр = 1000 куб. сантиметров;
• 1 куб. сантиметр = 1000 куб. миллиметров.

Рассмотрим ещё такую величину как литр. Для измерения вместимости сосудов употребляется литр. Литр является объёмом, который равен одному кубическому дециметру  (1 литр = 1 куб. дециметру).

Меры времени:

• 1 век (столетие) = 100 годам;
• 1 год = 12 месяцам;
• 1 месяц = 30 суткам;
• 1 неделя = 7 суткам;
• 1 сутки = 24 часам;
• 1 час = 60 минутам;
• 1 минута = 60 секундам;
• 1 секунда = 1000 миллисекундам.

Кроме того, используют такие единицы измерения времени, как квартал и декада.

• квартал — 3 месяца;
• декада — 10 суток.

Месяц принимается за  30  дней, если не требуется определить число и название месяца. Январь, март, май, июль, август, октябрь и декабрь —  31  день. Февраль в простом году —  28  дней, февраль в високосном году —  29  дней. Апрель, июнь, сентябрь, ноябрь —  30  дней.

Год представляет собой (приблизительно) то время, в течении которого Земля совершает полный оборот вокруг Солнца. Принято считать каждые три последовательных года по  365  дней, а следующий за ними четвёртый — в  366  дней. Год, содержащий в себе  366  дней, называется високосным, а годы, содержащие по  365  дней — простыми. К четвёртому году добавляют один лишний день по следующей причине. Время обращения Земли вокруг Солнца содержит в себе не ровно  365  суток, а  365  суток и  6  часов (приблизительно). Таким образом, простой год короче истинного года на  6  часов, а  4  простых года короче  4  истинных годов на  24  часа, т. е. на одни сутки. Поэтому к каждому четвёртому году добавляют одни сутки  (29 февраля).

Об остальных видах величин вы узнаете по мере дальнейшего изучения различных наук.

Сокращённые наименования мер

Сокращённые наименования мер принято записывать без точки:

Меры длины Километр — км Метр — м Дециметр — дм Сантиметр — см Миллиметр — мм	Меры веса/массы тонна — т центнер — ц килограмм — кг грамм — г миллиграмм — мг
Меры площади (квадратные меры) кв. километр — км2 гектар — га кв. метр — м2 кв. сантиметр — см2 кв. миллиметр — мм2	Меры объёма (кубические меры) куб. метр — м3 куб. дециметр — дм3 куб. сантиметр — см3 куб. миллиметр — мм3
Меры времени век — в год — г месяц — м или мес неделя — н или нед сутки — с или д (день) час — ч минута — м секунда — с миллисекунда — мс	Мера вместимости сосудов

	1 мм	1 см	1 дм	1 м	1 км
	1 мм2	1 см2	1 дм2	1 м2	1 км2
	1 мм3	1 см3	1 дм3	1 м3	1 км3

Измерительные приборы

Для измерения различных величин используются специальные измерительные приборы. Одни из них очень просты и предназначены для простых измерений. К таким приборам можно отнести измерительную линейку, рулетку, измерительный цилиндр и др. Другие измерительные приборы более сложные. К таким приборам можно отнести секундомеры, термометры, электронные весы и др.

Измерительные приборы, как правило, имеют измерительную шкалу (или кратко шкалу). Это значит, что на приборе нанесены штриховые деления, и рядом с каждым штриховым делением написано соответствующее значение величины. Расстояние между двумя штрихами, возле которых написано значение величины, может быть дополнительно разделено ещё на несколько более малых делений, эти деления чаще всего не обозначены числами.

Определить, какому значению величины соответствует каждое самое малое деление, не трудно. Так, например, на рисунке ниже изображена измерительная линейка:

Цифрами  1,  2,  3,  4  и т. д. обозначены расстояния между штрихами, которые разделены на  10  одинаковых делений. Следовательно, каждое деление (расстояние между ближайшими штрихами) соответствует  1 мм.  Эта величина называется ценой деления шкалы измерительного прибора.

Перед тем как приступить к измерению величины, следует определить цену деления шкалы используемого прибора.

Для того чтобы определить цену деления, необходимо:

1. Найти два ближайших штриха шкалы, возле которых написаны значения величины.
2. Вычесть из большего значения меньшее и полученное число разделить на число делений, находящихся между ними.

В качестве примера определим цену деления шкалы термометра, изображённого на рисунке слева.

Возьмём два штриха, около которых нанесены числовые значения измеряемой величины (температуры).

Например, штрихи с обозначениями  20 °С  и  30 °С.  Расстояние между этими штрихами разделено на  10  делений. Таким образом, цена каждого деления будет равна:

(30 °С – 20 °С) : 10 = 1 °С

Следовательно, термометр показывает  47 °С.

Измерять различные величины в повседневной жизни приходится постоянно каждому из нас. Например, чтобы прийти вовремя в школу или на работу, приходится измерять время, которое будет потрачено на дорогу. Метеорологи для предсказания погоды измеряют температуру, атмосферное давление, скорость ветра и т. д.

математиков | Определение, история и важность

Математика , наука о структуре, порядке и отношениях, которая возникла из элементарных практик подсчета, измерения и описания форм объектов. Он имеет дело с логическим рассуждением и количественным расчетом, и его развитие повлекло за собой все большую степень идеализации и абстракции предмета. С XVII века математика была незаменимым дополнением к физическим наукам и технологиям, а в последнее время она стала играть аналогичную роль в количественных аспектах наук о жизни.

Британская викторина

Математика

Какое число древние египтяне считали священным? Как называется многоугольник с тремя сторонами? Посмотрите, “складываются” ли ваши знания математики в этой викторине.

Во многих культурах – под влиянием потребностей практических занятий, таких как торговля и сельское хозяйство, – математика далеко вышла за рамки простого счета.Этот рост был наибольшим в обществах, достаточно сложных, чтобы поддерживать эту деятельность и предоставлять досуг для размышлений и возможность опираться на достижения более ранних математиков.

Все математические системы (например, евклидова геометрия) представляют собой комбинации наборов аксиом и теорем, которые могут быть логически выведены из аксиом. Исследования логической и философской основы математики сводятся к вопросу о том, обеспечивают ли аксиомы данной системы ее полноту и непротиворечивость.Для полного рассмотрения этого аспекта, см. математика, основы.

Эта статья посвящена истории математики с древнейших времен до наших дней. Вследствие экспоненциального роста науки большая часть математики развивалась с 15 века нашей эры, и историческим фактом является то, что с 15 века до конца 20 века новые разработки в математике были в основном сконцентрированы в Европе и Северной Америке. . По этим причинам основная часть данной статьи посвящена европейским разработкам с 1500 года.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

Это, однако, не означает, что события в других местах были несущественными. Действительно, чтобы понять историю математики в Европе, необходимо знать ее историю, по крайней мере, в древней Месопотамии и Египте, в Древней Греции и в исламской цивилизации с 9 по 15 века. То, как эти цивилизации влияли друг на друга, и важный прямой вклад Греции и ислама в более поздние события, обсуждаются в первых частях этой статьи.

Вклад Индии в развитие современной математики был сделан благодаря значительному влиянию достижений Индии на исламскую математику в годы ее становления. Отдельная статья «Математика в Южной Азии» посвящена ранней истории математики на Индийском субконтиненте и развитию там современной десятичной системы счисления с разрядами. Статья «Восточноазиатская математика» освещает в основном независимое развитие математики в Китае, Японии, Корее и Вьетнаме.

Основным разделам математики посвящено несколько статей. См. Алгебру ; анализ; арифметика; комбинаторика; теория игры; геометрия; теория чисел; числовой анализ; оптимизация; теория вероятности; теория множеств; статистика; тригонометрия.

6 Оценка аттестата по математике | Измерение того, что имеет значение: концептуальное руководство для оценки по математике

Внешние эффекты Оценки, такие как учебный тест (SAT) и тест Advanced Placement (AP), претерпевают фундаментальные изменения с повсеместным влиянием.Использование калькуляторов на экзамене AP по математическому анализу, например, оказывает глубокое влияние на многих учителей старших классов и на то, как они используют технологии в своих классах. ²⁵

Еще одним аспектом системных эффектов, которые преследуют многие усилия по реформированию, является изменение отношения родителей, политиков и других граждан к природе математики, которую необходимо изучать учащимся, и привлечение каждой группы к более близкой и более поддерживающей роли усилиями студентов. школа. Несмотря на то, что на сегодняшний день имеется мало данных об этих системных эффектах, важно будет оценить любые изменения в таком отношении и действиях, которые могут развиваться вместе с изменениями в оценке.

T HE E QUITY P RINCIPLE

Ключевые вопросы

Отдает ли оценка предпочтение одной группе над другими по причинам, не относящимся к тому, что она предназначена для измерения?

Насколько оправданы сравнения со стандартом или с показателями других?

Доступны ли задания этим учащимся?

Некоторые аспекты этого принципа требуют изучения и оценки.Первый аспект включает обычные вопросы, связанные со справедливостью оценки: традиционные вопросы справедливости и сопоставимости между группами, баллами, задачами и ситуациями. Второй аспект включает вопросы о том, имеют ли студенты возможность изучать важную математику (научили ли их оценивать важную математику). Третий аспект является более новым и связан с педагогикой, которая требует, чтобы все учащиеся находили задачи оценивания доступными, если они должны иметь необходимое положительное влияние на их обучение.

F ВОЗДУХА И C ВОЗМОЖНОСТЬ

Традиционные проблемы справедливого оценивания усиливаются или приобретают другое значение в контексте новых форм оценивания по математике. Например, когда оценка включает в себя несколько сложных задач, часто устанавливаемых в контекстах, не одинаково знакомых всем учащимся, любое систематическое несоответствие в способах разработки задач или

определение математики The Free Dictionary

существительное

Цитаты
«Насколько законы математики относятся к реальности, они не точны; и насколько они достоверны, они не относятся к реальности» [ Альберт Эйнштейн]
«Я часто восхищался мистическим образом Пифагора и тайной магией чисел» [Томас Браун Religio Medici ]
«Красота – это первое испытание; в мире нет постоянного места для уродливой математики» [Годфри Гарольд Харди A Mathematician’s Apology ]

Математика

Отрасли математики алгебра, анализ, аналитическая геометрия или координатная геометрия, прикладная математика, арифметика, булева алгебра, исчисление, геометрия хаоса, коники, дифференциальное исчисление, Евклидова геометрия, теория игр, геометрия, теория групп, интегральное исчисление, номография, неевклидова геометрия, теория чисел, численный анализ, теория вероятностей, о.у. re математика, теория множеств, статистика, топология, тригонометрия

Математические термины острый угол, сложение, алгоритм или алгоритм, угол, дуга, площадь, среднее, ось, основание, двоичный, биномиальный, кардинальное число, декартовы координаты, хорда, круг, окружность, замкнутое множество, коэффициент, общий знаменатель, общий множитель, комплексное число, концентрический, конус, постоянная, координата или координата, косеканс, косинус, котангенс, куб, кубический корень, кубоид, кривая, куспид , цилиндр, десятичный, десятичный, знаменатель, диагональ, диаметр, цифра, деление, додекаэдр, эллипс, равно, уравнение, равносторонний, четный, экспоненциальный, коэффициент, факториал, формула, дробь, частота, функция, график, спираль, полусфера , семиугольник, шестиугольник, гипербола, гипотенуза, икосаэдр, мнимое число, неправильная дробь, индекс, бесконечность, целое число, интеграл, пересечение, иррациональное число, равнобедренное число, геометрическое место, логарифм или log, наименьший общий знаменатель, наименьший общее кратное, множество Мандельброта, матрица, среднее значение, медиана, минус, мода, умножение, натуральный логарифм, натуральное число, узел, девятиугольник, число, числитель, продолговатый, тупой угол, восьмиугольник, октаэдр, нечетный, открытый набор, операция, оператор, порядковое число, начало координат, парабола, параллель, параллелограмм, пятиугольник, процент, идеальное число, пи, плюс, многоугольник, многогранник, полином, степень, простое число, призма, вероятность, произведение, доказательство, правильная дробь, теорема Пифагора, квадрант, квадратное уравнение, четырехугольник, частное, радиан, радиус, отношение, рациональное число, действительное число, обратная величина, прямоугольник, повторяющаяся десятичная дробь, угол отражения, остаток, ромб, прямой угол, прямоугольный треугольник, корень, скаляр, разносторонний, секущий, сектор , полукруг, множество, значащие числа, одновременные уравнения, синус, логическая линейка, твердое тело, сфера, квадрат, квадратный корень, странный аттрактор, подмножество, вычитание, сумма, surd, касательная, тетраэдр, тор, трапеция, треугольник, объединение, универсальное множество , значение, переменная, вектор, Диаграмма Венна баран, объем, вульгарная дробь, ось x, ось y, ось z, ноль

Mathematicians Мария Гаэтана Агнеси ( итальянский язык, ), Говард Хэтэуэй Айкен ( U.S. ), Жан Ле Ронд Аламбер ( французский язык ), Андре Мари Ампер ( французский язык ), Анаксимандр ( греческий язык ), Аполлоний Пергский ( греческий язык ), Архимед ( греческий язык ), Чарльз Бэббидж ( английский ), Иоганн Якоб Бальмер ( швейцарский ), Даниэль Бернулли ( швейцарский ), Жак Бернулли ( швейцарский ), Жан Бернулли ( швейцарский ), Фридрих Вильгельм Бессель ( немецкий ), Герман Бонди ( британский ), Джордж Буль ( английский ), Генри Бриггс ( английский ), Огюстен Луи Коши ( французский ), Артур Кейли ( английский ), Рудольф Юлиус Клаузиус ( немецкий ), Исидор Огюст Конт ( французский язык ), Джордж Ховард Дарвин ( английский язык ), Джулиус Вильгельм Ричард Дедекинд ( немецкий язык ), Джон Ди ( английский язык ), Рене Декарт ( французский язык ), Диофант ( греческий язык ), Питер Густав Лежен Дирихле ( Немецкий ), Альберт Эйнштейн ( U.S. ), Эратосфен ( греческий ), Евклид ( греческий ), Евдокс Книдский ( греческий ), Леонард Эйлер ( швейцарский ), Пьер де Ферма ( французский язык ), Леонардо Фибоначчи ( итальянский ), Жан Батист Жозеф Фурье ( французский язык ), Галилео ( итальянский язык ), Карл Фридрих Гаусс ( немецкий язык ), Джозия Уиллард Гиббс ( США ), Курт Гедель ( США ), Эдмунд Гюнтер ( Английский ), Эдмунд Галлей ( английский ), Уильям Роуэн Гамильтон ( ирландский ), Герой ( греческий ), Дэвид Гильберт ( немецкий ), Карл Густав Якоби Якоби ( немецкий ), Герман Кан ( U.С. ), Андрей Николаевич Колмогоров ( советский ), Жозеф Луи Лагранж ( французский язык ), Пьер Симон Лаплас ( французский язык ), Адриан Мари Лежандр ( французский язык ), Готфрид Вильгельм фон Лейбниц ( немецкий язык ) , Николай Иванович Лобачевский ( русский, ), Ада Лавлейс (, английский, ), Пьер Луи Моро де Мопертюи (, французский, ), Герард Меркатор (, фламандский, ), Герман Минковский (, немецкий, ), Джон Нэпьер (, шотландский ), Исаак Ньютон (, английский, ), Омар Хайям (, персидский, ), Николь д’Орем (, французский, ), Папп Александрийский (, греческий, ), Блез Паскаль (, французский, ), Карл Пирсон ().