Математика самоучка: Самоучка. Математика 2 класс. – Гайштут и его друзья

Математика для программистов-самоучек: собрали лайфхаки, книги и курсы

Bubble

21 января 2022, 12:28

На форуме Hacker News пользователь novakor спросил, как подтянуть математику — он программист-самоучка и чувствует большой пробел в знаниях. Мы собрали лучшие советы.

Вот, что ему порекомендовали:

• всегда помнить: если вы посмотрели курс лекций и уверены, что поняли тему — вы не поняли тему. Математику невозможно выучить, это процесс. Поэтому после каждой прочитанной темы нужно практиковаться и выполнять упражнения. Очень много упражнений;
• купить книгу по алгебре для подготовки к школьным экзаменам или для подготовки ко вступительным в университет. Когда освоите базу, можно пройти университетский вводный курс математики;
• ресурсы Khan Academy. На сайте проекта изучите раздел математики, а на YouTube-канале смотрите видео по нужным темам. Проект начал выходить и для русскоязычной аудитории, но пока доступны только две темы: тригонометрия и статистика для учеников средней школы;
• Лекции профессора Леонарда. По мнению одного из пользователей, они ничем не хуже лекций в университете;
• книги «Арифметика для практичного человека» Дж. Э. Томпсона, «Числовой дьявол: математические приключения» Ганса Магнуса Энценсбергера и «Исчисление с помощью аналитической геометрии» Ричарда Э. Джонсона и Фреда Л. Киокемейстера. Про последнюю пишут, что по ней занимались в Гарварде, и отмечают хороший набор упражнений;
• курс алгебры на платформе ALEX — «не бесплатно, но работает хорошо». Платформа поможет вам определить слабые места и сама подскажет нужные материалы;
• бесплатная книга по линейной алгебре от Джима Хефферона. Книга подходит тем, у кого уже есть какие-то знания, но он недостаточно их закрепил. Полный видео-курс линейной алгебры для колледжей от Хефферона в двух частях прилагается. Смотреть первую здесь, смотреть вторую тут;
• образовательный Youtube-канал про математику 3Blue1Brown. Охватывает темы от матанализа до нейросетей. У проекта также есть образовательно-развлекательный подкаст, а гостем одного из выпусков стал автор проекта Khan Academy.

Bubble тоже составил несколько рекомендаций:

• курс «Математика для всех» дает понимание, как работает математика в жизни и поможет перестать думать, что это невероятно сложный предмет для умников;
• курс «Линейная алгебра и аналитическая геометрия» будет отличным мостом между школьной и университетской программами, вы закрепите базовые знания и плавно перейдете на новый уровень;
• книга «Стратегия решения математических задач» от Альфреда Позаментье и Стивена Крулика. Все стратегии описываются на примерах бытовых ситуаций и через математику, а применять их вы сможете не только в математике и программировании;
•  курс школьной математики от Яндекс.Практикума;
• курс «Математика для всех» от Алексея Савватеева. Можно смотреть на Youtube или проходить на Coursera.

Материал может содержать партнерские ссылки. Это не отражается на стоимости сервисов или товаров. Партнеры не влияют на наши рекомендации и содержание текста. 

«‎‎Главная ошибка собеса — подгонять ответы»‎. Рекрутеры рассказали о найме в IT

Откуда берутся IT-рекрутеры, с какими трудностями они сталкиваются в попытках закрыть позиции и какие ошибки сами совершают на интервью — полезно знать перед тем, как искать работу.

Размещение рекламы на Bubble

Размещение рекламы на Bubble

Телеграм-канал про Образо­вание, карьеру и жизнь в IT

Телеграм-канал про Образо­вание, карьеру и жизнь в IT

Расти в IT

«Куда-то кликнул и все поломалось»: Что бесит айтишников в рабочей переписке

Bubble

Расти в IT

13 крутых книг по программированию. Советуют айтишники и Bubble

Bubble

Расти в IT

5 полезных аккаунтов в LinkedIn про то, как улучшить свою страницу в LinkedIn

Bubble

Расти в IT

Топ-9 полезных приложений, чтобы убить прокрастинацию и начать учебу

Bubble

Расти в IT

Кому в Web 3.

0 работать хорошо: кто создает новый интернет и неплохо на этом зарабатывает

Bubble

Расти в IT

Как выбрать полезную стажировку и не оплошать. Лайфхаки джунам

Bubble

Расти в IT

Расти в IT

Как вырасти до сеньора и тим-лида — гид по карьерному росту в айти

Мир содрогнулся, когда узнал, что читают разработчики по ночам…

Ничего криминального — только полезная еженедельная рассылка от Bubble. Тренды в айти, лайфхаки и советы экспертов.

Подписывайся!

Ты — котик! Проверяй почту

Нам нужен настоящий адрес эл. почты

Спецпредложения

Курсы со скидками для пользователей Bubble

Выбрать курс

Освоить за выходные

Экспресс-курсы программирования

Выбрать курс

Баг пофиксил

Курсы для QA-инженеров

Выбрать курс

Звездочка к резюме

Курсы по карьерному росту

Выбрать курс

Мы используем cookies, чтобы анализировать трафик и настраивать рекламу.

Уолтер Питтс: история великого математика-самоучки

Что бывает, когда ты никому не можешь доверять, кроме математики? В биографической истории Уолтера Питтса, основателя компьютерной нейролингвистики, всё настоящее — и наука, и дружба, и великие открытия, и одиночество вместе с депрессией. Увы, предательство своего первого верного друга, математики, он не стерпел.

Научно-популярный журнал Nautilus опубликовал статью об учёном-самоучке, широко известном в узких кругах интересующихся искусственным интеллектом. Подробную биографию Питтса редакция журнала восстановила по личным письмам Питтса, сохранившимся в архиве Американского философского общества.
Детство изгоя

Уолтер Питтс с детства был изгоем среди ровесников; добавьте к этому непростую семью во главе с отцом-котельщиком, нередко пускавшим в ход кулаки, и криминогенную обстановку Детройта. От жестоких насмешек соседских детишек Уолтер прятался в местной библиотеке. Там он и изучил основы греческого, латыни, логики и математики. Здесь, в спокойной сени полок с книгами, ему было гораздо комфортней, чем дома, где отец призывал Уолтера бросить школу и устроиться на работу.

Бездомный гений и алкоголик, Уолтер Питтс. Источник: nautil.us

В один из таких вечеров в библиотеке Питтс наткнулся на трёхтомник «Начала математики» (Бертран Рассел и Альфред Уайтхед, 1910-1913 гг.). Это фундаментальный труд по логике и философии математики, являющийся одним из самых влиятельных в истории. Три дня Питтс безотрывно поглощал 2 000 страниц этой научной работы, и в конце концов обнаружил несколько ошибок. Решив, что Бертрану Расселу необходимо о них узнать, мальчик написал математику подробное письмо с их указанием. Рассел не только ответил на сообщение мальчика, но и пригласил Питтса стать студентом магистратуры Кэмбриджского университета. Питтс, может быть, и согласился бы, да не мог — ему было лишь 12 лет на тот момент.

Но три года спустя, когда Рассел должен был нанести визит в Университет Чикаго, Питтс сбежал из дома и направился в Иллинойс. Больше он свою семью никогда не видел.

Пересечение двух судеб

В 1923 году, год спустя рождения Питтса, Уоррен МакКаллок как раз грыз гранит «Начал математики». На этом сходство между Питтсом и Уорреном заканчивается. МакКаллоку на тот момент исполнилось 25 лет, он был выходцем из образованной семьи юристов, врачей и инженеров и получил прекрасное образование — изучал математику в колледже Хэйверфорд в Пенсильвании, а затем философию и психологию в Йельском Университете. В 1923 году Уоррен готовился получить докторскую степень в области нейрофизиологии, в душе оставаясь философом. В то время пышным цветом распустилась теория психоанализа, но Уоррен не был её сторонником. Он был уверен, что все потайные уголки и загадки нашего сознания в основе своей имеют чисто механические связи между нейронами в мозге.

Невзирая на то, что судьбы МакКаллока и Питтса шли настолько разными путями, в итоге им было предначертано стать верными друзьями и коллегами до конца жизни. Вместе эти два человека создадут первую механистическую теорию сознания, первые математические модели нейрона, разработают компьютерную логику и станут основоположниками теории искусственного интеллекта. И всё же это история не только о плодотворном научном сотрудничестве. Это история о дружбе, хрупкости разума и беспомощности великой математической логики в нашем несовершенном жестоком мире.

Уоррен МакКаллок. Источник: nesfa.org

Странно выглядел этот альянс — МакКаллок и Питтс. МакКаллоку на момент знакомства с Питтсом было 42 года: уверенный в себе сероглазый бородач и полуночник, любитель покурить трубку, насладиться поэзией, философией и стаканом виски. Питтс — скромный невысокий восемнадцатилетний паренёк с высоким лбом, добавлявшим ему возраста, в очках, с пухлыми губами на квадратном лице. Познакомил их студент медицинского факультета Джером Леттвин. При первом же разговоре эти двое выяснили, что у них есть общий кумир: Готфрид Лейбниц.

Их обоих восхищала попытка философа XVII века создать азбуку человеческих мыслей, каждая буква которой соответствовала бы какой-либо концепции, что позволило бы оперировать ими так же, как числами.

МакКаллок в том разговоре рассказал Питтсу, что он пытался создать модель человеческого мозга, используя формальную логику Лейбница. Он был вдохновлён идеями «Начал математики», в которой вся математика сводилась к логике с помощью некоторого набора аксиом. Между аксиомами существовали отношения фундаментальных логических операций — конъюнкции («и»), дизъюнкции («или») или отрицания («не»). С помощью этих простейших операций создатели «Начал» и доказывали наиболее сложные теоремы современной математики.

МакКаллок же, читая этот труд, думал о нейронах. Он знал, что нейрон в мозге активируется только тогда, когда от близлежащих нейронов в синапс поступит достаточное количество сигналов. МакКаллок предположил, что нейроны действуют по бинарной схеме — они находятся либо во включенном состоянии, либо в выключенном.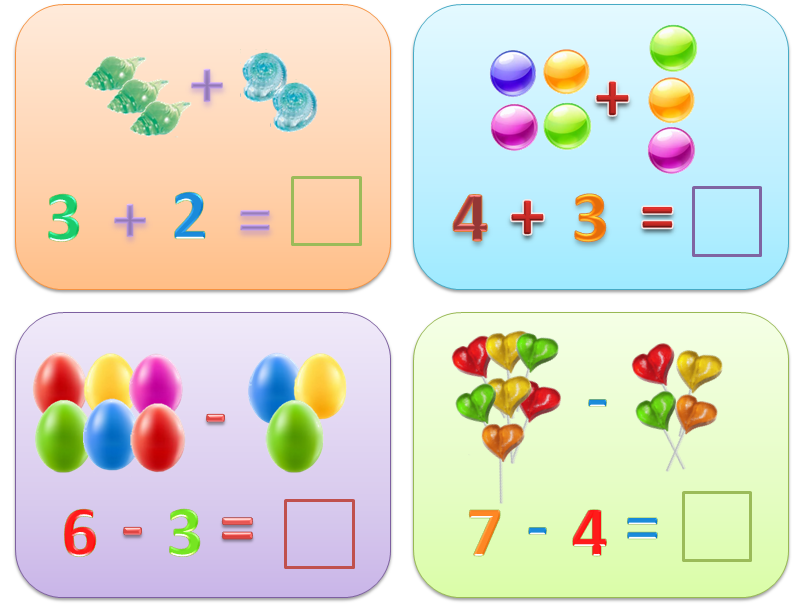 В этом смысле сигнал нейрона является аксиомой, а нейроны работают как логическая воронка — вбирая в себя несколько сигналов, а выпуская лишь один.

Схематическое изображение линейной воронки. Источник: wwwold.ecep.utep.edu

А потом вышло свежее исследование молодого британского математика Алана Тьюринга, которое доказывало, что машина способна произвести любые математические вычисления, и МакКаллок убедился в том, что наш мозг работает почти как машина Тьюринга, то есть использует логику нейросетей для произведения вычислений. Он полагал, что нейроны связаны друг с другом по законам формальной логики, и с помощью этих связей выстраиваются сложнейшие мыслительные цепочки.

Питтс сразу понял замысел МакКаллока и точно знал, какие математические инструменты использовать для доказательства этой гипотезы. В воодушевлении МакКаллок предложил юноше жить в своём загородном доме под Чикаго вместе со своей семьёй.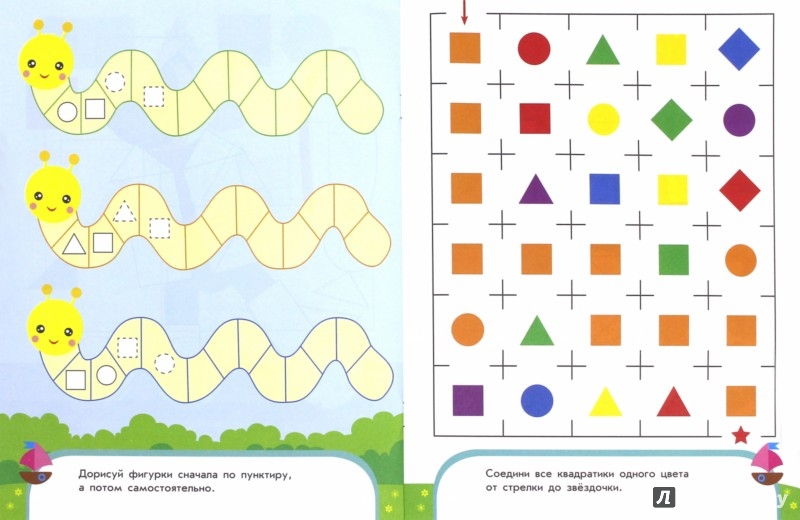 Это была типичная обитель творческой интеллигенции, где вечерами собирались представители разных её слоёв, обсуждали вопросы психологии, спорили о политике, читали стихи и слушали музыку на фонографе. А поздно ночью, когда жена и дети МакКаллока уже мирно спали, двое учёных, опустошая очередную бутылку виски, пытались создать компьютеризированную модель нейрона.

До знакомства с Питтсом МакКаллок никак не мог выбраться из исследовательского тупика: выходной сигнал последнего нейрона в цепи вполне мог становиться входным сигналом первого — нейронам ничто не мешало зацикливаться. У МакКаллока не было ни малейшего понятия. как смоделировать такую ситуацию математически. С точки зрения логики цикл имеет все признаки парадокса: следствие становится причиной и наоборот. МакКаллок каждой нейронной связи присваивал временную отметку: первый нейрон в цепочке активировался во время t, следующий — в t+1 и так далее. Но когда цепочка замыкалась, логика ломалась.

Питтс знал, как решить эту проблему. Он использовал модулярную арифметику, где значения в системе чисел повторяются после достижения определённого фиксированного модуля (так происходит с обозначением часов в сутках, например). Питтс показал своему другу, что в его вычислениях понятия «до» и «после» потеряли всякий смысл, поэтому временное значение стоит вовсе убрать из уравнения. Если вы видите молнию в небе, ваше зрение посылает сигнал в головной мозг, в нейронную цепь. Вы можете восстановить путь сигнала, начиная с любого нейрона в цепи, и определить длительность вспышки молнии. Это не работает, если нейронная цепь зациклена. В таком случае информация, в которой зашифрована вспышка молнии, просто бесконечно ходит по кругу. Она никак не связана с временным периодом, в который произошла эта вспышка. Эта информация становится «идеей в безвременье». Иными словами, памятью.

Отрывок из работы МакКаллока-Питтса «Логическое исчисление идей, относящихся к нервной активности». Источник: cse.buffalo. edu

Вычисления Питтса помогли друзьям получить механистическую модель мышления — первый аргумент в пользу того, что человеческий мозг является по сути процессором, обрабатывающим информацию. Объединяя простые бинарные нейроны в цепочки и циклы, учёные показали, что мозг может произвести любую возможную логическую операцию и произвести любые вычисления, доступные гипотетической машине Тьюринга. Это помогло понять, каким образом мозг осуществляет вычленение информации и строит из полученных элементов иерархические структуры — иными словами, каким образом происходит мышление.

Свои наблюдения МакКаллок и Питтс опубликовали в работе «Логическое исчисление идей, относящихся к нервной активности», опубликованной в 1943 г. Созданная ими модель работы мозга была слишком упрощена, чтобы быть биологически точной, но она блестяще доказывала основные принципы. По их догадке, мышление человека не может описываться мистическими обоснованиями Фрейда.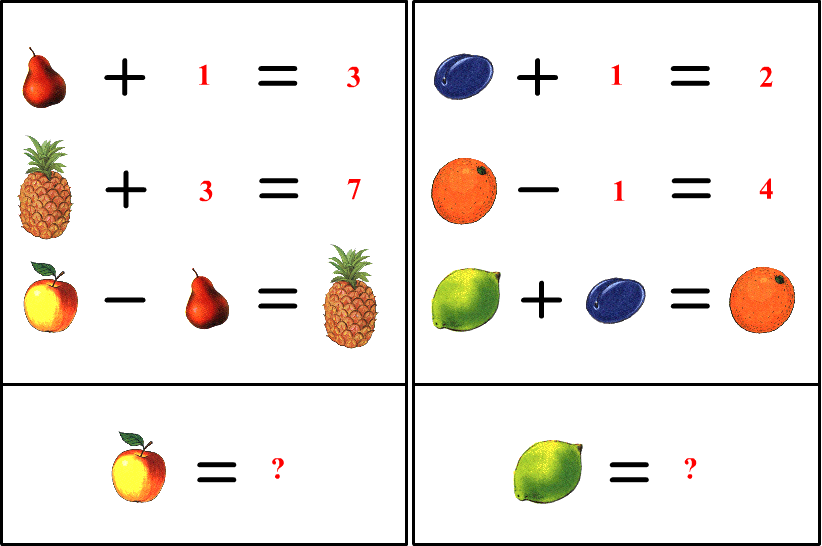 Вот что сказал МакКаллок своим студентам факультета философии:

Впервые в истории науки мы наконец знаем, как мы получаем знания.

Отношения с МакКаллоком стали для Питтса тем многим, чего ему не хватало в детстве — принятие интересов, дружба, интеллектуальное партнёрство. МакКаллок стал для Питтса отцом.

Великие амбиции

Вскоре Питтс познакомился с одним из ведущих интеллектуалов XX века, великим математиком и философом, основателем кибернетики Норбертом Винером. Встретились они в кабинете Винера в Массачусетском технологическом институте. Сами того не замечая, Винер и Питтс в ходе первой встречи убористо исписали две огромных учебных доски, висящих в кабинете — настолько они увлеклись сложным доказательством одной математической проблемы.

Винер предложил Питтсу получить докторскую степень по математике в МТИ. Это было против всех правил, поскольку Питтс не получил высшего образования. Но уже в 1943 г. Питтс стал студентом МТИ, где приступил к учёбе под наставничеством одного из самых влиятельных учёных мира.

Винер хотел, чтобы Питтс продолжил работу над созданием более реалистичной модели мозга. В продолжении таких исследований он видел будущую возможность использования нейросетей в робототехнике и будущем свершении киберреволюции. Он понимал, что для создания реалистичной модели мозга, состоящего из сотни миллиардов нейронов, необходимо иметь под рукой достаточный объём статистических данных. А уж в статистическом анализе и теории вероятностей Винер был силён как никто другой.

Норберт Винер в аудитории Массачусетского технологического института. Источник: norberwiener.umd.edu

Питтс начал свою работу с того, что понял один простой принцип: несмотря на то, что в генах человека зашифрована информация об основных свойствах нервной деятельности, они не могут предопределять развитие огромного количества синаптических связей в головном мозге. Поэтому возможно было начать с изучения случайно выбранных нейронных цепочек, в которых, скорее всего, и будет содержаться необходимая информация. С помощью статистической механики и процесса случайной модификации количества нейронных связей он собирался смоделировать процесс структурирования информации в мозге. Создание такой рабочей модели откроет путь к обучению машин.

В письме своему другу МакКаллоку в 1943 г. Питтс пишет:

[моя работа с Винером] станет первым компетентным обоснованием статистической механики в самом общем смысле и возможным её применением в выведении психологических принципов поведения человека из нейрофизиологических законов микромира… Разве не здорово?

Вскоре Питтс на конференции в Принстоне познакомился с легендарным Джоном фон Нейманом. Так постепенно сложилась первая научная группа кибернетиков: Винер, Питтс, МакКаллок, Леттвин (помните, тот студент, который познакомил МакКаллока с Питтсом?) и фон Нейман. И именно самоучка Питтс, некогда сбежавший из дома, был головным центром группы. Ни одна статья не публиковалась без согласия и правок Питтса. Леттвин вспоминает:

Он, без сомнений, был нашим гением. Он прекрасно разбирался в химии, физике, истории, ботанике… Его ответ на любой вопрос можно было записывать и выпускать в качестве учебника. В его восприятии мир представлялся чрезвычайно сложной и замысловатой структурой.

В 1945 г. фон Нейман начал работу над первым проектом отчёта о EDVAC, где было опубликовано описание логического устройства вычислительной машины с хранимой в памяти программой — та концепция, которая впоследствии стала известна как «архитектура фон Неймана».
EDVAC — это потомок культовой ЭВМ ЭНИАК, несовершенство которой быстро стало очевидным. ЭНИАК скорее вёл себя как гигантский электронный калькулятор, а не как компьютер. Для того, чтобы внести изменения в программу расчётов, необходим был утомительный процесс перекоммутации и длительная работа нескольких операторов по замене и сортировке перфокарт, а также по замене перегоревших ламп. После каждого перепрограммирования ЭНИАК как будто становился новым компьютером, и всю работу необходимо было начинать заново. Фон Нейман предположил, что избавление от необходимости перекоммутировать машину при перепрограммировании может значительно ускорить процесс обработки данных. Если бы компьютер мог запомнить свою конфигурацию, дело пошло бы гораздо быстрее. В этом и была идея EDVAC.

Джон фон Нейман рядом с компьютером IAS, прибл. 1950 г. Справа — обложка проекта отчёта по EDVAC. Источник: cacm.acm.org

В разработку проекта EDVAC фон Нейманом легли принципы работы нейросетей Питтса и МакКаллока. Только вместо нейронов использовались вакуумные трубки, игравшие роль логической воронки. В роли памяти компьютера выступали как раз циклы Питтса.

На Второй Конференции по кибернетике Питтс объявил, что он собирается написать докторскую диссертацию на основе построения трёхмерной модели нейросетей. Это стало одной из самых амбициозных математических задумок столетия. Но те, кто когда-либо работал с Питтсом, не сомневались, что он справится.

Резкое падение

Всё это время Питтс уже не жил в доме МакКаллока. Он квартировался на Бэйкон стрит в Бостоне вместе с другими студентами. И МакКаллок, и Питтс ощущали острую нехватку друг друга. Несмотря на научно-исследовательские успехи, Питтс пишет МакКаллоку:

Каждую неделю я испытываю острую тоску по нашим вечерам и ночным разговорам.

У Питтса в жизни был только один дом — дом МакКаллока. Без него он так и не научился чувствовать себя счастливым. МакКаллок испытывал примерно те же чувства без своего молодого друга и соратника.

В 1952 г. МакКаллоку предложили работу над новым проектом в Массачусетском технологическом институте, и он не раздумывая согласился променять свой уютный дом на обтрёпанную квартирку в Кембридже — ведь это означало совместную работу с Питтсом. Исследования проекта проводились на стыке теории информации, нейрофизиологии, статистической механики и компьютерных технологий — и с их помощью предполагалось понять, как в мозге человека зарождается мысль. Теперь Винер, Леттвин, МакКаллок и Питтс работали вместе в штаб-квартире на Вассар Стрит, 20.

Норберт Винер с супругой и незнакомцем. Источник: dl.tufts.edu

А потом разразился семейный скандал, связанный с супругой Винера. Маргарет Винер отличалась консервативными нравами, в отличие от супруги МакКаллока, которая с удовольствием принимала гостей в своём доме под Чикаго. Маргарет не переносила семьи МакКаллок, и известие о его переезде в Кембридж заставило её пойти на решительные меры. Она сообщила своему супругу, что несколько гостей МакКалока соблазнили их дочь Барбару, пока она гостила в их доме. Винер пришёл в ярость и порвал все связи с Питтсом и Леттвином:

Прошу сообщить [Питтсу и Леттвину], что я не желаю более иметь дела с вашими проектами. Пусть остаются вашей головной болью.

Для Питтса эта новость символизировала начало конца. Винер, который стал для него одним из первых наставников, изгнал его из своей жизни, не вступая в объяснения. Это стало не только большой эмоциональной потерей в жизни Питтса. Всё было гораздо хуже: это ещё раз подкосило такую хрупкую логику жестокого внешнего мира.

А потом произошла история с лягушками. В одном из подвалов лабораторий МТИ содержалась целая колония подопытных лягушек. В то время биологи полагали, что глаз работает подобно фотографической плёнке, регистрируя световые точки и планомерно посылая их к мозгу, где они и обрабатывались. Леттвин решил проверить эту гипотезу, вскрывая черепа лягушек и подсоединяя электроды к тканям зрительного нерва.

Питтс и Леттвин с подопытной участницей эксперимента. 1959 г. Источник: nautil.us

В компании с Питтсом, МакКаллоком и чилийским биологом Гумберто Матурана он подвергал лягушек различным опытам: зажигал и затенял свет, показывал цветные фотографии, запускал искусственных мух и регистрировал все сигналы, посылаемые от зрительного нерва лягушек в мозг. Ко всеобщему удивлению, глаз регистрировал вовсе не всё, что попадало в поле зрения, а фильтровал и анализировал информацию по контрасту, кривым и движению. В ставшей классической работе 1959 г. «Что говорит глаз лягушки мозгу лягушки» эта группа учёных напишет:

Глаз говорит с мозгом на языке, который уже обладает чертами высокой организации и интерпретации.

Это полностью сокрушило до этого стойкую картину мира Питтса. Вместо логичной чётко структурированной вычислительной работы головного мозга, понейронно обрабатывающего сигналы по законам формальной логики, получилось, что часть работы по интерпретации информации отдана хаотично организованной работе зрения. Как выяснилось, логика в нашем восприятии и обработке информации занимала отнюдь не центральное место.

Осознание этого факта привело Питтса к глубокой многолетней депрессии. Сам он писал о своих чувствах:

[моё состояние] разделят, пожалуй, все люди с избыточно развитой логикой, работающие в сфере прикладной математики. Этот пессимизм порождён собственной неспособностью более верить в принципы индукции или в принципы единства природы. Если никто не может доказать вероятную возможность того, что солнце завтра взойдёт, как же можно верить в то, что оно взойдёт?

Питтс ушёл в серьёзный хронический алкоголизм, отвернулся от друзей. Он отказался от получения докторской степени и сжёг свою диссертацию — уничтожил своими руками всё, над чем работал долгие годы, оставив своих коллег и последователей без ценнейшей научной информации.

Он всё ещё числился сотрудником МТИ, но в стенах университета его видели всё реже. Питтс так и остался двенадцатилетним мальчиком-изгоем. Только теперь он находил успокоение не в библиотеке, а в бутылке с алкоголем.

Вера в универсальность законов логики не позволила Питтсу создать практически применимую модель головного мозга, поэтому его работы остались в тени дальнейшего развития истории нейронауки. Питтс настолько полагался на незыблемость математических концепций, что не видел ограничений, которые они накладывают на реальный мир. Природа зачастую логике предпочитает непредсказуемость, и Питтс чувствовал себя обманутым. На этот раз его предали не близкие люди, а его главная жизненная опора — математика.

В 1969 году Питтс скончался в одиночестве от цирроза печени. Четыре месяца спустя ушёл из жизни и его главный друг, МакКаллок — как будто существование одного без другого представлялось этой хаотичной планете нелогичным.

• Как я не стал летчиком, а стал математиком

  Александр Кириллов

  О своем пути в математику, о первых поездках за рубеж, работе в США рассказал замечательный ученый, докт. физ.-мат. наук, профессор факультета математики Пенсильванского университета (США), главный научный сотрудник ИППИ РАН Александр Александрович Кириллов.

• Прорывы в математике плохо предсказуемы

  Сергей Ландо

  Сергей Ландо, докт. физ.-мат. наук, профессор факультета математики Высшей школы экономики, стоял у истоков возникновения факультета математики и исполнял обязанности декана с момента создания факультета в 2007 году до весны 2015 года. Людмила Сапченко расспросила Сергея Константиновича о его научной деятельности, о том, какое место занимают математические науки в современном мире, как создавался факультет, какие задачи ставятся перед факультетом в настоящее время.

• Джун Ху — математический гений, который поздно созрел, но всех одолел

  Теплым весенним утром Джун Ху шел в зал Макдоннелла Пристонского университета, где его ждали студенты. Однако он не был уверен, что идет в нужном направлении. Ху работает в элитарном Институте перспективных исследований, который располагается неподалеку от студгородка Принстона. Будучи сотрудником института, Ху не обязан преподавать. Тем не менее, он вызвался прочитать студентам продвинутый курс по коммутативной алгебре.

• Барьер сложности в современной математике

  В конце августа 2012 года японский математик Синичи Мочидзуки выложил на свою страницу в интернете четыре научные статьи. Их не сразу заметили, потому что не особенно ждали: без предварительных пресс-релизов, навязчивых анонсов и громких выступлений Мочидзуки опубликовал результат многолетнего самоотверженного труда, которому, вероятно, суждено совершить революцию в современной математике. Проблема лишь в том, что теорию Мочидзуки не торопится принимать научное сообщество – ее почти никто не может понять.

• Огюстен Луи Коши — человек и учёный

  Демьянов В. П.

  О продуктивности Коши-математика свидетельствует целый ряд терминов, определений и понятий, вошедших в науку, таких, как признак Коши, критерий Коши, задачи Коши, интеграл Коши, уравнения Коши–Римана и Коши–Ковалевской, относящиеся к разным разделам математического анализа, математической физики, теории чисел, и других дисциплин. Всего же он написал 700 работ (по другим источникам 800), с неимоверной легкостью переходя от одной области научного знания к другой.

• Михаил Бурцев: «Я решил заниматься наукой как хобби»

  Интервью о пути в науку, научной среде и популяризации науки с кандидатом физико-математических наук, заведующим Лабораторией нейроинтеллекта и нейроморфных систем НБИКС «Курчатовский Институт» Михаилом Бурцевым.

• Буквальная геометрия / The Discrete Charm of Geometry (2015)

  Это фильм в режиме включенного наблюдения, история о реальном исследовании, которое проводится в научно-исследовательском центре «Дискретизация в геометрии и динамике» Технического университета в Берлине. В центр постоянно приезжают математики русского происхождения, работающие по всему миру. Процесс ведения научных дискуссий, запечатленный на камеру, является уникальным по силе воздействия материалом: зритель становится свидетелем размышлений ученых, возникновения гениальных идей, погружается в работу команды и разделяет весь спектр эмоций участников.

• Математика и безумие: история Джона Нэша

  Американский математик, который внёс значительный вклад в теорию игр, более 30 лет страдал от тяжёлого психического расстройства. Каково это — быть гениальным сумасшедшим?

• Математические деформации Мариам Мирзахани

  Математика — это не только замечательная точная наука, но еще и удивительные человеческие судьбы. Девушка из Ирана по имени Мариам Мирзахани стала первой в мире женщиной, получившей Филдсовскую медаль — пожалуй, самую престижную награду в математике. Мариам показала как иранским ученым, так и простым людям, в частности женщинам, — чего может добиться человек собственным умом и собственной настойчивостью.

• Бесконечность / Infinity (1996)

  Фильм расскажет о молодости знаменитого американского физика-ядерщика Ричарда Фейнмана, о его первой любви, о его участии в создании атомной бомбы. В основе картины лежат две автобиографические книги ученого.

Далее >>>

Как научить себя математике

Немногие предметы вызывают столько воспоминания о боли и беспокойстве, как уроки математики. Сбивающие с толку символы, сложные процедуры и страшные графики и диаграммы.

Кое-кто теперь даже предполагает, что изучение математики может быть травмирующим опытом, чем-то выжившим, а не выученным.

Болезненная история многих людей с математикой — это позор, потому что математика невероятно полезна. Многие из лучших профессий выходят из областей STEM и полагаются на понимание математики. Понимание новостей и событий в мире все больше становится уроком статистики. Наконец, правильно понятая математика позволяет вам решать многие из ваших собственных проблем.

В этой статье я хотел бы объяснить, как вы можете самостоятельно изучить любую математику, будь то статистика, алгебра или алгоритмы.

Шаг первый: начните с объяснения

Первый шаг к изучению любой математики — получить предварительное объяснение темы.

Эту информацию можно получить во многих местах. Вот несколько хороших ресурсов, охватывающих широкий спектр тем:

• KhanAcademy — огромный бесплатный ресурс видео практически по всем темам математики
• MIT OCW — они начинаются на университетском уровне, но они решают много сложной математики
• Coursera — множество полных уроков по математике

Кроме того, существуют и специализированные ресурсы. Они, как правило, не охватывают все мыслимые темы, но часто более интересны, интуитивны и полезны для тех, кто ими занимается:

• BetterExplained — отличные статьи, дающие интуитивное представление об исчислении, алгебре, экспонентах и ​​многом другом
• 3Blue1Brown — отличные видеоролики на YouTube, подробно изучающие математические концепции
• Numberphile – Беседы с математиками на интересные математические темы

Где бы вы ни получили свое объяснение, ваш первый шаг — посмотреть его один раз, чтобы почувствовать, что вы понимаете основы того, как оно работает.

Что делать, если я не понимаю объяснение?

Если вы посмотрели объяснение, но не поняли его, возможны две проблемы:

1. Вам не хватает некоторых предпосылок для понимания этой части математики . Это означает, что вам нужно сделать резервную копию и пройти ее снова. Если вам кажется, что все «пошло слишком быстро» или вы не понимаете, что делает учитель, возможно, вам придется вернуться на несколько уроков назад и лучше выучить их, прежде чем продолжить.
2. Вы пытаетесь охватить слишком много без практики . Хороший способ — посмотреть кусок объяснения, а затем попробовать самому. Если вы только смотрите, но никогда не тренируетесь, это немного похоже на просмотр видео о катании на лыжах и никогда не катание по склонам. В конце концов объяснения перестанут иметь смысл, потому что у вас не будет личного опыта.

Попробуйте следующее: просмотрите объяснение один раз полностью в качестве отправной точки.

Шаг второй: Решайте задачи

Математика — это не то, что вы смотрите и запоминаете, а то, что вы делаете.

Если вы тратите все свое время на просмотр видео, а затем получаете набор задач, вам может быть очень трудно применить свои математические знания. Это может привести к ощущению, что вы «плохо разбираетесь в математике», хотя проблема лишь в том, что вы используете паршивый метод ее изучения.

Вы можете исправить это, приступив к решению проблем как можно скорее. Хорошая задача должна казаться сложной, но не невозможной. Если вы видите решение и даже не понимаете, как они его получили, скорее всего, вы слишком торопитесь — вернитесь и изучите некоторые основы, прежде чем двигаться дальше.

Что делать, если у меня нет проблем, которые нужно решать?

Если у вас нет предложенных задач, вы можете сделать несколько вещей:

• Решить задачи, указанные в объяснении, но не глядя на ответ.
• Создайте свои собственные проблемы и попытайтесь их решить.
• Попробуйте доказать понятия в классе. Это продвинутая техника, но она необходима для того, чтобы по-настоящему понять более сложную математику.

Попробуйте следующее: после просмотра объяснения выполните достаточное количество задач, чтобы чувствовать себя комфортно и понимать процедуру.

Шаг третий: поймите, почему математика работает

Интуитивное понимание очень важно для математики, в отличие от других предметов. Хотя интуиция для словарного запаса слов на иностранном языке может помочь, их все равно нужно запоминать. Однако заучивание математики может быть опасным, если оно заставляет вас учить ее без понимания.

Следующий шаг — убедить себя, что вы знаете, почему математика работает. Моя любимая техника для этого — Техника Фейнмана, которую я демонстрирую здесь:

Техника Фейнмана требует некоторого времени, поэтому вам не нужно полностью применять ее к каждому аспекту каждой математической задачи, с которой вы сталкиваетесь. Скорее применяйте его выборочно к наиболее важным понятиям и тем, которые кажутся вам запутанными, несмотря на достаточную практику.

Попробуйте следующее: определите основные понятия математики, которые вы изучаете, и используйте метод Фейнмана, чтобы убедить себя, что вы их понимаете.

Шаг четвертый: играйте с математикой

Практика — это хорошо, лучше понимать, но лучше всего играть с математикой.

После того, как вы решили некоторые заданные вам вопросы и убедились, что понимаете их, естественным продолжением этого будет попытка поиграть с математикой, которую вам дали. Как все меняется, когда вы пытаетесь изменить числа или применить их к другим задачам?

Допустим, вы только недавно научились рассчитывать сложные проценты. Вы можете выполнять простые расчеты процентов самостоятельно, и вы понимаете, почему они работают. Как вы могли играть с этой математикой?

• Вы могли видеть, что происходит по мере увеличения скорости начисления процентов.
• Что произойдет, если проценты будут отрицательными?
• Вы можете попытаться подсчитать собственные сбережения, если инвестируете их по разным ставкам.
• Попробуйте представить, сколько процентов по ипотеке вы платите по сравнению с основной суммой.

Excel — это хороший способ поэкспериментировать с математикой, так как вы можете вводить формулы напрямую, без необходимости выполнять алгебраические операции или повторять вычисления.

Попробуйте следующее: возьмите тему математики, которую вы недавно изучали, и посмотрите, как вы можете изменить переменные, применить их к разным вещам и изменить формулы.

Шаг пятый: применение математики вне класса

В конечном счете, целью изучения математики должно быть ее использование, а не просто сдача теста. Однако для этого вам нужно освободить свое понимание от примеров из учебника и применить его к реальным ситуациям.

Это сложнее, чем просто решить проблему. Когда вы решите проблему, вы начнете запоминать схему решения. Это часто позволяет вам решать проблемы без реального понимания принципов их работы.

Применение математики в реальной жизни, напротив, требует осознания ситуации, перевода ее в математику и решения созданной вами проблемы. Это сложнее, чем решать проблемы, поэтому, если вы хотите действительно использовать то, чему научились, вам нужно практиковаться.

Попробуйте следующее: возьмите тему, которую вы недавно изучали по математике, и попытайтесь найти реальную ситуацию, в которой вы могли бы вычислить ее, используя свои собственные числа или оценки, если они недоступны.

Похоже, это слишком много работы!

Выполнение всех этих пяти шагов по каждой теме, которую вы изучаете по математике, займет много времени. Это нормально, вам не нужно делать это для каждой мелочи, которую вам нужно выучить.

Вместо этого думайте об этом как о индикаторе выполнения. Каждое математическое понятие, которое вы изучаете, может проходить с первого по пятый этапы, углубляя ваши знания и увеличивая полезность математики каждый раз. Некоторые концепции будут достаточно важными, чтобы вы захотели их тщательно применить. Другие будут достаточно редкими, чтобы просто смотреть объяснения — это все время, которое вы можете сэкономить.

В частности, постарайтесь сосредоточиться на наиболее важных концепциях каждой идеи. Математика имеет тенденцию быть глубокой, поэтому часто в классе полного семестра может быть только несколько действительно больших идей, а все остальные идеи являются просто различными проявлениями этой базовой концепции.

Большинство курсов по математическому анализу для первого года обучения, например, сосредоточены на понятии производной, а все, что преподается, представляет собой просто различные расширения и приложения этой основной идеи. Если вы действительно понимаете, что такое дериватив и как он работает, вам будет намного легче выучить другие части.

Мои 9 шагов к самообучению

Если бы вы могли понимать простой английский и иметь доступ к Интернету, то вы определенно могли бы изучать математику самостоятельно .

После того, как вы выполните все в этом руководстве, вы узнаете, что никто не может научить вас быстрее и лучше, чем вы сами. (Особенно, если вы используете Anki!)

Небольшое предупреждение: хотя я сказал любой может это сделать, я на 100% уверен не каждый будет.

На самом деле это немного неудобно, особенно если вы делаете это впервые. (Но это очень полезно.)

В этом посте вы узнаете именно о 9-шаговом подходе, который я использовал, чтобы изучать математику, не полагаясь на кого-то, кто научил бы меня.

• Образ мышления №1, который многие упускают из виду при самостоятельном изучении математики
• Лучшие ресурсы для самостоятельного изучения математики
• Как вывести свои математические навыки на новый уровень

Приступим.

Можете ли вы действительно самостоятельно заниматься математикой?

Прежде всего, если вы думаете, что вы не «математик» (как, черт возьми, вообще выглядит математик), вы можете подумать, что вам нужен кто-то еще, чтобы учить вас математике в классе.

Но позвольте мне сказать вам вот что…

Со всеми доступными бесплатными материалами в Интернете — лекциями, программами, электронными книгами и МООК — вы, безусловно, можете легко изучать математику самостоятельно, как если бы вы учились в колледже.

Лучшая часть, вы делаете это в своем собственном темпе .

Никаких строгих графиков, только самоотверженность.

Однако вы должны думать об этом по-другому, если хотите пожинать плоды.

То есть признать , что умственные усилия, которые вы тратите на изучение математической темы, являются ценой, которую вы платите за то, чтобы упростить будущие математические навыки .

Или, точнее, это цена, которую вы платите за то, чтобы не усложнять себе обучение в будущем.

Математика это все о совокупное знание , знаете ли.

В отличие от школы, вы будете чувствовать себя паршиво, потому что вы не меняете темы в зависимости от времени — теперь вы меняете темы в зависимости от того, насколько быстро вы освоите навык .

Итак, вот руководство о том, как это сделать.

9 шагов к самостоятельному изучению математики

Я прерву вас на некоторое время, чтобы прояснить ситуацию: я создал это руководство, чтобы помочь людям, которые чувствуют, что отстают в своих математических знаниях и хотят просмотрите его, или люди, которые по какой-то причине просто хотят изучать математику самостоятельно.

Каждый пример, который я вам приведу, — это просто пример, который поможет вам понять то, что я пытаюсь донести. Вы все еще должны применить эти шаги к своей ситуации.

Шаг 1. Сначала определите, где вы хотите закончить

Математика строится сама на себе, поэтому, если вы хотите изучить какой-либо предмет, скажем, исчисление, всегда спрашивайте:

Какие предметы являются обязательными для изучения этого предмета?

В своем собственном исследовании я часто задаю себе вопросы, основанные на «навыках», а не на актуальные вопросы.

«Какие навыки мне нужно освоить, чтобы стать лучше в этом?»

В конце концов, решение проблем — это навык. Вы не сможете лучше решать проблемы, если у вас нет инструментов; индивидуальное освоение обязательных тем.

Что подводит меня к следующему пункту.

Шаг 2. Определите, с чего начать, очевидно

Теперь, когда вы определили конечную тему, пришло время решить, с какой общей темы начать.

Например, исчисление и его приложения станут проще, если у вас есть знания в области аналитической геометрии и тригонометрии.

Но в аналитическую геометрию включены некоторые элементы тригонометрии.

Итак, вы можете начать с тригонометрии.

Однако, если вы не знаете, «что является предварительным условием для чего», я настоятельно рекомендую вам найти онлайн-учебную программу.

Вот одна хорошая дорожная карта для тех, кто изучает математику для науки о данных.

Шаг 3. Найдите учебный план, чтобы избежать ненужной глубины

Если вы заблудились, вы идете на Google Maps.

Так что же делать, если у вас нет дорожной карты или последовательности изучения математики?

Используйте уже разработанную программу обучения. Они станут дорожной картой к вашему успеху в самообучении.

Как я уже упоминал ранее, их можно легко найти в Интернете.

Я имею в виду, что всего один поиск Google даст вам то, что вы ищете.

Или вы можете просто просмотреть ресурсы своего университета и проверить учебные планы по предметам по математике.

Шаг 4. Соберите свои справочные материалы, руководства по решению и книги типа «Решенные задачи»

Обычное обучение математике требует, чтобы вы ходили в школу, посещали занятия, выполняли домашнюю работу, а затем ждали проверки, прежде чем закончить петля обратной связи.

Я говорю, что это очень неэффективно.

Когда доступны руководства по решениям или книги типа «Решаемые проблемы», лучше использовать их одновременно с вашей собственной процедурой решения проблем.

Для этой, , мне нравится серия книг «Очерки Шаума».

Задачи довольно сложные, обсуждения краткие и прямолинейные, но вы, безусловно, ЛЕГКО научитесь решать проблемы.

Просто для ясности: я не говорю, что вы должны смотреть на решения каждый раз, когда решаете проблему, но всякий раз, когда вы застряли, вы можете легко выйти и на самом деле быстрее узнать решения.

Эта узкая петля обратной связи позволит нам изучать математику БЫСТРО и в СОБСТВЕННОМ темпе.

«Что делать, если я не понимаю материал?»

Либо вы не освоили предварительные условия (или вообще не освоили), либо используете слишком сложную книгу.

Наконец, здравый смысл подсказывает, что это руководство не является «самостоятельным изучением математики». Вы всегда можете проконсультироваться с другими, когда вы действительно застряли, даже если у вас есть руководство по решению (возможно, в нем есть опечатка или что-то в этом роде).

Шаг 5.

Расставьте приоритеты в углубленном, основанном на концепциях обучении

Это вытекает из пункта, поднятого выше, который заключается в использовании руководств по решениям для изучения математики, чтобы создать быструю петлю обратной связи.

Однако некоторые ученики неправильно его понимают.

Им кажется, что если они могут запомнить, как решается сложная проблема, то это хорошо.

БОЛЬШАЯ ошибка запоминать то, чего не понимаешь.

Соответственно, это тоже БОЛЬШАЯ ошибка просто что-то понимать, но не практиковать.

Узнайте, ПОЧЕМУ шаги работают, потому что если вы сделаете это, вы узнаете один раз и решите многие.

Шаг 6. Разместите ссылки на ресурсы в одном месте

Поскольку вы собираетесь в основном заниматься самообучением, используя цифровые ресурсы, удобно иметь их все в одном месте.

Возможно, сделайте их главной страницей вашего браузера.

Сделать ярлык или что-то в этом роде.

Дело в том, что вам НАСТОЛЬКО легко получить доступ к вашим ресурсам, чтобы вы не чувствовали трения, когда хотите учиться самостоятельно.

Это облегчает формирование ваших привычек к учебе, что всегда лучше в долгосрочной перспективе.

Шаг 7. Выделите время ОБА на изучение и решение проблем

Как я уже упоминал ранее, простого понимания недостаточно.

Вы должны практиковать то, чему научились.

Точно так же, как новичок не может сыграть шедевр на фортепиано сразу же после того, как кто-то хороший научит его этому, изучение новых вещей в математике не происходит в моменты «ага».

Обучение происходит, когда вы вспоминаете информацию из своей головы, а не когда пытаетесь что-то туда поместить.

Так что, помимо вашего «увлекательного» времени, выделите время для практики.

Шаг 8. Развивайте глубокую работу

Во время практики важно, чтобы вы не отвлекались.

Работа без внутренних и внешних отвлекающих факторов и преднамеренное сосредоточение на поставленной задаче, известная как «глубокая работа», улучшает совместную работу ваших нейронов при активации.

Это происходит из-за того, что оболочка, называемая миелиновой , формируется всякий раз, когда вы извлекаете часть информации или отрабатываете навык.

Когда ваше внимание направлено на решение задач, вы эффективно сообщаете своему мозгу, что ТОЛЬКО те нейроны, которые активируются во время решения задач, должны быть покрыты миелином.

Однако, когда вы отвлекаетесь, это явление происходит плохо, и обучающие фрагменты формируются не очень хорошо.

Шаг 9. Избегайте фразы «Практика, практика и еще раз практика», вместо этого делайте это

Это, вероятно, самый распространенный совет, который дают учащимся, которые спрашивают: «Как мне улучшить свои знания по математике?».

Нам не нужно больше времени на практику. Нам просто нужно потренироваться лучше .

Практика, безусловно, жизненно необходима, но есть два вида практики: Непродуктивная и Продуктивная Практика.

Если вы делаете все в течение длительного периода времени, нечасто в течение недели и просто повторяете одну и ту же проблему несколько раз, пока не «получите ее», прежде чем переходить к следующей, то это непродуктивная практика.

Продуктивная практика — это разумная практика.

Вот как это сделать. Два простых шага.

• Распространяйте свою практику на весь день и на неделю
• Когда вы получите основную идею концепции, не отвечайте на несколько задач одним и тем же решением; несколько ответов, несвязанных задач, не отсортированных по темам. (это называется чередующаяся практика )

Делая это, вы экономите ТОННУ времени и энергии на изучение математики.

Один из простых способов автоматизировать это — использовать Anki , но вам придется проявить немного творчества при создании колод и настроек.

В частности, как я рассказал в курсе по лучшему решению, вы можете создать «основную колоду» и «колоду упражнений/основной набор задач», используя определенные настройки колоды в зависимости от вашего уровня уверенности. (Более уверенно = более высокие интервалы)

Кто сказал, что изучение математики должно быть утомительным и занимать много времени? Это может быть эффективно, но, как я уже сказал… это должно быть более утомительно для ума.

Дополнительные ресурсы для самостоятельного изучения математики

Устали от бесконечного повторения сотен практических вопросов и получения дерьмовых оценок?

Вы не знаете, что делать, когда сталкиваетесь с совершенно новой проблемой?

Возможно, вы тренируетесь неправильно.

Узнайте больше о разнице между правильным и неправильным подходом к практике в Лучшее решение с Anki: получите отличные оценки по предметам решения задач (без бесконечного шлифования) . (Полное раскрытие: это мой собственный курс). Когда я начал свое путешествие по обучению металу, он был моим помощником. В конце концов, он закончил 4-летний курс информатики в Массачусетском технологическом институте всего за 12 месяцев. Я очень уважаю людей, которые делятся методами, основанными на их опыте.