Математика решить задачу 3 класс: Задачи по математике 4 класс

Составь и реши две задачи, обратные данной. ГДЗ по математике 3 класс Моро Часть 1 Порядок выполнения действий стр 27 задание 4 – Рамблер/класс

Составь и реши две задачи, обратные данной. ГДЗ по математике 3 класс Моро Часть 1 Порядок выполнения действий стр 27 задание 4 – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания “Останкино”?

Доброй ночи всем.

Вот подрядился помогать детям с домашкой…и застрял на вопросе:
Сшили 4 плаща, расходуя на каждый по 3 м ткани.Поставь вопрос и реши задачу. Составь и реши две задачи, обратные данной.
 Поможете?

ответы

Конечно! Мы недавно подобную решали)
4 • 3 = 12 м. Ответ: 12 м.
На 4 одинаковых плаща потратили 12 м ткани. Сколько ткани потратили на каждый плащ?
12 : 4 = 3 м.
Ответ: 3 м.
На несколько одинаковых плащей потратили 12 м ткани. Сколько сшили плащей, если на один расходуется 3 м ткани?
12 : 3 = 4 (шт.).
Ответ: 4 плаща

1) 4*3=12 (м) 
ответ:12 м ткани нужно использовать на 4 плаща
2) 12:3=4 (п)
ответ:4 плаща можно использовать за 12 м ткани 
3) 12:4=3 (м)
ответ:за 3 м можно сшить один плащ

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

5 класс

Репетитор

Химия

Алгебра

похожие вопросы 5

Решим задачу. Часть 1 Стр 12 задание 6 ГДЗ по математике 3 класс Моро

Доброй ночи, подскажите решение:
1.  Коля на 5 лет моложе Димы, но на 4 года старше Ани. На сколько лет Дима старше Ани?
2) (Подробнее…)

ЕГЭ3 классМатематикаМоро М.И.

Васильевых. 50 вариантов ответов по русскому языку. Вариант 31 ч.2 Задание 10

В приведённых ниже предложениях из прочитанного текста пронумерованы все запятые. Выпишите цифры, обозначающие запятые при вводной (Подробнее…)

ГДЗОГЭ9 класс

ЕГЭ Математика 11 класс. Ященко И. В. Тренировочная работа 15 Вопрос 9 . Какова вероятность того, что оба синих носка окажутся в одной кучке?

Привет. Выручайте с ответом по математике…
В ящике комода лежит 13 пар носков, из них одна пара синяя, а остальные чёрные. В (Подробнее…)

ЕГЭМатематикаЯщенко И.В.Семенов А.В.11 класс

ЕГЭ Математика 11 класс. Ященко И. В. Тренировочная работа 15 Вопрос 10 Найдите вероятность того, что в течение года перегорит ровно одна лампа.

Привет всем! Нужен ваш совет, как отвечать…
Помещение освещается фонарём с двумя лампами. Вероятность перегорания одной лампы в (Подробнее…)

ЕГЭМатематикаЯщенко И.В.Семенов А.В.11 класс

Вычислите № 317 ГДЗ Математика 4 класс Моро М.И.

88:44∙ 27            10 375 − (8 003 − 567)             25∙8∙0
99:33∙ 18            35 008 − (12 049 + 765)         9 :1 −9 (Подробнее…)

ГДЗМатематика4 классМоро М.И.

Почему я учу студентов нескольким стратегиям решения математических задач

Я большой сторонник обучения студентов нескольким стратегиям решения задач и предоставления студентам возможности выбрать лучшую стратегию, которая им подходит. Мне нравится, когда студенты могут взять на себя ответственность за определенный способ решения проблемы и добиться успеха. Они действительно понимают, почему это работает, и затем могут применить его к множеству других проблем.

Квалифицированные математические мыслители имеют в своем наборе инструментов множество стратегий решения задач и могут быстро и эффективно обращаться к ним. Они понимают, что одна и та же стратегия не работает для всех проблем, и способны применять лучшую, наиболее эффективную стратегию для каждой решаемой проблемы практически без усилий или даже не задумываясь об этом.

Я хочу, чтобы все мои ученики стали опытными математическими мыслителями и считали, что хорошо разбираются в математике .

Когда я учился в школе, я помню, как учительница писала, как решить задачу, и мы записывали, как она это делала, в свои тетради. Мы должны были скопировать в точности как она решила задачу и применить это ко всем задачам на странице наших учебников по математике. Вы помните, что вас так учили? В общем, был только один правильный путь  для решения проблемы. Интересно, как многого я упускал из-за того, что меня учили только одним способом. Я хорошо учился по математике, но мне она никогда не нравилась. Это было скучно, обыденно, и мы делали одно и то же каждый день.

Перенесемся к моим первым годам преподавания. Я стал заниматься профессиональным развитием, которое научило меня различным способам решения многозначных задач на сложение и вычитание, а также работе с дробями.

Моим глазам открылся совершенно новый мир. Я обнаружил, что хорошо разбираюсь в математике. Изучив несколько ключевых основополагающих идей, я обнаружил, что могу подойти к сложной проблеме и обдумать ее, выяснив свой собственный способ ее решения. Я любил математику. Именно этого я хочу для своих учеников.

Всякий раз, когда я размещаю эту фотографию на Facebook, она всегда привлекает массу внимания, как положительного, так и отрицательного. Я получаю «почему бы вам просто не научить их, как добавлять» комментариев, «какая классная идея» комментариев и все, что между ними.

Мне нравится использовать его, чтобы начать разговор об обучении нескольким стратегиям решения проблем. Это такой яркий пример того, как использовать 10 для решения фактов сложения.

Вы видите, что обучение студентов тому, как решать проблемы, используя различные стратегии, не является новой идеей. Помните новая математика в 80-х и начале 90-х? Это было оно. Это повторилось и в начале 2000-х. Учителя уже давно обучают стратегиям решения математических задач.

Однако Common Core и многие государственные стандарты теперь сделали его более явным и фактически поощряют использование нескольких стратегий до обучения традиционному алгоритму. С новыми стандартами и профессиональным развитием идея обучения нескольким стратегиям снова вышла на первый план.

Следует ли обучать традиционному алгоритму? Да. Но прежде чем его отдать учащимся, им нужно понять, почему работает ярлык традиционных алгоритмов и что делать, если он не работает (например, выяснить свою ошибку!).

Все дело в вычислениях в уме. Большинство из нас делают это автоматически в продуктовом магазине, когда выясняют, сколько мы хотим потратить. Хотя мы можем достать наш iPhone, зачастую быстрее сделать это в уме. В следующий раз, когда вы решите задачу на сложение в уме, подумайте, как вы решите проблему . Вы делаете десятку или округляете до следующего дружеского числа? Вы оцениваете? Вы удваиваете или делите число пополам? Как вы решаете проблему?

Держу пари, вы используете какую-то стратегию, которую либо изобрели сами, либо которой вас научили. Вы, вероятно, не думаете о традиционном алгоритме (хотя вы могли бы думать, если это все, чему вас учили).

[clickToTweet tweet=”Я хочу, чтобы все мои ученики стали квалифицированными математическими мыслителями, которые считают, что они хороши в математике” цитата=”Я хочу, чтобы все мои ученики стали квалифицированными математическими мыслителями, которые считают, что они хороши в математике.”]

Обучение студентов различным стратегиям помогает им переходить от бумажных и карандашных вычислений к вычислениям в уме. Большинство математических задач можно решить в уме, даже самые сложные, если мы сможем удержать в голове все числа. Студенты найдут стратегии, которые работают для них. Нам просто нужно обучить нескольким стратегиям, чтобы студенты могли найти те, которые им подходят.

Это приводит меня к . . .

В идеале мы хотим, чтобы учащиеся обладали гибким математическим мышлением. Мы хотим, чтобы они хорошо разбирались в математике и были уверены в своих способностях к «делать» математика. Для этого я учу студентов различным способам решения задач в надежде, что один из способов найдет отклик у каждого ученика.

Студенты находятся на разных этапах своего математического пути. Один из лучших инструментов, которые я видел для объяснения этого путешествия, — это Contexts for Learning. Ландшафт для обучения описывает пути, по которым учащиеся могут понять сложение и вычитание, а также умножение и деление. Каждый путь отличается, но есть тенденции, которые происходят.

В этих документах есть много слов, которые вам, возможно, придется поискать, но идея, которую я хочу подчеркнуть, заключается в том, что учащиеся постоянно находят новые способы решения проблем. Их математическое мышление не стоит на месте, а плавно перемещается по разным уровням по мере того, как они сталкиваются со все новыми и новыми проблемами. Обучение учащихся различным стратегиям решения проблем помогает им увидеть новые, более эффективные стратегии, которые могут им понравиться.

Мы хотим, чтобы учащиеся решали задачи правильно и эффективно. Обучение различным стратегиям поможет им увидеть разные способы решения проблем, и учащиеся будут тяготеть к тому способу, который лучше всего подходит для их текущей ситуации. Наша задача — подтолкнуть их немного дальше и стать более и более эффективными математическими мыслителями.

Это похоже на предыдущую идею в том смысле, что я хочу, чтобы учащиеся нашли стратегии, которые работают для них, но я также хочу подтолкнуть их к экспериментам и поиску новых стратегий, которые им могут быть просто недоступны.

В сообщениях моего блога, посвященных различным моделям и стратегиям сложения и вычитания двузначных чисел, я более подробно рассказываю о различных стратегиях сложения двузначных чисел. Эти стратегии способствуют обучению учащихся, чтобы они могли переходить от сложения однозначных чисел к сложению многозначных чисел и глубоко понимать, что происходит со значением разряда при сложении и вычитании.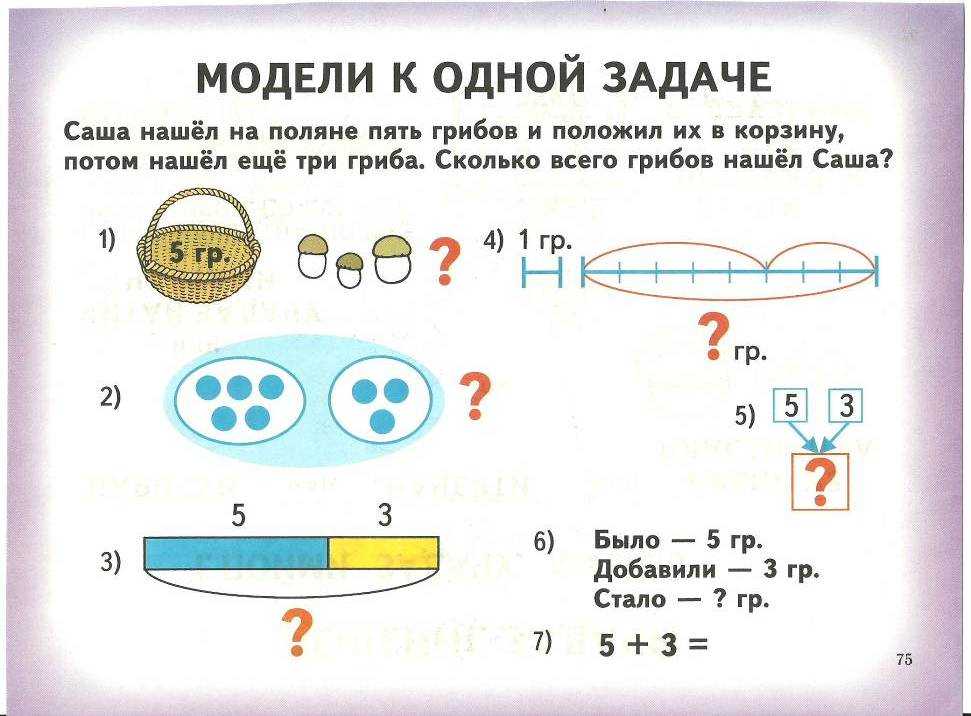

Теперь есть тонкая грань между обучением строительным лесам и предоставлением костылей. Ключевым моментом всегда является поощрение студентов попробовать что-то, что находится за пределами их уровня комфорта, который называется их зоной ближайшего развития. Мы всегда хотим подтолкнуть наших студентов сделать еще один шаг вперед, не слишком сильно, но ровно настолько, чтобы это побуждало их учиться больше.

У вас есть ученики, которые просто не любят математику? Те, кто не думают, что они хороши в математике? Это был я в детстве.

У меня не было мотивации заниматься математикой, потому что это было скучно. Однако я обнаружил, что, обучая студентов различным подходам к решению проблем, а затем немного отступая, мои ученики погружаются в проблемы и начинают исследовать их. Они гораздо более мотивированы работать во время занятий математикой, чем я когда-либо рос. Я дал учащимся точки входа в проблему и позволил им подойти к ней на своем уровне, используя базовые навыки, которые они знают и понимают.

Я дал учащимся возможность заниматься математикой, потому что я научил их различным стратегиям, которые можно добавить в их наборы инструментов.

Я обучаю множеству стратегий решения математических задач, потому что это:

• объясняет, что происходит у нас в голове
• помогает учащимся выбрать наиболее эффективную стратегию процесс
• мотивирует студентов хотеть узнать больше.

А ты? Обучаете ли вы студентов нескольким стратегиям решения математических задач? Мне бы хотелось услышать ваше мнение по этой теме в комментариях ниже.

---

Посмотрите ресурсы, которые я использую в своем классе, чтобы научить учащихся различным стратегиям решения математических задач. Нажмите на изображение, чтобы получить БЕСПЛАТНЫЙ образец этих ресурсов.
Двузначное сложение и вычитание?

Как решать задачи со словами

По мере того, как ваш ребенок будет учиться в школе, он столкнется с несколькими камнями преткновения. Есть некоторые проблемы, которые трудно понять многим учащимся. Наиболее распространенная проблема связана с текстовыми задачами. Студенты изо всех сил пытаются увидеть математику за словами.

 

 

 

Проверенный пошаговый метод решения текстовых задач на самом деле довольно прост.

• Прочтите задачу вслух про себя
• Нарисуй картинку
• Подумайте: «Что мне нужно найти?»
• Список того, что дается
• Найдите ключевые слова
• Решить
• Проверьте свою работу

Давайте применим эти шаги на практике. Рассмотрим задачу со словами ниже.

Пример: Кевин любит читать. Ему нравятся разные книги. У него 3 больших книжных шкафа, в каждом по 9 книг.полки на нем все заполнены его книгами. Если на каждой полке может поместиться 16 книг, сколько книг у Кевина?

Прочтите задачу вслух

Дети склонны торопиться с каждой задачей. Это связано с ограничениями по времени на классные работы и тесты. Если ваш ребенок не знает, о чем спрашивает проблема, то он не может ее решить. Когда ваш ребенок читает задачу вслух, он говорит и слышит задачу. Они могут сформировать в голове более четкую картину проблемы и более подготовлены к ее решению.

Нарисуй картинку

Учащиеся, особенно младшие школьники, должны визуализировать задачу, чтобы понять ее. Когда они становятся старше, они могут начать визуализировать в своей голове, но в юном возрасте они должны рисовать картинку, которая объясняет им, в чем проблема. Картина должна учитывать все аспекты проблемы.

Спросите: «Что мне нужно найти?»

Некоторые текстовые задачи прямолинейны со своими вопросами. Это может быть так просто, как «У Молли две собаки, у Джейсона три. Сколько собак у Молли и Джейсона вместе?» Однако об этом нам нужно подумать. Эта проблема состоит из более чем одного шага. Сначала нам нужно выяснить, сколько у него полок, а затем выяснить, сколько книг на всех полках, чтобы узнать, сколько всего у него книг.

Список того, что дано

Всегда хорошо начинать с перечисления того, что вы знаете. Если вы попытаетесь решить проблему, не зная, какие инструменты вам даны для ее решения, вы не получите правильного ответа. Вспомните, когда вы в последний раз пытались заполнить пробелы или предположить ответ, не зная всех фактов. Ваш результат, вероятно, не обернулся хорошо. Именно по этой причине нам нужно перечислять то, что дано перед любой проблемой. Учащийся должен записать его вверху или сбоку на листе бумаги, чтобы он всегда имел его в качестве справочного материала при решении задачи. Для этой задачи мой список того, что дано, будет:

• У Кевина 3 книжных шкафа
• Каждый книжный шкаф имеет 9 полок
• На каждой полке 16 книг

Поиск ключевых слов

Каждое слово «проблема» содержит ключевые слова, на которые нужно обращать внимание и которые говорят вам, какую операцию выполнять. По мере того, как ваш ребенок будет больше практиковаться в решении текстовых задач, поиск ключевых слов станет проще. Вот некоторые из самых популярных ключевых слов для текстовых задач:

Операция	Ключевые слова
Дополнение	«все вместе», «оба», «вместе», «всего»* «дополнительно»
Вычитание	«уменьшение», «разность», «меньше», «насколько больше», «насколько больше», «ушли», «остались»
Умножение	«удвоенный/утроенный», «каждый» «равные группы» «во всех», «из», «на»
Подразделение	«равные части» «разделенные» «разделенные», «проценты»

*это может быть ключевым словом для сложения и умножения

Решите

Согласно таблице выше, мы должны использовать умножение.