Разное

Математика правило 4 класс: Математика, 4 класс: уроки, тесты, задания

Содержание

Математика 4 класс

Фотоальбом

Педагоги

Рудик Наталья Николаевна

ГБОУ № 634 средняя общеобразовательная

школа с углубленным изучением

английского языка

 

Математика.

4 класс.

 
Тема: Правильные и неправильные дроби.
 
Тип урока: урок первичного предъявления новых знаний.
 
Дидактические цели урока:
– сформировать представление о правильных и неправильных дробях.
– учить сравнивать любую дробь с единицей.
– тренировать умение складывать и вычитать дробные числа.
  
Задачи:
метапредметные:
познавательные:
– осуществлять анализ материала с выделением существенных признаков.
– строить рассуждения учить группировать классифицировать материал, решать поставленную проблему;
коммуникативные: формировать умение сотрудничать с одноклассниками в паре, в группе;
регулятивные: обучать умению формулировать цели урока, принимать и сохранять учебную задачу;
личностные: учить адекватно оценивать свою деятельность и деятельность своих товарищей, выявлять причины неудач и успеха в учебной деятельности.
 
Методы обучения.
 
По характеру учебно-познавательной деятельности: проблемно-поисковые.
По способу организации и осуществления познавательной деятельности:
словесные, наглядные, практические.
По степени педагогического управления со стороны учителя: методы непосредственного управления учебно-познавательной деятельностью учащихся, методы опосредованного управления с помощью источников информации.
 
Формы организации учебной деятельности:
фронтальная, групповая.
 
Средства обучения: Петерсон Л. Г. Математика. Учебник для 4 класса. М.: Издательство «Ювента». 2009.
 
Раздаточный материал: по 2 равных круга на парту, цветные карандаши. Фрагмент презентации о С. Ковалевской.
Планируемые результаты:
 
Метапредметные: ученики получат возможность на практике познакомиться с правильными и неправильными дробями, осуществлять анализ материала с выявлением существенных признаков, группировать, классифицировать материал, сравнивать результат и делать выводы.
Коммуникативные: высказывать свою точку зрения, сотрудничать с одноклассниками в решении учебных задач.
Регулятивные: получат возможность учиться принимать и сохранять учебную задачу.
 
Ход урока.
 
– Если правильно выполните вычисление дробей, расшифруете фамилию выдающейся женщины-математика.
Ковалевская Софья Васильевна (1850-1891) жила во второй половине 19 века. Родилась в Москве в семье артиллерийского генерала. В те времена в России женщины не имели права учиться в университете, да и во многих университетах Европы. Софье Васильевне удалось убедить знаменитого немецкого математика Карла Вейерштрасса заниматься с ней лично. И уже через некоторое время получила ученую степень. Софья Ковалевская сделала ряд математических открытий, была удостоена множества наград и премий за достижения в области математики. Она занималась так же теорией дробей, которые мы с вами изучаем.
 
II Постановка проблемы.
– Разбить получившиеся дроби на 3 группы и записать в тетрадь.
1, 9/11   3/13   3/10   6/25
2. 7/7   6/6   9/9   3/3
3. 12/8   13/11   7/5
– Что заметили? С какими дробями мы не встречались? Можно ли эти записи назвать дробями? Проверим, выполнив практическую работу.
 
III Практическая работа. Открытие новых зданий.
  • 1) – Возьмите 2 равных круга и разделите их на 4 равные части.
– Сколько четвертых долей содержит один круг? Два круга?
– Запишем в тетрадь: 1=4/4     2=8/4
– Что необычного в этих дробях? Можно ли черту дроби понимать как знак деления?
Вывод: Значит, если числитель и знаменатель дроби равны, то дробь равна целому.

а/а=1
 
  • 2) – Заштрихуйте 5 четвертых долей круга цветным карандашом. Какой дробью можно выразить закрашенную часть? Запишем: 5/4
а/b>1, если а>b
 
 
Вывод: Следовательно, все записанные нами по группам дроби, существуют в математике. Как же они называются? (открывается тема урока на доске):
 
Правильные и неправильные дроби.
 
– Как думаете, какие дроби называются правильными? А неправильными?
  
а/b<1, если а<b
 
 
IV Первичное закрепление.
 
– Самостоятельно прочитайте правило в учебнике на с. 14. Повторение по опорным схемам.
– С.
13 № 2. По цепочке.
– № 4. Как обозначено целое на числовом луче? На сколько частей разделено целое? Самостоятельное выполнение задания. Взаимопроверка в парах.
 
V Самостоятельная работа.
 
– № 11. Работа по колонкам. С помощью данных чисел составить и записать по 3 правильные и неправильные дроби. Взаимопроверка и проверка по колонкам.
– Дополнительное задание: № 14 (самостоятельно).
 
VI  Итоги урока.
 
– Что нового узнали на уроке? Какие дроби называются правильными, неправильными?
 
Домашнее задание. С. 15 № 13, 3 14-а.

ГДЗ по математике 4 класс учебник Моро, Бантова 1 часть

  • Тип: ГДЗ, Решебник.
  • Автор: Моро М. И., Волкова С. И., Бантова М. А.
  • Год: 2020.
  • Серия: Школа России (ФГОС).
  • Издательство: Просвещение.

👉Ответы по математике за 4 класс, автор Моро и Бантова. Школа России.

Ответы к номерам: 151, 152, 153, 154, 155.Решебник – страница 37Готовое домашнее задание

Номер 151.

1) Прочитай таблицу единиц длины. Запиши и запомни ее.
2) Используя эту таблицу, узнай, сколько миллиметров в 1 дм, сколько сантиметров в 1 м.
3) Во сколько раз 1 м больше, чем 1 мм?

Ответ:

2) 1 дм = 10 ∙ 10 = 100 мм     1 м = 10 ∙ 10 = 100 см 3) 1 м = 100 см = 1000 мм, следовательно, 1 м больше в 1000 раз 1 мм.

Номер 152.

Спиши заполняя пропуски:

Ответ:

620 = 62 дес. 620 мм = 62 см 620 дм = 62 м
756 = 75 дес. 6 ед. 756 мм = 75 см 6 мм 756 дм = 75 м 6 дм
1000 см = 10 м 25000 м = 25 км 6000 мм = 6 м

Номер 153.

От двух остановок, расстояние между которыми 1 км, отошли два пешехода. Один из них прошел 140 м, а другой – 160 м. Каким стало расстояние между пешеходами?
1) Дополни условие, чтобы чертеж к задаче был таким, как на первой картинке.
2) Измени условие задачи, чтобы чертеж стал таким, как на второй картинке.
3) Реши обе задачи и сравни их решения.

Ответ:

1) От двух остановок, расстояние между которыми 1 км,     отошли два пешехода навстречу друг другу. Один из них прошел 140     метров, а другой 160 метров. Каким стало расстояние между пешеходами?

2) От двух остановок, расстояние между которыми 1 км,     отошли два пешехода в противоположные стороны. Один из них прошел     140 метров, а другой 160 метров. Каким стало расстояние между пешеходами?
3) Задача 1:     1 км = 1000 м     1000 – (160 + 140) = 1000 – 300 = 700 метров – расстояние между пешеходами.
    Задача 2:     1000 + 160 + 140 = 1300 метров – расстояние между пешеходами.

Номер 154.

Ответ:


Номер 155.

Найди правило, по которому составлен ряд чисел, и запиши еще 3 числа 24, 23, 21, 18, 17, 15, 12… .

Ответ:

Правило: сначала отнимаем 1, потом 2, потом 3. 24, 23, 21, 18, 17, 15, 12, 11, 9, 6.

Задание внизу страницы

Ответ:

1560 м = 1 км 560 м

Задание на полях страницы

Ребус.

Ответ:

Рейтинг

Выберите другую страницу

1 часть

Учебник Моро3456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111

2 часть

456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127

Ваше сообщение отправлено!

+

4 класс – единицы, величины, длина, время, площадь, масса, скорость.

Урок по математике

Дата публикации: .


Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Скачать:Единицы и меры измерения длины, площади, массы, времени (PDF)

Обучающие пособия и тренажеры в интернет-магазине “Интеграл” для 4 класса
Учебное пособие к учебнику М.И. Моро    Учебное пособие к учебнику Л.Г. Петерсон


Единицы и меры длины


Единицы длины мы используем в повседневной жизни очень часто. Например, на уроках математики, когда мы рисуем различные фигуры, мы используем сантиметры или миллиметры, иногда дециметры. Дома, измеряя длину комнаты, используем метры. Когда мы куда-либо отправляемся, например, в другой город или на дачу, мы используем единицу длины – километр.

Давайте вспомним, как они соотносятся друг с другом.

1 км = 1000 м

1 м = 10 дм
1 дм = 10 см
1 см = 10 мм
Ребята, ответьте на вопросы. Сколько сантиметров в 5 метрах, а в 3 дм? Сколько миллиметров в 4 дм? Во сколько раз 6 метров длиннее, чем 2 дм?

Часто мы определяем длину или расстояние “на глаз”. Это происходит из-за отсутствие линейки или метра под рукой. Чем точнее вы будете определять длину или расстояние, тем лучше у вас глазомер.

На данном рисунке нарисовано 3 отрезка. Определите “на глаз”, какова их длина. А теперь, попробуйте определить длину сторон треугольника и прямоугольника. Ещё несколько примеров и задач на определение длины. Какую меру длины надо использовать для того, чтобы измерить:
1. длину жука;
2. ширину парты;
3. расстояние до соседнего города;
4. длину и ширину комнаты;
5. длину реки;
6. ширину дороги.

Единицы и меры площади


Ребята, запомните, площадь всегда измеряется квадратами. Например, квадратный метр – это квадрат, сторона которого равно одному метру, а квадратный километр – это квадрат, сторона которого равна одному километру.

В письме словосочетание “квадратный метр” сокращается до записи м2. Если вы увидите такую запись, знайте, что речь идет о площади.
Как и в случае с длиной используют разные единицы измерения площади. Например, для измерения площади квартиры используют квадратные метры. Конечно можно использовать и квадратные сантиметры, но это будет не совсем удобно.
Рассмотрим, как величины площади соотносятся друг с другом.

1 км

2 = 1 000 000 м2
1 м2 = 100 дм2
1 дм2 = 100 см2
1 см2 = 100 мм2
Рассмотрим пример на расчет площади и выразим полученный результат через различные единицы измерения площади.
Для примера, рассмотрим обычное футбольное поле со сторонами 100 метров и 60 метров. Рассчитаем площадь такого поля.

S футбольного поля = 100 м х 60 м = 6 000 м

2 =
= 600 000 дм2 = 60 000 000 см2
Как видите, площадь можно выразить через квадратные метры, квадратные дециметры и т.д. Для данного примера м2 – это самая удобная единица измерения. Чтобы лучше понять данную тему потренируйтесь в определении площади. Укажите на рисунке следующие величины, если принять, что каждый квадратик имеет сторону, равную 1 мм:
1. квадратный миллиметр;
2. 3 квадратных сантиметра;
3. половину квадратного сантиметра.

Определите площадь первой и второй фигуры.

Единицы и меры массы


Ребята, вы уже знакомы с единицами массы – это граммы, килограммы и др. С этими мерами вы часто сталкиваетесь, особенно в продуктовом магазине. Там на каждый товар указана цена (обычно за 1 кг веса или за упаковку). Это очень удобно и практично. Если необходим использовать более крупные меры массы, например, для измерения веса автомобиля, то используются такие меры массы, как тонна или центнер.
Давайте рассмотрим, как они соотносятся с друг другом.
1 т = 10 ц

1 ц = 100 кг
1 кг = 1000 г
Ребята, ответьте на вопросы. Сколько грамм в двухкилограммовой пачке муки? Сколько центнеров в 8 тонной машине? Во сколько раз легковая машина весом 12 центнер легче автобуса весом 6 тонн?

Единицы времени


Понятие “времени” мы используем всегда и везде, без часов невозможно представить нашу жизнь. По расписанию работают магазины и заводы, школы, детские сады и другие учреждения. И прибор для измерения времени знаком всем – это часы. С древних времен человечество придумало единицы измерения времени на все случаи жизни. Посмотрите на таблицу.
1 век = 100 лет

1 год = 12 месяцев
1 месяц =30 или 31 день (кроме февраля, когда у нас 28 или 29 дней)
1 день = 24 часа
1 час = 60 минут
1 минута = 60 секунд
Ребята, ответьте на вопросы.
1. Сколько месяцев летом, осенью, зимой и весной?
2. Сколько дней в феврале?
3. Что такое “високосный” год?
4. Сколько часов и минут длятся 3 урока подряд?
5. Школьная библиотека начинает работать в 9 часов утра, а закрывается в 15 часов. Сколько часов работает библиотека? Сколько это будет в минутах?

Правила деления в математике

Предоставление учащимся инструментов для решения деления с помощью этих сокращений не только делает деление менее сложным, но и делает его похожим на забавную головоломку. Для многих наличие четкого набора правил и структуры помогает прояснить концепцию и помогает учащимся решать уравнения и манипулировать выражениями. Возможность проверки делимости может помочь во многих математических настройках, таких как возможность проверить решение, уменьшить дроби или проверить правильность расчета.

Каковы правила разделения?

Приступая к разделу о делении, обязательно поделитесь этими правилами с классом и обсудите их во время выступления по математике:

ДЕЛИМОСТЬ НА 2

Число, которое делится на 2, называется четным. Когда последняя цифра в числе равна 0 или даже четной, то есть 2, 4, 6 или 8, то число делится на 2. Например, 20 оканчивается на 0, поэтому оно делится на 2. Число 936 заканчивается в 6, а 6 четно. Значит, 936 делится на 2,9.0003

ДЕЛИМОСТЬ НА 3

Число делится на 3, если сумма цифр делится на 3. Чтобы использовать этот прием, учащиеся должны уметь делить, но проверка меньших чисел менее сложна, чем проверка больших. . Например, если вы спросите учащихся, делится ли 168 на 3, они должны ответить следующим образом:

1 + 6 + 8 = 15

15/3 = 5

Следовательно, 168 делится на 3.

ДЕЛИМОСТЬ НА 4

Если последние две цифры числа делятся на 4, то делится и все число. Например, в 1012 12 делится на 4. Однако в 1013 13 не делится. Следовательно, 1012 делится на 4, а 1013 — нет.

ДЕЛИМОСТЬ НА 5

Когда последняя цифра числа 0 или 5, число можно разделить на 5 без остатка. Таким образом, 5, 10, 15, 20, 25 и т. д. можно разделить на 5. Учащиеся могут посмотреть на большие числа и сразу сказать, можно ли их поровну разделить на пять частей.

ДЕЛИМОСТЬ НА 6

Числа, которые делятся на 6, также можно разделить на как на 3, так и на 2. Учащиеся должны проверить число с обоими правилами для 3 и 2. Если число проходит оба теста, его можно разделить на 6. Если он провалит хотя бы один тест, он не сможет. Например:

308 оканчивается на четную цифру, поэтому оно делится на 2. Однако 3 + 0 + 8 = 11, что не может делиться на 3 без остатка. Таким образом, 308 не делится на 6.

ДЕЛИМОСТЬ НА 8

Большое число делится на 8, если последние три цифры также делятся на 8 или равны 000. В числе 7120 120 можно разделить на 8 без остатка, поэтому 7120 также делится на 8.

ДЕЛИМОСТЬ НА 9

Правило делимости 9 такое же, как и 3. Если сумма цифр числа делится на 9, так же как и весь номер. Например:

В числе 549 5 + 4 + 9 = 18

18/9 = 2

Итак, 549 делится на 9.

ДЕЛИМОСТЬ НА 10

Если последняя цифра может быть 0, то число разделить поровну на 10.

Почему правила помогают и как их использовать

Эти правила позволяют учащимся рассматривать большие числа в менее сложном контексте. Правила делимости также позволяют им многое узнать о числе, просто взглянув на его цифры. Таким образом, вы должны поощрять учащихся использовать все правила при изучении числа. Глядя на что-то вроде 1159,350, учащиеся могут пройтись по списку делимости, отметив, на какие числа можно разделить большее число.

Конечно, на уроках математики вы будете говорить не только о четных делениях. Некоторые числа будут иметь остатки. Вы все еще можете использовать правила, чтобы говорить об этих числах. Предложите учащимся определить, будет ли у определенного числа остаток при делении на 2, 3, 4, 5, 6, 8 или 10. это вдохновляет учащихся увидеть ценность и цель математики в их повседневной жизни через полезные, реальные действия и уроки.

Связанные данные

  • Д-р Кэри Снейдер
    Руководитель писательской группы NGSS, доцент Портлендского государственного университета

  • Дженнифер Прескотт
    Форма Участник

  • Д-р Эми Эндо
    Директор по исследованиям в области образования, дополнительный язык и интервенция, грамотность

Правила делимости на 4 и 8 – Математика 3-го класса

Делимое число означает, что одно число можно разделить поровну на другое число.

Делимость Правила подобны ярлыкам для определения, может ли одно число делиться на другое.

Итак, вы выучили правила делимости на 2, 5 и 10 и правила делимости на 3, 6, 9. 

Теперь давайте изучим правила делимости на 4 и 8!

Делится на 4

Когда число делится на на 4 , последние две цифры делятся на 4!

Итак, важно знать свои двузначные числа, кратные 4:

4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 48

И эти тоже:

52, 56, 60, 64, 68, 72, 76, 80, 84, 88, 92, 96

Совет: Если вы не можете запомнить эти большие двузначные числа 👆, просто вычтите 40 из них и посмотрите, делится ли разница на 4.

Делится ли 44 на 4?

Если вы не можете вспомнить, вычтите 40 из 44:

44 – 40 = 4.

Делится ли 4 на 4? Да! Значит, 44 тоже делится на 4!

Теперь вы знаете все двузначные числа, которые делятся на 4.

Давайте потренируемся с большими числами!

4 , 388 делится на на 4?

Только посмотрите на две последние цифры!

4,3 88

88 делится на 4! 🌟

Значит, 4388 делится на 4.

Попробуем еще:

Делится ли 45 061 на 4?

Взгляните на две последние цифры:

45,0 61

Делится ли 61 на 4?

№ ❎

Это означает, что 45 061 не делится на 4.

Отличная работа! Теперь давайте узнаем о 8.

Делится на 8

Если последние 3 цифры числа делятся на 8, то все число делится на 8.

Для этого вам может понадобиться сделать немного длинное деление.

Давайте попробуем!

Делится ли 4 , 200 на 8?

Посмотрим, сможем ли мы разделить последние три цифры на 8 без остатка!

Мы не можем разделить 2 на 8, поэтому переходим к 20, делённому на 8. 

Теперь мы можем разделить 40 на 8.

Поскольку у нас нет остатка, мы знаем, что 4 , 200 делится на на 8 !

Попробуем еще! 😎

Делится ли 7 246 на 8 ?

Давайте решим задачу на деление с тремя последними цифрами:

Мы не можем разделить 8 на 2, поэтому мы делим на 24:

Можем ли мы разделить 6 на 8? 🤔

Нет! Итак, пишем 0 и находим остаток:

Поскольку 8 не делится на 246 без остатка, мы знаем, что 7246 — это , а не , делимое на 8 .

Отличная работа! 💪 Теперь вы знаете, как определить, делятся ли числа на 4 и 8!

Теперь завершите практику. Это поможет вам помнить дольше. 🤗 

Правило делимости на 4 – Методы, примеры

Правило делимости на 4 гласит, что данное число делится на 4, если последние две цифры числа – нули, или они образуют число, которое делится на 4 , Он также известен как проверка делимости на 4. Правило делимости на 4 помогает узнать, делится ли число на 4 или нет без выполнения деления. Первые четыре целых числа, которые делятся на 4, — это 0, 4, 8, 12 и 16. Все они кратны 4, и каждое кратное 4 полностью делится на 4.

1. Что такое правило делимости на 4?
2. Правило делимости на 4 для больших чисел
3. Правило делимости на 4 и 6
4. Признак делимости на 4 и 8
5. Часто задаваемые вопросы о правиле делимости числа 4

Что такое правило делимости на 4?

В соответствии с правилом делимости на 4, говорят, что целое число делится на 4, если оно удовлетворяет одному из двух условий:

  • Если последние две цифры данного числа – нули. Это означает, что число имеет нули в разряде десятков и разряде единиц. Например, в числе 300 последние две цифры 00, следовательно, 300 делится на 4.
  • Если последние две цифры данного числа образуют число, которое точно делится на 4. Например, в 316 последние две цифры образуют число 16, которое делится на 4. Следовательно, 316 делится на 4.

Правило делимости на 4 с примерами

Правило делимости на 4 можно понять с помощью следующих примеров.

Пример: Проверка делимость следующих чисел на 4.

a.) 1124

b. ) ) В 1124 последние две цифры в данном числе образуют число 24, которое делится на 4 (24 ÷ 4 = 6)
Таким образом, 1124 делится на 4. Это можно проверить следующим образом: 1124 ÷ 4 = 281

b.) В 1171 последние две цифры в данном числе образуют число 71, которое не делится полностью на 4 (71÷4 = 17 — частное, а 3 — остаток)
Таким образом, 1171 не делится на 4.

в.) В числе 1300 последние две цифры в данном числе — нули. Это означает, что 1300 полностью делится на 4.
1300 ÷ 4 = 325
Таким образом, 1300 делится на 4.

г) В числе 500 последние две цифры данного числа — нули. Это означает, что 500 полностью делится на 4.
500 ÷ 4 = 125
Таким образом, 500 делится на 4.

Правила делимости помогают решать задачи без процесса деления.

Правило делимости на 4 для больших чисел

Правило делимости на 4 гласит, что если число имеет два нуля в конце или две последние цифры образуют число, которое точно делится на 4, то данное число также делится на 4. Следовательно, для любых больших чисел мы проверяем последние две цифры и применяем правило делимости на 4 и можем узнать, делится ли большое число на 4 или нет.

Пример 1: в 238900 последние две цифры в разряде десятков и разряде единиц равны нулю. Это означает, что 238900 делится на 4.
238900 ÷ 4 = 59725
Таким образом, 238900 делится на 4.

Пример 2: В числе 148936 две последние цифры десятков и единиц образуют число 36, которое делится на 4 (36 ÷ 4 = 9).
148936 ÷ 4 = 37234
Таким образом, 148936 делится на 4.

Правило делимости на 4 и 6

Правила делимости 4 и 6 совершенно разные. В правиле делимости 4, если последние две цифры являются нулями или число, образованное двумя последними цифрами, точно делится на 4, то мы можем сказать, что число делится на 4. Однако, согласно правилу делимости 6 , говорят, что число делится на 6 только в том случае, если оно делится и на 2, и на 3.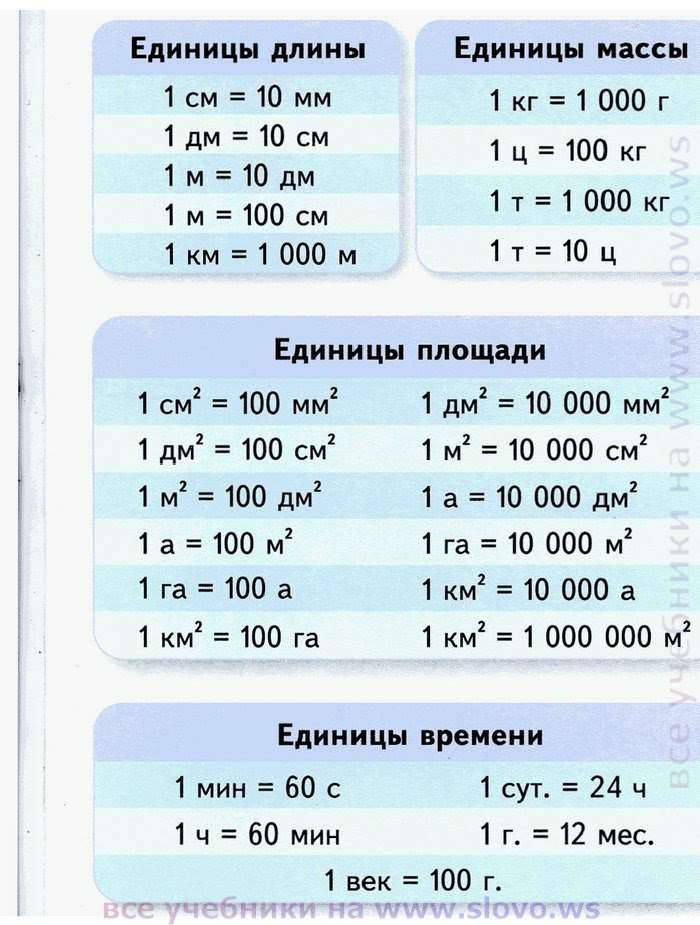 В тесте на делимость 4 мы проверяем две последние цифры, а в тесте на делимость 6 мы проверяем, все ли число делится на 2 и 3 или нет. Например, давайте проверим, если 936 делится на 6. Поскольку последняя цифра числа 936 четное число, можно сказать, что 936 делится на 2. Теперь проверим его делимость на 3. Сумма цифр равна 9 + 3 + 6 = 18, что делится на 3. Это означает, что 936 тоже делится на 3. Следовательно, можно сказать, что число 936 полностью делится на 6.

Признак делимости на 4 и 8

Признаки делимости 4 и 8 немного похожи. В тесте на делимость 4 мы проверяем две последние цифры, если последние две цифры – нули или число, образованное двумя последними цифрами числа, точно делится на 4, то исходное число также делится на 4. В тесте тест делимости 8, мы проверяем последние три цифры, если последние три цифры нули или число, образованное последними тремя цифрами числа, точно делится на 8, то исходное число также делится на 8. Например, пусть мы проверим, делится ли 61816 на 8. Если мы проверим последние 3 цифры, они образуют число 816, которое делится на 8. Следовательно, можно сказать, что 61816 делится на 8.

☛ Похожие темы

  • Правило делимости 3
  • Правило делимости числа 5
  • Правило делимости 6
  • Правило делимости числа 7
  • Правило делимости числа 8
  • Правило делимости числа 9
  • Правило делимости 11
  • Правило делимости 13

 

Правило делимости на 4 примера

  1. Пример 1: Узнать, делятся ли данные числа на 4 или нет, используя признак делимости на 4.

    а.) 380
    б.) 549
    в) 740

    Решение:

    а) В числе 380 последние две цифры образуют число 80, которое делится на 4. Следовательно, 380 делится на 4 (380 ÷ 4 = 95).

    б) В числе 549 последние две цифры образуют число 49, которое не делится на 4. Следовательно, 549 не делится на 4.

    в) В числе 740 последние две цифры образуют число 40, которое делится на 4. Следовательно, 740 делится на 4 (740 ÷ 4 = 185).

  2. Пример 2: Определите, делится ли наименьшее 6-значное число на 4 или нет, используя правило делимости на 4.

    Решение: последние две цифры наименьшего шестизначного числа — два нуля.
    (100000 ÷ 4 = 25000)

  3. Пример 3: Проверить, делится ли заданное большое число 434788 на 4, используя правило делимости на 4.

    Решение: В 434788 последние две цифры образуют число 88, а 88 делится на 4 точно, поэтому число 434788 делится на 4.
    (434788 ÷ 4 = 108697)

перейти к слайду перейти к слайду перейти к слайду

Отличное обучение в старшей школе с использованием простых подсказок

Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.

Записаться на бесплатный пробный урок

Практические вопросы по правилу делимости 4

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о правиле делимости числа 4

Что такое правило делимости на 4?

Правило делимости числа 4 гласит, что число считается делящимся на 4, если две последние цифры числа равны нулю или образуют число, которое делится на 4. Например, 2300 делится на 4, потому что два нуля в конце числа. Точно так же 488 также делится на 4, потому что последние две цифры 88 делятся на 4.

Используя правило делимости на 4, проверьте, делится ли 14540 на 4.

Сначала нам нужно проверить, делится ли число, состоящее из двух последних цифр заданного числа, на 4 или нет. В данном числе 14540 число, образованное двумя последними цифрами, равно 40, а 40 делится на 4. Таким образом, 14540 делится на 4.

Каково правило делимости 4 и 8?

Правила делимости на 4 и 8 немного похожи. В правиле делимости на 4 мы ориентируемся на две последние цифры числа. Если последние две цифры нули или число, образованное двумя последними цифрами числа, точно делится на 4, то можно сказать, что данное число также делится на 4. Например, 800, 900 и 348 делятся на 4, поскольку они удовлетворяют условию правила делимости на 4.

В правиле делимости на 8 мы фокусируемся на трех последних цифрах числа. Если последние три цифры – нули или число, образованное последними тремя цифрами числа, точно делится на 8, то мы можем сказать, что исходное число также делится на 8.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *