Математика плюс на плюс: Минус на плюс что дает?

Минус на плюс что дает?

Положительные и отрицательные числа придумали математики. Делать им было нечего, вот они и придумали. Правила умножения и деления положительных и отрицательных чисел придумали всё те же математики. Специально для того, чтобы нам жизнь мёдом не казалась. Как же нам быть? Нужно выучить эти правила, чтобы говорить математикам то, что они хотят от нас слышать.

Запомнить правила умножения или деления положительных и отрицательных чисел очень просто. Если два числа имеют разные знаки, в результате всегда будет знак минус.
Если два числа имеют одинаковые знаки, в результате всегда будет плюс.

Рассмотрим все возможные варианты. Что дает минус на плюс? При умножении и делении минус на плюс дает минус. Что дает плюс на минус? При умножении и делении в результате мы тоже получаем знак минус.

Минус на плюс, плюс на минус.

Как вы видите, все варианты умножения и деления положительных и отрицательных чисел исчерпаны, но знак плюс у нас так и не появился.

Это мы сформулировали правило для себя, чтобы запомнить. Что говорить математикам? При умножении или делении положительных и отрицательных чисел в результате получается отрицательное число. Всегда.

Что дает минус на минус? Всегда будет получаться плюс, если мы выполняем умножение или деление. Что дает плюс на плюс? Здесь совсем просто. Умножение или деление плюса на плюс дает всегда плюс.

 

Минус на минус, плюс на плюс.

Надеюсь, это вы запомнили: минус на минус дает плюс, плюс на плюс дает минус. Что говорить математикам? При умножении и делении положительных или отрицательных чисел в результате получается положительное число.

Если с умножением и делением двух плюсов всё понятно (в результате получается такой же плюс), то с двумя минусами ничего не понятно. По логике, если два плюса дают плюс, то два минуса должны давать минус.

Такой большой, жирный минус. Но не тут-то было. Математики думают иначе. Так почему минус и минус превращаются в плюс?

Могу вас заверить, что интуитивно математики правильно решили задачу на умножение и деление плюсов и минусов. Они записали правила в учебники, не особо вдаваясь в подробности. Для правильного ответа на вопрос, нам нужно разобраться, что же означают знаки плюс и минус в математике.

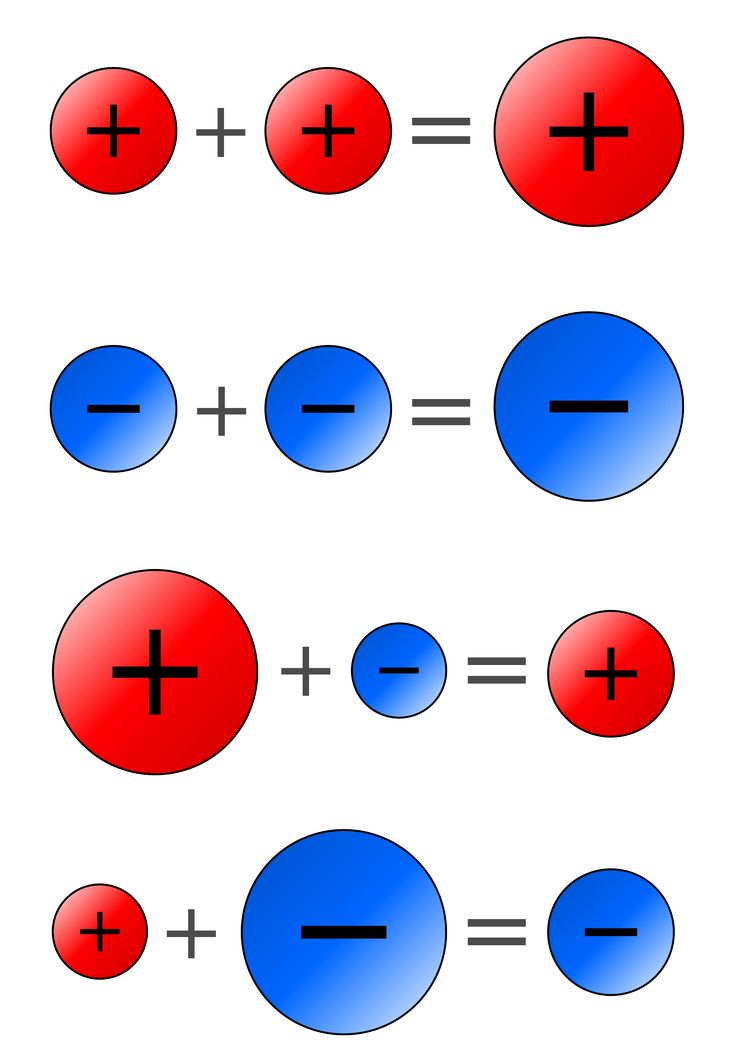
Давайте попробуем применить правило умножениея и деления положительных и отрицательных чисел на практике. Придумаем какой-нибудь пример из нашей жизни. Думаю, вы слышали про бочку мёда и ложку дёгтя, которая может испортить весь мёд. Пусть мёд – это положительные числа, а дёготь – это числа отрицательные. Пробуем. Смотрим на картинки и описываем правила.

Если в бочку дёгтя добавить ложку мёда, получится бочка дёгтя.
Если в бочку мёда добавить ложку дёгтя, получится бочка дёгтя.
Если в бочку дёгтя добавить ложку дёгтя, получится бочка мёда.
Если в бочку мёда добавить ложку мёда, получится бочка мёда.

Первых два примера с натяжкой можно принять. Последний пример вообще не вызывает вопросов. А вот с предпоследним примером возникают очень большие проблемы – в жизни такого не бывает.

Здесь возможны два варианта:
1. Математики не правильно записали свое правило.
2. Мы не правильно применяем математическое правило.

Лично я за второй вариант. Объясню почему. Математику не только нужно знать, но нею ещё нужно уметь пользоваться.

Приведу пример из собственного опыта. Один учитель математики на уроках нам говорил: «математика – это точная наука, два раза соври – получится правда». Это утверждение однажды мне очень пригодилось. Как-то я решал сложную задачу с длинным решением. Я точно знал, какой результат должен быть. Но результат был другим. Я долго искал ошибку в расчетах, но не смог ее найти. Тогда, за несколько действий до итогового результата, я изменил одно число так, чтобы результат получился правильным. Я в расчетах соврал два раза и получил правильный результат.

Математические вычисления в тот раз никто не проверял и я получил хорошую оценку. Это очень похоже на правило «минус на минус дает плюс», не так ли?

Но вернемся к нашим бочкам. Кстати, говорят, именно с бочек с вином математики срисовали знак “минус”. Виноделы этим знаком обозначали пустые бочки. После наполнения бочек вином они перечеркивали знак “минус” и получался знак “плюс”. По сути, знак “минус” заменял виноделам обычный ноль, ведь он обозначал отсутствие вина в бочке. Но математики ловко присобачили знак “минус” к числам и назвали их “отрицательными”.

Так что же не так с мёдом и дёгтем в бочках? Мои четыре примера описывают действие сложения – ведь мы прибавляем одно к другому, а математические правила мы рассматриваем для деления и умножения. Это абсолютно разные вещи, сколько бы математики не повторяли, что умножение это и есть сложение. Сложение – это изменение количества. Умножение – это изменение качества. При добавлении ложки дёгтя в бочку мёда, мёд не превращается в дёготь. 2

В этом примере буква а выполняет роль единицы измерения. Кстати, правило умножения отрицательных чисел наводит на ещё один вопрос математикам: сколько отрицательных чисел нужно сложить, чтобы получилось одно положительное число?

(-2)+(-2)=-4

(-2)*(-2)=+4

Так что же такое знаки “плюс” и “минус” в математике? Существуют ли отрицательные числа? Об этом мы поговорим как-нибудь в другой раз.

Узнаем как понять, почему «плюс» на «минус» дает «минус» ?

Слушая учителя математики, большинство учеников воспринимают материал как аксиому. При этом мало кто пытается добраться до сути и разобраться, почему «минус» на «плюс» дает знак «минус», а при умножении двух отрицательных чисел выходит положительное.

Законы математики

Большинство взрослых не в силах объяснить ни себе, ни своим детям, почему так получается. Они твердо усвоили этот материал в школе, но при этом даже не попытались выяснить, откуда взялись такие правила. А зря. Зачастую современные дети не столь доверчивы, им необходимо докопаться до самой сути и понять, скажем, почему «плюс» на «минус» дает «минус». А иногда сорванцы специально задают каверзные вопросы, дабы насладиться моментом, когда взрослые не могут дать вразумительного ответа. И совсем уж беда, если впросак попадает молодой учитель…

Кстати, следует отметить, что упомянутое выше правило действенно как для умножения, так и для деления. Произведение отрицательного и положительного числа даст лишь «минус. Если речь идет о двух цифрах со знаком «-», то в результате получится положительное число. То же касается и деления. Если одно из чисел будет отрицательным, то частное тоже будет со знаком «-».

Для объяснения правильности этого закона математики, необходимо сформулировать аксиомы кольца. Но для начала следует понять, что это такое. В математике кольцом принято называть множество, в котором задействованы две операции с двумя элементами. Но разбираться с этим лучше на примере.

Аксиома кольца

Существует несколько математических законов.

• Первый из них переместительный, согласно ему, C + V = V + C.
• Второй называется сочетательным (V + C) + D = V + (C + D).

Им же подчиняется и умножение (V х C) х D = V х (C х D).

Никто не отменял и правил, по которым открываются скобки (V + C) х D = V х D + C х D, также верно, что C х (V + D) = C х V + C х D.

Кроме того, установлено, что в кольцо можно ввести специальный, нейтральный по сложению элемент, при использовании которого будет верно следующее: C + 0 = C. Кроме того, для каждого C есть противоположный элемент, который можно обозначить, как (-C). При этом C + (-C) = 0.

Выведение аксиом для отрицательных чисел

Приняв приведенные выше утверждения, можно ответить на вопрос: «”Плюс” на “минус” дает какой знак?» Зная аксиому про умножение отрицательных чисел, необходимо подтвердить, что действительно (-C) х V = -(C х V). А также, что верно такое равенство: (-(-C)) = C.

Для этого придется вначале доказать, что у каждого из элементов существует лишь один ему противоположный «собрат». Рассмотрим следующий пример доказательства. Давайте попробуем представить, что для C противоположными являются два числа – V и D. Из этого следует, что C + V = 0 и C + D = 0, то есть C + V = 0 = C + D. Вспоминая о переместительных законах и о свойствах числа 0, можно рассмотреть сумму всех трех чисел: C, V и D. Попробуем выяснить значение V. Логично, что V = V + 0 = V + (C + D) = V + C + D, ведь значение C + D, как было принято выше, равняется 0. Значит, V = V + C + D.

Точно так же выводится и значение для D: D = V + C + D = (V + C) + D = 0 + D = D. Исходя из этого, становится ясно, что V = D.

Для того чтобы понять, почему все же «плюс» на «минус» дает «минус», необходимо разобраться со следующим. Так, для элемента (-C) противоположными являются C и (-(-C)), то есть между собой они равны.

Тогда очевидно, что 0 х V = (C + (-C)) х V = C х V + (-C) х V. Из этого следует, что C х V противоположно (-)C х V, значит, (-C) х V = -(C х V).

Для полной математической строгости необходимо еще подтвердить, что 0 х V = 0 для любого элемента. Если следовать логике, то 0 х V = (0 + 0) х V = 0 х V + 0 х V. А это значит, что прибавление произведения 0 х V никак не меняет установленную сумму. Ведь это произведение равняется нулю.

Зная все эти аксиомы, можно вывести не только, сколько «плюс» на «минус» дает, но и что получается при умножении отрицательных чисел.

Умножение и деление двух чисел со знаком «-»

Если не углубляться в математические нюансы, то можно попробовать более простым способом объяснить правила действий с отрицательными числами.

Допустим, что C – (-V) = D, исходя из этого, C = D + (-V), то есть C = D – V. Переносим V и получаем, что C + V = D. То есть C + V = C – (-V). Этот пример объясняет, почему в выражении, где идут два «минуса» подряд, упомянутые знаки следует поменять на «плюс». Теперь разберемся с умножением.

(-C) х (-V) = D, в выражение можно добавить и вычесть два одинаковых произведения, которые не поменяют его значения: (-C) х (-V) + (C х V) – (C х V) = D.

Вспомная о правилах работы со скобками, получаем:

1) (-C) х (-V) + (C х V) + (-C) х V = D;

2) (-C) х ((-V) + V) + C х V = D;

3) (-C) х 0 + C х V = D;

4) C х V = D.

Из этого следует, что C х V = (-C) х (-V).

Аналогично можно доказать, что и в результате деления двух отрицательных чисел выйдет положительное.

Общие математические правила

Конечно, такое объяснение не подойдет для школьников младших классов, которые только начинают учить абстрактные отрицательные числа. Им лучше объяснять на видимых предметах, манипулируя знакомым им термином зазеркалья. Например, придуманные, но не существующие игрушки находятся именно там. Их и можно отобразить со знаком «-». Умножение двух зазеркальных объектов переносит их в еще один мир, который приравнивается к настоящему, то есть в результате мы имеем положительные числа. А вот умножение абстрактного отрицательного числа на положительное лишь дает знакомый всем результат. Ведь «плюс» умножить на «минус» дает «минус». Правда, в младшем школьном возрасте дети не слишком-то пытаются вникнуть во все математические нюансы.

Хотя, если смотреть правде в глаза, для многих людей даже с высшим образованием так и остаются загадкой многие правила. Все принимают как данность то, что преподают им учителя, не затрудняясь вникать во все сложности, которые таит в себе математика. «Минус» на «минус» дает «плюс» – об этом знают все без исключения. Это верно как для целых, так и для дробных чисел.

Плюс-минус математика – Картина дня – Коммерсантъ

Школьная математика становится предметом ожесточенных споров не только среди педагогов и ученых, но и в обществе в целом. Все больше учеников не справляются со школьной программой, и правительства разных стран вынуждены искать пути выхода из ситуации. В США призывают программу упростить, во Франции убеждены, что само математическое знание потеряло престиж, и нужно срочно вкладываться в популяризацию. В России же математический курс пока только делают более сложным, несмотря на то что в прошлом году дети массово получили по ОГЭ двойки.

Фото: Алексей Танюшин, Коммерсантъ

Фото: Алексей Танюшин, Коммерсантъ

Перед математикой не все равны

«Подвергать детей нашего крупнейшего государства такому эксперименту — верх безответственности»,— говорится в открытом письме, под которым поставили подпись уже более полутора тысяч ученых, включая нескольких лауреатов самой престижной премии в математике — премии Филдса.

Письмо направлено против одной из крупнейших реформ математического образования, которую планируют провести в Калифорнии в наступившем году. Главная ее цель — сделать школьную математику привлекательной, в частности, чтобы ею хотели активнее заниматься национальные меньшинства и девочки, которые традиционно представлены в этом секторе меньше. Для этого авторы идеи предлагают убрать из программы наиболее сложные разделы алгебры, заменив их дисциплинами под общим названием «большие данные», упразднить существующее разделение классов в соответствии с математическими способностями и отменить экзамены в государственные математические школы, заменив их распределением мест по квотам.

Математик, профессор Калифорнийского университета в Ирвайне Светлана Житомирская

Фото: The Centre de Recherches Math?matiques, The Centre de Recherches Mathematiques

Математик, профессор Калифорнийского университета в Ирвайне Светлана Житомирская

Фото: The Centre de Recherches Math?matiques, The Centre de Recherches Mathematiques

«В Америке, особенно в последние полтора года, очень сильно движение за расовое и другие равенства, которое суперпрогрессивными левыми понимается как пропорциональное населению представительство во всем,— комментирует ситуацию математик, профессор Калифорнийского университета в Ирвайне Светлана Житомирская (в этом году Светлана приглашена в качестве пленарного докладчика на Международный конгресс математиков — крупнейшее и самое значимое научное мероприятие в этой сфере, что является признанием заслуг ученого.

—“Ъ”).— А представительство в продвинутых математических школах и классах часто очень непропорциональное. Зачастую здесь доминируют дети азиатского происхождения, а мальчиков традиционно намного больше, чем девочек. Нет нужды объяснять, что квоты для одних означают дискриминацию других. Мы все это проходили в Советском Союзе, где отвратительную дискриминацию в отношении евреев при приеме, скажем, на мехмат МГУ некоторые объясняли стремлением к пропорциональному представительству. Этому нет морального оправдания».

По словам эксперта, основная проблема предлагаемой калифорнийской реформы — значительное ослабление алгебраического фундамента, фактически его предлагают заменить на довольно пустой с математической точки зрения материал, якобы приближенный к современным нуждам «анализа данных». Также предполагается, что все, даже самые сильные, дети будут изучать алгебру только начиная с 9-го класса (с 14 лет), и в итоге у них просто не будет достаточно времени чтобы приобрести фундамент, необходимый для основ анализа, и пройти начала анализа, а последнее крайне желательно для тех, кто выберет технические специальности.

Вторая существенная проблема состоит в том, что предлагаемая программа игнорирует существование математических способностей.

«Хотя массовое математическое образование в Америке поставлено в целом из рук вон плохо и отстает от многих других стран, до сих пор был один очень хороший момент,— говорит Светлана Житомирская.— Во многих местах детей довольно рано на основании разных экзаменов делят на уровни и обучают раздельно. Большинство детей, у которых отмечаются способности, идут потом на технические специальности. Если новая программа будет утверждена, все они могут оказаться отброшенными назад по крайней мере на два года. При этом пострадают как раз дети из не самых обеспеченных семей, потому что остальные перейдут в частные школы, где математику будут преподавать так, как и прежде».

Отдельное опасение вызывает то, что Калифорния, как самый большой и наиболее густонаселенный штат, является законодателем мод в образовательной сфере, поэтому опыт в дальнейшем может быть экстраполирован на всю страну.

Долой Евклида!

Конечно, это не первый эксперимент радикальной реформы преподавания математики в школе. После Второй мировой войны во всех странах думали, как преподавать эффективнее. В США мощные преобразования начались в конце 1950-х годов. Президенту Кеннеди приписывают слова о том, что Америка проиграла космос русским «за школьной партой», которые Кеннеди якобы произнес после полета Гагарина в космос. С тех пор в США, а вслед за ними и в других западных странах начали внедрять «новую математику», которая должна была сделать науку более актуальной, понятной и доступной большинству учеников. При этом из школьного курса выкинули, например, Евклидову геометрию. «Евклид должен уйти» — так сформулировал постулат новой системы образования выдающийся французский математик Жан Дьёдонне. «Новая математика» продержалась вплоть до 1980-х годов, после чего этот опыт признали неудачным.

Предыдущая фотография

Математик, вице-президент Академии педагогических наук РСФСР Алексей Маркушевич

Фото: Н. Максимов / РИА Новости

Академик АН СССР и Академии педагогических наук СССР Андрей Николаевич Колмогоров

Фото: РИА Новости

Следующая фотография

1 / 2

Математик, вице-президент Академии педагогических наук РСФСР Алексей Маркушевич

Фото: Н. Максимов / РИА Новости

Академик АН СССР и Академии педагогических наук СССР Андрей Николаевич Колмогоров

Фото: РИА Новости

В СССР, как известно, реформа школьного математического образования стартовала чуть позже (до этого учились, например, по учебникам Киселева, написанным еще до революции) и была связана с именами математика Алексея Маркушевича и академика Андрея Колмогорова. Последний был председателем Комиссии по математическому образованию при Академии наук и лично написал учебник по алгебре, который переиздается до сих пор, а вот его учебник по геометрии скоро был изъят из обращения.

«У нас до сих пор жив миф о том, что советское математическое образование было лучшим в мире,— говорит педагог-математик, директор Центра непрерывного математического образования в РФ Иван Ященко. — Оно действительно было блестящим, но это касалось специализированных физмат школ, куда со всей страны собирали одаренных детей. При этом говорить о хорошем массовом математическом образовании не приходится. В школах давали огромный объем знаний, который приходилось зазубривать и решать механистически. В итоге те, кто умудрялся продраться сквозь этот поток, действительно становились прекрасными специалистами, но огромное количество школьников получали прививку против математики, не любили и не понимали ее всю жизнь. В итоговом контроле царила имитация, выпускные экзамены помогали выполнять учителя, а билеты устного экзамена по геометрии (кстати, замечательная по сути идея) массово зубрились наизусть без понимания».

Директор Центра непрерывного математического образования в РФ Иван Ященко

Фото: Дмитрий Лебедев, Коммерсантъ

Директор Центра непрерывного математического образования в РФ Иван Ященко

Фото: Дмитрий Лебедев, Коммерсантъ

По словам Ивана Ященко, когда в 2000-х годах в России ввели ЕГЭ, при всех его плюсах и минусах, появилась возможность реально увидеть то, о чем все знали и так: общий срез образования по стране, по математике в первую очередь, оказался очень слабым.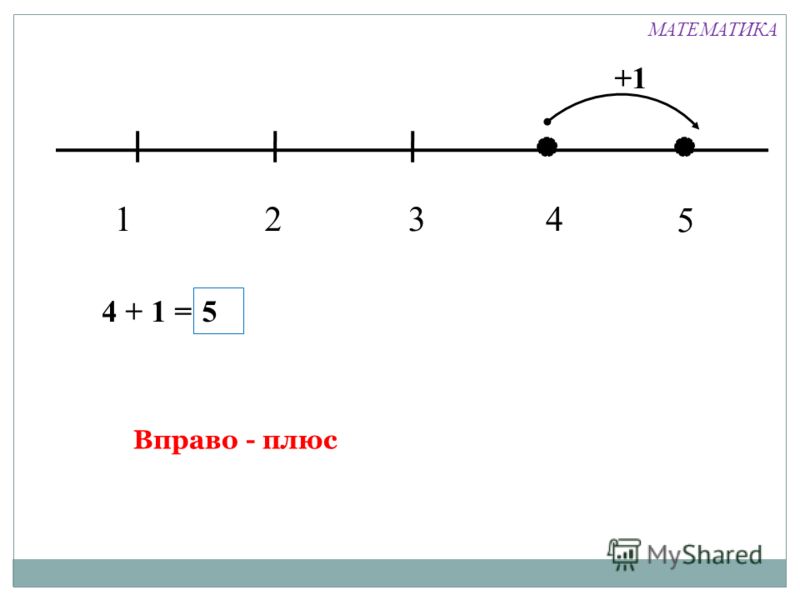 Аттестационный порог составлял три простейших задания, да еще и с выбором ответа. Особенно провальной оказалась геометрия, которую формально из российской программы никто не удалял, но в обязательном экзамене в 11-м классе ее не было.

Жертвы математики

Русский и советский педагог, «законодатель» школьной математики Андрей Киселев

Русский и советский педагог, «законодатель» школьной математики Андрей Киселев

Незнание математики современными школьниками лишь следствие общей нелюбви к точным наукам у большой части общества, считают эксперты. С тех пор как появились доступные информационные технологии и гаджеты, сложные математические умозаключения многим кажутся ненужными для жизни. Кризис интереса к математике в последнее время остается в центре новостной повестки газет во Франции. Здесь математику для изучения выбрало рекордно низкое количество студентов-первокурсников. Аналитики уже заявляют о том, что через несколько лет в стране не будет хватать инженеров и других высококлассных специалистов для воплощения технологической революции 4. 0, которая связана с информационными и цифровыми направлениями.

«Для большинства математика самый трудный школьный предмет, и очень многие ее усваивают совсем плохо, часто не столько в силу лени и отсутствия способностей или упорства, сколько в силу плохих программ или плохого преподавания,— комментирует Светлана Житомирская.— Поэтому желание эту ситуацию изменить совершенно естественно. Если те, кто принимает решения, сами математику не любят и не понимают, страдали от нее в детстве, то им, конечно, нравится идея внедрить курс, который будет даваться без труда. Действительно, на нашей памяти из школьных программ исчезли некоторые распространенные раньше вещи, например алгоритм извлечения квадратных корней. Кажется, что можно отказаться и от запоминания таблицы умножения, от алгоритма длинного деления или навыков строить графики вручную. Но опыт показал, что этого делать нельзя. Когда калькуляторами начинают пользоваться слишком рано, получаются очень плохие результаты в дальнейшем, так как отсутствует фундамент».

Математик Андрей Окуньков

Фото: Евгений Гурко, Коммерсантъ

Математик Андрей Окуньков

Фото: Евгений Гурко, Коммерсантъ

«Мои дети учились на Западе в начале 2000-х, и уже тогда меня поразило, что им преподавали физику без формул — только ее описательную часть,— комментирует профессор Колумбийского университета, Принстона, Калифорнийского университета в Беркли и Высшей школы экономики, профессор Сколтеха, лауреат премии Филдса Андрей Окуньков.— Сейчас такие тенденции доходят и до математики, ее пробуют превратить в описательную, почти гуманитарную науку. Мне очень странно слышать о повсеместных нападках на математику, на попытки изгнать ее из университетов, колледжей или школ, потому что сегодня именно эта наука лежит в основе технологического благополучия каждой страны. В наше время не пища, не энергия и уже даже не информация, а способность обрабатывать и понимать информацию стала самым стратегическим ресурсом. А этого невозможно сделать без большого количества специалистов с математическим образованием».

По словам экспертов, сегодня математически неграмотный человек постоянно становится жертвой более образованных. Огромное количество людей оказываются обманутыми именно потому, что не знают элементарных азов теории вероятности, которые лежат в основе многих финансовых операций на рынке.

«Конечно, преподавание математики на базовом уровне должно быть понятным, доступным и актуальным,— говорит Иван Ященко.— Например, сейчас в школьных программах много времени уделяется такой теме, как “оценивание порядка величин”. Оказывается, это знание очень важно в эпоху, когда мы во всем привыкли доверять гаджетам и компьютерам. Они сильно облегчают нам жизнь, но параллельно увеличивают опасность больших ошибок. В прошлом году газеты написали про забавный случай, когда жительница Австралии покупала туалетную бумагу в интернет-магазине и перепутала рулоны и коробки. Тот факт, что высветилась огромная сумма, в десятки раз больше той, которая должна была быть, ее не смутила. И в итоге ей привезли грузовик туалетной бумаги. Это было действительно смешно, а теперь представьте, если порядок величин перепутал врач, рассчитывающий дозу химиотерапии, или архитектор, проектирующий мосты. Другой важный предмет, который, кстати, с сентября 2022 года будет реализовываться в рамках ФГОС в России наравне с алгеброй и геометрией,— это статистика и теория вероятности,— за отсутствие которой уже много лет критиковалось наше школьное математическое образование. Чтобы продемонстрировать важность подобных знаний, достаточно вспомнить знаменитый исторический пример времен Второй мировой войны, который вошел в науку под названием “систематическая ошибка выжившего”. Когда открыли второй фронт, многие американские бомбардировщики возвращались на базу с пробоинами от зениток. Тогда было решено укрепить броню, выбрав места, куда снаряды попадали чаще всего. На ошибку такого подхода указал математик Абрахам Вальд, который сказал, что инженеры учли только те самолеты, которые вернулись, и, значит, получили некритические поражения, а укреплять нужно те места, повреждение которых вело к крушению самолета. Так что современный человек просто обязан обладать навыками математического мышления, логикой, умением соотносить данные и так далее».

Страшно далека она от народа

Основную проблему российского школьного математического образования эксперты видят как раз в его оторванности от жизни. Известно, что российские школьники год за годом побеждают в самых престижных международных математических олимпиадах и при этом показывают невысокие результаты при оценке так называемой функциональной математической грамотности. По сути, это способность школьника применять в жизни полученные в школе знания. Она оценивается раз в три года в рамках Международной программы по оценке образовательных достижений учащихся — PISA (Program for International Student Assessment). В 2018-м по математике Россия заняла 30-е место (на первых пяти — школьники Азиатского региона). Два года назад в рамках ОГЭ по математике ввели задачи как раз на функциональную грамотность: например, нужно было посчитать, какое оборудование выгоднее провести в дом — газовое или электрическое. Именно из-за таких заданий в прошлом году школьники получили рекордное количество двоек.

«Сейчас в России идет очень тяжелый переход от обязаловки и от зубрежки к осознанному подходу к предмету,— говорит Иван Ященко.— Но при этом мы наблюдаем среди школьников бум интереса к математике, которая сегодня стала социальным лифтом — в России постоянно фиксируется нехватка специалистов в сфере цифровых технологий, и есть крупные компании, которые готовы трудоустраивать выпускников. В России, в частности в Москве и Санкт-Петербурге, Татарстане уже реализуется все то лучшее, что хотят оставить в школьной программе те, кто выступает против нынешней реформы в Калифорнии. Уже несколько лет в школах Москвы введена так называемая Математическая вертикаль, когда практически в каждой школе дети могут учиться по разным программам — базу, причем современную, получают все; те, кому это интересно, могут освоить углубленный курс. А те, кто хочет еще большего,— учатся в ведущих математических школах, которые получают специальную поддержку». Реальную доступность качественного математического образования и развития таланта по всей стране обеспечивают массовые, разумеется бесплатные, математические олимпиады (такие, как проходящий онлайн школьный этап Всероссийской олимпиады школьников на платформе «Сириус», Математический праздник, «Я люблю математику»).

Правда, одновременно в стране год за годом отмечается самый большой дефицит учителей именно по математике — особенно в регионах. То есть программы хорошие, но учить по ним пока некому.

Математика с акцентом

«Российская математика внесла и, очень надеюсь, будет вносить гигантский вклад в развитие мировой математики. У нас много замечательной талантливой молодежи, очень живо интересующейся математикой, так что основания для такой надежды есть,— говорит Андрей Окуньков.— Но есть и волнение, потому что в последнее время связи между российской и мировой наукой во многих областях математики заметно ослабевают, и где-то уже наметилось, увы, некоторое отставание».

Чтобы не дать этому процессу зайти слишком далеко, несколько лет назад было решено провести Международный конгресс математиков в России, где молодежь сможет услышать самых ярких звезд математического олимпа. В последний раз столь значимое и масштабное математическое мероприятие проводилось у нас более полувека назад — в 1966 году.

«Когда конгресс замышлялся, никто и помыслить не мог, каков будет размер проблем на нашем пути. Разумеется, пандемия смешала все карты, многие международные мероприятия уже пали ее жертвой,— говорит Андрей Окуньков.— Но столь же трудно было предположить, что мы, организаторы конгресса, подвергнемся настоящей травле со стороны большого числа как отдельных коллег, так и целых профессиональных сообществ, неоднократно поднимавших вопрос о бойкоте конгресса. Очень нелегко сталкиваться с сознательным стремлением нанести вред, весьма вероятно подогреваемым подсознательным отторжением целой страны. Это особенно удивительно потому, что невозможно представить себе более универсального и объединяющего предмета, чем математика. Население Земли говорит на тысячах очень разных языков, а язык математики один для всех, один для всех стран, для всех категорий граждан, просто один. Он совершенно аполитичен, не знает авторитетов, минимально подвержен моде и выражает собой правду и истину настолько аккуратно, насколько человечество вообще способно об истине говорить. Поэтому каждый раз обидно, когда математика становится разменной монетой в общественных или политических спорах».

Елена Кудрявцева

Как правильно умножать отрицательные числа?

В 6 классе каждый школьник знает отличие между положительным и отрицательным числом и правила умножения. В этой статье объединим эти две темы и попрактикуемся в умножении отрицательных чисел.

Записывайтесь на онлайн-фестиваль для родителей SmartFest!

Ждём вас 8 октября в 13:00. Вместе с педагогами, психологами и другими экспертами в образовании и воспитании ответим на главные вопросы мам и пап.

Бесплатный урок по математике

Записаться

Основные определения

Вспомним, как отличить положительное число от отрицательного, что такое умножение и какие у него свойства.

Начнем с того, что проведем прямую и отметим на ней начало отсчета — точку нуль (0). А теперь укажем направление движения по прямой вправо от начала координат. В этом нам поможет красивая стрелка:

Два главных определения:

Положительные числа — это точки координатной прямой, которые лежат правее начала отсчета (нуля). Иногда рядом с ними ставят знак плюс — «+», но чаще всего положительные числа никак не обозначают. То есть «+1» и «1» — это одно и тоже число.

Запоминаем!

Положительные числа — это те, что больше нуля, а отрицательные — меньшие.

Отрицательные числа — это точки координатной прямой, которые лежат левее начала отсчета (нуля). Их всегда обозначают знаком минус — «-».

Нуль (0) — ни положительное, ни отрицательное число. Вот это ему повезло!

Числовую ось можно расположить как горизонтально (стрелка вверх), так и вертикально (стрелка вправо).

Если стрелка направлена вверх, то в верхней части от начала отсчета всегда расположены положительные числа, а в нижней — отрицательные. Смотрите:

Прямая, на которой отмечена начальная точка, положительное направление и единичный отрезок, называется координатной или числовой осью.

Умножение — арифметическое действие в котором участвуют два аргумента. Один множимый, второй множитель. Результат их умножения называется произведением.

Свойства умножения От перестановки множителей местами произведение не меняется. a * b = b * a Результат произведения трёх и более множителей не изменится, если любую группу заменить произведением. a * b * c = (a * b) * c = a * (b * c)

Вычислять можно в уме, при помощи таблицы умножения или в столбик. Продвинутые школьники могут использовать онлайн-калькулятор. 

Курсы ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Умножение отрицательных чисел

Правило умножения отрицательных чисел: чтобы умножить два отрицательных числа, нужно перемножить их модули. Это значит, что для любых отрицательных чисел -a, -b верно равенство:

• (-а) * (-b) = a * b

А вот как умножить два числа с разными знаками:

• перемножить модули этих чисел
• перед полученным числом поставить знак минус

А теперь упростим правила. Сформулируем их в легкой форме с минимумом слов, чтобы проще запомнить:

• «–» — при умножении минус на минус ответ будет положительным
  или минус на минус дает плюс
• «-+» — при умножении минуса на плюс ответ будет отрицательным
  или минус на плюс дает минус
• «+-» — при умножении плюса на минус ответ будет отрицательным
  или плюс на минус дает минус
• «++» — при умножении плюса на плюс ответ будет положительным
  или плюс на плюс дает плюс.

Примеры умножения отрицательных чисел

Пример 1. Вычислить: (-2)∗(-2) и (-3)∗(-7)

Как решаем:

Вспомним правило: отрицательное число умножить на отрицательное — получается ответ со знаком плюс. Считаем:

 

1. (-2)∗(-2) = 4


2. (-3)∗(-7) = 21

Ответ: 4; 21.

Пример 2. Вычислить: (-11)∗11 и (-20)∗2

Как решаем:

Вспомним правило: отрицательное число умножить на положительное — получается ответ со знаком минус. Считаем:

 

1. -11 * 11 = -121


2. (-20) * 2 = -40

 Ответ: -121; -40.

Пример 3. Вычислить произведение: 5∗(-5) и 12∗(-8)

Как решаем:

Вспомним правило: умножение положительного на отрицательное число дает отрицательный результат. Считаем:

 

1. 5 ∗ (-5)= -25


2. 12 ∗ (-8)= -96

Ответ: -25; -96.

Пример 4. Вычислить произведение: (-0,125 ) * (-6)

Как решаем:

 

1. Используем правило умножения отрицательных чисел:
   (-0,125 ) * (-6) = 0,125 * 6.


2. Выполним умножение десятичной дроби на натуральное число столбиком:
   

Ответ: 0,75.

 

Шпаргалки по математике родителей

Все формулы по математике под рукой

Минус на минус даёт плюс. А почему?

Репетиторы ❯ Математика ❯ Минус на минус даёт плюс. А почему?

Автор: Владимир Л., онлайн репетитор по математике

●

21.09.2011

●

Раздел: Математика

Минус на минус даёт плюс – это правило, которые мы выучили в школе и применяем всю жизнь. А кто из нас интересовался почему? Конечно, проще без лишних вопросов запомнить данное утверждение и глубоко не вникать в суть вопроса. Сейчас и без того достаточно информации, которую необходимо «переварить». Но для тех, кого всё же заинтересует этот вопрос, постараемся дать объяснение этому математическому явлению.

С древних времён люди пользуются положительными натуральными числами: 1, 2, 3, 4, 5,… С помощью чисел считали скот, урожай, врагов и т.д. При сложении и умножении двух положительных чисел получали всегда положительное число, при делении одних величин на другие  не всегда получали натуральные числа – так появились дробные числа. Что же с вычитанием?  С детских лет мы знаем, что лучше к большему прибавить меньшее и из большего вычесть меньшее, при этом мы опять же не используем отрицательные числа. Получается, если у меня есть 10 яблок, я могу отдать кому-то только меньше 10 или 10. Я никак не смогу отдать 13 яблок, потому что у меня их нет. Нужды в отрицательных числах не было долгое время.

Только с VII века н.э. отрицательные числа использовались в некоторых счётных системах, как вспомогательные величины, которые позволяли получить положительное число в ответе.

Рассмотрим пример, 6х – 30 = 3х – 9. Чтобы найти ответ, необходимо члены с неизвестными оставить в левой части, а остальные — в правую: 6х – 3х = 30 – 9, 3х = 21, х = 7. При решении этого уравнения нам даже не встретились отрицательные числа. Мы могли бы члены с неизвестными перенести в правую часть, а без неизвестных — в левую: 9 – 30 = 3х – 6х, (-21) = (-3х). При деление отрицательного числа на отрицательное получаем положительный ответ: х = 7.

Что мы видим?

Действия с использованием отрицательных чисел должны привести нас к такому же ответу, что и действия только с положительными числами. Мы можем больше не думать о практической непригодности и осмысленности действий – они помогают нам решить задачу гораздо быстрее, не приводя уравнение к виду только с положительными числами. В нашем примере мы не использовали сложных вычислений, но при большом количестве слагаемых вычисления с отрицательными числами могут облегчить нам работу.

Со временем, после проведения длительных опытов и вычислений удалось выявить правила, которым подчиняются все числа и действия над ними (в математике они называются аксиомами). Отсюда и появилась аксиома, которая утверждает, что при умножении двух отрицательных чисел получаем положительное.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Задать вопрос

Математика

Курсы по математике 10 класс

Математика

Курсы по математике 9 класс

Математика

Математика 11 класс

Математика

Курсы по геометрии 7 класс

Математика

Курсы по алгебре 7 класс

Математика

Алгебра 8 класс

Математика

Курсы по геометрии 8 класс

Французский язык

Курсы французского языка для начинающих

Откуда взялись плюс и минус?

На этот раз любопытные Кубик и Шарик решили выяснить, когда человечество стало использовать плюсы и минусы. Кажется, они были всегда…или нет?

– Шарик, расскажи, со знаками действий все же просто, да? Вот в Древнем Египте, как мне говорили, египтяне уже писали плюс и минус!

– Почти, Кубик. Смотри, в древнем Египте был иероглиф , которым обозначали сложение и вычитание. Согласно некоторым источникам, это был специальный знак, используемый только в математике. Действительно, в Московском папирусе есть такие знаки. Поскольку египтяне писали и справа налево, и слева направо, то этот символ означал и “прибавить” и “отнять” – в зависимости от направления текста .

– А что такое Московский папирус?

– Московский папирус – это один из двух египетских математических папирусов, дошедших до наших дней. Он составлен примерно в 1850 году до нашей эры и считается одним из древнейших математических текстов. Посмотри внимательно! Видишь, там есть ноги? Значит, что-то складывали или вычитали.

Текст Московского папируса

То, что ты видишь, не совсем настоящий папирус. Это специальный текст, переведенный учеными на белый лист, чтобы было легче расшифровывать и изучать его.

– Слушай, Шарик, а почему этот папирус “Московский”? Его что, в Москве нашли? Вот это да!

– Нет, Кубик, нашел его в Египте один из основателей русской египтологии Владимир Голенищев. А вот хранится “папирус Голенищева” в Москве, да не где-нибудь, а в Музее изобразительных искусств им. А. С. Пушкина. Ты его наверняка знаешь как “Пушкинский музей”.

– Теперь понятно. А что там с ногами?

– Ученые-египтологи тщательно расшифровывали и изучали папирус, и пришли к выводу, что эти знаки не были аналогами знаков “плюс” и “минус”, а были словами “добавить” и “отнять”. И в других, нематематических текстах они тоже встречаются.

– Наверное, дело в том, что в древние времена математика была практической дисциплиной, использовалась в основном для расчетов между людьми. Получается, абстрактные понятия и знаки были не нужны.

– Точно, Кубик. Ну что ж, символ есть, но это не знак, а слово…

– А я думал, мы уже все нашли и расследовали, а оказывается… Все начинать сначала! Где у нас там еще математикой занимались?

Шумерская таблица умножения

– Давай отправимся к шумерам, в Междуречье. До нас дошло огромное количество глиняных табличек, в том числе с математическими расчетами. Вот, например, таблица умножения: таких табличек найдено очень много, а часть из них с ошибками. Есть предположение, что таблицу умножения изучали в школах.

Каждая строчка начинается со слова “умножить”.

– Шарик, ну вот же, мы нашли! Вот же оно, обозначение умножения, сложения, вычитания…

– Дорогой Кубик, ты снова путаешь! Для нас сегодняшних это выглядит, как знаки, но на самом деле это не математические знаки, а слова!

– умножить, – отнять, – сложить.

Есть множество табличек, где ученые только по числам догадываются, что же делали с числами, то есть знаки действий не обозначались никак. Математика – это очень практическая дисциплина, она служила бытовым и религиозным целям. Абстрактных понятий пока еще нет, значит, и специальных знаков не нужно.

– Ну надо же! Раз в Месопотамии знаков нет, значит, и в Древней Греции их тоже нет?

– Не совсем так, Кубик. Древнегреческая цивилизация была первой, где создавались философские школы и изучались науки не с практической, а с исследовательской, научной целью. Были люди, которым интересно было познавать и открывать новое, а были люди, готовые за это платить. До нас дошло огромное количество греческих математических папирусов.

Греческий математический папирус

– Папирусов? Ты хочешь сказать, что и в Греции писали на папирусе?

– Конечно, потому что это был дешевый и легкий в изготовлении материал, очень удобный. Его использовали в средиземноморье вплоть до 12 века, пока он не был вытеснен бумагой.

Но вернемся к математике. В 3 веке до нашей эры, в Александрии, жил величайший математик Евклид. Он оставил огромный труд “Στοιχεῖα ” – “Начала” , или в английской традиции “Элементы”, которым, как учебником по геометрии, пользовались до середины 19 века. Сохранились несколько оригинальных листов, и многочисленные переводы на латинский и английский. Посмотри, вот греческий текст и перевод на английский, все описывается словами.

Евклидовы «Начала»

Чуть позднее, в работах Диофанта во 2 веке до нашей эры, появляются первые абстрактные символы, обозначающие возведение в степень и вычитание, а также символы для обозначения отрицательных чисел.

– Эврика! Нашли! Вот же они, первые математические символы!

Современные символы и символы Диофанта

– Да, Шарик, ты прав, это именно символы, не слова, но, увы, они остались только в книгах Диофанта и не были использованы другими математиками. Более того, каждая математическая школа придумывала свои символы или описывала действия словами. Никакой стройной системы не было.

– Как же так? Почему?

– Людей разделяли расстояния, войны и языки, одни философские школы и ученые не знали, что делается в других. Так продолжалось довольно долго, необходимость использовать символы вместо слов была, но единой записи пока не было. Самое удивительное, что аж до 15 века все действия даже в научных работах по-прежнему описывались словами или символами, используемыми только одним ученым.

Поскольку в те времена большинство научных книг писалось и издавалось на латыни, а все математические действия записывали словами, было не сразу понятно, что книга на самом деле посвящена математике.

– Вот бы их удивили наши учебники! Мало того, что везде какие-то непонятные знаки, так еще и язык не тот. Постой, Шарик, так кто же все-таки придумал плюс и минус?

– В 1417 году выходит “Книга о небе и мире” Николая Орема, в которой для обозначения сложения используется знак +. Поскольку книга была рукописная, то, скорее всего, это было сокращенное написание et, от которого осталась лишь буква t, похожая на привычный нам знак сложения. Писали, например, “4 et 5” , что в переводе с латинского означало “4 и 5”. До изобретения первого печатного станка оставалось еще почти 40 лет, поэтому записи легко могли сокращаться и писаться любыми символами, удобными автору.

– И что, вот теперь уже во всех книгах используют знак +?

– Нет, Кубик, информация в те времена распространялась медленно, и использование знака в одной книге не означало, что это увидели другие ученые. Некоторые из них использовали другие сокращения, которые им казались логичными и понятными. Например, в европейских книгах 15 века можно встретить обозначения p̄ и m̄ (p и m c чертой наверху), в переводе с итальянского più – “больше”, а meno – “меньше”.

– Шарик, я помню, что первая библия была напечатана Гутенбергом в 1455 году. Значит, после этого книги уже печатались, а не переписывались?

“Быстрый и наглядный счет для торговцев” Видмана

– Не совсем так, но довольно быстро этим величайшим изобретением стали пользоваться. Книги, безусловно, стали доступнее. В 1489 году немецкий математик Иоганн Видман публикует (именно публикует и довольно большим тиражом) книгу “Быстрый и наглядный счет для торговцев”, где впервые появляется привычная для нас запись арифметических действий. Однако в этой книге + и – обозначали еще не знаки действий, а дебиторскую и кредиторскую задолженность.

Но это была уже печатная книга, доступная по цене не только ценителям книг, но и торговцам, для которых она и писалась. Получается, об этой удобной записи могли узнать многие! В 1518 году в Германии издается книга Генриха Грамматеуса, где + и – уже используются для арифметических действий.

– Ну вот же! Смотри, уже и арабские цифры, и плюсы, и минусы, все уже выглядит привычно! Но где же знак “равно”?

– До его появления еще почти 40 лет, но помнишь, в древности почти ничего не менялось за 300 лет, а тут все стремительно меняется.

– Да уж, прошло всего-то сто лет с печати первой книги!

– Правильно! В 1557 году выходит книга Роберта Рекорда, валлийского математика и врача, преподавателя Оксфорда, где он впервые использует одновременно плюс и минус, а также в первый раз использует знак равенства.

Книга Рекорда

– Вот она, привычная нам запись! Знаки выглядят большими, но даже я могу разобрать, что там написано.

– Не только тебе понравилась такая запись, она довольно быстро распространилась среди ученого мира и стала общепринятой.

Вот такая непростая история у привычной нам записи математических действий. А вот знаки “умножить” и “разделить” даже сейчас в школах разных стран записывают по-разному!

Math Plus Academy — интерактивные онлайн-классы по повышению квалификации

• Зарегистрируйтесь сейчас

Научите своих детей ДУМАТЬ Не просто запоминать

Проверенные курсы математики от KG до алгебры 2

• Веселые, увлекательные занятия в небольших группах
• Под руководством сертифицированных учителей математики
• Частное репетиторство включено
• Еженедельные занятия и практика

Зарегистрируйтесь сегодня, количество мест ограничено!

Учащиеся учатся читать и писать цифры от 0 до 9, развивают понимание количества (больше/меньше) и …

Учащиеся осваивают сложение и вычитание однозначных чисел, используя различные стратегии, а также…

Учащиеся учатся складывать и вычитать дву- и трехзначные числа в уме, а также изучать сложные…

Учащиеся осваивают таблицы умножения и продвинутые методы вычитания, получая при этом…

Учащиеся осваивают продвинутые методы двух- и трехзначного умножения вместе с делением. ..

Учащиеся осваивают мощные техники умножения и деления с целым числа, десятичные дроби…

Учащиеся осваивают целые числа и целочисленные операции. Учащиеся учатся решать сложные задачи…

Учащиеся осваивают операции с целыми числами, показателями степени и порядком выполнения операций. Студенты учатся с…

Учащиеся узнают о геометрических построениях и жестких преобразованиях. Учащиеся знакомятся с…

Учащиеся изучают основное содержание Алгебры 2 с помощью последовательностей, шаблонов, визуальных моделей и ча…

Учащиеся Лаборатории программирования будут решать ряд задач! Каждый вызов…

Элементарная математика Участники команд участвуют в математических соревнованиях круглый год. Соревнования по математике…

Математическая команда средней школы Круглогодично готовится к математическим олимпиадам. Мы практикуем…

“Моя дочь посещала Кумон, но ей это не нравилось. Это было сплошное повторение, и я просто не видел в этом смысла. Я был в восторге, когда мы перешли в Академию Математика Плюс. Она любит ходить на занятия и даже выполняет домашнее задание по математике утром, прежде чем я отвожу ее в школу!»

— Г. Браун

“Спасибо за создание дополнительных онлайн-курсов по математике! Это было очень важно для моего сына, который посещает Академию Math Plus с первого класса и получает от этого удовольствие. ”

— В. Нарделла

“Я никогда не чувствовал, что мои дети испытывают трудности в школе. Я искал дополнительные занятия, которые были бы одновременно интересными и интересными!”

— Г. Ван

“Моей семье все нравится в Math Plus, , особенно то, как преподается математика, и подходы, которые они используют, чтобы научить детей понимать математику , а не просто решать суммы. ”

— П. Мурукутла

1. Выберите курс математики

В зависимости от класса и уровня способностей вашего ребенка.

2. Выберите время занятий

Выберите время занятий, которое соответствует вашему расписанию.

3. Присоединяйтесь к классам

Начните путь к долгосрочному успеху.

Отношение — это ВСЕ в математике

«Это не тот способ, которым я учился в школе, но мне так НАМНОГО больше нравится! Это намного проще!»

— JT о умственном умножении

«Я мог бы остаться в Math Plus навсегда… Мне здесь нравится. Хотел бы я, чтобы в школе преподавали математику так же».

— Эбигейл

“Мне это нравится! Это как тренировка для моего мозга!”

— Анджелина решает сложную задачу

“Сегодня вечером я отличился вычитанием! Я человек-калькулятор!”

— Нейт о умственном вычитании

21 век требует нового типа учеников — не того, кто может отвечать только наизусть, а того, кто может думать и решать проблемы . В Math Plus Academy ваш ребенок может обрести уверенность, вдохновиться и научиться думать , а не просто запоминать.

1

Проверенный учебный план

В отличие от традиционных репетиторских компаний, Math Plus Academy помогает учащимся преуспеть, сосредотачиваясь на том, чего не делают в школах, — арифметике в уме, решении задач и критическом мышлении.

2

Еженедельные уроки, которые бросают вызов

Еженедельные одночасовые занятия начинаются сразу после окончания школы. Мы обучаем стратегиям, которые дополняют то, что учащиеся изучают в школе, и помогают им развить более сильное чувство числа и навыки решения задач.

3

Увлеченные учителя и маленькие классы

Все наши учителя имеют сертификаты штата, хорошо подготовлены и любят математику. Наши классы ограничены 10 учениками с тремя инструкторами, поэтому мы можем бросить вызов каждому ребенку.

4

Программа вознаграждений

Наша программа вознаграждений основана на получении очков опыта, как в видеоигре. Студенты «повышают уровень», чтобы заработать привилегии и призы. Наша система вознаграждений мотивирует студентов стремиться к мастерству.

5

Легкий макияж и дополнительная поддержка один на один включены в комплект

Пропустили занятие? Просто найдите еще один в расписании и посетите этот класс в качестве макияжа. Вашему ребенку нужна помощь с заданиями? Забронируйте бесплатное занятие один на один с репетитором, когда вам это нужно.

---

Академия Математика Плюс

9681 Лесопилка ул.
Пауэлл, Огайо 43065

Условия | Политика конфиденциальности

Школа MathPlus | Newton MA Math School

Запросить бесплатную оценку

Спасибо за всю прекрасную работу, которую вы проделали с Лиамом. Теперь у него такая замечательная база в математике, и его уверенность в том, что он может сделать, переполняет всю комнату. Лиам не боится браться за сложные математические концепции и уравнения, даже если он еще не выучил эти концепции. Мы должны вам выразить огромную благодарность и признательность за то, что вы привели его к этому моменту. Ему очень понравились ваши занятия, и он с нетерпением ждет их каждую неделю.

Большое спасибо!

Cára Mezzetti Calmon

Math Plus — феноменальная программа, она действительно продвигает детей вперед в математике. Хотя первоначальные концепции могут показаться трудными для понимания, и так много областей затронуто, Белла сказала, что все будет хорошо, и так оно и было! Она закладывает отличный фундамент, как посадка семян, и к середине года они укореняются, растут и зацветают. Это было так важно для детей — иметь что-то сложное и веселое, видеть, как растет их уверенность и они преуспевают. Белла отлично ладит с детьми, очень ободряет и поддерживает, если им нужна помощь. Мы были рады порекомендовать наших друзей, многие из которых перешли с других программ — MathPlus охватывает больше материала, а обучение немного меньше, и месяц за месяцем. Настоятельно рекомендую!

Кэтрин Чан

Школа MathPlus — замечательная школа. У меня не хватает слов, чтобы похвалить академический уровень этой школы.

Мой 7-летний сын учится здесь пару месяцев, и его успехи очевидны. Теперь он может решать сложные задачи.

Миссис Белла Гершт, учитель математики, превосходна. Она очень добрая и терпеливая со всеми детьми. Ее методы обучения великолепны, как и ее математические книги и материалы. Студенты могут легко следовать ее объяснениям и решать проблемы без поддержки. Ее страсть к математике заразительна, и моему сыну это нравится.

Очень рекомендую отправлять сюда своих детей.

Александра Василиу

MathPlus спас жизнь в начале Covid. Мой сын (в то время 7 лет) был записан в программу, и я сразу же был уверен, что он многому научится, пока его обычная школа выясняет ситуацию. Как родитель, я могу сказать о MathPlus только положительные отзывы. Мой сын теперь просто любит математику и ждет нового интересного и понятного материала. Учебная программа, которую они предлагают, является прекрасной возможностью улучшить или расширить знания вашего ребенка по математике. Он охватывает не только основы математики, но также содержит раннее введение в геометрию и алгебру. Уроки перегружены, но мой 8-летний сын без проблем их выдерживает, время летит быстро, и он учится через понимание, а не просто запоминая. Он становится умнее с каждым днем ​​и повышает свой уровень математики с каждым уроком. Мы взяли весенний семестр 20-го года, летний класс и в настоящее время тоже зачислены. Я определенно рекомендую MathPlus и их замечательного учителя. Несколько моих друзей записались в этом году, и их детям это тоже нравится.

Победа

Наши девочки в MathPlus почти 2 года. Программа не только дает нашим дочерям базовые знания по математике, но и пробуждает в них радость и страсть к учебе. Они значительно улучшились за короткий период времени. Мы, родители, довольны прогрессом. Мы настоятельно рекомендуем MathPlus семьям, которые хотят получить сложную и всестороннюю учебную программу для своих детей.

Алиша и Уильям Нгуен (родители учащихся школы MathPlus)

После того, как наши дети начали посещать школу MathPlus, мы заметили значительный прогресс в их математических знаниях. Мы также заметили, как им нравится ходить на занятия, потому что задания интересные и веселые! Разнообразие задач и способов подачи классной и домашней работы велико. Кроме того, Белла очень хороший и талантливый учитель. Мы настоятельно рекомендуем школу MathPlus родителям, которые хотят вывести своих детей на новый уровень в математике.

Лариса Закирова

Мы присоединились к MathPlus, когда моя дочь была в 3-м классе, так как ее учитель в начальной школе Бруклина беспокоился о ее математических способностях. Я думал, что дополнительная математическая практика поможет ей достичь среднего уровня математики в школе. К моему удивлению, к концу третьего класса она стала лучшей ученицей по математике в своем классе. Мы продолжали посещать MathPlus, и моя дочь продолжала оставаться одной из лучших учениц в своем классе. И теперь она будет сдавать самый высокий уровень математики в средней школе. Она планирует посещать MathPlus во время учебы в старшей школе, чтобы подготовиться к вступительным экзаменам в колледж. Мы очень ценим прекрасную работу учителей MathPlus, их внимание к каждому ребенку и энтузиазм в изучении математики.

Юлия Голдберг

Я твердо верю, что отношения между ребенком и учителем являются основой успеха. Подход учителя к ученикам может сильно повлиять на результаты. Мой сын попробовал программу pre-k в другой математической школе, и это было непросто для нас обоих. Класс был слишком большим, он чувствовал себя потерянным и никогда по-настоящему не общался со своим учителем; он был несчастен, я чувствовал себя виноватым, и на этом все закончилось. Так что у меня были сомнения, когда он начал заниматься математикой в ​​детском саду в Math Plus с Беллой в сентябре этого года. Перенесемся на 4 месяца вперед; Я счастлив и чувствую облегчение – мой сын очень увлечен, любит ходить на занятия и чувствует себя частью группы. Классы небольшие (4-5 детей), и это лучшее из обоих миров, они по-прежнему полу-приватные, и они также могут общаться с другими детьми и учиться вместе. Мы оба с нетерпением ждем новых программ по математике и других программ в Math Plus в будущем.

Яна Рогозина

Моя дочь занимается в субботней утренней программе «Математика Плюс» с сентября 2015 года. В школе замечательный и очень индивидуальный подход к обучению математике. Дети ориентируются на «нестандартное мышление», разгадывая загадки и текстовые задачи и одновременно развивая прочную основу для базовых арифметических навыков. Навыки, приобретенные в математической школе, также пригодились ей при выполнении ее обычной школьной работы. Я с уверенностью рекомендую эту школу родителям, которые ищут индивидуальный и заботливый подход к развитию математических и логических навыков при работе с младшими учениками. Жаль, что я не знал об этой школе в прошлом году. Веселый, но дисциплинированный подход к обучению математике.

Зельфонд Аня, мама ученицы 1 класса.

Белла очень знающий учитель. Она делает занятия очень интересными и увлекательными для моих детей. Мы очень довольны успехами наших детей по математике, они любят ходить в Math Plus

Ирина Фикслер – мама 2 учеников Макса 2-го класса и Тима Детский сад

Мой сын начал заниматься математикой с Беллой в 3 года, что может показаться рано. Однако ей удалось организовать класс таким образом, чтобы развить их логику, когнитивные навыки в решении задач и загадок. Год спустя мой сын уже может легко писать числа, решать простые математические задачи и логически соединять точки. Очень рекомендуем Беллу.

Мать Леона-Лены Календжан

От всего сердца я хотел бы поблагодарить вас за прекрасный опыт работы с программой Pre-K Math. Моему сыну это очень нравится. Мне не нужно дважды просить его пойти на урок или сделать домашнее задание. Занятия проходят очень увлекательно и интересно. Идея создания историй, основанных на математике, очень интересна. Могу с уверенностью сказать, что у моего сына обострилось восприятие вещей и логика. Мне также нравится размер нашего класса. Я твердо чувствую, что каждый ребенок получает достаточно вашего личного внимания. Это очень важно. С нетерпением жду следующего года в программе детского сада.

Регина Сабитов

У Ника хорошие математические способности. В целом кажется, что его математическая работа для него несложна, и мы считаем, что субботний урок дает ему более сильную математическую основу для будущего обучения. Это обеспечивает полезную подготовку к алгебре и геометрии в средней школе. В целом программа оказалась очень полезной.

Арина Гоуэн 4 класс Ник

Мой сын начал заниматься математикой с Беллой в 3 года, что может показаться ранним. Тем не менее, она смогла организовать класс таким образом, чтобы развить их логику, когнитивные навыки в решении задач и загадок. Год спустя мой сын уже может легко писать числа, решать простые математические задачи и логически соединять точки. Очень рекомендуем Беллу.

Мать Леона-Лены Календжан

Мой 8-летний сын вообще аналитический и любознательный, поэтому я искала для него занятие типа STEM. Я так рада, что мы нашли Design Squad! Класс обеспечивает игровую атмосферу для обучения по очень широкому кругу тем. Мероприятия варьируются от изучения древней египетской культуры и ритуалов до создания роботов, изготовления натуральных средств из пчелиного воска и научных экспериментов — мой сын любит разнообразие! У инструктора, миссис Ник, масса энергии, и ей явно нравится то, что она делает — она может увлечь моего сына и поддерживать его интерес неделю за неделей.

Шрабштейн, Аннат – мама Ари, 8-летнего ученика группы дизайнеров

Я очень впечатлена школой Math Plus. Мой четырехлетний сын добился больших успехов за очень короткое время и сразу же очень заинтересовался математикой. В классе очень мало детей, поэтому каждый ребенок получает много внимания от учителя. Я особенно благодарен Белле Гершт за ее уникальную стратегию обучения. Она очень преданный и профессиональный учитель, который делает все возможное, чтобы убедиться, что ваш ребенок преуспевает в математике и других науках.

Катрина Генерозов, доктор фармацевтических наук

Когда мы начали отдавать нашу дочь в MathPlus в третьем классе, она говорила что-то вроде: «Я не силен в математике». Мы сразу же увидели улучшения в ее понимании и комфорте в математике. Через три года она неизменно была лучшей в своем классе по математике в своей французской двуязычной школе. В этом году она была отмечена за то, что вошла в 1% лучших по всему миру в Concours Kangourou, математическом конкурсе, проводимом учащимися французских школ по всему миру. Теперь она говорит: «Математика — мой любимый предмет!»

Тамара Кетт, мать ученицы 6-го класса

Моя дочь Рене посещает школу MathPluss с детского сада. Я видел, как сильно возросла ее любовь к изучению математики, и ее уверенность в себе взлетела, когда она понимает и решает задачи. Я очень доволен уровнем профессионализма в MathPlus и небольшим размером класса. Я убежден, что она находится на продвинутом уровне, потому что мы начали ее склоняться на уровне детского сада. Выученные методы продолжают делать математику веселой и легкой для Рене и во втором классе. Я настоятельно рекомендую MathPluss всем родителям, которые хотят заинтересовать своих детей и привить любовь к учебе с раннего возраста.

Симона Шустер Цеглин, родитель ученика MathPlus.

У меня двое сыновей, которые в этом году учатся в 3-м и 5-м классах. Я вижу, что они заинтересованы и очень вовлечены. Будучи весьма одаренными в математике, им все равно приходится тратить больше часа на выполнение домашнего задания по математике каждую неделю, так как задачи сложные и сложные. Я хотел бы поблагодарить преданных учителей MathPlus, которые помогают моим детям не только развивать математические навыки, но и ценить красоту математики.

Михаил Чумак, к.т.н. in Math, 179 School Graduate

Я просто хотел бы сказать, насколько я ценю подход MathPlus School к обучению математике. Математическая программа была тщательно разработана не только для того, чтобы преподавать предмет на действительно сложном уровне, но и для того, чтобы вдохновлять детей и развивать их подлинный интерес к математике. Учителя в школе очень опытны, хорошо осведомлены и стремятся обеспечить наилучшее математическое образование. Я очень впечатлен успехами моего сына в изучении предмета и могу рекомендовать эту программу детям, которые ищут сложную и дружелюбную среду для изучения математики.

Рубин Э. Магистр технических наук. Израильский технологический институт

Моя дочь посещает школу MathPlus в течение одного семестра. Она посещает уроки математики и русского языка. Лора уже значительно улучшила математические навыки с начала семестра. Теперь она может решать сложные задачи олимпиадного уровня. Благодаря уроку русского языка моя дочь может читать русскую литературу и писать по-русски. Спасибо школе MathPlus за прекрасную программу с широким выбором предметов.

Нина Ольчаный Инженер М.С. 57 Выпускник математической школы

Мои дети присоединились к программе MathPlus в прошлом году. Меня очень впечатлил уровень математической программы, который выходит далеко за рамки обычного школьного уровня. У моих детей наконец-то появился шанс полюбить математику. Это намного больше, чем мы могли бы ожидать от программы дополнительного образования после школы.

Дориана Фроим, доктор философии. кандидат биологических наук, выпускник Массачусетского технологического института

Отрицательные и положительные правила | Сложение, вычитание и примеры

Что такое целые числа?

Целое число — это число, которое можно записать без дробной части. Другими словами, целое число — это целое число, которое может быть положительным, отрицательным или равным нулю. Следовательно, мы можем сказать, что целые числа представляют собой совокупность целых чисел и отрицательных чисел. Набор целых чисел представлен Z и может быть записан как – 

Z = { …….. – 3, – 2 , – 1, 0, 1, 2, 3 …….. }

Какие отрицательные и положительные целые числа?

В соответствии с натуральными числами, 1, 2, 3, 4, 5 …… и т. д., мы создаем новые числа, -1, -2, -3, -4, -5 и так далее. Эти числа называются минус один, минус два, минус три и т. д. такие, что – 

1 + ( – 1 ) = 0

2 + ( – 2 ) = 0

3 + ( – 3 ) = 0

Итак, – 1 называется минусом 1, -2 называется минусом 2, и каждое отрицательное число противоположно своему положительному аналогу. Если мы объединим эти отрицательные числа с положительными, вместе мы получим набор чисел, которые мы называем целыми числами.

Числа 1, 2, 3, 4 ….. являются натуральными числами и называются положительными целыми числами, а числа – 1, – 2 , – 3 и т. д. называются отрицательными целыми числами.

Символ для отрицательных целых чисел

Мы используем символ «–» для обозначения отрицательных целых чисел, и тот же символ используется для обозначения вычитания. Однако контекст, в котором используется этот символ, проясняет, хотим ли мы использовать его для отрицательного целого числа или для вычитания. Давайте разберемся на примере.

Предположим, мы запишем число – 5. Это будет означать «минус пять». Точно так же – 17 будет читаться как «минус семнадцать».

Теперь напишем 5 – 3. Здесь мы видим, что «-» стоит между двумя числами. Это будет читаться как «пять минус три». Следовательно, здесь символ использовался для вычитания двух чисел.

Символ для положительных целых чисел

Мы используем символ «+» для обозначения положительных целых чисел, и тот же символ используется для обозначения сложения. Однако контекст, в котором используется этот символ, проясняет, хотим ли мы использовать его для положительного целого числа или для сложения. Давайте разберемся на примере.

Предположим, мы пишем число + 5. Это будет читаться как «плюс пять». Точно так же + 17 будет читаться как «плюс семнадцать».

Теперь напишем 5 + 3. Здесь мы видим, что «+» находится между двумя числами. Это будет читаться как «пять плюс три». Следовательно, здесь символ использовался для сложения двух чисел.

Здесь важно отметить, что если с числом не связан ни один знак, оно читается как положительное число. Например, + 5 также можно записать просто как 5. 

Отрицательные и положительные целые числа в числовой строке

Мы узнали, как представлять целые числа в числовой строке. для представления целых чисел на числовой прямой. Напомним, что числовая линия — это прямая горизонтальная линия с числами, расположенными через равные промежутки, которая обеспечивает визуальное представление чисел. Основные операции, такие как сложение, вычитание, умножение и деление, могут выполняться на числовой прямой. Числа увеличиваются, когда мы движемся к правой стороне числовой линии, и уменьшаются, когда мы движемся влево. Целые числа представлены в числовой строке, как показано ниже – 9. 0008

Выше показано визуальное представление стандартной числовой строки для представления целых чисел. Как хорошо видно, при движении слева направо значение целых чисел увеличивается, а при движении справа налево — уменьшается.

Давайте разберемся на примере

Построим 6 и – 6 на числовой прямой.

Правила сложения целых положительных и отрицательных чисел

Мы знаем, как складывать два целых числа. Мы можем складывать целые числа таким же образом, с той лишь разницей, что мы должны выполнять сложение и отрицательных чисел. следующие правила должны соблюдаться для сложения целых чисел –

1. Чтобы сложить два целых положительных или два отрицательных числа, мы складываем их абсолютные значения и присваиваем сумме знак слагаемого.
2. Чтобы сложить положительное или отрицательное целое число, мы определяем разность их абсолютных значений и присваиваем сумму слагаемого, имеющего большее абсолютное значение.

Давайте разберемся на примере.

Пример

Предположим, у нас есть два целых числа, 1258 и 3214, и мы хотим найти их сумму.

Решение

Сначала мы проверим знак обоих чисел. Мы видим, что оба числа одного знака и являются целыми положительными числами. Поэтому по правилам, изложенным выше, мы сложим абсолютное значение обоих чисел и присвоим им положительный знак. У нас будет

1258 + 3214 = 4473

. Рассмотрим другой пример.

Предположим, у нас есть два целых числа — 523 и 937, и мы хотим найти их сумму.

Решение

Мы видим, что складываемые числа имеют разные знаки, поэтому для их сложения находим разность их абсолютных значений и присваиваем знак слагаемого, имеющего большее абсолютное значение. Таким образом, мы будем иметь,

( – 5523 ) + 937 = 937 – 523 = 414

Вышеприведенные правила можно резюмировать как –

Правила вычитания положительных и отрицательных целых чисел

Мы знаем, как вычитать два целых числа числа. Важно помнить, что в целых числах мы не можем вычесть большее целое число из меньшего целого числа. В случае вычитания целых чисел из целых чисел мы можем вычесть большее целое из меньшего целого. Также важно помнить, что вычитание — это процесс, обратный сложению.

При вычитании целых чисел необходимо соблюдать следующее правило – 

Если a и b два целых числа, то для вычитания b из a меняем знак b и прибавляем его к a, т. е. a– b = a + ( – b ) 

Давайте разберемся на примере.

Пример

Предположим, мы хотим вычесть – 1235 из 4532

Решение

4532 – ( – 1235 ) = 4532 + 1235 = 5767

Следовательно, 4532 – ( – 1235 ) = 5767

Вышеприведенные правила можно суммировать как –

9

Мы знаем, что процесс нахождения произведения двух или более чисел называется умножением, а полученный таким образом результат называется произведением . Умножение целых чисел похоже на умножение натуральных чисел и целых чисел, за исключением того факта, что мы также должны позаботиться об умножении отрицательных чисел.

При умножении целых чисел соблюдаются следующие правила – 

Случай 1 – Когда у вас есть два целых числа противоположных знаков – Произведение двух целых чисел противоположных знаков равно аддитивной обратной величине произведения их абсолютные значения. Это означает, что для того, чтобы найти произведение положительного и отрицательного целых чисел, нам нужно найти произведение абсолютных значений и присвоить произведению знак минус. Давайте разберемся на примере.

Пример

Предположим, у вас есть два числа 7 и -4, и вы хотите найти произведение. Умножение 7 и -4 будет дано

7 x (– 4) = – (7 x 4) = – 28

Аналогично, (– 6) x 9 = – (6 x 9) =  = – 54

Случай 2 – Произведение двух целых чисел с одинаковыми знаками равно произведению их абсолютных значений. Это означает, что для того, чтобы найти произведение двух целых чисел, независимо от того, являются ли оба числа положительными или оба отрицательными, нам нужно будет найти произведение их абсолютных значений. Давайте разберемся в этом на примере.

Пример

Предположим, у вас есть два числа 7 и -4, и вы хотите найти произведение. Умножение – 7 и -4 будет равно

(– 7) x (– 4) = (7 x 4) = 28

Аналогично ( 6 ) x 9 = ( 6 x 9 ) = = 54

Приведенные выше правила можно резюмировать следующим образом: –

Правила деления положительных и отрицательных целых чисел

Мы знаем, что деление – это процесс повторяющегося вычитания. То же самое относится и к делению целых чисел. В делении есть четыре важных члена, а именно делитель, делимое, частное и остаток. Формула для делителя составляет все эти четыре термина. На самом деле именно соотношение этих четырех членов между собой определяет формулу деления. Если мы умножим делитель на частное и прибавим результат к остатку, то получим делимое. Это значит,

Делимое = Делитель x Частное + Остаток

Напомним, что деление целых чисел является обратным процессом умножения. Распространим ту же идею на деление целых чисел. Для деления целых чисел соблюдаются следующие правила: 

Случай 1 – Частное двух целых чисел, как положительных, так и отрицательных, является положительным целым числом, равным частному соответствующих абсолютных значений целых чисел. Это означает, что при делении двух целых чисел с одинаковыми знаками мы делим значения независимо от знака и ставим положительный знак в частном. Давайте разберемся на примере.

Пример

Предположим, у вас есть два числа — 20 и -4, и вы хотите разделить первое целое число на другое. У нас будет

-20 ÷ -4 = $\frac{20}{4}$ = 5

Случай 2 – Частное положительного и отрицательного целых чисел является отрицательным целым числом, и его абсолютное значение равно частное соответствующих модулей целых чисел. Это означает, что при делении целых чисел с разными знаками мы делим значение независимо от знака и ставим в частное знак минус. Давайте разберемся на примере.

Пример

Предположим, у вас есть два числа — 20 и 4, и вы хотите разделить первое целое число на другое. Мы будем иметь,

-20 ÷ 4 = – $\frac{20}{4}$ = – 5

Приведенные выше правила можно резюмировать как – 

Свойства отрицательных и положительных целых чисел

Давайте теперь обсудим некоторые свойства положительных и отрицательных целых чисел – 

Свойство замыкания

Свойство замыкания утверждает, что когда операция выполняется над двумя числами, результат также будет того же типа, что и числа, над которыми была выполнена операция выполненный.

Следовательно, сложение, вычитание и умножение как положительных, так и отрицательных целых чисел удовлетворяют свойству замыкания, в то время как деление целых чисел не удовлетворяет свойству замыкания.

Переместительное свойство

Переместительное свойство утверждает, что при выполнении операции над двумя числами порядок, в котором расположены числа, не имеет значения.

Для любых двух целых чисел, a и b,

a + b = b +a

a – b ≠ b – a

a x b = b x a

a ÷ b ≠ b ÷ a

Следовательно, сложение и умножение как положительных, так и отрицательных целых чисел удовлетворяют коммутативному свойству, в то время как вычитание и деление как положительных, так и отрицательных целых чисел не удовлетворяют коммутативное свойство.

Ассоциативное свойство

Ассоциативное свойство утверждает, что когда операция выполняется более чем с двумя числами, порядок, в котором расположены числа, не имеет значения.

Для любых трех целых чисел a, b и c

a + (b + c) = (a + b) + c

a – (b – c) ≠ (a – b) – c

a x ( b x c ) = ( a x b ) x c

a ÷ (b ÷ c ) ≠ (a ÷ b ) ÷ c

Следовательно, сложение и умножение положительных и отрицательных чисел удовлетворяет ассоциативному свойству, а вычитание и деление положительных также как отрицательные не удовлетворяют ассоциативному свойству.

Распределительное свойство умножения над сложением/вычитанием

Когда два положительных или отрицательных числа складывают или вычитают, а результат умножают на другое число, их можно умножать отдельно.

Следовательно, для любых трех целых чисел a, b и c дистрибутивное свойство умножения над сложением утверждает, что

a x ( b + c) = (a x b) + (a x c)

Аналогично, для любых трех чисел a, b и c, распределительное свойство умножения над вычитанием утверждает, что

a x (b – c) = (a x b) – (a x c)

Например, давайте сначала рассмотрим 10 x (18 + 12)

Мы будем использовать распределительное свойство умножения над сложением.

Мы имеем 10 x (18 + 12)

= (10 x 18) + (10 x 12)

= 180 + 120

= 300

Ключевые факты и резюме

1. . Интеллект является afteg число, которое можно записать без дробной части.
2. Числа 1, 2, 3, 4 ….. являются натуральными числами и называются целыми положительными числами, а числа – 1, – 2 , – 3 и т. д. называются целыми отрицательными.
3. Мы используем символ «-» для обозначения отрицательных целых чисел, и тот же символ используется для обозначения вычитания.
4. Мы используем символ «+» для обозначения положительных целых чисел, и тот же символ используется для обозначения сложения.
5. Числа увеличиваются, когда мы движемся вправо по числовой линии, и уменьшаются, когда мы движемся влево.
6. Чтобы сложить два целых положительных или два отрицательных числа, мы складываем их абсолютные значения и присваиваем сумме знак слагаемого.
7. Чтобы сложить положительное или отрицательное целое число, мы определяем разность их абсолютных значений и присваиваем сумму слагаемого, имеющего большее абсолютное значение.
8. Если a и b два целых числа, то чтобы вычесть b из a, мы меняем знак b и прибавляем его к a, т. 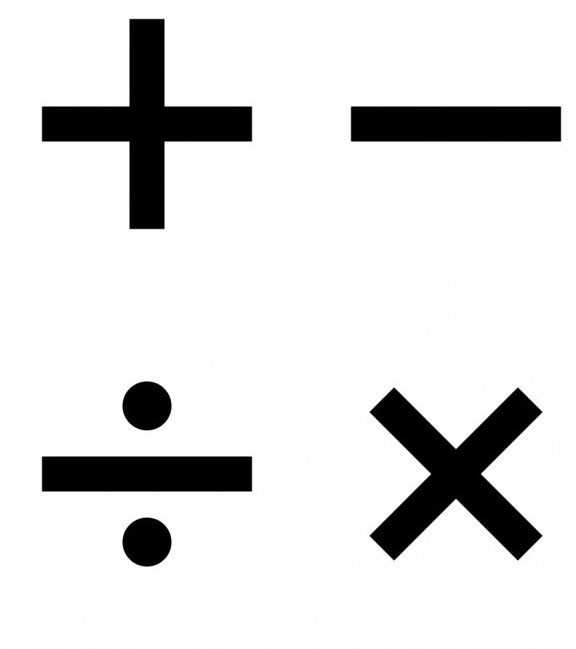е. a– b = a + ( – b ) 
9. Произведение двух целых противоположные знаки равны аддитивному обратному произведению их абсолютных значений.
10. Произведение двух целых чисел с одинаковыми знаками равно произведению их абсолютных значений.
11. Частное двух целых чисел, как положительных, так и отрицательных, — это положительное целое число, равное частному соответствующих абсолютных значений целых чисел.
12. Частное положительного и отрицательного целых чисел является отрицательным целым числом, и его абсолютное значение равно частному соответствующих абсолютных значений целых чисел.
13. Как положительные, так и отрицательные целые числа удовлетворяют свойству замыкания. Сложение и умножение как положительных, так и отрицательных целых чисел удовлетворяют коммутативным и ассоциативным свойствам. Вычитание и деление как положительных, так и отрицательных целых чисел не удовлетворяют коммутативным и ассоциативным свойствам.

Целые числа (на тему Дня Мертвых) Рабочие листы по математике
Понимание коммутативного и ассоциативного свойства сложения Рабочие листы по математике для 1-го класса
Распределительное свойство и алгебраические выражения Рабочие листы по математике для 6-го класса

Просмотреть все рабочие листы 7 Мы тратим много времени на изучение и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!

Целочисленные формулы – Что такое целые формулы? Примеры

Прежде чем изучать формулы для целых чисел, вспомним, что такое целые числа. Целое число — это число, которое не имеет десятичной или дробной части. Термин “целое число” был получен от латинского слова “целое число”, что означает “целое”. Давайте подробно изучим формулы для целых чисел в следующем разделе. Набор целых чисел представлен буквой «Z» и включает в себя:

• Все натуральные числа
• Отрицательные числа всех натуральных чисел
• Число ноль (0)

Что такое целые формулы?

Целочисленные формулы – это формулы/правила, которые используются для выполнения операций над целыми числами. Формулы целых чисел различаются для нахождения суммы/разности и произведения/частного. Вот формулы.

Формулы сложения/вычитания целых чисел

Чтобы сложить два целых числа с одинаковыми знаками, мы просто складываем их абсолютные значения и используем тот же знак, что и заданные целые числа, для результата. Чтобы сложить два целых числа разных знаков, мы вычитаем их абсолютные значения (в порядке большего числа минус меньшее число) и также используем знак большего числа к результату. Мы выполняем вычитание точно так же, как и сложение, но по правилу а – b = а + (-b). Таким образом, формулы сложения/вычитания целых чисел:

1. (+) + (+) = +
2. (-) + (-) = –
3. (+) + (-) = + (абсолютное значение положительного числа больше)
4. (+) + (-) = – (абсолютное значение отрицательного числа больше)

Примеры:

• 2 + 3 = 5
• (-2) + (-3) = -5
• 3 + (-2) = +1 (или) 1
• 2 + (-3) = -1

Умножение/деление целых чисел в формулах

Произведение/частное двух целых чисел одного знака всегда положительно, а произведение или частное двух целых чисел разных знаков всегда отрицательно. Таким образом, формулы умножения/деления целых чисел:

1. (+) × (+) = +; (+) ÷ (+) = +
2. (-) × (-) = +; (-) ÷ (-) = +
3. (+) × (-) = -; (+) ÷ (-) = –
4. (-) × (+) = -; (-) ÷ (+) = –

Примеры

• 2 × 3 = 6
• -2 × -3 = 6
• 2 × -3 = -6
• -2 × 3 = -6

Примечание: Множество целых чисел замкнуто, ассоциативно и коммутативно относительно сложения и умножения. Аддитивная идентичность 0 и мультипликативная идентичность 1 присутствуют в наборе целых чисел. Все целые числа имеют свои аддитивные инверсии в множестве целых чисел. Ни одно из целых чисел, кроме 1 и -1, не имеет своих мультипликативных инверсий в множестве целых чисел.

 

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами

Закажите бесплатный пробный урок

Давайте рассмотрим применение формул для целых чисел в следующих решенных примерах.

Примеры с использованием целочисленных формул

Пример 1:  Оцените следующее: a) 12 + (-3) b) 12 × -3

Решение:

а) В 12 + (-3) 12 со знаком + и 3 со знаком -. Итак, мы вычитаем абсолютные значения 12 и -3 (которые равны 12 и 3), вычитаем их (12 – 3 = 9) и присваиваем результату знак наибольшего абсолютного значения (знак 12, который равен +). .

Таким образом, 12 + (-3) = +9 (или) 9

б) 12 × -3

Используя одну из формул для целых чисел, (+) × (-) = – и 12 × 3 = 36.

Таким образом, 12 × -3 = -36.

Ответ: а) 9 б) -36.

Пример 2:  Запишите пару целых чисел в каждом из следующих случаев, используя формулы целых чисел: а) сумма которых равна -6   б) произведение которых равно -8.

Решение:

а) Рассмотрим 2 и -8. Их абсолютные значения равны 2 и 8.

Мы знаем, что 8 – 2 = 6, а среди 2 и -8 8 имеет наибольшее абсолютное значение. Таким образом, результат имеет знак минус (поскольку -8 имеет знак минус).

Таким образом, 2 + (-8) = -6.

б) Рассмотрим 2 и -4. Поскольку они имеют противоположные знаки, их произведение отрицательно. Таким образом,

2 × -4 = -8.

Ответ:  а) 2 и -8; б) 2 и -4.

Пример 3:  Оцените следующее: a) (-13) + (-12) + 2   b) -4 + (-2) × (3) + (-4) ÷ 2.

Решение:

Мы будем оценивать данные выражения, используя формулы целых чисел.

а) (-13) + (-12) – 2

= -25 + 2

= -23

б)  -4 + (-2) × (3) + (-4) ÷ 2

= -4 + -6 + (-2)

= -10 + (-2)

= -12

Ответ:  a) -23   b) -12

Часто задаваемые вопросы о формулах для целых чисел

Что такое формулы для целых чисел?

Целочисленные формулы — это формулы для сложения/вычитания и умножения/деления целых чисел. Эти формулы приведены ниже.

Формулы сложения/вычитания:

1. (+) + (+) = +
2. (-) + (-) = –
3. (+) + (-) = + (абсолютное значение положительного числа больше)
4. (+) + (-) = – (абсолютное значение отрицательного числа больше)

Формулы умножения/деления:

1. (+) × (+) = +; (+) ÷ (+) = +
2. (-) × (-) = +; (-) ÷ (-) = +
3. (+) × (-) = -; (+) ÷ (-) = –
4. (-) × (+) = -; (-) ÷ (+) = –

Как использовать формулы для целых чисел?

Мы можем использовать формулы целых чисел в зависимости от того, делаем ли мы сложение/вычитание/умножение/деление. Например, если нам нужно найти значение (-3) × (-2), мы используем формулу умножения целых чисел, которая гласит (-) × (-) = +. Используя это, (-3) × (-2) = 6 (поскольку 3 × 2 = 6).

Что такое -14 + 3 с использованием формул для целых чисел?

Абсолютные значения -14 и 3 равны 14 и 3 соответственно. Используя одну из формул для целых чисел, (-) + (+) = – (абсолютное значение отрицательного числа больше). Используя эту формулу, -14 + 3 = -11.

Что такое (-14) × 3 с помощью формул для целых чисел?

Мы знаем, что 14 × 3 = 42. Теперь, используя одну из формул для целых чисел, (+) × (-) = -. Таким образом, 14 × -3 = -42.

Ресурсы Mathplus

Предыдущий Следующий

Добро пожаловать в ресурсы Mathplus

Учителя, у которых еще нет учетной записи, пожалуйста, зарегистрируйтесь здесь . Для учащихся: попросите у преподавателя код учащегося для входа в систему. Гостям не требуется учетная запись для входа.

Войти как гость

Сенсо Эсквела Филиппины

---

Мобильные приложения Mathplus

Широко признано, что технологии открывают новые возможности для изучения математики. Действительно, за последние годы появилось множество математических приложений. Однако некоторые приложения не используют возможности технологий, поскольку они просто представляют один и тот же статический контент, используя другой носитель. В рамках проекта «Технологические инновации для математического мышления, статистического мышления и оценки», финансируемого Департамент науки и технологий – Филиппинский совет по исследованиям и разработкам в области промышленности, энергетики и новых технологий (DOST-PCIEERD), наша команда университетских преподавателей математики разрабатывает приложения, которые могут вовлечь студентов в математические задачи и стимулировать их к исследованию, делать предположения и применять свои рассуждения. Мы создаем организованный репозиторий приложений, чтобы учителя могли легко определить приложения, которые им нужны для преподавания определенной темы, как указано в официальной учебной программе. Этот проект поддерживает внедрение филиппинской системы математики от K до 12, поскольку он признает возможности технологий, включая объекты, которыми можно манипулировать, измерительные устройства, калькуляторы, компьютеры, смартфоны, планшеты и Интернет. Приложения, а также учебные пособия, разработанные командой, доступны по адресу mathplusresources.wordpress.com.

Senso Eskwela Pilipinas

Senso Eskwela Pilipinas (SEP) — ​​это веб-приложение, финансируемое DOST-PCIERD и предназначенное для для повышения статистической грамотности филиппинских учащихся с 1 по 11 классы. Он адаптирован из международного проекта, проводимого в разных странах, таких как США, Великобритании, Австралии и Новой Зеландии. SEP — это онлайн-репозиторий для сбора, хранение и извлечение достоверных данных, которые можно использовать для обучения и изучения статистики.

Под руководством учителя учащиеся должны пройти онлайн-опрос. Их ответы затем станут частью базы данных SEP, к которой можно получить доступ для использования в различные виды деятельности для статистического обучения.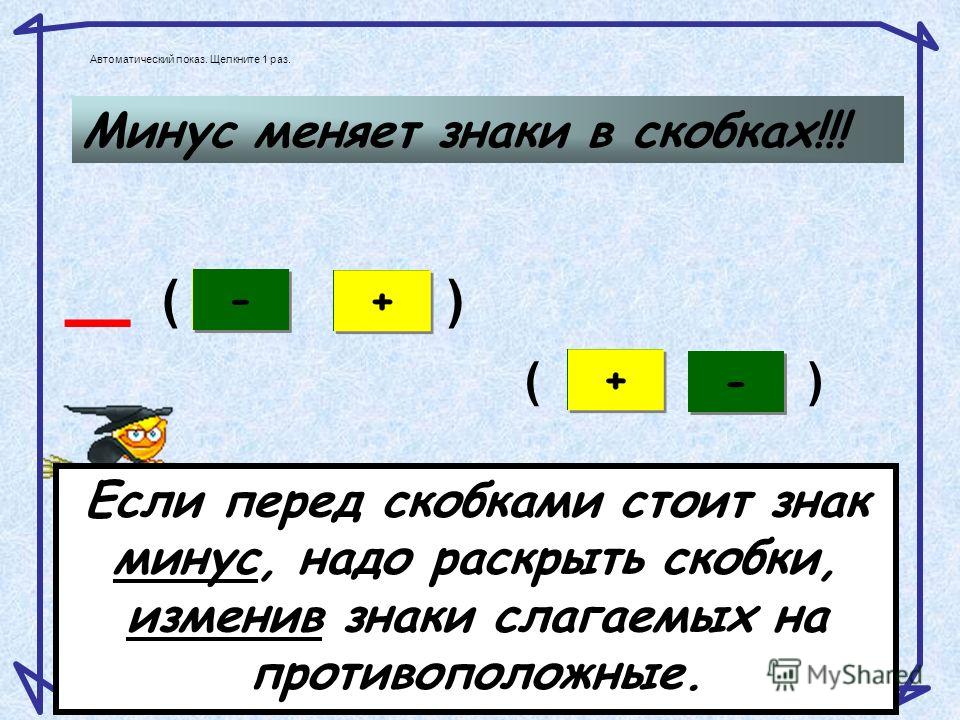 Через эту платформу, подлинную, актуальную, соответствующие данные предоставляются учителям и учащимся. Преподаватели и учащиеся могут получить доступ к данным своего класса. Более того, любой пользователь (в том числе гости, которым не требуется регистрация учетной записи) может загрузить случайную выборку из базы данных SEP.

Примечание. Создание учетной записи для учителей будет доступно позднее. По всем вопросам обращайтесь по адресу [email protected].

Отслеживание оценки Филиппины

Assessment Tracking Philippines (ATP) является одним из компонентов проекта «Технологические инновации для математического мышления, Статистическое мышление и оценка». Мы считаем, что оценивание является неотъемлемой частью образования, поскольку оно дает возможность для учителей, чтобы определить, достигнуты ли цели урока. Оценка также обеспечивает значительную обратную связь, которая влияет на учебные решения и учебный план.

ATP предлагает оценку основных навыков учащихся в основных операциях с целыми числами, дроби, десятичные и целые числа. Отчеты об успеваемости учащихся в каждом типе теста могут быть созданы и загружены. Мы надеемся, что это поможет учителям точно определить уровень знаний учащихся в основных областях математики.

Проверка электронной почты прошла успешно. Теперь вы можете войти, используя зарегистрированный адрес электронной почты и пароль

Войти как учитель

Войти как ученик

Введите код студента

Если у вас нет кода ученика, попросите его у преподавателя или вы можете войти в систему как гость.

Почему “±” с другой стороны?

Purplemath

В разделе «Решение квадратного корня» урока «Решение квадратичных уравнений» у нас была следующая задача и решение:

• Решите

  x ² – 4 = 0

Мои шаги были:

x ² – 4 = 0

x ² = 4

x = ± 2

. Затем мой раствор был:

9007 x = ± 2

. Затем мой раствор был 2

Содержание продолжается ниже

MathHelp.com

…и я объяснил форму решения, сказав:

Почему знак “±” (“плюс-минус”)? Потому что это могло быть положительное 2 или отрицательное 2, которое было возведено в квадрат, чтобы получить 4.

Хотя это и правильное объяснение, мы можем быть более точны с математической точки зрения относительно источника этого «плюс-минус».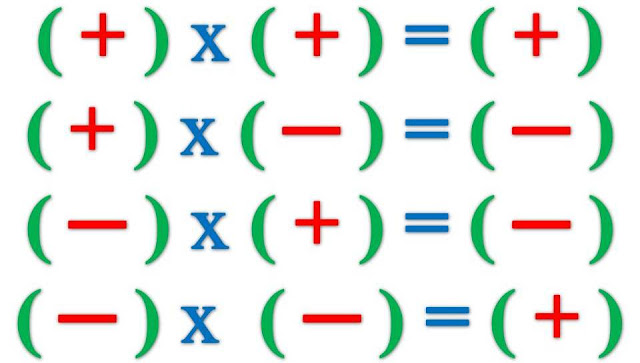 Объяснение может выглядеть следующим образом:

---

Предположим, нам дано уравнение « x ² = 4» и нам предлагается решить его. Когда мы «извлекаем квадратный корень» из любой части, мы делаем более короткий путь от обычного решения. Если вместо этого мы применим обычные методы факторизации к этому квадрату, мы сначала переместим все в одну сторону от знака «равно», сомножим и решим:0008

x ² = 4

x ² − 4 = 0

( x − 2)( x + 2) = 0

x = 2, −2

Поскольку мы факторизовали разность квадратов, мы пришли к двум решениям, равным во всем, кроме знаков. «Извлекая квадратный корень» из любой стороны первой вычислительной строки выше и ставя знак «плюс-минус» перед числовой частью уравнения, мы нашли бы два одинаковых значения решения, включая их разные знаки. , на один или два шага меньше. Но используемые рассуждения более ясны в факторизованной форме.

В приведенном выше примере мы извлекали квадратный корень из полного квадрата (а именно, 4), но процесс работает так же хорошо, когда строго числовая часть такого рода уравнения не является полным квадратом. Например:

x ² = 7

Это можно преобразовать в разность квадратов, если мы допускаем, что квадратный корень из семи является одним из возводимых в квадрат значений:

x ² = (кв.[7]) ²

Затем мы можем разложить как обычно:

x ² – (sqrt[7]) ² = 0

( x − sqrt[7])( x + sqrt[7]) = 0

x = ± sqrt[7]

Это тот же результат, который мы получили бы, «извлекая квадратный корень» из любой части исходного уравнения, а затем добавляя «±» перед числовой частью :

x ² = (квадрат[7]) ²

sqrt[ x ² ] = ± sqrt[7]

x = ± sqrt[7]

---

Другое объяснение наличия «±» с одной стороны уравнения гораздо более техническое, основанное на математических определениях:

---

Предположим, нам дают уравнение “ x ² = 4″ и нам говорят решить. Когда мы возьмем квадратный корень из любой стороны, мы получим следующее:

То есть, с технической точки зрения, у нас нет знака «±» перед квадратным корнем справа. Однако —

Техническое определение «квадратный корень из x в квадрате» — это «абсолютное значение x ». То есть:

Из-за этого весьма технического соображения уравнение на самом деле упрощается как:

x ² = 4

| х | = 2

Но x может быть положительным или отрицательным (но, очевидно, не нулевым). Чтобы решить это абсолютное уравнение, мы должны рассмотреть каждый из двух случаев. Если x положительно, то мы можем удалить столбцы абсолютных значений, ничего не меняя:

Если x > 0, то | х | = х , значит | х | = x = 2

С другой стороны, если x отрицательно, то мы должны изменить знак на x , когда мы удалим столбцы абсолютного значения, поэтому мы получим:

Если x < 0, то| х | = − x , поэтому | х | = − x = 2

.