Математика 3 класс как решать задачи: Задачи по математике 2 класс

Обзор – Группа изучения уроков

Что такое обучение через решение проблем?

При обучении через решение задач (TTP) учащиеся изучают новую математику, решая задачи. Учащиеся решают новую задачу, представляют и обсуждают стратегии решения и вместе создают следующую концепцию или процедуру в учебной программе по математике.

Обучение через решение проблем широко распространено в Японии, где учащиеся решают проблемы до того, как обучат методу или процедуре решения. Напротив, студенты в США проводят большую часть своего времени, выполняя упражнения, решая задачи, метод решения которых уже изучен.

Почему обучение через решение проблем?

По мере того, как учащиеся накапливают свои математические знания, они также:

• Научаются математическим рассуждениям, используя ранее полученные знания для создания новых идей
• Посмотрите на силу их объяснений и тщательно написанной работы, чтобы пробудить понимание для себя и своих одноклассников
• Ожидайте, что математика будет иметь смысл
• Наслаждайтесь решением незнакомых задач
• Испытайте математические открытия, которые естественным образом углубят их настойчивость

Этапы урока TTP

Загрузить

Обучение через решение проблем проходит через четыре этапа: 1. Понять проблему, 2. Попытаться решить проблему самостоятельно, 3. Представление и обсуждение своей работы (выбранные стратегии ) и 4. Обобщить и поразмышлять.

Нажмите на стрелки ниже, чтобы узнать, что делают учащиеся и учителя на каждом этапе, и посмотреть видео-примеры.

• 1. Осознайте проблему
• 2. Попробуйте решить
• 3. Представить и обсудить
• 4. Подвести итоги и обдумать
• Новые знания

ЧТО ДЕЛАЮТ СТУДЕНТЫ

• Понять проблему и развить интерес к ее решению.
• Подумайте, что они знают, что может помочь им решить проблему.

ЧТО ДЕЛАЮТ УЧИТЕЛЯ

• Покажите несколько дневниковых размышлений учащихся о предыдущем уроке.
• Поставьте задачу, которую учащиеся еще не знают, как решить.
• Заинтересуйте учащихся проблемой и размышлениями о своих собственных знаниях.

ЧТО ДЕЛАЮТ СТУДЕНТЫ

• Самостоятельно попробуйте решить задачу.
• Делайте , а не , просто следуя примеру решения учителя.
• Разрешить одноклассникам вносить свой вклад после некоторого времени самостоятельного обдумывания.

ЧТО ДЕЛАЮТ УЧИТЕЛЯ

• Распространите, используя схему рассадки, чтобы отметить подход к решению каждого учащегося.
• Определите работу, которую необходимо представить и обсудить на доске.
• Задавайте индивидуальные вопросы, чтобы стимулировать размышления, если некоторые учащиеся быстро закончат или не начнут.

ЧТО ДЕЛАЮТ СТУДЕНТЫ

• Представление и объяснение решений у доски, ответы на вопросы одноклассников и учителя. (2-3 ученика на уроке)
• Активно осмыслить представленную работу и выделить ключевые математические моменты. (Все студенты)
• Разрешить одноклассникам вносить свой вклад после некоторого времени самостоятельного обдумывания.

ЧТО ДЕЛАЮТ УЧИТЕЛЯ

• Стратегический выбор и последовательность презентаций работы учащихся у доски для построения новой математики. (Могут быть включены неправильные подходы.)
• Наблюдайте за обсуждением учащихся: все ли учащиеся замечают важные математические идеи?
• Добавляйте ходы учителя (вопросы, обсуждение, голосование) по мере необходимости, чтобы построить важную математику.

ЧТО ДЕЛАЮТ СТУДЕНТЫ

• Подумайте, что они узнали, и поделитесь своими мыслями с классом, чтобы помочь классу сформулировать итоги обучения. Скопируйте резюме в журнал.
• Напишите в журнале размышления о собственных выводах из урока.

ЧТО ДЕЛАЮТ УЧИТЕЛЯ

• Напишите на доске краткое изложение того, что класс узнал во время урока, по возможности используя идеи и слова учащихся.
• Попросите учащихся написать в своих дневниках, что они узнали на уроке.

Новое обучение — это то, что учащиеся на самом деле выносят из урока, что отражено в их дневниках, их работе и идеях во время занятий, а также в выходном задании, если таковое имеется.

Выявление того, что учащиеся вынесли из урока, и замечание хрупких или неполных идей позволяет учителям планировать следующий урок.

Как учителя помогают решать проблемы?

Хотя на уроке TTP большую часть разговоров и вопросов задают учащиеся, учителя играют решающую роль. Широко известный курс «5 практик организации математических дискуссий» был частично основан на TTP . Учителя изучают учебную программу, предвосхищают мысли учащихся, выбирают и упорядочивают презентации учащихся, которые позволяют классу построить новую математику. Процедуры в классе для презентации и обсуждения студенческих работ, организации доски и журналов по рефлексивной математике работают вместе, чтобы позволить учащимся выполнять тяжелую математическую работу. Чтобы узнать больше о журналах, работе совета директоров и обсуждениях в TTP, а также ознакомиться с другими ресурсами TTP и примерами TTP в действии, щелкните соответствующие вкладки в верхней части этой страницы.

Обучение решению задач по математике

2,4К акции

Каждый год мои ученики могут быть фантастическими в математике… пока они не начнут понимать математику словами. По какой-то причине, как только математика превращается в чтение, даже мои лучшие читатели начинают паниковать. Есть что-то в словесных задачах или решении задач, что заставляет детей думать, что они не знают, как их решать.

Каждый год занятий по математике я начинаю с обучения своих учеников навыкам и стратегиям решения задач. Каждый год они стонут и охают, что они знают их. Ежегодно – абзац первый выше. Это был порочный круг. Мне нужно было что-то новое.

Я собрал подразделение по решению проблем, которое немного больше сосредоточилось бы на стратегиях и шагах, в надежде, что это создаст звезды решения проблем.

Стратегии решения проблем

Во-первых, я хотел убедиться, что все мои ученики изучили различные стратегии решения задач, такие как угадывание и проверка, использование визуальных средств (нарисуйте картинку, разыграйте ее и смоделируйте), работа в обратном направлении и организационные методы (таблицы, диаграммы и списки). В прошлом я использовал страницы с рабочими листами, которые представляли одну стратегию и давали учащимся множество задач по отработке этой одной стратегии.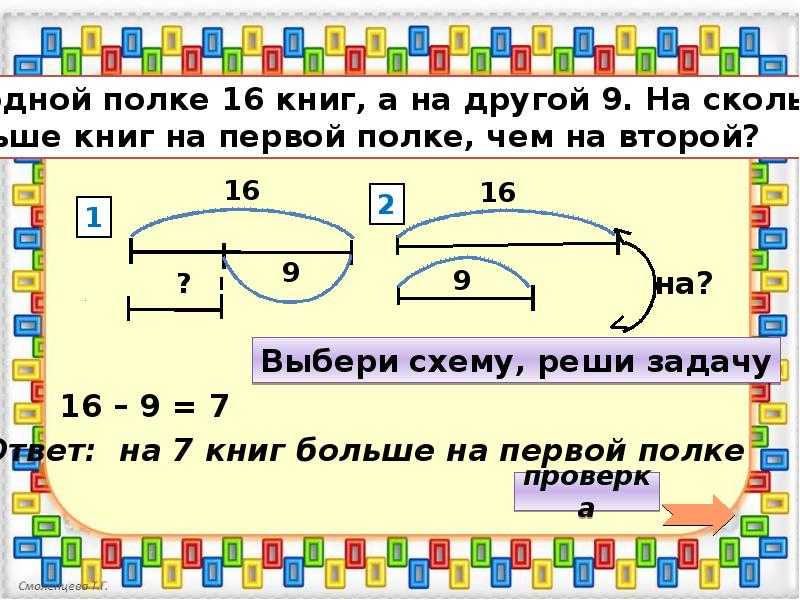 Мне это понравилось, потому что студенты могли больше сосредоточиться на отработке самой стратегии, но я также хотел, чтобы студенты знали, когда ее использовать, поэтому я убедился, что у них есть и то, и другое для практики.

Я дала ученикам возможность попрактиковаться в стратегиях, например, в этой игре «Угадай и проверь».

Также есть практика колеса визуальной стратегии.

Я также предоставил им бумажных кукол и различную одежду, чтобы составить упорядоченный список и определить, сколько нарядов будет у их «друга».

Затем, как я уже говорил выше, мы практиковались различными способами, чтобы точно знать, когда их использовать. Я действительно хотел убедиться, что они это сделали!

Так или иначе, после того как я узнал, что у них есть различные стратегии и когда их использовать, мы перешли к фактическим шагам решения проблемы.

Этапы решения задач

Я хотел, чтобы учащиеся поняли, что когда они видят задачку в рассказе, это не пугает. На самом деле это просто уравнение, записанное словами в реальной жизненной ситуации. Затем я дал им «ключи к успеху».

Шаг 1. Понимание проблемы.   Чтобы помочь учащимся понять задачу, я предоставил им образцы задач, и вместе мы сделали пять важных вещей:

• внимательно прочитать задачу
• переформулировать задачу своими словами
• зачеркнуть неважную информацию
• обвести любую важную информацию
• указать цель или вопрос, который необходимо решить

Мы делали это снова и снова с примерами задач .

Как только я почувствовал, что ученики устали, мы попрактиковались в эстафете решения задач. Учащиеся соревновались друг с другом, чтобы увидеть, как быстро они смогут справиться с мельчайшими задачами со словами. Мы не решали проблемы — пока.

Затем мы перешли к Шаг 2. Составьте план . Мы говорили о том, что именно здесь мы собирались выбрать, какую стратегию мы собираемся использовать.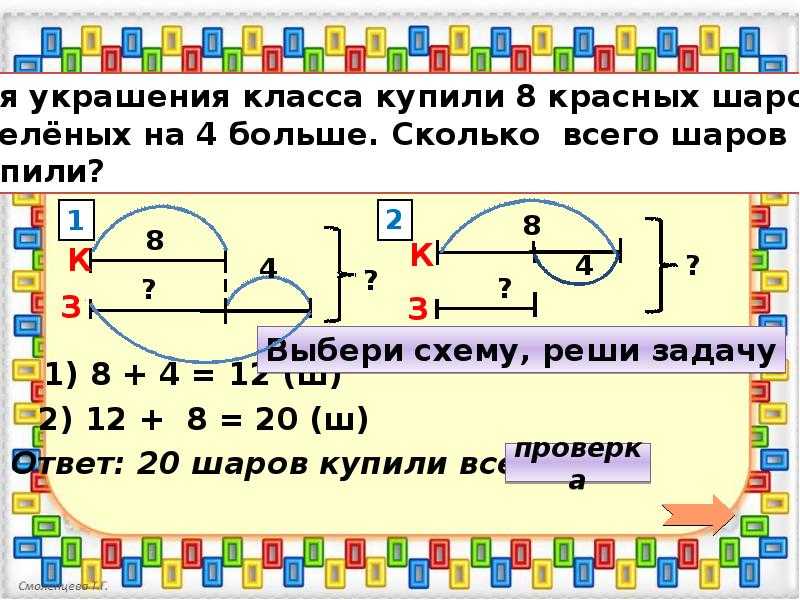 Мы также обсудили, как именно здесь мы собирались выяснить, какую операцию использовать. Я преподавал студентам концептуальную карту операции Шейлы Мелтон.

Мы говорили о том, что если вы знаете сумму и знаете, равна она или нет, это определит, какую операцию вы выполняете. Итак, мы взяли пример задачи, такой как:

Шелдон хочет испечь по кексу для каждого из своих 28 одноклассников. Из одной коробки смеси для кексов он может испечь 7 кексов. Сколько коробок ему нужно купить?

Мы начали с вопроса: «Знаем ли мы сумму?» Мы знаем, что всего 28 одноклассников. Так что да, мы расходимся. Затем мы спрашиваем: «Равно ли это?» Да, он хочет испечь кекс для КАЖДОГО из своих одноклассников. Итак, делим: 28 разделить на 7 = 4. Ему нужно будет купить 4 коробки. (На самом деле я пошел дальше и решил это здесь — это тоже следующий шаг.)

Шаг 3 – Решение проблемы . Мы говорили о том, что решение задачи включает в себя следующее:

• не спеша
• решение проблемы
• демонстрация всей нашей работы
• оценка ответа
• использование стратегий мышления

Мы говорили конкретно о стратегиях мышления. Как и в чтении, в математике есть стратегии мышления. Я хотел, чтобы студенты знали, что иногда, когда мы работаем над проблемой, определенная стратегия может не работать, и нам может потребоваться сменить стратегию. Мы также обсудили, что иногда нам может понадобиться переосмыслить проблему, подумать о соответствующем содержании или даже начать все сначала. Мы обсудили эти стратегии мышления:

• изменить стратегию или попробовать другую
• переосмыслить проблему
• подумать о связанном контенте
• начать сначала
• решить, нужно ли вам внести изменения
• проверить свою работу
• но самое главное… не сдаваться !

Чтобы убедиться, что они на практике используют эти стратегии мышления, я дал каждой группе лист бумаги с письмом от однокурсника (не настоящего студента), и они должны были дать совет, как помочь им решить свою проблему, используя описанные выше стратегии мышления.

Наконец, Шаг 4 – Проверьте.

  Этот шаг часто пропускают учащиеся. Я хотел подчеркнуть, насколько это важно! Я обсудил это с ними, обсудив, что, когда они проверяют свои проблемы, они всегда должны обращать внимание на следующие вещи:

• сравните свой ответ со своей оценкой
• проверьте правильность
• проверьте свои расчеты
• добавьте единицы
• переформулируйте вопрос в ответе
• объясните как вы решили задачу

Затем я раздал студентам тренировочные карточки. Я предоставил им карточки с примерами «учеников», которые уже выполнили свои задания, и я хотел, чтобы они были учителем. Им нужно было проверить работу и убедиться, что она выполнена правильно. Если это было не так, то им нужно было сказать, что они упустили, и исправить это.

Чтобы продемонстрировать их понимание устройства в целом, мы заполнили восхитительный журнал кругов (мой первый раз, когда я когда-либо собирал или даже создавал его – я был удивлен, насколько хорошо это получилось, на самом деле).

Это был отличный способ поместить туда все, что мы обсуждали.

После того, как мы все закончили, студенты официально приступили к решению задач S.T.A.R.S. Я просто часто напоминал студентам об этой аббревиатуре.

Стоп – Не спешите с решением; просто не торопитесь и осмотрите все.

Подумай – Не торопитесь, чтобы подумать о проблеме и ее решении.

Действие  – Примените стратегию и опробуйте ее.

Обзор – Просмотрите его и проверьте, есть ли у вас все детали.

Ух ты, настоящий боец, выкладывающийся в этом длинном посте! Подводя итог большей части того, что я здесь написал, у меня есть несколько БЕСПЛАТНЫХ закладок для решения задач, которые помогут вам запомнить и помочь вашим ученикам!

Вы можете получить эти закладки для решения проблем БЕСПЛАТНО, нажав здесь.

Вы можете реализовать любую из этих идей, ничего не покупая. Однако, если вы хотите сэкономить немного времени и энергии, то все они находятся в моем модуле решения задач Math Workshop.