Математическая линейка для дошкольников: «Арифметическая линейка»
Дошкольники: линейка без делений: klarissa45 — LiveJournal
?- Дети
- Cancel
Поскольку тема проходится в конце учебного года,
то учителя либо решают задачи с детьми достаточно халявно,
либо не решают эти задачи вообще.
В МГУ на мехмате когда-то был устный экзамен по математике,
и преподаватели любили задавать абитуриентам
задачи на построение треугольника по трем элементам (прямоугольника по двум элементам).
Решение этих задач в числе прочего хорошо тренирует логику.
Несколько лет назад я преподавала восьмиклассникам геометрию. В тот год как раз издали книгу
Голубева “Построение треугольников” и на факультативных занятиях мы почти два месяца решали
Так вот первая проблема. с которой я столкнулась, это была проблема “линейкабезделений”.
Ученики 8 класса были потрясены до глубины души: “И зачем она такая нужна?”
Эта история мне вспомнилась вчера на занятии с дошкольниками.
Мы рассматривали и обсуждали домики на картинке
“Логика в картинках”
Надо было объединить дома в группы по некоторым признакам.
Возник вопрос, как сравнить дома, стоящие в разных рядах, по высоте.
Полина, у которой есть старший брат-первоклассник, гордо вытащила линейку
из пенала: “А вот у нас есть линейка”.
Но я отказалась от ее помощи и предложала померять домики карандашом.
Дети грустно вертели в руках карандаши.
И тут я вдруг увидела счетные палочки Семена.
Экономные родители мальчика зашли в супермаркет
и попросили пару десятков деревянных палочек для мороженого.
Проблема измерения домиков была решена.
Мы взяли у Семена на время палочки и смогли померять наши домики, делая отметки карандашом.
Теперь надо объяснить родителям, что линейка с делениями для дошкольников – это зло.
Tags: 1 класс, 7 класс, Математическая вертикаль, дошкольники, кружок, малыши и математика, первый класс
Subscribe
Кружок 3-4 класса: графическое решение задач
Я уже рассказывала, что в учебнике Ивановой есть тема про схемы движения https://klarissa45.livejournal.com/210072.html Посмотрите на эти…
MathEdu — общедоступная электронная библиотека по вопросам преподавания математики
Я уже давала несколько ссылок на книжки из этой электронной библиотеки. Про неё либо забывают, либо вообще не знают. «Математическое…
Копилка идей
Последнее время я использую свой ЖЖ в качестве источника задач. И помечаю материалы, которые можно и нужно использовать на уроках и кружках тегом…
Photo
Hint http://pics.
livejournal.com/igrick/pic/000r1edq
Математические сказки для дошкольников
Плюсы и минусы
В древности у одного математика было трое учеников. Когда они в совершенстве овладели всеми арифметическими действиями, учитель призвал их и сказал:
– Теперь, когда вы достигли некоторых вершин в математике, пришла пора применить знания на практике, в жизни. Идите же и считайте, чего в мире больше – плюсов или минусов.
Ушли ученики, и пришли ровно через три года, как и договаривались.
– Ну, вот ты,- обратился он к первому ученику,- скажи, чего же в мире больше: плюсов или минусов?
– Конечно же, плюсов. Я встретил умную, красивую, богатую жену. У нас прекрасный дом, сады, чудесные фрукты. У меня за это время родилось двое замечательных детей. И вообще, я считаю, что минусы бывают только в математике, в жизни их вообще не существует.
– Ну, а ты что насчитал? – с грустью обратился он к другому своему ученику.
– Я считал… Все время считал… Золото, разные драгоценности, деньги.
Но меня ограбили. Кругом одни негодяи и жулики.
– Ну а как насчет моего задания? Чего больше: плюсов или минусов?
– Какие там плюсы? Вы их когда-нибудь видели в жизни? На каждом шагу одни только минусы.
Учитель погрустнел еще больше, махнул рукой и ничего не ответил.
– А ты что успел подсчитать? – спросил он с некоторой надеждой у своего третьего ученика.
– Я, учитель, ничего не успел. Видел я и плюсы, и минусы. Видел, что плюсы приносят людям радость, а минусы – горе. И мне захотелось сделать так, чтобы в жизни людей было как можно больше плюсов и как можно меньше минусов.
– Но такого не знает математика, – воскликнул учитель. И, помолчав, добавил:
– А всё-таки – это отличное действие. Больше плюсов, меньше минусов – ради этого стоит жить. Молодец, ты здорово усвоил мою науку!
А что вы думаете по этому поводу, ребята?
Путешествие по стране геометрии
Однажды Совёнок услышал незнакомое слово «геометрия». Ему стало очень интересно, что это такое, и он побежал к маме – Мудрой Сове.
Мама Сова взяла лист бумаги и карандаш и нарисовала там точку и прямую линию.
– Это точка, – сказала она.
– Точка, – повторил за ней Совёнок.
Мама Сова нарисовала теперь две точки и провела через неё черту (линию).
– Смотри внимательно, Совенок, это линия. Прямая линия. Попробуй, нарисуй и ты такую прямую линию, вот тебе линейка.
Совёнок очень обрадовался, когда у него получилась прямая линия и даже быстро сочинил вот такую песенку:
Прямая линия у нас
Нарисовалась в первый раз!
– Теперь я знаю, что такое геометрия. Она рисует прямые линии. Мудрая Сова засмеялась.
– Не торопись, Совёнок, геометрия изучает не только линии, посмотри: табуретка стоит слева от стула, а стул – справа от табуретки. А вот стоят мальчик и девочка. Скажи: кто из них стоит слева, а кто справа? А вот две точки, расположенные по разные стороны от прямой линии:
– Покажи, какая из них слева от прямой, какая справа?
– Знаю, знаю, – закричал Слонёнок, – геометрия изучает, кто стоит справа, а кто слева! Мудрая Сова покачала головой и продолжила свой рассказ:
– Геометрия ещё может очень много, например, помогает строить дома.
Посмотри в окно, видишь, строится дом. Над землёй уже поднялись два этажа, и строители возводят третий. Строителям помогает подъёмный кран. Он поднимает с земли большие плиты – перекрытия и подаёт их строителям. Под тяжестью груза стальной трос туго натянулся. Вот тебе еще прямая линия. Она протянулась точно сверху вниз. Такую линию называют вертикальной. Совёнок всё понял и на радостях придумал новую песенку:
Вот верёвочка моя!
Привязал к ней камень я,
И верёвка моментально
Натянулась вертикально!
– Строители часто используют в своей работе такую верёвочку с грузиком, -продолжала Сова.
– Для чего? – спросил Совёнок.
– Для того, чтобы проверить, вертикально ли стоит стена дома, не наклонилась ли она в какую-нибудь сторону. Если стена наклонилась, то верёвочка с грузиком пойдёт не по стене. Строители же должны стену поставить вертикально. Иначе дом может упасть.
Как родилась линия
В стране Геометрия жила-была маленькая точка. Это была очень красивая красная точка.
Однажды она подумала:
– Как мне хочется иметь много друзей! Отправляюсь-ка путешествовать и поищу себе подружек.
Только вышла красная точка за калитку, как на встречу ей тоже точка идёт, только зелёная. Подходит зелёная точка к красной и спрашивает, её куда та идёт.
– Иду искать друзей. Вставай со мной рядом и идём вместе путешествовать.
Через некоторое время встречают они синюю точку. Идут по дороге друзья – точки, и с каждым днём их становится всё больше и больше. И наконец, их стало так много, что выстроились они в один ряд, плечом к плечу и получилась линия. Когда точки идут прямо, получается линия прямая. Когда неровно, криво, – получается кривая линия.
Сказка об отрезке
Жил-был Карандаш. Был он очень любознательный и хотел всё знать. Увидит незнакомую линию и непременно спросит:
– Как эта линия называется?
Вышел однажды Карандаш на прямую линию и пошёл по этой прямой. Шёл, шёл по прямой линии, долго шёл. Устал. Остановился и говорит:
– Долго ли я ещё буду идти? Скоро ли конец прямой?
Засмеялась Прямая:
– Эх ты, Карандаш! Ведь ты не дойдёшь до конца: разве ты не знаешь, что у прямой нет конца?
– Тогда я поверну назад, – сказал Карандаш.
– Я, наверное, пошёл не в ту сторону.
– И в другую сторону не будет конца. У линии совсем нет концов. Она бесконечна…
– И Прямая даже пропела про себя песенку:
Без конца и края
Линия прямая!
Хоть сто лет по ней иди,
Не найти конца пути!
Опечалился Карандаш, узнав, что у линии совсем нет концов.
– Как же быть? Что же мне так и придётся идти и идти без конца?
– Ну, если ты не хочешь идти без конца, то отметь на прямой две точки, -подсказала Прямая.
– Ура! – закричал Карандаш. – Появились два конца, теперь я могу гулять по Прямой линии от одной точки до другой. Что же получилось на Прямой? Как это называется?
– Это мой отрезок, – улыбнулась Прямая линия.
– Отрезок прямой, отрезок прямой, – с удовольствием повторял Карандаш, прогуливаясь по отрезку от одного конца до другого. (Он был так рад, что от усталости не осталось и следа.)
Приключения точки
Жила-была Точка. Она хотела всё знать. Увидит незнакомую линию и непременно спросит:
– Как эта линия называется? Длинная она или короткая?
Подумала однажды Точка: «Как же я смогу всё узнать, если всегда буду жить на одном месте? Отправлюсь-ка я путешествовать!» Сказано – сделано.
Вышла Точка напрямую линию и пошла по этой линии.
Шла-Шла по прямой линии. Долго шла. Устала. Остановилась и говорит:
– Долго ли я ещё буду идти? Скоро ли конец прямой линии?
– Эх, ты, Точка! Ведь ты не дойдёшь до конца: разве ты не знаешь, что у прямой нет конца?
– Тогда я поверну назад, – сказала Точка. – Я, наверное, пошла не в ту сторону.
– И в другую сторону не будет конца. У прямой линии совсем нет концов.
Опечалилась Точка:
– Как же быть? Что же, мне так и придётся идти, идти без конца?
– Можно позвать на помощь Ножницы, – посоветовала Прямая. Тут, откуда ни возьмись, появились Ножницы, щёлкнули перед самым носом и разрезали Прямую.
– Ура! – закричала Точка. – Вот и конец получился! А теперь сделайте, пожалуйста, конец, с другой стороны.
– Можно и с другой, – послушно щёлкнули Ножницы.
– Как интересно! – воскликнула Точка. – Что же из моей прямой
получилось? С одной стороны – конец, с другой стороны конец. Как это
называется?
– Это отрезок, – сказали Ножницы.
– Можно нарезать много отрезков и даже разной длины: одни короткие, другие длинные. И разбросать их можно, как захочется.
– Ножницы быстро-быстро защелкали.
Посмотри, что получилось. Если нарисовать кружочек, получится солнышко с разными лучиками, – робко ответила Точка. – А как можно точно определить, какой из отрезков самый длинный и какой самый короткий?
– Нужно позвать на помощь Циркуль и Линейку.
Тут Ножницы кликнули помощников. Пришли Циркуль и Линейка и принялись за дело.
Циркуль расставил свои ноги и измерил один отрезок, затем подошёл к другому, самому маленькому, и Совёнок сразу увидел, что этот отрезок меньше первого.
– А линейка может точно ответить, насколько этот отрезок меньше, – важно ответил Циркуль, – а я могу снова соединить отрезки.
Циркуль подтянул лучи друг к другу, соединил их концами, и вот что получилось.
– Да, – воскликнула Точка, – это не прямая. Здесь прямо не пройдёшь, придётся поворачивать. Что же это такое? Как это называется?
– Это угол, – сказал Циркуль.
– Угол… Угол… – несколько раз повторила Точка новое для неё слово -Циркуль, а как называется то место, где соединяются лучи?
– Вершина угла. Сейчас ты Точка в вершине угла. А лучи, которые начинаются от тебя, – это стороны угла. Можно даже прокатиться разок-другой. Понравился Точке такой совет. Катится она и приговаривает:
От вершины по лучу
Словно с горки покачу.
только луч теперь – «она»,
Он зовется «сторона».
Покаталась Точка ещё немного по сторонам угла, а потом вернулась к вершине и обратилась к Циркулю:
– Я хочу катиться быстрее. Нельзя ли сделать горку круче?
– Можно, – ответил Циркуль.
– Он сдвинул стороны угла.
– Это уж слишком? – запищала Точка.
– Какой острый угол? С такой крутой горки кубарем покатишься? Не нужно так круто?
Циркуль раздвинул немного стороны угла.
– Теперь хорошо, – сказала Точка. – Но мне уже расхотелось кататься. Лучше расскажи мне всё, что ты знаешь об угле.
– Углы бывают разные: прямые; углы, которые шире прямых, называются тупыми углами; а углы, которые меньше прямых, называются острыми углами.
О треугольнике
Давным-давно в математическом царстве было геометрическое Государство и правил им король Треугольникус. Был он уже старым и часто болел. Однажды собирает он своих глашатаев и посылает их по сёлам и городам с заданием: найти человека, который вылечил бы Треугольникуса. И такой лекарь нашёлся в городке «Три стороны».
Пришёл он к королю с треугольным листом, на котором был изображён чертёж и поставлен вопрос: сколько на этом чертеже различных треугольников? Назови их. Король Треугольникус думал целый день. А когда решил, почувствовал себя сразу здоровым и помолодевшим.
Кто более или менее
С терпением знаком,
Считает он терпение
Совсем не пустяком.
Не случай, не везение
Тебе помогут вдруг.
Терпение, терпение
– Твой самый лучший друг.
Да, забыли вам сообщить самое главное.
Как только король сел за разгадывание количества треугольников на рисунке, послышалась музыка. Это пели треугольнички. Надеюсь, ты не забыл, что дело происходило в волшебной стране?Если хочешь, можешь даже выучить песенку треугольничков, Она ведь волшебная и поможет тебе веселее и быстрее разгадать любую задачу:
Ты на меня, ты на него,
На всех нас посмотри.
У нас всего, у нас всего,
У нас всего по три.
Три стороны и три угла
И столько же вершин.
И трижды трудные дела
Мы трижды совершим.
Все в нашем городе – друзья,
Дружнее не сыскать.
Мы треугольников семья,
Нас каждый должен знать.
В. Шитомирский
01.08.2021 в 20:39. Рубрики: Стихи и рассказы. Темы: Материалы по математике в детском саду
Ruler Games for Kids Online
Повседневная жизнь включает в себя множество оценочных измерений. Сколько времени потребуется, чтобы добраться до школы из дома, – это расчетная мера времени, которая требуется почти каждый день.
Другим примером является предполагаемая сумма денег, необходимая для совершения покупок. Приблизительное измерение длины — это ширина грязевой лужи, когда вы пересекаете ее, перепрыгивая через нее. Таким образом, измерение является неотъемлемой частью повседневной жизни человека. Что такое мера? Можно измерять время, вес, длину, емкость и т. д. Время можно измерять в секундах, минутах и часах. Для измерения веса, емкости и длины в основном используются два типа единиц измерения: метрические единицы и обычные единицы измерения. Метрические единицы измерения веса включают миллиграммы, граммы, килограммы и т. д., в то время как обычные единицы измерения — унции, фунты, тонны и т. д. Широко используемые единицы измерения температуры — Фаренгейты и градусы Цельсия. Метрическая единица длины включает в себя миллиметры, сантиметры, метры, километры и т. д. Обычные единицы длины включают дюймы, футы, ярды, мили и т. д. Емкость также может быть измерена, и общепринятыми единицами являются унции, пинты, чашки, кварты, галлоны и т.
д. единицы широко используются в Соединенных Штатах Америки.
Длина более важна, чем многие другие измерения в области геометрии, технического черчения, гражданского строительства и т. д. Линейки в основном используются для трех целей: для измерения, проведения прямых линий и в качестве прямой направляющей для резки лезвием.
Существуют различные типы линеек, такие как настольные линейки или масштабные линейки, цифровые линейки и т. д. Гибкие линейки похожи на масштабные линейки, но их также можно использовать для создания волнистых линий. Треугольные линейки используются для рисования горизонтальных, вертикальных и наклонных линий. Транспортир или конвейер используется для измерения углов. Линейки треугольной шкалы или скалометры имеют разные единицы измерения на каждой из сторон. В высшей и прикладной математике Т-линейки используются в технических чертежах. Программу линейки можно использовать для измерения пикселей на экране компьютера или мобильного телефона. Эти программы также известны как экранные линейки.
SplashLearn — один из лучших веб-сайтов по математике для учащихся, предлагающий хорошо сбалансированную учебную программу, основанную на общепринятых математических стандартах. В нем есть рабочие листы для дошкольников до 5 класса. Тема «линейки» рассматривается с большим количеством иллюстрированных примеров и заданий.
Знакомство с линейками с помощью математических манипуляций и упражнений Детям можно предоставить различные предметы для сравнительного анализа, например, две коробки совершенно разных размеров, и их можно попросить выбрать большую. Можно дать две палочки разной длины, чтобы выбрать меньшую и т. д. Развивающие игры для дошкольников на эту тему с красочными картинками вызовут интерес у малышей. Упорядочивание трех одинаковых предметов в соответствии с их размерами может быть дано на следующем уровне как деятельность по решению проблем. Можно дать небольшие измерительные палочки одинаковой длины, чтобы выстроить их в линию и фактически определить длину объекта.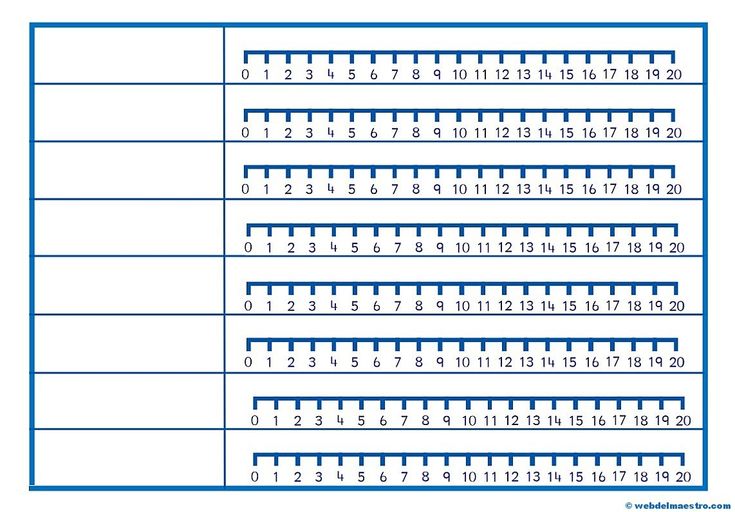
Такие интерактивные игры для детей можно проводить как групповые занятия. Действия по чтению измерений на линейке могут быть представлены на следующем уровне. Интересным занятием для детей будет непосредственный опыт измерения окружающих предметов с помощью настоящих линеек. В них должны быть введены линейки для измерения предметов с использованием различных типов метрических линеек и дюймовых линеек.
В Интернете доступно множество измерительных лент, размер которых можно изменить до линейки реального размера. Делая это, их можно превратить в печатные линейки. Печатные сантиметровые линейки или печатные миллиметровые линейки можно использовать при назначении групповых действий по измерению объектов в классе.
Математические онлайн-игры для детей для измерения длины заданного объекта помогают попрактиковаться в оценке и измерении длины.
Математические онлайн-игры для измерения доступны в метрических и обычных единицах измерения. Уровень сложности можно регулировать, выбирая соответствующие единицы, а также разделение каждого целого.
В детском саду дети узнают о различных измеряемых характеристиках одного объекта. Например, имея прямоугольную коробку, дети узнают, что ее размеры — высоту, ширину и длину — можно измерить. Еще одним измеримым атрибутом коробки является вес коробки. Они узнают об объеме коробки как о вещах, которые можно хранить внутри коробки. Обратите внимание, что они на самом деле не измеряют ни одну из этих величин. Еще одна тактика измерения, которая закладывает основу для фактической процедуры измерения, — это сравнение двух объектов. Это оценивается с использованием таких терминов, как больше/меньше, длиннее/короче, легче/тяжелее и т. д.
В 1-м классе они могут расположить три или более одинаковых объекта в соответствии с их измеримыми характеристиками, такими как длина, рост, вес и т. д. Дети учатся измерять длину объекта, складывая несколько копий более короткого объекта встык. Это закладывает фундамент для правителей.
Во 2 классе вводятся различные типы измерительных приборов, таких как линейки, измерительные линейки, критерия и рулетки.
Чтение линейки преподается на множестве иллюстрированных примеров. Оценка является еще одним методом, обсуждаемым на этом уровне. Словесные задачи, связанные со сложением и вычитанием длин, укрепляют понятия. На этом уровне все измерения строго ограничены целыми числами.
В 3 классе вводятся линейки, которыми обозначаются половинки и четверти. Дети учатся измерять длины с точностью до половины и четверти, используя различные типы линеек.
В программе четвертого класса по математике обсуждаются отношения между различными единицами в одной и той же системе единиц. Они применяют эти знания для математических преобразований больших чисел в математике пятого класса.
Методология обучения линейке Сравнение как основа измеренияПонятие длины вводится путем сравнения двух объектов разного размера.
Как только дети освоятся с понятиями, а также со словарным запасом длиннее/короче, больше/меньше и т. д., они могут сравнивать и располагать три или более похожих объекта.
На этом этапе вводится основной метод измерения с использованием нескольких копий более короткого объекта. Например, на картинке ниже длина карандаша измеряется количеством монет.
То есть длина карандаша равна длине 5 монет. Нужно быть осторожным, чтобы более короткий объект был правильно выровнен с более длинным объектом. Внутри измеряемых объектов не должно быть зазоров или перекрытий. Это закладывает основу для измерений линейки.
В SplashLearn есть большое количество рабочих тетрадей и листов для первого класса, доступных для практики по этой теме.
Линейки ВведениеЛинейки вводятся вместе с другими измерительными приборами, такими как линейки и рулетки.
Одной из самых распространенных линеек на этом уровне является 12-дюймовая линейка.
Может использоваться для измерения различных предметов, имеющихся в классе, таких как длина стола, скамьи, тряпки и т. д. являются наиболее распространенными.
Как правило, одна сторона линейки, используемой на этом уровне, будет отмечена в сантиметрах, а другая сторона – в дюймах.
Сначала детей учат читать линейку, используя изображения объектов и цифровую линейку.
Одним из самых важных моментов является совмещение начальной отметки линейки с кончиком измеряемого объекта. То есть длина нижнего мелка не 18 см, так как нижний конец мелка не совпадает с нулем линейки.
Чтобы укрепить эту концепцию чтения измерений, на этом уровне также обсуждается сравнение длин двух объектов.
Измерение объекта с помощью подходящей единицы требует некоторого логического мышления. Рассмотрим длину прямоугольника ниже. Это почти равно или немного меньше 13 см, тогда как точно равно 5 дюймам. В этом случае измерение длины в дюймах даст более точный ответ.
В SplashLearn доступны математические игры и задания для 2-го класса, а также тесты по математике, связанные с чтением и измерением линейки.
На следующем уровне дети знакомятся с более точными линейками, отмечающими половинки и четверти. У детей есть базовые знания о дробях, которые можно применить здесь. Они уже знают, что две половинки или четыре четверти составляют целое. Дети уже научились строить или читать дроби на числовой прямой. Это помогло бы им связать маркировку линейки с числовой линией.
Когда измерения на линейке составляют до половины целого, каждое целое делится поровну на два. В 12-дюймовой онлайн-линейке первая отметка после 0 будет равна ½, вторая — 1, четвертая — 1½ и так далее. На 12-дюймовой линейке будет 24 отметки.
Когда измерения на линейке составляют до четверти целого, каждое целое делится поровну на четыре части. В однодюймовой линейке первая отметка после 0 будет равна ¼, вторая — ½, третья — ¾, а четвертая — 1. Подобным образом каждое целое делится на 4.
ниже линейка имеет размеры половины и четверти дюйма:
Обычно 1/4 на линейке отмечены с одинаковой высотой, но короче отметки ½.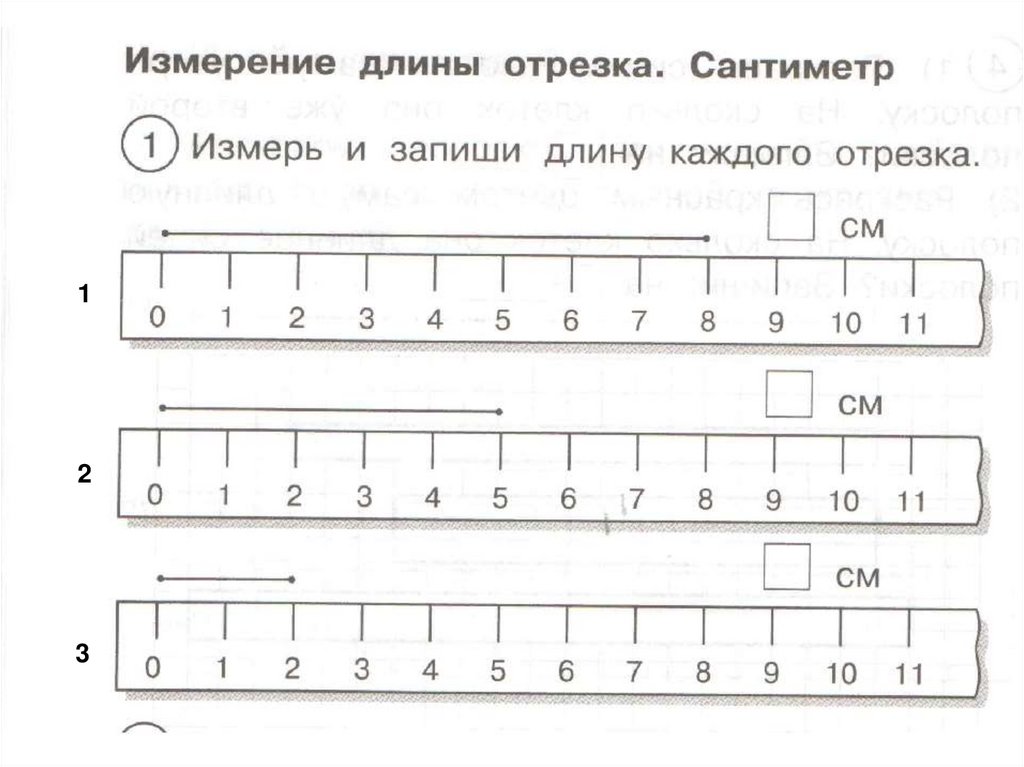
Когда дело доходит до линейки метрических единиц измерения, единица измерения, сантиметр, подразделяется на 10 маленьких линий, каждая размером в один миллиметр.
Рабочие листы для 3-х классов, доступные на SplashLearn для измерения объектов с помощью цифровой линейки, начинаются с более простых, измеряющих с точностью до дюйма. Постепенно он продвигается к измерению ближайших половинок и четвертей.
ОценкаОценка – это достаточно точное предположение или приближение объекта.
Они также узнают, какую меру и единицу измерения следует использовать для точного измерения данного объекта.
Дети узнают о предполагаемой длине частей тела человека, таких как длина руки около фута, размах рук около метра и т. д. Это помогает им получить более четкое представление о длине, чем использование точных измерений. с линейкой.
К тому времени дети уже имеют представление о различных единицах измерения и о том, сколько они измеряют.
Таким образом, дети могут применить эти знания для оценки длины объектов, которые они видят вокруг себя.
Оценка длины в метрических единицах, а также в обычных единицах измерения рассматривается в отдельных разделах SplashLearn с широким спектром не требующих пояснений математических задач.
Связь сложения и вычитания с длинойУ Чарли есть строка длиной 20 м, у Джозефа есть строка на 5 м длиннее, чем у Чарли. Какова общая длина обеих строк?
Веревка Джозефа на 5 м длиннее веревки Чарли. То есть на 5 м больше, чем на 20 м. Другими словами, (20 + 5) м = 25 м.
Теперь, чтобы найти общую длину двух цепочек, нужно сложить длины 20 м и 25 м.
Общая длина = 20 м + 25 м = 45 м.
Таким образом, общая длина двух цепочек составляет 45 м.
Этот тип текстовых задач на сложение и вычитание длин укрепляет концепцию измерения.
Преобразование в единицах измерения Дети учатся соотносить единицы длины в обычной или метрической системе единиц.
Они учатся выражать измерения в более крупных единицах измерения в единицах меньшего размера. То есть они понимают, что 1 фут равен 12 дюймам. Таким образом, 1 фут в 12 раз длиннее 1 дюйма. Некоторые расчеты выполняются как простые математические задачи в уме, тогда как некоторые требуют большого количества вычислений.
Позже они узнают, как переводить измерения в одной системе единиц. Например, 1 см = 10 миллиметров . Итак, 50 см равны (50 х 10) миллиметра или 500 миллиметрам. Рабочие листы преобразования единиц измерения для 4-го класса содержат таблицы измерений, которые необходимо заполнить. Аналогичные листы преобразования метрических показателей также доступны.
На этом уровне дети уже умеют умножать и делить десятичные дроби. Таким образом, они также могут обрабатывать преобразования измерений с использованием десятичных знаков. Знаний о простых делениях должно быть достаточно для этого. Преобразование общепринятых или стандартных мер в метрические обсуждается только в старших классах.
Далее они применяют эти знания в словесных задачах, связанных с переводом единиц.
Измерение для дошкольников – Корзиночки для маленьких ручек
Вот очень простое дошкольное измерительное задание для всей семьи! Ранние математические навыки начинаются с множества игровых возможностей, которые даже не нужно планировать заранее. Поощряйте математические исследования в детском саду и дошкольных учреждениях с помощью простого измерительного задания, подобного этому. Измерение различных предметов происходит каждый день, и здесь мы решили использовать наши кубики unifix для измерения рук и ног. Посмотрите все наши занятия по математике для дошкольников!
Дошкольное мероприятие по измерению с кубиками Unifix
ИЗМЕРЕНИЕ С ПОМОЩЬЮ КУБИКОВ UNIFIX Сегодня мы практиковались в измерении рук, ног и обуви. Все мы, включая папу! Цель состояла в том, чтобы увидеть путем измерения, у кого самая длинная рука и нога.
Хорошо, вроде легко сказать, но он был счастлив, выстраивая кубики unifix и считая их. Создание визуальных материалов и предоставление детям возможности изучать математику на практике жизненно важно для развития мозга.
ИЗМЕРЕНИЕ БЛОКАМИ?
Да! Хотя мы обычно думаем об измерении вещей, вытягивая линейку, мы можем научить детей дошкольного возраста концепции измерения с помощью этого простого действия.
Следует помнить пару важных моментов: предметы, которые вы используете для измерения, в нашем случае кубы unifix или DUPLO ниже, должны быть одного размера и типа. Они также должны быть аккуратно размещены встык. Использование набора объектов произвольного размера просто не сработает!
Измерение деятельности
Простая настройка Установка больших кусочков бумаги, маркеров и кубиков унификса (LEGO или небольшие блоки тоже работают!) 1. По очереди обведите свои руки, ноги и обувь на бумаге, при необходимости немного помогая.
Я попросил Лайама попрактиковаться в написании букв, написав М, Д и Л для каждого человека внутри каждой записи. В зависимости от буквы мы ставили точки, чтобы он следовал, направляли руку или давали ей. Мы также решили потренироваться писать его имя.
СОВЕТ: Не стесняйтесь раскрашивать и украшать ноги и руки, если вашему ребенку это интересно. Вы, безусловно, можете исследовать все направления раннего обучения, а не только математику.
ШАГ 2. Начните с нижней части каждой стопы, руки или обуви и аккуратно выстраивайте кубики unifix, пока не дойдете до самой высокой точки.
Мы немного поговорили о поиске самой высокой точки, и хотя верхняя часть руки могла быть в нескольких местах, мы искали самую высокую, самую высокую часть, чтобы выстроить наши кубики и измерить.
ШАГ 3. После того, как вы выровняете одну страницу (ногами вперед), подсчитайте количество кубиков унификса. Вы можете записать, сколько вы насчитали каждым.
ШАГ 4. Повторите эту же последовательность для каждой руки, ноги или обуви, а затем вернитесь, чтобы сравнить результаты. У кого были самые длинные руки или ноги?
Вы также можете использовать блоки или кубики для измерения высоты или длины игрушек. Измерьте комнату, измерьте высоту стола, измерьте длину обуви. Возможности безграничны!
Ищете простые в печати задания по математике для дошкольников?
У нас есть все для вас…
НАЖМИТЕ, ЧТОБЫ ПОЛУЧИТЬ БЕСПЛАТНЫЙ НАБОР МАТЕМАТИЧЕСКОГО НАБОРА!ЕЩЕ РАЗВЛЕКАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ ЗАДАНИЯ
- Работа на ферме
- LEGO Числа
- Тыквенная математика
- Рождественская математика
- Геометрические фигуры
ИЗМЕРИТЕЛЬНЫЕ ЗАДАНИЯ ДЛЯ ДОШКОЛЬНИКОВ
Посмотрите, какие еще занятия по математике для дошкольников нам очень нравятся! Щелкните фото.