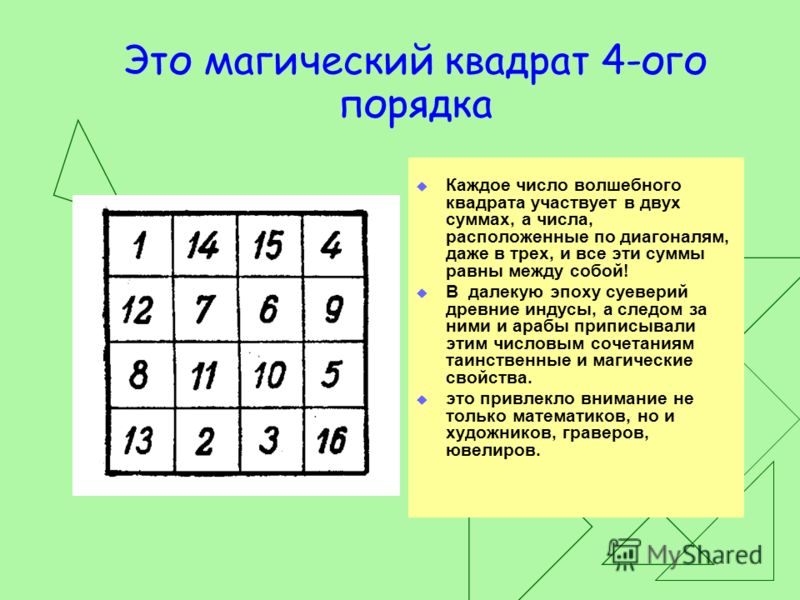
Магический квадрат онлайн решить онлайн: Магические квадраты: математические игры от ЛогикЛайк – Всё о детях – беременность, воспитание, уроки для детей

Содержание

Магические квадраты: математические игры от ЛогикЛайк

Математика и логика для детей / Математические игры

Игры с магическими квадратами нравятся всем, кто увлекается головоломками. В поисках магического числа, заполняя таблицу, ребенок развивает интерес к математике, логику и наблюдательность.

Выберите сложность, чтобы посмотреть

курс ЛогикЛайк «Магические квадраты»

5-8 лет

9-14 лет

Взрослый (15+)

На платформе LogicLike. com 3500 логических заданий с ответами: задачи, вопросы и головоломки. Решения и пояснения помогают научиться решать самые сложные задачи.

Как решать магические квадраты?

Разгадывать головоломки легче, когда точно понимаешь что нужно сделать и по каким правилам. Для начала нужно разобраться, что особенного в этих квадратных таблицах.

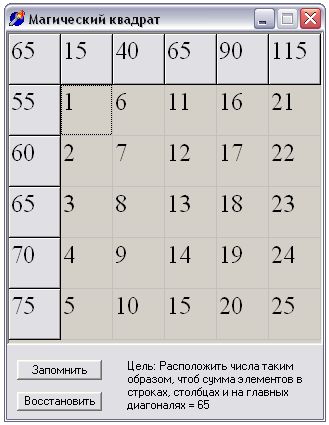
Решить магический квадрат — заполнить пустые ячейки так, чтобы сумма чисел по любой горизонтали, по вертикалям и диагоналям была одинаковой.

Сложите числа в решенной задаче в любой строке, в любом столбце, а также по обеим диагоналям.

Как ни складывай, получаем одну и ту же сумму.

Вот где магия, вот почему квадрат — магический!

Проверь себя

Помоги Клапану узнать, какой из 2 квадратов магический.

Узнать ответ

Ответ:

Первый, фиолетовый, квадрат.

Решение
В фиолетовом квадрате сумма чисел по всем направлениям равна 21.

В синем квадрате правила «магического» не выполняются.

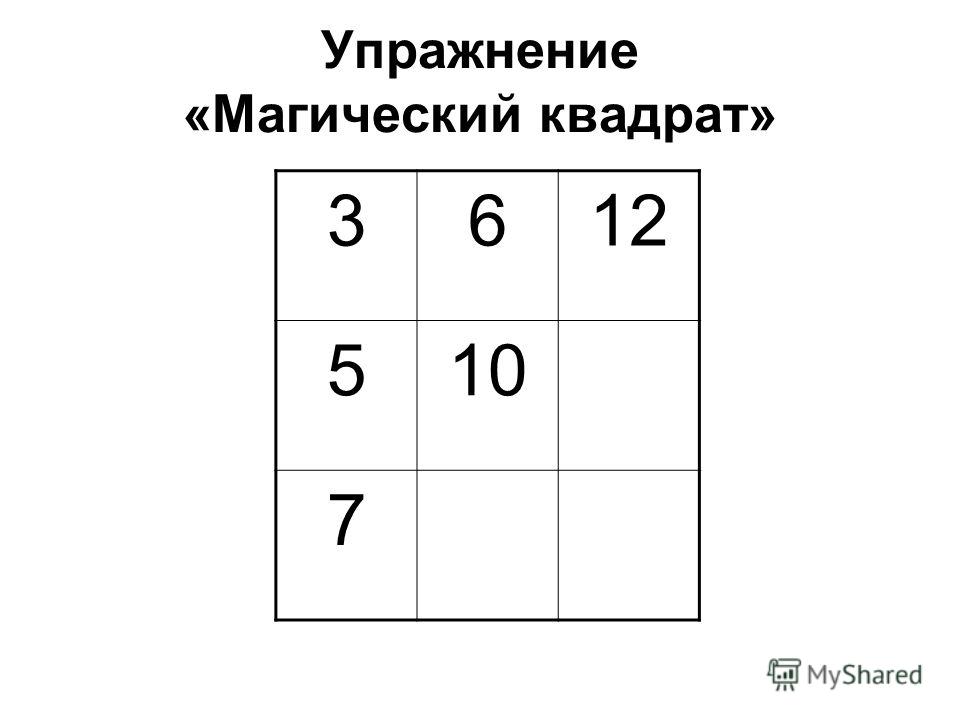
Познакомьтесь с примерами головоломок различного уровня сложности. Несколько заданий мы приводим с ответами и описанием решения.

Простые задания взрослый может выполнить в уме. Современным детям нравится решать головоломки и задачи онлайн.

Магические квадраты для 1-2 класса

Подборка заданий из обучающего курса ЛогикЛайк

Определи недостающее число

Чтобы решать задачи, нажмите Начать занятия!

Узнать ответ

Ответ:

Решение

Найти магическое число здесь можно множеством способов:
3+3+3 или 2+3+4 и т.п.
В математике это число называется магической константой и в данной головоломке равняется 9.
Находим пропущенное число:
9-2-2=5
или
9-3-1=5.

Чтобы решать задачи, нажмите «Начать занятия»!

Монстрики стерли некоторые числа в магическом квадрате.
Нужно заполнить пустые ячейки так, чтобы квадрат снова стал магическим.

Показать решение

1) Сначала нужно определить магическое число.

Для внимательных ребят это совсем просто: 5+3+1=9.
2) Находим недостающее число в первом столбце: 9-5-3=1.
3) Во 2-ой колонке: 9-3-1=5.
4) В 3-ем столбике: 9-1-5=3.

Помоги Иришке сделать квадрат магическим.

Чтобы решать задачи, нажмите «Начать занятия»!

В пустые клетки квадрата вставь числа 2, 3, 4.

Получить подсказку

Подсказка:

Магическое число = 4 + 3 + 2 = 9.
Интересно, что этот квадрат можно заполнить по правилам «Судоку».

Чтобы дети развивали логику и мышление с интересом, играючи, мы создали и развиваем онлайн-платформу «ЛогикЛайк».

Магические квадраты для 3-4 класса

Разгадать следующие головоломки в уме будет совсем непросто.
Можно вооружиться бумагой и ручкой или просто посмотреть примеры заданий. Интереснее всего – играть в магические квадраты онлайн (нажимайте «Начать занятия»).

Чтобы решать, нажмите «Начать занятия»

Профессор придумал магический квадрат, но из-за своей рассеянности не заполнил несколько клеток. Осталось заполнить всего 4 пропуска.

Чтобы решать, нажмите «Начать занятия»!

Монстрикам нужно поставить в пустые ячейки шесть различных чисел так, чтобы квадрат стал магическим.

Чтобы решать, нажмите «Начать занятия»!

Стань волшебником. Вставь в пустые клетки числа 5, 8, 9, 12, 13, 15 и сделай квадрат магическим.

Учим решать любые логические задачи

Более 150 000 детей и родителей со всего мира уже занимаются на сайте ЛогикЛайк. Подключайтесь и развивайте логику и мышление!

Начать обучение! Начать обучение!

Магический квадрат – виды, правила и примеры решения

Среди поклонников логических игр большой популярностью пользуется магический квадрат. Он представляет собой таблицу, заполненную особым образом цифрами. Причём сумма чисел одинакова по всем направлениям. Эту величину принято называть константой. Существует множество вариантов таких головоломок разной степени сложности.

Содержание

История и современное применение
Квадрат нечётного порядка
Одинарная чётность
- Вычисление магической константы
- Дальнейшие действия
Двойной порядок

История и современное применение

Первые подобные таблицы использовались ещё в Древней Греции и Китае. Это подтверждено археологическими находками. Арабы называли квадраты магическими, так как верили, что они обладают волшебными свойствами и могут защитить от многих напастей.

В середине XVI в. вопросом о том, как работает магический квадрат, заинтересовались математики в Европе. Они начали активно исследовать загадочные сочетания цифр. Учёные стремились вывести общие принципы построения квадратов и найти всё множество возможных вариантов.

В современной общеобразовательной школе разные виды магических квадратов используются на уроках математики. Они способствуют развитию логического мышления и вызывают у детей живой интерес.

С их помощью школьники учатся планировать свою работу и контролировать её. В клетки можно вписывать не только отдельные цифры, но и математические выражения. Задачи на эту тему часто предлагаются на математических олимпиадах. Решать такие числовые задачи можно и онлайн.

Квадрат нечётного порядка

Среди несложных магических квадратов по математике выделяют разновидности чётного и нечётного порядка. Первая группа подразделяется на таблицы одинарной и двойной чётности.

Начальным шагом во всех случаях будет определение магической константы. Делается это с помощью специальной формулы [n * (n2 + 1)] / 2. Разобраться с принципом решения задачи этого класса можно на самом простом примере. Для этого выстраивается таблица из 9 ячеек. В неё нужно расставить цифры от 1 до 9. Дальнейший алгоритм:

Подсчитывается сумма, которая должна получиться в каждой строке.

Для этого используется формула: 3 * (32 +1) / 2 = 3 * 10 / 2. Ответом будет число 15.

Числа в ячейках расставляются так, чтобы сумма их была равна 15 в каждой строчке. Это требует смекалки и воображения.

В средней клетке верхней строки вписывается 1.

Каждое следующее число ставится справа по диагонали вверх. Поставить цифру 2 нельзя, так как выше нет строк. Если мысленно добавить сверху ещё один квадрат, цифра 2 окажется в его нижнем правом углу. Значит, цифра 2 вписывается в нижнюю правую клетку.

По тому же принципу вписывается цифра 3. Она попадает в среднюю ячейку слева.

Если нужная клетка уже занята, очередной символ вписывается ниже предыдущего. Таким образом, 4 ставится под 3.

Записывается цифра 5 по диагонали вправо и вверх, а 6 в верхний угол справа.

Поскольку место цифры 7 уже занято, она вписывается ниже 6.

Восьмёрка занимает место в левом нижнем углу.

Оставшуюся клетку занимает девятка.

Общий алгоритм выполнения задания: каждый следующий знак пишется вверх и правее. Если там нет клетки — дорисовывается ещё один воображаемый квадрат. Если ячейка занята — число записывается ниже предыдущего. Таким способом можно составить любой квадрат нечётного порядка, включая самые сложные, с больши́м числом ячеек.

Одинарная чётность

Магические квадраты могут иметь порядок одинарной или двойной чётности. Для каждого случая предусмотрена отдельная методика вычисления. У таблиц одинарной чётности количество клеток в одной строке или столбце делится пополам, но не делится на четыре. Наименьшим квадратом, отвечающим этому требованию, будет прямоугольник 6х6. Фигуру 2х2 построить и заполнить невозможно.

Вычисление магической константы

Первый этап расчётов проводится по формуле [n * (n2 + 1)] / 2, где символом n обозначено число клеток в одном ряду. Если взять за пример квадрат 6х6, расчёт будет выглядеть следующим образом: [6 х (36 + 1)]: 2 = (6 х 37): 2 = 222:2.

Волшебная постоянная прямоугольника со стороной 6 клеток равна 111. Общая сумма чисел от 1 до 36 в каждой строке и в разных направлениях должна быть равна 111.

Рисунок делится на 4 одинаковые части. В каждой будет по 9 клеток (3х3). Каждую часть обозначают латинскими буквами: А — верхняя левая, С — верхняя правая, D — нижняя левая и В — нижняя правая часть. Если квадрат имеет другой размер, n делится на 2, чтобы узнать точную величину каждой из 4 частей.

Дальнейшие действия

Следующий шаг — вписывание в каждую часть ¼ всех чисел. В квадрант А вносятся числа от 1 до 9, в квадрант В — от 10 до 18, в части С — от 19 до 27, в D — от 28 до 36.

Последовательность вписывания такая же, как при заполнении простейшего нечётного квадрата:

Минимальное число, которым начинается заполнение ячеек, всегда ставится в верхнем ряду посередине. У каждой части эта ячейка находится отдельно.

Каждая часть заполняется как новый математический объект.

Даже если есть пустое место в другом квадрате, его в этих случаях игнорируют.

В блоках А и D на этой стадии решения сумма в строках и столбиках будет отличаться от постоянной. Чтобы это исправить, некоторые числа меняют местами между собой.

Алгоритм действий:

Начинать нужно с крайней левой клетки в верхней строке. Если фигура имеет размеры 6х6, выделяется только первая верхняя строка части А. В ней должно быть вписано число 8. Если величина таблицы составляет 10х10, выделяют 2 первые клетки в верхнем ряду. В них стоят 17 и 24.

Из выделенных клеток формируется промежуточный квадрат. В таблице с количеством строк и столбцов 6х6 он будет состоять из 1 клетки. Его условно обозначают А1.

Если размер 10х10, в верхней строке выделяется 2 первые ячейки. Вместе с ними выделяется ещё 2 клетки, во второй строке получается поле из 4 прилежащих друг к другу ячеек.

В следующей строке первая ячейка пропускается, затем выделяется столько клеток, сколько было в промежуточной таблице А1.

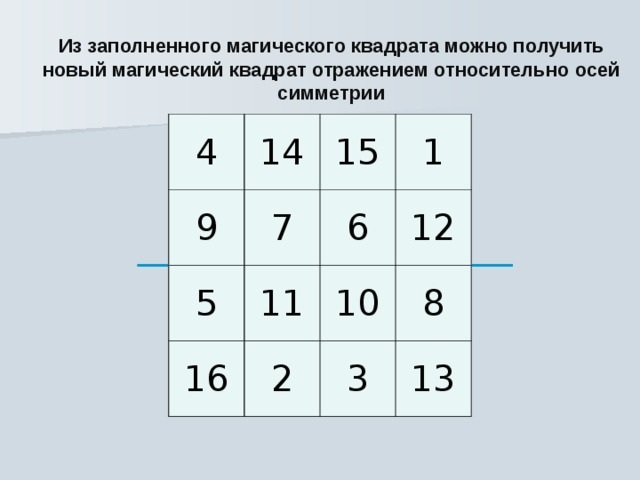Полученную фигуру можно обозначить А2.

Таким же способом строят промежуточный квадрат А3.

Эти 3 промежуточных фигуры формируют выделенную область А.

Далее переходят в квадрант D и формируют обособленную область D.

Цифры, которые были вписаны в выделенных треугольниках А и D, нужно поменять между собой местами. После этого сумма в каждой строке должна быть одинаковой. Она равняется вычисленной магической константе.

Двойной порядок

Если головоломка имеет порядок двойной чётности, количество окон в каждой горизонтальной строчке или вертикальном столбце должно делиться на 4. Минимальной фигурой с такими свойствами будет таблица 4х4.

Решать магические квадраты двойной чётности следует по тому же алгоритму, что и остальные. Первый шаг при заполнении — вычисление магической константы. Формула применяется та же, что для расчёта других квадратов. Для фигуры со стороной 4 клетки значение константы будет равно 34.

В каждом углу основного поля выделяются промежуточные таблицы. Их размер должен быть равен n/4. Эти области обозначают буквами A, B, C, D, располагая их против хода часовой стрелки. Величина промежуточных фигур зависит от размера исходного квадрата:

Если длина стороны составляет 4 ячейки, промежуточные зоны будут иметь по 1 клетке.

В таблице 8х8 эти области включают 4 элемента (2х2).

В квадрате 12х12 выделяются промежуточные фигуры размером 3х3.

Следующий этап — создание центрального промежуточного квадрата. Величина его стороны должна составлять n/2. Эта фигура не должна накладываться на периферические, но при этом соприкасаться с ними углами.

Далее в квадрат вносят цифры слева направо. Их допускается ставить только в свободные ячейки, которые входят в состав промежуточных областей. Например, при заполнении таблицы 4х4 порядок действий будет таким:

В первой сверху строке и первом слева столбце пишется 1.

В верхней клетке четвертого столбика — 4.

В центр второй горизонтальной строчки ставятся цифры 6 и 7.

В четвёртой строке слева пишется 13, а справа — 16.

По этому же принципу цифрами заполняются оставшиеся клетки. Числа проставляются слева в порядке уменьшения. Если всё сделано верно, сумма всех чисел в любой строчке будет одинаковой.

МатематикаАлгоритм Евклида – формулы, правила и примеры решения задач

МатематикаМинор матрицы – способы, порядок и примеры вычисления

Магические квадраты – презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Магические квадраты

Мальцева А.
Якупова А.
Морозова А.
Слободян Е.
Класс 5-1

2. Цели и задачи.

Цели:
1. Познакомиться с магическими квадратами.
2. Узнать историю возникновения квадратов.
3. Научиться правильно и быстро заполнять магические квадраты.
Задачи:
1. Изучить историю возникновения и развития магических
квадратов;
2. Изучить свойства магических квадратов;
3. Познакомиться с основными методами построения
магических квадратов.

3. Что такое «магический квадрат»? Магическим квадратом называется квадратная таблица, заполненная натуральными числами, суммы которых по в

4
9
2
3
5
7
8
1
6
Порядок магического квадрата.

Слово «порядок» означает в данном случае число клеток на одной
стороне квадрата. Квадрат 3 3 имеет третий порядок, а квадрат 5 5 –
пятый, и т.д.
История возникновения магических квадратов.
Название «магические» квадраты получили от арабов, которые усмотрели
в их свойствах нечто мистическое и потому принимали квадраты за
своеобразные талисманы, защищавшие тех, кто их носит, от многих
несчастий.
Магические квадраты возникли в глубокой древности в Китае. Вероятно,
самым «старым» из дошедших до нас магических квадратов является таблица
Ло Шу (ок. 2200 г. до н. э.). Она имеет размер 3×3 и заполнена натуральными
числами от 1 до 9. В этом квадрате сумма чисел в каждой строке, столбце и
диагонали равна 15.
Согласно одной из легенд, прообразом стал узор украшавший панцирь
огромной черепахи.

5. Разновидности магических квадратов.

Магический квадрат 3 порядка.
Сумма чисел в каждом ряду 15
Магический квадрат 4 порядка.

Сумма чисел в каждом ряду 34.
4
5
14
11
1
15
8
10
16
2
9
7
13
12
3
6
Магический квадрат 5 порядка.
Сумма чисел в каждом ряду 65.
11
24
7
20
3
4
12
25
8
16
17
5
13
21
9
10
18
1
14
22
23
6
19
2
15
Каждый элемент магического квадрата называется
клеткой. Квадрат, сторона которого состоит из n
клеток, содержит n² клеток и называется квадратом
n-го порядка. Например 3 клетки квадрат 3 –го
порядка, 4 клетки –квадрат 4 порядка, и т.д. В
большинстве магических квадратов используются
первые
последовательные натуральные чисел.
Сумма S чисел, стоящих в каждой строке, каждом
столбце и на любой диагонали, называется
постоянной квадрата и равна S = n(n²+1)/2. Для
квадрата 3-го порядка S = 15, 4-го порядка – S = 34,
5-го порядка – S = 65.

9. Магический квадрат Дюрера

В начале 16в.

знаменитый немецкий художник Альбрехт Дюрер
увековечил магический квадрат в искусстве, изобразив его на
гравюре «Меланхолия» . Квадрат Дюрера имеет размер 4 х 4 и
составлен из шестнадцати первых натуральных чисел, сумма
которых в каждой строке, столбце и на диагонали равна 34.

10. Применение в жизни.

Традиционной сферой применения магических квадратов
являются талисманы. К примеру, талисман Луны обладает
определенными свойствами: предохраняет от кораблекрушения и
болезней, делает человека любезным, способствует предотвращению
дурного намерения, а так же укрепляет здоровье. Его гравируют на
серебре в день и час Луны.
Судоку: японские головоломки. Эту игру, также известную как
магический квадрат придумал в 1783 году швейцарский математик
Леонард Эйлер.
Судоку (яп. «су» – число, «доку» – рядом, стоящее отдельно) –
японские числовые головоломки, где в квадрате 9х9 клеток нужно
расставить числа от 1 до 9 особым образом.

В настоящее время судоку широко распространены за пределами
Японии: их любят разгадывать как взрослые, так и дети по всему
миру.

11. Практическая часть .

Задача 1.
Впиши в пустые прямоугольники
недостающие числа от 1 до 16 так, чтобы в сумме по
всем столбикам и строкам и обеим диагоналям
получилось число 34.
Ответ:
5
13
3
6
1
9
11
8
10
5
2
13
3
16
7
12
6
9
14
1
15
4

12. Заключение.

В наше время магические квадраты продолжают
привлекать
к
себе
внимание
любителей
математических игр и развлечений. Возросло число
книг по занимательной математике, в которых
содержатся головоломки и задачи, связанные с
необычными квадратами. Для их успешного решения
требуются не столько специальные знания, сколько
смекалка
и
умение
подмечать
числовые
закономерности. Решение таких задач послужит
прекрасной «гимнастикой для ума».

Практическое использование получили не сами
магические квадраты, а методы, и целые разделы
современной математики, которые возникли и
развивались, благодаря решению задач составления и
анализа свойств магических квадратов.
Как и много веков назад, волшебные квадраты сейчас
используют только современные «маги», астрологи и
нумерологии.

14. Выводы.

1. Магические квадраты – это нечто удивительное,
интересное и увлекательное.
2. Заполнять магические квадраты несложно, но
необходимо знать некоторые правила.
3. Главными чертами магических квадратов являются не
только ясность, чёткость и логика, но и эстетичность,
стройность и красота.
Из полученной презентации мы узнали разновидности
магических квадратов, историю их возникновения , а также
применение в современном мире.

15. Список литературы.

1. Трошин В.В.. Магия чисел и фигур. М.: – ООО
«Глобус», 2007.
2. Энциклопедия для детей. – М.: Издательское
объединение «Аванта», 2003.

3. Сарвина Н.М. Неожиданная математика //
Математика для школьников 2005, №4
4. Файнштейн В. А. Заполним магический квадрат
// Математика в школе, 2000, №3
5. Интернет

English Русский Правила

МАГИЧЕСКИЙ КВАДРАТ | Энциклопедия Кругосвет

МАГИЧЕСКИЙ КВАДРАТ, квадратная таблица из целых чисел, в которой суммы чисел вдоль любой строки, любого столбца и любой из двух главных диагоналей равны одному и тому же числу.

Магический квадрат – древнекитайского происхождения. Согласно легенде, во времена правления императора Ю (ок. 2200 до н.э.) из вод Хуанхэ (Желтой реки) всплыла священная черепаха, на панцире которой были начертаны таинственные иероглифы (рис. 1,а), и эти знаки известны под названием ло-шу и равносильны магическому квадрату, изображенному на рис. 1,б. В 11 в. о магических квадратах узнали в Индии, а затем в Японии, где в 16 в. магическим квадратам была посвящена обширная литература. Европейцев с магическими квадратами познакомил в 15 в. византийский писатель Э.Мосхопулос. Первым квадратом, придуманным европейцем, считается квадрат А.Дюрера (рис. 2), изображенный на его знаменитой гравюре Меланхолия 1. Дата создания гравюры (1514) указана числами, стоящими в двух центральных клетках нижней строки. Магическим квадратам приписывали различные мистические свойства. В 16 в. Корнелий Генрих Агриппа построил квадраты 3-го, 4-го, 5-го, 6-го, 7-го, 8-го и 9-го порядков, которые были связаны с астрологией 7 планет. Бытовало поверье, что выгравированный на серебре магический квадрат защищает от чумы. Даже сегодня среди атрибутов европейских прорицателей можно увидеть магические квадраты.

В 19 и 20 вв. интерес к магическим квадратам вспыхнул с новой силой. Их стали исследовать с помощью методов высшей алгебры и операционного исчисления.

Каждый элемент магического квадрата называется клеткой. Квадрат, сторона которого состоит из n клеток, содержит n² клеток и называется квадратом n-го порядка. В большинстве магических квадратов используются первые n последовательных натуральных чисел. Сумма S чисел, стоящих в каждой строке, каждом столбце и на любой диагонали, называется постоянной квадрата и равна S = n(n² + 1)/2. Доказано, что n і 3. Для квадрата 3-го порядка S = 15, 4-го порядка – S = 34, 5-го порядка – S = 65.

Две диагонали, проходящие через центр квадрата, называются главными диагоналями. Ломаной называется диагональ, которая, дойдя до края квадрата, продолжается параллельно первому отрезку от противоположного края (такую диагональ образуют заштрихованные клетки на рис. 3). Клетки, симметричные относительно центра квадрата, называются кососимметричными. Таковы, например, клетки a и b на рис. 3.

Правила построения магических квадратов делятся на три категории в зависимости от того, каков порядок квадрата: нечетен, равен удвоенному нечетному числу или равен учетверенному нечетному числу.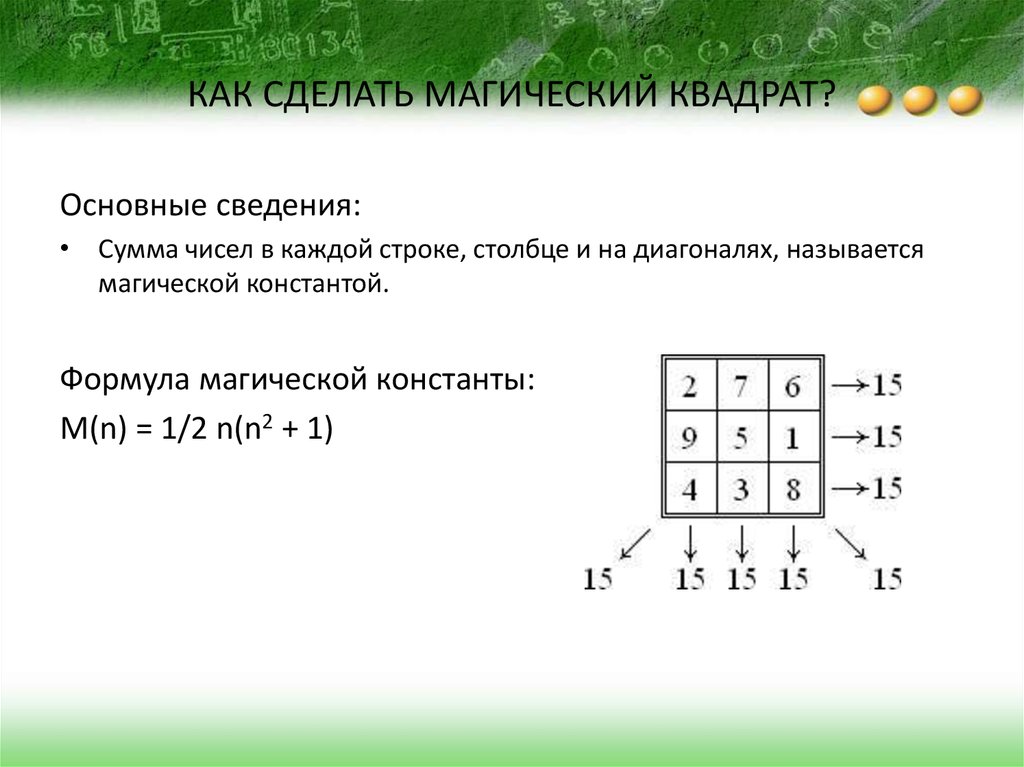 Общий метод построения всех квадратов неизвестен, хотя широко применяются различные схемы, некоторые из которых мы рассмотрим ниже.

Магические квадраты нечетного порядка можно построить с помощью метода французского геометра 17 в. А.де ла Лубера. Рассмотрим этот метод на примере квадрата 5-го порядка (рис. 4). Число 1 помещается в центральную клетку верхней строки. Все натуральные числа располагаются в естественном порядке циклически снизу вверх в клетках диагоналей справа налево. Дойдя до верхнего края квадрата (как в случае числа 1), продолжаем заполнять диагональ, начинающуюся от нижней клетки следующего столбца. Дойдя до правого края квадрата (число 3), продолжаем заполнять диагональ, идущую от левой клетки строкой выше. Дойдя до заполненной клетки (число 5) или угла (число 15), траектория спускается на одну клетку вниз, после чего процесс заполнения продолжается.

Метод Ф.де ла Ира (1640–1718) основан на двух первоначальных квадратах. На рис. 5 показано, как с помощью этого метода строится квадрат 5-го порядка. В клетку первого квадрата вписываются числа от 1 до 5 так, что число 3 повторяется в клетках главной диагонали, идущей вправо вверх, и ни одно число не встречается дважды в одной строке или в одном столбце. То же самое мы проделываем с числами 0, 5, 10, 15, 20 с той лишь разницей, что число 10 теперь повторяется в клетках главной диагонали, идущей сверху вниз (рис. 5,б). Поклеточная сумма этих двух квадратов (рис. 5,в) образует магический квадрат. Этот метод используется и при построении квадратов четного порядка.

Если известен способ построения квадратов порядка m и порядка n, то можно построить квадрат порядка mґn. Суть этого способа показана на рис. 6. Здесь m = 3 и n = 3. Более крупный квадрат 3-го порядка (с числами, помеченными штрихами) строится методом де ла Лубера. В клетку с числом 1ў (центральную клетку верхнего ряда) вписывается квадрат 3-го порядка из чисел от 1 до 9, также построенный методом де ла Лубера. В клетку с числом 2ў (правую в нижней строке) вписывается квадрат 3-го порядка с числами от 10 до 18; в клетку с числом 3ў – квадрат из чисел от 19 до 27 и т.д. В результате мы получим квадрат 9-го порядка. Такие квадраты называются составными.

Проверь себя!
Ответь на вопросы викторины «Математика»

Как звали математика, который в 19 лет решил задачу, не поддававшуюся усилиям лучших геометров со времен Евклида?

Пройти тест

Магические квадраты: головоломки с ответами для младших школьников

Магические квадраты 4 класс с ответами по математике

Как решать магические квадраты?

Сложите числа в решенной задаче в любой строке, в любом столбце, а также по обеим диагоналям.

Решить магический квадрат заполнить пустые ячейки так, чтобы сумма чисел по любой горизонтали, по вертикалям и диагоналям была одинаковой.

Logiclike. com

17.12.2020 21:11:08

2020-12-17 21:11:08

Источники:

Https://logiclike. com/math-logic/magicheskie-kvadraty

Как решать задачи на магические квадраты в 4-5 классе. Как составлять магические квадраты » /> » /> .keyword { color: red; }

Магические квадраты 4 класс с ответами по математике

Магический, или волшебный квадрат — это квадратная таблица, заполненная числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова. Минимальный размер магического квадрата — 3×3. Задачи на магический квадрат часто встречаются на математических олимпиадах для 4 и 5 класса.

Магическая константа M — сумма чисел в каждой строке, столбце и на диагоналях.

Для квадрата любой размерности N∙n минимальная магическая константа вычисляется по следующей формуле:

I. Магический квадрат 3×3

Для квадрата размера 3×3 минимально возможная магическая константа будет равна:

3(3 2 + 1)/2 = 3(9 + 1)/2 = 15

Подчеркнём, что 15 — это не единственно возможная магическая константа для квадрата 3×3, а константа, меньше которой других констант для этого квадрата быть не может.

Важное правило, которое вам пригодится при построении магического квадрата 3×3:

То есть, если у нас магическая константа M = 15, то в центре квадрата 3×3 будет стоять
15:3 = 5.

Для дальнейшего составления магического квадрата с магической константой M=15 расставьте по углам чётные числа 2,4,8,6.

Как видим, по сумма чисел на диагоналях квадрата равна 15, то есть магической константе.

Зная магическую константу и по два числа в ряду и столбце, мы можем вписать третье число в ряд и столбец. Определить это число очень просто — надо из магической константы вычесть два числа из ряда или столбца.

Применив этот метод, мы получим полностью заполненный магический квадрат:

Ещё одно важное правило построения магических квадратов:

Если у нас есть один магический квадрат, и мы все числа этого квадрата увеличим на одно и то же число или умножим на одно и то же число, то у нас опять получится квадрат. Это правило достаточно очевидно.

Пример 1. К числам в нашем магическом квадрате с M=15 прибавим 3 и 5

Как видим, у первого квадрата сумма чисел по вертикали, горизонтали и диагонали одинакова и составляет 24 (это и есть его магическая константа), а у второго квадрата магическая константа равна 30.

У этих двух квадратов число в центре по прежнему в три раза меньше, чем магическая константа (8 у первого квадрата и 10 у второго).

Пример 2. Числа нашего магического квадрата с M=15 умножим на 2 и на 3

Как видим, в первом случае, после умножения чисел на два, мы получили квадрат с магической константой 30 — та же самая константа, что и после того, как в первом примере мы увеличили все числа на 5. Но при этом, несмотря на то, что у этих двух магических квадратах одинаковые магические константы, числа при этом в клетках разные — а вот число в центральном квадрате одно и то же — это 10.

Так и должно быть, ведь, как было сказано выше, в магическом квадрате 3×3 число в центральной клетке должно быть в три раза меньше магической константы. Т. к. магическая константа у обеих магических квадратов одинаковая, то и центральное число одно и то же.

Постройте магический квадрат с магической константой 39.

Зная магическую константу, мы легко найдём число, которое должно быть в центральной клетке — нужно магическую константу разделить на 3. 39:3 = 13.

Далее можно или подбирать числа (помня о том, что сумма чисел по диагонали, по горизонтали и по вертикали должна быть равна магической константе) или, для ускорения процесса, воспользоваться знанием чисел магического квадрата с минимальной магической константой M = 15.

ВИДЕОКУРС 2plus2.online по решению Олимпиадных задач по математике для 4 класса и задач из Вступительных экзаменов в 5-й класс физматшколы.

Напомним этот квадрат:

В центре этого квадрата — число 5. В центре того квадрата, который мы должны построить — число 13.

Разница между этими числами составляет 8. И, как следует из правила, которое мы написали выше, если все числа одного магического квадрата увеличить на одно и то же число, то получится другой магический квадрат.

Достаточно запомнить, что в центре минимального магического квадрата — 5, а по углам — чётные числа 2, 4, 6, 8. Таким образом, нам надо увеличить эти числа на 8. Далее будет легко заполнить оставшиеся клетки (числа в них вычисляются как магическая константа минус числа в ряду или столбце).

В итоге получится вот такой квадрат:

Достройте магический квадрат

В этом квадрате мы знаем число в центральной клетке (9), а, значит, мы знаем магическую константу, которая в 3 раза больше и равна 27. Ну а зная магическую константу и три первоначальных числа, вписать оставшиеся числа в клетки не составит труда.

II. Магический квадрат 4×4

Мы не будем подробно останавливаться на магических квадратах 4×4 — они почти не встречаются на математических олимпиадах и вступительных экзаменах в физматшколы, но общее представление о них дадим.

Минимально возможная магическая константа вычисляется всё по той же формуле:

M = 4(4 2 + 1)/2 = 34.

У квадрата 4×4 обе стороны чётные, а это значит, что центральной клетки, в отличие от квадрата 3×3, у него нет, и нет соответствующей закономерности, с ним связанной.
Однако, у этого квадрата есть другие закономерности:

Помимо того, что у магического квадрата 4×4 равна сумма числе по диагонали, вертикали и горизонтали, у него сумма чисел в угловых квадратах 2×2 равна магической константе M, сумма чисел в центральном квадрате 2×2 также равна M, и сумма чисел в углах квадрата тоже равна M.

Сумма чисел в левом верхнем квадрате 2×2: 16+3+5+10 = 34. В трёх других угловых квадратах 2×2 сумма также равна магической константе, о чём и сказано выше.
Сумма чисел в центральном квадрате 2×2 также равна магической константе 34: 10+11+6+7 = 34.
Сумма чисел в углах магического квадрата тоже равна магической константе: 16+13+4+1 = 34

В итоге получится вот такой квадрат:

Магический квадрат 3×3

Для квадрата размера 3×3 минимально возможная магическая константа будет равна:

3(3 2 + 1)/2 = 3(9 + 1)/2 = 15

Важное правило, которое вам пригодится при построении магического квадрата 3×3:

То есть, если у нас магическая константа M = 15, то в центре квадрата 3×3 будет стоять
15:3 = 5.

Как видим, по сумма чисел на диагоналях квадрата равна 15, то есть магической константе.

Применив этот метод, мы получим полностью заполненный магический квадрат:

Ещё одно важное правило построения магических квадратов:

Пример 1. К числам в нашем магическом квадрате с M=15 прибавим 3 и 5

Пример 2. Числа нашего магического квадрата с M=15 умножим на 2 и на 3

Постройте магический квадрат с магической константой 39.

Напомним этот квадрат:

В центре этого квадрата — число 5. В центре того квадрата, который мы должны построить — число 13.

В итоге получится вот такой квадрат:

Достройте магический квадрат

Online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.

2plus2.online

22.12.2019 4:37:01

2019-12-22 04:37:01

Источники:

Https://2plus2.online/math-4-magic-square/90-Magicheskiy-kvadrat/

Урок математики в 4-м классе Формирование вычислительных навыков » /> » /> .keyword { color: red; }

Магические квадраты 4 класс с ответами по математике

Формирование вычислительного навыка требует выполнения большого количества однообразных упражнений. В то же время ученики младших классов в силу недостаточно развитого произвольного внимания не могут долго выполнять вычислительную работу. И здесь мы встречаемся с противоречием: чтобы правильно считать, нужно много считать – много считать нельзя, в связи с возрастными особенностями учащихся.

Опыт использования магических квадратов на уроках и во внеклассной работе показывает, что в первую очередь решение магических квадратов вызывает интерес у учащихся, дети с удовольствием принимаются их выполнять, что делает процесс формирования вычислительных навыков внутренне мотивированными. Кроме того, использование магических квадратов способствует не только формированию вычислительных навыков, но и развитию мышления, умения планировать и контролировать свою деятельность. Использование магических квадратов способствует так же математическому развитию.

Формировать вычислительные навыки. Развивать логическое мышление, умение планировать и контролировать свою деятельность. Создание благоприятного психологического климата для возможности раскрытия потенциала каждого ребенка; формировать качества взаимовыручки, ответственности, любознательности; развивать познавательную активность учащихся; воспитывать усидчивость, уверенность в своих возможностях.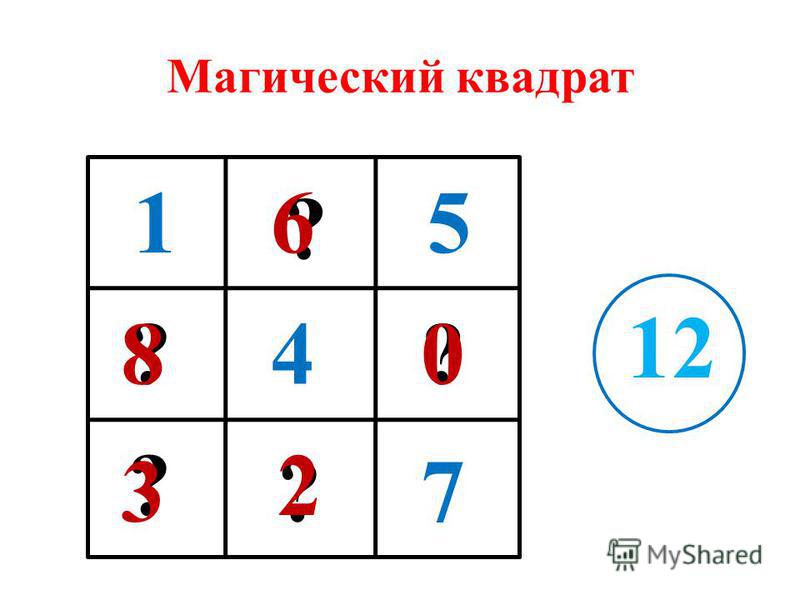

1. Организационный момент.

– Ребята! Готовы вы к уроку? (Да!)

– На вас надеюсь я, друзья.

– Мы хороший, дружный класс.

– Все получится у нас!

Я очень хочу, что бы урок получился интересным, познавательным, что бы мы вместе повторили и закрепили то, что мы уже знаем и постарались открыть новые секреты чисел и вычислений.

2. Актуализация знаний.

Мы привыкли пользоваться благами цивилизации – автомобилем, телефоном, телевизором и прочей техникой, делающей нашу жизнь легче и интереснее. Тысячи изобретений потребовались для этого, но самым важным из них были первыми – колесо и число. Без них не было бы всего нашего технического великолепия. У этих двух изобретений есть общая черта – ни колеса, ни числа в природе нет, и то, и другое – плод деятельности человеческого разума. Арабы принесли к нам способ записи чисел, которым мы сейчас пользуемся из Индии. Кто-то придумал знак нуля в Древнем Вавилоне. Кто-то из индейцев Майя – в Америке. Кто-то в Китае.

Числа настолько вошли в жизнь человека, что им стали приписывать всякие магические свойства. Так, многие не любят числа 13, число 666 называют звериным числом, приносящим несчастье.

В Древнем Китае четные числа называют женственными, а нечетные мужественные. Это какие?

Игра “Ай, да я!”. Дети цепочкой называют числа, хлопают в ладоши, если число четное, то вместо числа говорят: “Ай, да я!”.

При археологических раскопках в Китае и Индии были найдены квадратные амулеты. Квадрат разделен на девять квадратиков, в каждом из которых написано по одному числу от 1 до 9. Замечательно, что суммы чисел в каждой строке, в каждом столбце и по каждой из двух диагоналей были равны одному и тому же числу 15. Эту задачу решали тысячи лет назад китайские математики.

В средние века магические квадраты были очень популярны, они приносили счастье.

3. Постановка проблемы.

А вы хотите научиться решать магические квадраты? Эта задача – одна из самых древних задач в математике.

Какой квадрат можно назвать магическим?

Магический квадрат – это квадрат разделенный на клетки (количество клеток по вертикали и горизонтали одинаково), где в каждую клетку вписан последовательный ряд чисел. Числа записаны так, что их сумма по любым направлениям (диагоналям, горизонталям, вертикалям) постоянна. Каждое число магического квадрата участвует в нескольких разных суммах, и все эти суммы равны между собой! Этот любопытный, с точки зрения математики, факт вызывает большой интерес. Магия чисел завораживает.

4. Физминутка для глаз:

Упражнение повторять 4–5 раз.

Хотите узнать историю создания магических квадратов и способы их решения?

Пусть квадрат разделен на девять клеток (малых квадратов). Требуется разложить в них числа от 1 до 9 так, что бы сумма чисел в каждой строке, в каждом столбце, в каждой диагонали составляла 15.

Удобно запомнить следующее решение (Рис. 2).

1. Сначала напишем во всех 9 клетках по 5.
Понятно, что в этом случае сумма трех чисел в каждой строке составляет 15. Оставим в трех клетках по 5 (в средней клетке стоит 5). В двух рядом стоящих клетках добавим к пятеркам 1 и 2.

Дальше не трудно закончить составление таблицы. Проверь: получается ли по всем направлениям постоянная сумма 15?

Другой способ составления такого квадрата – использование симметрии (Рис. 3).

Начерти квадрат из 5 х 5 = 25 клеток. Внутри этого квадрата лесенкой напиши подряд числа от 1 до 9 (Рис. 3). “Перебрось” цифры 1 и 9 через цифру 5 и напиши их рядом с цифрой 5. То же самое проделай с цифрами 3 и 7.

Остальные клетки заполнить не трудно.

5. Расслабляющая гимнастика (на фоне релаксирующей музыки):

Пусть дети присядут на край стула как им хочется, в свободной позе. Не громко не торопливо произнесите:

Все умеют танцевать, бегать, прыгать, рисовать,
Но не все пока умеют расслабляться. Отдыхать.
Есть у нас игра такая – очень легкая, простая:
Замедляются движенья. Исчезает напряжение,
И становится понятно: расслабление приятно.

6. “Открытие” детьми нового знания.

А вы сами хотите создать магические квадраты?

В учебниках математики часто встречаются магические квадраты из девяти клеток (3 столбца и 3 строки). Их легко составить по простому правилу: запиши такой ряд из 9 чисел, в котором каждое следующее число на одно и то же число больше предыдущего.

Например: 14, 16, 18, 20, 22, 24, 26, 28, 30.

Возьми вторую тройку из этих чисел и запиши их по диагонали квадрата. Рядом с самым большим числом из этой тройки запиши самое маленькое число из ряда. Продолжи составление этого квадрата.

7. Первичное закрепление.

Проверь, что новые магические квадраты можно получить из данного, увеличивая или уменьшая каждое из записанных в нем чисел на одно и то же число (например, на 6) или в одно и то же число раз (например, в 2 раза).

Используя данный способ составьте свои магические квадраты и решите их.

Сумма чисел каждого ряда, столбца и каждой диагонали квадрата одинакова.

Произведение каждого ряда, столбца и диагонали квадрата одинаково.

Оцените свою работу в группе пословицей, поговоркой или изречением. Обведите пословицу или поговорку:

8. Физкультминутка.

Летел по небу шарик,
По небу шар летел.
Но знаем, что до неба
Наш шар не долетел.

При очередном прочтении закрывается по одному слову, заменяя его жестом (2 раза).

9. Самостоятельная работа с самопроверкой в классе.

Групповая работа (5 групп).

Задание для первой группы (средний уровень):

Докажите, что данный квадрат не является магическим:

Достаточно указать, что значение сумм чисел по диагоналям не равны: 12 + 15 + 18 ≠ 9 + 15 + 24.

Оцените свою работу в группе пословицей.

Задание для второй группы (высокий уровень):

В магическом квадрате суммы чисел по любым вертикалям, по любым горизонталям раны одному и тому же числу. Найдите это число. Укажите рациональный способ вычислений.

(Достаточно указать, найти значение одной, причем любой, из указанных в определении сумм. Более того ученик осознает необходимость в проведении рационального вычисления, т. к. простота вычислений в каждом случае будет разная. Например, найти сумму чисел 8 + 18 + 16).

Оцените свою работу в группе пословицей.

Задание для третьей группы (высокий уровень):

Дан магический квадрат. Какое число должно стоять в пустой клеточке?

(Можно рассуждать так: 1) найду постоянную сумму квадрата, для этого найду сумму левого столбика: 18 + 10 + 2 = 30; 2) найду сумму известных чисел в том столбике, где находится пустая клетка: 4 + 12 = 16; 3) найду число, которое должно стоять в пустой клетке: 30 – 16 = 14; 4) проверю, будет ли квадрат магическим, для этого найду сумму чисел в средней строке и сравню ее с постоянной с постоянной суммой квадрата: 14 + 6 + 10 = 30, 30 = 30, данный квадрат магический).

Оцените свою работу в группе пословицей.

Задание для четвертой группы (высокий уровень):

Дан магический квадрат. Докажите, что в клеточке со звездочкой (*) не может стоять число 32.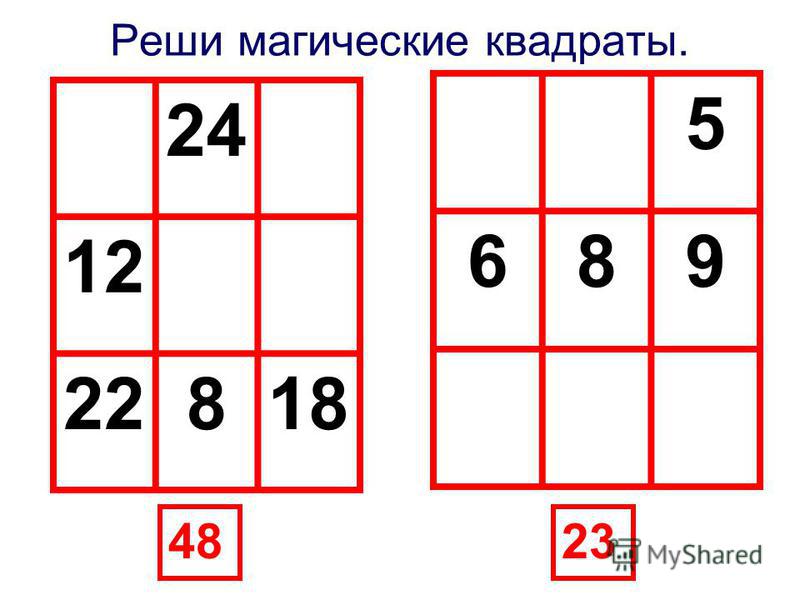

(Первый способ: можно с помощью вычислений установить, что в данной клеточке должно стоять число 14, поэтому не может стоять 32. Второй способ: найдем постоянную сумму: 8 + 6 + 16 = 30. Так как сумма должна быть не меньше каждого слагаемого, то все числа в клетках должны быть не больше 30. Но 32 > 30, значит 32 не может стоять вместо *).

Оцените свою работу в группе пословицей

Задание для пятой группы (низкий уровень):

В магическом квадрате суммы чисел по любым вертикалям, по любым горизонталям, по любым диагоналям равны одному и тому же числу. Проверьте будет ли данный квадрат магическим:

(Ученик должен сам составить в соответствии с условием все необходимые суммы, найти их значение и сделать вывод. Три суммы дают столбики, три суммы дают строчки, две суммы дают диагонали).

Летел по небу шарик,
По небу шар летел.
Но знаем, что до неба
Наш шар не долетел.

Все умеют танцевать, бегать, прыгать, рисовать,
Но не все пока умеют расслабляться. Отдыхать.
Есть у нас игра такая – очень легкая, простая:
Замедляются движенья. Исчезает напряжение,
И становится понятно: расслабление приятно.

Хотите узнать историю создания магических квадратов и способы их решения.

Urok.1sept. ru

30.05.2019 5:00:15

2018-10-06 06:25:59

Источники:

Https://urok.1sept. ru/articles/549824

Магический Квадрат читать онлайн Сильвия Брена, Иджинио Страффи (Страница 9)

— Вы меня простите, лейтенант Гаррет, но я действительно не могу быть вам полезна. С этим человеком, вашим Гейси, мои способности молчат. Мы ведь с вами однажды уже пробовали. Мне не удалось открыть канала доступа к информации о нем. К тому же я просто боюсь браться за это, у него слишком сильная и опасная отрицательная энергия. До свидания.

Трент видел, как мать, едва лейтенант ушел, упала в кресло словно подкошенная.

Юноша бесшумно скользнул в свою комнату. Какого рожна полиции искать помощь у медиума?

Он вновь сел к компьютеру и перечитал последнюю фразу: «Но одно мне ясно…» Вычеркнул ее.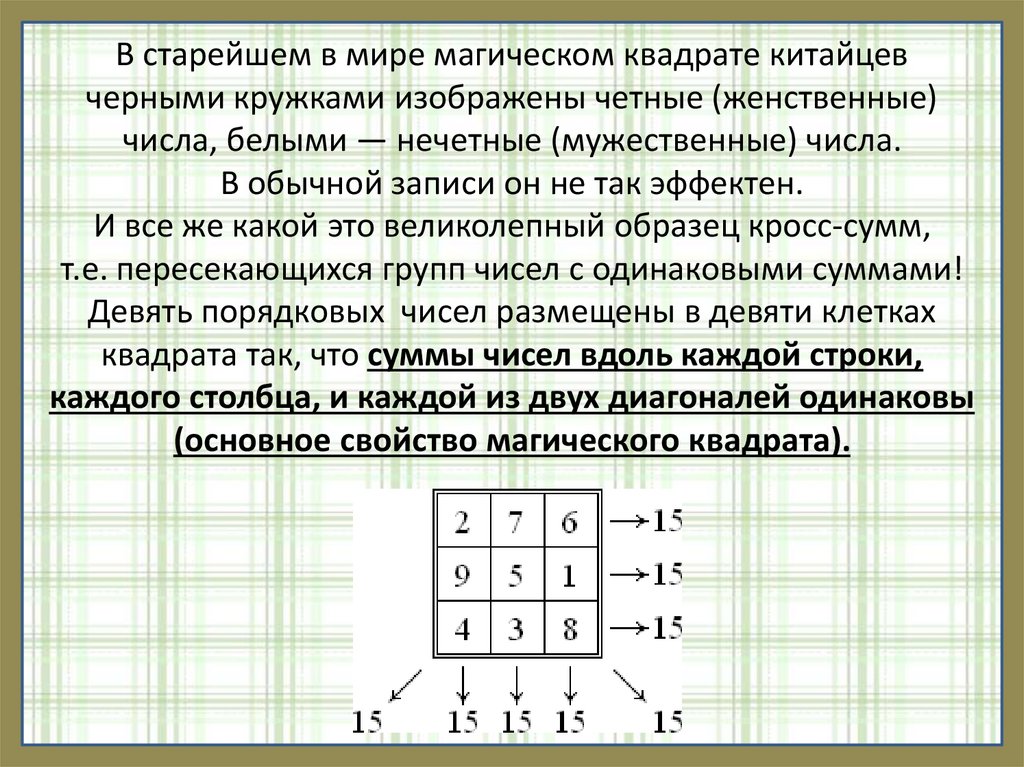 Нет, ничего мне не ясно, подумал Трент с горечью. «Я не знаю, что может произойти. Но одно мне ясно: я никогда не отрекусь от тебя», — так он закончил письмо. Не перечитывая, нажал клавишу «отправить» и отключил компьютер.

ГЛАВА 31

— Привет!

— Что тебе надо?

— Ко мне приходили из полиции. Я должна предупредить тебя: они напали на след Гейси.

ГЛАВА 32

— Это я.

— Профессор, что-то мы часто перезваниваемся в последнее время.

— На этот раз я действительно нуждаюсь в тебе.

— Зефс, вы меня утомляете, я это уже слышал от вас.

— Мне не до шуток, Гектор, или ты со мной, или ты за рамками дела.

— Я вас слушаю, только быстрее, пожалуйста. Мне надо закончить работу с одним очень интересным документом.

— За Гейси охотятся. Этот кретин… Я должен был предвидеть это. Не знаю, каким образом, но полиция его вычислила. Сегодня ему едва удалось сбежать от слежки.

— Это он сам вам рассказал?

— Нет, он исчез. Очевидно, он что-то от меня скрывает. У меня свои источники.

— А я здесь при чем?

— Тебе известно, что финал приближается, а мы еще не готовы. Нам не хватает главной детали. Ты же не хочешь, чтобы из-за этого имбецила сорвались наши планы?

Молодой человек с досадой захлопнул книжицу, которую держал в руках. Ему никак не удавалось до конца разобраться с этим окаянным Магическим Квадратом.

ГЛАВА 33

«Существует простой способ для того, чтобы: а) приручить мужчину своей мечты, oh теп, о yes!

б) избегать конфликтов с собственными мамашами, переживающими состояние менопаузы, вызывающей упадок гормонов;

в) избавиться от подруг, охотящихся за вашими ухажерами, настоящими и будущими.

МЫ ОТКРОЕМ ТЕБЕ ЭТОТ СПОСОБ! Развивай свои сенситивные способности и ИДИ ПО ЖИЗНИ С ВЫСОКО ПОДНЯТОЙ ГОЛОВОЙ!»

Валяясь на широкой Майиной кровати, подруги корчились от смеха. Сайт с советами о том, как открыть и развить собственные экстрасенсорные возможности, был безумно смешной. «Замечательная терапия, чтобы прогнать прочь беспокойство», — подумала Фло, краем глаза наблюдая за Майей.

«Начни с сенситивного правила 1. Вслушайся в себя. Интуиция — это способность прислушаться к своим инстинктам».

— Бум! — взорвалась Фло. — Хотите послушать, что я сделаю, если прислушаюсь к своим инстинктам? Во-первых, задушу Джона, он в последнее время просто невыносим!..

«Правило 2. Иди туда, куда ведет тебя твоя интуиция».

«Правило 3. Почувствуй в себе врожденный GPS. В каждом из нас есть подобный навигатор».

«Правило 4. Распознай в себе божественный дар. А если кто-то попытается покуситься на него, угости его волшебным напитком mala suerte».

— Девчонки, классный файл! Все интереснее и интереснее!..

— Oi sha san ga hi-tsu-yo des, что означает: если я делать так, я нужно к доктор.

— Юкико, ты у нас еще и острячка!

«Положи в глиняную чашку 200 граммов пчелиного воска, 900 граммов масла какао, 900 граммов каритэ; влей по полчашки оливкового и миндального масла и две чашки воды; добавь 10 капель масляного витамина Е, по 1 капле гиацинтового, женьшеневого и колокольчикового масла, 1 каплю ирландского мускуса. Затем все взбивай до тех пор, пока масса не загустеет. Намажь полученной мазью все тело, не оставляя несмазанным ни одного сантиметра. И не смывай два часа».

— Во как! А после бросьтесь в кипящее масло!

— Вы очень странные здесь, в Лондон. Вы такие смешно. Я дома рассказать…

— Даже не пытайся, Юкико, тебе никто не поверит.

— Стейси и Лиз говорить, что с некоторые вещи лучше не шутят.

— Стейси и Лиз — набитые дуры.

— О чем бы они ни говорили, они не имеют об этом никакого понятия.

— А ты, Майя, всегда иметь? Wa kari та sen. Может, я неправильно понимать, но Стейси говорить, ты делать хитрость с мертвецы.

— Что значит «хитрость с мертвецы»? Что она с ними, кокетничает, что ли?

— Кончай, Фло, Юкико имела в виду совсем другое.

— Arigato, Феба.

— Нет, Юкико, я не «хитрю с мертвецы». Просто иногда со мной случаются странные вещи. Они мне и самой не нравятся.

Голос Майи дрогнул. Она поднялась с кровати и пошла в ванную.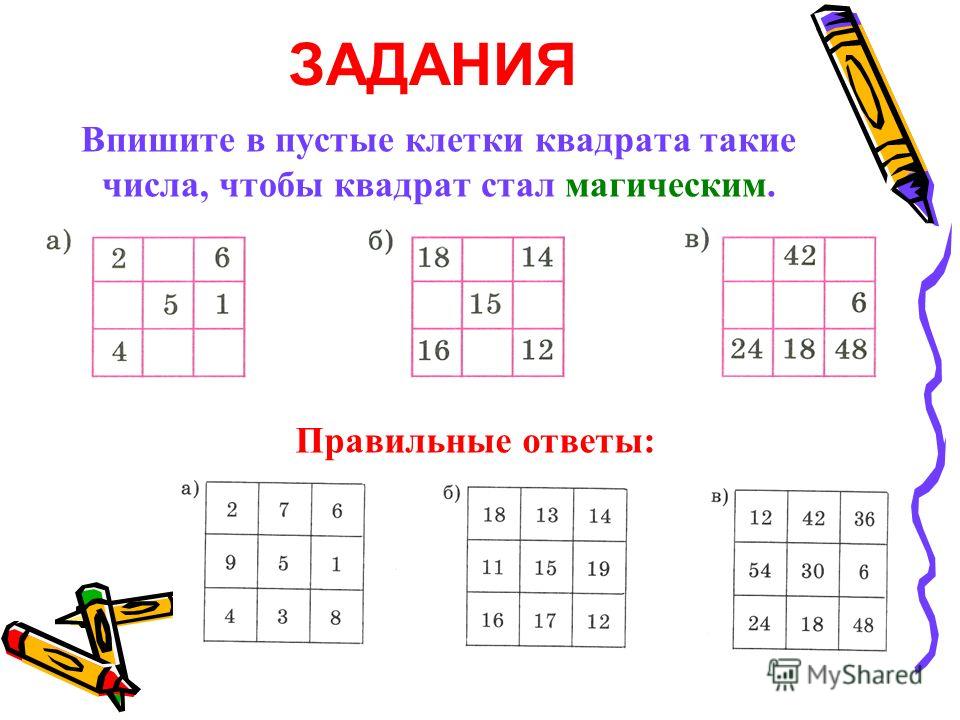 Фло с упреком посмотрела на Юкико и покачала головой. Та виновато потупила глаза. Феба пришла ей на помощь:

— Понимаешь, Юкико… у Майи случаются… скажем так, странные видения. Она называет их shining. В это время она, по ее словам, слышит голос своего отца, убитого три года назад. Знаешь, душевные травмы могут играть с человеком иногда нехорошие шутки.

— Go теп па sai, я очень сожалеть.

Фло тоже встала и пошла в ванную комнату, в которой укрылась Майя.

— Ты в порядке?

— Да-да, Фло, не беспокойся. Ты иди, я хочу немного побыть одна.

— Майя, я только хотела сказать тебе…

— Кончай, Фло, строить из себя заботливую мамочку.

— Нет, я просто подумала…

— Не надо думать, Фло. Я ценю твою заботу, но мне надо побыть одной.

— Хорошо, Майя… И все-таки я думаю, что нам стоит сходить в ту школу, о которой я тебе говорила. Может, там тебе помогут разобраться в себе. Гебе же будет лучше.

— Я там уже была.

— ???

— Позавчера вечером. Правда, внутрь не заходила. Может, ты и права, мне стоит попробовать. Только не бросай меня, Фло. Мы вместе пойдем в эту хваленую школу для магов и магш, где мне помогут обрести свое место среди ведьм-колдунов-заклинателей и всех мне подобных. Ты готова?

ГЛАВА 34

На этот раз вид белой виллы внушал больше доверия. Ничто не наталкивало на мысль о паранормальном. Вывеска имперского зеленого цвета свидетельствовала о древней и славной истории. «Колледж физических исследований, основан в 1884 году при активном содействии сэра Артура Конан Дойла…»

— Bay, Майя! Оказывается, великий сыщик Шерлок Холмс верил в привидения!

С восторгом разглядывая виллу, Фло остановилась в двух шагах от подруги.

Майя толкнула выкрашенную в черный цвет калитку и позвонила в дверной колокольчик. Никакого ответа. Позвонила еще раз.

Неожиданно в голове возникла забавная мысль, что этот странный дом заселен фантастическими эксцентричными старушками. Дверь внезапно распахнулась.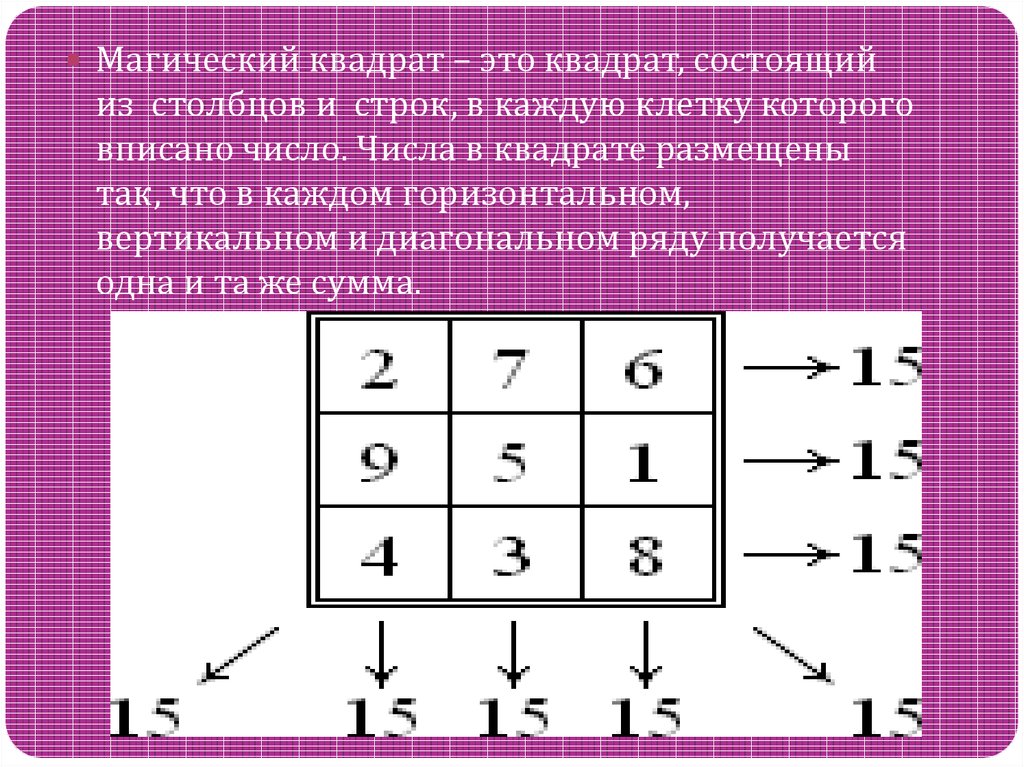

— Прошу вас, проходите. — И отдельно Майе: — Я ожидала твоего визита.

Майя и Фло украдкой переглянулись. Пожилая женщина, стоящая на пороге, без всяких колебаний обратилась именно к ней. Между тем женщина ничуть не была похожа на тех прозорливых медиумов, контактирующих с потусторонним миром, какими рисовались подругам обитатели колледжа. Прекрасный цвет лица, легкие морщинки в уголках пухлых губ, живые глаза, улыбка, излучающая радость и спокойствие, густые светлые волосы В виде длинного «конского хвоста».

— Добрый день, меня зовут Шейла. Мисс Шейла Купер. Здесь я… скажем так, занимаюсь всем понемногу. Можно сказать, я своего рода суперсекретарь. А также историческая память этого места. Следуйте, девочки, за мной.

Мисс Купер бесшумно заскользила по старинному паркету на подбитых кожей каблуках. Сделав несколько шагов, Майя и Фло огляделись по сторонам. Они находились в холле, из которого три двери вели в другие помещения, в глубине виднелась длинная лестница. Стены были желтого цвета, отчего казалось, что помещение залито солнечным светом. Тюлевые занавеси с ручной вышивкой целиком закрывали окна, защищая холл от нескромных взглядов снаружи. На небольшом столике под лестницей лежали стопки листовок и проспектов, рассказывающих о деятельности колледжа.

Майя задержалась взглядом на костюме мисс Купер в стиле шестидесятых годов: длинная до щиколоток цветная юбка, белая хлопковая блузка с романтическими кружевами на воротнике и на рукавах. Пальцы мисс Купер были унизаны множеством колец с разными камнями.

— Тебя заинтересовали мои кольца?

— Нет… То есть да… Особенно камни.

— Каждый из них имеет свой смысл. И обладает особой энергией. Ты должна бы знать это, раз носишь такую вещь.

И мисс Купер посмотрела поверх очков на кольцо на среднем пальце Майиной правой руки. Это было индейское кольцо наваратна, изготовленное по заказу Дэвида специально для Майи.

— Тебе известно, что за кольцо ты носишь?

— Более или менее.

— Юная леди, могущественные амулеты не носят, если не знают досконально их свойств и возможностей.

— Это подарок моего отца.

Идя за своей спутницей, Майя и Фло пересекли следующий зал, обстановка которого вызвала у них неподдельный восторг. Обои пастельных тонов, диваны красного бархата и множество картин, на которых были изображены закаты, рассветы и радуги. Шейла Купер провела их через анфиладу комнат и остановилась в последней. Это был просторный зал, представлявший собой идеальный квадрат, в центре которого стоял большой стол с нарисованной прямо на столешнице шахматной доской. Окна комнаты выходили во внутренний сад: были хорошо видны клумбы с розами и цветами разнообразных сортов, а также садовые беседки, усыпанные красными и оранжевыми листьями — знаками осени, которая никак не решалась уступить место зиме. Мисс Купер жестом попросила девушек занять два узких кресла в желто-белую полоску. Сама уселась на диван напротив. Но прежде разлила чай, который ждал, дымясь, в чайнике, рядом с блюдом, где высилась горка аппетитно выглядевших сэндвичей.

— Итак, ты ведь уже была здесь, не правда ли? — обратилась мисс Купер к Майе, слегка наклонившись в ее сторону и поглаживая ее руку кончиками пальцев. Майя отметила, что они горячие, как кипяток.

— Нет. Если быть точной.

— Была, была. Я тебя видела вчера вечером. Ты думаешь, девушка, одетая таким… оригинальным образом, не бросается в глаза?

Майя мысленно фыркнула: она не находила ничего оригинального в своей одежде. Обычный прикид готки, вот и все.

— А ты пришла из любопытства, девочка? — повернулась мисс Купер к Фло.

— Я? Нет… Просто Майя…

— Фло!.. — одернула Майя подругу.

— Майя — очень красивое имя. И многозначное.

— Ну, разумеется, народ майя с их древней культурой и прочее бла-бла-бла. Извините, но меня уже достали этой историей. Если хотите знать, мне самой противно мое имя.

— Речь не только о древних майя, дорогая. В индуистской философии «майя» означает начало мира. Такое же имя носили мать Будды и кормилица египетского фараона Тутанхамона. Так же называется одна из звезд Плеяд, самого загадочного созвездия. В общем, девочка, ты носишь весьма значительное имя. А теперь признавайтесь, вы здесь из-за того, что хотите научиться общаться с мертвыми?

Девушки в унисон утвердительно качнули головами.

— Все правильно. Уже ясно, что есть жизнь после смерти, — и это реальность. К такому выводу склоняется и обычная наука. Задача — научиться правильному способу преодоления барьера между мирами, иначе можно натворить дел.

— …

— Да-да, не смотрите на меня с таким недоверием. Я знаю, о чем говорю, девоньки. Я преподаю в колледже добрых тридцать пять лет. Представляете, сколько желающих стать медиумами, спиритами и магами прошло через мои руки за эти годы? Самое главное в нашем деле — осознать, что жизнь намного богаче, чем она нам, простодушным людям, кажется. Мы часто сами отказываемся видеть то, что природа и Бог поместили у нас перед глазами.

— Достаточно, Шейла, ты ведь не хочешь перепугать до смерти этих двух милых девушек своими разговорами?

Сорок лет максимум, мягкие черные брюки, прекрасно сидящие на мускулистом, хорошо развитом теле, черная шелковая рубашка с пуговицами из белого перламутра — эта женщина являла собой образец стиля. Картину дополнял водопад черных блестящих волос, ниспадающих до самых бедер. Но прежде всего девушек поразило ее лицо. Его кожа янтарного цвета. Казалось, оно соединяло в себе лучшие черты всех рас мира. Женщина могла быть индианкой, не будь ее кожа намного светлее. Уголки глубоких и слегка раскосых глаз, характерных для выходцев с Востока, были слегка приподняты вверх. Нежный и чувственный рот складывался в приятную улыбку.

— Добрый день, меня зовут Джоан Сен. Я директриса колледжа.

Девушки, покоряясь силе, исходившей от этой женщины, обе протянули ей руки.

— У нас более пятидесяти курсов. Вас интересует что-то особенное? Есть вечерние курсы для любителей, есть полноценные университетские курсы, дипломы колледжа признаются наравне с другими. Наши студенты получают глубокие знания по философии, неврологии, биологии, химии и физике человеческого организма и многим другим наукам.

— Но мы…

— Мы, — перебила подругу Майя, — мы здесь не для того, чтобы поступить в колледж, а из-за того… из-за меня… у меня есть проблема…

Женщина с мягкой улыбкой посмотрела на Майю. Ей явно понравилась прямота девушки.

— Дело в том, что я… я разговариваю со своим отцом, который уже три года как умер… Его убили.

Мисс Купер вновь погладила руку Майи своими горячими пальцами. Джоан Сен в свою очередь подбодрила ее улыбкой своих лучистых глаз.

— Он является мне. Нет, не то что он является мне на самом деле. Я ощущаю его присутствие, я слышу его голос. Впервые он появился месяц назад. Была очень скверная ситуация, и он спас мне жизнь. После я больше его не слышала. До позавчера. Но этот последний его визит сопровождался ужасной болью.

— Опиши мне, что ты чувствуешь, когда он приходит?

— Тепло. Очень сильное. Почти жар. Вот тут. — Майя показала рукой на солнечное сплетение. — Но последний раз я чувствовала острую пронизывающую боль. Словно от удара кинжалом.

— Твоего отца закололи ножом?

— Да.

— Я думаю, он сообщал тебе это.

— Да. Он добавил, что я должна пропустить через себя его смерть. Но я не хочу больше так страдать.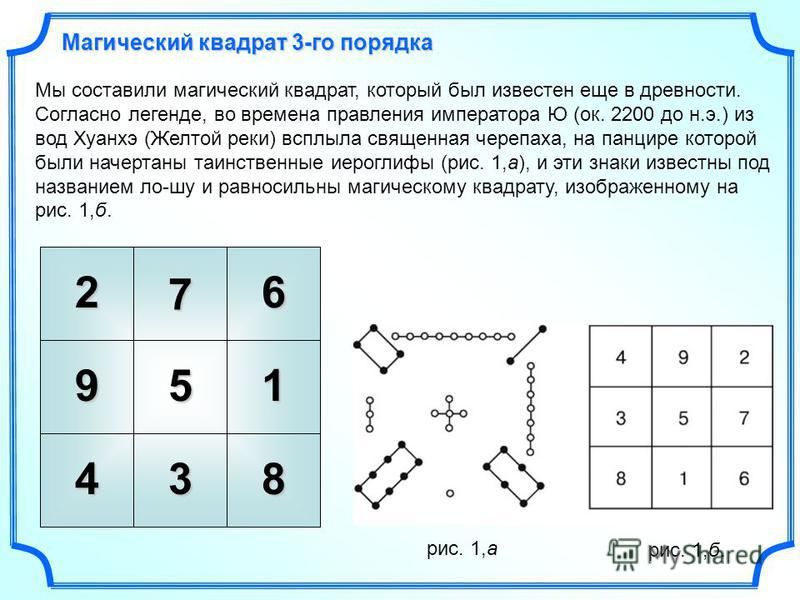 Это нестерпимо больно.

— Майя, ты, несомненно, обладаешь даром. Огромным даром. Отношения, которые связывают тебя и твоего отца, представляют собой, можно так сказать, любовь в концентрированном виде. А любовь — это энергия, дорогая…

— Которая, как утверждает наука, не исчезает… — Мисс Купер сопроводила свою реплику взмахом пухлой руки.

— Шейла права. Происходит превращение, но не уничтожение энергии. Она лишь принимает иные формы, отличные от первоначальной. Так и любовь не исчезает. Любовь, которая связывала тебя с отцом, позволила ему вернуться к тебе. У тебя явный дар, Майя. Им мало кто отмечен из живущих на земле. Ты антенна, умеющая принимать любовь. Поэтому твой отец может общаться с тобой. Но…

— Что «но»?.. — Фло с трудом сдерживала нетерпение.

— Но Майе необходимо, скажем так, научиться управлять открытием Двери между мирами.

— То есть?

— То, что Майя пережила позавчера, будет повторяться. Майя только в самом начале пути, который ведет к пониманию возможностей своего дара и к совершенному владению им.

— А если я этого не хочу? — воскликнула Майя. — Почему это происходит именно со мной? Почему этот дар дан мне, а не Фло, которой очень хотелось бы иметь его? Почему я не могу быть нормальным человеком?

— Ты и есть нормальный человек. И твой дар — вовсе не подарок свыше, не чудо. Нет, это врожденная способность выходить за пределы условностей, тонкая настройка твоего существа на более глубокое восприятие жизни и любви. Именно это и позволило тебе открыть Дверь туда, где находятся те, кого нет больше в этой жизни. Но тебе необходимо научиться открывать и закрывать ее по своей воле.

— Вы хотите сказать, что у меня нет пути назад? Что я не могу отказаться от этого проклятого дара?

— А ты могла бы отказаться от музыкального дара, допустим как у Моцарта? Или от интуиции, как у Эйнштейна? — подала реплику Шейла.

— Поэтому воспринимай shining как твой персональный паспорт в этой жизни. Так записано в Книге судеб, Майя. Так что прими это и радуйся жизни, которая позволяет тебе понимать вещи, недоступные другим человеческим существам. И научись управлять своим даром. Не позволяй ему сделать тебя своей рабыней.

— Но как я могу достичь этого?

— Всему свое время. Существуют упражнения…

— И исследования…

— Ты же училась включать и выключать свет? Вот так же ты привыкнешь открывать и закрывать Дверь. И решать сама, стоит общаться или нет с теми, кто ищет тебя из другого измерения.

— Но как? Я… я… я прошу вас, помогите мне!..

— Обязательно поможем. Только не сейчас. Твое время еще не пришло. Сначала ты должна окончить школу. А в следующем году, когда ты встанешь перед выбором пути, ты подумаешь и об этом. И если решишь обратиться к нам, мы примем тебя с распростертыми объятиями. А пока привыкай к своему дару. И доверься жизни.

Джоан Сен улыбнулась, поднялась, помахала подругам рукой и вышла из комнаты.

Улыбающаяся мисс Купер повела их к выходу.

Девушки безмолвно покинули виллу и захлопнули за собой черную калитку колледжа. Погруженные в раздумья, они не обратили внимания на слабый свет, вспыхнувший в окне второго этажа здания на противоположной стороне улицы, в одной из самых красивых патрицианских вилл Лондона.

Если бы они в эту секунду посмотрели туда, то смогли бы заметить пару глаз, внимательно изучающих их. Главным образом Майю.

Головоломки с магическими квадратами ОНЛАЙН + рабочие листы

Решайте головоломки с магическими квадратами онлайн. Решение магических квадратов 3х3. Генератор магических квадратов целых чисел. Скачать таблицу магических квадратов для печати в формате PDF. Математические магические квадраты в формате pdf. Решайте головоломки с магическими квадратами с ответами. Играйте в игру «Сложение квадратов» онлайн. Создайте рабочий лист магического квадрата 3×3 с ответами. Сложение магических квадратов для печати. Наслаждайтесь волшебным квадратом судоку онлайн. Математический магический квадрат онлайн.

Новая игра

Магическая константа:

Заполните пропуски так, чтобы числа в каждой строке, столбце и диагонали в сумме составляли одинаковую сумму.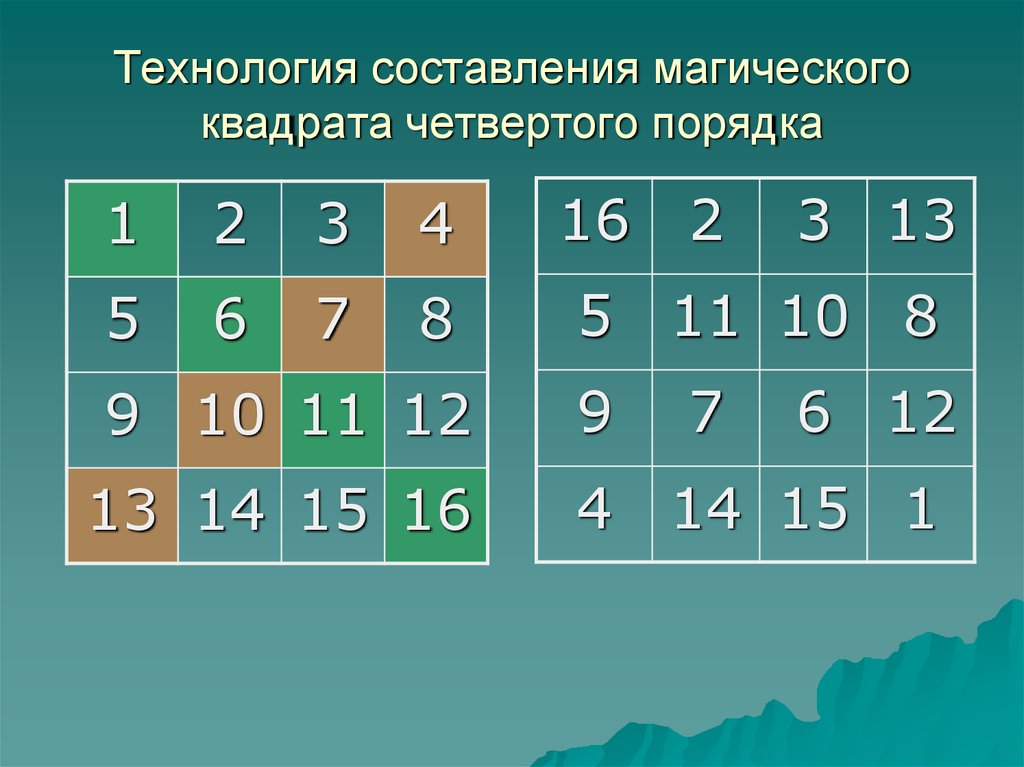

ПЕЧАТЬ ТАБЛИЦЫ »

Пожалуйста, поделитесь им:

Головоломки с магическими квадратами ОНЛАЙН

Решайте головоломки с магическими квадратами онлайн. Заполните пропущенные числа, чтобы операции в магическом квадрате были правильными. Магический квадрат составлен из чисел, расположенных так, что числа в каждом столбце, строке и на диагонали дают эквивалентную сумму. Эта сумма называется «магической константой». Каждый маленький квадрат будет иметь уникальное значение.

Загадки Магические квадраты с ответами

Нажмите “Проверить” , чтобы узнать, правильно ли заполнена головоломка с магическими квадратами. Правильные ответы будут зелеными, неправильные — красными. Нажать кнопку “Новая игра” и будет создана новая игра магических квадратов. ✨

Рабочие листы с магическими квадратами для печати PDF

Скачать магические квадраты для печати в формате PDF.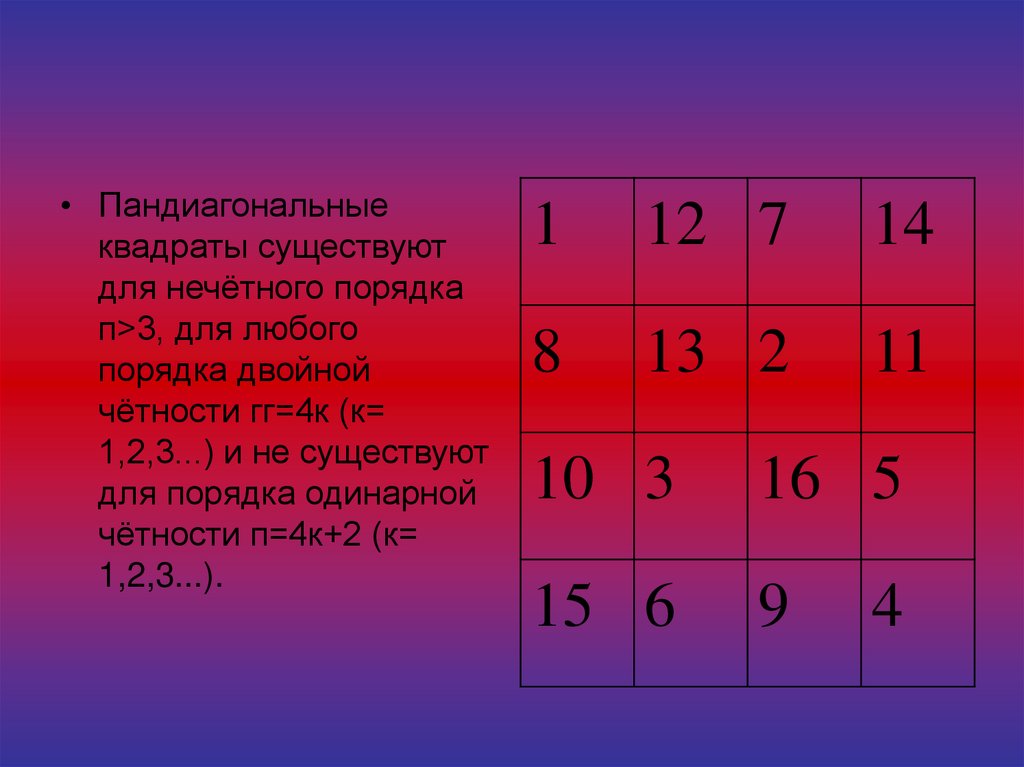 Каждый раз создается новый рабочий лист магических квадратов. Первая страница содержит четыре магических квадрата 3×3, вторая страница содержит головоломки магических квадратов с ответами. Магические константы варьируются от 12 до 100.

Нажмите на изображение ниже и загрузите бесплатную распечатанную таблицу магических квадратов в формате PDF:

Магические квадраты 3×3

Создать новый PDF

На этих рабочих листах с магическими квадратами вы найдете 4 головоломки с магическими квадратами – достаточно, чтобы развлечь детей. какое-то время, пока они осваивают эту забавную задачу. Вы можете найти больше бесплатных печатных рабочих листов здесь.

Магические квадраты ОНЛАЙН

Играйте в магические квадраты онлайн. Головоломки с магическими квадратами отлично подходят для обучения сложению в веселой и увлекательной форме. Эти магические квадраты онлайн улучшают не только сложение и вычитание, но и навыки решения задач и готовят детей для приближения к более сложным уравнениям позже в их учебном путешествии.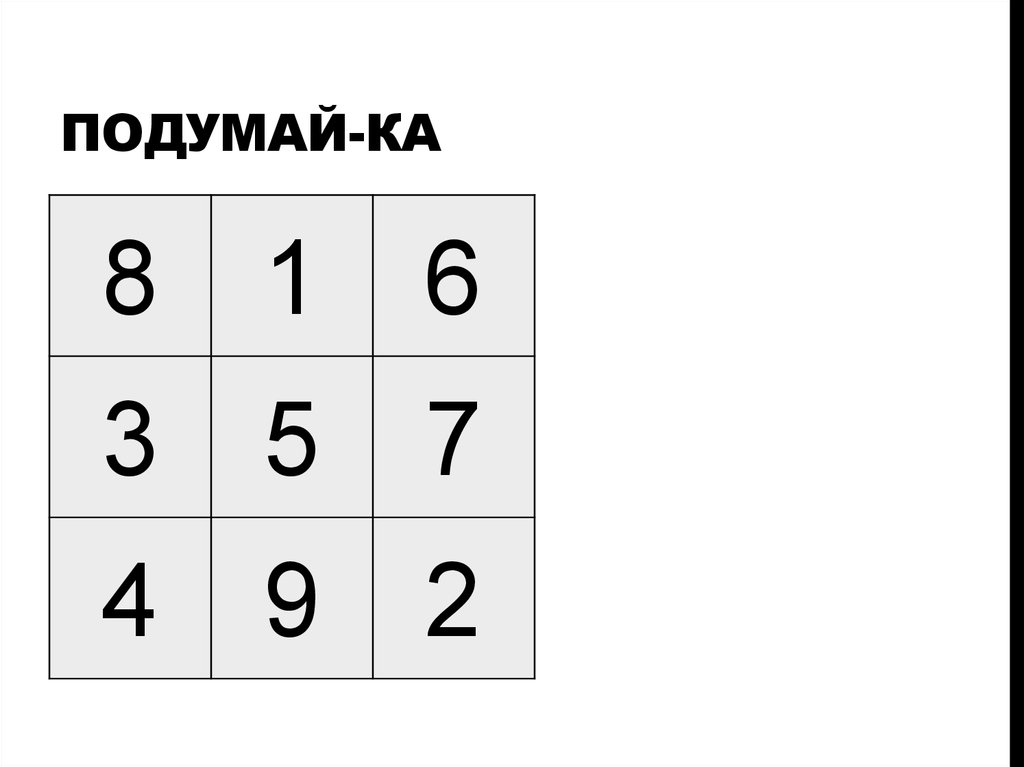

Чтобы решить эти головоломки со сложением квадратов, мы предполагаем, что дети уже умеют складывать и вычитать в пределах 100. Для практики сложения до 100 ознакомьтесь с этими сложение флешки, для вычитания до 100 проверить эти карточки вычитания флэш-памяти.

Вы также можете попробовать эти числовые кроссворды, которые также сочетают сложение и вычитание в пределах 100.

Магические квадраты 3х3

Наши магические квадраты 3×3 составлены из положительных целых чисел, расположенных так, что каждая вертикальная, горизонтальная и диагональная линия всегда добавляет к тому же значению. Каждый квадратик будет иметь уникальное значение, это означает, что эти значения больше не появятся.

Генератор магических квадратов целых чисел

Наша игра в магические квадраты генерирует магические квадраты 3×3. Вы можете выбрать диапазон магической константы: диапазон от 12 до 50 идеально подходит для детей первого и второго класса, предназначен диапазон от 51 до 100 для детей второго и третьего класса.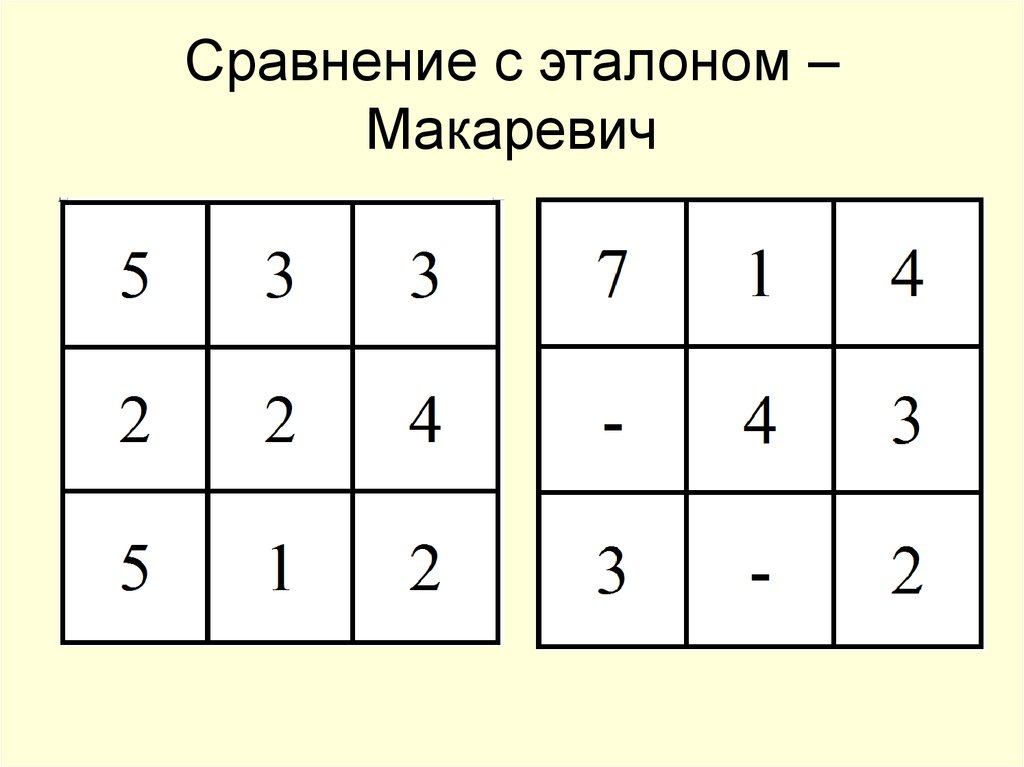

Что такое магические квадраты?

Согласно магическому квадрату Википедии представляет собой квадратный массив чисел. Это означает, что они являются последовательными числами. Наш генератор магических квадратов генерирует только те квадраты сложения, которые удовлетворяют условию: что все строки, столбцы и обе диагонали равны одному и тому же числу: магической константе.

Игра «Волшебные квадраты»

Вы можете сыграть в нашу онлайн-игру с магическими квадратами или распечатать лист магических квадратов 3×3 с ответами. Давая некоторые числа в головоломке с магическим квадратом, дети должны уметь вычислять недостающие числа.

Как решить эти головоломки на сложение квадратов?

Начните решать игру в магические квадраты со строками (или столбцами, или диагоналями), в которых заполнено наибольшее количество чисел, и подумайте, какое число необходимо для достижения целевой магической константы.

Обычно дети должны сначала сложить 2 заданных числа и вычесть результат из магической константы. И так продолжайте до тех пор, пока головоломка с магическим квадратом не будет полностью заполнена.

Категория:
Математические головоломки Дополнительные игры Игры на вычитание

Головоломки «Волшебный квадрат» с ответами

Головоломки / Логические головоломки

Кому нравятся головоломки, тому нравятся игры с магическими квадратами! В поисках магического числа ребенок заполняет таблицу. В то же время у него развивается интерес к математике, повышается логика и наблюдательность.

Решение магических квадратов

Когда вы поймете, как собирать ребусы и каким правилам следовать, процесс будет легким. Для начала следует понять, что же такого особенного в магических квадратах.

Решить магический квадрат означает заполнить пустые клетки так, чтобы сумма чисел по любым горизонтальным, вертикальным и диагональным линиям была одинаковой.

Суммируйте числа в любой строке, столбце и обеих диагоналях в решенной задаче.

Узнайте, является ли квадрат волшебным

Помогите Steam узнать, какой из двух квадратов волшебный.

Показать ответ

Ответ:

Левый квадрат.

Пояснения:
В фиолетовом квадрате сумма чисел во всех направлениях равна 21.
В синем квадрате не соблюдаются «магические» правила.

Познакомьтесь с головоломками любого уровня сложности. Для вас есть задания с ответами и описанием решения.

Вы можете делать самые простые задачи в уме. Тем не менее, все дети обожают решать головоломки онлайн.

Магические квадраты для учащихся 1 и 2 классов.

Подборка заданий из курса тренировки мозга LogicLike

Узнать пропавший номер

Показать ответ

Монстры стерли некоторые числа в магическом квадрате. Вы должны заполнить пустые клетки, чтобы квадрат снова стал волшебным.

Как решить

1) Сначала необходимо определить магическое число.
Для внимательных парней все очень просто: 5+3+1=9.
2) Найдите пропущенное число в первом столбце: 9-5-3=1.
3) Во 2-м столбце: 9-3-1=5.
4) В 3-м столбце: 9-1-5=3.

Помогите Энн сделать квадратный магический

Вставьте числа 2, 3, 4 в пустые квадратные клетки.

Показать подсказку

Магическое число = 4 + 3 + 2 = 9.
Любопытно, что этот квадрат можно заполнить по правилам судоку.

Мы создали и разрабатываем LogicLike, чтобы дать вам возможность держать свой мозг в тонусе. Улучшайте логику и навыки критического мышления и получайте удовольствие, играя в игры.

Магические квадраты для учащихся 3-4 классов.

Решать следующие головоломки в уме будет довольно сложно. Чтобы было проще, возьмите лист бумаги и ручку. Или вы можете просто наблюдать за примерами задач ниже. Самая увлекательная часть — играть в магические квадраты и решать другие логические головоломки онлайн.

Профессор придумал магический квадрат, но по рассеянности не заполнил несколько ячеек. Осталось заполнить 4 прохода.

Монстры должны поставить шесть разных чисел в пустые клетки, чтобы квадрат стал волшебным.

Станьте волшебником. Вставьте цифры 5, 8, 9, 9, 12, 13, 15 в пустые клетки и сделать квадрат волшебным.

Головоломка «Волшебный квадрат»

Постановка задачи «Волшебный квадрат»

Заполните таблицы 3 × 3 девятью различными целыми числами от 1 до 9 так, чтобы сумма чисел в каждой строке, столбце и на каждой диагонали была одинаковой. .

Решение Идея 1: Полный поиск

Основная идея состоит в том, чтобы изучить способы размещения чисел от 1 до 9 в таблице и проверить условие магического квадрата. Итак, главный вопрос: сколько существует способов заполнить такую таблицу? Дай подумать!

Мы можем начать заполнять таблицу одним числом за раз: начиная с размещения 1 где-нибудь и заканчивая размещением 9.

Существует девять уникальных способов разместить 1, за которыми следуют восемь способов поставить 2, и так до тех пор, пока последняя цифра 9 не будет помещена в единственную незанятую ячейку таблицы.
Значит, 9 · 8 · … · 1 = 9! = 362 880 способов расположить девять чисел в ячейках таблицы 3 × 3.
Таким образом, решение этой задачи с помощью полного перебора предполагает создание всех 362 880 возможных расположений различных целых чисел от 1 до 9.в таблице и проверяя для каждого из расположений, все ли его суммы строк, столбцов и диагоналей одинаковы.

Если мы еще больше увеличим значение n, то алгоритму исчерпывающего поиска потребуется изучить множество возможных решений, чтобы получить окончательный ответ. Таким образом, это решение неэффективно, потому что объем работы невозможно выполнить вручную. Даже компьютеру потребовалось бы значительное время, чтобы закончить работу!

Итак, главный вопрос: как решить эту проблему наиболее эффективно? Можем ли мы получить некоторое математическое представление о проблеме, чтобы решить ее, используя меньшее число шагов? Давай подумаем!

Эффективное решение Идея

Нетрудно решить эту головоломку, доказав два критических ограничения магического квадрата 3×3: 1) Значение общей суммы будет равно 15, что также называется магической суммой 2) Центральная ячейка должно содержать значение 5.

Поскольку мы знаем, что сумма всех столбцов, строк и диагоналей равна, поэтому магическая сумма = сумма всех чисел в ее строках, деленная на количество строк = сумма всех столбцов разделить на количество столбцов = (1 + 2 +··· + 9)/ 3 = 15. Таким образом, значение магической суммы равно 15.

Второй шаг — найти значение центральной ячейки. Предположим, что числа в строке 1, строке 2 и строке 3 равны: (a, b, c), (d, e, f), (g, h, i). Здесь «е» — значение числа в центральной ячейке. Как мы можем найти это значение? Давай подумаем!

Как мы знаем, сумма каждой строки, диагонали и столбца будет равна 15. Таким образом, мы суммируем строку, столбец и диагональ, включающие центральную клетку, т.е. мы складываем числа во второй строке, втором столбце и две главные диагонали. Вот уравнение:

=> (d + e + f) + (b + e + h) + (a + e + i) + (g + e + c) = 4*15

=> 3e + (a + b + в) + (d + e + f ) + (g + h + i) = 60

=> 3e + сумма чисел от 1 до 9 = 60

=> 3e + 45 = 60

=> e = 5

Центральная ячейка должна содержать значение 5, а сумма двух других значений строки, диагонали или столбца, включая центральную ячейку, должна быть равна 10. Для достижения магической суммы у нас будет четыре возможных пары оставшиеся 8 чисел, что дает сумму, равную 10: (1, 9), (2, 8), (3, 7) и (4, 6).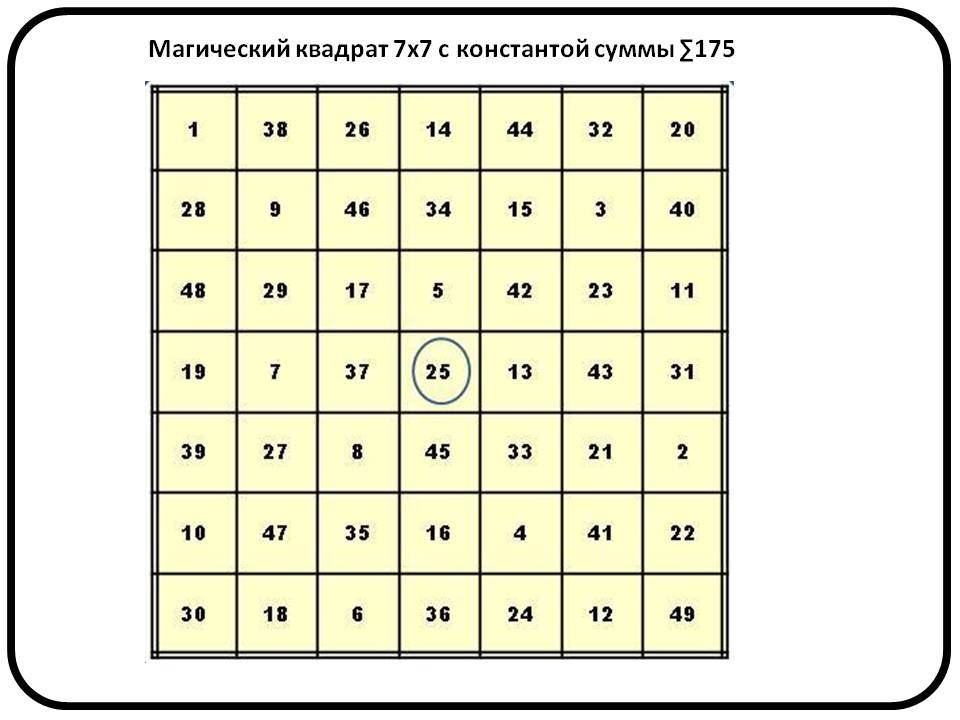 Итак, нам нужно построить магический квадрат, расположив вокруг центральной клетки четыре пары чисел. Считать! Глядя на симметрию стола, есть только два разных способа поставить 1 и 9: в углах стола и не в углах стола.

Но размещение чисел 1 и 9 в углах стола не может образовать магический квадрат. Считать! Предположим, мы поместили 1 в верхний левый угол и 9 в нижний правый угол. Если мы поместим число меньше 5 в верхний правый угол, у нас не будет волшебной суммы 15 в первой строке. Точно так же, если мы поместим число больше 5, у нас будет та же проблема с последним столбцом. Поэтому нам нужно игнорировать идею размещения пар (1, 9) в углах стола.

Теперь сосредоточимся на второй возможности поставить пару (1, 9) вокруг центральной строки или столбца таблицы. Есть четыре возможных способа поставить 1 и 9 в одну строку или в тот же столбец с 5. Для каждого варианта:

Строка, содержащая 1, должна быть заполнена 6 и 8.
Строка, содержащая 1, должна быть заполнена 2 и 4.
Строка, не содержащая 1 или 9, должна быть заполнена 3 и 7.

Как видно из рисунка, может быть 8 возможных магических квадратов 3 x 3. Для каждого возможного размещения пары (1, 9) мы можем получить два разных решения, которые являются отражением друг друга. Разумеется, все они симметричны и могут быть получены из одной из восьми вращением и отражением.

Некоторые важные факты, связанные с магическим квадратом 3×3:

Центральная ячейка должна содержать значение 5.
Значение магической суммы равно 15.
Диагональное расположение 1, 5 и 9 невозможно.
Строка, содержащая 1, должна быть заполнена 6 и 8.
Все 8 решений магического квадрата 3×3 симметричны и могут быть получены вращением и отражением друг друга

Критические идеи для изучения!

Количество различных магических квадратов порядка 2×2, 3×3, 4×4 и 5×5 равно 0, 1, 880, 275305224 (исключая полученные вращением и отражением). Точное количество магических квадратов 6×6 неизвестно.
С момента своего появления в древней Индии, Японии и Китае магические квадраты на протяжении тысячелетий очаровывали людей. Одна из нерешенных проблем заключается в том, как разработать общий алгоритм для генерации любого магического квадрата порядка NxN (N>2).
Можно использовать несколько известных алгоритмов для построения магических квадратов произвольного порядка n ≥ 3, которые особенно эффективны для нечетных n. Конечно, эти алгоритмы не основаны на исчерпывающем переборе!

Наслаждайтесь учебой, наслаждайтесь математикой!

Квадраты Эйлера

Автор(ы):

Элейн Янг

С недавней популяризацией судоку возродился интерес к родственным математическим играм, таким как магические квадраты и латинские квадраты. Головоломки судоку — это частный случай латинских квадратов; на самом деле любое решение головоломки судоку представляет собой латинский квадрат. Латинский квадрат – это квадратная сетка, заполненная символами таким образом, что каждый символ встречается один и только один раз в каждой строке или столбце. Например, латинский квадрат 3×3 будет иметь девять ячеек, в которых три различных символа будут расположены таким образом, чтобы ни один символ не повторялся ни по горизонтали, ни по вертикали (см. рис. 1).

А	Б	С
Б	С	А
С	А	Б

Рисунок 1: Латинский квадрат 3×3

Латинские квадраты были известны ранним арабским нумерологам. Эти мистические квадраты, известные как wafq majazi, , были найдены на исламских амулетах 13-го века [1] и набросаны на полях арабского медицинского текста 16-го века [2]. Знаменитый швейцарский математик Леонард Эйлер писал о латинских квадратах в своей статье Recherches sur une nouvelle espece de Quarres Magiques в 1782 году. Совсем недавно Артур Кэли (1821–1892), Рональд А. Фишер (1890–1962) и другие применяли латынь. квадраты в области агрономии, информатики, теории чисел, теории графов, теории кодирования, а также планирования и статистического анализа научных экспериментов [3] [4] [5].

Конвергенция

Автор(ы):

Элейн Янг

А	Б	С
Б	С	А
С	А	Б

Рисунок 1: Латинский квадрат 3×3

Латинские квадраты были известны ранним арабским нумерологам. Эти мистические квадраты, известные как wafq majazi, были найдены на исламских амулетах 13 века [1] и набросаны на полях арабского медицинского текста 16 века [2]. Знаменитый швейцарский математик Леонард Эйлер писал о латинских квадратах в своей статье Recherches sur une nouvelle espece de Quarres Magiques в 1782 году. Совсем недавно Артур Кэли (1821–1892), Рональд А. Фишер (1890–1962) и другие применяли латынь. квадраты в области агрономии, информатики, теории чисел, теории графов, теории кодирования, а также планирования и статистического анализа научных экспериментов [3] [4] [5].

Конвергенция

Автор(ы):

Элейн Янг

Квадраты Эйлера создаются путем наложения двух ортогональных латинских квадратов для включения двух атрибутов в каждую ячейку массива. Ортогональные латинские квадраты гарантируют, что каждая возможная пара двух атрибутов появляется в массиве ровно один раз. Теперь известные как греко-римские квадраты или квадраты Эйлера, эти массивы классифицируются по их «порядку» или количеству элементов вдоль одной стороны квадратного массива. Например, квадрат Эйлера 3×3 имеет третий порядок.

В 1694 году Жак Озанам [6] поставил задачу расположить 16 игральных карт в массиве 4 x 4 таким образом, чтобы ни одна строка или столбец не содержала более одной карты каждой масти и каждого ранга (рис. 2). Решение образует квадрат Эйлера четвертого порядка с атрибутами ранга и масти карт. Существует 144 возможных решения, не считая симметричных преобразований [7].

Рисунок 2. Одно решение проблемы с игральными картами0003

В 1779 году Эйлер исследовал теперь известную задачу об офицерах [8]:

Шесть различных полков имеют шесть офицеров, каждый из которых принадлежит к разным рангам. Могут ли эти 36 офицеров расположиться квадратным строем так, чтобы в каждом ряду и столбце было по одному офицеру каждого звания и по одному офицеру каждого полка?

Эйлер предположил, что не существует решения этой задачи, как и для любого другого квадрата Эйлера порядка 4 n +2. Эта знаменитая гипотеза просуществовала более 100 лет, пока Гастон Тарри, французский математик, не доказал отсутствие квадрата порядка шесть, перебрав вручную все возможные схемы за 19 лет.01. В 1960 году Паркер, Бозе и Шрикханде [9] использовали компьютер для создания квадрата Эйлера десятого порядка и впоследствии доказали, что единственные невозможные квадраты Эйлера имеют второй и шестой порядок.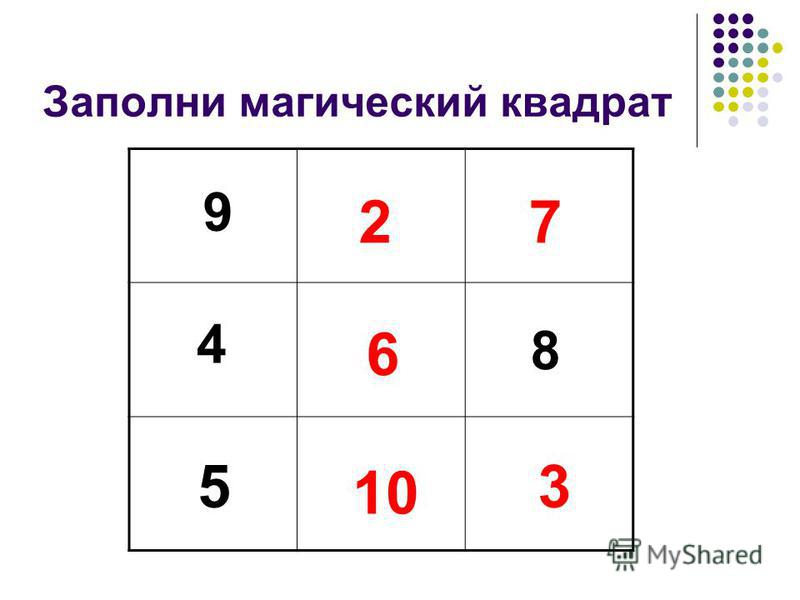 Пример квадрата Эйлера десятого порядка можно увидеть здесь. Квадрат Эйлера третьего порядка показан ниже с двойными атрибутами символа и цвета. Три символа и три цвета размещены так, чтобы ни один символ или цвет не повторялись ни в одной строке или столбце. Этот квадрат Эйлера можно разложить на два латинских квадрата, один из которых состоит из трех символов, а другой — из трех цветов (см. рис. 3). 9Рисунок 3: Квадрат Эйлера, разложенный на два латинских квадрата Девятнадцать учителей были объединены в группы для совместной работы и получили доску с пятью различными геометрическими фигурами пяти разных цветов (см. рис. 4). Автор благодарит ETA Cuisenaire за предоставление шести стержней Geo-Shapes для ее исследования.

Рис. 4. Колышка Geo-Shapes

Задача найти способ размещения колышков таким образом, чтобы ни одна форма или цвет не повторялись ни в одном ряду или столбце, группы наблюдались с использованием трех методов для поиска решения: диагонализация (показана выше на рис. 4), ход конем и навыки судоку.

Конвергенция

Автор(ы):

Элейн Янг

Этот метод начинается с размещения одного цвета по главной диагонали доски. Затем поместите другой цвет по параллельной диагонали, отметив, что это оставит единственный колышек этого цвета, который будет помещен в противоположный угол. Продолжайте диагонализовать по цветам. Это приятное для глаз и симметричное решение. Двойную диагонализацию можно выполнить, поместив цвет на одной главной диагонали, а фигуру на другой второй диагонали (см. рис. 5). 9Рис. 5. Решение двойной диагонализации Начав с цвета угла (розового), выберите другую форму (круг) и поместите этот цвет на доску, считая ходы коня в шахматах от двух до одного. Продолжайте размещать фигуры (квадрат, шестиугольник и треугольник) одного цвета, используя ход коня, «оборачиваясь» вокруг доски, когда это необходимо (см. стрелки на рис. 6). Продолжайте размещать фигуры в том же порядке, следя за тем, чтобы цвета располагались на ходу коня. Этот метод также производит диагонализацию по форме, но включает новый цветовой узор.

Рисунок 6. Обход с использованием хода конем

Конвергенция

Автор(ы):

Элейн Янг

Навыки, полученные при решении головоломок Эйлера, можно применить к квадрату. Однако это не простой метод, и, вероятно, его лучше всего применять после того, как вы начнете с двух описанных выше методов. Случайным образом размещайте колышки по диагоналям или рядам, а затем продолжайте, выбирая место на массиве и удаляя уже используемые цвета и формы для этой строки и столбца. Теперь выбирайте с умом из оставшихся колышков, корректируя при необходимости. Иногда последний цвет или последнюю форму можно разместить, проверив, какая строка или столбец еще не имеют этого атрибута. Этот метод решения был более случайным и не проявлял диагонализации или симметрии (см. рис. 7).

Рисунок 7. Использование навыков судоку для установки последней красной отметки для решения квадратов Эйлера.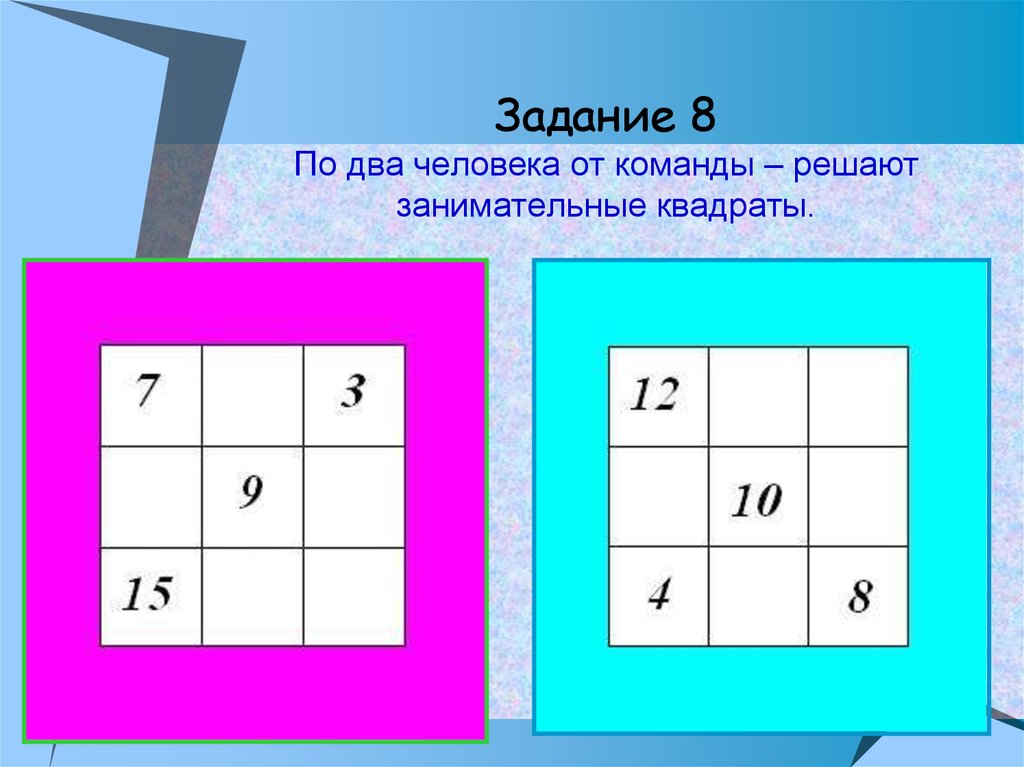 Затем инструктор предложил группам определить, сколько возможных решений может быть с использованием их конкретного метода. Группы, использующие диагонализацию, размышляли о перестановках своего текущего дизайна и обсуждали, какие из них были поворотами или отражениями, и считались ли эти шаблоны уникальными.

Другая группа начала расширять свои исследования, создав таблицу квадратов Эйлера возрастающего порядка. Вскоре они обнаружили, что квадрат Эйлера второго порядка составить невозможно. Однако, используя только один атрибут, они обнаружили два латинских квадрата. Они перешли к квадратам Эйлера более высокого порядка и начали считать, сколько существует решений. К концу урока они пытались определить формулу для предсказания количества решений, а также задавались вопросом, почему не существует квадрата Эйлера 6×6.

Простую детскую игрушку и интригующую историческую задачу можно объединить, чтобы стимулировать решение задач. Учителя не только узнали о квадратах Эйлера и связанных с ними математических темах, они многое узнали о себе и своих собственных мыслительных способностях. Сопутствующий Flash-модуль позволит читателю заняться этой исторической проблемой.

Конвергенция

Автор(ы):

Элейн Янг

Вопросы для исследования

1. Найдите латинский квадрат второго порядка. Сколько разных существует?

2. Докажите себе, что квадрата Эйлера второго порядка не существует.

3. Найдите латинский квадрат шестого порядка.

Интернет-ресурсы

Teddy Town — это интерактивная игра в латинские квадраты для детей 6-7 лет.

Квадраты Эйлера 4×4 можно распечатать и вырезать для создания игры. См. [7] для получения сопроводительной статьи и инструкций.

Построение ортогональных латинских квадратов — аплет Александра Богомольного.

Конвергенция

Автор(ы):

Элейн Янг

[1] Singmaster, D. (1998). Хронология рекреационной математики. Получено 2 сентября 2006 г. с http://www.eldar.org/~problemi/singmast/recchron.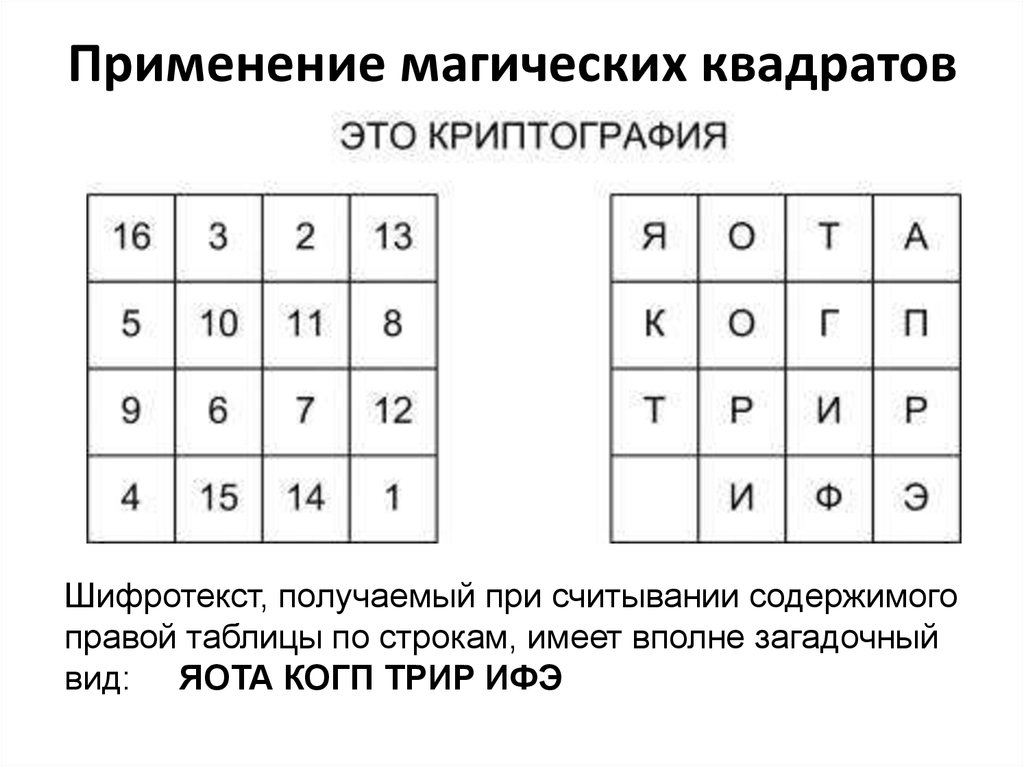 html

[2] Национальной медицинской библиотеки США. (2006). Исламские медицинские рукописи. Получено 2 сентября 2006 г. с http://www.nlm.nih.gov/hmd/arabic/

[3] Emanouilidis, E. (2005). Латинские и магические квадраты. Международный журнал математического образования в области науки и техники , 36(5), 546-9.

[4] Петерсен, И. (2000). Составление латинских квадратов. Новости науки в Интернете , 157 (19). Получено 2 сентября 2006 г. с http://www.sciencenews.org/articles/20000506/mathtrek.asp

[5] D’enes, J. & Keedwell, AD (1974). Латинские квадраты и их применение . Нью-Йорк: Академическая пресса.

[6] Озанам, Дж. (1694). Математический и физический отдых. Париж: Шарль-Антуан Жомбер.

[7] Паис, Дж., и Сингер, Р. (2004). Визуальные магические квадраты и групповые орбиты I. Получено 14 октября 2006 г. с http://www.mi.sanu.ac.rs/vismath/pais/pais.html 9.0003

[8] Sharp, J. (2005). Помимо Су Доку. Бесконечность, 1(3). Перепечатано в Преподавание математики в средней школе , 12 (3), 165–169.

[9] Бозе, Р.К., Шрикханде, С.С., и Паркер, Э.Т. (1960). Дальнейшие результаты о построении взаимно ортогональных латинских квадратов и ложности гипотезы Эйлера. Канадский журнал математики , 12, 189-203.

Конвергенция

Головоломка «Волшебные квадраты Ло Шу»

Тим Славин / Проекты по программированию и головоломки для детей / Октябрь 2014 г., выпуск

Алистер Янг на Flickr

Китайская головоломка с магическими квадратами, которой 4000 лет, — это и развлечение, и способ научиться базовым навыкам решения задач. Плюс черепахи.

Магические квадраты — это простая математическая головоломка с сеткой из равного количества столбцов и строк. Каждой ячейке сетки присваивается номер. Столбцы, строки и диагональные направления в сумме дают одинаковую сумму. Для детей старшего возраста и взрослых эта сумма называется магической константой.

Легенда гласит, что древний китайский император по имени Юй однажды вечером был на берегу Хуанхэ, когда заметил черепаху, плавающую у его ног. У черепахи были необычные отметины на панцире, которые образовывали магический квадрат, в котором сумма всех столбцов, строк и диагоналей была одинаковой. Вот узор из точек, который Ю увидел на панцире черепахи:

Википедия

Узор из точек на спине черепахи

Если вы любите числа, этот набор точек имеет удивительные отношения. Во-первых, обратите внимание, что числа 1, 2, 3, 4, 5, 6, 7, 8 и 9 состоят из точек, организованных в линии и прямоугольники. Сосчитайте сами от 1 до 9 на точечной схеме выше. Затем обратите внимание, что углы, начиная с верхнего правого угла, кратны 2. Числа 1, 3, 5, 7 и 9 находятся по краям или в центре этого узора.

Квадратная сетка 3 на 3 ячейки называется магическим квадратом Ло Шу в честь китайской сказки о узоре в виде звезды черепахи и реке Ло.

Головоломка «Математические квадраты»

Чтобы решить головоломку с математическими квадратами, сумма всех строк, столбцов и диагоналей должна быть одинаковой. Вы можете использовать каждый номер только один раз. Вот пустая сетка 3 на 3 ячейки, которую вы можете распечатать, чтобы попытаться решить:

Википедия

Пустая сетка-головоломка математических квадратов

Поскольку это сетка 3 на 3 ячейки, а числа можно использовать только один раз, 9 ячеек сообщают вам, что ваши доступные числа: 1, 2, 3, 4, 5, 6, 7, 8 и 9.

Сможете ли вы решить головоломку с помощью этих основных правил? Сколько времени это у тебя занимает?

Как решить головоломку с математическими квадратами

Самое простое решение — узор из точек, который император Юй увидел на спине черепахи. Обратите внимание, что в шаблоне каждая строка, столбец и диагонали точек в сумме дают 15:

Википедия

Узор из точек на спине черепахи

Конечно, просто ссылаться на узор из точек — обман. Гораздо интереснее посмотреть, есть ли математический способ решить любую головоломку с математическими квадратами.

Оказывается, есть способ вычислить сумму, которую нужно найти для каждой строки, столбца и диагонали в вашей сетке. Сложите все имеющиеся у вас числа и разделите на количество строк в вашей сетке:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45 / 3 = 15

Таким образом, квадратная сетка с тремя ячейками должна в сумме давать 15 для всех ее строк, столбцов и диагоналей. Точечный рисунок, который Ю увидел на спине черепахи, в сумме дает 15.

Способ суммирования до 15 оказывается довольно гибким. Вот восемь решений:

Национальный центр математического строительства

Возможные решения математических квадратов

Обратите внимание, что точечный узор Ю — это верхнее левое решение. Однако остальные семь решений также дают в сумме 15 по строкам, столбцам и диагоналям.

Большие квадратные сетки и математические пазлы

Если вы амбициозны или чокнуты, вам может быть интересно, верна ли эта математическая модель для больших квадратных сеток. Оно делает. Хотя легенда гласит, что император Китая Ю открыл магические квадраты, они появляются во многих культурах на протяжении истории. Вопрос о том, как расширить сетки магических квадратов с 3 ячеек на 3 ячейки, решил Тхаккура Феру в Индии в 1315 году нашей эры. Вы можете найти его решение и другие способы делать и обучать магическим квадратам по ссылкам ниже.

Узнать больше

Магические квадраты Ло Шу

http://en.wikipedia.org/wiki/Lo_Shu_Square

Magic Squares (Национальный центр математического строительства)

http://ncm.gu.se/media/maut/india/8_magic_square.pdf
http://ncm.gu.se/

Активность Сюзанны и Ричарда Алехандра в Ло Шу

http://mathforum.org/alejandre/magic.square/loshu1.html
http://mathforum.org/alejandre/magic.square/loshu2.html

Национальный совет учителей математики (NCTM)

Включает решение Тхаккуры Феру для больших головоломок с магическими квадратами.
http://illuminations.nctm.org/Lesson.aspx?id=655

Числа Бенджамина Франклина: незамеченная математическая одиссея

Некоторая скептическая подоплека легенды об императоре Ю с альтернативным происхождением.
http://books.google.com/books?id=UqugpLLyZUEC&pg=PA20&lpg=PA20&dq=emperor+yu,+mystic+symbol,+turtle,+magic+squares&source=bl&ots=NGVwCmLQtS&sig=zsTWHb_9NyT5GdRo8NXLf21nozM&hl=en&sa=X&ei=itMmVPiKIcWZsQSijIHYDw&ved= 0CB0Q6AEwADgK#v=onepage&q=emperor%20yu%2C%20mystic%20symbol%2C%20turtle%2C%20magic%20squares&f=false

Группа Magic Square на Flickr

https://www.flickr.com/groups/[электронная почта защищена]/

Также в выпуске за октябрь 2014 г.

Люди

Эндрю Миллс рассказывает о битах и байтах и о том, как разрабатывать игры

Эндрю создал Bits & Bytes, забавную карточную игру, чтобы научить детей вычислительным навыкам: логике, решению задач и критическому мышлению.

Прочитать статью

Люди

Тим Кропп рассказывает о создании игр для детей

Тим описывает, как он создал свою игровую компанию Glide Games и вместе со своим маленьким сыном создал две видеоигры: Elevator Adventures и Subway Adventures.

Прочитать статью

Проекты и пазлы

Пазл Lo Shu Magic Squares

Прочитать статью

История

История видеоигр

Можете ли вы назвать первую видеоигру? Вероятно, первой игрой был «Теннис для двоих» в 1958, но это могут быть космические войны! в 1962 или других играх. Все сложно.

Прочитать статью

Проекты и головоломки

Игра в Harvest Moon на японском языке

История англоговорящего человека, изучающего японский язык, играя в последнюю игру Harvest Moon, Connect to a New World, на оригинальном японском языке.

Прочитать статью

Люди

Венди Норман и Скайп в классе

Венди Норман, директор отдела социального обеспечения Microsoft, рассказывает об истории и особенностях службы Skype в классе для учителей.

Читать статью

Концепции

Игра

Вы можете использовать концепции игры, чтобы превратить почти любую задачу или информацию в игру. Предполагая, что вы можете определить игровой процесс.

Прочитать статью

Мероприятия

Maker Faire NY 2014

The Greatest Show and Tell на Земле оказалось массой развлечений для детей и родителей, а также местом, где можно побродить и найти новые технологии. Ссылки и видео.

Прочитать статью

Нам нужно рассказывать истории. В противном случае жизнь просто продолжается и продолжается, как число Пи.

Энг Ли

Дополнительные ссылки

Октябрь 2014 г. Дополнительные ссылки

Ссылки внизу всех статей за октябрь 2014 г., собранные в одном месте, чтобы вы могли распечатать, поделиться ими или добавить в закладки.

Прочитать статью

Язык месяца

Папирус

Этот язык позволяет модифицировать игру Skyrim, чтобы научиться кодировать игру, а также весело провести время, добавляя объекты и функциональные возможности в игру.

Прочитать статью

Новостная лента

Октябрь 2014 Новостная лента

Интересные истории о информатике, программировании и технологиях за сентябрь 2014 года.

Прочитать статью

Ноутбук

Unity, PyGame, GamePress

Три программных инструмента для создания игр, которые вы можете использовать для создания игр. Включает краткое описание и множество ссылок на эти и другие инструменты для создания игр.

Прочитать статью

Как решить магический квадрат?

Фокусники часто совершают действия , которые не являются строго магическими, но оставляют у зрителей ощущение, что они стали свидетелями чего-то невозможного. Примерами могут служить трюки с памятью, необычные научные демонстрации, игра в шахматы с завязанными глазами и быстрые вычисления в уме.

Успешные трюки такого рода говорят о том, что исполнитель обладает усиленным талантом. В некоторых случаях это действительно так — у них может быть необыкновенная память или они могут быть шахматными гроссмейстерами.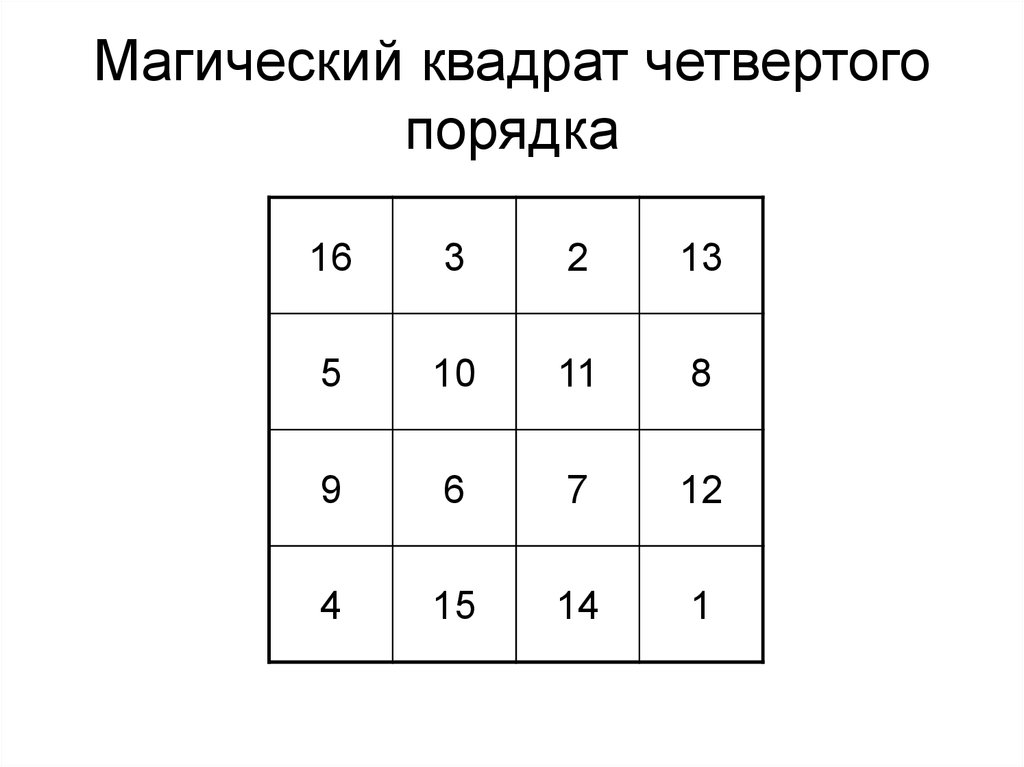 Но в большинстве случаев исполнитель использует систему. Эти системы могут быть простыми или требовать огромного мастерства, но они все равно проще, чем выполнение трюка вообще без какой-либо системы.

Популярным математическим трюком является создание «магического квадрата». Это сетка, чаще всего 3×3 или 4×4, заполненная числами. Числа в каждой строке в сумме дают одно и то же число. Вот пример:

Как видите, все строки в сумме дают 15. Обратите внимание, что каждое число от 1 до 9 используется один раз. Если бы вы могли повторять числа, многие магические квадраты стали бы тривиально простыми, как сетка, полностью состоящая из единиц, которые в сумме дают 3!

В этом нет ничего удивительного.

Составление магического квадрата перед аудиторией, если все сделано правильно, может стать впечатляющей демонстрацией очевидного владения математикой более высокого уровня. Я покажу вам, как это сделать, используя, казалось бы, более сложную сетку 4×4.

Возьмите визитную карточку и напишите на обороте магический квадрат 4×4:

Этот магический квадрат дает в сумме 34. Это наименьшая сумма, которую можно получить, используя числа от 1 до 16. Сохраните эту карточку, и вы сможете чтобы выполнить этот трюк в любое время вы хотите.

После обеда, скажем, переключите разговор на цифры и достаньте визитную карточку. Объясните основную идею магического квадрата; что каждый столбец и строка в сумме дают одно и то же число. Пусть ваши компаньоны проверят это, если захотят, добавив столбцы и строки.

Скажи им, что постараешься составить магический квадрат специально для них. Попросите их назвать вам любое двузначное число больше 34.

Предположим, вам дали число 87. Оставьте свою визитную карточку на видном месте и возьмите другой лист бумаги. Нарисуйте сетку 4×4. Из целевого числа, которое назвали ваши гости, вычтите число 34. В нашем примере 87 — это целевое число: 87 минус 34 = 53. Затем вы делите 53 на 4 до ближайшего целого числа. Это дает 13 с остатком 1 (13 x 4 = 52; 52 + 1 = 53).

Запомните число 13. Мы называем это частным, и это одно из двух специальных чисел, которые вам понадобятся. Другое специальное число — это частное плюс остаток. В нашем случае это 14 (13 + 1).

Теперь все готово. Сначала украдкой взгляните на свою визитную карточку. Посмотрите на верхний ряд. Добавьте свое первое специальное число к 8, которое появляется в строке 1, столбце 1 вашей карты: 13 + 8 = 21. Запишите это в соответствующем поле в новой сетке.

Вы продолжите в том же духе для всех 16 ячеек в сетке, за четырьмя исключениями. Когда вы дойдете до чисел 13, 14, 15 или 16 на исходной карте, вы должны добавить специальное число 9.0332 плюс остаток.

Правильно заполненная сетка будет выглядеть следующим образом:

Обратите внимание, что каждый результат в этой сетке представляет собой просто число с вашей исходной визитной карточки, добавленное к 13, за исключением четырех чисел, выделенных красным. Это ваши исходные числа плюс 14.

Теперь вы можете показать, что каждая строка и столбец в сумме дают 87.

Но подождите, это еще не все! Вам также удалось получить две диагонали в сумме 87, а также четыре числа в каждом из угловых квадрантов …

… и верхний центральный и нижний центральный квадранты!

К сожалению, два боковых квадранта добавят , а не к 87, но четыре угла большой сетки добавят!

Правда в том, что диагонали, квадранты и четыре угла на вашей оригинальной визитной карточке тоже составляют 34, но не раскрывайте это заранее. Сохраните это для магического квадрата, который вы сделаете для своих гостей.

Поскольку 87 — нечетное число, у нас был остаток, который нам нужно было использовать для ячеек с 13, 14, 15 и 16 в них. Если ваш зритель назовет четное число (например, 54), у вас не останется остатка.

Помните уравнение: 54 (целевое число) минус 34 (наша исходная сумма магического квадрата) = 20. Затем вы делите 20 на 4, чтобы получить 5 без остатка! Все, что вам нужно сделать, это добавить 5 к каждому из 16 чисел в вашей новой сетке, и все заработает.

Между прочим, если ваше целевое число равно четному , то эти два боковых квадранта также добавятся к целевому числу.

Если вы хотите, чтобы это выглядело сложнее, вы можете запомнить свой первоначальный магический квадрат, который в сумме дает 34. Таким образом, вам не придется смотреть на свою шпаргалка. Кроме того, вместо того, чтобы работать прямо через ряды по одному, вы можете попросить своего зрителя указать на любой пустой ящик, и вы можете добавить свой специальный номер (или специальный номер плюс остаток) к любому номеру, принадлежащему этому ящику.

Магические квадраты: математические игры от ЛогикЛайк

Как решать магические квадраты?

Проверь себя

Магические квадраты для 1-2 класса

Определи недостающее число

Магические квадраты для 3-4 класса

Магический квадрат – виды, правила и примеры решения

История и современное применение

Квадрат нечётного порядка

Одинарная чётность

Вычисление магической константы

Дальнейшие действия

Двойной порядок

Магические квадраты – презентация онлайн

1. Магические квадраты

2. Цели и задачи.

3. Что такое «магический квадрат»? Магическим квадратом называется квадратная таблица, заполненная натуральными числами, суммы которых по в

5. Разновидности магических квадратов.

9. Магический квадрат Дюрера

10. Применение в жизни.

11. Практическая часть .

12. Заключение.

14. Выводы.

15. Список литературы.

МАГИЧЕСКИЙ КВАДРАТ | Энциклопедия Кругосвет

Магические квадраты: головоломки с ответами для младших школьников

Как решать магические квадраты?

Источники:

I. Магический квадрат 3×3

II. Магический квадрат 4×4

Магический квадрат 3×3

Источники:

Источники:

Магический Квадрат читать онлайн Сильвия Брена, Иджинио Страффи (Страница 9)

Головоломки с магическими квадратами ОНЛАЙН + рабочие листы

Головоломки с магическими квадратами ОНЛАЙН

Загадки Магические квадраты с ответами

Рабочие листы с магическими квадратами для печати PDF

Магические квадраты 3×3

Магические квадраты ОНЛАЙН

Магические квадраты 3х3

Генератор магических квадратов целых чисел

Что такое магические квадраты?

Игра «Волшебные квадраты»

Как решить эти головоломки на сложение квадратов?

Головоломки «Волшебный квадрат» с ответами

Решение магических квадратов

Узнайте, является ли квадрат волшебным

Магические квадраты для учащихся 1 и 2 классов.

Узнать пропавший номер

Помогите Энн сделать квадратный магический

Магические квадраты для учащихся 3-4 классов.

Головоломка «Волшебный квадрат»

Постановка задачи «Волшебный квадрат»

Эффективное решение Идея

Критические идеи для изучения!

Квадраты Эйлера

Головоломка «Волшебные квадраты Ло Шу»

Головоломка «Математические квадраты»

Как решить головоломку с математическими квадратами

Большие квадратные сетки и математические пазлы

Узнать больше

Магические квадраты Ло Шу

Magic Squares (Национальный центр математического строительства)

Активность Сюзанны и Ричарда Алехандра в Ло Шу

Национальный совет учителей математики (NCTM)

Числа Бенджамина Франклина: незамеченная математическая одиссея

Группа Magic Square на Flickr

Также в выпуске за октябрь 2014 г.

Эндрю Миллс рассказывает о битах и ​​байтах и ​​о том, как разрабатывать игры

Тим Кропп рассказывает о создании игр для детей

Пазл Lo Shu Magic Squares

История видеоигр

Игра в Harvest Moon на японском языке

Венди Норман и Скайп в классе

Игра

Maker Faire NY 2014

Нам нужно рассказывать истории. В противном случае жизнь просто продолжается и продолжается, как число Пи.

Октябрь 2014 г. Дополнительные ссылки

Папирус

Эндрю Миллс рассказывает о битах и байтах и о том, как разрабатывать игры