Магический квадрат 4 класс решение с ответами – Магические квадраты: математические игры от ЛогикЛайк
Как решить магический квадрат для 4 класса
Как решить магический квадрат для 4 класса
Как решать магические квадраты?
17 ноября 2014
23842

Смотрите видео
Как решать магические квадраты?
Магическим квадратом принято называть головоломку наподобие судоку. Это квадрат, клетки которого заполнены числами так, чтобы сумма в конце любой строки, столбца и диагонали была одинаковой. В магических квадратах-головоломках некоторые числа пропущены, и требуется их расставить так, чтобы соблюсти описанное выше условие равной суммы. Как же решать магические квадраты?
Способы решения магических квадратов
Для того чтобы решение магических квадратов было верным, необходимо знать ту самую волшебную сумму, которая должна получаться при сложении чисел в строках, столбцах и диагоналях. После этого расставить недостающие числа становится существенно проще. Как же эту сумму найти?
Способ 1
Наипростейший вариант магического квадрата – когда одна из строк, один из столбцов или одна из диагоналей полностью заполнена числами. В таком случае остается только подсчитать сумму этих чисел и подбирать решения.
Сумму чисел на концах строк, столбцов и диагоналей можно высчитать по специальным формулам. При этом формула для квадратов с четным количеством ячеек в одной строке будет отличаться от квадратов с нечетным количеством ячеек.
Итак, для четных квадратов подходит формула:
n + ( (n+1) * n * (n-1) / 2), где n – количество ячеек в одной строке.
Для нечетных квадратов подходит формула:
n * ( n2 +1) / 2, где n – также количество ячеек в одной строке.
Пример решения
Рассмотрим решения магического квадрата из девяти ячеек с числами от 1 до 9. Сначала подсчитаем сумму, которая должна получаться на концах. В одной строке у нас 3 ячейки, то есть n = 3. Подставляем значение в формулу:
3 * ( 32 +1 ) / 2 = 3 * 10 / 2 = 15
Теперь подбираем числа так, чтобы сумма равнялась 15.
Далее алгоритм потребует немного пространственного воображения. Поставьте число 1 в середину верхней строки. Каждое следующее число мы ставим справа по диагонали вверх. Пробуем ставить 2. Но там нет ячеек, если мы подставим над нашим квадратом еще один такой же воображаемый, то число 2 окажется в правом нижнем углу этого нового
Похожие задачи:
Является ли рациональным или иррациональным числом сумма а + b, где а – 1,323223222… (группы цифр, состоящие из одной, двух, трёх двоек и т. д., разделяются тройками) и b = 2,313113111… (группы цифр, состоящие из одной, двух, трёх единиц и т. д., разделяются тройками)?смотреть решение >>
erricon.ru
Магический квадрат
Разделы: Математика
Цели работы:
Распознать сущность магических квадратов, их влияние на развитие познавательных интересов человека.
Задачи:
- Раскрыть исторические сведения о магических квадратах.
- Показать их связь с жизнью.
- Выяснить алгоритм построения магического квадрата.
- Познакомиться с другими магическими квадратами.
Древние люди куда больше зависели от природы, чем мы. Не имея метеорологических станций и спутников, центров для обработки наблюдений и прогнозирования, они предсказывали погоду по поведению птиц и животных, форме облаков, цвету восхода и заката Солнца. Найденные приметы передавались из поколения в поколение. Ими не пренебрегает и современная служба погоды.
Подобные приметы существовали не только для определения погоды, люди пытались найти связи для всех важных для них явлений с другими явлениями. Так родилась астрология, связывающая судьбы людей и народов с расположением небесных светил. А с появлением чисел им стали придавать и мистический смысл. До сих пор многие считают число 13 несчастливым, а уж если тринадцатое число месяца — пятница, то тут жди беды.
От беды нужно иметь защиту. Так появились разнообразные амулеты, предохраняющие человека от несчастий: драгоценные камни, когти и зубы животных, листья и травы. А в Китае и Индии с давних пор одним из видов амулета была бумажка с девятью цифрами, записанными в некотором порядке (рис.1). Цифры там были, конечно, не те, которыми мы пользуемся сейчас.
Рис. 1
Главное свойство такого расположения цифр в том, что их сумма в каждом горизонтальном ряду, в каждом вертикальном ряду и по каждой из двух диагоналей одна и та же.
По древней китайской легенде, император Ню, живший 4000 лет назад, однажды нашел на берегу реки священную черепаху, на панцире которой был изображен рисунок, состоящий из черных и белых кружков, соединенных черточками (рис.2). Этот рисунок назвали “ло-шу”.
Рис. 2
Подсчитав количество кружков в каждой из фигур, мы получим наш прежний магический квадрат. А существуют ли другие магические квадраты? Давайте подумаем.
Сначала выясним, чему может равняться сумма чисел в строке. Так как 1 + 2+3+4 + 5+6 + 7 + 8+9 = 45, то в каждой строке (столбце, диагонали) стоит треть от этого числа, т.е. 15.
Теперь определим число, стоящее в центре. Обозначим его через х и сложим все числа, стоящие на вертикали, горизонтали и диагоналях, проходящих через центр. При этом каждое число войдет в сумму по одному разу, а центральное — четыре раза, поэтому 4*15=(45 – х)+4х. Отсюда находим, что х = 5.
Из соображений четности следует, что в углах квадрата должны стоять четные числа, а в серединах сторон – нечетные.
Теперь уже нетрудно убедиться, что все магические квадраты получаются из квадрата “ло-шу” с помощью поворотов вокруг центра и симметрии относительно средних линий и диагоналей. Всего же их 8.
По образу квадрата “ло-шу” в дальнейшем стали придумывать магические квадраты большего размера. На картине знаменитого немецкого художника Альбрехта Дюрера “Меланхолия” мы видим магический квадрат размерами 4X4 (рис.3). Любопытно, что два числа в середине его нижней строки указывают год создания картины (1514 г.).
16 |
2 |
3 |
13 |
5 |
11 |
10 |
8 |
9 |
7 |
6 |
12 |
4 |
14 |
15 |
1 |
Магическим квадратом стали называть квадрат nхn, в клетках которого записаны числа от 1 до п2 так, что в каждой строке, каждом столбце и по каждой из двух его диагоналей сумма чисел одна и та же. Найти эту сумму не составляет труда, так как 1+2+…+n2=n2(n2+1)/2. Поэтому сумма в каждой строке (столбце, диагонали) равна n(n2+1)/2.
Долгое время составление магических квадратов было весьма популярным занятием математиков и любителей математики. Выдающийся американский общественный деятель, дипломат и ученый Бенджамин Франклин в молодости забавлялся составлением причудливых магических квадратов, скрашивая скучные часы на службе в Законодательном Собрании штата Пенсильвания. Его квадрат 8X8, изображенный на рисунке 4, обладает многими дополнительными свойствами.
52 |
61 |
4 |
13 |
20 |
29 |
36 |
45 |
14 |
3 |
62 |
51 |
46 |
35 |
30 |
19 |
63 |
60 |
5 |
12 |
21 |
28 |
37 |
44 |
11 |
6 |
59 |
54 |
43 |
38 |
27 |
22 |
55 |
58 |
7 |
10 |
23 |
26 |
39 |
42 |
9 |
8 |
57 |
56 |
41 |
40 |
25 |
24 |
50 |
63 |
2 |
15 |
18 |
31 |
34 |
47 |
16 |
1 |
64 |
49 |
48 |
33 |
32 |
17 |
Рис. 4
Сумма чисел в каждой строке здесь равна 8(64+1)/2=260. При этом сумма чисел в каждой половине строки и в каждой половине столбца равна 130. Четыре числа в углах вместе с четырьмя числами в центре вновь дают 260. И еще много подобных соотношений можно отыскать в этом квадрате.
Известны и небольшие квадраты с дополнительными свойствами. Так, квадрат 4X4, изображенный на рисунке 5, имеет сумму 34 не только по строкам, столбцам и диагоналям, но и по “разломанным диагоналям” (рис.6), а также в каждом квадрате 2X2. Если такими квадратами замостить плоскость, то каждый квадрат 4X4 в этой плоскости будет магическим.
1 |
12 |
6 |
15 |
8 |
13 |
3 |
10 |
11 |
2 |
16 |
5 |
14 |
7 |
9 |
4 |
Рис. 5
Создавались магические квадраты больших размеров. Известный немецкий математик М. Штифель в книге “Arithmetica integra”, вышедшей в 1544 году, приводит магический квадрат размерами 16X16. Известны магические квадраты размерами 43 X 43. Изготовление большого магического квадрата не составляет труда, поскольку имеются алгоритмы, позволяющие строить магические квадраты любых размеров.
Следует, правда, отметить, что магического квадрата 2X2 не существует.
Рис.6
При всем том, многое о магических квадратах неизвестно. Неизвестно, как зависит количество магических квадратов nхn от значения размера n. Известно лишь, что квадратов 4X4 существует 880, а квадратов 5X5 — около четверти миллиона. Прямой перебор всех возможностей даже для квадратов 5 X 5 на современных ЭВМ займет около 1000 лет!
Современных математиков магические квадраты интересуют из-за их связи с так называемыми “конечными геометриями”, в которых используется конечное число точек, а поэтому “прямые” и “плоскости” в таких геометриях также состоят из конечного числа точек.
Использованная литература:
- Физико-математический журнал для школьников и студентов “Квант” №4 1995 г.
- М.М. Постников “Магические квадраты”.
Презентация
2.08.2009
urok.1sept.ru
Как решать магические квадраты?
Как решать магические квадраты?


Магическим квадратом принято называть головоломку наподобие судоку. Это квадрат, клетки которого заполнены числами так, чтобы сумма в конце любой строки, столбца и диагонали была одинаковой. В магических квадратах-головоломках некоторые числа пропущены, и требуется их расставить так, чтобы соблюсти описанное выше условие равной суммы. Как же решать магические квадраты?
Способы решения магических квадратов
Для того чтобы решение магических квадратов было верным, необходимо знать ту самую волшебную сумму, которая должна получаться при сложении чисел в строках, столбцах и диагоналях. После этого расставить недостающие числа становится существенно проще. Как же эту сумму найти?
Способ 1
Наипростейший вариант магического квадрата – когда одна из строк, один из столбцов или одна из диагоналей полностью заполнена числами. В таком случае остается только подсчитать сумму этих чисел и подбирать решения.
Способ 2
Сумму чисел на концах строк, столбцов и диагоналей можно высчитать по специальным формулам. При этом формула для квадратов с четным количеством ячеек в одной строк
elhow.ru
Как решить магический квадрат 4 класса
ИНТЕРЕСНОЕ
Как решать магические квадраты?
17 ноября 2014
23842

Смотрите видео
Как решать магические квадраты?
Магическим квадратом принято называть головоломку наподобие судоку. Это квадрат, клетки которого заполнены числами так, чтобы сумма в конце любой строки, столбца и диагонали была одинаковой. В магических квадратах-головоломках некоторые числа пропущены, и требуется их расставить так, чтобы соблюсти описанное выше условие равной суммы. Как же решать магические квадраты?
Способы решения магических квадратов
Для того чтобы решение магических квадратов было верным, необходимо знать ту самую волшебную сумму, которая должна получаться при сложении чисел в строках, столбцах и диагоналях. После этого расставить недостающие числа становится существенно проще. Как же эту сумму найти?
Способ 1
Наипростейший вариант магического квадрата – когда одна из строк, один из столбцов или одна из диагоналей полностью заполнена числами. В таком случае остается только подсчитать сумму этих чисел и подбирать решения.
Способ 2
Сумму чисел на концах строк, столбцов и диагоналей можно высчитать по специальным формулам. При этом формула для квадратов с четным количеством ячеек в одной строке будет отличаться от квадратов с нечетным количеством ячеек.
Итак, для четных квадратов подходит формула:
n + ( (n+1) * n * (n-1) / 2) , где n – количество ячеек в одной строке.
Для нечетных квадратов подходит формула:
n * ( n2 +1) / 2 , где n – также количество ячеек в одной строке.
Пример решения
Рассмотрим решения магического квадрата из девяти ячеек с числами от 1 до 9. Сначала подсчитаем сумму, которая должна получаться на концах. В одной строке у нас 3 ячейки, то есть n = 3. Подставляем значение в формулу:
3 * ( 32 +1 ) / 2 = 3 * 10 / 2 = 15
Теперь подбираем числа так, чтобы сумма равнялась 15.
Далее алгоритм потребует немного пространственного воображения. Поставьте число 1 в середину верхней строки. Каждое следующее число мы ставим справа по диагонали вверх. Пробуем ставить 2. Но там нет ячеек, если мы подставим над нашим квадратом еще один такой же воображаемый, то число 2 окажется в правом нижнем углу этого нового
tvoiznaniya.com
Магические квадраты – Оценок.нет
Магический квадрат – квадратная таблица, заполненная натуральными числами, в которой сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова.
Магический квадрат родом из Древнего Китая. По легенде, во времена правления императора Ю (ок. 2200 до н.э.) однажды из реки Хуанхэ выплыла громадная черепаха, на панцире которой был начертан таинственный узор.
Со временем узор превратился в знаменитый план “девяти квадратов “. Каждый квадрат ассоциируется с направлением и содержит число. Это называется “диаграммой ло-шу”, или “первоначальным планом” и является основой школы Блуждающих или Летящих Звезд в искусстве фэн-шуй. Интересный аспект плана девяти квадратов заключается в том, что вы можете сложить любые три числа по прямой линии – вверх, вниз, поперек или по диагонали – и всегда получите в сумме число 15.
Магическим квадратам приписывали различные мистические свойства. Бытовало поверье, что выгравированный на серебре магический квадрат защищает от чумы.
Каждый элемент магического квадрата называется клеткой. Квадрат, сторона которого состоит из n клеток, содержит n2 клеток и называется квадратом n-го порядка. В большинстве магических квадратов используются первые n последовательных натуральных чисел. Сумма S чисел, стоящих в каждой строке, каждом столбце и на любой диагонали, называется постоянной квадрата и равна S = n(n2 + 1)/2.
Для квадрата 3-го порядка S = 15
Для квадрата 4-го порядка S = 34
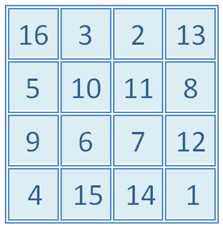
Для квадрата 5-го порядка S = 65
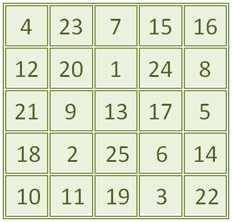
Cвойства магических квадратов.
Свойство 1. Магический квадрат останется магическим, если все числа, входящие в его состав, увеличить или уменьшить на одно и то же число.
Свойство 2. Магический квадрат останется магическим, если умножить или разделить все его числа на одно и то же число.
Свойство 3. Если квадрат является магическим для какой-нибудь арифметической прогрессии, то он будет магическим для так же расположенной арифме
ozenok.net
Как решить магический квадрат 4 класса
ИНТЕРЕСНОЕ
Как решать магические квадраты?
17 ноября 2014
23842

Смотрите видео
Как решать магические квадраты?
Магическим квадратом принято называть головоломку наподобие судоку. Это квадрат, клетки которого заполнены числами так, чтобы сумма в конце любой строки, столбца и диагонали была одинаковой. В магических квадратах-головоломках некоторые числа пропущены, и требуется их расставить так, чтобы соблюсти описанное выше условие равной суммы. Как же решать магические квадраты?
Способы решения магических квадратов
Для того чтобы решение магических квадратов было верным, необходимо знать ту самую волшебную сумму, которая должна получаться при сложении чисел в строках, столбцах и диагоналях. После этого расставить недостающие числа становится существенно проще. Как же эту сумму найти?
Способ 1
Наипростейший вариант магического квадрата – когда одна из строк, один из столбцов или одна из диагоналей полностью заполнена числами. В таком случае остается только подсчитать сумму этих чисел и подбирать решения.
Способ 2
Сумму чисел на концах строк, столбцов и диагоналей можно высчитать по специальным формулам. При этом формула для квадратов с четным количеством ячеек в одной строке будет отличаться от квадратов с нечетным количеством ячеек.
Итак, для четных квадратов подходит формула:
n + ( (n+1) * n * (n-1) / 2) , где n – количество ячеек в одной строке.
Для нечетных квадратов подходит формула:
n * ( n2 +1) / 2 , где n – также количество ячеек в одной строке.
Пример решения
Рассмотрим решения магического квадрата из девяти ячеек с числами от 1 до 9. Сначала подсчитаем сумму, которая должна получаться на концах. В одной строке у нас 3 ячейки, то есть n = 3. Подставляем значение в формулу:
3 * ( 32 +1 ) / 2 = 3 * 10 / 2 = 15
Теперь подбираем числа так, чтобы сумма равнялась 15.
Далее алгоритм потребует немного пространственного воображения. Поставьте число 1 в середину верхней строки. Каждое следующее число мы ставим справа по диагонали вверх. Пробуем ставить 2. Но там нет ячеек, если мы подставим над нашим квадратом еще один такой же воображаемый, то число 2 окажется в правом нижнем углу этого нового
Оцени ответ
napyaterku.com
Учебный проект по математике “Магический квадрат” (4 класс)
История появления магических квадратов.
В давние времена, научившись считать и выполнять арифметические действия, люди с удивление обнаружили, что числа имеют самостоятельную жизнь, удивительную и таинственную.
Китайский император Ню, живший 4 тысячи лет назад, однажды гулял по берегу реки. И вдруг увидел черепаху. На её панцире был изображён рисунок из белых и чёрных кружков.
« Да, она священна!», – воскликнул он.
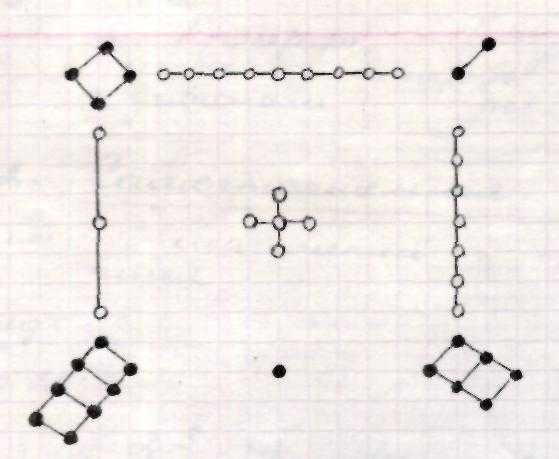
Если заменить каждую фигуру числом, показывающим, сколько в ней кружков, получится такая таблица.
9
2
3
5
7
8
1
6
(Сумма чисел строк равна сумме чисел столбцов, равна сумме чисел диагоналей и равна 15.)
Сейчас любую квадратную таблицу, составленную из чисел и обладающую таким свойством, называют магическим квадратом.
Определение магического квадрата.
Магический квадрат – квадратная таблица из целых чисел, в которой суммы чисел вдоль любой строки, любого столбца и любой из двух главных диагоналей равны одному и тому же числу.
Наверное, эту легенду китайцы придумали, когда нашли расположение чисел от 1 до 9 со столь замечательным свойством. Рисунок они назвали «ло-шу» и стали считать его магическим символом. Первое специальное упоминание о таком квадрате найдено около 1 века до н.э. Вплоть до 10 века н.э. магические квадраты были воплощены в амулетах, заклинаниях. Они использовались в качестве талисманов по всей Индии. Их рисовали на кувшинах удачи, медицинских кружках. До сих пор они используются у некоторых восточных народов как талисман.
Полного описания всех возможных магических квадратов не получено и до сего времени. Магических квадратов 2*2 не существует. Существует единственный магический квадрат 3*3, так как остальные магические квадраты 3*3 получаются из него либо перестановкой строк (рис. 4а) или столбцов (рис. 4б) либо путем поворота исходного квадрата на 900 (рис. 4в) или на 1800 (рис 4г).
27
6
9
5
1
4
3
8
8
1
6
3
5
7
4
9
2
2
9
4
7
5
3
6
1
8
6
1
8
7
5
3
2
9
4
а б в г
В IX веке интерес к магическим квадратам вспыхнул с новой силой. Получение магических квадратов считалось популярным развлечением среди математиков. Ими создавались огромные квадраты, например, 45*45, содержащий числа от 1 до 2025, Были придуманы способы построения магических квадратов любого размера.
В XIII веке математик Ян Хэй занялся проблемой методов построения магических квадратов. Его исследования были, потом продолжены другими китайскими математиками. Из Китая магические квадраты распространились сначала в Индию, а затем и в другие страны.
Редкостью является использование магического квадрата в изобразительном искусстве, а не в научном или литературном произведении. Впервые это сделал немецкий художник Альбрехт Дюрер (1471 – 1528), выпустивший в гравюру «Меланхолия», на которой есть изображение магического квадрата четвёртого порядка. Причем два числа в середине нижней строки указывают на год создания гравюры – 1514.Этот факт говорит об умении в то время составлять магические квадраты с определённым заданным расположением некоторых чисел. Говорят, что гравюра А.Дюрера послужила толчком для знаменитых пророчеств его современника Мишеля Нострадамуса (1503-1566).
Применение магических квадратов .
Традиционной сферой применения магических квадратов являются талисманы. К примеру, талисман Луны обладает определенными свойствами: предохраняет от кораблекрушения и болезней, делает человека любезным, способствует предотвращению дурного намерения, а так же укрепляет здоровье. Его гравируют на серебре в день и час Луны, когда Солнце или Луна находится в первых десяти градусах Рака. Магический квадрат 9-ого порядка вписывается в девятиугольник (9 – число Луны, см. ниже) и окружается специальными символами.
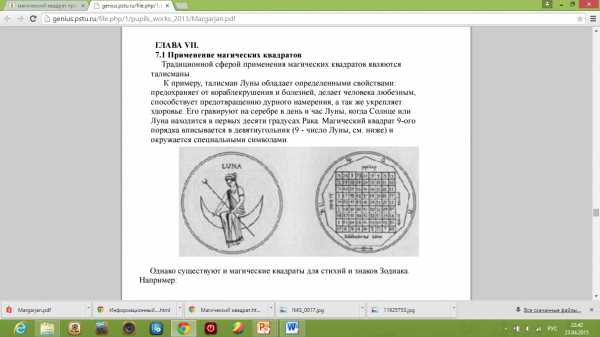
В наши дни магические квадраты можно встретить на палубах больших пассажирских судов как площадку для игры. Известная головоломка – пазл с числами – судоку, появившаяся примерно 30 лет назад и популярная во многих странах мира, тоже содержит магические квадраты.
За последнее столетие значительно возросло число книг по занимательной математике, в которых содержатся головоломки и задачки, связанные с необычными квадратами. В наше время магические квадраты продолжают привлекать к себе внимание не только специалистов, но и любителей математических игр и развлечений.
|
infourok.ru