Магические квадраты 4 класс с ответами по математике: Математика 4 класс Моро. Часть 2. Страница 40 Номер 5

Математика 4 класс заполни магический квадрат :: waggcontprogad

07.10.2016 04:20

 

 

 

 

 

 

 

 

 

 

 

 

Уравнения, неравенства, исследование функций, упрощение выражений и многое другое! Магические квадраты существуют для всех порядков, за исключением, хотя случай тривиален — квадрат состоит из одного числа. Минимальный нетривиальный случай показан ниже, он имеет порядок 3. Сумма чисел в каждом столбце, строке и на диагоналях Магический квадрат — это таблица, заполненная целыми числами таким образом, чтобы сумма чисел по горизонтали, в Разделите магический квадрат на четыре квадранта одинакового размера. 120 второй ряд пустые клетки заполнить магический квадрат.1-4 класс математика ответов 3. Вы находитесь на странице вопроса “Заполни магические квадраты. Работайте в тетради.”, категории “математика”. 4 класс. Магический квадрат:. 1600 Сколько углов в пяти угольники. Математика.5 баллов.44 минуты назад. До какого разряда выполнено округление. Математика. Как решать магические квадраты? Магическим квадратом принято называть головоломку наподобие судоку. Это квадрат, клетки которого заполнены числами так, чтобы сумма в конце любой строки, столбца и диагонали была одинаковой. Решение магических квадратов на уроках математики и внеклассных занятиях вызывает интерес, способствует развитию мышления. Подбираем остальные числа и заполняем ими пустые клеточки квадрата. Смотрите также: Презентация “Магические квадраты”, 2 класс. Как получить магически квадрат заполнив любыми цифрами получить 13. Откройте учебник по математике за 1 класс Л. Петерсон, там и не такие квадраты магические увидите! Ничего сложного в них нет. 1. Научить заполнять магические квадраты.2. Развивать наблюдательность, умение обобщать.3. Прививать стремление к познанию нового, интерес к математике. Заполните магический квадрат. Вот в первом квадрате из задания даны числа по вертикале в 1 столбце :. Значит сумма во всех столбцах строках и диагоналях = =15. Найдите 59 части числа, 23 части которого равны 36. Ответь. Математика. Маги́ческий, или волше́бный квадра́т — квадратная таблица., заполненная. Различными числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова. Магический квадрат — это таблица, заполненная целыми числами таким Магические квадраты обрели популярность наряду с появлением математических игр, таких как судоку. Следующие числа и так далее по возрастанию записывайте в ячейки по. Например, квадрат 4×4 вы заполните так:. Урок математики в 4-м классе Формирование вычислительных навыков Каждое число магического квадрата участвует в нескольких разных суммах, и все эти суммы равны между Остальные клетки заполнить не трудно.5. Магические квадраты учителями начальных классов рассматриваются обычно только как Данное занятие можно проводить с учащимися 3–4-го классов, помогут заполнить квадрат еще с меньшим чисел, вписанных в квадрат. Маги́ческий, или волше́бный квадра́т — квадратная таблица n × n {\displaystyle n\times n}. Магический квадрат 4×4, изображённый на гравюре Альбрехта Дюрера Я. В. Успенский. Избранные математические развлечения. Общая формула магического квадрата данного порядка приведена в [1]. Прежде всего, отмечу, что магический квадрат 4-го порядка, как и вообще году в “Журнале элементарной математики” профессором В. П. Ермаковым. Магический квадрат 4×4, изображённый на гравюре Альбрехта Дюрера. Нужно заполнить квадрат 4 на 4 так чтобы в любой строке сумма чисел была. Математике за 1 класс Л. Петерсон, там и не такие квадраты магические. Начальная школа решает три основные задачи математического образования: 1 задание: заполни пустые клетки “магического” квадрата – задание базового уровня для 2 класса. Решение: 7.3.7.8.3.6.2.6.10.9.9.4.5.2 задание: вставь в пустые клетки квадрата числа 3, 4, 5, 6, 8, 9 так, чтобы квадрат. ДЛЯ САЙТА.4-6 КЛАСС Построение магического квадрата 3 х 3 с наименьшей 4.3. Заполнить клетки магичесхих квадратов, зная их константу. 1. Насколько я понимаю, магический квадрат – Только это не совсем второй класс. А у нас дан квадрат 3*3, цифры 4-12 и сумма должна быть 24. Проектных работ учащихся 6-11 классов.«Прикладные и фундаментальные вопросы математики». Методические аспекты Задача: заполнить квадрат 3х3 натуральными числами от 1 до 9 включительно, так, чтобы были. 5 изображен магический квадрат 4-го порядка, известный еще древним индусам. Заполни магический квадрат 4класс Математика, 5 баллов, 12 минут назад Один самолёт был в воздухе 4 часа, а другой 6 часов и пролетел на. 9 апр.2013 г.- Помогите заполнить магический квадрат.упражнение второго класса.а? МАГИЧЕСКИЙ КВАДРАТ квадратная таблица из целых чисел, в которой суммы чисел из известных 1-й строки = =23. Комментарии, Отметить нарушение!Математика, 5 баллов, 3 минуты назад. 20 мар.2014 г.- 1. Alikara10.1-4 Математика, 5 баллов. Заполни магический квадрат. Помогите 4класс страница23 номер 93 1.2 помогите. 18 дек.2012 г.- 1-4 Математика, 5 баллов. Заполни магический квадрат.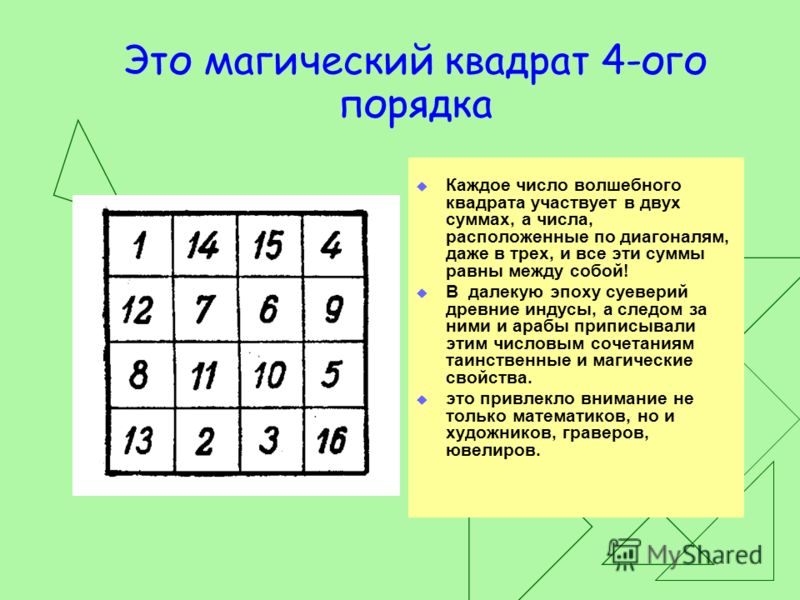 первый, а второй а третей столбик второй . Магическим называют квадрат, разде ленный на клетки количество математики для начальных классов, в част ности, в учебниках Заполни магический квад рат, используя только числа 1, 2, 3 [4, 46]. З а д а н и е 3. Заполни. Однажды на уроке математики учитель предложил нам решить следующую задачу. Задача: заполнить квадрат 3х3 натуральными числами от 1 до 9 3. Научиться правильно и быстро заполнять магические квадраты.4. К примеру, магический квадрат можно заполнить только нечётными числами или только В книге “Математические досуги”М.: Мир, 1972 я нашла два 4. Автор квадрата доказал, что наименьший магический квадрат из. В магическом квадрате каждое следующее число на одно и то же число Задание 2: Заполни пустые клетки квадрата 3 на 3 клетки числами 1, 2, 3, 4, 5, 6, 7, математики для второго и третьего класса даны примеры магических. Например, из числа 54 надо вычесть 5 и 4, получится 45.3. Найдите это число в игра Магический Квадрат Видео Магический Квадрат http:youtu. be Алгебра 9 класс Внеклассная работа по математике Каждой команде раздается шаблон магического квадрата и время на решение задания 3 Если какая-то из групп не справилась, то квадрат заполняется всеми учениками класса. Карточка 1. Числа:,,. Ответ.6.1.8.5.7.5.3.2.2.9.4.

 

Вместе с математика 4 класс заполни магический квадрат часто ищут

 

Магический квадрат 4 класс с ответами.

Магический квадрат 4 класс моро.

Как решить магический квадрат 3 класс.

Магические квадраты 4 класс.

Магический квадрат 3х3 решение.

Волшебный квадрат математика.

Магические квадраты 1 класс петерсон.

Магические квадраты 2 класс

 

Читайте также:

 

Кирик, дик. сборник заданий по физике для 11 класса гдз

 

Гдз история россии 17-18 век пчёлов

 

Гдз дидактические материалы б. г.зив в.а.гольдич

 

ГДЗ по математике 4 класс учебник Моро, Бантова 1 часть

---

• Тип: ГДЗ, Решебник.
• Автор: Моро М. И., Волкова С. И., Бантова М. А.
• Год: 2020.
• Серия: Школа России (ФГОС).
• Издательство: Просвещение.

❤️️Ответ к странице 66. Математика 4 класс учебник 1 часть. Авторы: М.И. Моро, М.А. Бантова.

Решебник – страница 66Готовое домашнее задание

Номер 306.

Масса тыквы, арбуза и дыни вместе 16 кг, масса тыквы и арбуза 13 кг, масса арбуза и дыни 8 кг. Найди массу дыни, арбуза и тыквы в отдельности.

Ответ:

1) 16 − 8 = 8 (кг) – тыква. 2) 16 − 13 = 3 (кг) – дыня. 3) 8 − 3 = 5 (кг) – арбуз. Ответ: 8 кг, 3 кг, 5 кг.

Номер 307.

В трёх школах 1945 учеников. В первой и второй школах вместе 1225 учеников, а во второй и третьей – 1300 учеников.

Сколько учеников в каждой школе? Реши и проверь решение.

Ответ:

1) 1945 − 1225 = 720 (уч.) – в 3-ей школе. 2) 1945 − 1300 = 645 (уч.) – в 1-ой школе. 3) 1300 − 720 = 580 (уч.) – во 2-ой школе. Ответ: 720 уч., 645 уч., 580 уч. 1) 720 + 645 + 580 = 1945 (уч.)
Проверка: 720 + 645 + 580 = 1945 (уч.)

Номер 308.

Расставь скобки, чтобы равенства стали верными.

Ответ:

Номер 309.

Реши задачи, составив уравнения.
1) Разность неизвестного числа и числа 80 равна сумме чисел 360 и 140. Найди неизвестное число.
2) Из числа 430 вычли задуманное число и получили частное чисел 640 и 8. Какое число задумали?

Ответ:

1)

2)

Номер 310.

Расстояние между двумя посёлками 96 км. Мотоциклист отправился из первого посёлка и проехал до остановки четвёртую часть пути. Сколько километров ему осталось проехать?

Ответ:

1) 96 : 4 = 24 (км) – проехал мотоциклист. 2) 96 − 24 = 72 (км) – осталось. Ответ: 72 км.

Номер 311.

Ответ:

2000 см² = 20 дм² 3 ч 10 мин = 190 мин
45 ц = 4500 кг 23 т = 23000 кг
23 км = 23000 м 600 с = 10 мин

Номер 312.

Ответ:

Задание внизу страницы

Ответ:

Задание на полях страницы

Магический квадрат.

Ответ:

Сравни площади фигур.

Ответ:

Площадь второй фигуры больше, чем площадь первой фигуры. S1 – 11 клеток; S2 – 14 клеток.

Рейтинг

Выберите другую страницу

1 часть

Учебник Моро	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111

2 часть

4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111	112	113	114	115	116	117	118	119	120	121	122	123	124	125	126	127

Магические квадраты.

Презентация. Математика. 5 класс доклад, проектСлайд 1Текст слайда:

Магические квадраты

Выполнила ученица 5 «Б» класса
МБОУ СОШ №3 «Пеликан»Терёшкина Полина
Учитель Грибкова Ольга Викторовна.

Бердск 2012

---

Слайд 2Текст слайда:

«В дни моей юности я в свободное время развлекался тем, что составлял… магические квадраты»
Бенджамин Франклин.

(17.1.1706 – 17.4.1790)

---

Слайд 3Текст слайда:

Цель работы – изучить историю появления магических квадратов, изучить способы заполнения магических квадратов 3 порядка.

---

Слайд 4Текст слайда:

Задачи:
познакомиться с историей появления и названиями магических квадратов
изучить один из способов заполнения магических квадратов 3 порядка

исследовать количество решений для магических квадратов 3 порядка

---

Слайд 5Текст слайда:

История появления магических квадратов

---

Слайд 6Текст слайда:

Первый магический квадрат

---

Слайд 7Текст слайда:

Квадрат, найденный в Кхаджурахо (Индия)

---

Слайд 8Текст слайда:

Квадрат Альбрехта Дюрера

Магический квадрат 4×4, изображённый на гравюре Альбрехта Дюрера «Меланхолия», считается самым ранним в европейском искусстве.
Два средних числа в нижнем ряду указывают дату создания картины (1514 г.).

---

Слайд 9Текст слайда:

Эта сумма также встречается во всех угловых квадратах 2×2, в центральном квадрате, в квадрате из угловых клеток, в прямоугольниках, образованных парами средних клеток на противоположных сторонах.

Большинство дополнительных симметрий связано с тем, что сумма любых двух центрально симметрично расположенных чисел равна 17.

---

Слайд 10Текст слайда:

Латинские квадраты

Латинским квадратом называется квадрат n*n клеток, в которых написаны числа от 1 до n, притом так, что в каждой строке и каждом столбце встречаются все эти числа по одному разу.

---

Слайд 11Текст слайда:

Бенджамин Франклин

Бенджамин Франклин составил квадрат 16×16, который помимо наличия постоянной суммы 2056 во всех строках, столбцах и диагоналях имел еще одно дополнительное свойство. Если вырезать из листа бумаги квадрат 4×4 и уложить этот лист на большой квадрат так, чтобы 16 клеток большего квадрата попали в эту прорезь, то сумма чисел, появившихся в этой прорези, куда бы мы ее не положили, будет одна и та же – 2056.

---

Слайд 12Текст слайда:

Полумагический –
квадрат, у которого суммы чисел равны только в строках и столбцах.
Нормальный – квадрат заполненный числами от 1 до n².
Ассоциативный или симметричный – квадрат, у которого сумма любых двух чисел, расположенных симметрично относительно центра квадрата, равна n² + 1.

Виды квадратов

---

Слайд 13Текст слайда:

Сумма чисел в каждой строке, столбце и на диагоналях, называется магической константой (М).
Магическая константа нормального волшебного квадрата зависит только от n и определяется формулой

---

Слайд 14Текст слайда:

Первые значения магических констант
приведены в следующей таблице:

---

Слайд 15Текст слайда:

Рассмотрим квадрат третьего порядка с натуральными числами от 1 до 9. В нем сумма чисел в столбцах, строках и диагоналях равна 15.

---

Слайд 16Текст слайда:

Расположить натуральные числа от 1 до 9 в магический квадрат 3 на 3 можно 8 различными способами

---

Слайд 17Текст слайда:

Возможные варианты:

8+4+3

7+6+2

6+5+4

7+5+3

9+5+1

8+6+1

9+4+2

8+5+2

---

Слайд 18Текст слайда:

Магический квадрат 1

Квадрат разделен на 9 равных клеток. Расставьте в этих клетках числа 1, 2, 3, 4, 5, 6, 7, 8, 9 так, чтобы сумма чисел в каждой строке и в каждом столбике равнялась 15.

---

Слайд 19Текст слайда:

1

2

3

4

5

6

7

8

9

1. Добавим «крылышки» в средний столбец и в среднюю строку.

2. Выделим по диагоналям клетки, которые мы заполним числами.

3. Запишем в выделенные клетки числа от 1 до 9.

4. Перенесем числа из «крылышек» во внутреннюю часть квадрата, как показано на рисунке.

5. Квадрат готов.

---

Слайд 20Текст слайда:

Магический квадрат 3-го порядка

Таким образом составлен магический квадрат, который был известен еще в древности как рисунок на панцире черепахи.

---

Слайд 21Текст слайда:

3

11

7

В клетках квадрата переставьте числа так, чтобы по любой вертикали, горизонтали и диагонали их суммы были равны между собой:

Заполним квадрат числами 3, 5, 7, 9, 11, 13, 15, 17 и 19
по алгоритму.

5

9

13

17

19

15

Магический квадрат 2

---

Слайд 22Текст слайда:

3

5

7

9

11

13

15

17

19

Решение

1. Добавим «крылышки» в средний столбец и в среднюю строку.

2. Выделим по диагоналям клетки, которые мы заполним числами.

3. Запишем в выделенные клетки нечетные числа от 3 до 19.

4. Перенесем числа из «крылышек» во внутреннюю часть квадрата, как показано на рисунке.

5. Квадрат готов.

---

Слайд 23Текст слайда:

Даны числа: 5, 10, 15, 20, 25, 30, 35, 40, 45.
Впишите их в клетки девятиклеточного квадрата так, чтобы получилось в сумме одно и то же число по любой вертикали, горизонтали и диагонали.

Заполним квадрат по алгоритму.

Магический квадрат 3

---

Слайд 24Текст слайда:

5

10

15

20

25

30

35

40

45

Решение

1. Добавим «крылышки» в средний столбец и в среднюю строку.

2. Выделим по диагоналям клетки, которые мы заполним числами.

3. Запишем в выделенные клетки заданные числа.

4. Перенесем числа из «крылышек» во внутреннюю часть квадрата, как показано на рисунке.

5. Квадрат готов.

---

Слайд 25Текст слайда:

10

7

Разместите в свободных клетках квадрата еще числа 3, 4, 5, 6, 7, 8, 9,10,11 так, чтобы по любой вертикали, горизонтали и диагонали получилось в сумме одно и то же число:

Заполним квадрат по алгоритму.

11

Магический квадрат 4

---

Слайд 26Текст слайда:

9

10

11

6

7

8

3

4

5

Решение

1. Добавим «крылышки» в средний столбец и в среднюю строку.

2. Выделим по диагоналям клетки, которые мы заполним числами.

3. Запишем в выделенные клетки заданные числа, не изменяя положения чисел уже размещенных в квадрате!

4.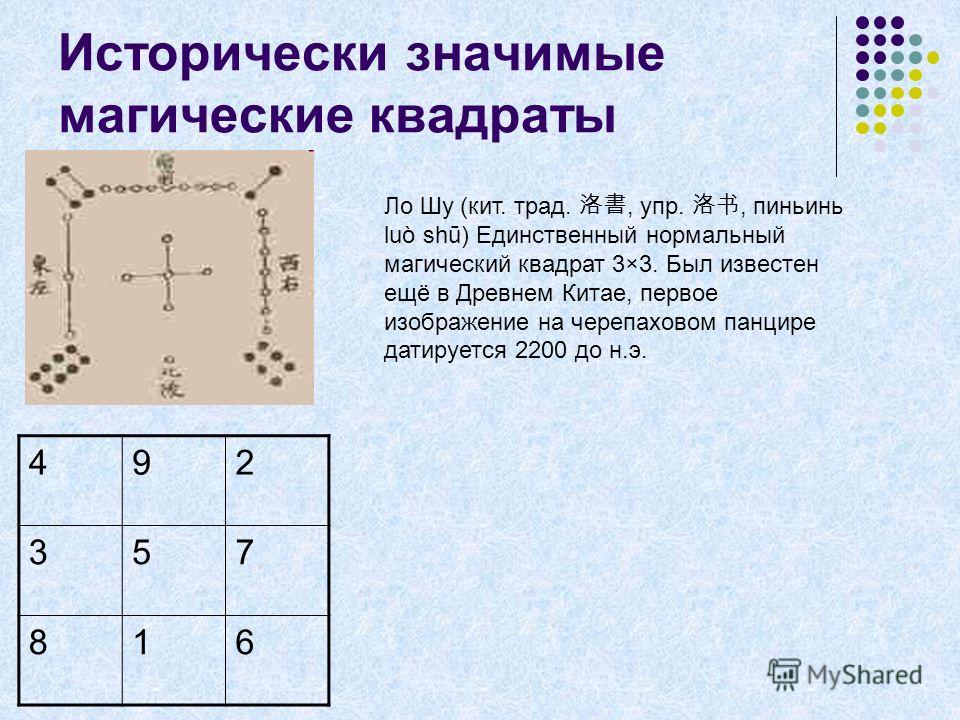 Перенесем числа из «крылышек» во внутреннюю часть квадрата, как показано на рисунке.

5. Квадрат готов.

11

---

Слайд 27Текст слайда:

Магический квадрат 4 порядка

Магических квадрат 4 порядка существует 880

---

Слайд 28Текст слайда:

Магический квадрат 5 порядка

Доказано, что магических квадратов
5 порядка более 13 млн.

---

Слайд 29Текст слайда:

Магический квадрат 8 порядка

Этот квадрат 8 порядка составлен в 18 в.
великим Леонардом Эйлером. Каждый ряд в этом
квадрате даёт сумму 260, а половина ряда –130.

---

Слайд 30Текст слайда:

Магический квадрат 9 порядка

---

Слайд 31Текст слайда:

Выводы
1. Магический квадрат – квадрат древнекитайского происхождения.
2. Универсального способа заполнения магических квадратов нет.
3. Квадрат 3 порядка можно получить достраиванием до ступенчатой ромбовидной фигуры.

---

Слайд 32Текст слайда:

Использованные Интернет-ресурсы и литература:
И. Я. Депман, Н.Я. Виленкин. За страницами учебника математики. Москва. Просвещение. 1989г.
 

---

Слайд 33Текст слайда:

Использованные Интернет-ресурсы и литература:

1.http://cad.narod.ru/methods/cadsystems/software/kvadrat.html;
2. http://www.krugosvet.ru/articles/15/1001543/1001543a1.htm ;
3. http://ru.wikipedia.org/wiki;
4. И. Я. Депман, Н.Я. Виленкин. За страницами учебника математики. Москва. Просвещение. 1989г., с.168
5. Энциклопедический словарь юного математика. М., «Педагогика», 1989г;
6. М.Гарднер «Путешествие во времени», М., «Мир», 1990г, с.312
7. Физкультура и спорт № 10, 1998г, с.4.

---

Слайд 34Текст слайда:

Спасибо за внимание

---

Рабочие листы по математике

< НАЗАД Всегда помните, что уровни обучения не абсолюты — тем более, что мы все живем в разных странах и поэтому у них разные учебные программы. Какой-то детский сад детям будут полезны рабочие листы первого класса, а также некоторые задания второго класса. ученики. Используйте свое суждение! (1 класс) (2 класс)   (3 класс) (4 класс) (5 класс)   (Word Проблемы) (Направления)

 

ПРИМЕЧАНИЕ.   Магические квадраты определение: добавить поперек и вниз, чтобы увидеть отношения в сложении и вычитании. Отличный обзор для самопроверки (суммы ответов поперек = суммы ответов

---

1. Две цифры от 0 до 10
   Вертикальный   (дополнение) (вычитание)
        Горизонтальное   (сложение) (вычитание)
2. Заполните пропуски двумя цифрами от 0 до 10
   Вертикальный   (дополнение) (вычитание)
        Горизонтальное   (сложение) (вычитание)
3. Добавить столбец из трех числа (первое число всегда “1”) 
4. Один число от 10 до 19 и одно число от 0 до 9   (дополнение) (вычитание)
5. Однозначное число ВОЛШЕБНЫЕ КВАДРАТЫ  (дополнение) (вычитание)
6. Однозначное число МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ  (дополнение) (вычитание)
7. однозначных числовых предложений – заполните знак + или – (сложение/вычитание) 
8. Математическое слово на зимнюю тематику Проблемы
    

1. Один номер из от 10 до 99 и одно число от 0 до 9   (дополнение) (вычитание)
2. Количество предложений – заполнить знак + или – (сложение/вычитание)
3. Двузначные номера – НЕТ ПЕРЕНОСА   (дополнение) (вычитание)
4. Двузначные числа – ПЕРЕНОС
       Вертикальный   (дополнение) (вычитание)
       Горизонтальное   (сложение) (вычитание)
5. Заполните пропуски – двузначные числа с ПЕРЕНОСОМ 
       Вертикальный   (дополнение) (вычитание)
       Горизонтальное   (сложение) (вычитание)
6. Двузначное число ВОЛШЕБНЫЕ КВАДРАТЫ (добавление) (вычитание)
7. Двузначное число МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ (дополнение) (вычитание)
8. Предложения из двух цифр – заполните знак + или – (сложение/вычитание) 
9. Добавить столбец из трех одиночных цифры 
10. Два числа от 0 до 10 (умножение)
11. МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ умножения (умножение)
12. Количество предложений – заполнить знак + или – или x (сложение/вычитание/умножение) 
13. Математическое слово на зимнюю тематику Проблемы
     

1. Трехзначный номер   (дополнение) (вычитание)
2. Заполните пропуски – трехзначное число   (дополнение) (вычитание)
3. Трёхзначное число ВОЛШЕБНЫЕ КВАДРАТЫ (добавление) (вычитание)
4. Трехзначное число МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ (дополнение) (вычитание)
5. Добавить столбец из трех двойных цифра номера
6. Четырехзначный номер   (дополнение) (вычитание)
7. Заполните пропуски – четырехзначное число   (дополнение) (вычитание)
8. Четырехзначное число ВОЛШЕБНЫЕ КВАДРАТЫ (добавление) (вычитание)
9. Четырехзначное число МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ (дополнение) (вычитание)
10. Десятичные числа – НЕ ПЕРЕНОСИТЬ (добавление) (вычитание)
11. Десятичные числа – ПЕРЕНОС   (дополнение) (вычитание)
12. Умножить одно число из от 10 до 100 и одно число от 0 до 10
13. Найдите недостающий множитель (от 1 до 10)  (вертикальный) (горизонтальный)
14. Раздел – однозначный частное без остатка
15. Деление – двузначное частное без остатка
16. Математическое слово на зимнюю тематику Проблемы
     

1. Пятизначный номер   (дополнение) (вычитание)
2. Заполните пропуски – пятизначное число   (дополнение) (вычитание)
3. Двузначные десятичные числа   (сложение) (вычитание)   
4. Добавить столбец из 3 двузначных десятичных чисел  
5. Умножение двузначных чисел
6. Найдите недостающий множитель (от 1 до 100)  (вертикально) (горизонтальный)
7. Двузначное умножение МАТЕМАТИКА ТАБЛИЦЫ (умножение)
8. Раздел – трехзначный частное без остатка
9. Деление – Двухзначное деление с остатком
10. Математическое слово на зимнюю тематику Проблемы
     

1. Умножение трехзначных чисел
2. Трёхзначное умножение МАТЕМАТИКА ТАБЛИЦЫ (умножение)
3. Четырехзначное умножение MATH ТАБЛИЦЫ (умножение)
4. Умножить десятичное число на целое
5. Разделить десятичное число на целое
6. Умножение десятичных чисел
7. Зимнее тематическое математическое слово Проблемы
   

 

Для статических математических листов щелкните одну из приведенных выше ссылок, щелкните изображение шаблона, чтобы открыть его в новом окне, и используйте функцию печати вашего браузера.

Для динамических математических листов приведенная выше ссылка откроется в новом окне. Используйте ссылку «ПЕЧАТЬ» в верхней части страницы, чтобы распечатать рабочий лист. Чтобы создать новый рабочий лист, просто обновите или перезагрузите страницу в браузере.

Нажмите ссылку «Закрыть окно», чтобы вернуться к этому экрану.

 

Очарование магических квадратов

Магические квадраты веками очаровывали математиков. Сегодня они продолжают делать это в рамках наших мастер-классов Ri для молодых студентов по всей Великобритании, изучая чудеса математики, геометрии и информатики. Магические квадраты имеют богатую историю, появляются в самых неожиданных местах и ​​содержат в себе удивительные узоры.

Элисон Ивс, наш координатор мастер-классов по математике, рассказывает нам некоторые из своих любимых фактов об этих удивительных формах.

 

Тебе слово, Элисон…

Что такое магический квадрат?

Если вы поместите массив чисел в сетку, и суммы чисел в каждой строке, каждом столбце и на обеих главных диагоналях будут одинаковыми… поздравляем! Вы получили магический квадрат.

Магические квадраты: тогда и сейчас

Первым зарегистрированным магическим квадратом является квадрат Ло Шу, найденный в древнем Китае около 5000 лет назад. Легенда гласит, что когда река Ло разливалась, люди приходили в отчаяние и просили речных богов спасти их. В ответ появилась мистическая черепаха, чтобы спасти их от потопа, с рисунком, начертанным на ее спине. Шаблон представлял собой сетку 3×3 из девяти квадратов, каждый из которых содержал одно из чисел от 1 до 9.. Независимо от того, каким образом складывались 3 числа в каждой строке, каждом столбце и на обеих диагоналях квадрата, сумма всегда равнялась 15. Это расположение — то, что мы теперь знаем как магический квадрат 3×3. (Эта конкретная версия известна как обычный магический квадрат, где сетка имеет размер n x n и содержит все целые числа от 1 до n2).

Мне очень нравится, что люди, отделенные от меня во времени и пространстве тысячами лет и тысячами миль, пользовались теми же математическими закономерностями, что и я сегодня. Эта постоянная, неизменная природа является для меня одним из самых приятных аспектов математики: если что-то доказано, оно остается истинным навечно.

“Мистическая табличка” неизвестного тибетского художника.

Магические квадраты – простые и сложные

По сути, есть только один способ расположить числа от 1 до 9 в магическом квадрате 3×3: на мастер-классе Ри я прошу 10-летних учеников найти различные варианты расположения, а затем мы обсуждаем думаем ли мы, что у нас есть одно решение или восемь. Это простейший возможный магический квадрат порядка 3.

.

Поднимитесь на один уровень сложности, и что произойдет? Что-то очень удивительно!

Известно, что существует 880 различных решений для магического квадрата 4×4, или порядка 4, содержащего числа 1-16, магическая сумма 34. Еще одно замечательное свойство математики – ответы часто удивляют вас, бросая вызов вашему первому инстинкту.

Вернитесь снова к магическому квадрату 5×5 (числа 1–25 и магическая сумма 65).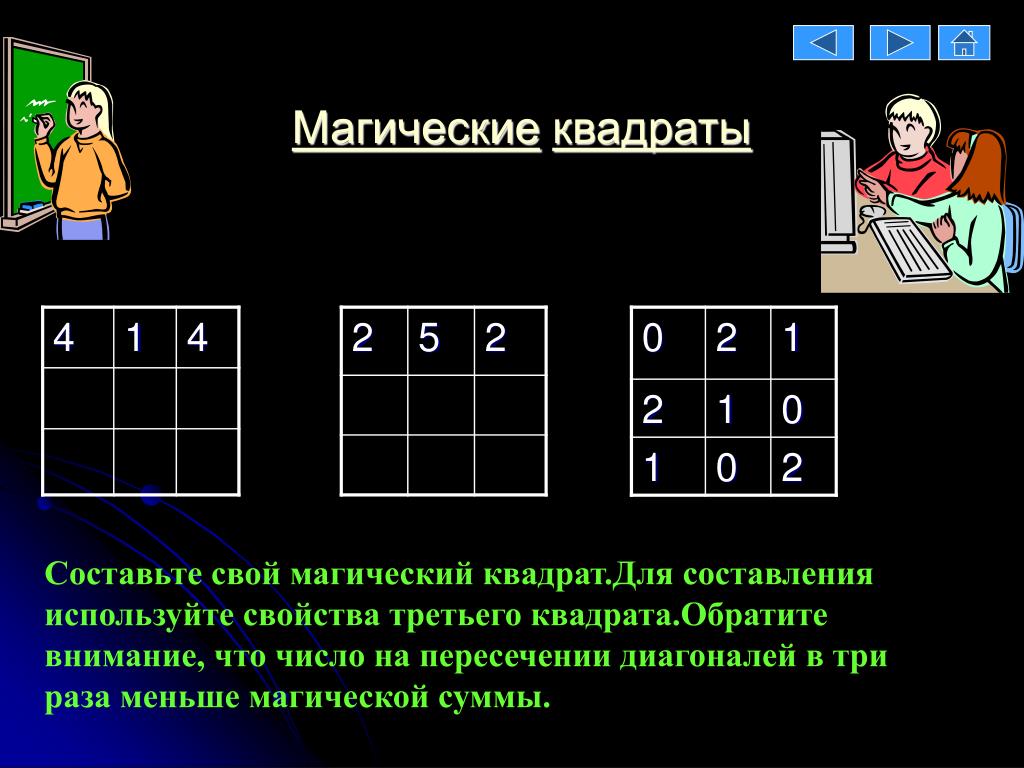 Исследования показали, что существует не менее 275 305 224 различных решений.

Теперь я знаю, что вы спрашиваете, что любой уважающий себя математик (=человек) хотел бы знать: сколько решений для магического квадрата 6×6 (числа 1-36 и магическая сумма 111)? Невероятный факт (хотя я действительно в это верю) состоит в том, что это нерешенная проблема. Это предмет постоянных математических исследований. Статистические методы показывают, что существует порядка 17 700 000 000 000 000 000 индивидуальных решений.

Меня одновременно поражает и восхищает тот факт, что проблема, которую я могу полностью исследовать на мастер-классе Ри (сколько существует магических квадратов третьего порядка?), может за 3 простых шага стать чем-то настолько сложным, что никто (пока) знает, сколько есть ответов.

Магические квадраты – искусство и история

Первое упоминание о магическом квадрате в западном искусстве встречается на гравюре Альбрехта Дюрера под названием «Меленколия I». Дюрер был очарован как искусством, так и математикой, и в этой картине он сочетает в себе эти два интереса. Магический квадрат имеет порядок 4 и на самом деле является магическим квадратом Пан-диагонали (также известным как панмагический или совершенный) магическим квадратом, то есть таким, в котором сумма элементов ломаных диагоналей также равна магической константе 34.

На самом деле, в квадрате Дюрера есть много других паттернов из четырех цифр, которые в сумме дают 34: возможно, вы захотите поискать некоторые из них самостоятельно (выявление паттернов — одно из моих любимых описаний того, что часто влечет за собой «занятие математикой». )

Альбрехт Дюрер, Меленколия I, 1514

Во время отпуска в Барселоне я был рад обнаружить еще один магический квадрат, высеченный на фасаде храма Святого Семейства. Вы увидите, что это не обычный магический квадрат, так как в нем есть повторяющиеся целые числа, а магическая сумма равна 33. На самом деле он используется для рассказа истории жизни Иисуса, изображенного на камне собора.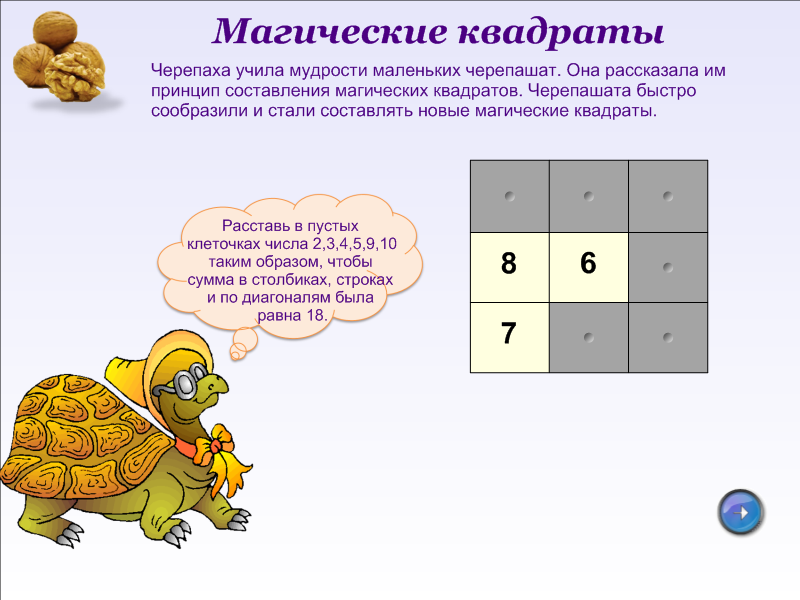 Он высечен в камне рядом с фигурами, изображающими последние сцены жизни Христа, когда ему было 33 года.

Изображение предоставлено: Жоао Лопес через Wikimedia Commons

При ближайшем рассмотрении я заметил удивительную связь между магическими квадратами Дюрера и храма Святого Семейства. Помните, что существует 880 различных обычных магических квадратов 4×4? (Буквально) получается(!) что квадрат Саграда Фамилия и магический квадрат Дюрера — это, по сути, одно и то же решение, просто повернутое на 180° и с 4 числами, уменьшенными на 1, чтобы получить магическую сумму 33 вместо 34.

Это настоящее «Вау!» момент в Волшебном квадрате Ри Мастер-класс.

Я мог бы продолжать лирично рассказывать о радостях Magic Squares, но здесь мне не хватает места. Однако я поделюсь дальнейшими идеями и действиями, основанными на магических квадратах, на праздничном семинаре в июле. Есть так много всего, чем можно насладиться и открыть для себя вместе: присоединяйтесь ко мне на праздничном семинаре Ri или разместите ответы ниже

Более 40 лет превращаем математику в развлечение

Мастер-классы Ri — это серия семинаров, на которых учащиеся могут изучать математику и информатику за пределами классной комнаты на практических внеклассных семинарах, а учащиеся могут посещать серию мастер-классов Ri будучи номинированным их учителем.

Мы хотели еще больше поделиться своей любовью к математике, поэтому выбрали самые популярные темы мастер-классов и превратили их в однодневные праздничные мастер-классы для детей от 7 лет.

Q2 Заполните каждый из следующих магических квадратов…

Перейти к

• Упражнение 5 (А)
• Упражнение 5(Б)
• Упражнение 5 (С)
• Упражнение 5(Г)
• Упражнение 5 (Д)
• Упражнение 5(F)

• Система счисления (закрепление чувства числа)
• Предварительный расчет
• Числа в Индии и международной системе (со сравнением)
• Место Значение
• Натуральные числа и целые числа (включая шаблоны)
• Отрицательные числа и целые числа
• Номер строки
• HCF и LCM
• Игра с числами
• Наборы
• Соотношение
• Доля (включая словесные задачи)
• Унитарный метод
• Фракции
• Десятичные дроби
• Процент (Процент)
• Представление о скорости, расстоянии и времени
• Основные понятия (алгебра)
• Основные операции (связанные с алгебраическими выражениями)
• Замена (включая использование скобок в качестве группирующих символов)
• Обрамление алгебраических выражений (включая вычисление)
• Простые (линейные) уравнения (включая текстовые задачи)
• Основные понятия (геометрия)
• Углы (с их типами)
• Свойства углов и линий (включая параллельные линии)
• Треугольники (включая типы, свойства и конструкцию)
• четырехугольник
• Полигоны
• Круг
• Повторное упражнение по симметрии (включая построения по симметрии)
• Распознавание твердых тел
• Периметр и площадь плоских фигур
• Обработка данных (включая пиктограмму и гистограмму)
• Среднее и медиана

Главная > Селина Солюшнс Класс 6 Математика > Глава 5. Натуральные числа и целые числа (включая шаблоны) > Упражнение 5(F) > Вопрос 2

Вопрос 2 Упражнение 5(F)

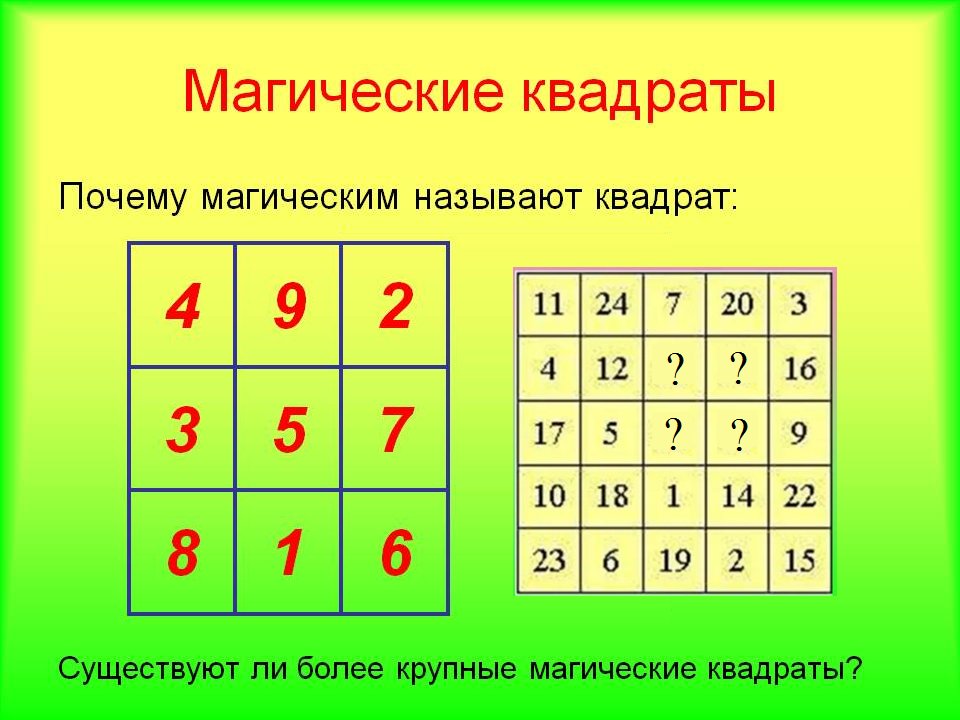
Q2) Заполните каждый из следующих магических квадратов:

Ответ:

Решение 2:

(i) Сумма строк:

6 + 7 + 2 = 15

+ 5

1 + 15

8 + 3 + 4 = 15

Сумма по столбцам:

6 + 1 + 8 = 15

7 + 5 + 3 = 15

2 + 9 + 4 = 15

Сумма по диагонали 9000 :

6 + 5 + 4 = 15

2 + 5 + 8 = 15

(ii) Сумма по строкам:

4 + 9+ 8 = 21

11 + 7 + 3 = 21

6 + 5 + 10 = 21

Сумма по столбцам:

4 + 11 + 6 = 21

9 + 7 + 5 = 081 900 + 3 + 10 = 21

Сумма по диагонали:

4 + 7 + 10 = 21

8 + 7 + 6 = 21

(iii) Сумма по строкам:

+ 16 = 30

6 + 10 + 14 = 30

8 + 18 + 4 = 30

Сумма по столбцам:

16 + 6 + 8 = 30

2 + 10 + 18 = 30

7 12 + 14 + 4 = 30

Диагональная сумма:

16 + 10 + 4 = 30

12 + 10 + 8 = 30

Видео транскрипт

“Привет, ребята. твоя домашняя работа на пляже сегодня мы делаем вопрос номер два в котором мы должны выполнить каждый из следующие магические квадраты теперь, что вы подразумеваете под магическими квадратами что вы должны выполнить следующие квадрат в таких числах, что в любом случае вы добавляете числа любым способом это диагональ в сверху снизу все они три числа должны в сумме одно и то же число, поэтому давайте сделаем их один за другим так что в первом случае как видите диагональ в диагонали все числа даны так что 6 плюс 5 будет 11 11 плюс четыре пятнадцать так что сумма этого магического числа так что магическое число этого магического квадрата пятнадцать так везде сумма должна быть пятнадцать теперь начнем с первого ряда в первом ряду шесть плюс семь, значит, шесть плюс Семь плюс это число, это точка точка точка должен дать вам 15 поэтому 13 плюс это число равно 15 поэтому это число равно 2 так что это будет иметь 2 в нем аналогично эта часть получит 1, используя тот же метод 8 плюс 4 равно 12, поэтому эта часть даст нам 3 и это и, таким образом, этот волшебный магический квадрат все кончено, секундочку да так давайте посмотрим на это полностью хорошо, так что это ответ на этот первый вопрос, который мы сделали прямо сейчас в спереди тебя так что давайте поместим это здесь, и я стереть эту часть которые мы решили прямо сейчас, хорошо, давайте перейти к второй секунде вторая часть вопроса прямо второй вопрос, который этот квадрат теперь в этом квадрате 4 плюс 7 плюс 10 это диагональ дает ответ как 11 плюс 10, что 21 хорошо, поэтому ответ 21 поэтому теперь 4 плюс эта точка точка плюс 8 должно быть 21, значит 4 плюс 8 будет 12, значит 12 плюс это число равно 21, поэтому это число напрямую 9. так что это 9. сейчас теперь пойдем по этому пути так что 8 плюс 10 18 18 плюс 21 18 плюс 3 будет 21 поэтому это это 3 нормально так это 3 теперь 3 плюс 7 будет 10 10 плюс 21 10 плюс 11 будет 21, поэтому это 11 лет теперь 4 плюс 11 будет 15 15 плюс 21 15 плюс 6 это 21 это 6. теперь 6 плюс точка точка так 6 плюс 10 плюс пунктирная точка это 21 это 21 поэтому 16 плюс точка точка равна 21, поэтому эта точка точка или это пространство будет заполнено 16 21 минус 16, что 5 так что давайте проверим, если наши ответы правильно, я знаю, что это может выглядеть немного сбивает с толку поэтому я ставлю последний ответ изображение прямо сейчас перед вами так что просто дайте мне одну секунду и вот ваш ответ, так что просто проверьте, если это было правильно, как то, что мы делали раньше и да это абсолютно правильно так давайте перейдем к третьему или последний снова даны диагонали, которые 16 плюс 10 плюс 4 что даст нам 26 на 30. так что магическое число в данном случае 30 нормально Итак, давайте узнаем их всех, так что 16 плюс 2 равно 18 18 плюс 12 это 30. так что это 12. 12 плюс х или пунктирная точка плюс 4 равно 30. поэтому 16 плюс хх 16 плюс пунктирная точка 30, так что здесь мы получим 4 или здесь мы получим 14. в этом случае у нас есть 10 плюс 14 24 24 плюс есть 30 так воля быть заполненным шестью шесть плюс 16 будет 22 это осталось что выйдет восемь восемь плюс четыре будет двенадцать и это осталось, что будет 18, поэтому наш магический квадрат номер 3 тоже завершен давайте еще раз проверим наш ответ правильно и да, это абсолютно правильный еще раз большое спасибо, ребята, если вы но есть другие сомнения прежде всего сделайте этот скриншот эти ответы, если хочешь если у вас еще есть какие-либо сомнения, пожалуйста дайте мне знать в комментариях ниже и я вернусь как можно скорее также ставьте лайк этому видео и подпишись на канал большое спасибо ребята”

Связанные вопросы

Q1)(i) 1 × 9 + 1 = 1012 × 9 + 2 = 110123 × 9 + 3 = 1110 (ii) 9 × 9 + 7 = 8898 × ​​9 + 6 = 888987 × 9 + . ..

Q3) Внимательно посмотрите на следующую схему: (i) Если n обозначает номер цифры, а S обозначает число…

Q5) В каждом из следующих шаблонов постройте следующую фигуру. (i) В каждом случае, если n обозначает число…

Фейсбук WhatsApp

Копировать ссылку

Было ли это полезно?

Упражнения

Упражнение 5(A)

Упражнение 5(B)

Упражнение 5(C)

Упражнение 5(D)

Упражнение 5(E)

Упражнение 5(F)

Главы

Система счисления (консолидация смысла числа)

Оценка

Числа в Индии и международной системе (со сравнением)

Числовая строка

HCF и LCM

Игра с числами

Наборы

Отношение

Пропорции (включая задачи со словами)

Унитарный метод

Фракции

Десятичные фракции

процент (процент)

Идея скорости, расстояния и времени

Фундаментальные концепции (алгебра)

Фундаментальные операции (связанные с алгебрамическими выражениями)

Равирование (включая использование брекетов в группе.