Логика математика 1 класс: Логические задачи для 1 класса с ответами и решениями, развивающие задания на логику для детей 7-8 лет
Информатика логика математика 1 класс Юным умникам и умницам Методическое пособие Холодова ОА
138
Артикул:
H00000289920
Есть в наличии
153
Скидки от 10% до 25%
Цена действует только при заказе через интернет магазин!
Кол-во товара
В корзину! Перейти в корзину
Избранное Удалить
В избранное!
Сравнить Удалить
Добавить к сравнению
| Система скидок при заказе с сайта | ||
| Сумма заказа | Скидка | Цена товара |
до 5000 р. | 10% | 138 |
| от 5000 р. | 15% | 130 |
| от 10000 р. | 20% | 122 |
| от 15000 р. | 25% | 115 |
- Переплет: мягкий
- Предмет: Математика и информатика
- Автор: Холодова
- Класс: 1 класс
- Год выпуска: 2016/2017/2019/2020
- УМК/Линия Учебников: Начальное общее образование 1-4 класс
- Тип литературы: Методическое пособие
- Уровень образования: Начальное общее образование 1-4 класс
- ISBN: 5-905279-78-2
- Издательство: РОСТ
- Относится к УМК: Юным умникам и умницам
- Описание
- В наличии: в
1 магазинах
Пособие представляет собой методические рекомендации по работе с рабочими тетрадями “Юным умникам и умницам 6-7 лет (1 класс)”.
 В нём раскрывается смысл и цели данных тетрадей и приведены подробные указания по проведению занятий по РПС (развитию познавательных способностей). Данный систематический курс создает условия для развития у детей познавательных интересов, формирует стремление ребёнка к размышлению и поиску, вызывает у него чувство уверенности в своих силах, в возможностях своего интеллекта. Во время занятий по предложенному курсу происходит становление у детей развитых форм самосознания и самоконтроля, у них исчезает боязнь ошибочных шагов, снижается тревожность и необоснованное беспокойство. В результате этих занятий ребята достигают значительных успехов в своём развитии, они многому научаются и эти умения применяют в учебной работе, что приводит к успехам. В настящее издание включена программа курса “РПС”. Пособие адресовано учителям начальной школы, воспитателям групп продлённого дня, педагогам дополнительного образования детей, родителям, а также всем тем, кто интересуется развитием познавательных способностей детей младшего школьного возраста.
В нём раскрывается смысл и цели данных тетрадей и приведены подробные указания по проведению занятий по РПС (развитию познавательных способностей). Данный систематический курс создает условия для развития у детей познавательных интересов, формирует стремление ребёнка к размышлению и поиску, вызывает у него чувство уверенности в своих силах, в возможностях своего интеллекта. Во время занятий по предложенному курсу происходит становление у детей развитых форм самосознания и самоконтроля, у них исчезает боязнь ошибочных шагов, снижается тревожность и необоснованное беспокойство. В результате этих занятий ребята достигают значительных успехов в своём развитии, они многому научаются и эти умения применяют в учебной работе, что приводит к успехам. В настящее издание включена программа курса “РПС”. Пособие адресовано учителям начальной школы, воспитателям групп продлённого дня, педагогам дополнительного образования детей, родителям, а также всем тем, кто интересуется развитием познавательных способностей детей младшего школьного возраста.
Название магазина и адрес Время работы магазинов Остаток Книжный магазин “Эдвис”
г.Уфа, Маршала Жукова, 8
8 (347) 241-07-70Пн-Сб: 10.00-20.00 Вс: 10.00-19.00 Много
| Название магазина и адрес | Время работы магазинов | Остаток | ||
|---|---|---|---|---|
| Книжный магазин “Эдвис” г.Уфа, Маршала Жукова, 8 8 (347) 241-07-70 | Пн-Сб: 10.00-20.00 Вс: 10.00-19.00 | Много |
Тренажёр. ФГОС. Юным умникам и умницам. Информатика, логика, математика 1 класс, в 2 частях, комплект.
 Холодова О. А. Тренажёр. ФГОС. Юным умникам и умницам. Информатика, логика, математика 1 класс, в 2 частях, комплект. Холодова О. А.
Холодова О. А. Тренажёр. ФГОС. Юным умникам и умницам. Информатика, логика, математика 1 класс, в 2 частях, комплект. Холодова О. А.- Главная
- О магазине
- Доставка
- Контакты
- Канцтовары
- Посуда
- Спорт и туризм
- Хозтовары
- Швейная галантерея
- Мебель
- Игрушки
- Творчество
- Книги
- Сувениры
- Праздники
- Текстиль
- Одежда и обувь
- Авто и мото
- Летние товары
- Сад и огород
- Баня и сауна
- Детские товары
- Зоотовары
- Строительство и ремонт
- Интерьер
- Аксессуары
- Красота и здоровье
- Бытовая техника и электроника
- Собственное производство
- Оборудование для бизнеса и производства
- Освещение
- Упаковка
- Товары с любимыми героями
- Наша разработка
Связаться с нами
Дюссельдорф
- clo.ru/adorable_potoo_of_wealth:images/7124877/0/700.webp”>
О товаре
- Страна производитель: Россия
- Торговая марка: РОСТкнига
- Артикул: 7124877
- Мин. кол-во для заказа: 1
- Набор: да
- Школьный предмет: информатика, математика
- Школьный класс: 1
- Количество страниц: 112
- Год издания: 2020
- Автор:
холодова о.
 а.
а. - Тип обложки: мягкий переплёт
- Автор: холодова ольга леонидовна
- Вид пособия: тренажёры
- Наличие: нет в наличии
Все характеристики
648 RUB P
405 p* *при покупке от 25 шт.
нет в наличии
Описание и характеристики
Доставка и оплата
Характеристики
- Страна производитель Россия
- Торговая марка РОСТкнига
- Артикул 7124877
- Мин.
 кол-во для заказа
1
кол-во для заказа
1 - Набор да
- Школьный предмет информатика, математика
- Школьный класс 1
- Год издания 2020
- Автор
холодова о.
 а.
а. - Тип обложки мягкий переплёт
- Автор холодова ольга леонидовна
- Соответствие стандарту (ФГОС) да
- Вид пособия тренажёры
- Длина упаковки 28.5
- Высота упаковки
0.
 5
5 - Ширина упаковки 21.5
- Объем упаковки, куб. дм 0.306
- Объем продукта, л 0.2552
- Объем бокса, л 7.656
- Вес, г 250
- Материал Бумага
- Количество в упаковке 1
- Тип индивидуальной упаковки Полиэтиленовая пленка
- Кол-во страниц 112
Описание
Данное пособие представляет систему специально разработанных заданий по развитию познавательных способностей детей 6-7 лет. Оно рассчитано на программу 1 класса общеобразовательной школы. Упражнения, выполненные в определенной последовательности, обеспечивают комплексное развития различных видов памяти, внимания, развивают наблюдательность, воображение; способствует развитию сенсорной и двигательной сфер ребенка, формируют нестандартное мышление. Задания, разработанные в системе, могут быть использованы на уроках математики, информатики, логики. Пособие поможет также воспитателям групп продленного дня при организации свободного времени учащихся и руководителям кружковой работы при составлении заданий игрового и творческого характера.
Оно рассчитано на программу 1 класса общеобразовательной школы. Упражнения, выполненные в определенной последовательности, обеспечивают комплексное развития различных видов памяти, внимания, развивают наблюдательность, воображение; способствует развитию сенсорной и двигательной сфер ребенка, формируют нестандартное мышление. Задания, разработанные в системе, могут быть использованы на уроках математики, информатики, логики. Пособие поможет также воспитателям групп продленного дня при организации свободного времени учащихся и руководителям кружковой работы при составлении заданий игрового и творческого характера.
В пособии использована авторская система, разработанная кандидатом педагогических наук Н. К. Винокуровой.
Передача в доставку до 03.05.2023
(Ваш заказ будет отправлен в течение 5 рабочих дней после оплаты).
Стоимость доставки оплачивается при получении заказа.
Мы принимаем к оплате
Доставка в Дюссельдорф
Популярное
Сенсация Тайна (новое издание). Берн Р.
1539 p
Кремлёвская школа переговоров. Рызов И. Р.
1038 p
Жутко громко и запредельно близко
1258 p
Зубная щетка R.O.C.S. Baby для детей от 0 до 3 лет микс
243 p
Сто лет одиночества
730 p
Раскраска «Модный показ», 12 стр.
26 p
Настольный баскетбол «Штрафной бросок», цвета МИКС
29 p
Рында латунь 12 см
4857 p
Лента для декора и подарков 0,5 см х 500 м, белая
256 p
Вывеска светодиодная LED 48*25 см. “ОТКРЫТО/ЗАКРЫТО”, 2 режима 220V
1869 p
Логика и решение задач 1-го класса
Перейти к основному содержаниюКнопка профиля
Вход для поиска по сайту
- Войти
Индивидуальный Школа
Вход для поиска по сайту
(17) результаты найдены
Предметы
Математика
Музыка
Музыка Национальный стандарт содержания 8
Загрузка
Добавить в избранноеСОЗДАТЬ НОВУЮ ПАПКУ
Предметы:
Измерение
Математика
Логика и решение задач
Скачать
Добавить в избранноеСОЗДАТЬ НОВУЮ ПАПКУ
Предметы:
Логика и решение задач
Математика
Скачать
Добавить в избранноеСОЗДАТЬ НОВУЮ ПАПКУ
Предметы:
Измерения
Метрическая система
Математика
Скачать
Добавить в избранноеСОЗДАТЬ НОВУЮ ПАПКУ
Темы:
Учить не Нормана: История золотой рыбки
Животные (зоология)
Книги
Скачать
Добавить в избранноеСОЗДАТЬ НОВУЮ ПАПКУ
Предметы:
Словесные задачи
Математика
Логика и решение задач
Скачать
Добавить в избранноеСОЗДАТЬ НОВУЮ ПАПКУ
Предметы:
Математика
Логика и решение задач
Скачать
Добавить в избранноеСОЗДАТЬ НОВУЮ ПАПКУ
Предметы:
Логика и решение задач
Словесные задачи
Математика
Скачать
Добавить в избранноеСОЗДАТЬ НОВУЮ ПАПКУ
Предметы:
Математика
Логика и решение задач
Рисование
Скачать
Добавить в избранноеСОЗДАТЬ НОВУЮ ПАПКУ
Темы:
Математика
Естествознание
Логика и решение задач
Загрузка
Добавить в избранноеСОЗДАТЬ НОВУЮ ПАПКУ
Предметы:
Математика
Логика и решение задач
Скачать
Добавить в избранноеСОЗДАТЬ НОВУЮ ПАПКУ
Предметы:
Математика
Логика и решение задач
Скачать
Добавить в избранноеСОЗДАТЬ НОВУЮ ПАПКУ
Предметы:
Математика
Логика и решение задач
Скачать
Добавить в избранноеСОЗДАТЬ НОВУЮ ПАПКУ
Предметы:
Логика и решение задач
Математика
Скачать
Добавить в избранноеСОЗДАТЬ НОВУЮ ПАПКУ
Предметы:
Логика и решение задач
Словесные задачи
Математика
Скачать
Добавить в избранноеСОЗДАТЬ НОВУЮ ПАПКУ
Предметы:
Логика и решение задач
Математика
Скачать
Добавить в избранноеСОЗДАТЬ НОВУЮ ПАПКУ
Предметы:
Животные (зоология)
Биология
Наука
Скачать
Добавить в избранноеСОЗДАТЬ НОВУЮ ПАПКУ
© 2022 Sandbox Networks Inc. Все права защищены. Sandbox Learning является частью компании Sandbox & Co., занимающейся цифровым обучением.
Все права защищены. Sandbox Learning является частью компании Sandbox & Co., занимающейся цифровым обучением.
1.1 Логические операции
Математика обычно включает в себя объединение истинных (или гипотетически истинных) утверждения различными способами для получения (или доказательства) новых истинных утверждений. Начнем с разъяснения некоторых из этих фундаментальных идей.
предложение мы имеем в виду утверждение, имеющее определенное истинностное значение , истина (T) или ложь (F) — например,
«В 1492 году Колумб плыл по синему океану». (T)
«Наполеон выиграл битву при Ватерлоо». (Ф)
В более общем смысле под формулой мы подразумеваем
утверждение, возможно, с некоторыми переменными, которое либо истинно, либо
false всякий раз, когда мы присваиваем определенные значения каждой из переменных.
Мы будем использовать заглавные буквы для обозначения формул. Если правда а
формула зависит от значений, скажем, $x$, $y$ и $z$, мы будем использовать
обозначение типа $P(x,y,z)$ для обозначения формулы. 92+y = 12$”, то $P(2,8)$ и $P(3,3)$
верно, а $P(1,4)$ и $P(0,6)$ ложны. Если $Q(x,y,z)$ равно “$x+y
92+y = 12$”, то $P(2,8)$ и $P(3,3)$
верно, а $P(1,4)$ и $P(0,6)$ ложны. Если $Q(x,y,z)$ равно “$x+y
Является ли предложение истинным или ложным, обычно зависит от того, что мы говорят о том, что одно и то же предложение может быть истинным или ложным в зависимости от по контексту; например, формула $x|y$ означает, что `$x$ делит $у$’. То есть $x|y$, если существует некоторый $z$ такой, что $y=x\cdot z$. Сейчас, правда ли, что $3|2$? Это зависит: если мы говорим о целых числах, ответ – нет; если мы говорим о рациональных числах, то ответ да, потому что $2=3\cdot(2/3)$. (Конечно, если $x\not=0$ и $y$ любые рациональных чисел, затем $x|y$, так что это не очень полезное понятие. При обычном использовании внешний вид формулы “$x|y$” подразумевает , что $x$ и $y$ являются целыми числами.)
вселенная дискурса для конкретной области математики представляет собой набор, который
содержит все, что представляет интерес для этой темы. Когда мы
изучение математических формул типа «$x$ делит $y$» на переменные
предполагается, что они принимают значения в любом дискурсивном универсуме
подходит для конкретного предмета. Вселенная дискурса
обычно ясно из обсуждения, но иногда нам нужно будет
идентифицируйте его явно для ясности.
Вселенная дискурса обычно обозначается $U$.
Вселенная дискурса
обычно ясно из обсуждения, но иногда нам нужно будет
идентифицируйте его явно для ясности.
Вселенная дискурса обычно обозначается $U$.
Сложные предложения и формулы составляются из более простых, используя небольшое количество логических операций . Просто горстка этих операций позволит нам сказать все, что мы должны сказать в математика.
Если $P$ — это формула, то «не $P$» — это другая формула. формула, которую мы символически запишем как $\lnot P$. Конечно, $\lне P$ ложно, если $P$ истинно, и наоборот, например,
«6 не является простым числом» или «Неверно, что 6 премьер” или “$\lnot(\hbox{6 простое число})$” (T)
«Рональд Рейган не был президентом». (Ф)
Предположим, что $P$ и $Q$ — формулы. Затем «$P$ и $Q$» — это формула, записанная символически как $P\land Q$, называемое соединением из $P$ и $Q$. Чтобы $P\land Q$ были истинными как $P$, так и $Q$ должно быть истинным, иначе оно ложно, например,
«5 долларов = 6 долларов и 7 долларов = 8 долларов». (F)
(F)
«Сиэтл находится в Вашингтоне, а Бойсе — в Айдахо». (T)
«Толстой был русским, а Диккенс был Французский.” (Ф)
Если $P$ и $Q$ являются формулами, то формула “$P$ или $Q$” записывается символически как $P\lor Q$, называемая дизъюнкция $P$ и $Q$. Это важно отметить, что это включительно или, то есть, «либо или оба”. Итак, если $P$, $Q$ или оба $P$ и $Q$ верны, то же самое и с $P\lor Q$. Единственный случай, когда $P\lor Q$ может быть ложным, состоит в том, что оба $P$ и $Q$ ложны, например,
«Вашингтон в Канаде или Лондон в Англии». (T)
“$5
«Ленин был испанцем или Ганди был итальянцем». (Ф)
Если $P$ и $Q$ – формулы, то “если $P$, то $Q$”
или “$P$ означает, что $Q$” написано
$P\подразумевает Q$, используя условный символ ,
$\подразумевает$. Не очевидно (по крайней мере, для большинства людей), под чем
обстоятельства $P\имеет Q$ должно быть правдой. Отчасти это потому, что
«if… then» используется в обычном английском языке более чем одним способом, однако
нам нужно исправить правило, которое позволит нам точно знать, когда $P\ подразумевает
Q$ верно. Конечно, если $P$ истинно, а $Q$ ложно, $P$ не может
подразумевают $Q$, поэтому $P\implis Q$ в этом случае ложно. Чтобы помочь нам с
в других случаях рассмотрим следующее утверждение:
Конечно, если $P$ истинно, а $Q$ ложно, $P$ не может
подразумевают $Q$, поэтому $P\implis Q$ в этом случае ложно. Чтобы помочь нам с
в других случаях рассмотрим следующее утверждение:
«Если $x$ меньше 2, то $x$ меньше 4».
Это утверждение должно быть верным независимо от значения $x$. (при условии, что вселенная дискурса является чем-то знакомым, например целые числа). Если $x$ равно 1, оно оценивается как $\rm T\имплицитно T$, если $x$ равно 3, оно становится $\rm F\implis T$, а если $x$ равно 5, становится $\rm F\ подразумевает F$. Таким образом, оказывается, что $P\implis Q$ истинно, если только $P$ истинно, а $Q$ ложно. Это правило, которое мы принимаем.
Наконец, бикондиционал , написанный $\Leftrightarrow$, соответствует фраза «если и только если» или «если» для краткости. Таким образом, $P \Leftrightarrow Q$ истинно, когда и $P$, и $Q$ имеют одинаковое истинностное значение, иначе оно ложно.
Пример 1.1.2 Предположим, что $P(x,y)$ равно “$x+y=2$” и $Q(x,y)$
равно “$xy>1$”. Тогда, когда $x=1$ и $y=1$,
$\lnot P(x,y)$, $P(x,y)\land Q(x,y)$, $P(x,y)\lor Q(x,y)$,
$P(x,y)\имеет Q(x,y)$ и $P(x,y)\Leftrightarrow Q(x,y)$
имеют значения истинности F, F, T, F, F соответственно, а когда
$x=2$ и $y=3$ имеют истинностные значения
Т, Ф, Т, Т, Ф соответственно.
$\квадрат$
Тогда, когда $x=1$ и $y=1$,
$\lnot P(x,y)$, $P(x,y)\land Q(x,y)$, $P(x,y)\lor Q(x,y)$,
$P(x,y)\имеет Q(x,y)$ и $P(x,y)\Leftrightarrow Q(x,y)$
имеют значения истинности F, F, T, F, F соответственно, а когда
$x=2$ и $y=3$ имеют истинностные значения
Т, Ф, Т, Т, Ф соответственно.
$\квадрат$
Используя операции $\lnot$, $\land$, $\lor$, $\implies$,
$\Leftrightarrow$, мы можем построить составных выражения , таких как
$$
(P\land (\lnot Q))\ подразумевает ((\lnot R)\lor ((\lnot P)\land Q)).
$$
Как показывает этот пример, иногда необходимо
включать много круглых скобок, чтобы группировать термины
в формуле ясно. Как и в алгебре, где
умножение имеет приоритет перед сложением, мы можем
убрать некоторые скобки
согласование определенного порядка, в котором логически
операции выполняются. Мы
будет применять операции в этом порядке, начиная с
от первого к последнему: $\lnot$, $\land$, $\lor$, $\implies$
и $\Leftrightarrow$. Так
$$A\подразумевает B\или C\land\lnot D
$$
сокращение от
$$A\подразумевает (B\или (C\land (\lnot D))). $$
Как и в алгебре, часто разумно включать
несколько дополнительных скобок, чтобы убедиться, что предполагаемый смысл понятен.
Большая часть информации, которую мы обсудили, может быть резюмирована в таблицы истинности . Например, таблица истинности для
$\lnot P$:
$$
Как и в алгебре, часто разумно включать
несколько дополнительных скобок, чтобы убедиться, что предполагаемый смысл понятен.
Большая часть информации, которую мы обсудили, может быть резюмирована в таблицы истинности . Например, таблица истинности для
$\lnot P$:
| $P$ | $\lnot P$ |
|---|---|
| Т | Ж |
| Ф | Т |
В этой таблице две строки, потому что есть только две возможности для истинное значение $P$. Другие логические операции используют две переменные, поэтому им требуется 4 строки в их таблицах истинности.
| $P$ | $Q$ | $P\land Q$ | $P\lor Q$ | $P\Rightarrow Q$ | $P\Leftrightarrow Q$ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Т | Т | Т | Т | Т | Т | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ф | Т | Ф | Т | Т | Ф | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Т | Ж | Ж | Т | Ж | Ж | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ф | Ф | Ф | Ф 9п$
строки в таблице, потому что есть много разных способов назначить
T и F для $n$ простых формул в составном выражении. Таблица истинности для $(P\land Q)\lor \lnot R$ такова: Таблица истинности для $(P\land Q)\lor \lnot R$ такова:
Обратите внимание, как включение промежуточных шагов облегчает работу с таблицей. Тавтология — это логическое выражение, которое всегда оценивается как T, то есть последний столбец его таблицы истинности состоит только из Т. Иногда говорят, что тавтология равна 9.0252 действительный ; хотя «действительный» используется в других контекстах как ну, это не должно вызывать путаницы. Например, $(P\land Q)\lor P\Leftrightarrow P$ является тавтологией, поскольку ее таблица истинности такова:
Мы перечисляем несколько важных тавтологий в следующей теореме. Теорема 1.1.3. Справедливы следующие утверждения. а) $P\стрелка влево \lnot\lnot P$ б) $P\lor Q\Leftrightarrow Q\lor P$ c) $P\land Q\Стрелка влево Q\land P$ d) $(P\land Q)\land R\Стрелка влево P\land(Q\land R)$ e) $(P\lor Q)\lor R\Стрелка влево P\lor(Q\lor R)$ f) $P\land (Q\lor R)\Leftrightarrow (P\land Q)\lor (P\land R)$ g) $P\lor (Q\land R)\Стрелка влево (P\lor Q)\land (P\lor R)$ h) $(P\подразумевает Q)\Стрелка влево (\lnot P\lor Q)$ i) $P\подразумевает (P\или Q)$ j) $P\land Q\подразумевает Q$ k) $(P\стрелка влево Q)\стрелка влево ((P\подразумевает Q)\land (Q\подразумевает P))$ l) $(P\подразумевается Q)\стрелка влево (\lnot Q\подразумевается \lnot P)$ Доказательство. Доказательства оставлены в качестве упражнений. $\qed$ Заметим, что (b) и (c) — коммутативные законы, (d) и (e) —
ассоциативные законы и (е) и (ж) говорят, что $\land$
и $\lor$ распределяются друг над другом. Если две формулы всегда принимают одно и то же истинностное значение независимо от того, элементы из вселенной дискурса, которые мы заменяем различными переменные, то мы говорим, что они эквивалентны . Стоимость эквивалента формулы в том, что они говорят одно и то же. Это всегда правильный шаг в доказательстве заменить некоторую формулу эквивалентной. Кроме того, многие тавтологии содержат важные идеи для построения доказательств. Для например, (k) говорит, что если вы хотите показать, что $P\Leftrightarrow Q$, это можно (и часто целесообразно) разбить доказательство на два части, одна из которых доказывает импликацию $P\implis Q$, а вторая доказывая обратное , $Q\подразумевает P$. При чтении теоремы 1.1.3 у вас может возникнуть
заметил, что $\land$ и $\lor$ обладают многими схожими свойствами. Джордж Буль. Буль
(1815–1864) имел только обычное школьное образование, хотя и выучил
Греческий и латынь самостоятельно. Он начал свою карьеру в качестве элементарного
школьным учителем, но решил, что ему нужно больше узнать о
математики, поэтому он начал изучать математику, а также
языки, необходимые ему для чтения современной литературы на
математика. В 1847 году он опубликовал короткую книгу «Математический анализ».
Анализ логики , который, можно справедливо сказать, лег в основу исследования.
математической логики. Ключевой вклад работы заключался в
переопределить «математику» так, чтобы она означала не просто «изучение чисел и
величина», но изучение символов и манипулирование ими в соответствии с
к определенным правилам. В «Исследовании законов мысли» , опубликованном в 1854 г.,
Буль установил настоящую формальную логику, развивая то, что сегодня называется
Булева алгебра или иногда алгебра множеств . Он использовал символы для
сложение и умножение как операторы, но в совершенно абстрактном
смысл. Сегодня эти символы все еще иногда используются в булевых выражениях.
алгебре, хотя символы `$\land$’ и `$\lor$’, и `$\cap$’ и
`$\cup$’ также используются. Буль применил алгебраическую манипуляцию к
процесс рассуждения. Вот простой пример типа
манипуляцию, которую он проделал: уравнение $xy=x$ (которое сегодня можно было бы записать
$x\land y = x$ или $x\cap y = x$) означает, что «все вещи, удовлетворяющие
$x$ удовлетворяет $y$’, или, говоря нашим языком, $x\имеет y$. Если также $yz=y$ (что
есть $y\implis z$), то подстановка $y=yz$ в $xy=x$ дает
$x(yz)=x$ или $(xy)z=x$. Информация здесь взята из A History of Mathematics, by Карл Б. Бойер, Нью-Йорк: John Wiley and Sons, 1968. Подробнее информацию см. в Lectures on Ten British Mathematicians , by Александр Макфарлейн, Нью-Йорк: John Wiley & Sons, 1916. Пример 1.1.1 Постройте таблицы истинности для следующих логических выражений: а) $(P\land Q)\или \lnot P$ б) $P\имеет (Q\land P)$ c) $(P\land Q)\Стрелка влево (P\lor \lnot R)$ d) $\lnot P\имеет в виду \lnot(Q\lor R)$ Пример 1.1.2 Проверьте тавтологии в теореме 1.1.3. Пример 1.1.3 Предположим, что $P(x,y)$ — это формула «$x+y=4$», а $Q(x,y)$ — это формула “$x $P(x,y)\land Q(x,y)$, $\lnot P(x,y)\lor Q(x,y)$, $P(x,y)\подразумевает \lnot Q(x,y)$, $\lnot(P(x,y)\Leftrightarrow Q(x,y))$, , используя значения:
|
 посчитай и прочитай.
посчитай и прочитай.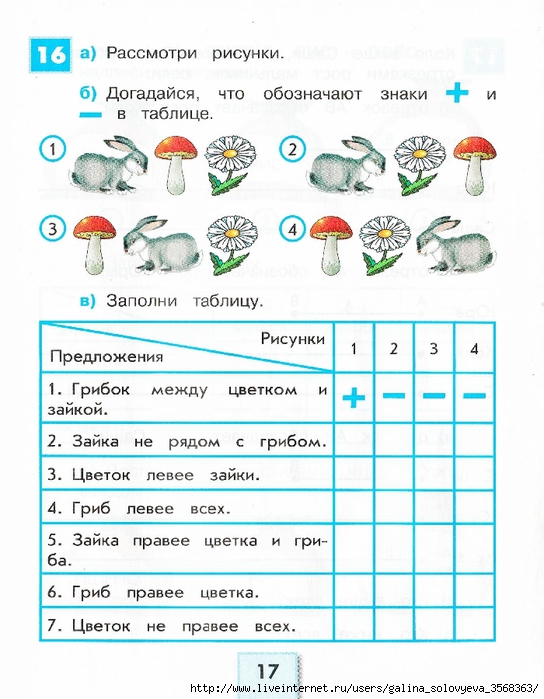
 Это говорит о том, что существует
форма алгебры для логических выражений, аналогичная алгебре
для числовых выражений. Этот предмет называется Булева алгебра и имеет множество применений.
особенно в информатике.
Это говорит о том, что существует
форма алгебры для логических выражений, аналогичная алгебре
для числовых выражений. Этот предмет называется Булева алгебра и имеет множество применений.
особенно в информатике. Они называются «двойственными» понятиями — для любого свойства
один, есть почти идентичное свойство, которому удовлетворяет другой,
экземпляры двух операций поменялись местами. Это часто
означает, что когда мы доказываем результат, включающий одно понятие, мы получаем
соответствующий результат для своего двойственного без дополнительной работы.
Они называются «двойственными» понятиями — для любого свойства
один, есть почти идентичное свойство, которому удовлетворяет другой,
экземпляры двух операций поменялись местами. Это часто
означает, что когда мы доказываем результат, включающий одно понятие, мы получаем
соответствующий результат для своего двойственного без дополнительной работы. Важность этого уровня абстракции для
будущее математики трудно переоценить. Вероятно, на
Благодаря этой работе он перешел на должность в Куинс-колледж в Корке.
Важность этого уровня абстракции для
будущее математики трудно переоценить. Вероятно, на
Благодаря этой работе он перешел на должность в Куинс-колледж в Корке. Заменив $xy$ на $x$, получим $xz=x$, или
$x\подразумевает z$. Этот простой пример логического рассуждения используется более
и далее по математике.
92+bD+c=0$, обработка
$D$ как номер , предоставляет информацию о решениях для
дифференциальное уравнение.
Заменив $xy$ на $x$, получим $xz=x$, или
$x\подразумевает z$. Этот простой пример логического рассуждения используется более
и далее по математике.
92+bD+c=0$, обработка
$D$ как номер , предоставляет информацию о решениях для
дифференциальное уравнение.