Логика математического развития детей дошкольного возраста: Статья Логико-математическое развитие детей дошкольного возраста как важная задача дошкольного образования
Статья Логико-математическое развитие детей дошкольного возраста как важная задача дошкольного образования
Логико-математическое развитие детей
дошкольного возраста как важная задача
дошкольного образования
Е.А. Егорова
МБДОУ детский сад № 63 «Буратино»
г. Ульяновск
Аннотация: в статье раскрыто логическое и математическое развитие детей дошкольного
возраста как важная задача дошкольного образования. Логическое мышление
формируется на основе образного и выше стадия развития мышления. Достижение
этой стадии является длительным и сложным процессом, поскольку полное развитие
логического мышления требует не только высокой активности умственной
деятельности, но и обобщенное знание общих и существенных особенностей
предметов и реальности, которые закреплены словами и характерно для старшего
возраста. Однако навыки, способности, приобретенные в дошкольный период,
послужат фундаментом для получение знаний и развитие логического мышления.
Однако навыки, способности, приобретенные в дошкольный период,
послужат фундаментом для получение знаний и развитие логического мышления.
Ключевые слова: логическое и математическое развитие, дети старшего дошкольного возраста, логические приемы, логическое мышление.
Логическое и математическое развитие дошкольников – это сдвиги и изменения познавательной деятельности ребёнка, происходящие в результате формирования элементарных математических представлений и связанных с ними логических операций. Иными словами, в методологии математического развития дошкольников развитие логики ребёнка означает развитие логических приёмов мыслительной деятельности, а также умение понимать, прослеживать причинно-следственные связи явлений, строить на их основе простые выводы.
Логическими приемами умственных действий являются: сравнение, обобщение, анализ, синтез, сериация, абстрагирование, классификация, аналогия, систематизация.
Изучению проблемы развития
логико-математического развития детей дошкольного возраста посвящены труды
отечественных и зарубежных ученных, педагогов: Л.
Логическое мышление – это способность оперировать абстрактными понятиями, это управляемое мышление; это мышление рассуждениями, это строгое следование законам логики, это совершенное создание отношений причины и следствия. В частности, эта способность выполнять простейшие логические операции: определение понятий (определение).
Логика мышления не дается человеку с
самого рождения. Он захватывает его в течение жизни, на тренировках.
Подчеркивая ценность математики в воспитании логического мышления, необходимо
подбирать общие положения организации такого образования: – продолжительность
процесса воспитания культуры мышления, его ежедневная реализация; –
недопустимость ошибки в логике изложения и обоснования; – привлечение детей к
полноценной работе по совершенствованию мышления, которая будет рассматриваться
ими как личностно значимая задача; – включение в содержание обучения системы
определенных теоретических знаний, прежде всего, знания способов ориентации при
выполнении интеллектуальных действий.
Первой и основной составляющей содержания математического развития детей дошкольного возраста являются [4, стр. 146]:
1) свойства и отношения. В ходе различных действий с объектами потомки овладевают такими свойствами, как форма, размер, количество, пространственное расположение. Важнейшая предпосылка абстрактного мышления – способность к абстракции формируется у детей.
2) В ходе реализации практических действий дети обучаются различным геометрическим фигурам и постепенно переходят к их группированию по количеству углов, сторон и вершин. У детей развиваются конструктивные способности и пространственное мышление. Они овладевают способностью мысленно повернуть объект, посмотреть на него с разных сторон, разобрать, собрать, изменить его.
3) В знании размеров дети переходят от прямых путей (навязывание, применение) к опосредованным способам их сравнения (посредством измерения с условной мерой).
Это позволяет организовать предметы по их свойствам (размер, высота, длина,
толщина, масса).
4) Пространственные и временные представления – самые сложные для дошкольника, осваиваются через реально представленные отношения (далеко, близко, сегодня-завтра).
5) Знание чисел и освоение действий с числами является важнейшей составляющей содержания математического развития. Посредством числа выражается число и значения. Подсчитывая разные по размеру, пространственному расположению предмета, дети приходят к пониманию независимости числа от других свойств предмета, знакомятся с цифрами и знаками.
Задачи логического и математического развития детей дошкольного возраста:
1. Разработка сенсорных способов познания математических свойств и отношений: исследование, согласование, группирование, упорядочение, разбиение.
2. Детское освоение математических способов познания реальности: счет, измерение, простые вычисления.
3. Дети развивают логические способы
познания математических свойств и отношений (анализ, абстракция, отрицание,
сравнение, обобщение, классификация, сериализация).
4. Представление о математических свойствах и взаимосвязях объектов, конкретных величинах, числах, геометрических фигурах, зависимостях и узорах.
5. Детское освоение экспериментальных методов исследования познания математического содержания (рекреация, экспериментирование, моделирование, трансформация).
6. Развитие точной, аргументированной и доказательной речи, обогащение детского словаря.
7. Развитие интеллектуальных и творческих проявлений детей: находчивость, подкованность, угадывание, умность и т. д. [3, с. 396].
Умение мыслить логически включает в себя ряд составляющих: умение ориентироваться на существенные признаки объектов и явлений, умение подчиняться законам логики, выстраивать действия в соответствии с ними, умение совершать логические операции, сознательно аргументируя их, умение выстраивать гипотезы и выводить следствия из данных посылок.
В свою очередь, логико-математическая
компетентность дошкольника предполагает владение логическими приемами
мыслительной деятельности, а также умение понимать, прослеживать
причинно-следственные связи явлений, выстраивать на их основе простейшие
умозаключения.
Логическими приемами умственных действий являются: сравнение, обобщение, анализ, синтез, сериация, абстрагирование, классификация, аналогия, систематизация. Рассмотрим их более детально.
Сравнение – мыслительная операция, которая состоит в сопоставлении познаваемых объектов по некоторому основанию с целью выявления сходства и различия между ними. Сравнение неотделимо от других мыслительных операций и осуществляется на основе определенных качеств и свойств (анализ) с последующим установлением связи между ними (синтез) [5, с. 215].
Обобщение – мысленное объединение предметов и явлений по их общим и
существенным признакам. Обобщение является переходом на более высокую ступень
абстракций путем выявления общих признаков (свойств, отношений, тенденций
развития и т.п.) предметов рассматриваемой области; влечет за собой появление
новых понятий, законов, теорий. Обобщение обеспечивает мышлению определенность
и последовательность. Обобщение осуществляется на основе
абстракции.
Абстракция – форма познания, основанная на мысленном выделении существенных свойств и связей предмета и отвлечении от других, частных его свойств и связей.
Классификация – логическая операция распределения предметов какого-либо рода на классы согласно наиболее существенным признакам, присущим предметам данного рода и отличающим их от предметов других родов.
Для проведения классификации необходимо уметь анализировать материал, сравнивать (соотносить) его отдельные элементы друг с другом, находить в них общие черты, обобщать на этой основе, распределять объекты по группам на основе общих черт, выделенных в них и отраженных в слове – название группы – общих признаков.
Систематизация – умственная деятельность, при которой исследуемые объекты организованы в определённую систему на основе выбранного принципа. Систематизации предшествует анализ, синтез, обобщение, сравнение [2, стр. 121].
Анализ – мысленная операция
разложение сложного объекта на детали или характеристики.
Синтез – это объединение элементов, свойств (сторон) исследуемого объекта в единое целое (систему). Синтез – одна из основных мыслительных операций. Это связано с тем, что характерной чертой восприятия является целостность; концепция формируется путём синтеза определённых существенных черт объектов и явлений; синтез входит в творческую деятельность мышления и воображения по созданию нового образа; на основе синтеза объединяют компоненты в процессе формирования моторного мастерства. Синтез неразрывно связан с анализом и не существует отдельно от него, а также с обобщением, систематизацией, сравнением, вместе с чем составляет логический аппарат мышления и способствует более глубокому познанию реальности [1, с. 144].
Суждение – форма мышления, в которой утверждается или отрицается что-либо относительно каких-то объектов, предметов, явлений. Суждения бывают истинные и ложные; общие, частные и единичные; утвердительные и отрицательные.
Умозаключение – умственное действие,
в результате которого из одного или нескольких известных и определенным образом
связанных суждений получается новое суждение.
Доказательство – это рассуждение, устанавливающее истинность какого-либо утверждения путем приведения других утверждений, истинность которых уже не вызывает сомнений.
В доказательстве различаются тезис – утверждение, которое нужно доказать, и основание, или аргументы, – те утверждения, с помощью которых доказывается тезис [5, с. 220].
Таким образом, логическое мышление формируется на основе образного процесса и является высшей ступенью в развитии мышления. Достижение этого этапа является длительным и сложным процессом, так как полное развитие логического мышления требует не только высокой активности умственной деятельности, но и обобщённых знаний об общих и значимых особенностях предметов и явлений реальности, которые закреплены словами и характерны для старшего возраста. Однако полученные в дошкольный период навыки послужат основой для получения знаний и развития логического мышления.
Список литературы
1.
Богоявленская Д.Б. Умственные способности как компонент интеллектуальной
активности / Д. Б. Богоявленская, И.Л. Петухова // Психологические исследования
интеллектуальной деятельности / Под ред. О.К. Тихомирова. – М.: АСТ, 2012. –
161 с.
Б. Богоявленская, И.Л. Петухова // Психологические исследования
интеллектуальной деятельности / Под ред. О.К. Тихомирова. – М.: АСТ, 2012. –
161 с.
2. Воспитание дошкольников / Под ред. А.С. Стасова. – М.: Академия, 2012. – 121 с.
3. Выгодский М.Я. Справочник по элементарной математике / М.Я. Выгодский. – М.: ЮНИТИ, 2011. – 396 с.
4. Гончарова М.А. Развитие у дошкольников математических представлений, воображения и мышления / М.А. Гончарова. М.: Антал, 2012. – 146 с.
5. Данилова В. Математическая подготовка в дошкольных учреждениях / В.Данилова. – М.: ЮНИТИ, 2011. – 215 с.
Развитие логического мышления дошкольников при формировании счетной деятельности
%PDF-1.5 % 1 0 obj > /Metadata 4 0 R >> endobj 5 0 obj /Title >> endobj 2 0 obj > endobj 3 0 obj > endobj 4 0 obj > stream
 52017-11-24T11:04:54+05:002017-11-24T11:04:54+05:00
endstream
endobj
6 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/XObject >
>>
/MediaBox [0 0 595.
52017-11-24T11:04:54+05:002017-11-24T11:04:54+05:00
endstream
endobj
6 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/XObject >
>>
/MediaBox [0 0 595. 2 841.92]
/Contents [98 0 R 99 0 R 100 0 R]
/Group >
/Tabs /S
/StructParents 0
/Annots [101 0 R]
>>
endobj
7 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 103 0 R
/Group >
/Tabs /S
/StructParents 1
>>
endobj
8 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 104 0 R
/Group >
/Tabs /S
/StructParents 2
>>
endobj
9 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 105 0 R
/Group >
/Tabs /S
/StructParents 3
>>
endobj
10 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 107 0 R
/Group >
/Tabs /S
/StructParents 4
>>
endobj
11 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 108 0 R
/Group >
/Tabs /S
/StructParents 5
>>
endobj
12 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
2 841.92]
/Contents [98 0 R 99 0 R 100 0 R]
/Group >
/Tabs /S
/StructParents 0
/Annots [101 0 R]
>>
endobj
7 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 103 0 R
/Group >
/Tabs /S
/StructParents 1
>>
endobj
8 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 104 0 R
/Group >
/Tabs /S
/StructParents 2
>>
endobj
9 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 105 0 R
/Group >
/Tabs /S
/StructParents 3
>>
endobj
10 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 107 0 R
/Group >
/Tabs /S
/StructParents 4
>>
endobj
11 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 108 0 R
/Group >
/Tabs /S
/StructParents 5
>>
endobj
12 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 2 841.92]
/Contents 109 0 R
/Group >
/Tabs /S
/StructParents 6
>>
endobj
13 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 110 0 R
/Group >
/Tabs /S
/StructParents 7
>>
endobj
14 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 111 0 R
/Group >
/Tabs /S
/StructParents 8
>>
endobj
15 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 112 0 R
/Group >
/Tabs /S
/StructParents 9
>>
endobj
16 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 113 0 R
/Group >
/Tabs /S
/StructParents 10
>>
endobj
17 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 114 0 R
/Group >
/Tabs /S
/StructParents 11
>>
endobj
18 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
2 841.92]
/Contents 109 0 R
/Group >
/Tabs /S
/StructParents 6
>>
endobj
13 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 110 0 R
/Group >
/Tabs /S
/StructParents 7
>>
endobj
14 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 111 0 R
/Group >
/Tabs /S
/StructParents 8
>>
endobj
15 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 112 0 R
/Group >
/Tabs /S
/StructParents 9
>>
endobj
16 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 113 0 R
/Group >
/Tabs /S
/StructParents 10
>>
endobj
17 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 114 0 R
/Group >
/Tabs /S
/StructParents 11
>>
endobj
18 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 2 841.92]
/Contents 115 0 R
/Group >
/Tabs /S
/StructParents 12
>>
endobj
19 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 116 0 R
/Group >
/Tabs /S
/StructParents 13
>>
endobj
20 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 117 0 R
/Group >
/Tabs /S
/StructParents 14
>>
endobj
21 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 118 0 R
/Group >
/Tabs /S
/StructParents 15
>>
endobj
22 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 119 0 R
/Group >
/Tabs /S
/StructParents 16
>>
endobj
23 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 120 0 R
/Group >
/Tabs /S
/StructParents 17
>>
endobj
24 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
2 841.92]
/Contents 115 0 R
/Group >
/Tabs /S
/StructParents 12
>>
endobj
19 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 116 0 R
/Group >
/Tabs /S
/StructParents 13
>>
endobj
20 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 117 0 R
/Group >
/Tabs /S
/StructParents 14
>>
endobj
21 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 118 0 R
/Group >
/Tabs /S
/StructParents 15
>>
endobj
22 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 119 0 R
/Group >
/Tabs /S
/StructParents 16
>>
endobj
23 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 120 0 R
/Group >
/Tabs /S
/StructParents 17
>>
endobj
24 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 2 841.92]
/Contents 121 0 R
/Group >
/Tabs /S
/StructParents 18
>>
endobj
25 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 122 0 R
/Group >
/Tabs /S
/StructParents 19
>>
endobj
26 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 124 0 R
/Group >
/Tabs /S
/StructParents 20
>>
endobj
27 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 125 0 R
/Group >
/Tabs /S
/StructParents 21
>>
endobj
28 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 126 0 R
/Group >
/Tabs /S
/StructParents 22
>>
endobj
29 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 127 0 R
/Group >
/Tabs /S
/StructParents 23
>>
endobj
30 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
2 841.92]
/Contents 121 0 R
/Group >
/Tabs /S
/StructParents 18
>>
endobj
25 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 122 0 R
/Group >
/Tabs /S
/StructParents 19
>>
endobj
26 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 124 0 R
/Group >
/Tabs /S
/StructParents 20
>>
endobj
27 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 125 0 R
/Group >
/Tabs /S
/StructParents 21
>>
endobj
28 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 126 0 R
/Group >
/Tabs /S
/StructParents 22
>>
endobj
29 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 127 0 R
/Group >
/Tabs /S
/StructParents 23
>>
endobj
30 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 2 841.92]
/Contents 128 0 R
/Group >
/Tabs /S
/StructParents 24
>>
endobj
31 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 129 0 R
/Group >
/Tabs /S
/StructParents 25
>>
endobj
32 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 130 0 R
/Group >
/Tabs /S
/StructParents 26
>>
endobj
33 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 131 0 R
/Group >
/Tabs /S
/StructParents 27
>>
endobj
34 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 132 0 R
/Group >
/Tabs /S
/StructParents 28
>>
endobj
35 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 133 0 R
/Group >
/Tabs /S
/StructParents 29
>>
endobj
36 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
2 841.92]
/Contents 128 0 R
/Group >
/Tabs /S
/StructParents 24
>>
endobj
31 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 129 0 R
/Group >
/Tabs /S
/StructParents 25
>>
endobj
32 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 130 0 R
/Group >
/Tabs /S
/StructParents 26
>>
endobj
33 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 131 0 R
/Group >
/Tabs /S
/StructParents 27
>>
endobj
34 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 132 0 R
/Group >
/Tabs /S
/StructParents 28
>>
endobj
35 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 133 0 R
/Group >
/Tabs /S
/StructParents 29
>>
endobj
36 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 2 841.92]
/Contents 134 0 R
/Group >
/Tabs /S
/StructParents 30
>>
endobj
37 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 135 0 R
/Group >
/Tabs /S
/StructParents 31
>>
endobj
38 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 136 0 R
/Group >
/Tabs /S
/StructParents 32
>>
endobj
39 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 138 0 R
/Group >
/Tabs /S
/StructParents 33
>>
endobj
40 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 139 0 R
/Group >
/Tabs /S
/StructParents 34
>>
endobj
41 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 140 0 R
/Group >
/Tabs /S
/StructParents 35
>>
endobj
42 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
2 841.92]
/Contents 134 0 R
/Group >
/Tabs /S
/StructParents 30
>>
endobj
37 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 135 0 R
/Group >
/Tabs /S
/StructParents 31
>>
endobj
38 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 136 0 R
/Group >
/Tabs /S
/StructParents 32
>>
endobj
39 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 138 0 R
/Group >
/Tabs /S
/StructParents 33
>>
endobj
40 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 139 0 R
/Group >
/Tabs /S
/StructParents 34
>>
endobj
41 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 140 0 R
/Group >
/Tabs /S
/StructParents 35
>>
endobj
42 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 2 841.92]
/Contents 141 0 R
/Group >
/Tabs /S
/StructParents 36
>>
endobj
43 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 142 0 R
/Group >
/Tabs /S
/StructParents 37
>>
endobj
44 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 144 0 R
/Group >
/Tabs /S
/StructParents 38
>>
endobj
45 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 145 0 R
/Group >
/Tabs /S
/StructParents 39
>>
endobj
46 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 147 0 R
/Group >
/Tabs /S
/StructParents 40
>>
endobj
47 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 148 0 R
/Group >
/Tabs /S
/StructParents 41
>>
endobj
48 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
2 841.92]
/Contents 141 0 R
/Group >
/Tabs /S
/StructParents 36
>>
endobj
43 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 142 0 R
/Group >
/Tabs /S
/StructParents 37
>>
endobj
44 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 144 0 R
/Group >
/Tabs /S
/StructParents 38
>>
endobj
45 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 145 0 R
/Group >
/Tabs /S
/StructParents 39
>>
endobj
46 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 147 0 R
/Group >
/Tabs /S
/StructParents 40
>>
endobj
47 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 148 0 R
/Group >
/Tabs /S
/StructParents 41
>>
endobj
48 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 2 841.92]
/Contents 149 0 R
/Group >
/Tabs /S
/StructParents 42
>>
endobj
49 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 151 0 R
/Group >
/Tabs /S
/StructParents 43
>>
endobj
50 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 152 0 R
/Group >
/Tabs /S
/StructParents 44
>>
endobj
51 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 153 0 R
/Group >
/Tabs /S
/StructParents 45
>>
endobj
52 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 154 0 R
/Group >
/Tabs /S
/StructParents 46
>>
endobj
53 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 155 0 R
/Group >
/Tabs /S
/StructParents 47
>>
endobj
54 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
2 841.92]
/Contents 149 0 R
/Group >
/Tabs /S
/StructParents 42
>>
endobj
49 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 151 0 R
/Group >
/Tabs /S
/StructParents 43
>>
endobj
50 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 152 0 R
/Group >
/Tabs /S
/StructParents 44
>>
endobj
51 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 153 0 R
/Group >
/Tabs /S
/StructParents 45
>>
endobj
52 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 154 0 R
/Group >
/Tabs /S
/StructParents 46
>>
endobj
53 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 155 0 R
/Group >
/Tabs /S
/StructParents 47
>>
endobj
54 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 2 841.92]
/Contents 156 0 R
/Group >
/Tabs /S
/StructParents 48
>>
endobj
55 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 157 0 R
/Group >
/Tabs /S
/StructParents 49
>>
endobj
56 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 158 0 R
/Group >
/Tabs /S
/StructParents 50
>>
endobj
57 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 161 0 R
/Group >
/Tabs /S
/StructParents 51
>>
endobj
58 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 164 0 R
/Group >
/Tabs /S
/StructParents 52
>>
endobj
59 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 167 0 R
/Group >
/Tabs /S
/StructParents 53
>>
endobj
60 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
2 841.92]
/Contents 156 0 R
/Group >
/Tabs /S
/StructParents 48
>>
endobj
55 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 157 0 R
/Group >
/Tabs /S
/StructParents 49
>>
endobj
56 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 158 0 R
/Group >
/Tabs /S
/StructParents 50
>>
endobj
57 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 161 0 R
/Group >
/Tabs /S
/StructParents 51
>>
endobj
58 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 164 0 R
/Group >
/Tabs /S
/StructParents 52
>>
endobj
59 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 167 0 R
/Group >
/Tabs /S
/StructParents 53
>>
endobj
60 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 2 841.92]
/Contents 168 0 R
/Group >
/Tabs /S
/StructParents 54
>>
endobj
61 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 171 0 R
/Group >
/Tabs /S
/StructParents 55
>>
endobj
62 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 172 0 R
/Group >
/Tabs /S
/StructParents 56
>>
endobj
63 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 173 0 R
/Group >
/Tabs /S
/StructParents 57
>>
endobj
64 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 174 0 R
/Group >
/Tabs /S
/StructParents 58
>>
endobj
65 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 175 0 R
/Group >
/Tabs /S
/StructParents 59
>>
endobj
66 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/Annots [177 0 R 178 0 R]
/MediaBox [0 0 595.
2 841.92]
/Contents 168 0 R
/Group >
/Tabs /S
/StructParents 54
>>
endobj
61 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 171 0 R
/Group >
/Tabs /S
/StructParents 55
>>
endobj
62 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 172 0 R
/Group >
/Tabs /S
/StructParents 56
>>
endobj
63 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 173 0 R
/Group >
/Tabs /S
/StructParents 57
>>
endobj
64 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 174 0 R
/Group >
/Tabs /S
/StructParents 58
>>
endobj
65 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 175 0 R
/Group >
/Tabs /S
/StructParents 59
>>
endobj
66 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/Annots [177 0 R 178 0 R]
/MediaBox [0 0 595. 2 841.92]
/Contents 179 0 R
/Group >
/Tabs /S
/StructParents 60
>>
endobj
67 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 180 0 R
/Group >
/Tabs /S
/StructParents 63
>>
endobj
68 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 181 0 R
/Group >
/Tabs /S
/StructParents 64
>>
endobj
69 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 182 0 R
/Group >
/Tabs /S
/StructParents 65
>>
endobj
70 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/Annots [183 0 R]
/MediaBox [0 0 595.2 841.92]
/Contents 184 0 R
/Group >
/Tabs /S
/StructParents 66
>>
endobj
71 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 186 0 R
/Group >
/Tabs /S
/StructParents 68
>>
endobj
72 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
2 841.92]
/Contents 179 0 R
/Group >
/Tabs /S
/StructParents 60
>>
endobj
67 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 180 0 R
/Group >
/Tabs /S
/StructParents 63
>>
endobj
68 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 181 0 R
/Group >
/Tabs /S
/StructParents 64
>>
endobj
69 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 182 0 R
/Group >
/Tabs /S
/StructParents 65
>>
endobj
70 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/Annots [183 0 R]
/MediaBox [0 0 595.2 841.92]
/Contents 184 0 R
/Group >
/Tabs /S
/StructParents 66
>>
endobj
71 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 186 0 R
/Group >
/Tabs /S
/StructParents 68
>>
endobj
72 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 2 841.92]
/Contents 190 0 R
/Group >
/Tabs /S
/StructParents 69
>>
endobj
73 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 193 0 R
/Group >
/Tabs /S
/StructParents 70
>>
endobj
74 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 194 0 R
/Group >
/Tabs /S
/StructParents 71
>>
endobj
75 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 195 0 R
/Group >
/Tabs /S
/StructParents 72
>>
endobj
76 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 196 0 R
/Group >
/Tabs /S
/StructParents 73
>>
endobj
77 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 199 0 R
/Group >
/Tabs /S
/StructParents 74
>>
endobj
78 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
2 841.92]
/Contents 190 0 R
/Group >
/Tabs /S
/StructParents 69
>>
endobj
73 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 193 0 R
/Group >
/Tabs /S
/StructParents 70
>>
endobj
74 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 194 0 R
/Group >
/Tabs /S
/StructParents 71
>>
endobj
75 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 195 0 R
/Group >
/Tabs /S
/StructParents 72
>>
endobj
76 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 196 0 R
/Group >
/Tabs /S
/StructParents 73
>>
endobj
77 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 199 0 R
/Group >
/Tabs /S
/StructParents 74
>>
endobj
78 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 2 841.92]
/Contents 203 0 R
/Group >
/Tabs /S
/StructParents 75
>>
endobj
79 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 205 0 R
/Group >
/Tabs /S
/StructParents 76
>>
endobj
80 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 206 0 R
/Group >
/Tabs /S
/StructParents 77
>>
endobj
81 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 207 0 R
/Group >
/Tabs /S
/StructParents 78
>>
endobj
82 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 209 0 R
/Group >
/Tabs /S
/StructParents 79
>>
endobj
83 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 210 0 R
/Group >
/Tabs /S
/StructParents 80
>>
endobj
84 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
2 841.92]
/Contents 203 0 R
/Group >
/Tabs /S
/StructParents 75
>>
endobj
79 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 205 0 R
/Group >
/Tabs /S
/StructParents 76
>>
endobj
80 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 206 0 R
/Group >
/Tabs /S
/StructParents 77
>>
endobj
81 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 207 0 R
/Group >
/Tabs /S
/StructParents 78
>>
endobj
82 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 209 0 R
/Group >
/Tabs /S
/StructParents 79
>>
endobj
83 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 210 0 R
/Group >
/Tabs /S
/StructParents 80
>>
endobj
84 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 2 841.92]
/Contents 212 0 R
/Group >
/Tabs /S
/StructParents 81
>>
endobj
85 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 214 0 R
/Group >
/Tabs /S
/StructParents 82
>>
endobj
86 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 216 0 R
/Group >
/Tabs /S
/StructParents 83
>>
endobj
87 0 obj
>
endobj
88 0 obj
>
endobj
89 0 obj
>
endobj
90 0 obj
>
endobj
91 0 obj
>
endobj
92 0 obj
>
endobj
93 0 obj
>
endobj
94 0 obj
>
endobj
95 0 obj
>
endobj
96 0 obj
>
endobj
97 0 obj
>
stream
x
2 841.92]
/Contents 212 0 R
/Group >
/Tabs /S
/StructParents 81
>>
endobj
85 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 214 0 R
/Group >
/Tabs /S
/StructParents 82
>>
endobj
86 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.2 841.92]
/Contents 216 0 R
/Group >
/Tabs /S
/StructParents 83
>>
endobj
87 0 obj
>
endobj
88 0 obj
>
endobj
89 0 obj
>
endobj
90 0 obj
>
endobj
91 0 obj
>
endobj
92 0 obj
>
endobj
93 0 obj
>
endobj
94 0 obj
>
endobj
95 0 obj
>
endobj
96 0 obj
>
endobj
97 0 obj
>
stream
xметодическая копилка
МБДОУ Пестречинский детский сад №3 “Солнышко”/ МБДОУ Питрәч муниципаль районы 3 нче номерлы “Кояшкай””
Математическое развитие дошкольников по программе «Детство».
Дошкольные годы – период наиболее интенсивного развития ребенка, возраст больших потенциальных возможностей, рождения личности, становление основ самосознания и ценных ориентаций, освоение ребенком основных видов деятельности, проявление первых творческих потенций ребенка, его индивидуальности.
Психологи считают, что в дошкольном возрасте не следует стремиться к искусственной умственной акселерации детей. Важно другое: активно обогащать те стороны развития, к которым каждый возраст наиболее чувствителен, наиболее восприимчив обучению дошкольников началам математики должно, отводиться важное место. Это вызвано целым рядом причин: подготовкой к школьному обучению, обилием информации, получаемой ребенком, повышением внимания к компьютеризации, желанием делать процесс обучения более интенсивным, стремлением родителей в связи с этим как можно раньше научить ребенка узнавать цифры, считать, решать различного рода задачи. Преследуется главная цель: вырастить детей людьми, умеющими думать, хорошо ориентироваться во всем, что их окружает, правильно оценивать различные ситуации, с которыми они сталкиваются в жизни, принимать самостоятельные решения.
Следуя основным принципам программы развития и воспитания детей в детском саду «Детство», где сказано: «Активность ребенка, направленная на познание, реализуется в содержательной самостоятельной игровой и практической деятельности, в организуемых воспитателем познавательных, развивающих играх», в своей педагогической практике использую математические развивающие игры, которые способствуют развитию у дошкольника мыслительной деятельности и приобщают к умственной деятельности.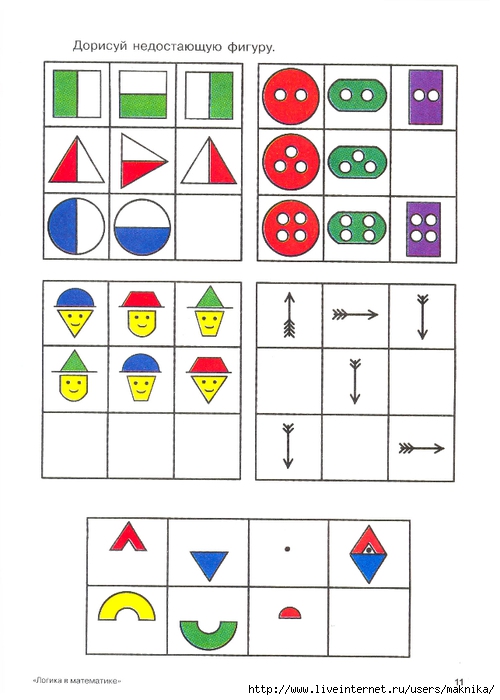 У детей вызывают живой интерес такие игры, как: «Логическая мозаика», «Кубики для всех», «Кубики «Хамелеон», «Сложи узор», «Уникуб», «Кростики», «Логический экран» и конечно же блоки Дьенеша и цветные палочки Кюинезера. Такие игры помогают ребенку вычленить анализируемый предмет, увидеть его во всем многообразии свойств, установить связи и зависимости, определить отношение сходства и различия.
У детей вызывают живой интерес такие игры, как: «Логическая мозаика», «Кубики для всех», «Кубики «Хамелеон», «Сложи узор», «Уникуб», «Кростики», «Логический экран» и конечно же блоки Дьенеша и цветные палочки Кюинезера. Такие игры помогают ребенку вычленить анализируемый предмет, увидеть его во всем многообразии свойств, установить связи и зависимости, определить отношение сходства и различия.
Использование таких развивающих игр способствует познавательному, творческому развитию ребенка и воспитанию оценки своих действий и решений, побуждают к выработке активных поисковых действий и решений.
Игровые ситуации, используемые на занятиях по математическому развитию, содержат увлекательные, развивающие сообразительность, смекалку игровые задачи и упражнения, которые составлены с учетом стремления детей к активной преобразующей деятельности. Благодаря заинтересованности детей в развитии сюжета игры – сопереживая его героям, дети активной познавательной деятельности переживают положительные эмоции, благоприятно сказывающиеся на улучшении его психо – эмоционального состояния. Решение творческой задачи дает толчок к желанию включиться в выполнение разнообразных действий, мотивированных логикой развития сюжета.
Решение творческой задачи дает толчок к желанию включиться в выполнение разнообразных действий, мотивированных логикой развития сюжета.
Играя с цветным конструктором, блоками Дьенеша палочками Кюинезера, дети реализуют представленную им возможность действовать самостоятельно, совершать поиск и нахождение поставленной перед ним творческой задачи.
Привлекая детей к оценке результатов, как своих собственных действий, так и сказочных героев, а так же других детей, мне приходилось пользоваться положительной оценкой, для того, чтобы стимулировать детскую активность и желание заниматься далее умственной деятельностью. Подводя итог очередного занятия по математическому развитию с использованием развивающих игр, давая положительную оценку ребенку, выражая доброжелательную эмоциональную поддержку, стремлюсь вызвать в нем желание преодолевать свои ошибки и не бояться прибегать к иным решениям поставленных задач, не бояться самостоятельно, экспериментировать.
У дошкольника появляется потребность самостоятельно, творчески применять освоенные действия и помогать другому выполнять их. Меняется отношение к способу достижения результата деятельности. От простого повтора нахождения решения, показанного воспитателем, ребенок отказывается и прилагаем все усилия, накопленный опыт и полученные навыки, чтобы перейти к решению поставленной перед ним задачи иным «своим» путем.
Используемые дидактические и развивающие игры в свободной игровой деятельности способствуют развитию умственной деятельности. Активность детей, направленная на познание, реализовывается через систему по развитию у ребенка логико-математических представлений и умений, основанной на использовании игр и материалов развивающего характера – уникальных по своим возможностям: блокам Дьенеша, палочкам Кюинезера, моделях и других дидактических средств.
Играя, в логико-математические игры дети овладевают, умением сравнивать и обобщать группы предметов по двум-трем признакам; уметь находить сходство и различие; они выявляют зависимости между предметами по количеству, расположению и другим признакам.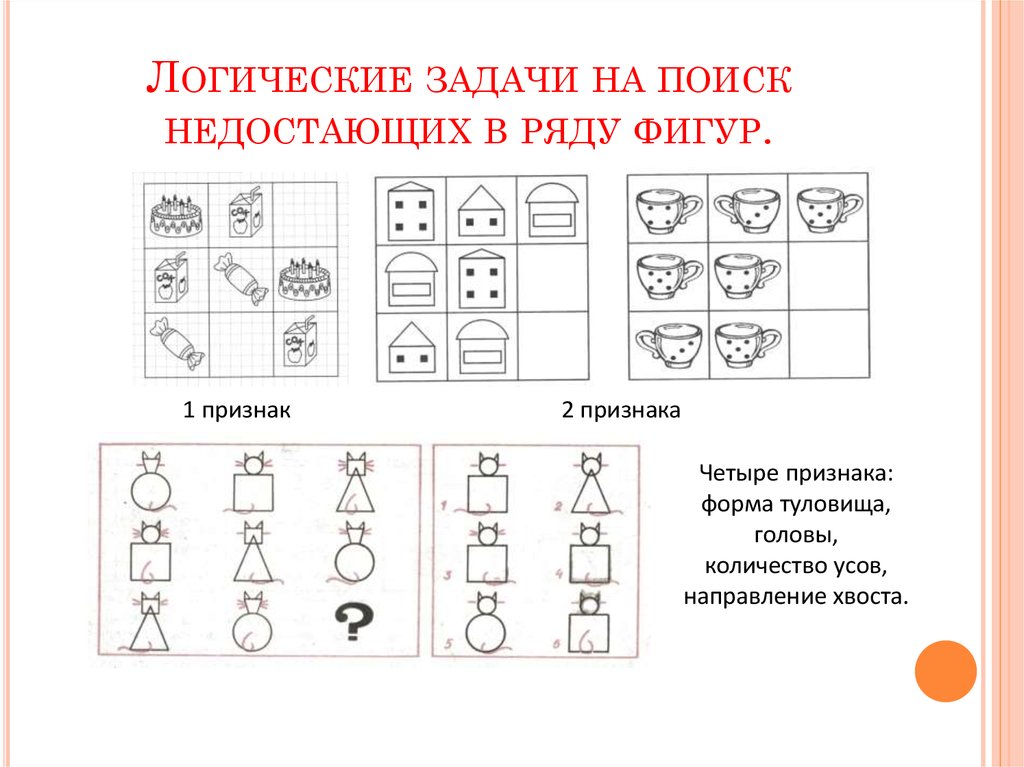
Освоение это довольно сложного, но способствующего развитию мышления, содержания, осуществляется при решении наглядно-представленных логических задач, а в дальнейшем – словесных.
Результат использования развивающих игр в математическом развитии дошкольника:
– развитие умственной деятельности, познавательного интереса, мыслительной активности;
– развитие логического мышления детей, памяти, сообразительности и смекалки;
– развитие творческого воображения, самостоятельной познавательной игровой деятельности;
– умение активно действовать в условиях простых проблемных ситуациях;
— умение анализировать, сравнивать, обобщать предметы по их свойствам, количеству, расположению, назначению;
– умение сосчитывать предметы и пользоваться счетом для оценки количества объектов.
В процессе специальных игр и упражнений дети осваивают элементы логики математики.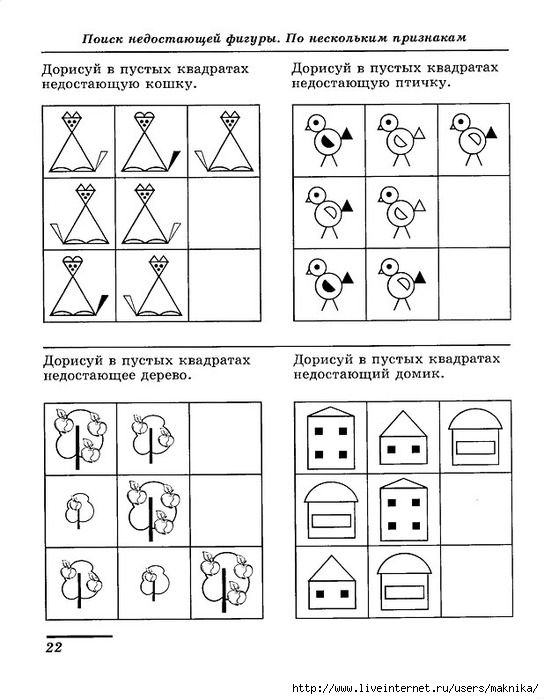 У них складывается представление об отношениях, эквивалентности, сохранении, алгоритмах, разбиении множеств и др.
У них складывается представление об отношениях, эквивалентности, сохранении, алгоритмах, разбиении множеств и др.
Выдвижение в программе «Детство» развивающих задач, дает возможность педагогу конструировать воспитательный процесс с позиции интеграции содержания. В контексте любой деятельности: природоведческой, художественной и других – осуществляется общее умственное и личностное развитие ребенка-дошкольника.
Математическое развитие в первой младшей группе.
Основные задачи: Привлечение внимания детей к свойствам и соотношениям окружающих предметов; название цвета и формы, расположение или увеличения с чисто практической, игровой целью; в организации разнообразной, интересной детям деятельности, направленной на их сенсорное развитие.
Используемые методические пособия:
|
№ |
Методические пособия |
Авторы |
|
1. |
Математика – это интересно. Игровые ситуации для детей дошкольного возраста. В пособи представлены игровые ситуации для детей от 2 до 7 лет, включающие игровой сюжет, описание игровой обстановки, учебно – игровые задачи, методику вовлечения ребенка в деятельность по овладению сравнением, соотнесением, группировкой, упорядочиванием по заданным свойствам.
|
З. |
|
2. |
Конспекты занятий в первой младшей группе детского сада. Дидактические игры. Накопление сенсорно – двигательного навыка, соотнесение по форме, группирование по форме, величине и цвету. |
Н.А.Карпухина |
|
3. |
Комплексные развивающие занятия с детьми раннего возраста. Накопление ориентировки в пространстве, времени, по величине, по цвету, группировка предметов. |
Е.Е. Хомякова |
Динамика уровня математического развития детей в первой младшей группе.
Математическое развитие во второй младшей группе.
Основные задачи: Способствовать освоению свойств предметов, отношений идентичности, порядка и неравенства, простых зависимостей между предметами в повседневной детской деятельности и использованию с целью совершенствования игр, практических действий; развивать самостоятельность познания. Поощрять проявление элементов творческой инициативы.
Используемые методические пособия:
|
№ |
Методические пособия |
Авторы |
||
|
1. |
Математика – это интересно. Игровые ситуации для детей дошкольного возраста. В пособие представлены игровые ситуации для детей от 2 до 7 лет, включающие игровой сюжет, описание игровой обстановки, учебно – игровые задачи, методику вовлечения ребенка в деятельность по овладению сравнением, соотнесением, группировкой, упорядочиванием по заданным свойствам.
|
З.А. Михайлова, И.Н.Чеплашкина |
||
|
2. |
Математика вторая младшая группа. В пособие представлены дидактические и развивающие игры, задания и упражнения для детей. |
Е.С. Маклакова |
||
|
3. |
Математика в детском саду. В пособие представлены знакомство с величиной и формой предметов, пространственными и временными ориентировками и с количеством. |
В.П. Новикова |
||
|
4. |
Математика от трех до семи. В пособие представлены описание игр и игровые упражнения с математическим содержанием, приведенные сценарии математических праздников. |
З.А. Михайлова, Э.Н. Иоффе, Н.С. Камышн и Т.В. Лагода. |
||
Динамика уровня математического развития детей во второй младшей группе.
Математическое развитие в средней группе.
Основные задачи: Оперировать свойствами, отношениями предметов, числами; выявлять простейшие изменения и зависимости их по форме, размеру; сравнивать, обобщать группы предметов, соотносить, вычленять закономерности чередования и следования, оперировать в плане представлений, стремиться к творчеству; проявлять инициативу в деятельности, самостоятельность в уточнении или выдвижении цели, в ходе рассуждений, в выполнении и достижении результата; рассказывать о выполняемом или выполненном действии.
Используемые методические пособия:
|
№ |
Методические пособия |
Авторы |
|
1. |
Математика – это интересно. Игровые ситуации для детей дошкольного возраста. В пособие представлены игровые ситуации для детей от 2 до 7 лет, включающие игровой сюжет, описание игровой обстановки, учебно – игровые задачи, методику вовлечения ребенка в деятельность по овладению сравнением, соотнесением, группировкой, упорядочиванием по заданным свойствам.
|
З.А. Михайлова, И.Н.Чеплашкина |
|
2. |
Математика от трех до семи. В пособие представлены описание игр и игровые упражнения с математическим содержанием, приведенные сценарии математических праздников |
З.А. Михайлова, Э.Н. Иоффе, Н.С. Камышн и Т.В. Лагода |
|
3. |
Развернутое перспективное планирование по программе «Детство». Осваивают счет, пользуются числами, осуществляют элементарные вычисления по наглядной основе и устно, осваивают простейшие временные и пространственные отношения, преобразуют предметы различных форм и размеров.
. |
Е.А.Мартынова, И.М.Сучкова |
Динамика уровня математического развития детей в средне группе.
Математическое развитие в старшей группе.
Основные задачи: Самостоятельно применять доступные им способы познания с целью освоения зависимости между предметами, числами, строить простые высказывания о сущности выполненного действия; находить нужный способ выполнения задания, ведущий к результату наиболее экономным путем; свободно разговаривать со взрослыми по по поводу игры, практических заданий, упражнений, в том числе и придуманных детьми.
Используемые методические пособия:
|
№ |
Методические пособия |
Авторы |
|
1. |
Математика – это интересно. Игровые ситуации для детей дошкольного возраста. В пособие представлены игровые ситуации для детей от 2 до 7 лет, включающие игровой сюжет, описание игровой обстановки, учебно – игровые задачи, методику вовлечения ребенка в деятельность по овладению сравнением, соотнесением, группировкой, упорядочиванием по заданным свойствам.
|
З. |
|
2. |
Математика от трех до семи. В пособие представлены описание игр и игровые упражнения с математическим содержанием, приведенные сценарии математических праздников |
З.А. Михайлова, Э.Н. Иоффе, Н.С. Камышн и Т.В. Лагода |
|
3. |
Развернутое перспективное планирование по программе «Детство». Осваивают счет, пользуются числами, осуществляют элементарные вычисления по наглядной основе и устно, осваивают простейшие временные и пространственные отношения, преобразуют предметы различных форм и размеров.
. |
Е. |
|
4. |
Математика до школы. В пособие представлены игровые упражнения с нестандартными средствами математического развития. |
А.А. Смоленцева, О.В. Пустовойт |
|
5.
|
Игры – головоломки. В пособие представлены описания и чертежи 8 разных по сложности игр – головоломок, способствующих развитию пространственного воображения и мышления детей.
|
З. М. Михайлова,
Р.
|
Динамика уровня математического развития детей в старшей группе.
Математическое развитие в подготовительной группе.
Основные задачи: Самостоятельно применять доступные им способы познания с целью освоения зависимостей между предметами, числами, строить простые высказывания о сущности выполненного действия; находить нужный способ выполнения задания, ведущий к результату наиболее экономным путем; активно включать в коллективную игру, помогать сверстнику в случае необходимости; свободно разговаривать со взрослыми по поводу игры, практических заданий, упражнений, в том числе и придуманных детьми.
Используемые методические пособия:
|
№ |
Методические пособия |
Авторы |
|
1. |
Математика – это интересно. Игровые ситуации для детей дошкольного возраста. В пособие представлены игровые ситуации для детей от 2 до 7 лет, включающие игровой сюжет, описание игровой обстановки, учебно – игровые задачи, методику вовлечения ребенка в деятельность по овладению сравнением, соотнесением, группировкой, упорядочиванием по заданным свойствам.
|
З.А. Михайлова, И.Н.Чеплашкина |
|
2. |
Математика от трех до семи. В пособие представлены описание игр и игровые упражнения с математическим содержанием, приведенные сценарии математических праздников |
З.А. Михайлова, Э.Н. Иоффе, Н.С. Камышн и Т.В. Лагода |
|
3. |
Развернутое перспективное планирование по программе «Детство». Осваивают счет, пользуются числами, осуществляют элементарные вычисления по наглядной основе и устно, осваивают простейшие временные и пространственные отношения, преобразуют предметы различных форм и размеров.
. |
Е.А.Мартынова, И.М.Сучкова |
|
4. |
Математика до школы. В пособие представлены игровые упражнения с нестандартными средствами математического развития. |
А.А. Смоленцева, О.В. Пустовойт |
|
5.
|
Игры – головоломки.
|
З. М. Михайлова,
Р.Л. Непомнящая
|
|
6.
|
Комплексные занятия в подготовительной группе детского сада. Воспитывает у детей стойкий интерес к математике, развивает память, внимание, мышление.
|
Т.М. Бодаренко
|
Динамика уровня математического развития детей в подготовительной группе.
|
МУНИЦИПАЛЬНОЕ АВТОНОМНОЕ ДОШКОЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ МУНИЦИПАЛЬНОГО ОБРАЗОВАНИЯ Светловский городской округ Детский сад №1 «Пчелка»
Тема: «Развитие логико-математических способностей у детей старшего дошкольного возраста» Выполнил воспитатель: Добрякова И.В. Развитие логико-математических способностей у детей старшего дошкольного возраста Каждый день мы сталкиваемся со множеством задач, решение которых требует от нас способности к логическому мышлению. Основы логического мышления закладываются ещё в детстве. С помощью логического мышления, человек может анализировать ситуации и выбирать самые наилучшие варианты действий в сложившихся условиях. Многие родители полагают, что главное при подготовке к школе – это познакомить ребенка с цифрами и научить его писать, считать, складывать и вычитать (на деле это обычно выливается в попытку выучить наизусть результаты сложения и вычитания в пределах 10). Однако при обучении математике по учебникам современных развивающих систем эти умения очень недолго выручают ребенка на уроках математики. Запас заученных знаний кончается очень быстро (через месяц-два), и несформированность собственного умения продуктивно мыслить (то есть самостоятельно выполнять указанные выше мыслительные действия на математическом содержании) очень быстро приводит к появлению «проблем с математикой». В то же время ребенок с развитым логическим мышлением всегда имеет больше шансов быть успешным в математике, даже если он не был заранее научен элементам школьной программы (счету, вычислениям и
Однако не следует думать, что развитое логическое мышление – это природный дар, с наличием или отсутствием которого следует смириться. Существует большое количество исследований, подтверждающих, что развитием логического мышления можно и нужно заниматься (даже в тех случаях, когда природные задатки ребенка в этой области весьма скромны). В 5-6 лет ребенок смотрит на мир широко открытыми глазами. Ему все интересно, его все манит и привлекает. Он постигает мир под девизом “Хочу все знать!”. Уровень развития мыслительных операций ребенка старшего дошкольного возраста помогает ему более осознанно и глубоко воспринимать и постигать имеющиеся сведения о мире, разбираться в них, устанавливать различные связи и зависимости. Развивать логическое мышление дошкольника целесообразнее всего в русле математического развития. Как научить маленького ребенка думать? Очевидно, что научить ребенка этому можно лишь в ситуации, требующей осмысления. В математике главное – научить мыслить, логически рассуждать, находить скрытые для непосредственного восприятия математические взаимосвязи и взаимозависимости и т.д. Именно поэтому, начинать надо не со счета, а с понимания математических отношений: больше, меньше, поровну. Необходимо развивать мышление ребенка, нужно научить его сравнивать, обобщать, анализировать, развивать речь. Так как механическое запоминание разнообразной информации, копирование взрослых рассуждений ничего не дает для развития мышления детей. В.А. Сухомлинский писал: “…Не обрушивайте на ребёнка лавину знаний…- под лавиной знаний могут быть погребены пытливость и любознательность. Умейте открыть перед ребёнком в окружающем мире что-то одно, но открыть так, чтобы кусочек жизни заиграл перед детьми всеми цветами радуги. Один из основных залогов успешного обучения детей – это использование в работе с дошкольниками занимательного наглядного материала. На занятиях большое внимание следует уделять его разнообразию, так как он способствует привлечению внимания детей, развивает наглядно-образное мышление, которое, в свою очередь, стимулирует познавательную активность ребёнка. И родители, и педагоги знают, что математика – это мощный фактор интеллектуального развития ребенка, формирования его познавательных и творческих способностей. Самое главное – это привить ребенку интерес к познанию. Для этого занятия должны проходить в увлекательной игровой форме. Поэтому обучение и развитие ребёнка должны быть непринужденными, осуществляться через свойственные конкретному возрасту виды деятельности и педагогические средства. Таким развивающим средством для старших дошкольников выступает игра. Несмотря на то, что игра постепенно перестает выступать в качестве ведущего вида деятельности в старшем дошкольном возрасте, но она не теряет развивающих функций. Развитие логического мышления включает в себя использование дидактических игр, смекалок, головоломок, решение различных логических игр и лабиринтов и вызывает у детей большой интерес. В этой деятельности у детей формируются важные качества личности: самостоятельность, находчивость, сообразительность, вырабатывается усидчивость, развиваются конструктивные умения. Дети учатся планировать свои действия, обдумывать их, догадываться в поиске результата, проявляя при этом творчество. Игры логического содержания помогают воспитывать у детей познавательный интерес, способствовать к исследовательскому и творческому поиску, желание и умение учиться. Дидактические игры как один из наиболее естественных видов деятельности детей и способствует становлению и развитию интеллектуальных и творческих проявлений, самовыражению и самостоятельности. Разновидностью математических игр и задач являются логические игры, задачи, упражнения. Они направлены на тренировку мышления при выполнении логических операций и действий. С целью развития мышления детей используют различные виды несложных задач и упражнений. Это задачи на нахождение пропущенной фигуры, продолжение ряда фигур, на поиск чисел, недостающих в ряду фигур (нахождение закономерностей, лежащих в основе выбора этой фигуры и т. д.) Следовательно, логико-математические игры это игры, в которых смоделированы математические отношения, закономерности, предполагающие выполнение логических операций и действий. В логико-математических играх и упражнениях используются специальный структурированный материал, позволяющий наглядно представить абстрактные понятия и отношения между ними. Кроме этого, таким играм свойственна познавательная и игровая мотивация, которая вносит оживление, стимулирует выбор ребенком необходимых практических и умственных результативных действий. В процессе логико-математических игр допустимы свободное взаимодействие и общение ребенка со взрослыми и сверстниками, что создает условия для проявления активности и самореализации личности ребенка в деятельности. Взрослый вызывает интерес к игре и поддерживает его, не подавляя инициативу ребенка. Итак, в заключении можно сделать вывод, что развитие логического мышления, умения классифицировать, обобщать, группировать предметы, строить графические модели, развитие интеллектуальных и личностных качеств, самовыражение и самостоятельность имеет важное значение для успешного умственного развития и последующего школьного обучения. Обучение детей классификации способствует успешному овладению более сложным способом запоминания – смысловой группировкой, с которой дети встречаются в школе. Развитие у дошкольников способности мыслить приводит к определенным изменениям в поведении и психике детей: возрастает самоконтроль и самостоятельность их деятельности. В процессе игры дети усваивают сложные математические понятия, учатся считать, читать и писать, а в развитии этих навыков ребенку помогают близкие люди – его родители и педагог. Обучая детей в процессе игры, идет стремление, чтобы радость от игровой деятельности постепенно перешла в радость учения. Учение должно быть радостным. СПИСОК ЛИТЕРАТУРЫ 1. Белкин А.С. Основы возрастной педагогики: Учебное пособие для студентов высш. пед. учебных заведений. – М.: Изд. центр “Академия”, 2005. 2. Консультации для воспитателей. Тема: Развитие логического мышления у дошкольников средствами логико-математических игр. Автор: Макарова Р.Х. http://www.moi-detsad.ru/konsultac553.html 3. Михайлова З.А., Носова Е.А. «Логико-математическое развитие дошкольников». – СПб.: ОООО «ИЗДАТЕЛЬСТВО «ДЕТСТВО-ПРЕСС», 2013. – 128 С. 4. Носова Е.А., Непомнящая Р.Л. Логика и математика для дошкольников. 5. Пантина Н.С. Выходные элементы психических структур в раннем детстве. /Вопросы психологии, № 3, 1993. 6. Смоленцева А.А., Суворова О.В. Математика в проблемных ситуациях для маленьких детей: Учебно-методическое пособие – СПб.: ОООО «ИЗДАТЕЛЬСТВО «ДЕТСТВО-ПРЕСС», 2010. – 112 с. 7. Статья с Фестиваля педагогических идей “Открытый урок”. Тема: Развитие элементарного логического мышления у детей старшего дошкольного возраста. http://ds82.ru/doshkolnik/4359-.html 8. Сухомлинский В.А. О воспитании. – М., 1985. жүктеу/скачать 24.2 Kb. Достарыңызбен бөлісу: |
Развитие элементов логического мышления посредством обучающих логико-математических игр
Введение
Актуальность темы. Логическое мышление формируется на основе образного и является высшей стадией развития мышления. Достижение этой стадии – длительный и сложный процесс, так как полноценное развитие логического мышления требует не только высокой активности умственной деятельности, но и обобщенных знаний об общих и существенных признаках предметов и явлений действительности, которые закреплены в словах. Не следует ждать, когда ребенку исполнится 14 лет, и он достигнет стадии формально – логических оᴨераций, когда его мышление приобретает черты, характерные для мыслительной деятельности взрослых. Начинать развитие логического мышления следует в дошкольном детстве.
Достижение этой стадии – длительный и сложный процесс, так как полноценное развитие логического мышления требует не только высокой активности умственной деятельности, но и обобщенных знаний об общих и существенных признаках предметов и явлений действительности, которые закреплены в словах. Не следует ждать, когда ребенку исполнится 14 лет, и он достигнет стадии формально – логических оᴨераций, когда его мышление приобретает черты, характерные для мыслительной деятельности взрослых. Начинать развитие логического мышления следует в дошкольном детстве.
Но зачем логика маленькому ребенку, дошкольнику? Дело в том, что на каждом возрастном этаᴨе создается как бы определенный «этаж», на котором формируются психические функции, важные для ᴨерехода следующему этапу. Итак, навыки, умения, приобретенные в дошкольный ᴨериод, будут служить фундаментом для получения знаний и развития способностей в более старшем возрасте – в школе. И важнейшим среди этих навыков является навык логического мышления, способность «действовать в уме». Ребенку, не овладевшему приемами логического мышления, труднее будет даваться учеба – решение задач, выполнение упражнений потребуют больших затрат времени и сил. В результате может пострадать здоровье ребенка, ослабнет, а то и вовсе угаснет интерес к учению.
Ребенку, не овладевшему приемами логического мышления, труднее будет даваться учеба – решение задач, выполнение упражнений потребуют больших затрат времени и сил. В результате может пострадать здоровье ребенка, ослабнет, а то и вовсе угаснет интерес к учению.
В целях развития логического мышления нужно предлагать ребенку самостоятельно производить анализ, синтез, сравнение, классификацию, обобщение, строить индуктивные и дедуктивные умозаключения.
Овладев логическими оᴨерациями, ребенок станет более внимательным, научится мыслить ясно и четко, сумеет в нужный момент сконцентрироваться на сути проблемы и сможет убедить других в своей правоте. Учиться станет легче, а значит, и процесс учебы, и сама школьная жизнь будут приносить радость и удовлетворение.
Данную проблему рассматривали такие отечественные и зарубежные педагоги-психологи как Л.С.Выготского, П.П.Блонского, П.П.Гольперина, С.Л.Рубинштейна, В.В.Давыдова, А.И.Мещерякова, И.А.Менчинской, Д.Б. Эльконина, А.В. Запорожца, М.Монтессори и другие.
Запорожца, М.Монтессори и другие.
Проанализировав методическую литературу по данной проблеме, была выделена цель исследования – рассмотреть логико-математические игры в работе с детьми старшего дошкольного возраста.
В соответствии с целью исследования были определены следующие задачи:
1.Рассмотреть представления о возрастных особенностях мышления у старших дошкольников.
2. Изучить формирование и развитие логической сферы детей старшего дошкольного возраста.
3. Рассмотреть логико-математические игры как средство формирования логического мышления у старших дошкольников.
Объектом исследования является мышление старших дошкольников.
Предметом исследования являются логико-математические игры как средство формирования логического мышления.
Методы исследования: теоретический анализ научных источников и литературы по теме исследования.
Структура работы: введение, две главы, выводы по главам, заключение список литературы.
Период от рождения до поступления в школу является, по признанию специалистов всего мира, возрастом наиболее стремительного физического и психологического развития ребенка, первоначального формирования физических и психологических качеств, необходимых человеку в течение всей последующей жизни, качеств и свойств, делающих его человеком. [5, 136 с.]
Любопытствующие вопросы становятся естественным сопровождением становления психики ребенка. Чтобы самостоятельно ответить на них, ребенок должен обратиться к процессу мышления. С помощью мышления мы получаем знания, которые не могут дать органы чувств. Мышление соотносит данные ощущений и восприятий, сопоставляет, различает и раскрывает отношения между окружающими явлениями. Результатом мышления является мысль, выраженная в слове.
Согласно концепции Л.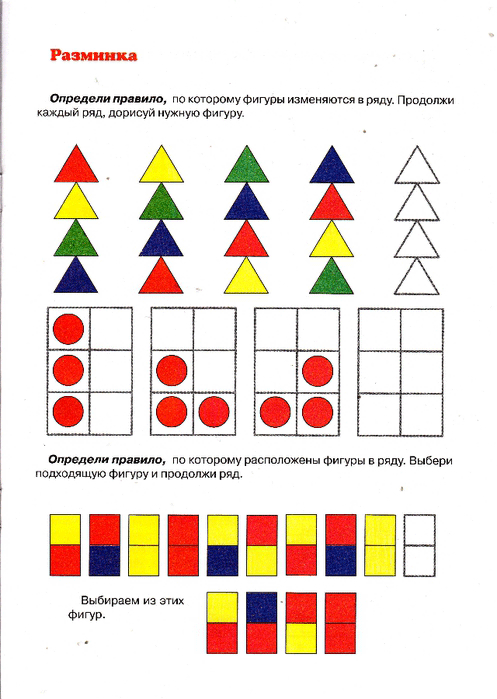 С.Выготского, в переходный период от дошкольного к младшему школьному возрасту происходит перестройка структуры сознания, и благодаря этому все другие психические процессы интеллектуализируются. Оценивая подсменные возможности организованного обучения, Л.С. Выготский писал, что «обучение может дать в развитии больше, чем то, что содержится в его непосредственных результатах. Приложенное к одной точке в сфере детской мысли, оно видоизменяет и перестраивает многие другие точки. Оно может иметь в развитии отдаленное, а не только ближайшие последствия». [5, 210 с.]
С.Выготского, в переходный период от дошкольного к младшему школьному возрасту происходит перестройка структуры сознания, и благодаря этому все другие психические процессы интеллектуализируются. Оценивая подсменные возможности организованного обучения, Л.С. Выготский писал, что «обучение может дать в развитии больше, чем то, что содержится в его непосредственных результатах. Приложенное к одной точке в сфере детской мысли, оно видоизменяет и перестраивает многие другие точки. Оно может иметь в развитии отдаленное, а не только ближайшие последствия». [5, 210 с.]
Для дошкольного возраста характерны следующие формы мышления:
Наглядно-действенное – форма мышления, манипулирующая предметной сферой. Оно характерно для детей до 1,5 лет.
На развитие наглядно-действенного мышления дошкольников работают картинки, пазлы, детали конструктора “Лего”, разные модели кубика Рубика, головоломки из подвижно сцепленных колец, треугольников и других фигур.
Как пишет детский психолог В.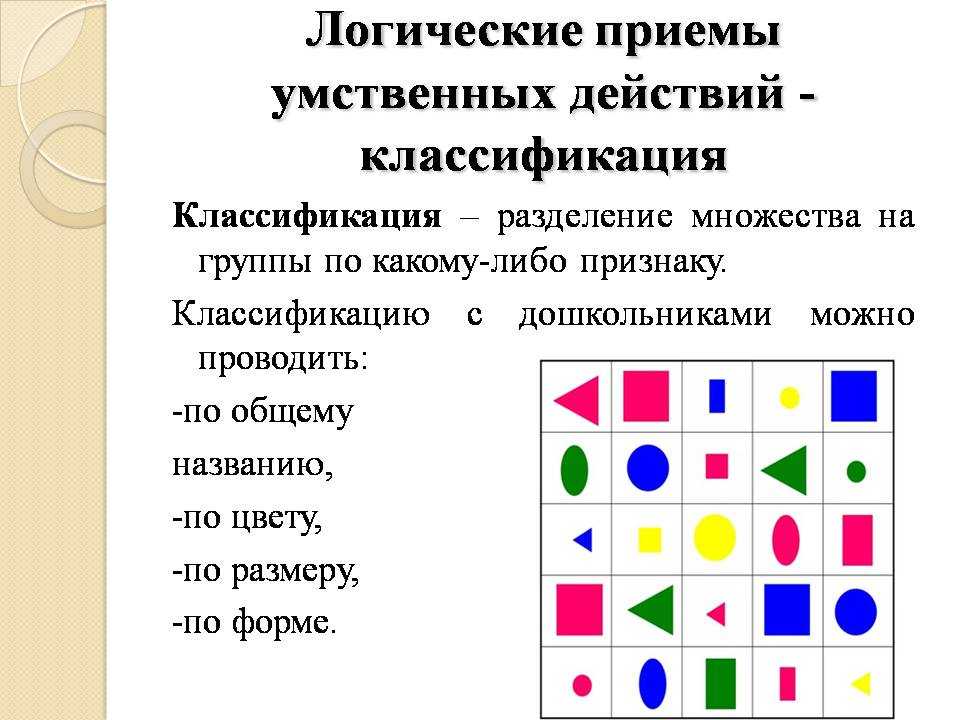 С. Мухина, к старшему дошкольному возрасту появляются задачи нового типа, где результат действия будет не прямым, а косвенным и для его достижения ребенку необходимо будет учитывать связи между двумя или несколькими явлениями, происходящими одновременно или последовательно. Например, такие задачи возникают в играх с механическими игрушками (если поместить шарик в определенном месте игрового поля и определенным образом дернуть за рычажок, то шарик окажется в нужном месте), в конструировании (от величины основания постройки зависит ее устойчивость) и т. д. [3, 105 с.]
С. Мухина, к старшему дошкольному возрасту появляются задачи нового типа, где результат действия будет не прямым, а косвенным и для его достижения ребенку необходимо будет учитывать связи между двумя или несколькими явлениями, происходящими одновременно или последовательно. Например, такие задачи возникают в играх с механическими игрушками (если поместить шарик в определенном месте игрового поля и определенным образом дернуть за рычажок, то шарик окажется в нужном месте), в конструировании (от величины основания постройки зависит ее устойчивость) и т. д. [3, 105 с.]
Наглядно-образное – задачи решаются с помощью существующего, реального объекта. Формирование этой формы мышления активно происходит в возрасте от 1,5 – до 5 лет.
При решении подобных задач с косвенным результатом дети четырех-пяти лет начинают переходить от внешних действий с предметами к действиям с образами этих предметов, совершаемым в уме. Так развивается наглядно-образное мышление, которое опирается на образы: ребенку необязательно брать предмет в руки, достаточно отчетливо представить его. В процессе наглядно-образного мышления идет сравнение зрительных представлений, вследствие чего задачка решается.
В процессе наглядно-образного мышления идет сравнение зрительных представлений, вследствие чего задачка решается.
Возможность решения задач в уме возникает благодаря тому, что образы, которыми пользуется ребенок, приобретают обобщенный характер. То есть в них отображаются не все особенности предмета, а только те, которые существенны для решения определенной задачи. То есть в сознании ребенка возникают схемы, модели. Особенно ярко модельно-образные формы мышления развиваются и проявляются в рисовании, конструировании и других видах продуктивной деятельности.
Так, детские рисунки в большинстве случаев представляют собой схему, в которой передается связь основных частей изображенного предмета, и отсутствуют его индивидуальные черты. Скажем, при срисовывании домика на рисунке изображается основание и крыша, при этом расположение, форма окон, дверей, какие-то детали интерьера не учитываются.
Например, с пяти лет ребенок может найти в помещении спрятанный предмет, пользуясь отметкой на плане, выбрать нужный путь в разветвленной системе дорожек, основываясь на схеме типа географической карты.
Овладение моделями выводит на новый уровень способы получения детьми знаний. Если при словесном объяснении ребенок не всегда может понять, скажем, некоторые первичные математические действия, звуковой состав слова, то с опорой на модель он это сделает легко.
Образные формы обнаруживают свою ограниченность, когда перед ребенком возникают задачи, которые требуют выделения таких свойств и отношений, которые нельзя наглядно представить. Такой тип задач описал знаменитый швейцарский психолог Ж.Пиаже и назвал их “задачи на сохранение количества вещества”. Например, ребенку предъявляется два одинаковых шарика из пластилина. Один из них на глазах ребенка превращается в лепешку. Ребенка спрашивают, где пластилина больше: в шарике или лепешке. Дошкольник отвечает, что в лепешке. [1, 25 с.]
При решении подобных задач ребенок не может независимо рассмотреть наглядно происходящие с объектом перемены (например, изменение площади) и остающееся постоянным количество вещества. Ведь для этого требуется переход от суждений на основе образов к суждениям на основе словесных понятий.
Абстрактно-логическое – мышление абстракциями — категориями, которых нет в природе. Эта форма мышления начинает формироваться у дошкольников с 5 лет.
Абстрактно – логическое мышление самое сложное, оно оперирует не конкретными образами, а сложными отвлеченными понятиями, выраженными словами. В дошкольном возрасте можно говорить лишь о предпосылках развития этого вида мышления.
Слово начинает использоваться как самостоятельное средство мышления по мере усвоения ребенком выработанных человечеством понятий – знаний об общих и существенных признаках предметов и явлений действительности, закрепленных в словах. Взрослые часто ошибаются, считая, что слова имеют для них и дошкольников один и тот же смысл. Для ребенка используемые слова – это слова-представления. Скажем, слово “цветок” может в сознании ребенка быть крепко связанным с образом конкретного цветка (например, розы), и предъявленный кактус в качестве цветка не рассматривается. На протяжении дошкольного возраста ребенок постепенно переходит от единичных понятий к общим. [13, 31 с.]
[13, 31 с.]
Проблема развития детского мышления является предметом научного исследования психологов и педагогов в течение многих лет.
Современная концепция общего образования во главу утла ставит идею развития личности ребенка, формирования его творческих способностей, воспитания важных личностных качеств. Если до недавнего времени основное внимание ученых было обращено на школьный возраст, где, как казалось, ребенок приобретает необходимые каждому знания и умения, развивает свои силы и способности, то теперь положение коренным образом изменилось. Значительную роль в этом сыграл “информационный взрыв” – знамение нашего времени. Сегодняшние дети умнее своих предшественников – это признанный всеми факт. Это связано в первую очередь со средствами массовой информации, опоясавшими мир каналами связи, с утра до ночи льющими поток разнообразных знаний в детские умы. Сегодня становится все больше детей с ярким общим интеллектуальным развитием, их способности постигать сложный современный мир проявляются очень рано – в 3–4 года.
Дошкольное детство – небольшой отрезок в жизни человека. Но за это время ребенок приобретает значительно больше, чем за всю последующую жизнь. “Программа” дошкольного детства поистине огромна: овладение речью, мышлением, воображением, восприятием и т.п.
В психологии есть такое понятие: сензитивность (чувствительность к воздействиям определенного рода). Так, наибольшая сензитивность к языку у детей в 2–3 года, 5-летние дети легче и лучше, чем дети другого возраста, обучаются чтению. К сожалению, в дошкольном детстве пока не выделены все сенситивные периоды, в частности обучения игре в шахматы. Но достоверно известно одно: не стоит пропускать эти годы, иначе происходит необратимый процесс. Упущено время – потеряны возможности легко и безболезненно усвоить главное для этого возраста. Дошкольники необычайно чувствительны к разного рода воздействиям, и если мы не замечаем результатов каких-то воздействий, то это еще не свидетельствует, что они ничего не значат. Дети, как губка, впитывают впечатления, знания, но далеко не сразу выдают результаты. Возможности маленького человека велики и путем специально организованного обучения можно сформировать у дошкольников такие знания и умения, которые ранее считались доступными лишь детям значительно более старших возрастов.
Возможности маленького человека велики и путем специально организованного обучения можно сформировать у дошкольников такие знания и умения, которые ранее считались доступными лишь детям значительно более старших возрастов.
И это очень важно, так как школа в наше время предъявляет к малышу, оказавшемуся на ее пороге, массу серьезных требований. С первых же дней учебы первоклассник должен ответственно к ней относиться, подчиняться требованиям и правилам школьной жизни, должен обладать развитыми волевыми качествами – без них он не сможет сознательно регулировать свое поведение, подчинять его решению учебных задач, организованно вести себя на уроке. Произвольным, управляемым должно быть не только внешнее поведение, но и умственная деятельность ребенка – его внимание, память, мышление.
Ребенку необходимо уметь наблюдать, слушать, запоминать, добиваться решения поставленной учителем задачи. И еще надо последовательно овладевать системой понятий, а для этого требуется развитие отвлеченного, логического мышления. К тому же наибольшие трудности в начальной школе испытывают не те дети, которые имеют к концу дошкольного возраста недостаточный объем знаний и навыков, а те, которые проявляют интеллектуальную пассивность, у которых отсутствует желание и привычка думать, решать задачи. А это закладывается с раннего детства.
К тому же наибольшие трудности в начальной школе испытывают не те дети, которые имеют к концу дошкольного возраста недостаточный объем знаний и навыков, а те, которые проявляют интеллектуальную пассивность, у которых отсутствует желание и привычка думать, решать задачи. А это закладывается с раннего детства.
Первая особенность мышления — его опосредованный характер. То, что человек не может познать прямо, непосредственно, он познаёт косвенно, опосредованно: одни свойства через другие, неизвестное — через известное. Мышление всегда опирается на данные чувственного опыта — ощущения, восприятия, представления — и на ранее приобретённые теоретические знания. Косвенное познание и есть познание опосредованное.
Вторая особенность мышления — его обобщённость. Обобщение как познание общего и существенного в объектах действительности возможно потому, что все свойства этих объектов связаны друг с другом. Общее существует и проявляется лишь в отдельном, в конкретном.
Полуторагодовалый ребенок может прогнозировать и указывать направление движения, место расположения знакомых предметов, решать в сенсомоторном плане простейшие задачи, связанные с преодолением препятствий на пути к желанной цели. После полуторагодовалого возраста формируется реакция выбора объектов по наиболее ярким и простым признакам, прежде .всего по форме.
На протяжении раннего детства происходит постепенный переход от наглядно-действенного к наглядно-образному мышлению, которое отличается тем, что действия с материальными предметами здесь заменяются действиями с их образами. Внутреннее развитие мышления в свою очередь идет по двум основным направлениям: развитие интеллектуальных операций и формирование понятий.
Способность решать задачи в уме несколько отстает в этом возрасте от развития способности решать задачи в практическом плане. Вначале обобщения, лежащие в основе формирования понятий, производятся без пользования словом и проявляются в практике как перенос предметного действия с одних объектов и ситуаций на другие, отличающиеся от тех, где соответствующее действие исходно было образовано. На этой стадии ребенок может абстрагировать и выделять форму и цвет предмета. При решении задачи группировки предметов по их признакам дети в первую очередь ориентируются на размер и цвет предметов. Около двух лет основанием для выделения предметов становятся многие существенные и несущественные признаки: зрительные, слуховые, осязательные. В возрасте примерно 2,5 лет предметы уже классифицируются детьми по каким-либо существенным признакам, им присущим. В качестве таких признаков детьми последовательно выделяются и используются цвет, форма и величина предмета.
На этой стадии ребенок может абстрагировать и выделять форму и цвет предмета. При решении задачи группировки предметов по их признакам дети в первую очередь ориентируются на размер и цвет предметов. Около двух лет основанием для выделения предметов становятся многие существенные и несущественные признаки: зрительные, слуховые, осязательные. В возрасте примерно 2,5 лет предметы уже классифицируются детьми по каким-либо существенным признакам, им присущим. В качестве таких признаков детьми последовательно выделяются и используются цвет, форма и величина предмета.
Заметим, что в это время речь ребенка с его мышлением еще не связана. Понимание и говорение внешне представляют собой акты общения, а внутренне строятся на простых переходах от знака — воспринятого слова к значению — конкретному предмету, который это слово обозначает, или наоборот — от значения к знаку. Со второй половины раннего дошкольного возраста, т. е. приблизительно с 1,5— 2 лет, значение слова постепенно становится обобщением, насыщается смыслом, абстрагируется, отделяется от конкретного содержания.
Первый из рассмотренных этапов развития связан с наглядно-действенным мышлением, которое практически осуществляется независимо от речи, второй же представляет собой начало формирования и функционирования образного, точнее, наглядно-образного мышления, так как образ сам по себе представляет некоторое абстрагирование свойств предметов. В образе знак связан со значением, но уже отделен от непосредственного восприятия обозначаемого им предмета. За значением детского слова в дошкольном детстве зачастую скрывается обобщенное, образное восприятие действительности.
Хронологически начало формирования у детей наглядно-образного мышления приурочено к концу раннего возраста и по времени обычно совпадает с двумя событиями: становлением элементарного самосознания и началом развития способности к произвольной саморегуляции. Сопровождается все это достаточно развитым воображением ребенка. Сначала, когда ребенок находится еще на стадии наглядно-действенного мышления, он имеет возможность познавать окружающий мир, решать задачи, наблюдая за ним и производя реальные действия с предметами, находящимися в поле его зрения. Затем появляются образы этих предметов и возникает способность оперировать ими. Наконец, образ предмета может быть назван и поддержан в сознании ребенка не только внешними предметными сигналами, но и произнесенным словом. Это знаменует собой переход от наглядно-действенного к наглядно-образному мышлению, которое в свою очередь предшествует и готовит почву для становления к концу дошкольного детства высшей формы мышления — словесно-логической.
Затем появляются образы этих предметов и возникает способность оперировать ими. Наконец, образ предмета может быть назван и поддержан в сознании ребенка не только внешними предметными сигналами, но и произнесенным словом. Это знаменует собой переход от наглядно-действенного к наглядно-образному мышлению, которое в свою очередь предшествует и готовит почву для становления к концу дошкольного детства высшей формы мышления — словесно-логической.
Словесно-логическое мышление ребенка, которое начинает развиваться в конце дошкольного возраста, предполагает уже умение оперировать словами и понимать логику рассуждений. Способность использовать словесные рассуждения при решении ребенком задач можно обнаружить уже в среднем дошкольном возрасте, но наиболее ярко она проявляется в феномене эгоцентрической речи, описанном Ж.Пиаже. Другое явление, открытое им же и относящееся к детям данного возраста, нелогичность детских рассуждений при сравнении, например, величины и количества предметов — свидетельствует о том, что даже к концу дошкольного детства, т е. к возрасту около 6 лет, многие дети еще совершенно не владеют логикой.
к возрасту около 6 лет, многие дети еще совершенно не владеют логикой.
Развитие словесно-логического мышления у детей проходит как минимум два этапа. На первом из них ребенок усваивает знания слов, относящихся к предметам и действиям, научается пользоваться ими при решении задач, а на втором этапе им познается система понятий, обозначающих отношения, и усваиваются правила логики рассуждений. Последнее обычно относится уже к началу школьного обучения.
Н.Н. Поддьяков специально изучал, как идет у детей дошкольного возраста формирование внутреннего плана действий, характерных для логического мышления, и выделил шесть этапов развития этого процесса от младшего до старшего дошкольного возраста [14, 84 с.].
Эти этапы следующие.
1. Ребенок еще не в состоянии действовать в уме, но уже способен с помощью рук, манипулируя вещами, решать задачи в наглядно-действенном плане, преобразуя соответствующим образом проблемную ситуацию.
2. В процесс решения задачи ребенком уже включена речь, но она используется им только для называния предметов, с которыми он манипулирует в наглядно-действенном плане. В основном же ребенок по-прежнему решает задачи «руками и глазами», хотя в речевой форме им уже может быть выражен и сформулирован результат выполненного практического действия.
В основном же ребенок по-прежнему решает задачи «руками и глазами», хотя в речевой форме им уже может быть выражен и сформулирован результат выполненного практического действия.
3. Задача решается в образном плане через манипулирование представлениями объектов. Здесь, вероятно, осознаются и могут быть словесно обозначены способы выполнения действий, направленных на преобразование ситуации с целью найти решение поставленной задачи. Одновременно происходит дифференциация во внутреннем плане конечной (теоретической) и промежуточных (практических) целей действия. Возникает элементарная форма рассуждения вслух, не отделенного еще от выполнения реального практического действия, но уже направленного на теоретическое выяснение способа преобразования ситуации или условий задачи.
4. Задача решается ребенком по заранее составленному, продуманному и внутренне представленному плану. В его основе — память и опыт, накопленные в процессе предыдущих попыток решения подобного рода задач.
5. Задача решается в плане действий в уме с последующим выполнением той же самой задачи в наглядно-действенном плане с целью подкрепить найденный в уме ответ и далее сформулировать его словами.
Задача решается в плане действий в уме с последующим выполнением той же самой задачи в наглядно-действенном плане с целью подкрепить найденный в уме ответ и далее сформулировать его словами.
6. Решение задачи осуществляется только во внутреннем плане с выдачей готового словесного решения без последующего обращения к реальным, практическим действиям с предметами.
Важный вывод, который был сделан Н.Н.Поддьяковым из исследований развития детского мышления, заключается в том, что у детей пройденные этапы и достижения в совершенствовании мыслительных действий и операций полностью не исчезают, но преобразуются, заменяются новыми, более совершенными. Они трансформируются в «структурные уровни организации процесса мышления» и «выступают как функциональные ступени решения творческих задач». При возникновении новой проблемной ситуации, или задачи, все эти уровни снова могут включаться в поиск процесса ее решения как относительно самостоятельные и вместе с тем как составляющие логические звенья целостного процесса поиска ее решения. Иными словами, детский интеллект уже в этом возрасте функционирует на основе принципа системности. В нем представлены и при необходимости одновременно включаются в работу все виды и уровни мышления: наглядно-действенное, наглядно-образное и словесно-логическое. [5, 175 с.]
Иными словами, детский интеллект уже в этом возрасте функционирует на основе принципа системности. В нем представлены и при необходимости одновременно включаются в работу все виды и уровни мышления: наглядно-действенное, наглядно-образное и словесно-логическое. [5, 175 с.]
В дошкольном возрасте начинается развитие понятий, в итоге чего примерно к подростковому возрасту у детей полностью оформляется словесно-логическое, понятийное или абстрактное мышление (его иногда называют теоретическим). Как же идет этот специфический процесс?
Трех – четырехлетний ребенок может использовать слова, которые мы, взрослые, анализируя смысловую структуру языка и речи, называем понятиями. Однако использует он их иначе, чем взрослый, зачастую не полностью понимая их значение. Ребенок пользуется ими как ярлыками, заменяющими действие или предмет. Ж. Пиаже назвал эту стадию рече-мыслительного развития детей, ограничив ее 2—7 годами, дооперациональной по той причине, что здесь ребенок еще фактически не знает и практически не применяет прямых и обратных операций, которые, в свою очередь, функционально связаны с пользованием понятиями, по крайней мере в их начальной, конкретной форме.
Развитие мышления в детском возрасте представляет особую форму труда, которую осваивает ребенок. Это умственный труд. Труд сложный и интересный. Кого-то он может напрягать и пугать, а у кого-то умственный труд связан с приятной эмоцией удивления. Удивления, открывающего дверь в мир, который можно познать.
§ 1.2. Особенности использования логико-математических игр в процессе развития мыслительных операций у дошкольников Формирование логических приемов является важным фактором, непосредственно способствующим развитию процесса мышления старшего дошкольника. Практически все психологические исследования, посвященные анализу способов и условий развития мышления ребенка, единодушны в том, что методическое руководство этим процессом не только возможно, но и является высокоэффективным, т. е. при организации специальной работы по формированию и развитию логических приемов мышления наблюдается значительное повышение результативности этого процесса независимо от исходного уровня развития ребенка [6, с. 13].
13].
Рассмотрим возможности активного включения в процесс математического развития ребенка старшего дошкольного возраста различных приемов умственных действий на математическом материале.
Сериация – построение упорядоченных возрастающих или убывающих рядов. Классический пример сериации: матрешки, пирамидки, вкладные мисочки и т. д. Сериации можно организовать по размеру: по длине, по высоте, по ширине – если предметы одного типа (куклы, палочки, ленты, камешки и т. д.) и просто «по величине» (с указанием того, что считать «величиной») – если предметы разного типа (рассадить игрушки по росту). Сериации могут быть организованы по цвету: по степени интенсивности окраски.
Анализ – выделение свойств объекта, выделение объекта из группы или выделение группы объектов по определенному признаку.
Например, задан признак: кислый. Сначала у каждого объекта множества проверяется наличие или отсутствие этого признака, а затем они выделяются и объединяются в группу по признаку «кислые».
Синтез – соединение различных элементов (признаков, свойств) в единое целое. В психологии анализ и синтез рассматриваются как взаимодополняющие друг друга процессы (анализ осуществляется через синтез, а синтез – через анализ).
Логические игры предоставляют возможность развивать у детей произвольность таких психических процессов, как внимание, память, речь. Логико-математические игровые задания развивают у детей смекалку, находчивость, сообразительность, наблюдательность, самостоятельность, требуют умения построить высказывание, суждение, умозаключение; включают не только умственные, но и волевые усилия – организованность, выдержку, умение соблюдать правила игры, подчинять свои интересы интересам коллектива.
Логико-математические игры и упражнения позволяют на доступном детям математическом материале, в опоре на жизненный опыт, строить правильные суждения без предварительного теоретического освоения самих законов и правил логики. В процессе логических упражнений дети практически учатся сравнивать математические объекты, выполнять простейшие виды анализа и синтеза, устанавливать связи между родовыми и видовыми понятиями.
В дошкольном возрасте предлагаемые детям логические упражнения не требуют вычислений, а лишь побуждают выполнять правильные суждения и приводить несложные доказательства. Сами же упражнения носят занимательный характер, поэтому они содействуют возникновению интереса у детей к процессу мыслительной деятельности (одна из самых важных задач учебно-воспитательного процесса старших дошкольников) [11, 128 с.].
Логические упражнения представляют собой одно из средств, с помощью которого происходит формирование у детей правильного мышления. Когда говорят о логическом мышлении, то имеют в виду мышление, по содержанию находящееся в полном соответствии с объективной реальностью.
Логические упражнения позволяют на доступном детям математическом материале, в опоре на жизненный опыт строить правильные суждения без предварительного теоретического освоения самих законов и правил логики.
В процессе логических упражнений дети практически учатся сравнивать математические объекты, выполнять простейшие виды анализа и синтеза, устанавливать связи между родовыми и видовыми понятиями.
Чаще всего предлагаемые детям логические упражнения не требуют вычислений, а лишь заставляют детей выполнять правильные суждения и приводить несложные доказательства. Сами же упражнения носят занимательный характер, поэтому они содействуют возникновению интереса у детей к процессу мыслительной деятельности. А это одна из кардинальных задач учебно-воспитательного процесса старших дошкольников.
Вследствие того, что логические упражнения представляют собой упражнения в мыслительной деятельности, а мышление старших дошкольников в основном конкретное, образное, то на уроках применяют наглядность. В зависимости от особенностей упражнений в качестве наглядности применяют рисунки, чертежи, краткие условия задач, записи терминов-понятий.
Выводы по I главе При проведении непосредственно образовательной и самостоятельной деятельности по математике для детей дошкольного возраста необходимо использовать логико-математические игры, так как это приведёт к развитию творческих и интеллектуальных способностей детей, к развитию их воображения, логического мышления и повышению уровня знаний по развитию элементарных математических представлений.
Продолжение статьи
Список используемой литературы1. Беженова М. Математическая азбука. Формирование элементарных математических представлений. – М.: Эксмо, СКИФ, 2005 – 64 с.
2. Белошистая А.В. Готовимся к математике. Методические рекомендации для организации занятий с детьми 5-6 лет. – М.: Ювента, 2006 – 239 с.
3. Белошистая А.В. Формирование и развитие математических способностей дошкольников: Вопросы теории и практики: Курс лекций для студ. дошк. факультетов высш. учеб. заведений. – М.: Гуманит. изд. центр ВЛАДОС, 2003. – 400 с.
4. Волчкова В.Н., Степанова Н.В. Конспекты занятий в старшей группе детского сада. Математика. Практическое пособие для воспитателей и методистов ДОУ. – М.: ТЦ «Учитель», 2007 – 132 с.
5. Гогоберидзе А.Г. Дошкольная педагогика с основами методик воспитания и обучения: учебник для бакалавров по направлению “Педагогика” / А.Г.Гогоберидзе, О.В.Солнцева. – Санкт-Петербург : Питер, 2013. – 464 с.
– 464 с.
6.Касабуцкий, Н. И. Давайте поиграем: математические игры для детей: книга для воспитателей детского сада и родителей / Н.И.Касабуцкий, Г.Н.Скобелев, А. А. Столяр, Т. М. Чеботаревская. – М. : Просвещение, 2001 – 84 с.
7.Метлина Л.С. Занятия по математике в детском саду. Пособие для воспитателя детского сада. – М.: «Просвещение», 1985.
8. Михайлова З.А. Игровые занимательные задачи для дошкольников 2-е изд. – М.: Просвещение, 1990. – 94 с.
9. Михайлова З.А. и др. Теории и технологии математического развития детей дошкольного возраста. – СПб.: «ДЕТСТВО-ПРЕСС», 2008.- 384 с.
10. Носова Е.А., Непомнящая Р.Л. Логика и математика для дошкольников. – М.: Детство-Пресс, 2007 – 79 с.
11. Петерсон Л.Г., Кочемасова Е.Е. Игралочка. Практический курс математики для дошкольников. Методические рекомендации. – М.: Ювента, 2006 – 224 с.
12.Столяр А.А. Давайте поиграем. Математические игры для детей 5-6 лет. – М.: «Просвещение», 1991 – 84 с.
13. Сычева Г.Е. Формирование элементарных математических представлений у дошкольников. – М.: Книголюб, 2007 – 104 с.
Сычева Г.Е. Формирование элементарных математических представлений у дошкольников. – М.: Книголюб, 2007 – 104 с.
14. Щербакова Е.И. Методика обучения математике в детском саду. – М.: Издательский центр «Академия», 2004 – 272 с.
15. Шалаева Г. Математика для маленьких гениев дома и в детском саду. – М.: АСТ, Слово, 2009 – 208 с.
Развитие математических способностей и логического мышления у детей
Чтобы ученик успешно обучался в школе математике, нужно постараться обучить его некоторым азам еще в дошкольном возрасте. Основными знаниями являются счет в прямом и обратном направлении, графическое изображение и узнавание цифр, представления о составе числа. Полезны будут домашние занятия в виде игр. Как научить ребенка составу числа до 10, подскажут рекомендации педагогов.
Читать далее…
Счетные палочки для малышей – что это? Учеба или игра? Ответить помогут психологи, которые утверждают, что детское мышление можно развивать даже с помощью такого нехитрого приспособления, как палочки для счета. С ними можно познавать мир, развивать математические способности, формировать интеллект вашего чада. Главная задача родителей – сделать обучение для крохи увлекательной и интересной игрой.
С ними можно познавать мир, развивать математические способности, формировать интеллект вашего чада. Главная задача родителей – сделать обучение для крохи увлекательной и интересной игрой.
Читать далее…
Каждый родитель стремится максимально подготовить свое чадо к школьному обучению. Прилагается много усилий на посещение подготовительных курсов, где используются специальные методики. Ребенку дается максимум знаний и умений, причем особого внимания заслуживает математика для дошкольников. Зная программу детской математики, родители могут начать домашние занятия с детками уже в раннем возрасте.
Читать далее…
В современном обучении детей все более популярными становятся методики, основанные на естественной потребности ребенка: играть, творить. Педагоги рекомендуют использовать наиболее простые и эффективные из них в домашнем обучении. Одной из таких методик, показавших хороший результат, стали “палочки Кюизенера”. Плюсом является то, что палочки легко изготовить в домашних условиях.
Плюсом является то, что палочки легко изготовить в домашних условиях.
Читать далее…
Нужно ли развивать абстрактное мышление у младших школьников? Достаточно ли школьных занятий? Cпециалисты считают, что абстрактное мышление необходимо маленьким ученикам, так как дает возможность успешно овладевать теми науками, которые базируются на нем: математика, физика, астрономия. Родители могут помочь детям развить все формы абстрактного мышления при помощи специальных упражнений.
Читать далее…
Как научить ребенка считать дома? Многие родители задаются этим вопросом, как только малыш начинает подрастать. Обучение счёту помогает развивать логическое мышление, интеллект. Самым оптимальным периодом является возраст 2 – 3 лет, а начинать нужно со счета предметов в пределах от 1 до 5. Для обучения использовать повседневные события, игры, стихи, считалочки.
Читать далее. ..
..
Довольно сложная для родителей задача – ознакомление детей с геометрическими фигурами – решается легко и быстро на домашних занятиях, если знать требования к уровню знаний дошколят и использовать эффективные средства обучения. Формированию у детей представлений о геометрических фигурах помогут игры, стихи, развивающие книжки, мультики.
Читать далее…
Чтобы успешно обучаться в начальной школе, анализировать учебные тексты, решать задачи, составлять рассказы, детям необходимо иметь хорошо развитое логическое мышление. Логика развивается постепенно, поэтому начинать работу надо с младшего возраста. Для достижения лучшего результата родители должны сделать интеллектуальное общение с ребенком образом жизни. Им помогут в работе с детьми интересные логические игры, тренировочные упражнения, решение головоломок, ребусов, шарад.
Читать далее…
Ориентировка в пространстве ‒ важный навык для дошкольников, он является основой для будущего обучения письму и математике. В методике развития пространственных представлений накоплено много игр и упражнений, которые помогут родителям в домашних занятиях с детьми.
В методике развития пространственных представлений накоплено много игр и упражнений, которые помогут родителям в домашних занятиях с детьми.
Читать далее…
Ребенок все чаще и чаще задает вопросы: “А когда мы пойдем в парк?”, “А когда у меня следующая тренировка?”, “А когда папа не пойдет на работу и будет играть со мной?”. Можно ответить: “В воскресенье”, “В четверг” и т.п. Но если ребенок этого не понимает, приходится очень долго объяснять, когда наступит этот день. А может пора с ребенком выучить дни недели? И тогда вы будете со своим чадом разговаривать на одном языке.
Читать далее…
Зачастую родители стремясь научить всему своего малыша как можно раньше упускают, что любые знания должны усваиваться в определенной последовательности. Можно научить маленького ребенка пользоваться часами, но не будет понимания самого течения времени. Когда, как и в какой последовательности обучать ребенка узнавать время по часам?
Читать далее. ..
..
Хотите чтобы ребенок вырос умным? Тогда система игр Дьенеша для Вашего ребенка. Играя блоками Дьенеша дети получают базовые знания не только о свойствах предметов (цвет, форма, размер), но также учатся сравнивать их, группировать и объединять в множества по определенному признаку. Также эти блоки можно применить для развития мелкой моторики, воображения или в активных играх.
Читать далее…
Начните играть с ребенком в одну из игр и Вы не заметите как сами увлеклись: фантазия подсказывает продолжение сказочных сюжетов, а ребенок, глядя на Вас разгадывает загадки и выполняет задания, которые порой ставят в тупик даже взрослого.
Читать далее…
Как многие авторы методик раннего развития детей, инженер-физик Вячеслав Воскобович создавал свои игры для собственных детей. Он постарался совместить игру и обучение. А положив в основу игр сказочный сюжет простимулировал ребенка доводить дело до конца, несмотря на усложнение заданий по мере продвижения к цели.
Читать далее…
Цикл «Занимательная математика» посвящен деткам увлекающимся математикой и родителям, которые уделяют время развитию своих детей, «подкидывая» им интересные и занимательные задачки, головоломки. Эта статья посвящена правилу Гаусса, рассмотрены задачки и решения по этой теме.
Читать далее…
Логический математический интеллект для детей
Амина Решма
Чтение через 3 мин
Что такое логический математический интеллект?
Логический математический интеллект — это один из восьми видов интеллекта или способностей, определенных Говардом Гарднером в его книге «Структура разума: теория множественного интеллекта». Определяется как « Способность логически анализировать ситуации или проблемы, находить решения, проводить научные исследования и легко решать логические/математические операции. ” 1
” 1
Проще говоря, логико-математический интеллект — это способность понимать, манипулировать и применять логику, числа и рассуждения, чтобы понять, как что-то работает, обнаружить существующую структуру или шаблон или даже создать что-то.
Люди с высоким уровнем логического математического интеллекта используют логику для анализа данных и поиска причинно-следственных связей.
Они часто избегают работы с субъективной информацией в пользу четких фактов и достоверных данных. Люди с математическим интеллектом также обладают сильной способностью делать выводы и делать наблюдения. Их разум работает как компьютер в фоновом режиме, несмотря на то, что временами они кажутся сбитыми с толку. 1
Математика, информатика, технология, черчение, дизайн, химия и другие «точные науки» популярны среди детей с высоким логическим математическим интеллектом. Вы можете заметить, что они предпочитают логический порядок в инструкциях и лучше работают в структурированных, организованных условиях. 1
1
Какие характеристики отличают людей с логическим математическим интеллектом?
У детей с логическим математическим интеллектом есть несколько преимуществ, и вы можете выделить такие характеристики, как:
- Они отлично разбираются в числах, закономерностях и их связях.
- Они обладают сильными способностями к решению проблем и лучше всего учатся, рассуждая, выстраивая логическую последовательность и анализируя.
- Им нравится быть хорошо организованными, а также классифицировать предметы.
- Им нравится работать с абстрактными понятиями и проводить научные эксперименты.
- Им нравится использовать логику и факты для решения проблем, и они основывают свои решения на фактах и здравом смысле, а не на эмоциях и личных чувствах.
- Обладают хорошими математическими способностями и легко оперируют числами.
Теперь, когда вы знаете наиболее важные характеристики логического математического интеллекта, вы можете начать наблюдать за своим ребенком, чтобы определить, «сообразительны ли они в математике». Согласно Sage Journals, дети в возрасте 4 или 5 лет могут отдавать предпочтение одному типу интеллекта перед другим. Когда дело доходит до маленьких детей, вы можете просто понаблюдать за ними и создать «профиль интеллекта» на основе этого. 2
Согласно Sage Journals, дети в возрасте 4 или 5 лет могут отдавать предпочтение одному типу интеллекта перед другим. Когда дело доходит до маленьких детей, вы можете просто понаблюдать за ними и создать «профиль интеллекта» на основе этого. 2
Учебные предпочтения детей с логическим математическим интеллектом
Как упоминалось ранее, решение проблем, упорядочивание сложных ситуаций и логические теории — это лучшие способы помочь детям с логическим математическим интеллектом учиться. Наглядные материалы, компьютеры, статистические и аналитические программы, а также практические проекты помогают детям с логическим математическим стилем обучения более эффективно обрабатывать информацию. Они предпочитают структурированную, целенаправленную деятельность, основанную на математических рассуждениях и логике, неструктурированной творческой деятельности с нечетко определенными целями обучения. Представьте, что вы строите конкретную модель Lego® или рисуете без подсказок. 2
2
Помощь в обучении для детей с логико-математическим интеллектом
- Если ваш ребенок учится логически, вы можете помочь ему разными способами. Вовлекайте их в стратегические игры и логические головоломки во время семейного отдыха, давайте им планировщики в классе и устанавливайте четкие правила дома. По возможности просите ребенка помочь вам с математическими задачами. Покупая продукты, попросите ребенка подсчитать счет до того, как вы подойдете к кассе. Если они старше и могут рассчитывать проценты, попросите их рассчитать скидку на один или два товара.
- Поощряйте вашего логического ребенка-математика использовать такие инструменты, как графики, диаграммы, временные шкалы или схемы для понимания абстрактных понятий, если вы подозреваете, что у него проблемы с видением общей картины.
- Вы можете поощрить критическое мышление вашего ребенка, попросив его объяснить причины своих решений всякий раз, когда появляется возможность.
 Удивительно наблюдать, как ваш ребенок решает задачи с изобретательскими решениями, о которых вы, возможно, и не подозревали.
Удивительно наблюдать, как ваш ребенок решает задачи с изобретательскими решениями, о которых вы, возможно, и не подозревали. - Вам также может быть полезно общаться с учителем вашего ребенка. Дайте им понять, что их ученик обладает высоким уровнем логического математического интеллекта и получит пользу от обучения в той манере, которая ему нравится. 3
Если ваш ребенок обладает естественными способностями к логическому математическому интеллекту, вы можете помочь ему улучшить свои навыки, используя игры на запоминание или логику, математические головоломки, компьютерные программы, практические проекты, распознавание образов, анализ данных и другие занятия. Хотя обычно считается, что те, кто хочет улучшить свой логический интеллект, должны хорошо разбираться в математике, это не всегда так. Вы можете улучшить свой логический математический интеллект, если будете прилагать усилия и прилагать усилия.
Если эта статья заинтересовала вас, посетите блог BYJU’S FutureSchool Blog, где вы найдете больше развлекательных и образовательных материалов.
Ссылки:
- Примеры логического математического интеллекта – MentalUP . (н.д.). Получено 16 июня 2022 г. с https://www.mentalup.co/blog/logical-mathematical-intelligence
- Лучшие занятия для логического математического интеллекта — . (н.д.). Получено 16 июня 2022 г. с https://whatdoesmammasay.com/activities-for-logical-mathematical-intelligence/ 9.0040
- Обучение детей с помощью логико-математического интеллекта (множественный интеллект) – Занятия, Игрушки, Материалы, Примеры . (н.д.). Получено 16 июня 2022 г. с https://www.parentree.in/Blogs/841-teaching-children-through-logical-mathematical-intelligence-multiple-intelligence-activities-toys-materials-examples
- Внутри: Несколько Интеллект Логико-математический интеллект Логико-математический интеллект в Монтессори Зачем покупать разноцветные пластиковые гаджеты для младенцев? Внешний порядок для малышей Конкретная математика в Доме ребенка Много дум в Начальной школе! Среднее отделение Логико-математический интеллект жив дома Логико-математический интеллект Логико-математический интеллект Международные школы Монтессори и центры развития ребенка Брюссель, Бельгия .
 (н.д.). Получено 16 июня 2022 г. с сайта www.international-montessori.org
(н.д.). Получено 16 июня 2022 г. с сайта www.international-montessori.org - Логический математический интеллект: определение и примеры – видео и расшифровка урока | Study.com . (н.д.). Получено 16 июня 2022 г. с https://study.com/academy/lesson/logical-mathematical-intelligence-definition-examples-quiz.html
Учись с математикой, математика
Вам также может понравиться
Что такое Пентагон и каковы примеры из реальной жизни?Большинство из вас знакомы с некоторыми основными геометрическими формами, которые нас окружают, такими как квадраты, пирамиды, прямоугольники, круги и другие. Но Подробнее…
Математические методы для детей младшего возраста
Доступные форматы
- ПДФ
- электронная книга
Условия использования
Атрибуция
СС ПО
отзывов
Узнайте больше об отзывах.
Отзыв Цици Ньябандо, доцента Университета Восточного Нью-Мексико, 01. 06.22
06.22
Текст охватывает соответствующие инструкции по математике для периода раннего детства. В нем хорошо обсуждается важность развития зарождающейся математики и подходящие для развития способы помочь маленьким детям развить основы математики… читать далее
Отзыв Цици Ньябандо, доцента Университета Восточного Нью-Мексико, 01.06.22
Полнота рейтинг: 5 видеть меньше
Учебник содержит соответствующие инструкции по математике для детей младшего возраста. В нем хорошо обсуждается важность развития зарождающейся математики и подходящие для развития способы помочь маленьким детям развить базовые математические навыки и отношения. Автор обсудил стратегии и примеры деятельности для разных этапов раннего детства. Несколько иллюстраций в книге улучшают или дополняют знания о математических концепциях и действиях, которые обсуждает автор. Преподаватели могут использовать различные вспомогательные ресурсы для занятий в классе или управляемого обучения вне класса.
Точность содержания рейтинг: 5
Содержание кажется точным, связанным с исследованиями, а источники заслуживают доверия. Я не видел никакого предвзятого контента.
Актуальность/долговечность рейтинг: 5
Автор включил соответствующие идеи и мероприятия. Автор также предоставил ссылки на статьи, видеоролики и веб-сайты, которые можно легко обновить в случае необходимости. Содержание напрямую связано с преподаванием математики в дошкольных классах.
Ясность рейтинг: 5
Автор представил информацию в понятной и понятной форме. Примеры и визуальные эффекты помогают повысить ясность. В главе 4 автор представил обзор стандартов по математике для детей младшего возраста в штате Канзас. Части стандартов штата Канзас также несколько раз цитируются в других частях книги. Хотя между различными государственными стандартами могут существовать некоторые сходства, это может быть недостатком. Как правило, автор предоставил контекст и четкие описания, чтобы помочь читателям из других штатов понять содержание.
Последовательность рейтинг: 5
Автор был последователен в подаче материала. Формат каждой главы одинаков. Автор использовал терминологию, с которой воспитатели дошкольного образования знакомы на протяжении всего учебника. В конце текста есть глоссарий, а язык книги прост и понятен воспитателям дошкольного образования.
Модульность рейтинг: 5
Различные разделы текста могут быть легко назначены на разные точки курса. Заголовки полезны для навигации.
Организация/Структура/Поток рейтинг: 5
Главы организованы логически. Подзаголовки позволяют легко находить информацию и следить за обсуждением. Изображения помогают разбить текст и внести ясность, а страницы не выглядят загроможденными.
Интерфейс рейтинг: 4
В некоторых областях размер шрифта слишком велик или слишком мал. Это может отвлечь читателя. Все ссылки в книге работают, и я могу перемещаться по главам электронной книги с помощью боковой панели в левой части страницы. Поскольку в книге есть ссылки на вспомогательные ресурсы, читатели получат больше пользы, если воспользуются электронной книгой.
Поскольку в книге есть ссылки на вспомогательные ресурсы, читатели получат больше пользы, если воспользуются электронной книгой.
Грамматические ошибки рейтинг: 5
Грамматических ошибок не заметил.
Культурная значимость рейтинг: 5
На картинках в книге изображены разные дети и взрослые. Я не заметил каких-либо культурно нечувствительных или оскорбительных тем или информации.
КомментарииЯ думаю, что это хорошо написанный учебник, и я буду использовать его в своих курсах.
Отзыв Стефани Даниэль, доцента Общественного колледжа им. Дж. Сарджанта Рейнольдса, 29 марта 2022 г.
В целом, этот учебник построен в логическом порядке и включает актуальные математические темы, подходящие для обучения детей младшего возраста. Существует оглавление и глоссарий, которые очень полезны при поиске по конкретным темам. читать далее
Отзыв Стефани Даниэль, доцента Общественного колледжа им. Дж. Сарджанта Рейнольдса, 29 марта 2022 г.
Полнота рейтинг: 5 видеть меньше
В целом, этот учебник построен в логическом порядке и включает актуальные математические темы, подходящие для обучения детей младшего возраста. Существует оглавление и глоссарий, которые очень полезны при поиске по конкретным темам.
Точность содержания рейтинг: 5
В книге отражена точная информация. Я преподавал этот курс, используя другие ресурсы, и я считаю, что информация в этом тексте является точной и актуальной. Никаких ошибок или предвзятости, на мой взгляд, в моей рецензии на учебник замечено не было.
Актуальность/долговечность рейтинг: 5
Этот учебник включает в себя соответствующие темы, которые организованы в логическом порядке. Информация о Национальном совете учителей математики была тщательно составлена вместе с предлагаемыми мероприятиями, которые полезны для учителей дошкольного образования, особенно потому, что большинство учителей уже работают в этой области.
Ясность рейтинг: 4
Книга хорошо написана. За ходом текста было легко следить. Я ценю изображения по всему тексту как визуальные эффекты для обсуждаемого содержания. Всегда здорово иметь визуальные эффекты, соответствующие тексту. Для некоторых читателей это делает контент осмысленным и легким для восприятия, особенно когда на одной странице много текста. Единственная добавленная обратная связь, возможно, заключается в том, чтобы убедиться, что весь текст имеет один и тот же шрифт, если он не является заголовком. Некоторый текст был мелким шрифтом и крупным шрифтом в одном предложении. Может быть, поработать над форматом, чтобы сделать его последовательным.
За ходом текста было легко следить. Я ценю изображения по всему тексту как визуальные эффекты для обсуждаемого содержания. Всегда здорово иметь визуальные эффекты, соответствующие тексту. Для некоторых читателей это делает контент осмысленным и легким для восприятия, особенно когда на одной странице много текста. Единственная добавленная обратная связь, возможно, заключается в том, чтобы убедиться, что весь текст имеет один и тот же шрифт, если он не является заголовком. Некоторый текст был мелким шрифтом и крупным шрифтом в одном предложении. Может быть, поработать над форматом, чтобы сделать его последовательным.
Последовательность рейтинг: 4
Текст несколько соответствует текущим исследованиям. Я не уверен, когда была написана книга, но некоторым ссылкам более 10 лет. Может быть, пересмотреть текст, добавив больше текущих исследований, чтобы поддержать содержание. Кроме того, возможно, добавление целей и введение к каждой главе может помочь с последовательностью.
Модульность рейтинг: 5
Текст каждой главы четкий и лаконичный, включая заголовки глав и несколько иллюстраций по всему тексту. Информация представлена управляемыми порциями, что опять же облегчает чтение текста. Единственное добавленное предложение — это, возможно, добавление целей главы, как указано в предыдущем рейтинге.
Информация представлена управляемыми порциями, что опять же облегчает чтение текста. Единственное добавленное предложение — это, возможно, добавление целей главы, как указано в предыдущем рейтинге.
Организация/Структура/Поток рейтинг: 4
В целом, текст представлен хорошо, за исключением того, что некоторые части шрифта немного смещены в абзацах. Тем не менее, содержание каждой главы разделено на разделы, что упрощает навигацию по тексту.
Интерфейс рейтинг: 4
В целом интерфейс выполнен хорошо. Я скачал его в формате PDF, и в нем было легко ориентироваться. Большая часть контента легко читается, и другим должно быть легко ориентироваться. Опять же, единственное предложение состоит в том, чтобы пересмотреть некоторые элементы форматирования текста. Для некоторых читателей разница в размере текста может быть проблемой, особенно если они используют программу чтения с экрана.
Грамматические ошибки рейтинг: 5
Профессионально и точно, без грамматических, орфографических и структурных ошибок.
Культурная значимость рейтинг: 4
Большая часть контента сосредоточена на государственных стандартах, поэтому, возможно, включение легко оцениваемых гиперссылок или примечаний, где можно найти культурно значимый контент, было бы дополнительным преимуществом учебника.
КомментарииВ целом, это хорошо написанная книга, в которой подробно рассматриваются математические методы обучения детей младшего возраста. Мне понравилось просматривать этот ресурс, и я планирую использовать некоторые главы в своем курсе CHD146 «Математика, естествознание и социальные науки для детей».
Отзыв Даун Хендрикс, инструктора муниципального колледжа Клакамас, 23 февраля 2022 г.
«Главы охватывают компоненты математики для детей младшего возраста. Указатель не включен. Имеется глоссарий. Существует достаточно информации о математических стандартах. Тем не менее, существует не так много практических идей или стратегий того, как… читать далее
Отзыв Даун Хендрикс, инструктора муниципального колледжа Клакамас, 23 февраля 2022 г.
Полнота рейтинг: 3 видеть меньше
“Главы охватывают компоненты математики для детей младшего возраста. Указатель не включен. Имеется глоссарий.
Имеется достаточно информации о математических стандартах. Однако не так много практических идей или стратегий того, как учителя могут способствовать обучению детей математике в соответствии со стандартами. Информация о том, как продвигать математические знания для младенцев и детей ясельного возраста, скудна».
Точность содержания рейтинг: 5
Содержимое соответствует математическим стандартам Канзаса. Однако, поскольку основное внимание уделяется математическим стандартам Канзаса, было бы сложно использовать или адаптировать эту книгу в других штатах.
Актуальность/долговечность рейтинг: 5
Содержание относительности будет легко обновляться новыми исследованиями, поскольку каждому компоненту математики посвящена отдельная глава.
Ясность рейтинг: 5
Использование профессионального жаргона сведено к минимуму, при необходимости включаются простые в использовании определения.
Последовательность рейтинг: 5
Используемая терминология соответствует стандартам в области математики для детей младшего возраста.
Модульность рейтинг: 5
Каждая глава разбита на более мелкие разделы, которые легко читать.
Организация/Структура/Поток рейтинг: 5
Темы представлены организованно, последовательно
Интерфейс рейтинг: 4
При непосредственном доступе к книге через Интернет интерфейс организован, понятен и прост в использовании. Однако при загрузке версий PDF и Word шрифт отличается и плохо отформатирован.
Грамматические ошибки рейтинг: 5
Грамматических ошибок не обнаружено.
Культурная значимость рейтинг: 5
Содержимое выглядит непредвзятым.
Содержание
- 1. Важность математики в раннем детстве
- 2. Вехи математики
- 3. Математика в дошкольных учреждениях
- 4.
 Математические стандарты
Математические стандарты - 5. Обучение математике посредством решения задач
- 6. Ранние понятия числа и чувство числа
- 7. Целое число Разрядное значение
- 8. Вычисление целых чисел
- 9. Ранние концепции фракций
- 10. Геометрия и измерения
- 11. Алгебраическое мышление
- 12. Данные и анализ данных
- 13. Глоссарий
Вспомогательный материал
О книге
Добро пожаловать в школу математики для детей младшего возраста! Этот курс соответствует унифицированным требованиям раннего детства в штате Канзас для лицензии на преподавание с рождения до 3 класса.
Большинство людей согласны с тем, что раннее детство включает в себя период от младенчества до восьмилетнего возраста, характеризующийся быстрым и сложным развитием в физической, когнитивной и социальной областях. Математическим навыкам необходимо обучать с раннего детства. Детям должна быть предоставлена основа для достижения успеха в начальной школе и за ее пределами. Учителя должны сосредоточить уроки в раннем детстве на основных навыках, которые помогут в будущем продвигать математику. От дошкольного возраста до окончания начальной школы дети закладывают основу для будущих жизненных навыков.
Математическим навыкам необходимо обучать с раннего детства. Детям должна быть предоставлена основа для достижения успеха в начальной школе и за ее пределами. Учителя должны сосредоточить уроки в раннем детстве на основных навыках, которые помогут в будущем продвигать математику. От дошкольного возраста до окончания начальной школы дети закладывают основу для будущих жизненных навыков.
Изучение математики — это «естественное» и подходящее для развития ребенка занятие» (Гинзберг, Ли и Бойд, 2008). Благодаря повседневному взаимодействию с миром у многих детей формируются неформальные представления о пространстве, количестве, размере, закономерностях и операциях. К сожалению, не у всех детей есть одинаковые возможности для построения этих неформальных и основополагающих математических концепций в их повседневной жизни (Sherman-LeVos, 2010).
Маленькие дети от природы любознательны, и лучше всего начинать заниматься математикой в то время, когда мозг маленького ребенка быстро развивается. Математика в раннем детстве помогает детям развивать навыки критического мышления и рассуждения в раннем возрасте и – это ключ к успеху в школьные годы.
Математика в раннем детстве помогает детям развивать навыки критического мышления и рассуждения в раннем возрасте и – это ключ к успеху в школьные годы.
О вкладчиках
Автор
Джанет Страмел, Государственный университет Форт-Хейс
Внести вклад в эту страницу
Предложить изменение этой записи книгиКлассификация и сортировка
Что включает в себя классификация и сортировка?
Классифицировать и сортировать можно любые объекты как с одинаковыми, так и с разными характеристиками, сортируя их по их характеристикам, таким как класс, вид или размер. Согласно Harris, (2013) , классификация и сортировка включают три этапа:
- Дети решают, по какой характеристике сортировать по
- Дети физически сортируют объекты
- Дети могут предоставить и описать свое обоснование для своей классификации
Исторически, с точки зрения обучения как последовательного, тесно связанного с возрастом, это привело к построению соответствующей развитию практики (DAP). Однако более современные взгляды, такие как конструктивизм, рассматривают детей как врожденно способных и утверждают, что обучение ведет к развитию, а не развитие управляет обучением (Артур 9).0013 и др. , 2014). В результате дети должны знакомиться с математикой и получать богатый, неограниченный опыт счета с раннего возраста, чтобы поддерживать их развитие, а не ждать, пока они не будут признаны готовыми к развитию. Классификация и сортировка, а также любой математический опыт наиболее эффективны, когда они правильно включены в повседневную жизнь детей. Детям важно видеть математику в реальном мире, чтобы понять ее место и использование ( Harris, 2013 ).
Однако более современные взгляды, такие как конструктивизм, рассматривают детей как врожденно способных и утверждают, что обучение ведет к развитию, а не развитие управляет обучением (Артур 9).0013 и др. , 2014). В результате дети должны знакомиться с математикой и получать богатый, неограниченный опыт счета с раннего возраста, чтобы поддерживать их развитие, а не ждать, пока они не будут признаны готовыми к развитию. Классификация и сортировка, а также любой математический опыт наиболее эффективны, когда они правильно включены в повседневную жизнь детей. Детям важно видеть математику в реальном мире, чтобы понять ее место и использование ( Harris, 2013 ).
В частности, ранние математические концепции, такие как классификация, сортировка, сравнение и решение проблем, которые при этом используются, являются основой для более позднего, более сложного математического мышления ( Дэймон, (н.д.
). Классификация и сортировка важны для развитие числовых понятий и способности группировать числа и наборы, важные для решения сложных сумм в старших классах начальной школы Путем классификации и сортировки логическое мышление применяется к повседневным объектам, что важно для более поздней математики, а также для принятия всех решений ( Рене, 2011 ). Примечательно, что исследования показали, что умение считать, возникающее в раннем возрасте, повышает успеваемость по всем предметам в последующем школьном обучении (, Дараганова и Эйнли, 2011, ).
Примечательно, что исследования показали, что умение считать, возникающее в раннем возрасте, повышает успеваемость по всем предметам в последующем школьном обучении (, Дараганова и Эйнли, 2011, ).Источник: mrsmclennan.blogspot.com.au
Упражнение 1: Загадочная коробка
Принесите загадочную коробку с различными классами предметов внутри. Обсудите различия и сходства с группой детей и поговорите о том, как мы могли бы сгруппировать предметы в соответствии с их сходством. Следуйте предложениям и идеям детей и целенаправленно и совместно работайте с ними, чтобы научить их классифицировать и сортировать. Разложите предметы на земле в соответствии с их классификациями и поинтересуйтесь вместе с детьми, как еще мы могли бы их классифицировать. Совместно классифицируйте объекты. Примеры классификации могут включать искусственные и природные, тяжелые и легкие, длинные и короткие, животные и насекомые или разные цвета. Включите увеличительные стекла, весы и измерительные инструменты, чтобы дети могли исследовать различия.
Упражнение 1: Связи с австралийской учебной программой Математика Наука Предоставлено theinspiredapple.blogspot.com.au | Связи с Early Years Learning Framework Результат 1: У детей сильно развито чувство идентичности; Результат 4: Дети уверены в себе и вовлечены в процесс обучения; |
Мероприятие 2: Незакрепленные детали
Источник: www.aneverydaystory.com
Предоставьте детям отдельные детали, чтобы они могли практиковаться в переписке 1:1, раскладывая предметы по соответствующим номерам. Предметы разного размера, текстуры и цвета, такие как пуговицы, игральные кости и крышки от бутылок, шарики или, в частности, натуральные и органолептические материалы с разным запахом и происхождением, такие как орехи, цветы, травы, ракушки, камни, перья, цветы и палки. Это позволяет детям проводить более интересные и аутентичные классификации, например, по запаху или местоположению (например, пляж, кусты и сад). Включите различные материалы с цифрами на них, такие как банки, орехи и камни, нарисованные как домино с цифрой, а также с другой стороны, чтобы сделать действие более преднамеренным. Предоставление таких материалов, как весы для взвешивания, линейки/рулетки, позволяет детям сравнивать материалы по их весу и размеру.
Это позволяет детям проводить более интересные и аутентичные классификации, например, по запаху или местоположению (например, пляж, кусты и сад). Включите различные материалы с цифрами на них, такие как банки, орехи и камни, нарисованные как домино с цифрой, а также с другой стороны, чтобы сделать действие более преднамеренным. Предоставление таких материалов, как весы для взвешивания, линейки/рулетки, позволяет детям сравнивать материалы по их весу и размеру.
Предметы, с помощью которых дети могут создавать узоры, например бусины разного цвета и размера.
Разнообразие 2D- и 3D-форм для сортировки из различных материалов, например, сферы из стволов деревьев, кубические кубики, мраморные сферы
Используйте предметы, имеющие личное и культурное значение для учащихся.
Для получения дополнительной информации о преимуществах «Незакрепленных деталей» посетите страницу . Ежедневная история
| Занятие 2: Связи с австралийской учебной программой Математика Наука | Подключения к системе раннего обучения Результат 4: Дети уверены в себе и вовлечены в процесс обучения; Результат 5: Дети эффективно общаются; |
| Чего следует избегать при обучении классификации и сортировке Избегайте прямых инструкций по классификации и сортировке и позволяйте детям исследовать и вместо этого получать подсказки с более открытыми вопросами. Когда математические занятия скучны и не позволяют детям исследовать, у них может развиться негативное отношение к математике. Источник: creativestarlearning.co.uk Возможности для практики в окружающей среде
Используйте преднамеренные вопросы, когда дети взаимодействуют с такими материалами, как: | Как научить классифицировать и сортировать с помощью игрового подхода Крайне важно, чтобы дети развивали позитивное отношение к учебе и учились на протяжении всей жизни, поэтому опыт счета должен быть приятным и увлекательным.
Источник: theimaginationtree.com |
Примеры практики
| youtube.com/embed/z2Z5nqcC9Og?wmode=opaque” frameborder=”0″ allowfullscreen=””> |
Для ссылок на страницы и дополнительной информации о представлении классификации и сортировки: Артур Л., Бичер Б., Смерть Э., Докетт С., Фармер С. (2014). Программирование и планирование в начале Настройки детства. (6-е изд.). Южный Мельбурн, Австралия: Cengage Learning Australia. Дарагонова, Г. и Эйнли, Дж. (2011). Навыки счета детей. Получено с http://www.growingupinaustralia.gov.au/pubs/asr/2011/asr2011h.html_ Harris, A. (2013). Сопоставление и сортировка являются ранними этапами развития математики. Рене. (2011). Дошкольные и детские сады Сортировка и классификация деятельности. Получено с http://www.schoolsparks.com/blog/preschool-and-kindergarten-sorting-and-classifying-activitiesДополнительные ресурсы http://www.andnextcomesl.com/2014/ 08/reggio-inspired-preschool-math-tray.html – поднос для коврика облегчает изучение математики. «Искусство преподавания — это искусство помогать открывать» — Марк Ван Дорен |
Использование игры для обучения математике
Образовательный фонд Джорджа Лукаса
EdutopiaEdutopia
Поиск
Социальное и эмоциональное обучение (SEL)
Математика не должна быть серьезной. Один учитель считает, что игра — это ключ к пониманию математики для всех возрастов.
Один учитель считает, что игра — это ключ к пониманию математики для всех возрастов.
Мэтью Олдридж
24 июля 2019 г.
mladn61/ iStock
Концепция игры часто ограничивается младшими учениками и менее академическими усилиями, но игра может быть полезной стратегией в маловероятной дисциплине: математике.
Математика известна как холодная, логичная и строгая, но этот предмет не получает должного внимания за свой истинный озорной дух, хорошо скрытый от мира. Учебные программы по математике для K–12 могут занять время и пространство, чтобы поиграть с концепциями и идеями, даже в спешке по обязательным темам.
В своем исследовании для выступления на TEDxKitchenerEd в 2017 году под названием «Математика — это игра» я нашел несколько материалов о радости от математики в старших классах. Большая часть литературы об игре как подходе к обучению основана на ранних годах, особенно в детском саду, где она является общепринятым педагогическим методом.
Маленькие дети во время игры часто достигают состояния, которое психолог Михай Чиксентмихайи называет “потоком”, неуловимого состояния ума, когда время, кажется, исчезает, когда они глубоко сосредотачиваются на том, что делают. Чтобы достичь этого идеального состояния в классе, требуется нечто большее, чем свобода играть — учителя также должны реагировать на идеи учащихся и направлять их через такие понятия, как счет и числа. Этот тип управляемой игры требует принятия решения о том, как и когда давать прямые инструкции. Создавая свободу и в то же время предлагая направление, можно продуктивно играть, открывая учащимся умы для лучшего понимания сложных математических концепций.
Чтобы достичь этого идеального состояния в классе, требуется нечто большее, чем свобода играть — учителя также должны реагировать на идеи учащихся и направлять их через такие понятия, как счет и числа. Этот тип управляемой игры требует принятия решения о том, как и когда давать прямые инструкции. Создавая свободу и в то же время предлагая направление, можно продуктивно играть, открывая учащимся умы для лучшего понимания сложных математических концепций.
Количество игр на «серьезные» академические темы, такие как математика, похоже, обратно пропорционально возрасту учащихся, но это не обязательно так. Игровую педагогику математики можно систематизировать и сделать реальной, строгой и аутентичной.
Примите и включите игру
В моей книге Преподавание математики посредством решения задач в классах K–12 я написал о необходимости признать, что люди рождены для игры. Игра неудержимо человечна, и мы можем играть, чтобы учиться. Игра и мышление не противоречат друг другу. Хотя игра обычно связана с отключением мышления и отдачей себя приятной деятельности, работа над интересными задачами может стать триггером потока. Есть благоприятный момент, часто около 30 минут работы над интересной проблемой, когда идеи начинают становиться решениями.
Хотя игра обычно связана с отключением мышления и отдачей себя приятной деятельности, работа над интересными задачами может стать триггером потока. Есть благоприятный момент, часто около 30 минут работы над интересной проблемой, когда идеи начинают становиться решениями.
Создайте культуру, в которой математические идеи – это не просто формулы на странице, а концепции, которые нужно обсуждать и обдумывать. Игра продвигает обучение математике от механического заучивания к более широкому пониманию математики. Поощряйте студентов говорить, думать, рассуждать и задаваться вопросом, когда они решают проблемы. Создание чувства любопытства, даже для простых понятий, вовлекает учащихся в игровой форме.
Простые стратегии, такие как «покажи и поговори», могут создать возможности для совместного обучения в игровой форме. Использование подсказок в повседневной работе в классе может сделать математические концепции увлекательными. Такие сайты, как Visual Patterns, Fraction Talks или Estimation180, предлагают простые и быстрые способы сделать математические концепции интересными.
Погрузитесь в неизвестное
Математика полна сюрпризов, которые могут быть интересными и забавными. Для решения многих проблем нет единого пути или стратегии. Будьте восприимчивы к сюрпризам в том, как ваши ученики думают о проблемах и решают их. Открытость к неожиданностям может способствовать формированию культуры игривого любопытства в классе. Игривый ученик математики полон надежд и оптимистичен — элементы мышления, которые помогают учащимся лучше понимать сложные понятия.
Примите беспорядок процесса решения проблем. Мышление беспорядочно. У нас не всегда все получается с первого раза. Нужны корректировки курса, исправления и даже полная трансформация работы.
Наблюдайте за своими учениками во время работы. Где блокпосты? Как они адаптируются к конкретным вызовам? Прислушивайтесь к своему собственному разговору с самим собой во время работы и используйте свои проблемы, чтобы продумать, как ваши ученики могут столкнуться с трудностями. Решения важны, но не менее важен и процесс. Слушая и разговаривая со своими учениками во время их работы, вы можете давать хорошие отзывы и получать данные об оценках.
Слушая и разговаривая со своими учениками во время их работы, вы можете давать хорошие отзывы и получать данные об оценках.
Игра создает открытые пространства для размышлений, где учителя могут помочь учащимся разобраться с большими и интересными идеями математики.
Использование конкретных методов
Физические или цифровые манипуляции, такие как кубы привязки, блоки шаблонов и реляционные стержни, — все это инструменты, которые могут помочь учащимся воплотить математику в жизнь — процесс, называемый представлением. Учителя могут использовать колоды карт, игральные кости или предметы для счета, чтобы помочь учащимся отработать свои основные навыки.
Например, младшие школьники могут практиковаться в умножении фактов до 6 раз 6, бросая два кубика и умножая результаты. Учащиеся старшего возраста могут использовать колоды карт, чтобы практиковать операции с целыми числами, где красные масти являются отрицательными, а черные — положительными. Для младших школьников, изучающих базовые навыки работы с числами, выделите один день в неделю для целенаправленной практики с использованием игр.
Визуальное представление математических идей может быть игривым. Например, дайте учащимся крышку от консервной банки или другой круглый предмет, веревку и рулетку, чтобы попытаться найти соотношение между окружностью и диаметром.
Использование физических или цифровых элементов дает учащимся пространство для игры с более абстрактными концепциями и идеями. Свобода игровой среды создает возможности для более глубокого вовлечения. Как я сказал в своем выступлении: «Пусть играют. Пусть говорят, думают, строят предположения и удивляются. Пусть играют».
Filed Under
- Social & Emotional Learning (SEL)
- Teaching Strategies
- Math
- K-2 Primary
- 3-5 Upper Elementary
- 6- 8 Средняя школа
- 9-12 старшая школа
Математическое и научное мышление у трех- и четырехлетних детей — Better Kid Care — Penn State Extension
Дошкольные годы, в возрасте трех и четырех лет, — это время, когда маленькие дети погружаются в обширные исследования тем, которые их интересуют. Дошкольники быстро развивают умственные способности мыслить математическим и научным образом, чтобы изучать и понимать свои любимые темы. Дошкольники также видят доказательства использования математических и научных концепций в повседневной жизни: от раскладывания нужного количества салфеток для перекуса до предсказания и проверки направления, в котором будет двигаться мяч при ударе по нему. Изучите способности, развиваемые дошкольниками, которые помогают им мыслить более сложными способами.
Дошкольники быстро развивают умственные способности мыслить математическим и научным образом, чтобы изучать и понимать свои любимые темы. Дошкольники также видят доказательства использования математических и научных концепций в повседневной жизни: от раскладывания нужного количества салфеток для перекуса до предсказания и проверки направления, в котором будет двигаться мяч при ударе по нему. Изучите способности, развиваемые дошкольниками, которые помогают им мыслить более сложными способами.
Разборка и сборка
Что делают дети
Тройки и четверки играют с понятиями частей и целых. Они очарованы внутренностями вещей и тем, как различные части заставляют целое работать. Они понимают, как собрать части вместе, чтобы сделать целое. Все, что они создают, становится более сложным и продуманным.
Что могут предоставить лица, осуществляющие уход
- Выброшенные мелкие бытовые приборы и настоящие инструменты для их разборки.
- Книги, иллюстрирующие внутренности животных, растений, зданий, машин и т.
 д.
д. - Инструменты для исследования (лупы, пинцеты), а также бумага и карандаши для записи увиденного.
Что могут говорить и делать воспитатели
- Имейте место для хранения незавершенной работы, чтобы помочь детям расширить свои исследования на несколько дней.
- Стимулируйте и развивайте любознательность детей. («Интересно, как он выглядит внутри. Как вы думаете, что мы там найдем? Как мы могли узнать?»)
- Попросите детей описать свои мысли и решения по мере того, как они строят («Что вы сделали дальше?», «Что делает эта часть?», «Что еще вам нужно?»).
Наблюдение за изменениями в себе
Что делают дети
Дошкольники очень любопытны к себе и любят смотреть и обсуждать свои младшие фотографии. Они гордятся тем, как они выросли и изменились. Это возможность познакомить учащихся с измерениями, составлением графиков, записью наблюдений и другими математическими и естественными навыками.
Что могут предоставить лица, осуществляющие уход
- Инструменты для измерения роста и веса (начните с нестандартных способов измерения, а затем введите стандартные инструменты измерения, такие как линейки, позже).
- Детские книги о росте и изменении детей и фотографии детей в младенческом и раннем возрасте.
Что могут сказать и сделать опекуны
- Заставьте детей замечать и записывать свой собственный рост с течением времени, а не сравнивать их с другими детьми.
- Помимо размера, помогите детям определить и записать другие способы их изменения.
- Распространите интерес детей к собственному росту на рост и развитие других живых существ.
- Поощряйте измерения, подсчеты, составление графиков и запись.
Создание представлений
Что делают дети
Дошкольники умеют и заинтересованы в воссоздании точных моделей вещей, которые они наблюдали. Рисование или лепка объекта часто является частью научного исследования и может увеличить внимание к деталям, что может вызвать любопытство. Даже младшие дошкольники проявляют удивительный уровень внимания, сосредоточенности и интереса, когда изобразительное рисование и лепка являются частью их исследования.
Рисование или лепка объекта часто является частью научного исследования и может увеличить внимание к деталям, что может вызвать любопытство. Даже младшие дошкольники проявляют удивительный уровень внимания, сосредоточенности и интереса, когда изобразительное рисование и лепка являются частью их исследования.
Что могут предоставить лица, осуществляющие уход
- Инструменты для рисования и раскрашивания, помогающие рисовать детали (цветные карандаши, маркеры с тонкими точками).
- Плотная пластилин для лепки (вместо пластилина) и инструменты для лепки.
- Зона, где дети могут выставить свои скульптуры или сфотографироваться с моделями.
Что могут сказать и сделать воспитатели
- Поговорите с детьми о создании моделей на основе наблюдений и о том, чем это отличается от создания моделей на основе их воображения.
- Говорите с детьми о том, что они видят. Прокомментируйте детали, представленные в их модели.

Распознавание цифр
Что делают дети
В дошкольном возрасте дети устанавливают связь, что определенный письменный символ – «5» – обозначает количество и соответствует словесному обозначению этого количества. Поскольку в символе, похожем на сумму, нет ничего, дети узнают названия и символы для каждой суммы посредством многократного воздействия и использования цифр в игре и повседневной деятельности.
Что могут предложить опекуны
- Игры с написанием цифр.
- Головоломки, книги, схемы и другие материалы, связывающие написанные цифры с их количеством.
Что могут говорить и делать лица, осуществляющие уход
- Включите счет, словесные ярлыки и письменные символы в повседневную деятельность. («Сколько детей хотят добавить клубнику в свой йогурт? Один, два, три, четыре — хорошо, четверо детей. Давайте напишем цифру 4 в нашей таблице».)
- Дайте детям образцы числительных, на которые они могут ссылаться, но не беспокойтесь о точности их первых попыток.
 Со временем они улучшатся.
Со временем они улучшатся.
Имейте в виду: научное мышление включает в себя предсказание того, что произойдет дальше, проверку этих предсказаний и наблюдение за результатом, запись этого результата каким-то образом и сообщение другим об обнаруженных фактах. Математическое мышление включает в себя знание цифр, счет, создание моделей, распознавание геометрических фигур, измерение и организацию числовой информации с использованием диаграмм и графиков. Дошкольники могут освоить все эти навыки, если эти навыки встроены в деятельность и исследования, которые сосредоточены на детских интересах и любознательности.
Советы 16-12
Скачать публикацию
Математическое и научное мышление у трех- и четырехлетних детей (PDF)
Детали статьи
Трех- и четырехлетнее научное мышление в Заголовке
Математическое годовалыеЭта публикация доступна в альтернативных СМИ на запрос.
Страница не найдена – Фонд Наффилда
Страница не найдена – Фонд Наффилда Страница, которую вы ищете, не может быть найдена. Пожалуйста, попробуйте использовать либо главное меню, либо поиск по сайту.
Пожалуйста, попробуйте использовать либо главное меню, либо поиск по сайту.
Поиск проектов, новостей, воздействия, события
Поиск
Образование 640 Когнитивные и некогнитивные навыки 32Curriculum и субъект. 30-летний 1611111 год. образование и навыки 93Primary Education 128Q-шаг 26School Эффективность 45 Сторонного образования 153 Специальные потребности в образовании и инвалидность 53 Проблемы по промышленности образования. интеллект 3Помощь при смерти 1Дополненная реальность 0Преимущества 51Обязанности по уходу 27Сообщества и социальная сплоченность 63Страна рождения 24COVID-19327Прогнозирование преступности 2Данные для общественного блага 27Цифровой вред и дезинформация 33Цифровая интеграция и исключение 14Цифровые навыки 16Цифровое общество 47Инвалидность 13Экономика, государственные расходы и услуги 175Этническая принадлежность 47Семья и семейная динамика 115Гендер 42Глобальное неравенство в отношении здоровья и нуждающиеся дети 73Психическое здоровье 90Заболевания опорно-двигательного аппарата 11Пенсии 16Физическое здоровье 43Бедность и уровень жизни 107Производительность и инновации 6Общественное здравоохранение 150Социальные сети 2Социоэкономика старения 24Социоэкономика раннего взросления 40Спортивная наука 1Злоупотребление психоактивными веществами 11Налоги 46Доверие к демократии 65Оценка данных 5
ProjectsNewsEventsImpactOpinionPublicationsSeriesReportsEducation 640Cognitive and non-cognitive skills 32Curriculum and subject choice 30Early years 161Education workforce 74Educational assessment 28Higher education 91Language and literacy 78Lifelong learning 14Nuffield Research Placements 23Numeracy 83Parenting 73Pedagogy 19Post-16 education and skills 93Primary education 128Q-Step 26School effectiveness 45Secondary education 153Special educational needs и инвалидность 53Системные проблемы образования 97justice 230 к правосудию 36 Административное правосудие 23Civil юстиции 21 Корт.
 А. Михайлова, И.Н.Чеплашкина
А. Михайлова, И.Н.Чеплашкина
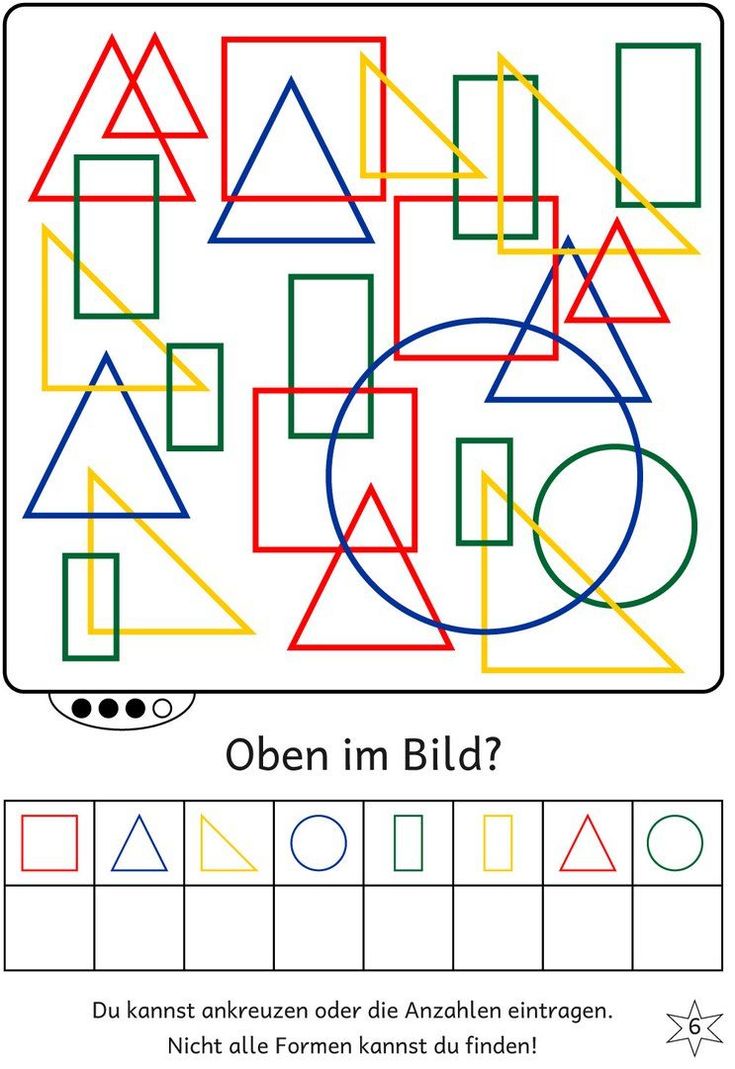

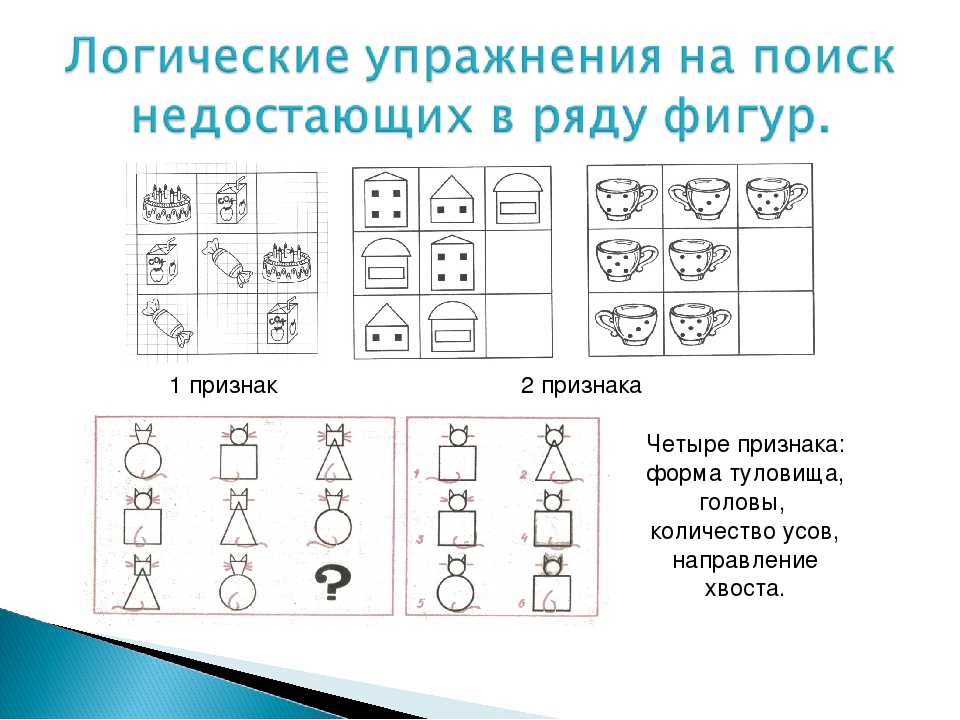
 А. Михайлова, И.Н.Чеплашкина
А. Михайлова, И.Н.Чеплашкина А.Мартынова, И.М.Сучкова
А.Мартынова, И.М.Сучкова Л. Непомнящая
Л. Непомнящая
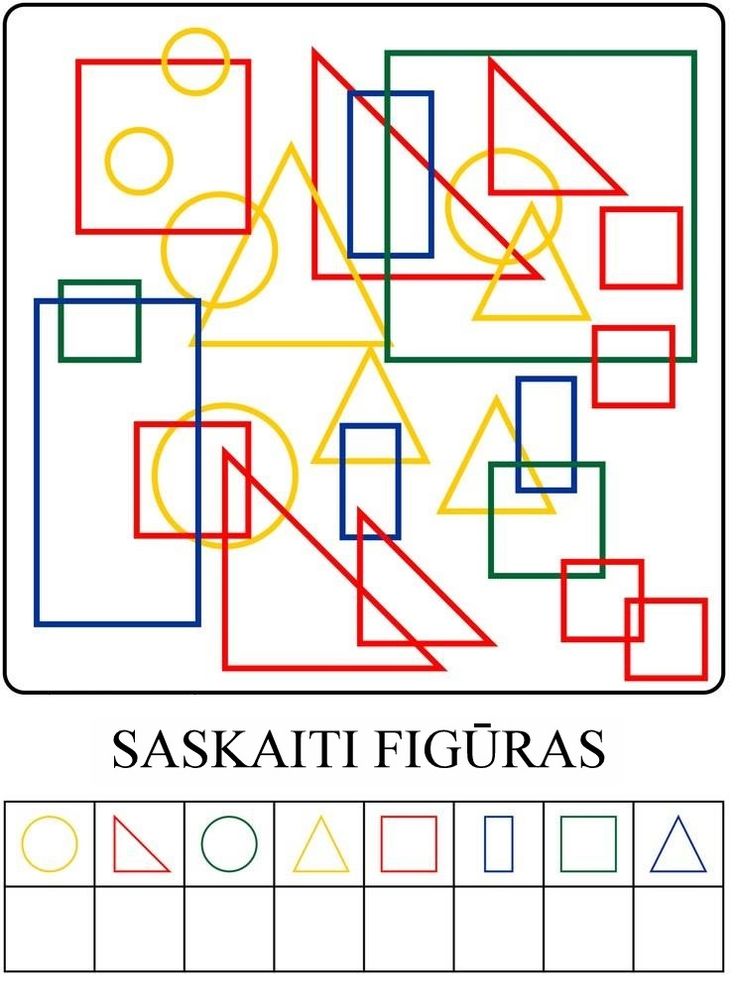
 В пособие представлены описания и чертежи 8 разных по сложности игр – головоломок, способствующих развитию пространственного воображения и мышления детей.
В пособие представлены описания и чертежи 8 разных по сложности игр – головоломок, способствующих развитию пространственного воображения и мышления детей. Но большая часть людей мыслит стереотипно, поскольку у них плохо развито логическое мышление. Логика нуждается в постоянных тренировках и делать это надо с раннего детства.
Но большая часть людей мыслит стереотипно, поскольку у них плохо развито логическое мышление. Логика нуждается в постоянных тренировках и делать это надо с раннего детства.
 п.)
п.)
 Таковой является ситуация, с которой начинается процесс размышления. Осознание трудностей, невозможность разрешить их привычным путем побуждают ребенка к активному поиску новых средств и способов решения задач и открытию мира математики.
Таковой является ситуация, с которой начинается процесс размышления. Осознание трудностей, невозможность разрешить их привычным путем побуждают ребенка к активному поиску новых средств и способов решения задач и открытию мира математики.
 Открывайте всегда что-то недосказанное, чтобы ребёнку хотелось ещё и ещё раз возвратиться к тому, что он узнал”.
Открывайте всегда что-то недосказанное, чтобы ребёнку хотелось ещё и ещё раз возвратиться к тому, что он узнал”.




 – М.: Детство-Пресс, 2007.
– М.: Детство-Пресс, 2007.