Логические задания по математике 1 класс в картинках: Логические задачи для 1 класса с ответами и решениями, развивающие задания на логику для детей 7-8 лет

Логические задания к недели математики 1-4 классы.

 

 

 

 

 

 

 

 

Задания для недели математики, логики, информатики  подготовлены на основе рабочих тетрадей «Юным умникам и умницам: Задания по развитию познавательных способностей (6-10 лет)»

 для 2, 3, 4 класса. О.Холодова., Москва: РОСТ книга, 2007

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Математический диктант, 2 класс

Сантиметр,  дециметр,  килограмм,  квадрат,  треугольник,  четырёхугольник, многоугольник, периметр,  минута,  часы, слагаемое,  сумма,  разность,  уменьшаемое, вычитаемое, множитель, произведение, делимое, делитель, частное.

Математический диктант, 3класс

Миллиметр,  дециметр, километр, длина, длинный,  периметр, площадь, параллелепипед, треугольник, килограмм, грамм,  масса, цена, количество, стоимость.

Математический диктант, 4 класс

Миллиметр,  дециметр, километр, длина, окружность, радиус, скорость, расстояние, периметр, площадь,  класс миллионов, килограмм, центнер, тонна, секунда.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Логика. Информатика. Математика.

1 тур, 1 класс

1.     Найди закономерность.

Ø Нарисуй недостающий флажок.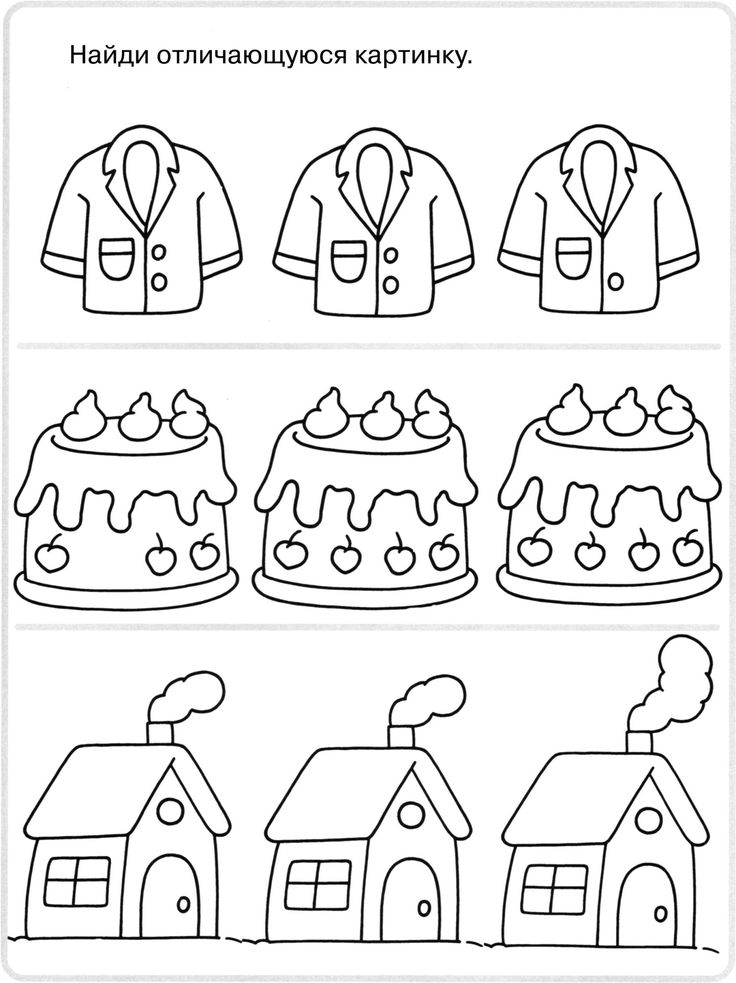

Ø Впиши недостающее число.

Ø Догадайся, какие слова вписаны в окружность.

Что лежит в твоей кровати                                   «Должность»

под одеялом на матрасе?                                  повелительницы снегов

                                                                            из сказки Г.Х.Андерсена

      

2.     Тренировка зрительной памяти.

Ø Найди двух одинаковых котов. Раскрась их.

 

          

 

 

 

Ø Найди фигуры А, В, С в квадрате справа. Напиши в фигурах их номера. Раскрась одинаковые фигуры одним цветом.

3.     Совершенствование воображения.

Ø Отгадайте, какие слова спрятались на картинках (такие картинки называются изографами)

4.     Логически-поисковые задания.

Ø 1. На столе стоят матрёшки. В каждой из трёх больших матрёшек умещаются 5 маленьких. Сосчитай, сколько всего матрёшек на столе?

___________________________

___________________________

___________________________

 

Ø 2.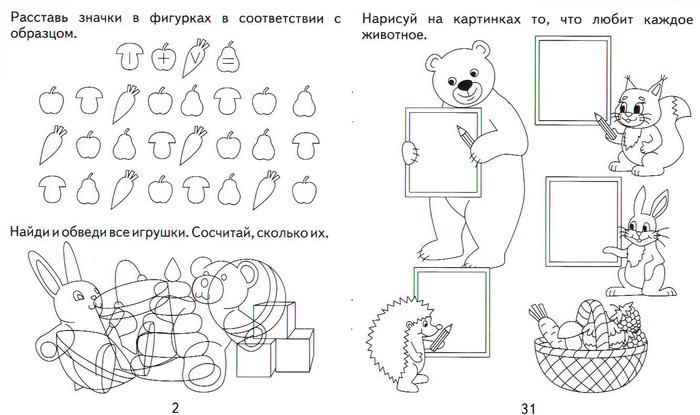 Вставь пропущенные знаки действий, чтобы получились верные равенства.

5 4 3 2 1=1                     5 4 3 2 1 =3                   5 4 3 2 1 =5

Ø 3.Составь слова и найди «лишнее» слово, зачеркни его.

ЖИАРФ              НОЛС                 ЛОВК                    ЛОТС

_______               _______            _________                ________

Ø 4.Ребята сидели на скамейке. В каком порядке они сидели, если известно, что Маша сидела справа от Серёжи, а Серёжа справа от Иры?

 

_____________________         Ты молодец!

Логика. Информатика. Математика.

1       тур, 2 класс

1.     Найди закономерность.

Ø Вставь нужную фигуру из 6 пронумерованных.

Ø Впиши недостающее число.

Ø Найди закономерность, впиши недостающее число.

                

2       Тренировка зрительной памяти.

Ø Отражение нарисовано неточно. Художник допустил здесь 7 ошибок. Найди их. Соедини.

 

          

 

Ø В пятиугольнике слева найди такие же фигуры, как фигуры О, К, И. Впиши в фигуры их номера. Раскрась одинаковые фигуры одним цветом.

3       Совершенствование воображения.

Ø Отгадайте, какие слова спрятались на картинках (такие картинки называются изографами)

4       Логически-поисковые задания.

Ø 1Впиши числа, чтобы сумма их по всем направлениям была равна.

Ø 2.Вставь пропущенные знаки действий, чтобы получились верные равенства.

 

Ø 3.Ребята сидели на скамейке. В каком порядке они сидели, если известно, что Маша сидела справа от Серёжи, а Серёжа справа от Иры?

 

_____________________     Ты молодец!

Логика. Информатика. Математика.

1       тур, 3 класс

1.     Найди закономерность.

Ø Вставь нужную фигуру из 4 пронумерованных.

 

Ø Впиши недостающее число.

Ø Догадайся, какие слова вписаны в окружность. Запись может читаться по часовой стрелке или против.

              Головная боль                                                 Детская игра

              для дворника            

 

 

 

 

 

 

2.     Тренировка зрительной памяти.

Ø Напиши номер части, которую отрезали от листа.

          

Ø В пятиугольнике слева найди такие же фигуры, как фигуры О, К, И. Впиши в фигуры их номера. Раскрась одинаковые фигуры одним цветом.

3.     Совершенствование воображения.

Ø Отгадайте, какие слова спрятались на картинках (такие картинки называются изографами)

4.     Логически-поисковые задания.

Ø 1.Найди по три числа в каждом ряду, сумма которых равна числу, данному в кружке.

        

Ø 2.Реши анаграммы и исключи лишнее слово.

АТСЕН             ТИВОНКР              РАКЫШ              КООН

______________________________________________________

Ø 3.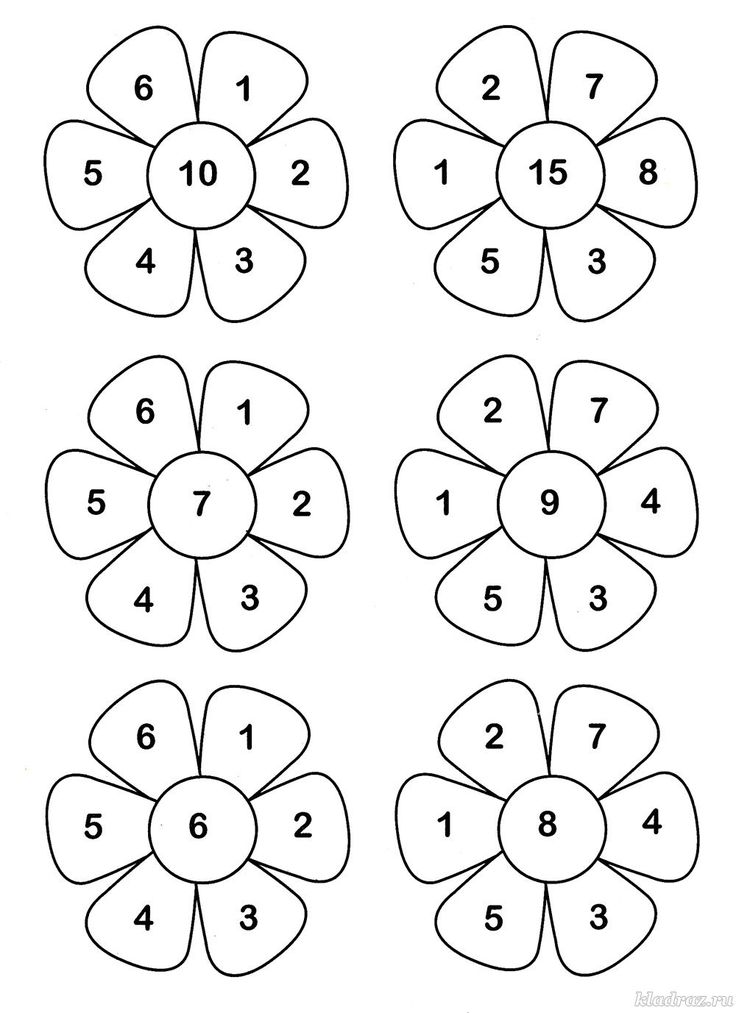 В клетках квадрата поставлены числа 1,15,20. Расставь в свободных клетках  цифры 2,3,4,5,6,8 так, чтобы произведение чисел в каждом столбце и в каждой строке было равно 120.

 

У тебя всё получится!

Логика. Информатика. Математика.

1       тур, 4 класс

1.     Найди закономерность.

Ø Вставь нужную фигуру из 6 пронумерованных.

Ø Впиши недостающее число.

      

Ø Догадайся, какие слова вписаны в окружность. Запись может читаться по часовой стрелке или против.

              Головная боль                                                 Детская игра

              для дворника            

 

 

 

 

 

2.     Тренировка зрительной памяти.

Ø Какая из частей дополняет колесо.

                    

Ø Какие две фигуры одинаковые? Обведи их номера.

 

 

 

 

 

3.      Совершенствование воображения.

Ø Отгадайте, какие слова спрятались на картинках (такие картинки называются изографами)

4.     Логически-поисковые задания.

Ø 1.Когда Оля спросила у дедушки, сколько ему лет, дед ответил: «Если проживу ещё половину того, что я прожил, да ещё один год, то мне будет сто лет». Сколько лет Олиному дедушке?

_________________________________________________________

_________________________________________________________

        

Ø 2. Владик был в деревне с 15 июля по 7 августа включительно. Сколько дней был Владик в деревне?

_________________________________________________________

_________________________________________________________

Ø 3.Реши анаграммы и исключи лишнее слово.

АТСЕН             ТИВОНКР              РАКЫШ              КООН

_________________________________________________________

______________________________________________________

Ø 4. В клетках квадрата поставлены числа 1,15,20. Расставь в свободных клетках  цифры 2,3,4,5,6,8 так, чтобы произведение чисел в каждом столбце и в каждой строке было равно 120.

 

У тебя всё получится!

Логика. Информатика. Математика. Ответы.

1       тур, 1 класс

1.     Найди закономерность.

Ø Нарисуй недостающий флажок.

Ø Впиши недостающее число.

Ø Догадайся, какие слова вписаны в окружность.

Что лежит в твоей кровати                                   «Должность»

под одеялом на матрасе?                                  повелительницы снегов

                                                                            из сказки Г.Х.Андерсена

Простыня                                                              Королева

      

2.Тренировка зрительной памяти.

Ø Найди двух одинаковых котов. Раскрась их. (1,5)

 

          

 

 

 

Ø Найди фигуры А, В, С в квадрате справа. Напиши в фигурах их номера. Раскрась одинаковые фигуры одним цветом. А-3, В-2, С-10

3. Совершенствование воображения.

Ø Отгадайте, какие слова спрятались на картинках (такие картинки называются изографами)

                        Дом                                             Аист

4. Логически-поисковые задания.

Ø 1. На столе стоят матрёшки. В каждой из трёх больших матрёшек умещаются 5 маленьких. Сосчитай, сколько всего матрёшек на столе?

5+5+5=15 (м) маленьких

5+3=8(м)________________

Ответ: 8 матрёшек________

 

Ø 2.Вставь пропущенные знаки действий, чтобы получились верные равенства.

5-4+ 3-2-1=1                     5+4-3-2-1 =3                   5+4-3-2+1 =5

Ø 3.Составь слова и найди «лишнее» слово, зачеркни его.

ЖИАРФ              НОЛС                 ЛОВК                    ЛОТС

ЖИРАФ              СЛОН                  ВОЛК                   СТОЛ

Ø 4.Ребята сидели на скамейке. В каком порядке они сидели, если известно, что Маша сидела справа от Серёжи, а Серёжа справа от Иры?

 

Ира, Серёжа, Маша   Ты молодец!

Логика. Информатика. Математика. Ответы.

1       тур, 2 класс

1.     Найди закономерность.

Ø Вставь нужную фигуру из 6 пронумерованных.

Ø Впиши недостающее число.

Ø Найди закономерность, впиши недостающее число.

                

2       Тренировка зрительной памяти.

Ø Отражение нарисовано неточно. Художник допустил здесь 7 ошибок. Найди их. Соедини.

 

           

Ø В пятиугольнике слева найди такие же фигуры, как фигуры О, К, И. Впиши в фигуры их номера. Раскрась одинаковые фигуры одним цветом. О-2, К- 5, И-6

3       Совершенствование воображения.

Ø Отгадайте, какие слова спрятались на картинках (такие картинки называются изографами)

           Часы           Утюг                      Гусь

4       Логически-поисковые задания.

Ø 1Впиши числа, чтобы сумма их по всем направлениям была равна.

Ø 2.Вставь пропущенные знаки действий, чтобы получились верные равенства.

 

Ø 3.Ребята сидели на скамейке. В каком порядке они сидели, если известно, что Маша сидела справа от Серёжи, а Серёжа справа от Иры?             Ира, Серёжа, Маша          Ты молодец!

Логика. Информатика. Математика. Ответы.

1       тур, 3 класс

1.     Найди закономерность.

Ø Вставь нужную фигуру из 4 пронумерованных.

 

Ø Впиши недостающее число.

Ø Догадайся, какие слова вписаны в окружность. Запись может читаться по часовой стрелке или против.

              Головная боль                                                 Детская игра

              для дворника    Мусор                          Прятки        

 

 

 

2       Тренировка зрительной памяти.

Ø Напиши номер части, которую отрезали от листа. 3

          

Ø В пятиугольнике слева найди такие же фигуры, как фигуры О, К, И. Впиши в фигуры их номера. Раскрась одинаковые фигуры одним цветом. О-2, К- 5, И-6

3       Совершенствование воображения.

Ø Отгадайте, какие слова спрятались на картинках (такие картинки называются изографами)

  Луноход                              Паровоз                      Колокол

4       Логически-поисковые задания.

Ø 1.Найди по три числа в каждом ряду, сумма которых равна числу, данному в кружке.

        

Ø 2.Реши анаграммы и исключи лишнее слово.

АТСЕН             ТИВОНКР              РАКЫШ              КООН

стена                                                        крыша               окно

Ø 3. В клетках квадрата поставлены числа 1,15,20. Расставь в свободных клетках  цифры 2,3,4,5,6,8 так, чтобы произведение чисел в каждом столбце и в каждой строке было равно 120.

Логика. Информатика. Математика. Ответы.

1       тур, 4 класс

1.     Найди закономерность.

Ø Вставь нужную фигуру из 6 пронумерованных.

Ø Впиши недостающее число.

      

Ø Догадайся, какие слова вписаны в окружность. Запись может читаться по часовой стрелке или против.

              Головная боль                                                 Детская игра

              для дворника     Мусор                  Прятки       

 

 

 

2       Тренировка зрительной памяти.

Ø Какая из частей дополняет колесо. 4

                     

Ø Какие две фигуры одинаковые? Обведи их номера. 3,7

 

 

 

 

3       Совершенствование воображения.

Ø Отгадайте, какие слова спрятались на картинках (такие картинки называются изографами)

Луноход                              Паровоз                      Колокол

4       Логически-поисковые задания.

Ø 1.Когда Оля спросила у дедушки, сколько ему лет, дед ответил: «Если проживу ещё половину того, что я прожил, да ещё один год, то мне будет сто лет». Сколько лет Олиному дедушке?

(100 – 1): 2= 49,5

Дедушке 49 лет и 6 месяцев.

        

Ø 2. Владик был в деревне с 15 июля по 7 августа включительно. Сколько дней был Владик в деревне?

24 дня

_________________________________________________________

Ø 3. Реши анаграммы и исключи лишнее слово.

АТСЕН             ТИВОНКР              РАКЫШ              КООН

стена                                                        крыша               окно

Ø 4. В клетках квадрата поставлены числа 1,15,20. Расставь в свободных клетках  цифры 2,3,4,5,6,8 так, чтобы произведение чисел в каждом столбце и в каждой строке было равно 120.

 

 

 

IQ Тест “Законы логики”: только очень сообразительные ответят на все вопросы. Dropi

11 Марта, 22:49 / Автор: Мария

IQ тест поможет вам потренировать логическое мышление и проверить эрудицию – ведь без неё проверка силы интеллекта была бы неполноценной! А ещё вы обязательно устройте встряску своей внимательности – так что будьте внимательны!

Тесты IQ #IQ тесты

Вопрос 1 из 10

Что из следующего не является анаграммой музыкального термина:

БОР ТАНИ

ОК! ЦЕНТР

ПОРА! СОН

УРА! КИРА! ТАК!

СПОР ДА И Я

Вопрос 2 из 10

Какой рисунок необходимо добавить вместо знака вопроса?

1

2

3

4

5

6

Вопрос 3 из 10

Это анаграмма одной известной фразы: О, БЕС! МЕДЬ НЕ НАМ.

a” data-question-id=”d0!1a!%9q!*b” data-test-id=”2130″ data-post-id=”6658″ data-answer-count=”3110″> В

Г

Вопрос 5 из 10

Заполните недостающее слово в скобках по примеру: 12, 32 (ЮБКА) 2, 1; 23, 5 (…) 21, 10

ДУША

ДУНЯ

БАЮК

ДУХИ

КЕДЫ

КЕПИ

Вопрос 6 из 10

Восстановите высказывание Козьмы Пруткова.

8@jyi2m2#” data-test-id=”2130″ data-post-id=”6658″ data-answer-count=”1372″> Л, М

Вопрос 8 из 10

Анаграммой какого слова является словосочетание ВЕГА СТОЛБ. Подсказка: колокольный звон. Слово-ответ заканчивается на:

Л

Б

Т

А

Е

Вопрос 9 из 10

Какое из предложенных ниже чисел должно стоять в пустой ячейке?

417

926

138

172

428

Вопрос 10 из 10

Измените по одной букве в каждом слове и отгадайте известное выражение: ЛИХА ОКРАИНСКАЯ ДОЧЬ

Фраза получилась!

Покажите ответ. ..

Комментарии

Дополнительные математические рабочие листы с математическими упражнениями и текстовыми задачами для математических классов с 1 по 6.

Выберите одну из следующих категорий для 1–6 классов дополнительный рабочий лист . Все наши рабочие листы для начальной школы бесплатны и их можно распечатать.

Дополнение с картинками

Номер строки

Добавление 1 цифры номера

Сумма до 20

Сумма 100 (без перегруппировки)

Сумма 100 (с перегруппировкой)

До 200 (2 + 2 цифры)

До 1000 (3 + 2 цифры)

До 1000 (3 + 3 цифры)

Добавление 4-х и 5-значных номеров

Отсутствующие дополнения

Добавление десятичных знаков

Сложение/вычитание подобных дробей

Сложение/вычитание непохожих дробей

Сложение/вычитание целых чисел

Головоломки с дополнительными числами

Дополнение Кроссворды

Дополнительные квадраты

Оценка сумм

Добавление до 10

(уровень 1)

Добавить и цвет

(уровень 1)

. Создание 9

(уровень 1)

. Создание 10

(уровень 1)

55959965. Изготовление 15

(уровень 1)

Добавьте до 15

(уровень 1)

Добавьте до 20

(уровень 1)

Добавьте до 20

(уровень 1)

Нажмите здесь, чтобы узнать больше Дополнение с картинками рабочие листы

На этой странице вы найдете наши основные рабочие листы по математике, предназначенные для 1-6 классов по математике. Наши дополнительные упражнения и рабочие листы подходят для любой математической школы, онлайн-обучения математике, и коррекционное сложение и математическая практика. Для математического класса 1 у нас есть большой выбор рабочих листов для сложения изображений, рабочих листов для сложения строк, задач на сложение одной цифры, сложения до 100 рабочих листов, упражнений на сложение связей и рабочих листов с упражнениями на подсчет пропусков.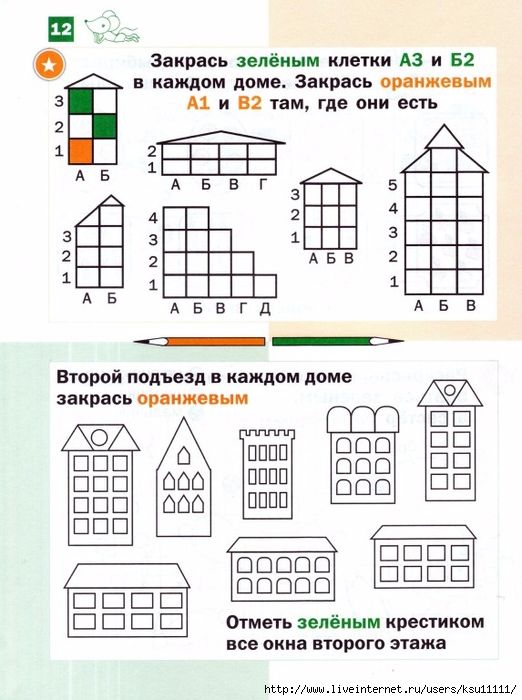

Для второго и третьего математических классов вы можете использовать наше дополнение до 1000 и 10000 рабочих листов, 3- и 4-значные листы сложения, добавление одинаковых рабочих листов дробей, пропуск подсчета по 2-значным рабочим листам, отсутствующие слагаемые и пропущенные рабочие листы цифр и наши головоломки на сложение и квадраты на сложение. Наши головоломки на сложение — отличный способ для студентов, изучающих математику, попрактиковаться в общей логике и математических навыках.

Для старших классов начальных классов по математике мы предлагаем задания на сложение больших чисел, сложение различных дробей, сложение десятичных дробей, сложение целых чисел и более сложные уровни наших математических головоломок на сложение. Отличный способ научиться сложению и математике — выполнить нашу оценку материалов для задач на сложение. Это придаст учащимся больше уверенности в проверке и оценке своей работы и дополнительных навыков.

Наши головоломки-сложения Fubuki имеют 3 уровня сложности, и цель состоит в том, чтобы заполнить сетки 3 на 3 числами от 1 до 9 так, чтобы все строки и столбцы складывались в заданные суммы.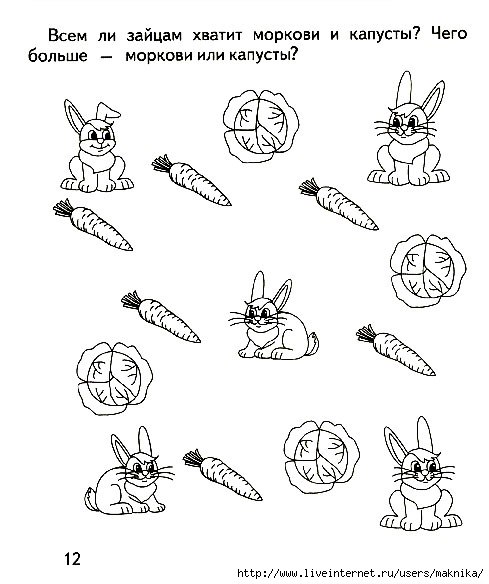 Очень сложно и здорово тренировать математический мозг.

Квадраты сложения также являются сложными математическими задачами. Учащимся необходимо заполнить таблицы и вычислить значения недостающих слагаемых в квадратах. Поиск решений этих головоломок на сложение требует навыков как на сложение, так и на вычитание.

Наши рабочие листы для сложения по математике с 1 по 6 классы охватывают: рабочие листы сложения в картинках, рабочие листы сложения строк, рабочие листы для сложения числовых связей, рабочие листы для сложения однозначных чисел, упражнения по сложению с пропуском счета, добавление рабочих листов для сложения 2, 3 и 4 цифр, добавление рабочих листов с большими числами, добавление рабочих листов с дробями, добавление десятичных знаков, добавление целых и отрицательных чисел, оценка сумм сложения, математические головоломки на сложение, головоломки на сложение квадратов, рабочие листы с отсутствующими сложениями и смешанные рабочие листы на сложение и вычитание.

Наши коррекционные дополнительные ресурсы основаны на следующих математических темах Сингапурской учебной программы:

• Завершение дополнительных связей и семейных фактов
• Решение задач на сложение с помощью изображений
• Способность показать работу шагов сложения в числовых рядах
• Возможность складывать однозначные числа с перегруппировкой и без нее
• Добавление 2- и 3-значных чисел до 1000
• Сложение больших чисел до десятков тысяч, сотен тысяч и миллионов
• Знание соотношения между сложением и вычитанием
• Способность находить и вычислять недостающие слагаемые
• Способность оценивать суммы и результаты задач на сложение
• Умение складывать похожие и разные дроби
• Возможность складывать десятичные числа
• Возможность складывать отрицательные и целые числа

Наши новые материалы? Подписывайтесь на нас.

Посмотрите наши

Головоломки

Испытай себя

Активное решение проблем Института пятиборья

Обучение решению проблем, которые постоянно претерпевают изменения

Программа «Математическое пятиборье» ^® дает опыт мыслительных процессов, необходимых для активного решения проблем. Серия из 20 игр по математическому пятиборью дает ученикам K-7 опыт дедуктивных и индуктивных рассуждений за счет многократного использования последовательного мышления, а также нелинейного, интуитивного мышления. Воздействие таких форм мышления помогает учащимся относиться к реальным жизненным ситуациям решения проблем и учиться «думать на ходу».

Четыре раздела, приведенные ниже, объясняют следующее: Определение активного решения задач, что такое математика, три типа математического мышления и концептуальное понимание с использованием конкретных и графических моделей.

---

СЕКЦИЯ 1

Определение активного решения проблем

Решение проблем можно разделить на две категории:

Обычные и нестандартные

Решение рутинных проблем , подчеркивает использование наборов известных или предписанных процедур (алгоритмов) для решения проблем. Сила этого подхода в том, что его легко оценить с помощью бумажно-карандашных тестов. Поскольку современные компьютеры и калькуляторы могут быстро и точно выполнять самые сложные схемы алгоритмов для решения многоэтапных рутинных задач, типичное рабочее место не требует высокого уровня квалификации в решении рутинных задач. Однако сегодняшнее рабочее место требует от многих сотрудников умения решать нестандартные задачи.

Решение нестандартных задач , подчеркивает использование эвристики и часто практически не требует использования алгоритмов. В отличие от алгоритмов, эвристики — это процедуры или стратегии, которые не гарантируют решение проблемы, но обеспечивают более вероятный метод обнаружения решения. Построение модели и рисование картины проблемы — две основные эвристики решения проблем. Изучение ситуаций в конце игры дает учащимся опыт использования эвристики сведения задачи к аналогичной, но более простой задаче и решения задачи в обратном направлении, то есть от ее решения к исходному состоянию. Другие эвристики включают описание проблемной ситуации, классификацию информации и поиск ненужной информации.

Существует две категории решения нестандартных задач:

Статическая и активная

Статические-нестандартные проблемы имеют фиксированную известную цель и фиксированные известные элементы, которые используются для решения проблемы. Решение головоломки является примером статической-нестандартной задачи. Имея все части головоломки и изображение цели, учащимся предлагается расположить части так, чтобы завершить картину. Различные эвристики, такие как классификация частей по цвету, соединение частей, образующих границу, или соединение частей, которые образуют характерный элемент головоломки, например, флагштока, являются типичными способами, которыми люди пытаются решить такие проблемы.

Активно-нестандартные задачи могут иметь фиксированную цель с изменяющимися элементами, изменяющуюся цель или альтернативные цели с фиксированными элементами или изменяющиеся или альтернативные цели с изменяющимися элементами. Эвристики, используемые в этой форме решения проблем, известны как стратегии. Люди, изучающие такие проблемы, должны научиться изменять или адаптировать свои стратегии по мере развития проблемы.

---

РАЗДЕЛ 2

Что такое математика?

В математическом сообществе, как и в обществе в целом, растет убеждение в том, что изучение математики должно развивать у всех учащихся понимание математики, которое сохраняется на протяжении всей жизни и развивается в соответствии с постоянно меняющимися ситуациями и переменными. С нашей точки зрения, математика — это область исследований, которая развивает способность критически наблюдать, классифицировать, описывать и анализировать данные логическим образом с использованием как индуктивных, так и дедуктивных методов. В отличие от стерилизованного и бессвязного метода, в котором часто преподавалась школьная математика, математика представляет собой творческое и эстетическое изучение закономерностей, геометрических и числовых отношений. Он динамичен, а не пассивен по своей природе и должен вовлекать студентов в стратегическое мышление, исследуя множество возможностей и переменных, которые постоянно меняются, как и жизнь.

Программа «Математическое пятиборье®», объединяющая «Приключения в решении задач», рабочие тетради I и II, игры «Математическое пятиборье®» и исследовательские упражнения, книги I и II, была разработана для реализации определения математики, описанного выше. Игры разделены на четыре уровня по классам: К-1, 2-3, 4-5 и 6-7, по пять игр на каждом уровне.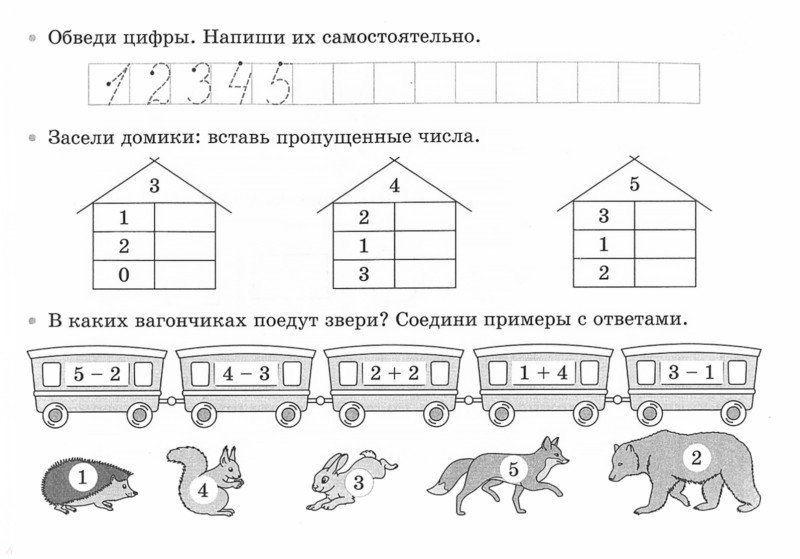 Название программы «Математическое пятиборье®» было придумано, чтобы уподобить ее всемирной серии спортивных соревнований, составляющей десятиборье Олимпийских игр. В мире легкой атлетики Decathlon ценится за то, что ценит и вознаграждает людей, развивших разнообразные спортивные способности. Напротив, математическое сообщество в целом редко ценит или вознаграждает людей с разнообразными математическими способностями. Игры Mathematics Pentathlon® способствуют разнообразию математического мышления, объединяя пространственное/геометрическое, арифметическое/вычислительное и логическое/научное мышление на каждом уровне раздела. Поскольку каждая из 5 игр требует от учащихся расширения их мыслительных процессов, она привлекает учащихся самых разных уровней способностей, от тех, кто считается «одаренным и талантливым», до «средних» и «групп риска».

Формат игр был выбран по двум причинам. Во-первых, игры стратегического характера требуют, чтобы учащиеся рассмотрели несколько вариантов и сформулировали стратегии, основанные на ожидаемых ответных действиях другого игрока. Математическое пятиборье® еще больше развивает этот тип мышления, объединяя учащихся в группы по четыре человека и команды по два человека. Команды поочередно ходят по очереди, а партнеры по команде поочередно принимают решения о конкретных розыгрышах, обсуждая вслух различные варианты и возможности. Таким образом, все члены группы лучше понимают множество вариантов и стратегий. По мере того, как учащиеся играют в эти игры с течением времени, они учатся составлять план на основе лучших доступных вариантов, а также переоценивать и корректировать этот план на основе того, что действовала другая команда, чтобы изменить свои предыдущие идеи. Благодаря этому интерактивному процессу обмена идеями и возможностями учащиеся учатся думать на много шагов вперед, сочетая индуктивное и дедуктивное мышление. Во-вторых, в качестве формата были выбраны игры, поскольку они являются мощным мотивационным инструментом, привлекающим учащихся с различными способностями и уровнями интересов, чтобы они проводили больше времени над заданием, развивая базовые навыки, а также навыки решения проблем. В то время как азартные игры, основанные на гонках, обычно используются в классах, они обычно не вызывают любопытства учащихся в течение длительного периода времени. Учащиеся могут сыграть в такие игры один или два раза, но затем теряют интерес, так как они не вызывают серьезных затруднений. Игры Mathematics Pentathlon® поставили перед учащимися серьезную задачу по развитию их способности мыслить стратегически и решать проблемы, которые постоянно претерпевают изменения. В результате мы рассматриваем активное решение проблем и стратегическое мышление, как описано выше, как важнейший фокус учебной программы по математике.

---

РАЗДЕЛ 3

3 типа математического мышления

Интеграция пространственного/геометрического, вычислительного,
и логического/научного рассуждений

В большинстве занятий по математике упор делается на знание учащимися основных арифметических фактов. В то время как программа математического пятиборья обеспечивает большую практику с овладением основными фактами, она выходит далеко за рамки обучения арифметическим навыкам. Таблица математического содержания и стандартов для 20 игр по математическому пятиборью показывает, как каждая игра решает несколько задач математического содержания и процесса (см. на задней обложке руководства). Эти цели были сгруппированы в логические/научные рассуждения, вычислительные рассуждения и пространственные/геометрические рассуждения. Каждая из этих категорий описана ниже.

Пространственное/геометрическое мышление

Пространственная визуализация включает в себя способность представлять объекты и изображения мысленным взором, а также способность мысленно преобразовывать положения и исследовать свойства этих объектов/изображений. Большое количество математических исследований приходит к выводу, что способность к пространственному мышлению тесно связана с решением математических задач более высокого уровня и геометрическими навыками, а также с общими достижениями учащихся в математике. Многие игры по математическому пятиборью делают акцент на пространственных рассуждениях, а некоторые объединяют эту форму мышления с логическими и вычислительными рассуждениями.

Вычислительное мышление

Многие игры по математическому пятиборью включают вычисления в структуру игры. Уделение большего количества времени отработке арифметических навыков действительно приводит к повышению успеваемости учащихся в классе, а также при выполнении стандартных тестов. Но в играх по математическому пятиборью, в которых упор делается на вычисления, недостаточно полагаться только на арифметические навыки. Чтобы добиться успеха в этих играх, учащиеся также должны использовать свои способности к логическому мышлению, чтобы рассмотреть несколько вариантов и решить, какие из них максимизируют их способность достичь цели (целей) игры.

Логическое/научное мышление

Одним из самых важных жизненных навыков, не говоря уже о математических способностях, является способность мыслить логически. Для логических рассуждений необходимы процесс наблюдения, классификации, выдвижения гипотез, экспериментирования, индуктивного и дедуктивного мышления. Но где дети учатся этим фундаментальным жизненным навыкам? Стратегические игры дают учащимся возможность развивать эту форму мышления. Каждая из игр «Математическое пятиборье» представляет собой стратегическую игру, которая развивает у учащихся навыки логического мышления в процессе исследования различных вариантов и выбора лучших вариантов. В то же время учащиеся развивают навыки научного мышления, учась лучше наблюдать за игровыми переменными и вариантами. Игра в игры с течением времени позволяет развивать гипотетические рассуждения, поскольку учащиеся анализируют последовательности ситуаций «если-то» и делают выбор, связывая индуктивное и дедуктивное мышление.

Хотя в каждой из 20 игр одна форма математического мышления может быть поставлена ​​выше другой, каждая игра объединяет как минимум две категории математического мышления. Кроме того, пять игр на каждом уровне дивизиона уравновешивают три типа рассуждений.

---

РАЗДЕЛ 4

Концептуальное понимание с использованием конкретных и графических моделей Понимание

С момента своего создания Национальный совет учителей математики (NCTM) призывал к созданию концептуальной учебной программы в школах по всей стране. Самые последние психологические и педагогические исследования показали, что концептуальное понимание является ключевым свойством людей, хорошо разбирающихся в математике. Кроме того, большое количество исследований, проведенных за последние четыре десятилетия, показывает, что эффективное использование физических и изобразительных моделей математических понятий улучшает концептуальное понимание учащихся, навыки решения задач и общие достижения в математике. Исследования также показывают, что использование конкретных и изобразительных моделей улучшает пространственное воображение и геометрическое мышление.

  Математическое пятиборье ^®   Программа  включает в себя различные конкретные и графические модели для развития у учащихся концептуального понимания многих важных математических концепций, которые включают вычислительные, пространственные и логические рассуждения. Кроме того, играя в эти игры в кооперативных группах, как предлагается в этой публикации, учащиеся также улучшают свои устные и письменные коммуникативные навыки посредством обсуждения математических идей и отношений.