Квадрат фибоначчи: Web in Math: Магия чисел Фибоначчи: математика, которая вдохновляет

Web in Math: Магия чисел Фибоначчи: математика, которая вдохновляет

Числа Фибоначчи – один из самых популярных “математических” поисковых запросов в сети Интернет. В этом легко убедиться: если вы попробуете ввести слово “числа” в поисковую систему Google, то увидите, что первый по популярности запрос, состоящий из двух слов, первое из которых “числа” – это именно “числа фибоначчи”.

Математика логична, функциональна и просто… невероятна. Математический маг Артур Бенджамин (Arthur Benjamin) в своем выступлении на TED раскрывает непревзойденную магию чисел Фибоначчи, исследует скрытые свойства странного и чудесного набора чисел – последовательности Фибоначчи. (И он напоминает вам, что математика может вдохновлять!)

Почему мы изучаем математику? По сути, есть три причины: расчёт, приложение и последняя (к сожалению, наименее важная с точки зрения времени, которое мы ей уделяем) – это вдохновение.

Математика – это наука о моделях, и мы изучаем её, чтобы научиться мыслить логично, критично и творчески, но та математика, которую мы изучаем в школе чаще всего неэффективно мотивирована, и когда наши студенты спрашивают: «Почему мы это изучаем?» – то им часто приходится слышать, что это необходимо в предстоящем математическом классе или для будущих тестов. Но было бы здорово, если бы мы хоть иногда занимались математикой просто потому, что это весело или красиво или потому, что она волнует ум. Я знаю, что многие люди не имеют возможности увидеть, как это происходит, поэтому позвольте мне показать вам небольшой пример из моей любимой коллекции чисел, чисел Фибоначчи. (Аплодисменты)

Да! Тут уже есть фанаты Фибоначчи. Это здорово.

Эти цифры могут быть истолкованы различными способами. С точки зрения вычислений, их так же легко понять, как 1 + 1 = 2. Тогда 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8, и так далее. На самом деле человек, которого мы называем Фибоначчи, носил имя Леонардо из Пизы, и эти цифры появляются в его книге Liber Abaci, которая научила западный мир методам арифметических операций, используемых сегодня. С точки зрения приложений, числа Фибоначчи появляются в природе удивительно часто. Количество лепестков на цветке – это типичное число Фибоначчи. Количество спиралей на подсолнухе или ананасе также тяготеет к числу Фибоначчи.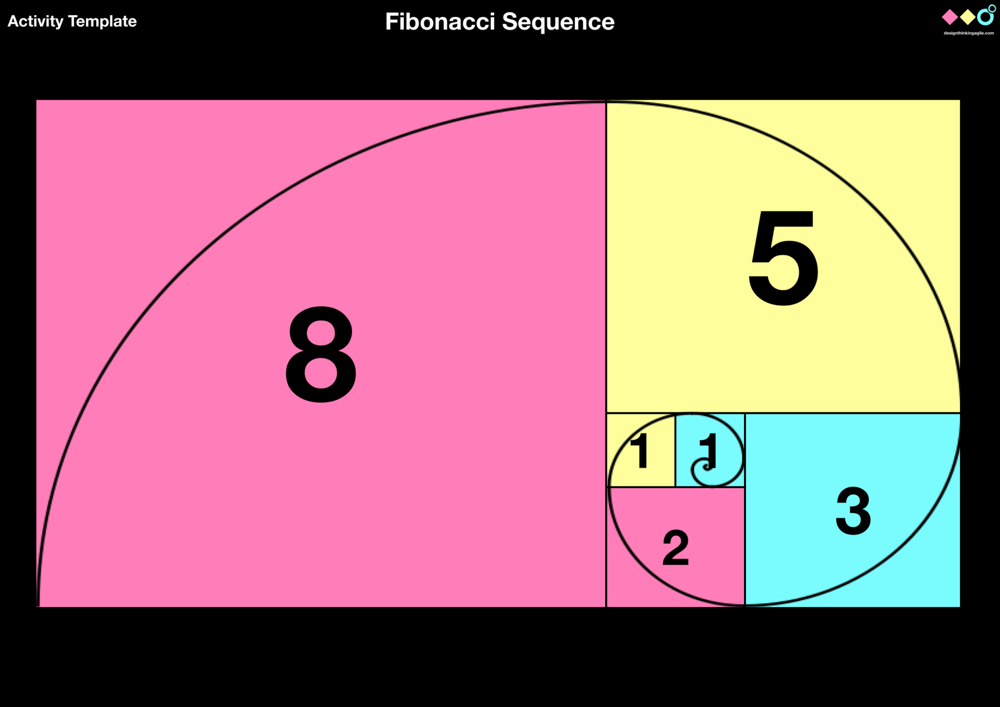

В самом деле, есть много больше применений чисел Фибоначчи, но наиболее вдохновляющими, по моему мнению, являются прекрасные цифровые образцы, которые они демонстрируют. Позвольте мне показать вам один из моих любимых. Предположим, что вы хотите возвести число в квадрат, и, честно говоря, кто не хотел бы? (Смех)

Давайте посмотрим на квадраты первых нескольких чисел Фибоначчи. 1 в квадрате равно 1, 2 в квадрате – 4, 3 в квадрате – это 9, 5 в квадрате – 25 и так далее. Теперь известно, что при сложении последовательных чисел Фибоначчи вы получите следующее число Фибоначчи. Верно? Вот как они созданы. Но вы не ожидаете ничего особенного от сложения их квадратов. Но давайте проверим это. 1 + 1 = 2, и 1 + 4 = 5. И 4 + 9 = 13, 9 + 25 = 34, и да, шаблон повторяется.

Фактически тут есть ещё один шаблон. Предположим, вы хотите проанализировать сложение квадратов нескольких первых чисел Фибоначчи. Давайте посмотрим, что мы получим. Так что 1 + 1 + 4 = 6. Добавляем к этому 9 и получаем 15.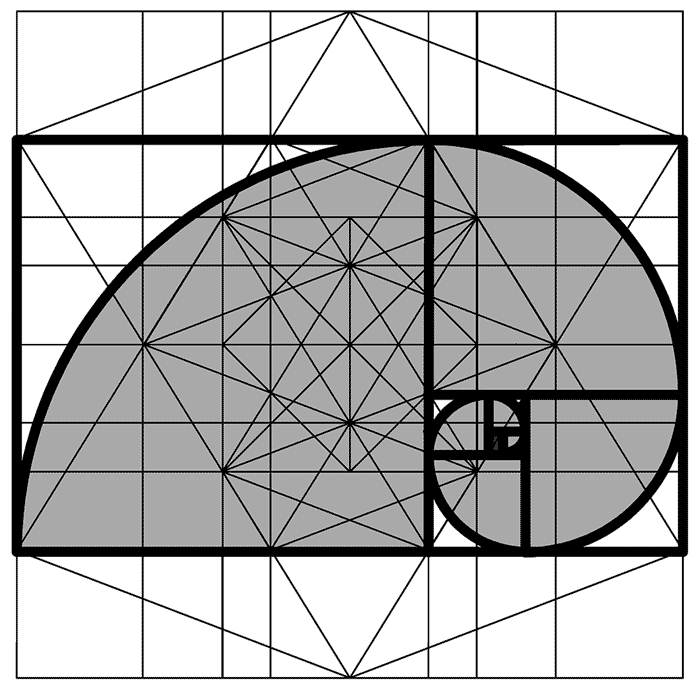 Добавив 25, мы получаем 40. Добавив 64, мы получаем 104. Теперь посмотрите на эти цифры. Они не являются числами Фибоначчи, но если вы посмотрите на них внимательно, вы увидите, что числа Фибоначчи скрыты внутри них.

Вы это видите? Я покажу вам это. 6 – это 2 × 3, 15 — это 3 × 5, 40 — это 5 × 8, 2, 3, 5, 8 – кому мы должны быть признательны?

(Смех)

Фибоначчи! Конечно.

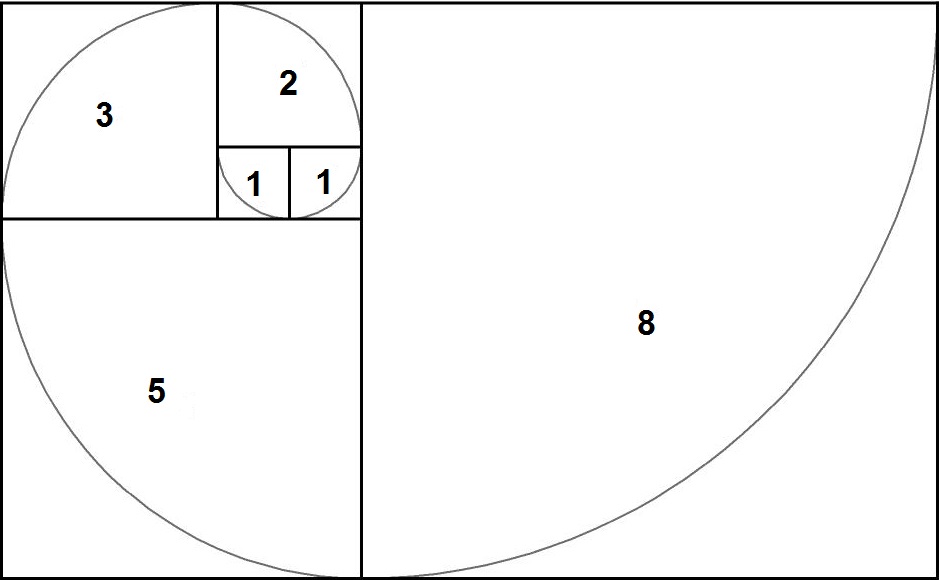
Обнаружить эти шаблоны было забавно, но ещё большее удовлетворение – понять, почему они являются подлинными. Давайте посмотрим на последнее уравнение. Почему квадраты 1, 1, 2, 3, 5 и 8 составляют 8 × 13? Я покажу вам это, нарисовав простую картину. Мы начнем с квадрата единицы, и рядом с этим ещё один квадрат единицы. Вместе они образуют прямоугольник один на два. Ниже я поставлю квадрат 2 на 2, потом квадрат 3 на 3, под ним квадрат 5 на 5, и затем квадрат 8 на 8, получается один гигантский прямоугольник, правильно?

Теперь позвольте мне задать вам простой вопрос: какова площадь прямоугольника? С одной стороны, это сумма площадей квадратов внутри него, правильно? Так же, как мы создали его.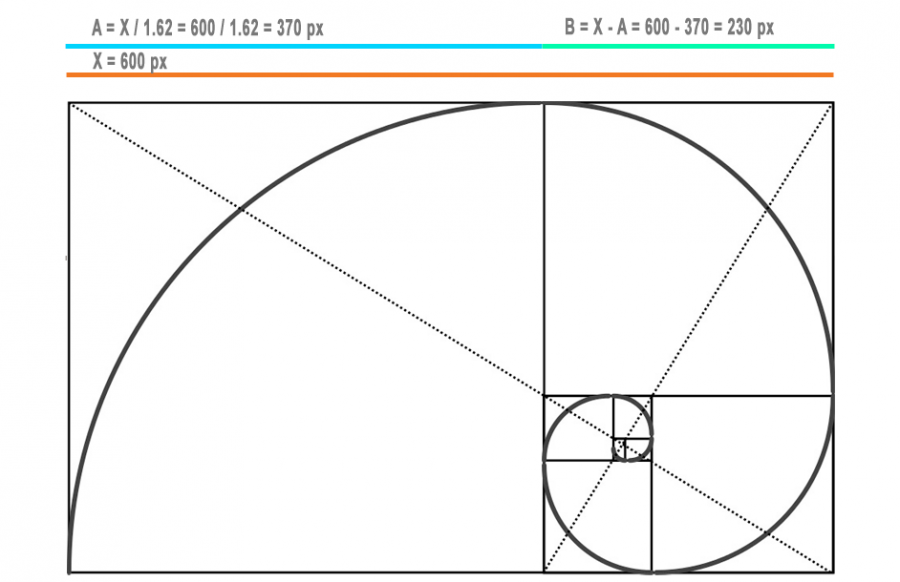 Это 1 в квадрате плюс 1 в квадрате плюс 2 в квадрате плюс 3 в квадрате плюс 5 в квадрате плюс 8 в квадрате. Верно? Это площадь. С другой стороны, поскольку это прямоугольник, площадь равна его высоте, умноженной на ширину. Высота равна 8, а ширина – 5 + 8, чем и является следующее число Фибоначчи 13. Верно? Таким образом, площадь равна 8 × 13. Так как мы правильно рассчитали площадь двумя разными способами, числа должны быть одинаковыми, и вот почему квадраты 1, 1, 2, 3, 5 и 8 складываются в 8 × 13.

Если мы продолжим этот процесс, мы создадим прямоугольники размером 13 на 21, 21 на 34 и так далее.

Теперь проверьте это. Если вы разделите 13 на 8, вы получите 1,625. И если вы разделите большее число на меньшее число, то эти коэффициенты становятся всё ближе и ближе к числу 1.618, известному многим людям как Золотое сечение, числу, которое очаровывало математиков, учёных и художников на протяжении многих веков.

Я показываю всё это вам потому, что много что в математике имеет красивые стороны, которые, боюсь, не получают достаточного внимания в наших школах. Мы тратим много времени на изучение вычислений, но давайте не забывать и о применении, которое включает, возможно, наиболее важное применение – научиться думать.

Если я мог бы обобщить это в одном предложении, это звучало бы так: математика — это не только поиск решений для Х, но также и поиск причин таких решений.

Большое спасибо.

(Аплодисменты)

Исчезающая клетка и числа Фибоначчи / Модели // Математические этюды

Чтобы было легче разгля­деть этот парал­ле­лограмм, посмот­рим на ана­лог «тре­уголь­ника Гард­нера» меньшего размера — со сто­ро­нами $3$ и $5$.

Все вершины всех частей лежат в узлах квад­рат­ной сетки. И в том, что гра­ницы частей не скла­ды­ваются в прямую линию, а обра­зуют сто­роны парал­ле­лограмма (с верши­нами в узлах), легко убе­диться, посчи­тав по кле­точ­кам наклон каж­дого отрезка. В прямо­уголь­нике $5\times 13$ в жёл­том тре­уголь­нике отноше­ние кате­тов равно $\tg \alpha=\dfrac{3}{8}$, а для синей трапе­ции тангенс «того же» угла равен $\dfrac{2}{5}$. Для софизма с тре­уголь­ни­ком: в вари­анте Гард­нера $\dfrac{2}{5}\ne \dfrac{3}{8}$, в уменьшен­ном вари­анте $\dfrac{1}{2}\ne \dfrac{2}{3}$. Во всех слу­чаях сто­роны парал­ле­лограмма, как и должно быть, попарно равны и парал­лельны. Вершины парал­ле­лограмма лежат в узлах сетки, а вот внутри парал­ле­лограмма нет ни одного узла. Что, впро­чем, неуди­ви­тельно, если вспом­нить, что площадь равна еди­нице и ⁠⁠формулу Пика.

Разо­бравшись с несты­ков­кой, задума­емся, как кон­стру­и­ро­вать подоб­ные софизмы. Можно заме­тить, что встре­чавши­еся числа $1,$ $2,$ $3,$ $5,$ $8,$ $13$ являются нача­лом знаме­ни­той после­до­ва­тель­но­сти чисел Фибо­наччи

$ \{1,$ $1,$ $2,$ $3,$ $5,$ $8,$ $13,$ $21,$ $34,$ $55,$ $89,\ \dotso\}.$

Эта после­до­ва­тель­ность зада­ётся рекур­рент­ным соот­ноше­нием $$ F_n=F_{n-1}+F_{n-2} $$ и парой началь­ных чисел $F_0=1$, $F_1=1$.

Между чис­лами Фибо­наччи суще­ствует много инте­рес­ных соот­ноше­ний. 2$ и прак­ти­че­ски нераз­ли­чимы.

Появившийся еди­нич­ный парал­ле­лограмм и его диаго­наль являются объек­тами кра­си­вой науки, начала кото­рой заложил Герман Мин­ков­ский, — геомет­рии чисел. Более точно — геомет­ри­че­ской интер­пре­тации цеп­ных дро­бей.

На рисунке пока­зана прямая $x=\dfrac{1+\sqrt{5}}2y$ и отме­чены наи­бо­лее близ­кие к ней узлы сетки. Их коор­ди­наты — сосед­ние числа Фибо­наччи, а сами точки, пры­гая пооче­рёдно то выше прямой, то ниже, при­ближаются к ней. А отноше­ния сосед­них чисел Фибо­наччи дают в неко­то­ром смысле наи­лучшие раци­о­наль­ные при­ближе­ния золо­того сече­ния… Заин­триго­ван­ному чита­телю сове­туем брошюру Вла­ди­мира Иго­ре­вича Арнольда «Цеп­ные дроби».

Каза­лось бы, про­сто фокус, про­сто кар­тинки, ходящие в интер­нете… А сколько нетри­ви­аль­ной матема­тики в них заложено!

Лите­ра­тура

Игна­тьев Е. И. В цар­стве сме­калки или арифме­тика для всех: книга для семьи и школы. Книга вто­рая. — Санкт-Петер­бург, 1909. — [Раз­дел «Геомет­ри­че­ские софизмы»]. — [Сле­дует смот­реть изда­ния 1908—1924 годов — они суще­ственно пол­нее и содержа­тель­нее после­дующих].

Кор­дем­ский Б. А. Матема­ти­че­ская сме­калка. — М.: ГТТЛ, 1954. — [Глава 14 «Числа древ­ние, но вечно юные», Б. «Числа Фибо­наччи»].

Sillke T. Geometrical Paradox. — [Стоит обра­тить внима­ние на обшир­ный спи­сок лите­ра­туры].

Спи­вак А. В. Числа Фибо­наччи // Новая школь­ная энцик­лопе­дия. Т. «Небес­ные тела. Числа и фигуры». — М.: Росмэн-пресс, Мир книги, 2005. — Стр. 396—401. — [Пере­из­да­ние: «Матема­тика: пол­ная энцик­лопе­дия». — М.: Росмэн-пресс, 2020].

Воро­бьёв Н. Н. Числа Фибо­наччи. — 4‐е изд., доп. — М.: Наука, 1978. — (Попу­ляр­ные лекции по матема­тике; Вып. 6).

Грэ­хем Р., Кнут Д., Паташ­ник О. Кон­крет­ная матема­тика: Осно­ва­ние информа­тики. — М.: Мир, 1998. — [2‐e изд.: М.: Мир, Бином, 2009].  — [§ 6.6 «Числа Фибо­наччи»].

Кокс­тер Г. С. М. Вве­де­ние в геомет­рию. — М.: Наука, 1966. — [Глава 11 «Золо­тое сече­ние и фил­ло­так­сис», стр. 236—252].

Арнольд В. И. Цеп­ные дроби. — М.: МЦНМО, 2009. — (Биб­лио­тека «Матема­ти­че­ское про­свеще­ние»; Вып. 14).

Фил­ло­так­сис // Матема­ти­че­ская состав­ляющая / Ред.-сост. Н. Н. Андреев, С. П. Коно­ва­лов, Н. М. Паню­нин. — Вто­рое изда­ние, расши­рен­ное и допол­нен­ное. — М. : Матема­ти­че­ские этюды, 2019. — С. 78, 318.

Другие модели раздела «Площади фигур и равносоставленность»

  Площадь трапеции  Разбиение Дьюдени  Площадь правильного двенадцатиугольникаЗадача о диване

Математические этюды

Фибоначчи и квадратные числа – Первые шаги

Вы здесь

Главная » Публикации МАА » Периодические издания » Конвергенция » Фибоначчи и квадратные числа – Первые шаги

‹ Фибоначчи и квадратные числа – Суд Фридриха II вверх Числа Фибоначчи и квадратные числа – соответствующие числа ›

Автор(ы): 

Патрик Хедли

Как найти два квадрата, сумма которых равна квадрату? Леонардо отвечает на этот вопрос несколькими способами, причем первый метод следует из простого наблюдения, которое вдохновляет на протяжении всей книги:

Я думал о происхождении всех квадратных чисел и обнаружил, что они возникают из возрастающей последовательности нечетных чисел; ибо единица есть квадрат, и из нее сделан первый квадрат, а именно 1; к этой единице прибавляется 3, образуя второй квадрат, а именно 4, с корнем 2; если к сумме добавить третье нечетное число, а именно 5, получится третий квадрат, а именно 9, с корнем 3; и, таким образом, суммы последовательных нечетных чисел и последовательность квадратов возникают вместе в порядке [стр. 4].

Таким образом, суммы 1 + 3 + 5 + 7 = 16 и 1 + 3 + 5 + 7 + 9 = 25 являются квадратами. Поскольку мы добавляем квадрат 9 к первой сумме, чтобы получить вторую, мы имеем 16 + 9 = 25 как сумму двух квадратов, добавленных к третьему квадрату. Леонардо объясняет, что мы могли бы использовать любой нечетный квадрат вместо 9, чтобы сделать то же самое. Например, используя 49, мы получаем 1 + 3 + … + 47 = 576 и 1 + 3 + … + 49 = 625, поэтому 576 + 49 = 625 — еще одна сумма той же формы. Далее Леонардо отмечает, что последние два или более членов этих сумм нечетных чисел также могут в сумме давать квадрат. Например, четный квадрат можно разделить на последовательные нечетные числа, например 17 + 19.= 36. Так как 1 + 3 + … + 15 = 64 и 1 + 3 + … + 19 = 100, мы получаем 64 + 36 = 100.

Продолжая, Леонардо ставит следующую задачу:

Я хочу найти три квадрата так, чтобы сумма первого и второго, а также всех трех чисел была квадратными числами [стр. 105].

Он объясняет свое решение так:

Я найду первые два квадратных числа, сумма которых равна квадрату и которые взаимно просты. Пусть даны 9 и 16, у которых в сумме 25, квадратное число. Я возьму квадрат, представляющий собой сумму всех нечетных чисел, меньших 25, а именно квадрат 144, корень которого является средним между крайними значениями тех же нечетных чисел, а именно 1 и 23. Из суммы 144 и 25 результатов, по факту 169, который представляет собой квадратное число. И таким образом находятся три квадратных числа, для которых суммы первых двух и всех трех вместе являются квадратными числами [стр. 105].

Фактически, Леонардо указывает, что этот метод можно распространить на любое количество квадратов, поскольку (1 + 3 + … + 167) + 169 = 7056 + 169 = 84 ² + 13 ² = 85 ² = 7225, и (1 + 3 + … + 7223) + 7225 = 3612

2 + 85 ² = 3613 ² . Таким образом, мы получаем следующую последовательность квадратов: 92,\end{массив}\]

и так далее.

Патрик Хедли, «Фибоначчи и квадратные числа — первые шаги», Convergence (август 2011 г.)

Convergence

Dummy View — НЕ УДАЛЯТЬ

Зарегистрируйтесь сейчас для AMC 8 и 12/10

Ваш новый портал для участников MAA запущен!

подписчикам скидка 25%

Плитки и спираль Фибоначчи

Числа Фибоначчи — это ряды чисел или последовательность , где каждое следующее число является суммой двух предыдущих чисел. Последовательность начинается с 0 , а следующее число — 1 . Третье число тоже 1 , потому что 0 + 1 = 1 . Следующие за ним числа: 1 + 1 = 2 , 1 + 2 = 3 и так далее. Для первых 10 чисел в последовательности имеем:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34

Из-за того, что каждое число в последовательности является суммой двух предыдущих, числа Фибоначчи иногда используются для представления естественных темпов роста.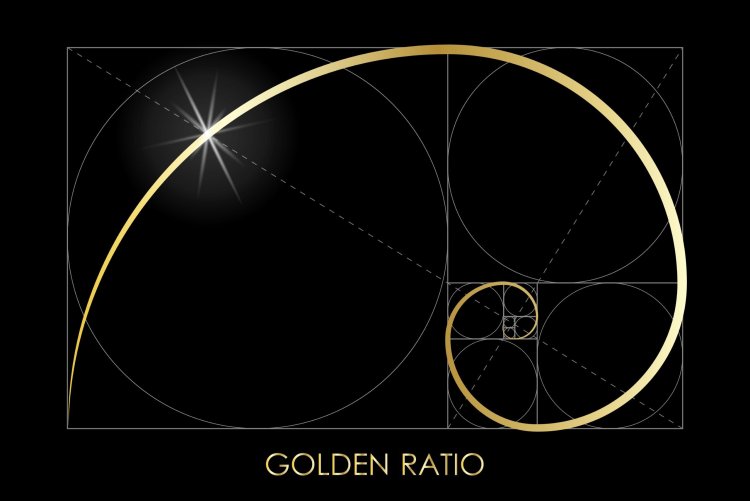

На рисунке выше нарисованы квадраты со сторонами, длина которых равна числу Фибоначчи. Вы видите, что квадраты идеально выложены вместе по спирали, начиная с самого маленького квадрата и затем двигаясь против часовой стрелки. Кроме того, настоящая спираль вписана в квадраты с использованием дуг четверти окружности, которые являются радиусом числа Фибоначчи для этого квадрата. По мере рисования большего количества квадратов и дуг поверхность рисования будет заполняться «естественным образом». Каждый больший квадрат будет располагаться рядом с меньшими без каких-либо зазоров, а спираль будет плавно расти с естественным изгибом.

Генерация чисел Фибоначчи

Простой способ показать числа Фибоначчи — сгенерировать их в цикле, а затем показать каждое число как счет игры. Вот способ показать первые 10 чисел:

 пусть f0 = 0
пусть f1 = 1
пусть фибо = 0
для (пусть я = 0; я < 10; я ++) {
    info.setScore (фибоначчи)
    f0 = f1
    f1 = Фибоначчи
    Фибоначчи = f1 + f0
    пауза(1000)
} 

Мозаика Фибоначчи

Мозаика Фибоначчи — это спрайты с квадратными изображениями.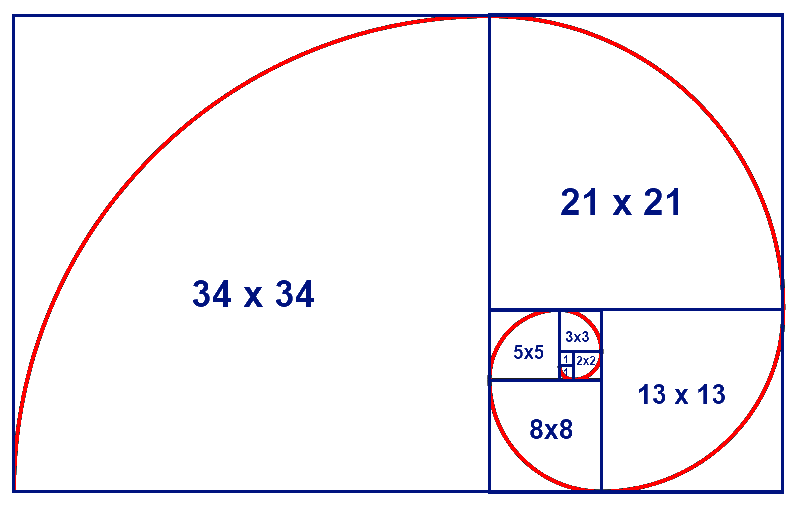 Стороны квадратного изображения — это длина текущего числа Фибоначчи. По мере создания каждого квадратного спрайта они располагаются рядом с предыдущим квадратом по схеме против часовой стрелки. Для этого мы используем последовательность вращения из 4 шагов, которая размещает новые квадраты рядом с предыдущим квадратом в правильном месте.

Текущий шаг вращения сохраняется в переменной вращения . Полный поворот происходит за 4 шага, поэтому переменная rotate сбрасывается на 0 после того, как квадратный спрайт помещается в шаг вращения 4 .

Мы должны помнить местоположение каждого предыдущего спрайта, чтобы следующий спрайт располагался в нужном месте. Предыдущий спрайт сохраняется в переменной

fibSprite0 . Первый квадрат является «виртуальным», так как длина его сторон равна 9.0073 0 .

Последовательность выполняется для 14 квадратов, и для каждого квадрата используется свой цвет.

 пусть fibSprite: Sprite = null
пусть fibSquare: Image = null
пусть вращается = 0
пусть клр = 1
позвольте повторить = 14
пусть f = 0
пусть f0 = 0
пусть f1 = 1
пусть fibSprite0 = sprites.create(img`.`, 0)
fibSprite0.top += 20
game.onUpdateInterval(1000, функция () {
    если (повторить > 0) {
        f0 = f1
        f1 = f
        f = f1 + f0
        информация.setScore(f)
        повтор += -1
        fibSquare = image.create(f, f)
        fibSquare.fillRect(0, 0, f, f, clr)
        клр += 1
        fibSprite = sprites.create(fibSquare, 0)
        если (повернуть == 0) {
            fibSprite.верхний = fibSprite0.нижний
            fibSprite.left = fibSprite0.left
            повернуть += 1
        } иначе если (повернуть == 1) {
            fibSprite.bottom = fibSprite0.bottom
            fibSprite.left = fibSprite0.right
            повернуть += 1
        } иначе если (повернуть == 2) {
            fibSprite.bottom = fibSprite0.top
            fibSprite.right = fibSprite0.right
            повернуть += 1
        } иначе если (повернуть == 3) {
            fibSprite.  top = fibSprite0.top
            fibSprite.right = fibSprite0.left
            повернуть = 0
        }
        fibSprite0 = fibSprite
    }
}) 

Спираль Фибоначчи

Мы можем добавить спираль Фибоначчи к квадратам в приведенной выше программе, используя функцию рисования дуг. Функция может использовать текущее значение числа Фибоначчи в качестве радиуса дуги. Чтобы узнать направление рисования дуги, следует последовательность вращения. Дуги рисуются на изображениях квадратов с помощью случайных точек, которые рисуют линию дуги.

 пусть f = 0
пусть х = 0
пусть у = 0
пусть вращается = 0
пусть fibSquare: Image = null
функция drawArc() {
    // рисуем дугу окружности, используя случайные точки!
    для (пусть я = 0; я < 100000; я ++) {
        х = случайный (0, f)
        у = случайный (0, f)
        // проверяем, будет ли точка рисовать круг
        если (x * x + y * y >= (f - 1) ** 2 && x * x + y * y < (f + 1) ** 2) {
            если (повернуть == 0) {
                х = е - х
                у = е - у
            } иначе если (повернуть == 1) {
                х = е - х
            } иначе если (повернуть == 3) {
                у = е - у
            }
            fibSquare.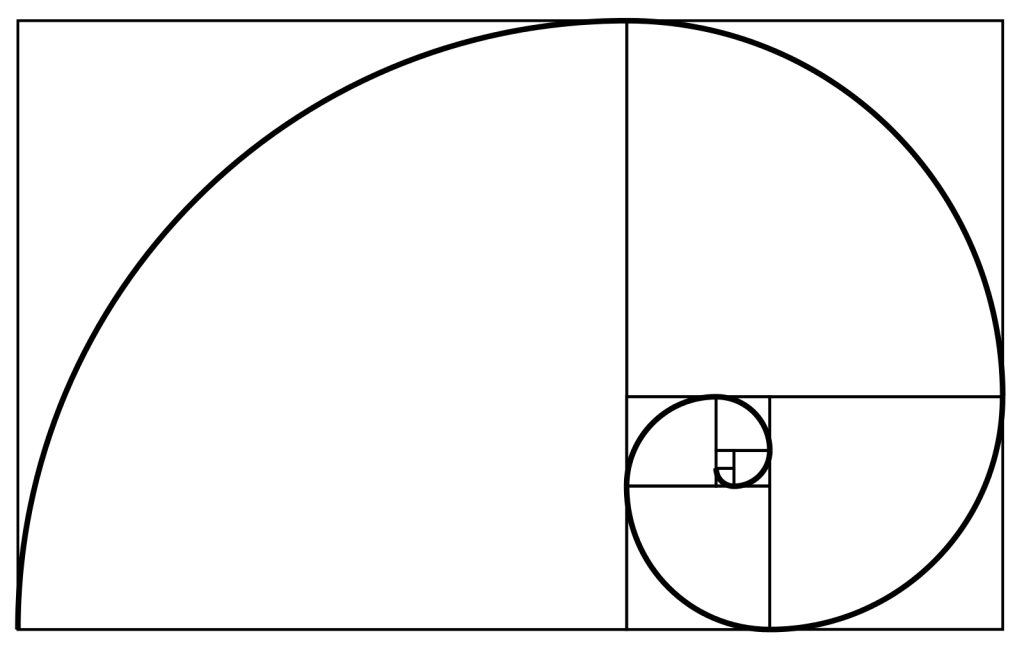 setPixel(x, y, 1)
        }
    }
}
рисовать дугу() 

Добавьте функцию drawArc в предыдущую программу и вызовите функцию непосредственно перед обновлением предыдущего спрайта Фибоначчи:

 let fibSprite0: Sprite = null
пусть fibSprite: Sprite = null
функция drawArc() {}
рисовать дугу()
fibSprite0 = fibSprite 

Pan the View

Квадраты и спирали в конечном итоге заполнятся за пределами вида на экране. Чтобы увидеть все квадраты, вы можете добавить код для прокрутки экрана. В следующем коде кнопки со стрелками используются для изменения центра обзора камеры, чтобы прокручивать изображение на экране в 4 направлениях.

 пусть cx = scene.screenWidth() / 2
пусть cy = scene.screenHeight () / 2
controller.left.onEvent (ControllerButtonEvent.Pressed, функция () {
    сх += -20
    scene.centerCameraAt(cx, cy)
})
controller.right.onEvent (ControllerButtonEvent.Pressed, функция () {
    сх += 20
    scene.centerCameraAt(cx, cy)
})
controller. up.onEvent (ControllerButtonEvent.Pressed, функция () {
    су += -15
    scene.centerCameraAt(cx, cy)
})
controller.down.onEvent (ControllerButtonEvent.Pressed, функция () {
    су += 15
    scene.centerCameraAt(cx, cy)
}) 

Полная программа

Полная программа содержит код рисования плитки, функцию дуги для рисования спирали и код панорамирования экрана.

 пусть fibSprite: Sprite = null
пусть fibSquare: Image = null
пусть вращается = 0
пусть х = 0
пусть у = 0
пусть клр = 1
позвольте повторить = 14
пусть f = 0
пусть f0 = 0
пусть f1 = 1
пусть fibSprite0 = sprites.create(img`.`, 0)
пусть cx = scene.screenWidth () / 2
пусть cy = scene.screenHeight () / 2
fibSprite0.top += 20
game.onUpdateInterval(1000, функция () {
 если (повторить > 0) {
 f0 = f1
 f1 = f
 f = f1 + f0
 информация.setScore(f)
 повтор += -1
 fibSquare = image.create(f, f)
 fibSquare.fillRect(0, 0, f, f, clr)
 клр += 1
 fibSprite = sprites. create(fibSquare, 0)
 если (повернуть == 0) {
 fibSprite.верхний = fibSprite0.нижний
 fibSprite.left = fibSprite0.left
 повернуть += 1
 } иначе если (повернуть == 1) {
 fibSprite.bottom = fibSprite0.bottom
 fibSprite.left = fibSprite0.right
 повернуть += 1
 } иначе если (повернуть == 2) {
 fibSprite.bottom = fibSprite0.top
 fibSprite.right = fibSprite0.right
 повернуть += 1
 } иначе если (повернуть == 3) {
 fibSprite.top = fibSprite0.top
 fibSprite.right = fibSprite0.left
 повернуть = 0
 }
 рисовать дугу()
 fibSprite0 = fibSprite
 }
})
функция drawArc() {
 // рисуем дугу окружности, используя случайные точки!
 для (пусть я = 0; я < 100000; я ++) {
 х = случайный (0, f)
 у = случайный (0, f)
 // проверяем, будет ли точка рисовать круг
 если (x * x + y * y >= (f - 1) ** 2 && x * x + y * y < (f + 1) ** 2) {
 если (повернуть == 0) {
 х = е - х
 у = е - у
 } иначе если (повернуть == 1) {
 х = е - х
 } иначе если (повернуть == 3) {
 у = е - у
 }
 fibSquare.