Круговые схемы эйлера: 1.6. Круговые схемы Эйлера. Логика. Учебное пособие
1.6. Круговые схемы Эйлера. Логика. Учебное пособие
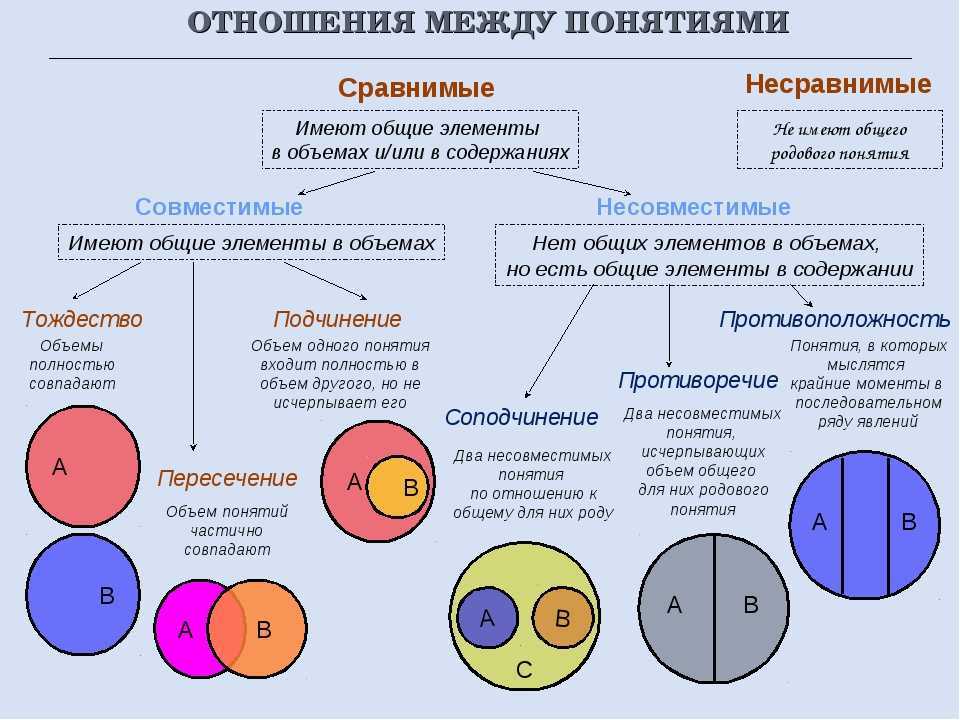
1.6. Круговые схемы Эйлера
Как мы уже знаем, в логике выделяется шесть вариантов отношений между понятиями. Два любых сравнимых понятия обязательно находятся в одном из этих отношений. Например, понятия писатель и россиянин находятся в отношении пересечения, писатель и человек – подчинения, Москва и столица России – равнозначности, Москва и Петербург – соподчинения, мокрая дорога и сухая дорога – противоположности, Антарктида и материк – подчинения, Антарктида и Африка – соподчинения и т. д. и т. п.
Надо обратить внимание на то, что если два понятия обозначают часть и целое, например месяц и год, то они находятся в отношении соподчинения, хотя может показаться, что между ними отношение подчинения, ведь месяц входит в год. Однако, если бы понятия месяц и год были подчиненными, то тогда надо было бы утверждать, что месяц – это обязательно год, а год – это не обязательно месяц (вспомним отношение подчинения на примере понятий 
Месяц – это не год, а год – это не месяц, но и то, и другое – отрезок времени, следовательно, понятия месяц и год, так же, как и понятия книга и страница книги, автомобиль и колесо автомобиля, молекула и атом и т. п., находятся в отношении соподчинения, т. к. часть и целое – не то же самое, что вид и род.
В начале говорилось о том, что понятия бывают сравнимыми и несравнимыми. Считается, что рассмотренные шесть вариантов отношений применимы только к сравнимым понятиям. Однако возможно утверждать, что все несравнимые понятия находятся между собой в отношении соподчинения. Например, такие несравнимые понятия, как пингвин и небесное тело возможно рассматривать как соподчиненные, ведь пингвин – это не небесное тело и наоборот, но в то же время объемы понятий пингвин и небесное тело входят в более широкий объем третьего понятия, родового по отношению к ним: это может быть понятие объект окружающего мира или форма материи (ведь и пингвин и небесное тело – это различные объекты окружающего мира или различные формы материи).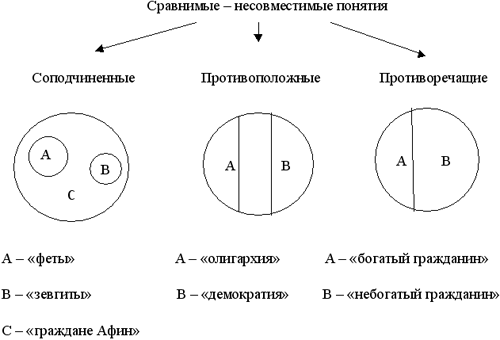
Если же одно понятие обозначает что-то материальное, а другое – нематериальное (например, дерево и мысль), то родовым для этих (как возможно утверждать) соподчиненных понятий является понятие форма бытия, т. к. и дерево, и мысль, и что угодно еще – это различные формы бытия.
Как нам уже известно, отношения между понятиями изображаются круговыми схемами Эйлера. Причем до сих пор мы изображали схематично отношения между двумя понятиями, а это можно сделать и с большим количеством понятий. Например, отношения между понятиями
Взаимное расположение кругов показывает, что понятия боксер и негр находятся в отношении пересечения (боксер может быть негром и может им не быть, а также негр может быть боксером и может им не быть), а понятия боксер и человек, так же как и понятия негр и человек находятся в отношении подчинения (ведь любой боксер и любой негр – это обязательно человек, но человек может не быть ни боксером, ни негром).
Рассмотрим отношения между понятиями дедушка, отец, мужчина, человек с помощью круговой схемы:
Как видим, указанные четыре понятия находятся в отношении последовательного подчинения: дедушка – это обязательно отец, а отец – не обязательно дедушка; любой отец – это обязательно мужчина, однако не всякий мужчина является отцом; и, наконец, мужчина – это обязательно человек, но человеком может быть не только мужчина. Отношения между понятиями хищник, рыба, акула, пиранья, щука, живое существо изображаются следующей схемой:
Попробуйте самостоятельно прокомментировать эту схему, установив все имеющиеся на ней виды отношений между понятиями.
Подытоживая сказанное, отметим, что отношения между понятиями – это отношения между их объемами. Значит, для того, чтобы было возможно установить отношения между понятиями, их объем должен быть резким, а содержание, соответственно, ясным, т. е. эти понятия должны быть определенными. Что касается неопределенных понятий, о которых шла речь выше, то установить точные отношения между ними достаточно сложно, фактически невозможно, ведь из-за неясности их содержания и нерезкости объема два каких-нибудь неопределенных понятия можно будет характеризовать как равнозначные или как пересекающиеся, или как подчиняющиеся и т.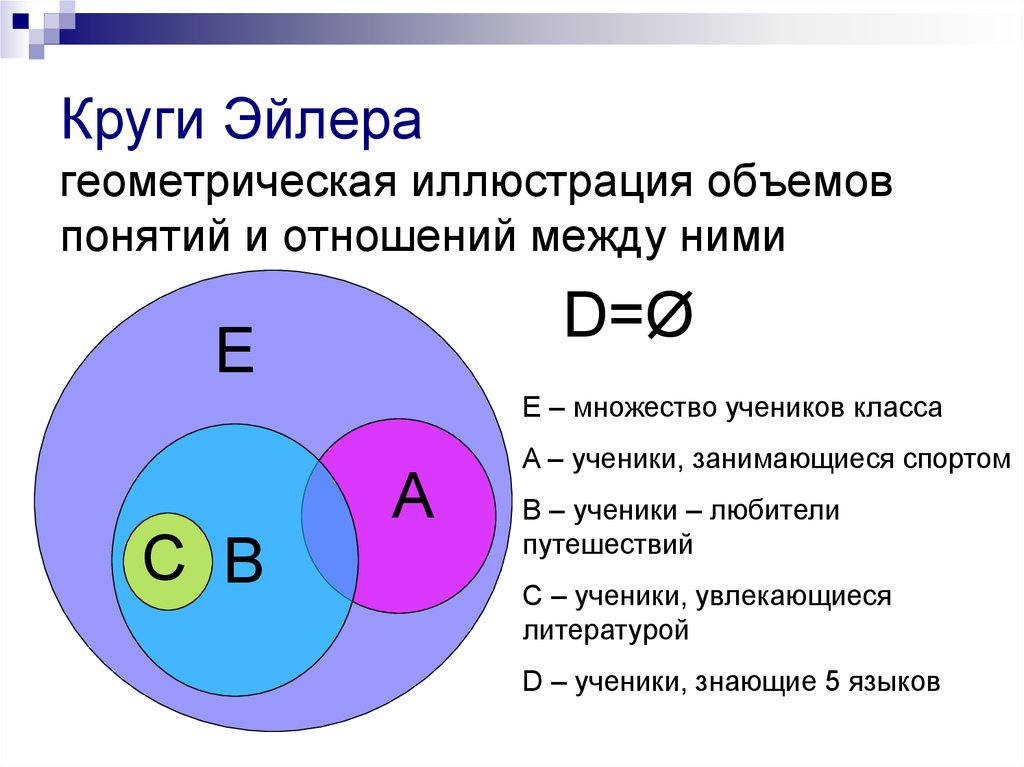
Данный текст является ознакомительным фрагментом.
9.1. Графические схемы структуры аргументации
9.1. Графические схемы структуры аргументации
Всякая аргументация начинается с установления и обсуждения некоторых фактов, которые в дальнейшем будут называться данными, и с помощью которых выдвигается и обосновывается некоторое заключение.
Комментарии и схемы
Комментарии и схемы Учение, в основе которого лежит внутренняя работа личности, не могло бы пережить саму эту личность без приливов новой внутренней работы новых личностей. Тех, кто увидел для себя особый смысл в этом учении. Меняются условия существования, приходит
Нравственная философия Толстого и Достоевского в рамках ницшеанской схемы нигилизма
Нравственная философия Толстого и Достоевского в рамках ницшеанской схемы нигилизма Начиная с последней четверти прошлого века проблема нигилизма выходит на одно из первых мест в числе важнейших проблем западноевропейской философии. Своим «статусом» она прежде всего
СХЕМЫ ПРАВИЛЬНЫХ РАССУЖДЕНИЙ
СХЕМЫ ПРАВИЛЬНЫХ РАССУЖДЕНИЙ
Вот два примера дедуктивных выводов из рассказа русского юмориста начала века В.
Билибина. «Если бы на свете не существовало солнца, то пришлось бы постоянно жечь свечи и керосин. Если бы пришлось постоянно жечь свечи и керосин, то чиновникам
Теоретические схемы и абстрактные объекты технической теории
Теоретические схемы и абстрактные объекты технической теории Теоретические схемыпредставляют собой совокупность абстрактных объектов, ориентированных, с одной стороны, на применение соответствующего математического аппарата, а с другой, – на мысленный эксперимент,
2. Диалектика схемы, аллегории и символа
2. Диалектика схемы, аллегории и символа Какие же возможны вообще виды этого взаимоотношения? Их очень много. Но, следуя Шеллингу, можно указать три основных таких вида. При этом будем иметь в виду, что наши термины «внутреннее» и «внешнее» – очень общие термины и их можно
Иконография как система методов: схемы и угрозы
Иконография как система методов: схемы и угрозы
Сама практика иконографического анализа сформировала «проверенную схему» последовательных исследовательских действий.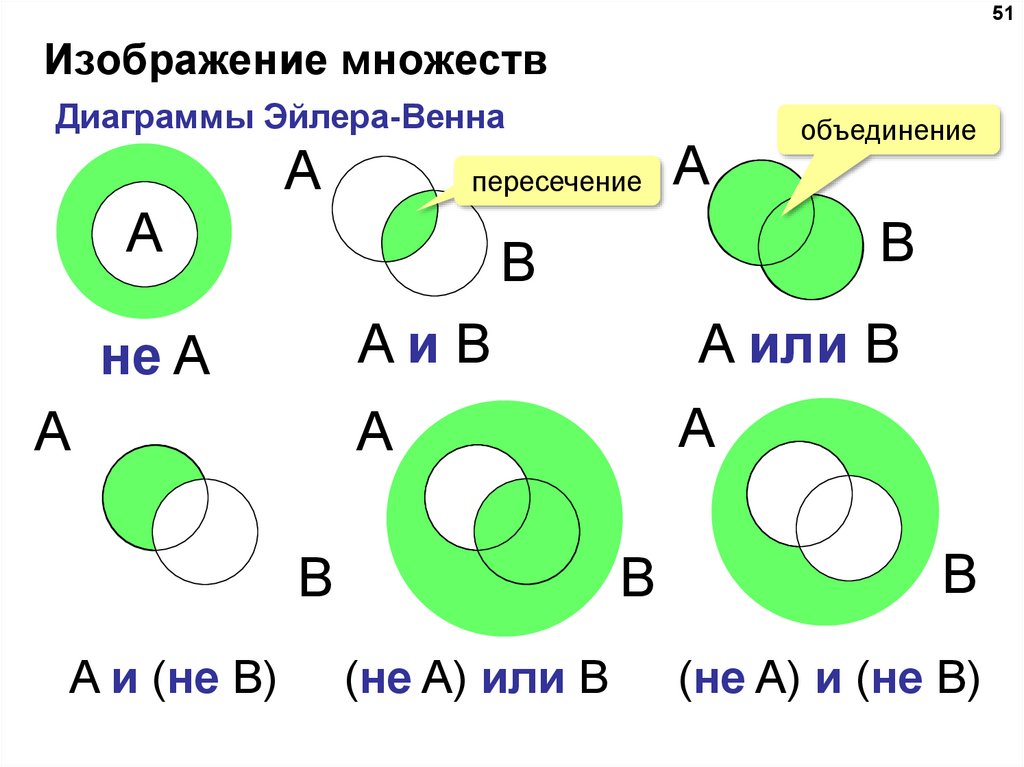
Схема подразумевает:– уяснение исторического значения мотива – с точки зрения времени (момент
2.1.1. Нормы-схемы речевого общения: речевой этикет
2.1.1. Нормы-схемы речевого общения: речевой этикет Выбор первой проблемной области – речевого этикета – обусловлен следующим. При определении сущностных характеристик нормы мы начали движение от социальных норм, при этом заметили, что их существование в полной мере
2.1.2. Семиотически закрепленные нормы-схемы: жанры
2.1.2. Семиотически закрепленные нормы-схемы: жанры Основой противопоставления социально и семиотически закрепленных норм, как было сказано в главе I, является способ их закрепления в социокультурной практике. Первые – неписаные законы – становятся программами, схемами
Круговые схемы Эйлера и диаграммы Венна для выражения отношений между понятиями
Разделительная связка
в языке обычно выражается с помощью
союзов «или», «либо».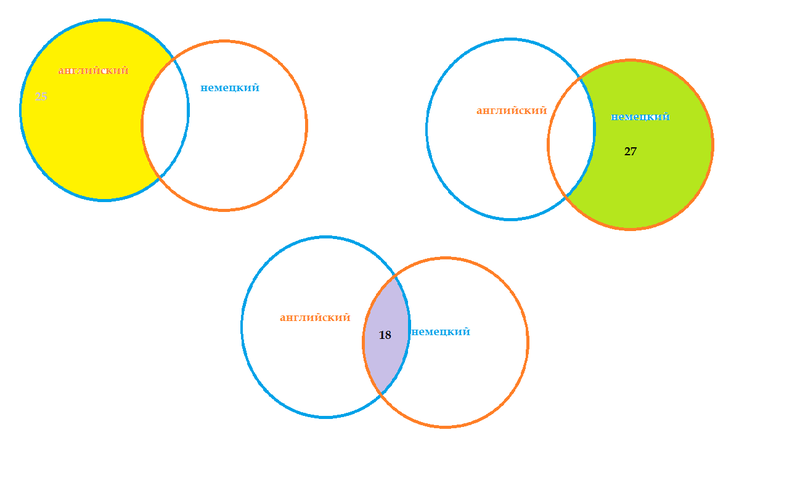
С целью усиления дизъюнкции до альтернативного
значения нередко употребляют удвоенные
союзы: вместо выражения «р или q» употребляют «или р, или q», а вместе «р либо q» — «либо р, либо q».Поскольку
в грамматике отсутствуют однозначные
союзы для нестрогого и строгого разделения,
то вопрос о типе дизъюнкции в юридических
и других текстах должен решаться содержательным
анализом соответствующих суждений.
Полная и неполная дизъюнкция. Среди дизъюнктивных суждений следует различать полную и неполную дизъюнкцию.
Полным или закрытым называют дизъюнктивное суждение, в котором перечислены все признаки или все виды определенного рода.
Символически это суждение можно записать следующим образом:
<р v q v r>.
Например: «Леса бывают лиственные, хвойные или смешанные». Полнота этого разделения (в символической записи обозначается знаком <…>) определяется тем, что не существует, помимо указанных, других видов лесов.
Неполным или
открытым называют дизъюнктивное суждение,
в котором перечислены не все
признаки или не все виды определенного рода.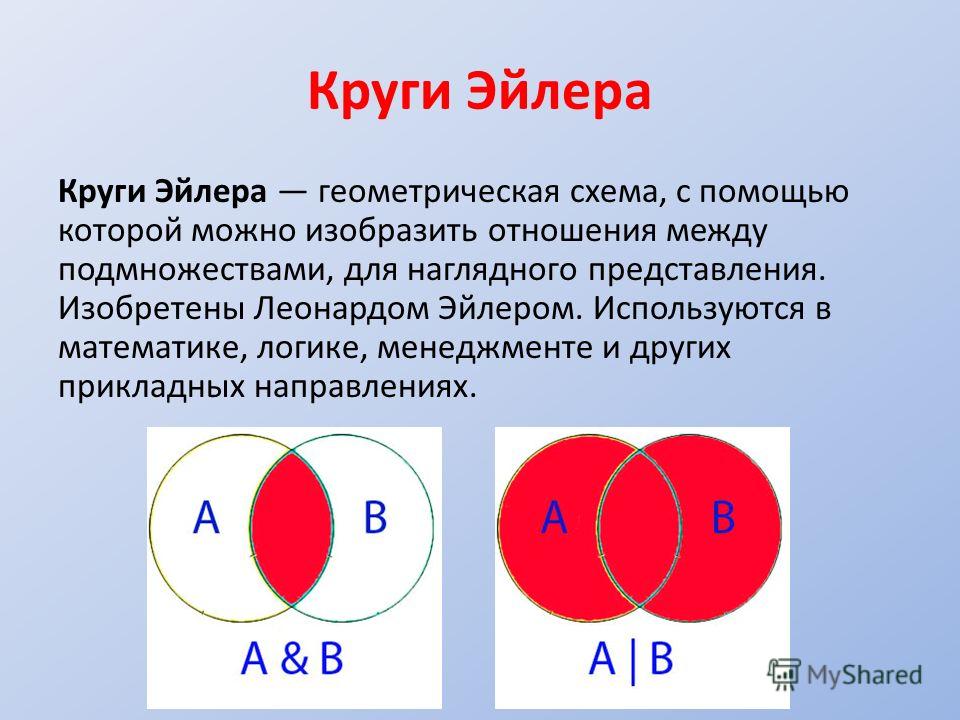
В символической записи неполнота дизъюнкции
может быть выражена многоточием:
р v q v r v…
В естественном языке неполнота дизъюнкции выражается словами: «и т.д.», «и др.», «и тому подобное», «иные» и другими.
3. Условные (импликативные) суждения.5
Условным, или импликативным,
называют суждение, состоящее из двух
простых, связанных логической связкой
«если.., то…». Например: «Если предохранитель
плавится, то электролампа гаснет». Первое
суждение — «Предохранитель плавится»
называют антецедентом (
В естественном языке для выражения условных суждений используется
не только союз«если…, то…», но и другие
союзы: «там…, где», «тогда…, когда…», «постольку…, поскольку…» и
т.п. В форме условных суждений в языке
могут быть представлены такие виды объективных
связей, как причинные, функциональные,
пространственные, временные, правовые,
а также семантические, логические и другие
зависимости.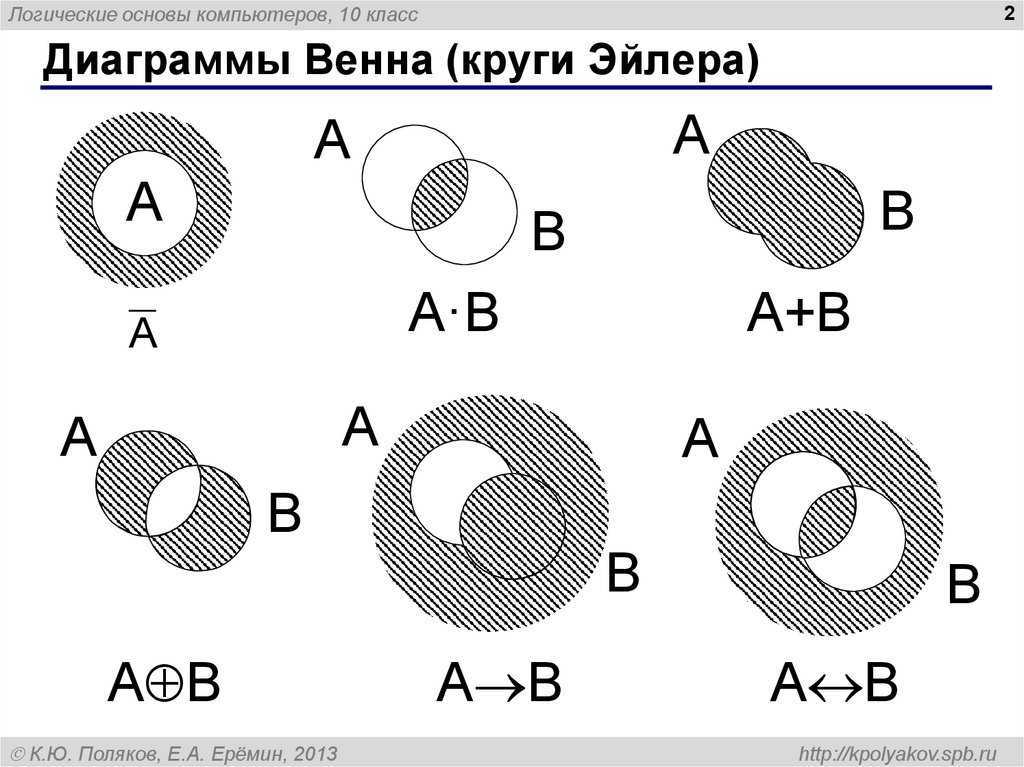
Примером причинного суждения
может служить следующее высказывание:
«Если воду нагреть при нормальном атмосферном
давлении до 100°С, то она закипит». Пример
семантической зависимости: «Если число
делится на 2 без остатка, то оно четное».
В форме условных суждений нередко выражают логические зависимости между высказываниями. Например: «Если верно, что некоторые птицы улетают зимой в теплые края, то неверно, что ни одна птица не улетает в теплые края».
В условном суждении антецедент
выполняет функцию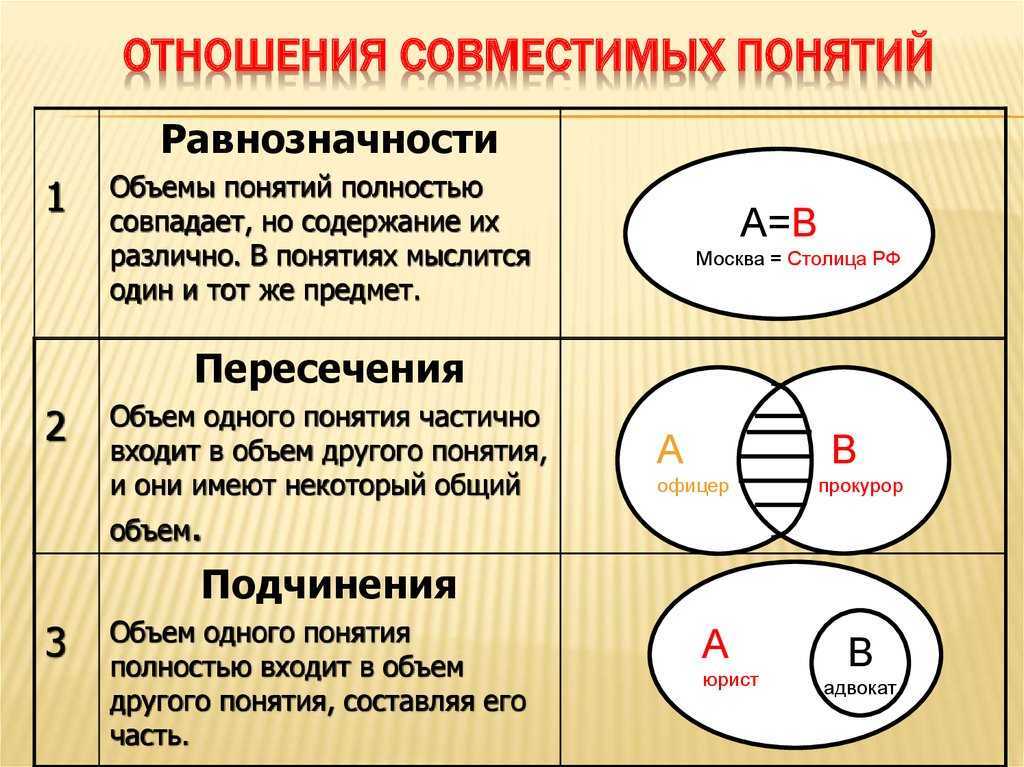 
4. Эквивалентные суждения (двойная импликация).
Эквивалентным, называют суждение, включающее в качестве составных два суждения, связанных двойной (прямой и обратной) условной зависимостью, выражаемой логической связкой «если и только если…, то…». Например: «Если и только если человек награжден орденами и медалями (р), то он имеет право на ношение соответствующих орденских планок (q)».
Логическая характеристика этого суждения состоит в том, что истинность утверждения о награждении (р) рассматривается как необходимое и достаточное условие истинности утверждения о наличии права на ношение орденских планок (q). Точно так же истинность утверждения о наличии права на ношение орденских планок (q) является необходимым и достаточным условием истинности утверждения о том, что данное лицо награждено соответствующими орденом или медалью (р).
В естественном языке
для выражения эквивалентных суждений используют союзы: «лишь при условии что…, то.
..»,
«в том и только в том случае когда…, тогда…»,
«только тогда когда…, то…» и другие.
3.Тест:
Суждение «Бога нет» является:
а) релятивным;
б) атрибутивным;
в) экзистенциональным;
г) конъюнктивным
Ответ: в)
Список используемой литературы
- Кириллов В.И., Старченко А.А. Логика: учебник. – М.: Юристъ, 2008.
– с.230
- Гетманова А.Д. Учебник по логике. 2-ое изд. – М.: «ВЛАДОС», 1995.
– с. 304
- Логика;электронно-Библиотечная Система,учебное пособие; Батурин В.К./Москва 2012
1 Логика;электронно-Библиотечная Система,учебное пособие; Батурин В.К./Москва 2012
2 Кириллов В.
И., Старченко А.А. Логика: учебник. – М.:
Юристъ, 2008.– с.230
3 Логика;электронно-Библиотечная Система,учебное пособие; Батурин В.К./Москва 2012
Гетманова А.Д. Учебник по логике. 2-ое изд. – М.: «ВЛАДОС», 1995.– с. 304
4 Логика;электронно-Библиотечная Система,учебное пособие; Батурин В.К./Москва 2012
5 Логика;электронно-Библиотечная Система,учебное пособие; Батурин В.К./Москва 2012
Математика — это больше, чем соревнования.
Вы старшеклассник, который любит математику? Вы находите традиционную учебную программу по математике слишком простой? Вы хотите изучать увлекательную и сложную математику? Вы хотите работать над задачами и подружиться с математически мыслящими сверстниками? Если это так, вы пришли в нужное место!
What Euler Circle — математический институт для продвинутых студентов, любящих математику. Мы предлагаем ряд занятий по математике на уровне колледжа, специально адаптированных к потребностям старшеклассников, многие из которых исчерпали учебную программу по математике в своих школах и хотят узнать больше.
Каждый предлагаемый нами курс эквивалентен уроку математики в колледже. На каждом занятии учащиеся решают множество задач, чтобы ознакомиться с новым материалом, а на продвинутых занятиях каждый учащийся пишет пояснительную работу по теме, связанной с материалом занятия.
Классы устроены таким образом, чтобы обеспечить путь к независимым исследованиям. Многие из наших наборов задач в продвинутых классах включают нерешенные проблемы, которые учащиеся могут исследовать после того, как освоят материал, представленный в классе. Мы предлагаем встречи в небольших группах для студентов, заинтересованных в работе над исследовательскими проблемами, после того, как они продемонстрировали способность усердно работать над сложными задачами. Подробнее об исследованиях см. в круге Эйлера.
Почему Математика — это больше, чем соревнования. Тем не менее, у старшеклассников мало ресурсов, чтобы узнать об остальном чудесном мире математики. Мы считаем, что многие студенты хотели бы увидеть, что еще есть, и мы хотим поделиться тем, что знаем.
Прием заявок на зимние классы открыт. Осенние занятия можно будет посещать онлайн или лично в Пало-Альто. Таким образом, студенты со всего мира могут подать заявку.
Осенью у нас будет промежуточный класс по переходу к доказательствам в комбинаторике, класс между средним и продвинутым уровнем по основам высшей математики с упором на реальный анализ и продвинутый класс по жемчужинам линейной алгебры. Занятия будут проходить в гибридном очном и онлайн-формате, поэтому подавать заявки могут студенты со всего мира.
Вот даты и время зимних занятий:
| Класс | Дата начала | Дата окончания | Все | Онлайн | Лично |
|---|---|---|---|---|---|
| Переход к корректуре | 9 января | 15 марта | Понедельник 17:00–18:00 | Вторник 17:00–19:00 | Среда 18:30–20:30 |
| Основы высшей математики | 9 января | 15 марта | Понедельник 17:00-18:30 | Среда 17:00–19:00 | Среда 18:30–20:30 |
| Жемчужины линейной алгебры | 9 января | 15 марта | Понедельник 18:30–20:30 | Вторник 17:00–19:00 | Среда 18:30–20:30 |
Заявки на зимние курсы принимаются 20 ноября .
После этого мы продолжим принимать заявки, пока места остаются на постоянной основе. Нажмите здесь, чтобы подать заявку!
Нажмите здесь, чтобы подписаться на рассылку!
Эйлера 9Точечный круг | Математические ресурсы IB от Intermathematics
30 сентября 2017 г. по геометрии
Если вы учитель, пожалуйста, посетите мой новый сайт: intermathematics.com, где вы найдете более 2000+ страниц ресурсов в формате PDF для обучения математике IB!
Девятиточечный круг Эйлера
Это хорошее введение в некоторые из красивых геометрических построений. Этот раздел математики то популярен, то теряет популярность — еще во времена Евклида построения с использованием линий и окружностей были краеугольным камнем математических доказательств, позже интерес возродился в 1800-х годах благодаря проективной геометрии Понсело, что позже привело к новой области ненаучных исследований. Евклидова геометрия. Это снова немного вышло из моды, но стало более доступным, чем когда-либо, благодаря таким программам, как Geogebra (на которых были построены приведенные ниже диаграммы).
9точечная окружность (или, по крайней мере, шеститочечная окружность была открыта немцем Карлом Вильгельмом фон Фейербахом в 1820-х годах. К сожалению, для Фейербаха ее часто вместо этого называют кругом Эйлера — в честь одного из величайших математиков всех времен, Леонарда Эйлера.
Итак, , как нарисовать 9-конечный круг Эйлера? Это немного сложно, так что не сдавайтесь!
Шаг 1: Нарисуйте треугольник:
Шаг 2: Нарисуйте серединные перпендикуляры к трем сторонам и отметьте точка, где они все пересекаются (D).0003
Шаг 3: Проведите окружность через точку D.
Шаг 4: От каждой линии треугольника проведите перпендикуляр через его третий угол. Например, для линии AC нарисуйте перпендикулярную линию, которая проходит через AC и угол B. (Высоты треугольника). Соедините 3 высоты, которые встретятся в точке (E).
Шаг 5. Соедините середины каждой стороны треугольника с оставшимся углом. Например, найдите середину треугольника AC и соедините эту точку с углом B.
(Средние линии треугольника). Обозначьте точку, где пересекаются 3 линии, буквой F.
Шаг 6. Удалите все вспомогательные линии. Теперь вы можете видеть, что у нас есть 3 точки в линии. D — центр окружности, проходящей через точки ABC, E — место, где встречаются высоты треугольника (ортоцентр ABC), а F — место, где встречаются медианы (центроид ABC).
Шаг 7. Соедините 3 точки — они лежат на одной линии.
Шаг 8. Увеличьте круг, проходящий через точки A B C, с коэффициентом масштабирования -1/2 с центром в точке F.
Шаг 9: Теперь у нас есть круг из 9 точек. Посмотрите на точки пересечения внутренней окружности с треугольником ABC. Вы можете видеть, что точки M N O показывают точки, где основания высот (из шага 4) встречаются с треугольником.
Точки P Q R показывают точки, где начинаются биссектрисы прямых (т. е. середины прямых AB, AC, BC). линии между E и вершинами A, B, C.
Шаг 10. Мы можем перетаскивать вершины треугольника, и описанные выше отношения сохранятся.
Во втором случае мы имеем E и D вне треугольника.
В третьем случае мы имеем E и F в одной и той же точке.
В четвертом случае мы имеем D и E на противоположных сторонах треугольника.
Итак, поехали — кто сказал, что математика некрасива?
Основные ресурсы для преподавателей IB
1) Intermathematics.com
Если вы учитель , пожалуйста, также посетите мой новый сайт. Это было разработано специально для учителей математики в международных школах. Контент теперь включает более 2000 страниц содержимого в формате PDF для всей программы SL и HL Analysis, а также программы SL Applications. Некоторые материалы включают в себя:
- Оригинальные рабочие листы в формате PDF (с полными решениями), предназначенные для охвата всех тем программы. Из них получаются отличные листы с домашним заданием или листы с заданиями в классе, и каждый из них рассчитан на продолжительность от 40 минут до 1 часа.
