Круги эйлера примеры решения логика: Решение задач с помощью кругов Эйлера

Решение задач с помощью кругов Эйлера

Пояснительная записка

Очень часто решение задачи помогает найти рисунок. Использование рисунка делает решение простым и наглядным.

В данной разработке приведены примеры решения задач с помощью кругов Эйлера. Это не просто занимательная и интересная штука, но и весьма полезный метод решения задач. Они помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.

С данным способом решения задач учащихся можно познакомить как на уроках, так и на кружковых занятиях.

Главной целью этой работы является помощь учителям математики для подготовки учащихся к олимпиадам, а также к экзаменам.

Основные понятия

Понятие множества − одно из первичных в математике. Поэтому очень трудно дать ему какое-либо определение, которое бы не заменяло слово «множество» каким-нибудь равнозначным выражением, например, совокупность, собрание элементов и т.

д. Элементы множества − это то, из чего это множество состоит, например, каждый ученик вашего класса есть элемент множества школьников.

Пересечение множеств в теории множеств – это множество, которому принадлежат те и только те элементы, которые одновременно принадлежат всем данным множествам.

Круги Эйлера – геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Леонардом Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях.

2. Решение задач с помощью кругов Эйлера

2.1. “Обитаемый остров” и “Стиляги”

Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек – фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?

Решение:

Чертим два множества таким образом:

6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств.

1. 15 – 6 = 9 – человек, которые смотрели только «Обитаемый остров»,

2. 11- 6 = 5 – человек, которые смотрели только «Стиляги».

Получаем:

Ответ: 5 человек.

2.2. Задача про библиотеки

Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги в школьной библиотеке, 20 – в районной.

Сколько шестиклассников:

1. Являются читателями обеих библиотек;
2. Не являются читателями районной библиотеки;
3. Не являются читателями школьной библиотеки;
4. Являются читателями только районной библиотеки;
5. Являются читателями только школьной библиотеки?

Решение:

Чертим два множества таким образом:

1) 20+ 25 – 35 = 10 (человек) – являются читателями обеих библиотек. На схеме это общая часть кругов. Мы определили единственную неизвестную нам величину. Теперь, глядя на схему, легко даем ответы на поставленные вопросы.

2) 35 – 20 = 15 (человек) – не являются читателями районной библиотеки,

3) 35 – 25 = 10 (человек) – не являются читателями школьной библиотеки,

4) 35- 20 = 10 (человек) – являются читателями только районной библиотеки,

5) 35- 20 = 15 (человек) – являются читателями только школьной библиотеки.

Очевидно, что вопросы 2 и 5, а также 3 и 4 – равнозначны и ответы на них совпадают.

Ответ: 10 человек; 15 человек; 10 человек; 10 человек; 15 человек.

2.3. Гарри Поттер, Рон и Гермиона

На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал только Рон?

Решение:

Учитывая условия задачи, сделаем чертеж:

Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги – Гермиона, то 11 – 4 – 2 = 5 – книг прочитал только Гарри.

Следовательно, 26 – 7 – 2 – 5 – 4 = 8 – книг прочитал только Рон.

Ответ: 8 книг.

2.4. Задача про любимые мультфильмы

Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах. Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок», шестерым – «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма. У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка Боб Квадратные Штаны».

Решение:

Чертим три круга, таким образом:

Из условия знаем, что трем ученикам нравиться и «Белоснежка и семь гномов», и «Волк и теленок», шестерым – «Белоснежка и семь гномов» и «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма.

Мы помним, что по условиям задачи среди фанатов мультфильма «Волк и теленок» пятеро ребят выбрали два мультфильма сразу, т.е. 5 – 3 = 2 – ученика выбрали «Волк и теленок» и «Губка Боб Квадратные Штаны».

1) 21 – 3 – 1 – 6 = 11 – учеников выбрали только «Белоснежка и семь гномов»,

2) 13 – 3 – 1 – 2 = 7 – учеников выбрали – «Волк и теленок»,

3) 38 – (11 + 3 + 1 + 2 + 6 + 7) = 8 – ребят выбрали «Губка Боб Квадратные Штаны».

4) 8 + 2 + 1 + 6 = 17 – человек выбрали мультик «Губка Боб Квадратные Штаны».

Ответ: 17 учеников.

2.5. Задача про Крейсер и Линкор

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.

Запрос	Найдено страниц, тыс.
Крейсер и Линкор	7000
Крейсер	4800
Линкор	4500

Какое количество страниц (в тысячах) будет найдено по запросу Крейсер и Линкор? (Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

)

Решение:

При помощи кругов Эйлера изобразим условия задачи.

1) 4800 + 4500 – 7000 = 2300 (тыс. страниц) – найдено по запросу Крейсер и Линкор,

2) 4800 – 2300 = 2500 (тыс. страниц) – найдено по запросу Крейсер,

3) 4500 – 2300 = 2200 (тыс. страниц) – найдено по запросу Линкор.

Ответ: 2300 тыс. страниц.

2.6. Задача про блондинок

Каждый ученик класса – либо девочка, либо блондин, либо любит математику. В классе 20 девочек, из них 12 блондинок, но одна блондинка любит математику. Всего в классе 24 ученика – блондина, математику из них любят 12, а всего учеников (мальчиков и девочек), которые любят математику, 17, из них 6 девочек. Сколько учеников в данном классе?

Решение:

Изобразим с помощью кругов Эйлера данные из задачи:

1) 12 – 1 = 11 (учеников) – девочек блондинок,

2) 12 – 1 = 11 (учеников) – блондины и любят математику,

3) 6 – 1 = 5 (учеников) – девочек, которые любят математику,

4) 20 – 11 – 1 – 5 = 3 (ученика) – девочки,

5) 24 – 11 – 1 – 11 = 1 (ученик) – блондин,

6) 17- 5 – 1 – 11 = 0 (учеников) – любят математику,

7) 3 + 1 + 0 + 5 + 11 + 11 + 1 = 32 (ученика) – всего в классе.

Ответ: 32 ученика.

2.7. Задача про кружки

В трёх седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?

Решение:

Учитывая условия задачи, сделаем чертеж:

1) 10 – 3 = 7 (ребят) – посещают драмкружок и хор,

2) 6 – 3 = 3 (ребят) – поют в хоре и занимаются спортом,

3) 8 – 3 = 5 (ребят) – занимаются спортом и посещают драмкружок,

4) 27 – 7 – 3 – 5 = 12 (ребят) – посещают драмкружок,

5) 32 – 7 3 – 3 = 19 (ребят) – поют в хоре,

6) 22 – 5 – 3 – 3 = 11 (ребят) – увлекаются спортом,

7) 70 – (12 + 19 + 11 + 5+ 7 + 3 + 3) = 10 (ребят) – не поют в хоре, не увлекаются спортом и не занимаются в драмкружке.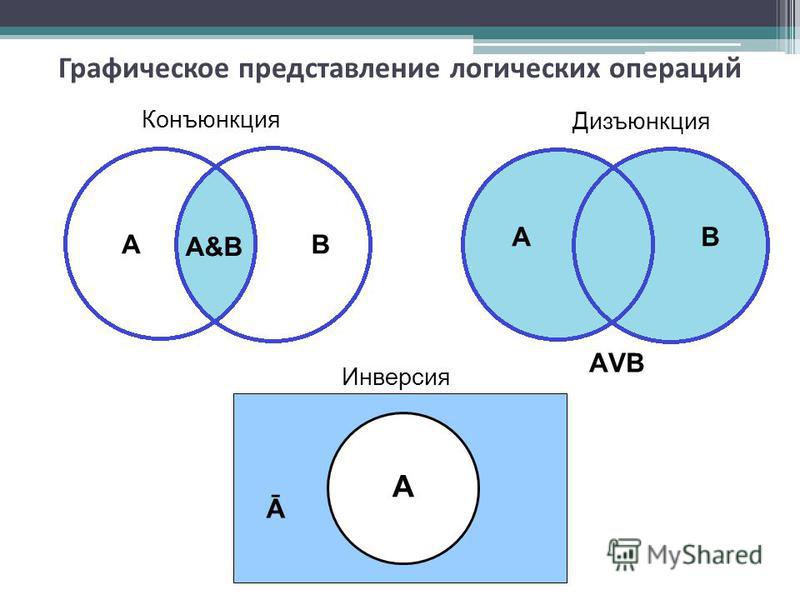

Ответ: 10 человек и 11 человек.

Задачи для самостоятельного решения

1. На фирме работают 67 человек. Из них 47 знают английский язык, 35 – немецкий язык, а 23 – оба языка. Сколько человек фирмы не знают ни английского, ни немецкого языков?

2. Из 40 учащихся нашего класса 32 любят молоко, 21 – лимонад, а 15 – и молоко, и лимонад. Сколько ребят в нашем классе не любят ни молоко, ни лимонад?

3. 12 моих одноклассников любят читать детективы, 18 – фантастику, трое с удовольствием читают и то, и другое, а один вообще ничего не читает. Сколько учеников в нашем классе?

4. Из тех 18 моих одноклассников, которые любят смотреть триллеры, только 12 не прочь посмотреть и мультфильмы. Сколько моих одноклассников смотрят одни «мультики», если всего в нашем классе 25 учеников, каждый из которых любит смотреть или триллеры, или мультфильмы, или и то и другое?

5. Из 29 мальчишек нашего двора только двое не занимаются спортом, а остальные посещают футбольную или теннисную секции, а то и обе.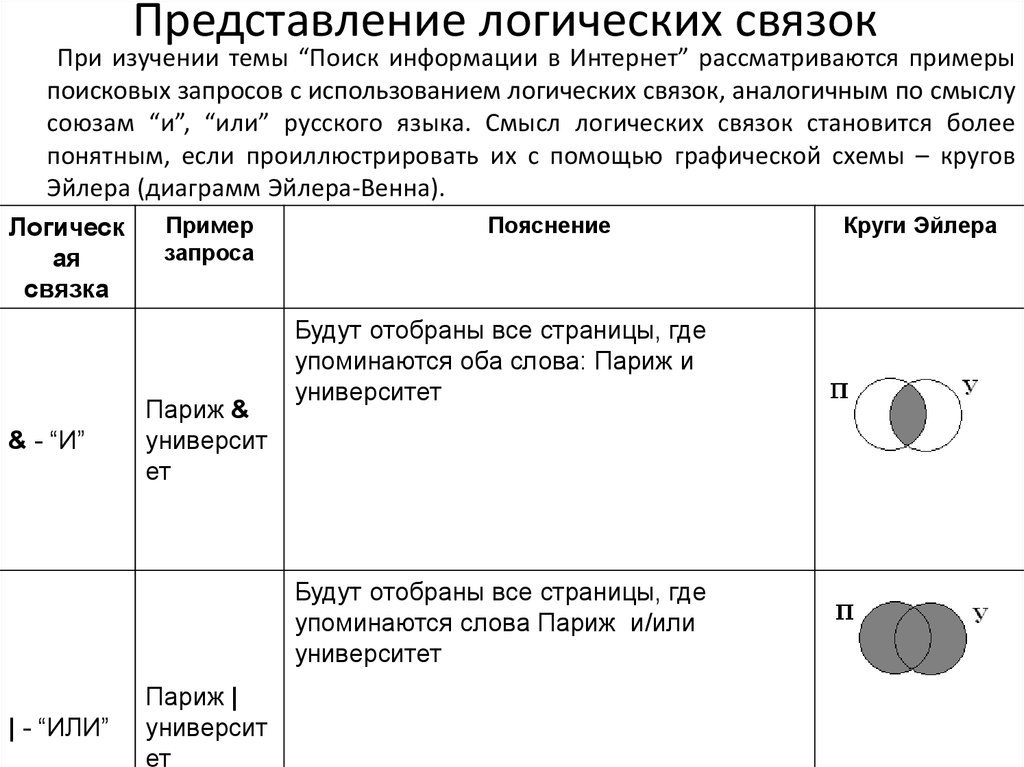 Футболом занимается 17 мальчишек, а теннисом – 19. Сколько футболистов играет в теннис? Сколько теннисистов играет в футбол?

6. В одном классе 25 учеников. Из них 7 любят груши, 11 – черешню. Двое любят груши и черешню; 6 – груши и яблоки; 5 – яблоки и черешню. Но есть в классе два ученика, которые любят все и четверо таких, что не любят фруктов вообще. Сколько учеников этого класса любят яблоки?

7. В конкурсе красоты участвовали 22 девушки. Из них 10 было красивых, 12 – умных и 9 – добрых. Только 2 девушки были и красивыми, и умными; 6 девушек были умными и одновременно добрыми. Определите, сколько было красивых и в то же время добрых девушек, если я скажу вам, что среди участниц не оказалось ни одной умной, доброй и вместе с тем красивой девушки?

8. В нашем классе 35 учеников. За первую четверть пятерки по русскому языку имели 14 учеников; по математике – 12; по истории – 23. По русскому и математике – 4; по математике и истории – 9; по русскому языку и истории – 5.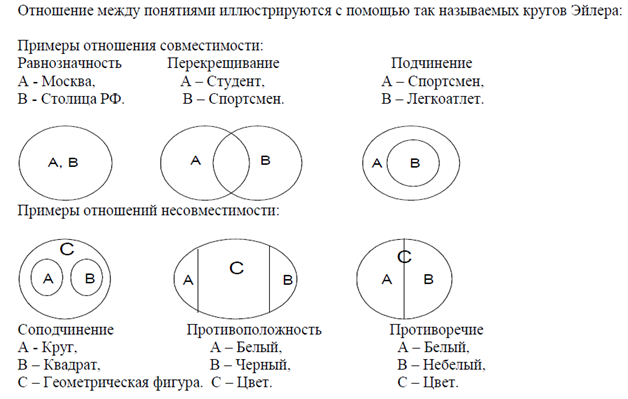 Сколько учеников имеют пятерки по всем трем предметам, если в классе нет ни одного ученика, не имеющего пятерки хотя бы по одному из этих предметов?

9. Из 100 человек 85 знают английский язык, 80 – испанский, 75 – немецкий. Все владеют, по крайней мере, одним иностранным языком. Среди них нет таких, которые знают два иностранных языка, но есть владеющие тремя языками. Сколько человек из этих 100 знают три языка?

10. Из сотрудников фирмы 16 побывали во Франции, 10 – в Италии, 6 – в Англии; в Англии и Италии – 5; в Англии и Франции – 6; во всех трех странах – 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них побывал хотя бы в одной из названных стран?

Список использованных источников

1. Баженов И.И, Порошкин А.Г., Тимофеев А.Ю., Яковлев В.Д. Задачи для школьных математических кружков: учеб. пособие / Сыктывкар: Сыктывкарский университет, 2006.

2. Марков И.С. Новые олимпиады по математике – Ростов н/Д: Феникс, 2005.

3. https://ru.wikipedia.org/wiki/

4. http://logika.vobrazovanie.ru

5. http://www.otvet-prost.ru/load/diskretnaja_matematika/na_krugi_ehjlera/zadacha_na_krugi_ehjlera/18-1-0-22

6. http://urok.1sept.ru/articles/550092/

7. http://www.tutoronline.ru/blog/reshit-zadachu-pomogut-krugi-jejlera

Круги Эйлера в информатике

Сегодня разберём задачи на круги Эйлера в информатике.

Леонард Эйлер – швейцарский, немецкий и российский математик и механик, сыгравший огромную роль в развитии этих наук.

Задача (Простая)

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Пушкин	3500
Лермонтов	2000
Пушкин | Лермонтов	4500

Какое количество страниц (в тысячах) будет найдено по запросу Пушкин & Лермонтов? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

Видим, что по запросу “Пушкин” в поисковике нашлось 3500 страниц. По запросу “Лермонтов” – 2000 страниц.

Запрос “Пушкин | Лермонтов” обозначает, что поисковик выдаст страницы, где есть слова про “Пушкина”, и страницы, где есть слова про “Лермонтова”, а так же могут быть страницы, где написано и про “Пушкина”, и про “Лермонтова” одновременно.

Если сложить страницы, в которых написано про “Пушкина” и про “Лермонтова” получается 3500 + 2000 = 5500 страниц. Но почему же при запросе “Пушкин | Лермонтов” получается меньше страниц, всего 4500 ?

Этот факт обозначает то, что когда мы подсчитывали страницы про “Пушкина” (3500 страниц), мы подсчитали и те страницы, где было написано и про “Пушкина”, и про “Лермонтова” одновременно.

Тоже самое и для количества страниц, где написано про “Лермонтова” (2000 страниц). В этом числе находятся и те, в которых одновременно упоминается и про “Пушкина”, и про “Лермонтова”.

В вопросе спрашивается, сколько страниц будет по запросу “Пушкин & Лермонтов“. Это обозначает, что как раз нужно найти количество страниц, где будет одновременно написано и про “Пушкина”, и про “Лермонтова”.

Отсюда получается:

Пушкин & Лермонтов = (3500 + 2000) – 4500 = 5500 – 4500 = 1000 страниц.

Это и будет ответ!

Теперь решим эту задачу с помощью Кругов Эйлера!

У нас всего есть две сущности: “Пушкин” и “Лермонтов”. Поэтому рисуем два пересекающихся круга, желательно разными цветами.

Объединение двух кругов в общую фигуру (показано фиолетовым цветом), показывает операцию “Пушкин | Лермонтов”. Эта операция всегда стремится увеличить площадь, объединить площади других фигур!

Обратите внимание, что круги пересекаются, из-за этого сумма площадей двух кругов по отдельности (3500 + 2000 = 5500) больше чем у фигуры, которая характеризует логическую операцию «ИЛИ» “Пушкин | Лермонтов” (4500).

Нужно найти площадь фигуры Пушкин & Лермонтов, которая закрашена золотистым цветом. Данная логическая операция «И» стремится уменьшить площадь. Она обозначает общую площадь других фигур.

Найдём сначала заштрихованную часть синего круга. Она равна: площадь фиолетовой фигуры (4500) минус площадь красного круга (3500).

Теперь легко найти площадь золотистой фигуры. Для этого нужно от площади синего круга вычесть площадь заштрихованной части. Получается:

Пушкин & Лермонтов (Количество страниц) = 2000 – 1000 = 1000

Получается, что по запросу Пушкин & Лермонтов будет найдено 1000 страниц.

Ответ: 1000

Рассмотрим ещё одну не сложную разминочную задачу.

Задача (Разминочная)

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Кокос | Ананас	3400
Кокос & Ананас	900
Кокос	2100

Какое количество страниц (в тысячах) будет найдено по запросу Ананас?

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

У нас две сущности: Кокос и Ананас. Нарисуем два круга Эйлера, которые пересекаются между собой. Так же отменим все имеющееся данные.

Найдём заштрихованную часть красного круга.

Весь красный круг 2100. Золотистая область равна 900. Заштрихованная часть равна 2100 – 900 = 1200.

После того, как нашли заштрихованную часть (такой полумесяц), можно найти уже площадь синего круга. Для этого нужно от площади фиолетовой фигуры отнять площадь заштрихованной части!

Ананас (Количество страниц) = 3400 – 1200 = 2200

Ответ: 2200

Разберём классическую задачу из информатики по кругам Эйлера.

Задача (Классическая)

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
(Космос & Звезда) | (Космос & Планета)	1100
Космос & Планета	600
Космос & Планета & Звезда	50

Какое количество страниц (в тыс. ) будет найдено по запросу Космос & Звезда?

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

В этой задаче у нас три сущности: Космос, Планета, Звезда. Поэтому рисуем три круга Эйлера, которые пересекаются между собой.

Могут ли круги не пересекаться ? Могут! Если мы докажем, что площади по отдельности двух кругов в сумме дают площадь фигуры, которая получается при применении операции логического “ИЛИ”.

Теперь отметим на нашем рисунке запрос (Космос & Звезда) | (Космос & Планета).

Сначала отменим для себя то, что находится в скобках. Первое Космос & Звезда

Теперь отметим вторую скобку Космос & Планета.

В выражении (Космос & Звезда) | (Космос & Планета) две скобки соединяет знак логического “ИЛИ”. Значит, эти две области нужно объединить! Область (Космос & Звезда) | (Космос & Планета) отмечена фиолетовым цветом!

Отметим Космос & Планета ещё раз, т.к. для этого выражения известно количество страниц.

Площадь фигуры для выражения Космос & Планета & Звезда будет очень маленькая. Это общая часть для всех трёх кругов. Отметим её оранжевым цветом! Каждая точка этой фигуры должна одновременно быть в трёх кругах!

Найти нужно Космос & Звезда. Отменим на рисунке чёрным цветом ту область, которую нужно найти. Мы эту область уже отмечали салатовым цветом.

Теперь у нас есть все компоненты, чтобы решить эту задачу.

Найдём заштрихованную область.

Вся область Космос & Планета равна 600. А заштрихованная часть равна: область Космос & Планета (600) минус оранжевая область (50).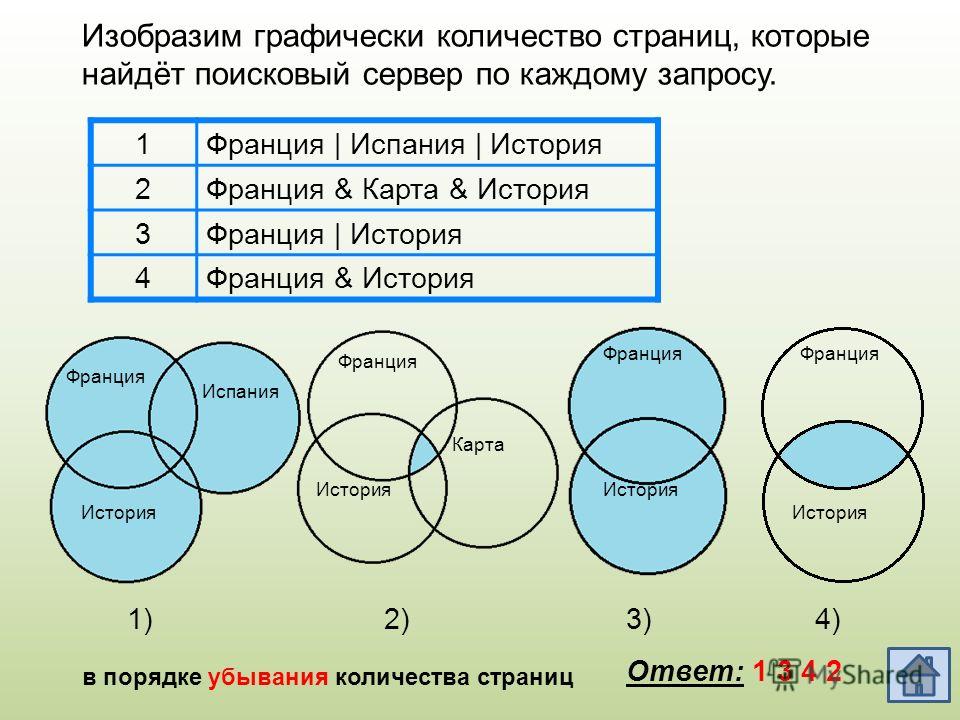

Количество страниц в заштрихованной части = 600 – 50 = 550

Тогда черная область легко находится: фиолетовая область (1100) минус заштрихованная область (550).

Количество страниц (при запросе Космос & Звезда) = 1100 – 550 = 550

Ответ: 550

Закрепляем материал по задачам на Круги Эйлера.

Задача (На закрепление)

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Море & Солнце	290
Море & Пляж	355
Море & (Пляж | Солнце)	465

Какое количество страниц (в тысячах) будет найдено по запросу Море & Пляж & Солнце? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.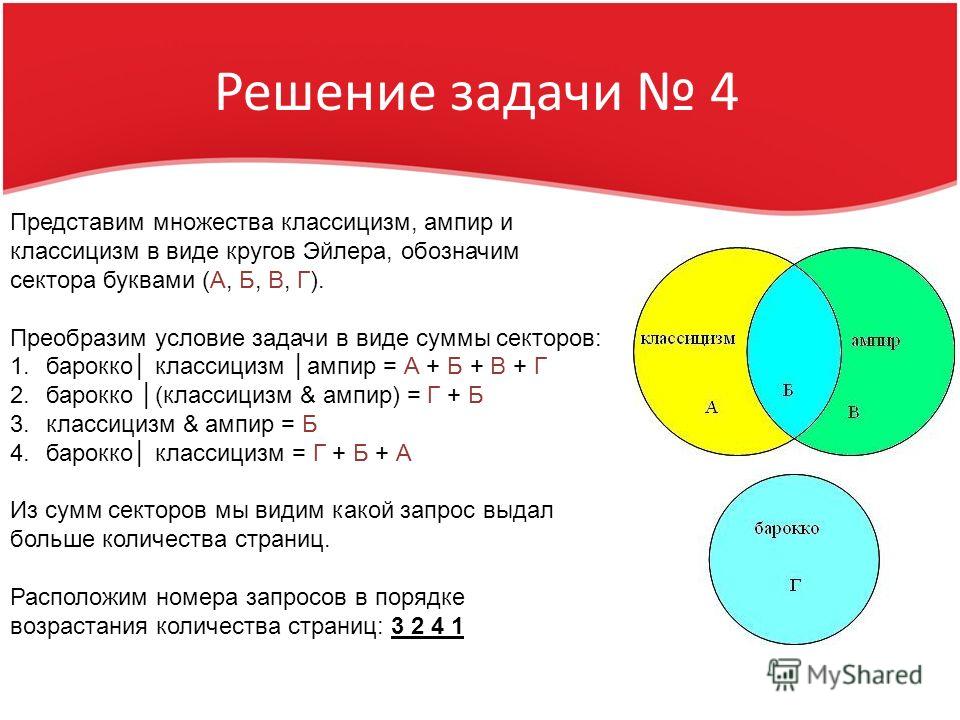

Решение:

В задаче используются три сущности: Море, Пляж, Солнце. Поэтому нарисуем три пересекающихся круга Эйлера.

Отметим все области для которых нам даны количество страниц.

В начале отметим Море & (Пляж | Солнце). Для начало нарисуем область, которая в скобках (Пляж | Солнце)

Теперь нужно очертить общую часть фиолетовой области и зелёного круга и получится Море & (Пляж | Солнце). Отметим оранжевым цветом.

Теперь отметим Море & Пляж.

Теперь отметим Море & Солнце.

Найти нужно ту область, которая получается в результате выделения общей части для всех трёх кругов! Обозначим её чёрным цветом!

Найдём заштрихованную область!

Количество страниц (в заштрихованной области) =
= Количество страниц (В оранжевой области) – Море & Солнце =
= 465 – 290 = 175

Чтобы найти искомую чёрную область, нужно из Море & Пляж (355) вычесть заштрихованную область (175).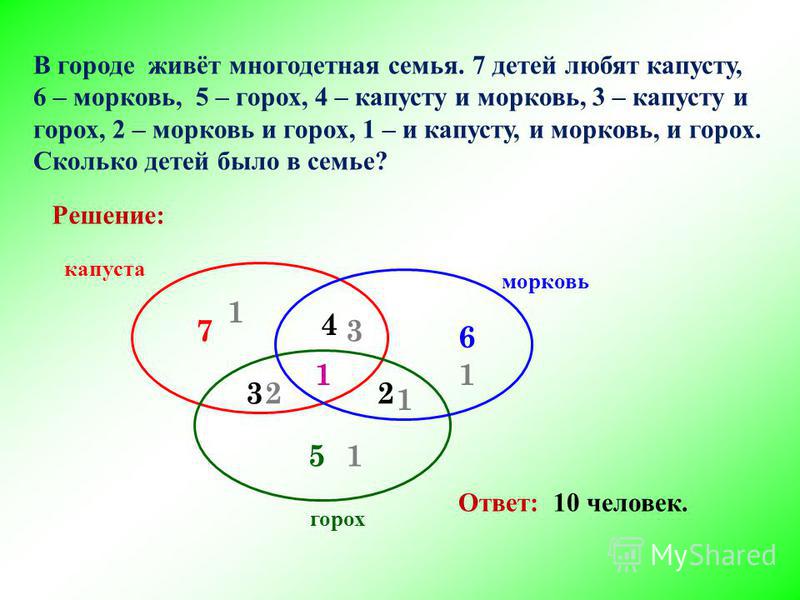

Количество страниц (Море & Пляж & Солнце) =
= Море & Пляж (355) – Количество страниц (в заштрихованной области) 175 =
= 355 – 175 = 180

Ответ: 180

Решим ещё одну тренировочную задачу из информатики на Круги Эйлера.

Задача (с 4 сущностями)

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Англия & (Уэльс & Шотландия | Ирландия)	450
Англия & Уэльс & Шотландия	213
Англия & Уэльс & Шотландия & Ирландия	87

Какое количество страниц (в тысячах) будет найдено по запросу

Англия & Ирландия?

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

Нужно нарисовать 4 пересекающихся круга. Сначала нарисуем три круга, как обычно, оставив немного места для четвёртого круга.

Четвёртый круг для Ирландии нужно нарисовать так, чтобы он проходил через область (Англия & Уэльс & Шотландия). Это нам подсказывает сама таблица, где есть количество страниц для Англия & Уэльс & Шотландия, а так же для Англия & Уэльс & Шотландия & Ирландия.

Нужно отметить на рисунке Англия & (Уэльс & Шотландия | Ирландия). Это будем делать, как всегда поэтапно.

Область Уэльс & Шотландия выглядит так:

Добавим к этой области Ирландию через логическое “ИЛИ”. Получается область (Уэльс & Шотландия | Ирландия). Произошло объединение серой области и жёлтого круга!

Теперь нужно сделать операцию логического “И” получившийся области с “Англией”. Тогда область Англия & (Уэльс & Шотландия | Ирландия) примет вид:

Т.е. это общее между предыдущем серым контуром и красным кругом!

Отметим Англия & Уэльс & Шотландия – это общая территория трёх кругов: Красного, Синего и Зелёного. Отмечено оранжевым цветом.

Отметим Англия & Уэльс & Шотландия & Ирландия – это общая территория четырёх кругов. Область получается ещё меньше. Если взять точку в этой области, то мы будем находится сразу в четырёх кругах одновременно. Отмечено фиолетовым цветом.

Отметим то, что нужно найти Англия & Ирландия чёрным цветом.

Искомую чёрную область легко найти, если из серой области вычесть кусочек, окрашенный в бирюзовый цвет!

Найдём, сколько страниц приходится на бирюзовый кусочек:

Количество страниц (для бирюзового кусочка) =
= Англия & Уэльс & Шотландия (213) – Англия & Уэльс & Шотландия & Ирландия (87) =
= 213 – 87 = 126

Найдём искомую чёрную область.

Количество станиц (для чёрной области) =
= Англия & (Уэльс & Шотландия | Ирландия) (450) – Количество (для бирюзового кусочка) =
450 – 126 = 324

Это и будет ответ!

Ответ: 324.

Разберём задачу из реального экзамена по информатике, которая была в 2019 году в Москве! (Сейчас в 2021 задачи не встречаются на Круги Эйлера)

Задача (ЕГЭ по информатике, 2019, Москва)

В таблице приведены запросы и количество страниц, которые нашёл поисковый сервер по этим запросам в некоторым сегменте Интернета:

Запрос	Найдено страниц (в тысячах)
Суфле	450
Корзина	200
Эклер	490
Суфле & Корзина	70
Суфле & Эклер	160
Корзина & Эклер	0

Сколько страниц (в тысячах) будет найдено по запросу

Суфле | Корзина | Эклер

Решение:

Видим, что у нас три поисковых разных слова, поэтому будет три разных круга Эйлера!

Так же видим, что логическое “И” между словами Корзина и Эклер даёт 0 страниц. Это значит, что эти круги не пересекаются! Так же круги бы не пересекались, если бы операция логического “ИЛИ” совпадала бы с суммой этих кругов.

Видим, что Суфле имеет с двумя кругами пересечения, а Корзина и Эклер не пересекаются.

Отметим всё, что нам дано в условии.

Жёлтым цветом отмечено Суфле | Корзина | Эклер . Объединение всех трёх кругов. Это то, что нужно найти.

Искомая жёлтая фигура складывается из заштрихованных областей и красного круга! Площадь красного круга мы знаем. Нужно найти площади заштрихованных частей.

Левая заштрихованная область находится просто:

Количество страниц (лев. заштрих. область) =
= Эклер (490) – Суфле & Эклер (160) = 330

Так же найдём площадь правой заштрихованной области:

Количество страниц (прав. заштрих. область) =
= Корзина (200) – Суфле & Корзина (70) = 130

Теперь можно найти искомую жёлтую область

Количество страниц (Суфле | Корзина | Эклер) =
= Красный круг (450) + лев. 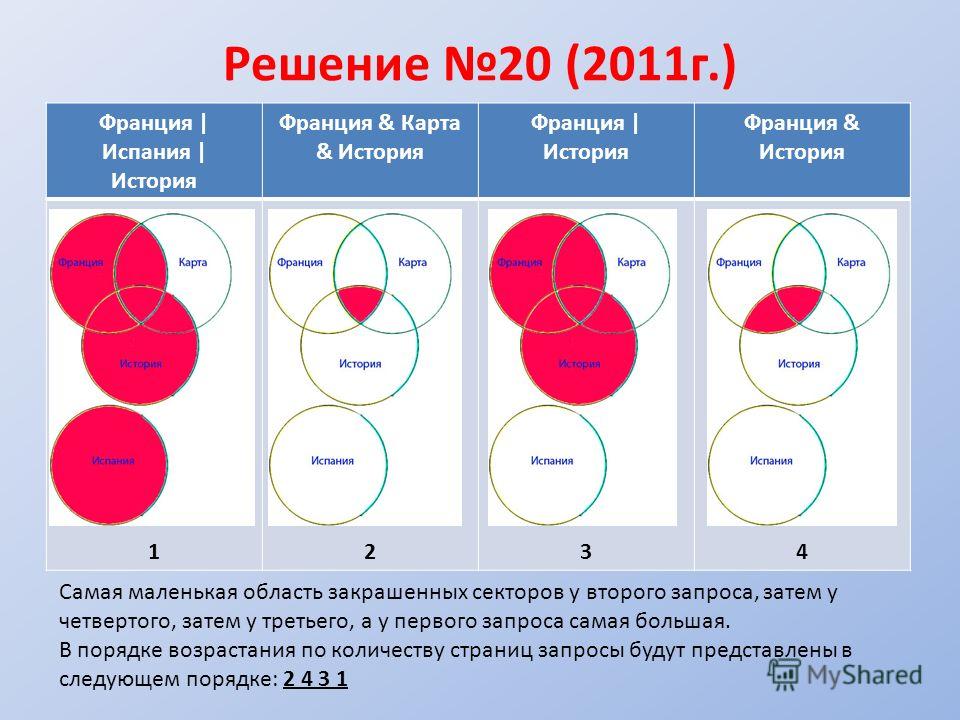заштрих. область (310) + прав. заштрих. область (130) =
= 450 + 330 + 130 = 910

Задача решена, можно писать ответ.

Ответ: 910

Разберём ещё одну задачу из реального ЕГЭ уже 2020 года

Задача (ЕГЭ по информатике, 2020, Москва)

В таблице приведены запросы и количество страниц, которые нашёл поисковый сервер по этим запросам в некоторым сегменте Интернета:

Запрос	Найдено страниц (в тысячах)
Аврора	50
Крейсер	45
Заря	23
Аврора & Заря	9
Заря & Крейсер	0
Заря | Крейсер | Аврора	93

Сколько страниц (в тысячах) будет найдено по запросу

Аврора & Крейсер

Решение:

Количество страниц при запросе Заря & Крейсер равно нулю. Значит, эти два круга не будут пересекаться.

Нарисуем все данные на рисунке.

Нужно найти для начала заштрихованную правую часть.

Количество страниц (для двух заштрих. частей) =
З | К | А (93) – Красный круг (50) = 43

Левую заштрихованную область легко найти.

Количество страниц (для левой заштрих. части) =
Синий круг (23) – А & З (9) = 14

Тогда для правой заштрихованной области получается:

Колич. страниц (для правой заштрих. части) =
Колич. страниц (для двух заштрих. частей) (43) – Колич. страниц (для лев. заштрих. части) (14) =
= 43 – 14 = 29

Тогда искомую область легко найти:

Колич. страниц (А & K) =
Зелёный круг (45) – Колич. страниц (для правой заштрих. части) (29) =
45 – 29 = 16

Ответ: 16

На этом всё! Надеюсь, вы теперь будете с удовольствием решать задачи по информатике с помощью Кругов Эйлера.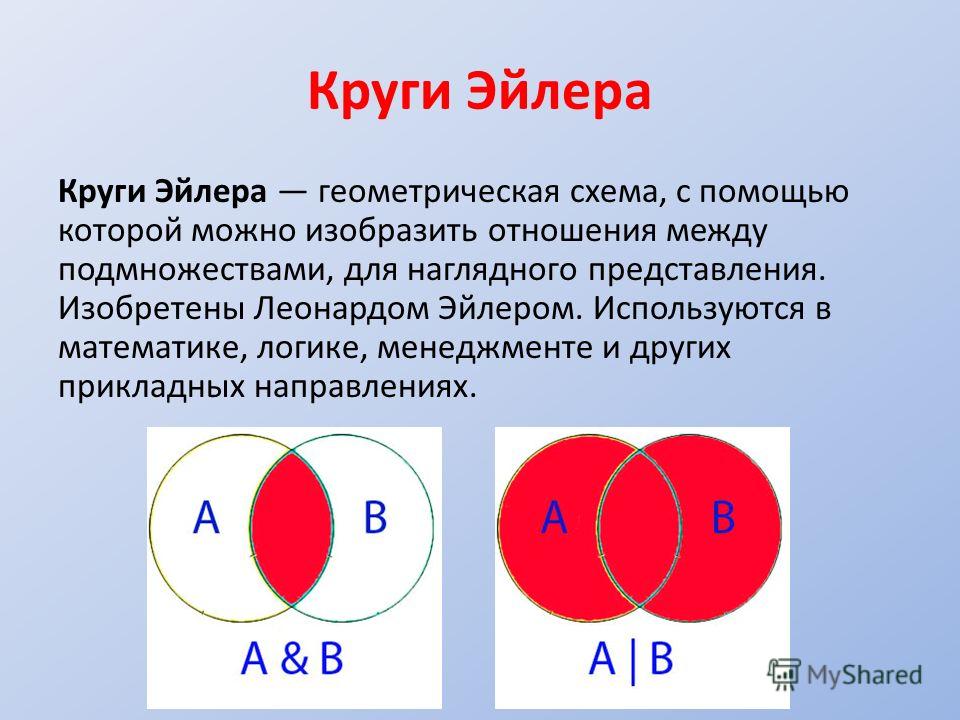

Как анализировать аргументы с помощью диаграмм Эйлера

На экзамене по конечной математике вас могут попросить проанализировать аргумент с помощью визуального подхода с использованием диаграммы Эйлера. Эта изобразительная техника используется для проверки правильности аргумента.

Аргумент может быть классифицирован как допустимый или недопустимый. Действительный аргумент возникает в ситуациях, когда, если посылки верны, то и заключение должно быть верным. И аргумент может быть верным, даже если вывод ложный.

Следующий аргумент имеет две предпосылки: (1) «У всех собак есть блохи». (2) «Хэнк — собака». Вывод таков, что, следовательно, у Хэнка блохи.

Эти аргументы обычно имеют следующий формат с предпосылками, перечисленными первыми, и выводом, подчеркнутым горизонтальной линией:

Используя диаграмму Эйлера для анализа этого аргумента, нарисуйте круг, содержащий все объекты, на которых есть блохи. Внутри круга поместите еще один круг, чтобы содержать всех собак. А внутри круга собак посади Хэнка. Рисунок иллюстрирует этот подход.

У бедного Хэнка блохи.

Этот аргумент не обязательно верен, потому что вы знаете, что не у всех собак есть блохи. Все это показывает, что аргумент равен действительный . Если обе посылки верны, то и заключение должно быть верным.

Теперь рассмотрим аргумент, включающий прямоугольники и треугольники. Многоугольник — это фигура, состоящая из отрезков, соединенных концами.

При анализе правильности этого аргумента диаграмма Эйлера начинается с круга, содержащего все многоугольники, как показано здесь.

Два типа полигонов.

Два круга нарисованы внутри большего круга — один содержит прямоугольники, а другой — треугольники. Два круга не пересекаются, потому что у прямоугольников четыре стороны, а у треугольников три стороны.

Аргумент недействителен . Прямоугольники — это не треугольники, даже иногда.

Аргументы могут иметь более двух посылок. Например:

Одна диаграмма Эйлера, которая может представить эту ситуацию, имеет три пересекающихся круга, как показано здесь.

Президент Авраам Линкольн и другие юристы штата Иллинойс.

Как видно из диаграммы, могут быть президенты, родившиеся в Кентукки, которые не были юристами в Иллинойсе, и могут быть президенты, которые были юристами в Иллинойсе, но не родились в Кентукки. Аргумент равен неверный . Чтобы быть действительным, оно всегда должно быть истинным.

Эта статья из книги:

• Конечная математика для чайников,

Об авторе книги:

Мэри Джейн Стерлинг является автором Алгебра I для чайников, Алгебра для чайников, и многих других Для чайников книг. Она преподавала в Университете Брэдли в Пеории, штат Иллинойс, более 30 лет, преподавая алгебру, бизнес-расчеты, геометрию и конечную математику.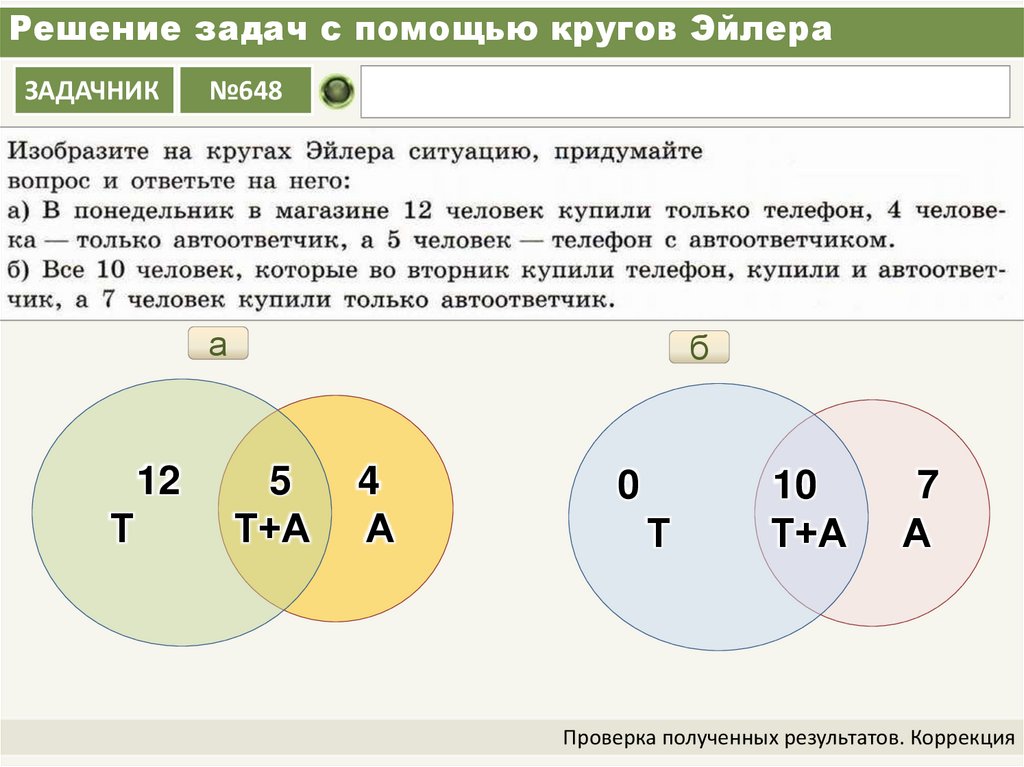

Эту статью можно найти в категории:

• Расчет и анализ,

17.9: Оценка дедуктивных аргументов с помощью диаграмм Эйлера

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

41408

• Дэвид Липпман
• Колледж Пирса через OpenTextBookStore

Мы можем визуально интерпретировать дедуктивный аргумент с помощью диаграммы Эйлера, которая по сути является тем же самым, что и диаграмма Венна. Это может облегчить определение того, является ли аргумент действительным или недействительным.

Пример 31

Рассмотрим дедуктивный аргумент «Все кошки — млекопитающие, а тигр — кошка, поэтому тигр — млекопитающее». Является ли этот аргумент действительным?

Решение

Помещения:

Все кошки млекопитающие.

Тигр – это кошка.

Вывод:

Тигр – млекопитающее.

Обе посылки верны. Чтобы увидеть, что посылки должны логически вести к заключению, мы можем использовать диаграмму Венна. Исходя из первой посылки, мы рисуем множество кошек как подмножество множества млекопитающих. Из второй посылки нам говорят, что тигр содержится в множестве кошек. Из этого мы видим на диаграмме Венна, что тигр также должен быть внутри множества млекопитающих, так что вывод верен.

Анализ аргументов с помощью диаграмм Эйлера

Чтобы проанализировать аргумент с помощью диаграммы Эйлера:

1) Нарисуйте диаграмму Эйлера на основе предпосылок аргумента

2) Аргумент недействителен, если есть способ нарисовать диаграмму что делает вывод ложным

3) Аргумент действителен, если нельзя построить диаграмму, чтобы сделать вывод ложным

4) Если посылок недостаточно для определения местоположения элемента или множества, упомянутых в заключении, то аргумент неверный.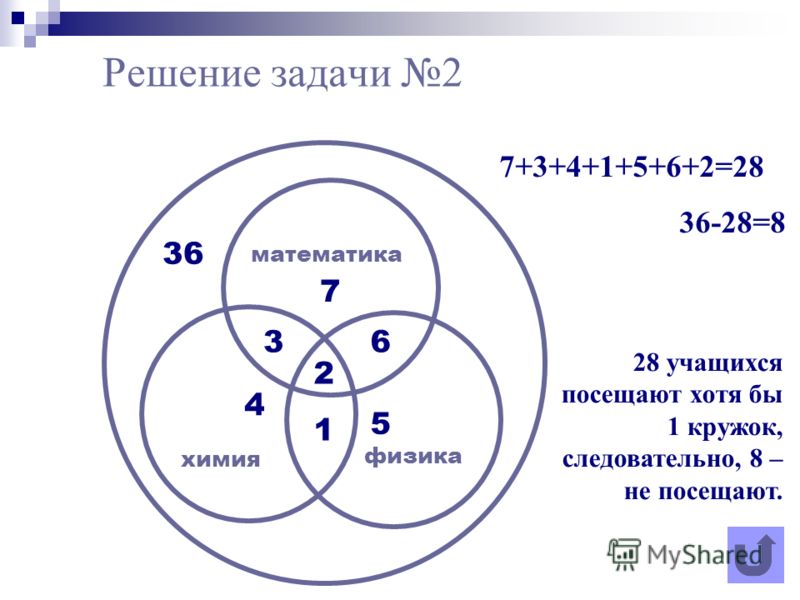

Попробуйте сейчас 9

Определите правильность этого аргумента:

\(\begin{array} {ll} \text{Предпосылка:} & \text{Все кошки боятся пылесосов.} \\ \text {Предпосылка:} & \text{Макс – кошка.} \\ \text{Вывод:} & \text{Макс боится пылесосов.} \end{array}\)

Ответ

Действителен. Кошки — это подмножество существ, которых пугают пылесосы. Макс входит в набор котов, значит, он тоже должен быть в наборе существ, которых пугают пылесосы.

Пример 32

\(\begin{array} {ll} \text{Предпосылка:} & \text{Все пожарные знают СЛР.} \\ \text{Посылка:} & \text{Джилл знает СЛР.} \ \ \text{Вывод:} & \text{Джилл – пожарный.} \end{array}\)

Решение

Из первой посылки мы знаем, что все пожарные находятся внутри набора тех, кто знает СЛР. (Пожарные — это подмножество людей, знающих СЛР.) Из второй посылки мы знаем, что Джилл является членом этой большей группы, но у нас недостаточно информации, чтобы узнать, является ли она также членом меньшей подгруппы, т. е. пожарные.

Поскольку вывод не обязательно следует из посылок, это неверный аргумент. Возможно, что Джилл — пожарный, но структура аргумента не позволяет сделать вывод, что это определенно так.

Важно отметить, что действительно ли Джилл пожарный или нет, не имеет значения для оценки обоснованности аргумента; нас интересует, достаточно ли посылок для доказательства вывода.

Попробуйте сейчас 10

Определите правильность этого аргумента:

\(\begin{array} {ll} \text{Посылка:} & \text{Все велосипеды имеют два колеса.} \\ \text{Посылка:} & \text{Это У Harley-Davidson два колеса.} \\ \text{Вывод:} & \text{Этот Harley-Davidson — велосипед.} \end{array}\)

Ответ

Недействительно. Множество велосипедов является подмножеством множества транспортных средств с двумя колесами; Harley-Davidson входит в число двухколесных транспортных средств, но не обязательно в меньший круг.

Попробуйте сейчас 11

Определите правильность этого аргумента:

\(\begin{array} {ll} \text{Предпосылка:} & \text{Нет фиолетовых коров.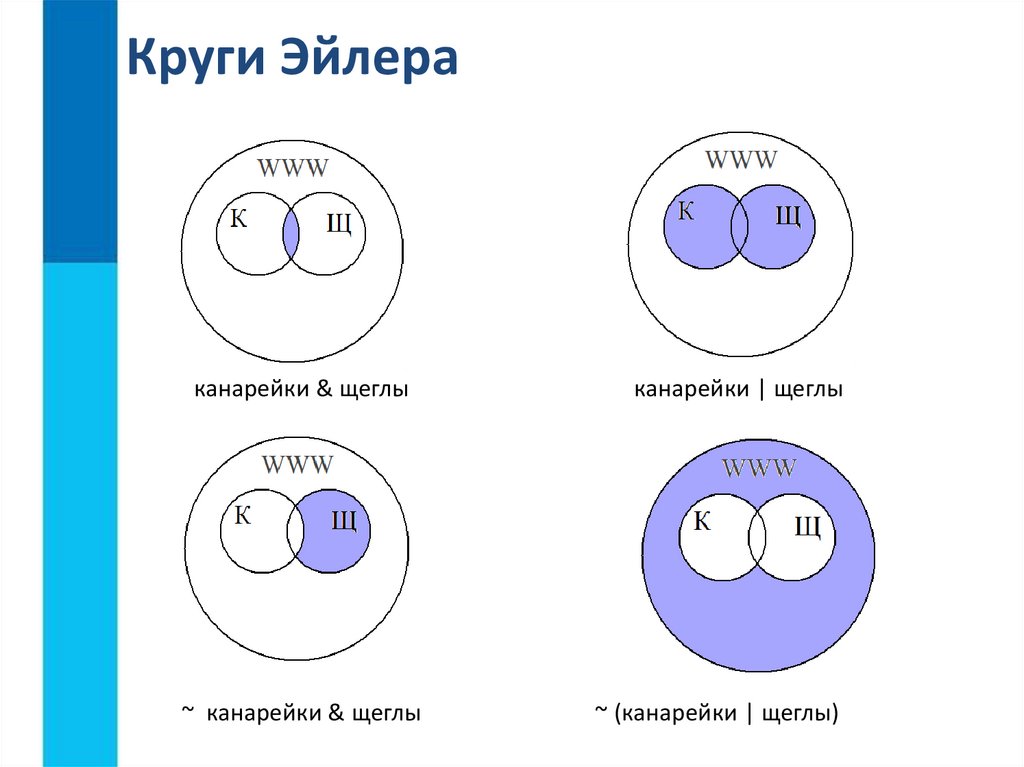 } \\ \text{Предпосылка: } & \text{Фидо не корова.} \\ \text{Вывод:} & \text{Фидо фиолетовый.} \end{массив}\)

Ответ

Недействительно. Поскольку фиолетовых коров нет, мы знаем, что набор коров и набор фиолетовых вещей не пересекаются. Мы знаем, что Фидо не находится в наборе коров, но этого недостаточно, чтобы сделать вывод, что Фидо находится в наборе фиолетовых вещей.

Помимо этих категориальных стилевых посылок вида «все ___», «некоторые ____» и «нет ____», также часто встречаются условные посылки.

Пример 33

\(\begin{array} {ll} \text{Предпосылка:} & \text{Если вы живете в Сиэтле, вы живете в Вашингтоне.} \\ \text{Предпосылка:} & \text{Маркус не живет в Сиэтле.} \\ \text{Вывод:} & \text{Маркус не живет в Вашингтоне.} \end{array}\)

Решение

Из первой посылки мы знаем, что множество людей, живущих в Сиэтле, находится внутри множества тех, кто живет в Вашингтоне. Из второй посылки мы знаем, что Маркус не входит в набор Сиэтла, но у нас недостаточно информации, чтобы узнать, живет ли Маркус в Вашингтоне или нет. Это неверный аргумент.

Попробуй сейчас 12

Определите правильность этого аргумента:

\(\begin{array} {ll} \text{Предпосылка:} & \text{Если у вас есть помада на воротнике, то вы изменяешь мне.} \\ \text{Предпосылка:} & \text{Если ты мне изменяешь, я разведусь с тобой.} \\ \text{Предпосылка:} & \text{ У тебя нет помады на губах воротник.} \\ \text{Вывод:} & \text{Я с вами не разведусь.} \end{array}\)

Ответить

Недействительно. Помада на твоем воротнике — это подмножество сценариев, в которых ты изменяешь, а обман — это подмножество сценариев, в которых я разведусь с тобой. Хотя прекрасно, что у тебя на воротнике нет помады, ты все равно можешь мне изменять, и я разведусь с тобой. На самом деле, даже если ты мне не изменяешь, я могу развестись с тобой по другой причине. Тебе лучше привести себя в форму.

---

Эта страница называется 17.9: Оценка дедуктивных аргументов с помощью диаграмм Эйлера распространяется под лицензией CC BY-SA 3.