Картинки многоугольники для детей: Геометрические фигуры из многоугольников для дошкольников
Многоугольники, виды многоугольников — ISaloni — студия интерьера, салон обоев
Содержание
стороны, вершины, диагонали. Периметр многоугольника
Многоугольник — это геометрическая фигура, ограниченная замкнутой ломаной линией, не имеющей самопересечений.
Звенья ломаной называются сторонами многоугольника, а её вершины — вершинами многоугольника.
Углами многоугольника называются внутренние углы, образованные соседними сторонами. Число углов многоугольника равно числу его вершин и сторон.
Многоугольникам даются названия по количеству сторон. Многоугольник с наименьшим количеством сторон называется треугольником, он имеет всего три стороны. Многоугольник с четырьмя сторонами называется четырёхугольником, с пятью — пятиугольником и т. д.
Обозначение многоугольника составляют из букв, стоящих при его вершинах, называя их по порядку (по часовой или против часовой стрелки). Например, говорят или пишут: пятиугольник ABCDE
:
В пятиугольнике
ABCDE точки

Выпуклые и вогнутые
Многоугольник называется выпуклым, если ни одна из его сторон, продолженная до прямой линии, его не пересекает. В обратном случае многоугольник называется вогнутым:
Периметр
Сумма длин всех сторон многоугольника называется его периметром.
Периметр многоугольника ABCDE равен:
AB + BC + CD + DE + EA.
Если у многоугольника равны все стороны и все углы, то его называют правильным. Правильными многоугольниками могут быть только выпуклые многоугольники.
Диагональ
Диагональ многоугольника — это отрезок, соединяющий вершины двух углов, не имеющих общей стороны. Например, отрезок AD является диагональю:
Единственным многоугольником, который не имеет ни одной диагонали, является треугольник, так как в нём нет углов, не имеющих общих сторон.
Если из какой-нибудь вершины многоугольника провести все возможные диагонали, то они разделят многоугольник на треугольники:
Треугольников будет ровно на два меньше, чем сторон:
t = n — 2,
где t — это количество треугольников, а n — количество сторон.
Разделение многоугольника на треугольники с помощью диагоналей используется для нахождения площади многоугольника, так как чтобы найти площадь какого-нибудь многоугольника, нужно разбить его на треугольники, найти площадь этих треугольников и полученные результаты сложить
.
Polygon: от подвижных геометрических фигур до картин
Новости с курса Подвижная математика с Desmos: первые шаги.
В этом модуле мы учились воссоздавать с помощью несложного набора записей геометрические объекты, необходимые нам для визуализации задач по геометрии.
Но это совсем другие задачи — подвижной геометрии.
Причем, нам не нужна даже специальная среда desmos.geometry, знакомство с которой мы отложим до следующего нашего курса.
Здесь мы обойдемся одними аналитическими записями. Можно считать, что да, это аналитическая геометрия.
Несколько примеров того, как мы это делали:
Подвижные отрезки и ломаные
Подвижная ломаная https://www. desmos.com/calculator/18848b1dac
desmos.com/calculator/18848b1dac
Подвижные многоугольники
1. Подвижный многоугольник с помощью таблицы
2. Подвижный закрашенный многоугольник с помощью таблицы и polygon(A,B,C,D,E)
Используя подвижные точки, отрезки, ломаные, многоугольники, можно создать интерактивные задания на множество математических тем:
от задач из «Математической шкатулки» до задач из школьного курса геометрии.
Вот здесь вы можете увидеть примеры таких задач, а ниже — ссылки на апплеты
Desmos-апплеты, использованные в активности
Модель картины с помощью команды polygon
С помощью подвижных многоугольников можно также моделировать картины, в которых много геометрических фигур.
Шаблон Картина Мондриана
Здесь, воспользовавшись образцом — картиной Мондриана, нужно сделать модель картины с помощью подвижных прямоугольников. Для этого ученику необходимо мысленно разметить имеющееся в распоряжении клетчатое пространство (справа).
Линейные размеры не так важны, важнее пропорции и относительное расположении фигур. Отличительная черта этой учебной задачи в том, что нет никаких особенных инструкций по использованию инструментов: ученик должен сам для себя открыть возможность перемещать точки и менять положение и размеры объектов на клетчатой плоскости. В то же время, он имеет возможность самостоятельно проверять правильность своей модели, визуально сравнивая ее с образцом (слева). У ученика здесь есть та самая, упомянутая выше, возможность “возиться” с объектами.
Шаблон Sandor Bortnyik, Composition, 1922
Из картин подобных авторов «собирать» в desmos можно и более сложные в геометрическом плане картины. Например, эту. Заготовка
Предоставляю участникам возможность самим поискать подобные картины и создать шаблоны для их моделирования на основе предложенных прототипов.
Задачи от участников МК
Задачу на построение в интерактивной среде предложила Авраменко Владислава
https://www. desmos.com/calculator/u5ghtuswy3
desmos.com/calculator/u5ghtuswy3
Задачу на вычисление площади многоугольника с помощью вспомогательных линий предложила Юткина Наталья https://www.desmos.com/calculator/s7tiekyzqh
Ирина Кузнецова предложила задачу Участки https://www.desmos.com/calculator/0skab6jmfs
Вот одно из решений https://www.desmos.com/calculator/al5lrl3uta
Лехова Ирина придумала как визуализировать задачу Козы и капуста
https://www.desmos.com/calculator/ddakrfrdtl
Татьяна Кротова предложила визуализацию знаменитой задачи Кобона
https://www.desmos.com/calculator/27qi8xh6pw
Игру Гонки https://www.
desmos.com/calculator/ufw2xikyhj создала Медведева Милана
Ждем новых идей и задач от участников!
Наш курс продолжается…
Публикации по теме
Многоугольные рамки для фото и картин
Многоугольные — в этой статье рассмотрим вопрос изготовления рамок, которые в некотором роде связаны с многоугольными формами. Лучше всего начать с того, что нужно вспомнить из далекой начальной школы, что такое многоугольник.
Лучше всего начать с того, что нужно вспомнить из далекой начальной школы, что такое многоугольник.
Многоугольные и математика для них
- Плоские замкнутые ломаные линии — общий случай;
- Плоские замкнутые ломаные линии без самопересечений — простые многоугольные;
- Часть плоскости, ограниченная замкнутыми ломаными линиями без самопересечений.
На рисунке ниже: (а) пятиугольник; (b) шестиугольник; (c) не является многоугольником, потому что он не замкнут; (d) не является многоугольником, потому что есть линии самопересечений; и (e) не является многоугольные, так как не все его линии являются прямыми.
Виды многоугольников, с разным числом ребер и их имена показаны на рисунке ниже.
Многоугольные формы
Обычные многоугольники имеют свойство, они находятся в кругу, который называется окружностью и соприкасается со всеми вершинами многоугольника. Центром правильного многоугольника всегда является центр его круга.
Допустим, что наш многоугольник имеет количество углов = N, круг имеет всегда 3600 и градус угла определяем из формулы 3600/N.
Например, шестиугольник имеет N=6 углов и образует угол в центре круга равный 3600/6 = 600.
Внутренние углы нашего многоугольника одинаковы и равны 180 0( N-2 )/N градусов.
Например, внутренние углы квадрата равны 1800( 4-2 )/4 = 900; у восьмиугольника 1800( 8-2 )/8 = 1350.
По мере увеличения числа ребер в многоугольнике, длина ребра будет уменьшаться и в конечном итоге они сойдутся в одну окружность.
Некоторые изделия, имеющие многоугольную форму, без изменения размеров сторон показаны на рисунке ниже. Шкатулка имеет форму восьмиугольника, рамки для зеркала, которые имеют прямоугольную и шестиугольную формы. Разделочная доска, не правильный многоугольник, он состоит из двух форм, квадрата и восьмиугольника. Некоторые изделия, имеющие многоугольную форму, с изменением размеров сторон показаны на рисунке ниже. Ваза имеет семь сторон с наклоном в наружу, то есть снизу вверх, настольная лампа, наоборот, имеет наклон во внутрь с шестью сторонами.
Ваза имеет семь сторон с наклоном в наружу, то есть снизу вверх, настольная лампа, наоборот, имеет наклон во внутрь с шестью сторонами.
Равносторонний многоугольник.
Главными переменными на многоугольные формы есть внутренние углы, длина ребер, и площадь изделия. Как видно из рисунка сегмент N-углов вписан в две окружности, обозначим их, как внутренний и внешний круг. Обозначим три стороны треугольника (стороны R, r, и l) его стороны образованы радиусами и ребром, обозначим три угла, которые расположены в треугольнике (А 1, А2 и А3). Между концами этих радиусов внутри двух кругов проведем линию с одной конечной точкой в месте касания к внутреннему кругу и другой точкой в месте касания к внешнему кругу. Радиус — отрезок, соединяющий центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка R.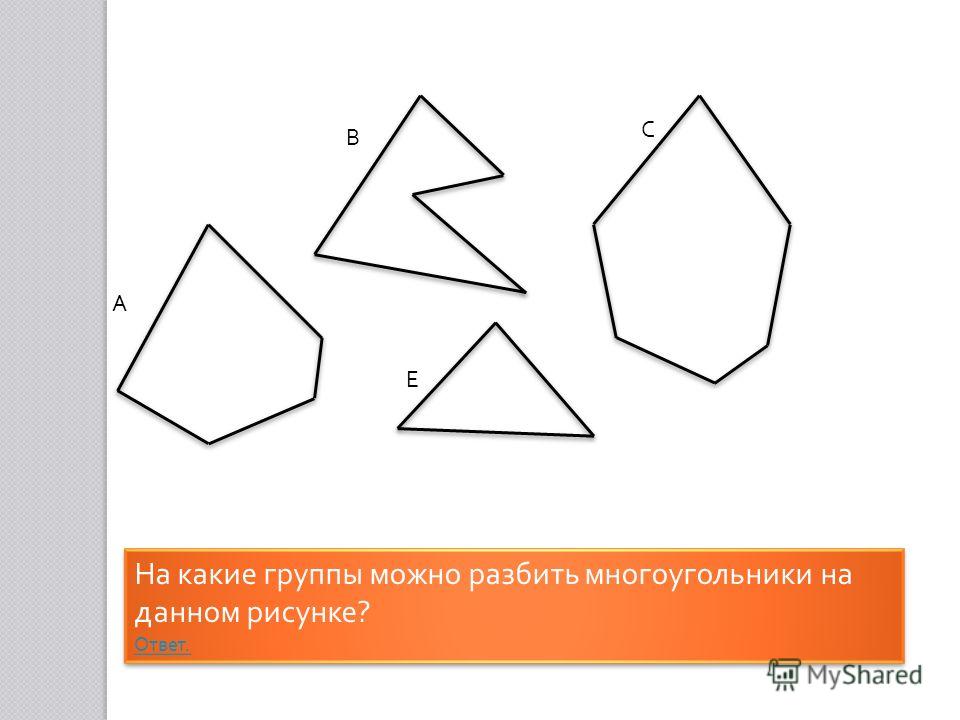 Радиус составляет половину диаметра 2R.
Радиус составляет половину диаметра 2R.
Угол A1 составляет половину центрального угла и равен 1800/N для N-углов. Угол А2 = 900, потому что радиус круга (r) касается к сегменту (l) под прямым углом.
Это означает, что угол А3 и радиус (R) есть составляющие угла А1 и поэтому А3
=900-А1=900(N-2)/N. который является половиной внутреннего угла.
Две стороны определяют третью сторону треугольника, потому что R2=r2+l2. Определим стороны r и l по отношению к углу А1: r=Rcos А1 и l=Rsin А1.
Определим длину ребра L: L=2l=2Rsin А1, это формулы определения градусов в N-углах. [su_note note_color=»#c3f8a3″ radius=»6″].
Пример: Рассмотрим пятиугольник имеющий длину стороны L=1 дюйм. Угол А1=1800/5=360, угол А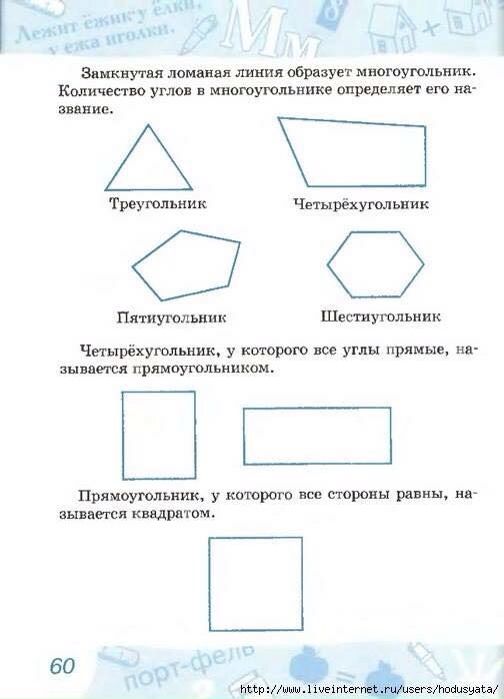
Пятиугольник лежит внутри окружность радиуса R=L/(2sin А1)=1/(2sin 360)=0,85 дюйма.
Пример: Рассмотрим шестиугольник, внутренний круг, имеет диаметр 1,7 дюйма. Определяем радиус окружности R=1,7/2=0,85 дюйма. Угол А1=1800/6=300 и угол А3=600. Длина ребра равна L=2Rsin=1.7sin300=0,85 дюйма.[/su_note]
Углы А1 и А3 важны в создании формы правильного многоугольника и они отмечены в таблице для:
квадрата, пятиугольника, шестиугольника, восьмиугольника.
| N углов | центральный угол | внутренний угол | A1 | A3 |
| 4 | 90 | 90 | 45 | 45 |
| 5 | 72 | 108 | 36 | 54 |
| 6 | 60 | 120 | 30 | 60 |
| 8 | 45 | 135 | 22,5 | 67,5 |
Разносторонние многоугольные.
Разносторонние многоугольники — те, которые имеют стороны не равной длины. Примеры угловых шкафов на рисунке ниже. Здесь углы и ребра разной длины и зависят от конкретных условий.
Те, кому интересна тригонометрия, формулы и примеры:
http://dls-website.com/documents/WoodworkingNotes/Compound%20Miters.pdf http://www.woodcentral.com/bparticles/miter_formula.shtml http://www.woodworkersguildofga.org/ShopHelpers/CompoundMiterTable.pdf Также существует программа написанная на языке Frink, которая позволяет делать расчеты для углов многоугольников на настольных компьютерах и смартфонах, Android-ах и iPhon-ах, она работает с компьютерами на платформе Андроид. Frink — компьютерный язык-программирования, на котором написана программа. Сама программа расположена по адресу: http://dls-website.com/documents/WoodworkingNotes/Compound%20Miters.pdf, там же описание программы и ее настройки. Инструкции по использованию языка-программирования можно получить бесплатно с сайтов: https://play.
http://www.woodworkersguildofga.org/ShopHelpers/MiterCalculator.htm
http://jansson.us/jcompound.html
http://www.pdxtex.com/canoe/compound.htm
Торцовочное приспособление на многоугольные. Торцовочное приспособление необходимо в различных проектах многоугольников, имеющих наклонные стороны. Ниже на рисунке показаны два необходимых реза под углом на циркулярном станке. Один из них создает углы торцов изделия, которые соединяют стороны многоугольника между собой, а другой рез создает углы наклона во внутрь или в наружу для каждой стороны, смотрите рисунок ниже.
Многогранники
Многоугольники являются двухмерными изделиями. Закрытые трехмерные изделия могут быть изготовлены из них путем присоединения многоугольников вдоль их краев. Объекты, полученные таким образом, называются многогранники. Куб полученный соединением шести квадратов является примером многогранника. Другим примером является додекаэдр, он показаны на рисунке слева и на рисунке ниже: (а) античная многогранная шкатулка; (б) додекаэдрическая система динамиков; (с) додекаэдрические солнечные часы, они построены из двенадцати одинаковых пятиугольников. Каждая пятиугольная грань составляет 0,5 дюйма толщиной красного дерева с использованием шаблона метод резки на рисунке ниже.
Важное значение в построении многогранников имеют скошенные уголки его многоугольных граней, детальнее: http://dls-website.com/documents/PolyhedralSundials.pdf
Любовные «многоугольники» Фрэнка Синатры — РИА Новости, 10.12.2010
И если бы не Ава Гарднер, то, возможно, на свет появился бы и еще один список фавориток. С Авой Фрэнк познакомился на съемках фильма «Джентльмены предпочитают блондинок». Молодая актриса не просто попала в список Синатры, она оказалась там единственной. Фрэнк настолько сильно увлекся Гарднер, что буквально вымаливал у своей супруги развод. После долгих уговоров Нэнси согласилась: Синатра и Гарднер обвенчались. Но…
С Авой Фрэнк познакомился на съемках фильма «Джентльмены предпочитают блондинок». Молодая актриса не просто попала в список Синатры, она оказалась там единственной. Фрэнк настолько сильно увлекся Гарднер, что буквально вымаливал у своей супруги развод. После долгих уговоров Нэнси согласилась: Синатра и Гарднер обвенчались. Но…
И эта история завершилась размолвкой. В какой-то момент Ава стала успешнее своего возлюбленного. Разлад в отношениях стал наиболее явным, когда Фрэнк подарил Гарднер кольцо с бриллиантом, не сказав при этом, что купил его на деньги, снятые с ее кредитной карточки. «Я была замужем два раза, но никогда так долго», — иронизировала актриса на устроенной в эту честь вечеринке. Очередной удар по самолюбию Фрэнка, он уезжает на съемки фильма Ф. Циннемана «Отныне и во веки веков», где блестяще сыграл итальянца, солдата американской армии, забитого насмерть в тюрьме.
И вновь громкий успех, толпы поклонниц, мечтающих об одном — хотя бы на секунду оказаться в объятьях знаменитого сердцееда. Все это, безусловно, тешило самолюбие молодого артиста, он был невероятно заносчив, постоянно грубил, что жутко расстраивало Аву. В 1953 году их отношениям пришел конец. И для Синатры это обернулось настоящей трагедией.
Все это, безусловно, тешило самолюбие молодого артиста, он был невероятно заносчив, постоянно грубил, что жутко расстраивало Аву. В 1953 году их отношениям пришел конец. И для Синатры это обернулось настоящей трагедией.
«Гангстер» 30-х
Синатру неоднократно обвиняли в связях с крупнейшими мафиози. Его приглашали участвовать в слетах и съездах международной мафии, он был тесно знаком с Джо Фишетти, племянником самого Аль Капоне.
«Тайм» писал о Синатре: «Мужчина, безусловно, внешне похож на общепринятый стандарт гангстера образца 1929 года. У него яркие, неистовые глаза, в его движениях угадываешь пружинящую сталь; он говорит сквозь зубы. Он одевается с супермодным блеском Джорджа Рафта — носит богатые темные рубашки и галстуки с белым рисунком… согласно последним данным, у него были запонки, примерно стоившие 30 000 долларов… Он терпеть не может фотографироваться или появляться на людях без шляпы или иного головного убора, скрывающего отступающую линию волос».
Тридцать девять лет — расцвет карьеры Фрэнка: награда академии за роль в картине «Отныне и вовеки веков», звание «первого великого певца спален наших дней». О себе в известном справочнике «Кто есть кто» он написал коротко и ясно — «баритон». Новая пассия — Лорен Бейколл, на которой он хотел жениться, но впоследствии передумал, ведь его ждала Мэрилин — Мэрилин Монро.
«Невинная» Монро
Виды многоугольников
Виды многоугольников:
Четырехугольники
Четырехугольники, соответственно, состоят из 4-х сторон и углов.
Стороны и углы, расположенные напротив друг друга, называются противоположными.
Диагонали делят выпуклые четырехугольники на треугольники (см. на рисунке).
Сумма углов выпуклого четырехугольника равна 360° (по формуле: (4-2)*180°).
Параллелограммы
Параллелограмм — это выпуклый четырехугольник с противоположными параллельными сторонами (на рис.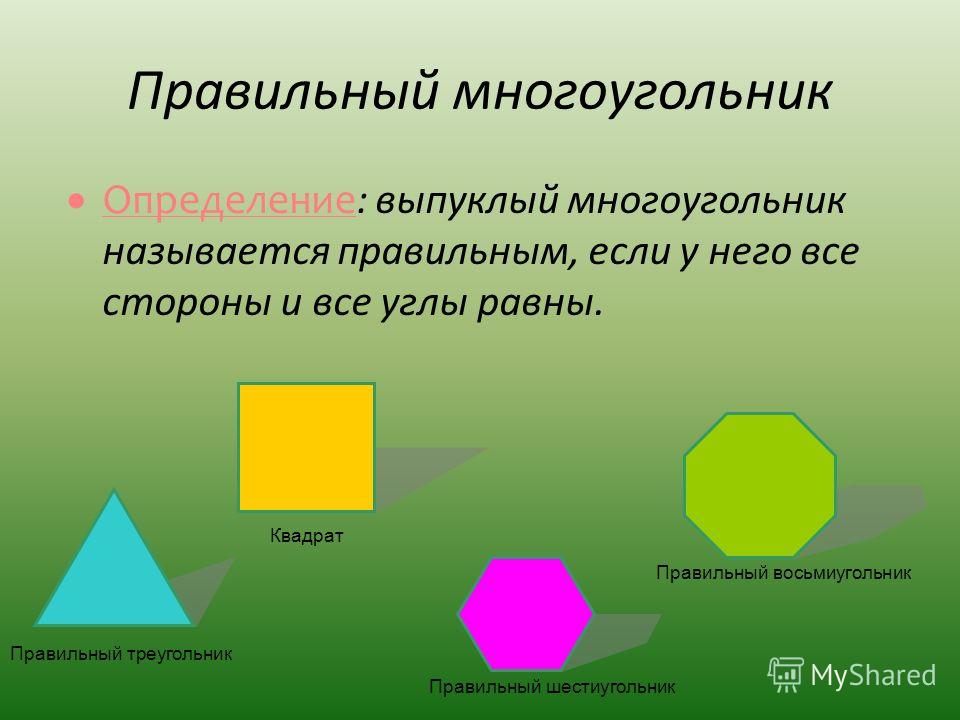 под номером 1).
под номером 1).
Противоположные стороны и углы в параллелограмме всегда равны.
А диагонали в точке пересечения делятся пополам.
Трапеции
Трапеция — это тоже четырехугольник, и в трапеции параллельны только две стороны, которые называются основаниями. Другие стороны — это боковые стороны.
Трапеция на рисунке под номером 2 и 7.
Как и в треугольнике:
— если боковые стороны равны, то трапеция — равнобедренная;
— если один из углов прямой, то трапеция — прямоугольная.
Средняя линия трапеции равна полусумме оснований и параллельна им.
Ромб
Ромб — это параллелограмм, у которого все стороны равны.
Помимо свойств параллелограмма, ромбы имеют своё особое свойство — диагонали ромба перпендикулярны друг другу и делят углы ромба пополам.
На рисунке ромб под номером 5.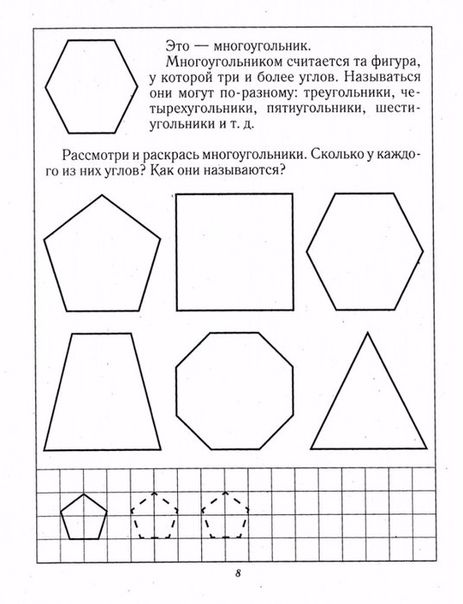
Прямоугольники
Прямоугольник — это параллелограмм, у которого каждый угол прямой (см. на рис. под номером 8).
Помимо свойств параллелограмма, прямоугольники имеют своё особое свойство — диагонали прямоугольника равны.
Квадраты
Квадрат — это прямоугольник, у которого все стороны равны (№4).
Обладает свойствами прямоугольника и ромба (так как все стороны равны).
Редактировать этот урок и/или добавить задание Добавить свой урок и/или задание
Добавить интересную новость
Эффект боке в фотографии — Уроки фотографии
Наверняка вы слышали восхищенные возгласы типа «Ах, какое у него боке!» или «Мне так нравятся фотографии с боке!». Что означает это странное слово? И почему это боке в фотографии так всем нравится? Давайте разберемся вместе!
Что означает это странное слово? И почему это боке в фотографии так всем нравится? Давайте разберемся вместе!
Слово «боке» (правильно произносить «бокЭ» с ударением на последний слог) пришло в русский язык от японского «??» (бокэ) «размытие, нечеткость». Боке в фотографии называют элемент изображения, которое оказалось вне зоны резкости. Именно характер размытия на фотографии зависит от формы и качества боке. Зачастую под боке понимают цветные пятна, которые получаются при размытии небольших световых пятен в зоне нерезкости (фонари, лучи света сквозь листву, вечерние окна домов и т.д.). И это не ошибка, потому что именно в этом случае можно детально разглядеть форму и характер боке.
На самом деле такими размытыми пятнами становятся все детали в зоне размытия на фотографии, и из таких маленьких «бокешек» складывается изображение в зоне нерезкости. Одно боке накладывается на другое, и мы получаем размытое изображение. Только вот разные объективы по-разному размывают фон. Это зависит от конструктивных особенностей конкретного объектива, которые влияют на форму боке. Посмотрим, какие виды боке встречаются и отчего это зависит.
Это зависит от конструктивных особенностей конкретного объектива, которые влияют на форму боке. Посмотрим, какие виды боке встречаются и отчего это зависит.
Боке в видеIMG_7810-web[1] пятиугольников. Объектив Canon 50 mm 1.8, диафрагма 3.5, 5 лепестков диафрагмы
Форма боке в фотографии. Вы наверняка замечали, что на некоторых снимках световые пятна на заднем плане превращаются в размытые кружочки, а на других – в пяти-, шести- или восьмигранники. Дело в том, что форма боке зависит от строения диафрагмы объектива, а именно от количества лепестков. Чем больше лепестков, тем более округлым получается боке на фотографии. При меньшем количестве лепестков получаются многоугольники.
Практически идеально круглое боке. Объектив Canon 70-200 mm 4L, диафрагма 4, 8 лепестков диафрагмы
Более качественные и дорогие объективы обладают диафрагмой со множеством лепестков (8-10), что позволяет рисовать округлое боке. Традиционно считается, что идеальное боке с точки зрения художественности – это круглое пятно, которое дает объектив идеальной конструкции с максимально открытой диафрагмой. Однако интересного эффекта можно добиться и с объективами, которые рисуют боке в фотографии в виде многоугольника.
Традиционно считается, что идеальное боке с точки зрения художественности – это круглое пятно, которое дает объектив идеальной конструкции с максимально открытой диафрагмой. Однако интересного эффекта можно добиться и с объективами, которые рисуют боке в фотографии в виде многоугольника.
На форму боке также влияет степень открытия диафрагмы. При полностью открытой диафрагме (f=1.2, 1.4, 1.8) лепестки разъезжаются до максимального значения, образуя максимально округлое отверстие. При закрытии диафрагмы лепестки сужаются, образуя тупые углы между каждым из элементов конструкции, и отверстие приобретает форму многоугольника с количеством углов, равным количеству лепестков. Также не забывайте, что чем сильнее закрыта диафрагма, тем меньше размытия на фотографии. Поэтому чтобы получить красивое боке в фотографии, сильнее открывайте диафрагму объектива.
Степень яркости боке в фотографии. Еще одна характеристика качества боке – это распределение яркости. В зависимости от этого выделяют три типа боке:
- Боке с высокой яркостью в центре и неяркими краями.
 Это мягкое боке, которое дает плавное и мягкое размытие. Множество размытых таким образом пятен накладываются друг на друга неяркими (размытыми) краями, и получается плавное размытие фона.
Это мягкое боке, которое дает плавное и мягкое размытие. Множество размытых таким образом пятен накладываются друг на друга неяркими (размытыми) краями, и получается плавное размытие фона. - Боке с низкой яркостью в центре и яркими краями (такие колечки или бублики). Это жесткое боке, которое приводит к не совсем красивому размытию. Порой такой тип боке дает задвоение контуров объектов в зоне нерезкости, что отвлекает внимание от главного объекта в кадре.
- Боке в равномерно распределенной яркостью. Это боке называют нейтральным, и оно может встретиться только у идеального объектива (с диафрагмой 1, то есть практически без диафрагмы в конструктивном смысле).
Как получить эффект боке на фотографии? Здесь под боке будем понимать именно размытые световые пятна, которые так нравятся многим ценителям фотографии. Такие пятна придают снимку атмосферность. Добиться эффекта боке достаточно просто: выберите объект съемки (человека или предмет), расположите его на фоне с множеством небольших источников света, которые могут превратиться в красивые цветные пятна. Теперь максимально открывайте диафрагму, фокусируйтесь на главном объекте и нажимайте кнопку спуска. Вуаля! Фотография с красивым боке у вас в портфолио!
Теперь максимально открывайте диафрагму, фокусируйтесь на главном объекте и нажимайте кнопку спуска. Вуаля! Фотография с красивым боке у вас в портфолио!
Если не получается с первого раза подобрать правильную выдержку для нормальной экспозиции, прочитайте мою статью про экспозицию в фотографии тут.
Хороших вам снимков!
Как создать многоугольник в CorelDRAW
Инструмент Многоугольник на первый взгляд не создает впечатление креативного инструмента с широкими возможностями, ведь он предназначен для создания многосторонних многоугольников. Но этот урок убедит вас в обратном.
Как создать многоугольник в CorelDRAW
Для начала нам нужно начертить простой многоугольник. Для этого щелкните инструмент «Многоугольник» и протащите курсор в окне рисования, пока многоугольник не достигнет желаемых размеров.
Совет: для создания симметричного многоугольника (многоугольника с равными сторонами) удерживайте клавишу Ctrl, а для создания многоугольника от центра наружу — клавишу Shift.
После того, как многоугольник создан, выделите его с помощью инструмента Указатель. Количество сторон многоугольника может быть изменено в любой момент. Для этого в поле Точки или стороны на панели свойств нужно ввести число сторон. Помните, что для внесения изменений в объект его нужно выделить с помощью инструмента Указатель.
У нашего многоугольника 8 восемь сторон (восьмиугольник).
После того, как многоугольник создан, щелкните инструмент Форма и нарисуйте окно вокруг многоугольника.
Будут выделены два узла, а на панели свойств отобразятся параметры редактирования узлов. Нажмите значок Преобразовать в кривые.
На первый взгляд изменения не будут заметны. Однако, щелкнув один из узлов или путь многоугольника с помощью инструмента Форма и протащив курсор внутрь или наружу, вы заметите, что стороны многоугольника искривляются. Это позволяет создавать разнообразные формы. Посмотрите:
Посмотрите:
Вы можете продолжать изменять форму многоугольника. Для этого нужно щелкнуть и перетащить узлы и опорные маркеры.
Кроме того, к многоугольнику можно применить заливку цветом. Как видите, здесь я залила многоугольник черным цветом, щелкнув нужный образец цвета на цветовой палитре.
Замечательная особенность состоит в том, что в течение всего процесса исходный многоугольник можно модифицировать — изменять количество сторон многоугольника можно столько раз, сколько нужно.
Каждый раз при изменении количества сторон многоугольника будет создаваться новая фигура.
Попробуйте: выделите многоугольник и измените количество сторон. Для этого в поле Точки или стороны на панели свойств введите нужное число. Как и в этом примере, ваш многоугольник будет автоматически преобразован в новую форму.
Вы сможете взаимодействовать с каждым многоугольником в этом файле и убедиться в универсальности и огромных возможностях инструмента CorelDRAW Многоугольник.
Ссылка на источник
12 лучших низкополигональных генераторов для ярких фонов и изображений
Раскрытие информации: Ваша поддержка помогает поддерживать работу сайта! Мы зарабатываем реферальный сбор за некоторые услуги, которые мы рекомендуем на этой странице. Узнать больше
Поделиться — это забота!
Последнее обновление
Низкополигональные генераторы могут добавить интерес к вашим изображениям. А когда они используются в качестве фона, они помогают придать вашему сайту элегантный, но в то же время ретро-вид.
Этот стиль вошел в моду еще тогда, когда дизайнеры осознали, что могут использовать смелую и яркую геометрию для создания узоров или изображений, которые могут вызывать трехмерный вид.Но благодаря тому, насколько просты низкополигональные конструкции, они не требуют много места для хранения и пропускной способности.
Эта статья представляет собой введение в низкополигональные изображения, а также ссылки на лучшие бесплатные генераторы для создания с их помощью отличных фонов и других изображений.
Просто хотите приобрести один из низкополигональных генераторов? Переходите прямо к фоновым или специализированным генераторам!
История низкополигональных изображений
Низкополигональные изображения восходят к тому времени, когда началась компьютерная анимация.Многие из техник, используемых в этой форме анимации, восходят к началу 1940-х годов, когда в компьютерах даже не было экранов.
Спустя десятилетия компьютерная анимация стала мейнстримом и широко распространена.
К 1980-м годам трехмерные фигуры начали строиться с использованием полигональных сеток, что привело к появлению трехмерных видеоигр. В свою очередь, это привело к использованию компьютерной анимации и 3D-персонажей в таких фильмах, как Terminator 2 .
Изображение с сайта Pixabay
Низкополигональная игра использовалась в видеоиграх из-за быстрого рендеринга.Вы можете думать о лоу-поли как о особом виде мозаики, в которой используются многоугольные формы (треугольники, безусловно, являются наиболее распространенными).
Ключевыми примерами этого вида дизайна являются сетка треугольников, составляющих текстуры, типичные компьютерные фоновые изображения и даже целые изображения, в которых изображения имеют геометрические фигуры, соединенные друг с другом.
Низкополигональную мозаику можно рассматривать как особый вид мозаики, в которой используются многоугольные формы, причем треугольники являются наиболее распространенными.
При выполнении 3D-рендеринга дизайнеры достигают желаемого эффекта создания реалистичного персонажа, используя больше полигонов на изображении.
В веб-дизайне, однако, — полная противоположность . Количество используемых многоугольников сведено к абсолютному минимуму, поскольку основная идея здесь заключается в том, чтобы треугольные конструкции были четко видны.
Зачем нужны низкополигональные генераторы и искусство?
Дизайнеру часто приходится визуализировать трехмерное искусство, если он хочет отобразить такие качества, как освещение и анимация. Раньше для этого требовалось много вычислительной мощности и дорогих суперкомпьютеров.
Раньше для этого требовалось много вычислительной мощности и дорогих суперкомпьютеров.
С годами дизайнеры узнали, что для уменьшения рабочей нагрузки и, следовательно, минимизации потребности в дорогостоящих суперкомпьютерах, достаточно , исключив количество полигонов в сетках.Это то, что мы сейчас называем «low poly».
Изображение через Pxhere
Несмотря на то, что сегодня вы можете купить ноутбук, достаточно мощный для рендеринга продвинутой компьютерной анимации, используя миллионы многоугольников на кадр, low poly по-прежнему процветает , потому что возвращает нас в более простые времена и Дизайнеры help создают более ретро-стиль.
Хотя вы всегда можете использовать фоторедакторы, такие как GIMP или Photoshop, для создания изображений для вашего веб-сайта, если вы хотите заполнить его геометрией, вы обычно будете использовать генераторы low poly или генераторы фона.
С учетом сказанного, вот список некоторых из лучших генераторов low poly на сегодняшний день.
Низкополигональные генераторы фона
Все следующие низкополигональные генераторы бесплатны. Если вам нужна еще большая мощность, у DMesh и HalftonePro есть недорогие премиум-версии.
1. Trianglify
Trianglify — это тот инструмент, который вам нужен, если вы хотите создавать низкополигональные фоны как можно быстрее…
Trianglify — это простое в использовании приложение, которое позволяет создавать низкополигональные фоны очень быстро. Небольшое время.Вы можете скачать их как файлы PNG.
Используемые цвета выбираются случайным образом и меняются со всеми новыми творениями. Вы можете легко контролировать размер и вариацию форм. Trianglify — это инструмент , который вам понадобится , если вы хотите как можно быстрее создавать низкополигональные фоны.
Trianglify предлагает на выбор 27 изысканных цветовых схем, которые надежны. Однако, если вам не нравится какой-либо из них, вы можете просто создать свою собственную цветовую схему с помощью 24-битной палитры цветов, предлагаемой в программе.
Однако, если вам не нравится какой-либо из них, вы можете просто создать свою собственную цветовую схему с помощью 24-битной палитры цветов, предлагаемой в программе.
Снимок экрана с помощью Trianglify
2. DMesh
Гениальность DMesh заключается в том, что он может легко превращать уже существующие изображения в низкополигональные файлы, просто накладывая желаемую трехмерную треугольную сетку на двухмерное изображение.
DMesh на самом деле разработан для новичков…
Вы можете даже автоматически сгенерировать очки, но если вы хотите более изысканный вид, вам рекомендуется создавать свои собственные точки.
Хотя DMesh может выглядеть как продвинутый генератор фона или программа для редактирования изображений, на самом деле он разработан для новичков.Вот почему вы найдете такие полезные функции, как , автоматическое создание точек , что делает его очень простым в использовании.
Бесплатная версия DMesh не позволяет вам контролировать количество используемых полигонов или плотность распределения. Но с помощью ластика вы можете легко уменьшить количество треугольников, отображаемых в вашем изображении, после того, как это произошло.
С помощью DMesh вы можете экспортировать готовые файлы в форматы растрового изображения, Wavefront OBJ или PDF.
Снимок экрана через DMesh
3.HalftonePro
Это векторный генератор многоугольников с широким набором опций настройки, позволяющих создавать шестиугольные заголовки и кристаллические покрытия. Однако это не самый простой инструмент.
HalftonePro позволяет создавать детализированные градиенты с каждой настройкой, радикально меняющей изображение…
HalftonePro имеет широкий спектр сложных под поверхностью, что придает ему удивительные качества, которыми восхищается почти каждый дизайнер.
С помощью этого инструмента вы можете легко создавать детализированные градиенты с каждым параметром , радикально меняющим изображение и предоставляя вам больше возможностей обработки изображений.
Хотя это прекрасное дополнение, оно означает, что вы должны быть очень осторожны с количеством настроек, которые вы делаете, чтобы получить идеальный фон заголовка.
HalftonePro дает вам практически безграничные комбинации. Но он также предоставляет инструмент изменения размера, что означает, что вам не нужно использовать какие-либо другие редакторы изображений, если вы хотите уменьшить окончательное изображение до нужного размера.
Снимок экрана с помощью HalftonePro
4. Генератор треугольников Делоне
Прежде чем мы поговорим об этом низкополигональном генераторе, лучше всего объяснить «триангуляцию Делоне» в целом.
Генератор треугольников Делоне предоставляет вам до семи виртуальных источников света, которые значительно помогают, отбрасывая окружающий свет на холст…
Триангуляция Делоне — это математическая функция, которая определяет треугольник на основе массива точек. В этом дизайне ни одна из точек не находится внутри описанной окружности других треугольников. Это означает, что эта конструкция максимально избегает острых углов и в результате дает очень широкие и большие формы.
В этом дизайне ни одна из точек не находится внутри описанной окружности других треугольников. Это означает, что эта конструкция максимально избегает острых углов и в результате дает очень широкие и большие формы.
Генератор треугольников Делоне основан на этих принципах. Инструмент дает вам до семи виртуальных источников света , которые очень помогают, отбрасывая окружающий свет на холст. Вы можете легко настроить цвета, а также их интенсивность.
Самое главное, однако, вы можете изменить количество полигонов, а также их мягкость.
Если вы хотите создать фон с великолепным люминесцентным узором и, как правило, элегантными изображениями, этот инструмент для вас.
Снимок экрана через MSurguy.github.io
5. Polyshaper
Polyshaper — простой в использовании, но мощный низкополигональный генератор…
Polyshaper — это веб-приложение, которое создает низкополигональное изображение на основе обычного изображения. Но это дает большой контроль.
Но это дает большой контроль.
С Polyshaper вы можете вводить свои собственные баллы (но это не обязательно). А с помощью отдельных инструментов вы можете добавлять и удалять лишние треугольники.
Можно включать и выключать формы границ, а также заливку. Вы также можете изменить прозрачность этих элементов.
Кроме того, в Polyshaper есть инструментов для манипулирования цветом , которые позволяют получить ваше низкополигональное изображение именно таким, каким вы его хотите.
Снимок экрана с помощью Polyshaper
6.Генератор изображений триангуляции
Триангулятор — это очень простой в использовании низкополигональный генератор…
Генератор изображений триангуляции триангуляторов — очень простой в использовании инструмент. У него не так много вариантов, но он отлично подходит, если вам нужно низкополигональное изображение, но вас не слишком заботят его детали.
Как и многие генераторы low poly, Triangulator начинается с базового изображения и создает из него низкополигональное изображение. У него есть изображение по умолчанию, которое вы можете использовать.
Triangulator предлагает 3 алгоритма : Yape06 (с элементами управления Laplacian и Mineigen), Yape (с контролем радиуса) и Fast Corners (с контролем порогового значения). Yape06 обеспечивает максимальный контроль, а Fast Corners создает более типичные низкополигональные изображения.
Вы также можете установить любой размер изображения в соответствии с базовым изображением или 720p, 1080p и 2160p.
Снимок экрана через SnapBuilder
7. Генератор низкополигонального фона
С помощью низкополигонального генератора фона вы можете создать практически любой фон, который хотите…
Генератор низкополигонального фона прост в использовании. -используем еще и мощный .
-используем еще и мощный .
Вы можете установить следующие значения:
- Размер изображения
- Вариант ячейки
- Размер ячейки
- Глубина ячейки
- Количество цветов
- Цвета
С помощью этих функций вы сможете создать почти любой фон по вашему желанию.
Снимок экрана через Codepen
Специализированные низкополигональные генераторы
Инструменты в этом разделе более специализированы, чем те, что указаны выше.Большинством из них интересно пользоваться. Но более того, они полезны блогерам для различных целей.
1. PolyGen
Это, безусловно, один из лучших низкополигональных генераторов, доступных для мобильных устройств (его можно найти как в App Store, так и в Play Store).
Безусловно, один из лучших низкополигональных генераторов, доступных для мобильных…
PolyGen действительно создан для личного использования, например для создания фоновых изображений и аватаров телефонов. Но он может быть полезен дизайнерам, которые в основном работают в дороге и на своих телефонах, чтобы создавать изображения, идеально подходящие для их мобильных проектов.
Но он может быть полезен дизайнерам, которые в основном работают в дороге и на своих телефонах, чтобы создавать изображения, идеально подходящие для их мобильных проектов.
PolyGen, несомненно, невелик, но это не значит, что ему не хватает отличного контента. Он имеет список функций , который идет в ногу с любым полнофункциональным низкополигональным генератором для ПК, представленным сегодня на рынке. Кроме того, его можно использовать для создания красивых шаблонов дизайна или просто для упрощения изображений.
Можно было бы ожидать, что инструмента, который долгое время был монополистом на рынке мобильных низкополигональных генераторов, в некоторых областях будет немного не хватать. Будьте уверены, что это не относится к PolyGen.
Этот инструмент нисколько не жертвует качеством. Вот почему это инструмент для создания low-poly для мобильных пользователей и дизайнеров.
Снимок экрана через Google Play Store
2.
 I ♥ Δ
I ♥ ΔI ♥ Δ уникален для запуска в веб-браузере из кода на вашем локальном компьютере…
I ♥ Δ — это простой но забавный инструмент. Он позволяет импортировать растровую графику. Затем на основе этого изображения он создает поверх него слой, содержащий рандомизированные треугольники на основе изображения.
Можно объединить два изображения, изменив непрозрачность низкополигонального изображения. Однако, если вы хотите загрузить это изображение, вам нужно будет сделать снимок экрана. В противном случае вы можете сохранить только низкополигональное изображение в формате SVG или PNG.
I ♥ Δ уникален тем, что вы загружаете код на локальный компьютер, а затем запускаете его в веб-браузере. Это очень просто и быстро.
Снимок экрана через Игоря Борисенко
3. Триангуляция
Триангуляция позволяет легко преобразовать обычное изображение в низкополигональное…
Триангуляция — это веб-приложение, которое позволяет легко создавать низкополигональные изображения. поли изображения на основе изображения.Вы просто перетаскиваете изображение в него . Как только он появится, вы сможете контролировать количество точек, ширину обводки, размытие и точность.
поли изображения на основе изображения.Вы просто перетаскиваете изображение в него . Как только он появится, вы сможете контролировать количество точек, ширину обводки, размытие и точность.
Триангуляция также имеет кнопку случайного выбора. Он рандомизирует четыре элемента управления, упомянутых выше. Это очень интересно, потому что это вырывает вас из ваших обычных склонностей и часто создает действительно необычные образы.
Помимо перетаскивания, изображения можно загружать или брать с веб-камеры. Вы также можете скачать изображение в формате PNG или SVG.И, наконец, вы можете поделиться им в Facebook, Twitter и Reddit.
Снимок экрана через snorpey.github.io
4. Poly Maker
Polymaker — это мощный инструмент, который не только интересен в использовании…
Poly Maker — удивительно мощный инструмент для тех, кто так много весело работать.
Это необычно во многих отношениях, но особенно с точки зрения того, что он использует для создания низкополигонального изображения: 4 выбранные пользователем точки, которые соответствуют кубической кривой Безье.Итак, вы запускаете любой проект, щелкнув 4 места на экране. Вы быстро узнаете, как эти точки определяют окончательное изображение.
Poly Maker имеет различные способы изменения изображения. Например, можно задать количество используемых шагов , а также двухцветную схему . Также есть много других настроек.
Вы также можете скачать изображения в формате PNG. При желании можно отобразить код SVG. Этот код можно скопировать и вставить в локальный файл.
Снимок экрана с помощью Aerotwist.com
5. Polygonize
Polygonize предоставляет простой способ сделать ваши изображения более интересными…
Polygonize — невероятно простой инструмент, но его можно использовать, чтобы оживить ваш блог .
Вы загружаете изображение (или вводите URL-адрес), а затем выбираете один из 15 фильтров Polygonize. Большинство фильтров представляют собой простые низкополигональные изображения, но некоторые сочетают их с другими графическими элементами.
Онлайн-версия ограничена изображениями размером 700 пикселей и менее.Если вам нужно более высокое разрешение, доступна недорогая версия для Windows.
Снимок экрана с помощью Polygonize
Как выбрать правильный низкополигональный генератор
Выбор правильного низкополигонального генератора действительно зависит от ваших общих дизайнерских навыков и того, чего вы хотите достичь в конечном итоге. Более продвинутые дизайнеры будут довольны очень сложными инструментами, такими как HalftonePro, в то время как те, кто только начинает, могут захотеть использовать DMesh или PolyGen.
Что вы хотите сделать, так это найти инструмент, обладающий следующими качествами:
- Простота использования
- Предоставляет вам больше всего вариантов, когда дело доходит до цветовой схемы
- Имеет большинство настроек, не будучи слишком сложными
- Позволяет вам для экспорта готовой работы в желаемый формат
- Имеет широкую сеть поддержки в Интернете
Любой из вышеупомянутых низкополигональных генераторов соответствует этим требованиям, но не так прост в использовании, и именно здесь проявляются ваш опыт и предпочтения играть.
Хотя всегда легче загружать готовые изображения, лучше использовать любой из этих низкополигональных генераторов для создания или изменения собственных, поскольку добавляет уникальный элемент на ваш веб-сайт .
Используйте любой из этих генераторов low poly, чтобы улучшить свой блог или другие проекты!
Фрэнк работает в Интернете с 1987 года. Когда блоги впервые появились, он отверг их как костыли, которыми пользуются люди, не умеющие программировать. Но в 2008 году он завел личный блог и влюбился.С тех пор он опубликовал около 10 000 сообщений в блогах.
Color by Polygon в App Store
Раскрашивайте по полигонам с помощью PolyColor! Поднимите раскраску на СЛЕДУЮЩИЙ БОЛЬШОЙ уровень! Создайте свои собственные художественные работы в стиле Low-Poly! Воображение запрещено!
Приготовьтесь к опыту Unique Polygon R T! Это НОВАЯ горячая тенденция в окрашивании, от которой невозможно отстать! Создайте свой собственный мозаичный шедевр из крошечных треугольников! Изображения превратились в причудливые геометрические произведения искусства!
Думаете, вы действительно не можете создавать картинки из тех, кто не из этого мира? Подумай еще раз! Никакого специального набора навыков не требуется! Выберите картинку, свяжитесь со своим внутренним художником и раскрасьте его по-своему с помощью потрясающего набора палитр и классных цветовых комбинаций! От яркого, энергичного, веселого до мрачного и драматичного! Придайте ему причудливую, футуристическую или просто настоящую цветовую атмосферу!
Используйте Poly Cam, чтобы сделать снимок, или выберите любое изображение, которое вам нравится, и превратите его в раскраску с геометрическим рисунком!
Если вы ищете расслабляющий и увлекательный способ развить свое творчество, вы его нашли! Простые геометрические фигуры расположены бок о бок! Отпустите свои заботы, расслабьтесь и погрузитесь в творческое настроение с PolyColor! Намного легче, чем вы думали!
ОСОБЕННОСТИ:
• Полигональное искусство! Мега потрясающий способ раскраски нового поколения!
• Сделайте потрясающие низкополигональные изображения!
• Сила идеального соответствия цветов! Стильная палитра для любых и всех картинок!
• Огромная коллекция картинок с угловатым рисунком! Скоро будут регулярные обновления!
• Используйте многоугольную камеру, чтобы сделать потрясающий снимок и превратить его в многоугольник!
• Супер-легкий антистресс! Не подчеркнул? Просто выпустите своего творческого зверя!
• Развлечения для всей семьи! И для взрослых, и для детей!
• Запишите процесс создания с помощью замедленных видеороликов!
• Удивите друзей и поделитесь своими шедеврами!
• Простой, чистый, минималистичный внешний вид!
Не стесняйтесь написать нам: support @ exosmart. uk.com
uk.com
Получить PolyColor Premium
Подпишитесь на Premium, чтобы получить неограниченный доступ к полной коллекции полигональных изображений. Погрузитесь в мир современного футуристического искусства без ограничений!
-3 варианта подписки: еженедельная (7,99 долларов США, 3-дневная бесплатная пробная версия), ежемесячная (7,99 долларов США), годовая (39,99 долларов США).
-Подписавшись, вы получаете неограниченный доступ ко всем функциям приложения на весь период подписки.
— Оплата будет снята с учетной записи iTunes при подтверждении покупки.
-Подписка автоматически продлевается, если автоматическое продление не отключено по крайней мере за 24 часа до окончания текущего периода.
-Счет будет взиматься плата за продление в течение 24 часов до окончания текущего периода. «Бесплатная пробная версия»> 7,99 долл. США в неделю или продление соответствует выбранной первоначальной подписке и ее текущей цене, если не предлагается специальная цена.
-Вы можете отменить бесплатную пробную версию, управлять своей подпиской и отключить автоматическое продление в любое время через настройки своей учетной записи. Это необходимо сделать за 24 часа до окончания бесплатного пробного периода или периода подписки, чтобы избежать списания средств.
Это необходимо сделать за 24 часа до окончания бесплатного пробного периода или периода подписки, чтобы избежать списания средств.
-Политика конфиденциальности: http://exosmart.uk.com/index.php/privacy-policy/
-Условия использования: http://exosmart.uk.com/index.php/terms-of-use/
-Как только вы приобретете подписку, любая неиспользованная часть или период бесплатного пробного периода будет аннулирован.
Создание многоугольника в App Store
PolyGen — приложение для низкополигонального искусства. Он позволяет создавать кристаллические узоры автоматически или вручную вручную.
Иногда в приложениях не так много возможностей для игры, что ограничивает ваше творчество.Из-за этого мы привыкаем выбирать предустановленные обои или использовать те же старые фильтры. Если бы только был инструмент, который позволил бы вам без особых усилий создавать красивые дизайны …
Откройте для себя PolyGen, приложение, которое позволяет каждому быть художником.
С помощью PolyGen вы можете:
— Создавать бесконечное количество полигонов
— Выбирать цвета, размеры, контраст и многое другое
— Создавать красивое абстрактное искусство
— И преобразовывать фотографии в геометрическое искусство
— Переключаться в редактор и размещать точки самостоятельно
— Используйте узор в качестве обоев вашего смартфона
— Или создайте аватары, фоны социальных сетей и многое другое
Некоторые из обзоров:
TUAW: PolyGen — это полезное приложение, которое позволяет вашему дому iOS и экранам блокировки выглядеть так, как вы может постоянно освежаться.
JC7133: Я давно искал подобное приложение. Количество настроек (огромное количество) настолько велико.
Cyberspace: нравится тот факт, что оно поддерживает размеры экрана рабочего стола. Больше не нужно искать в Интернете абстрактные обои!
PolyGen предлагает простые и полезные решения, заключенные в легкий в использовании интерфейс. Вы можете создавать новые полигональные узоры одним простым касанием. При желании вы можете контролировать процесс, а также легко «заблокировать» свои любимые атрибуты.Редактировать вершины фигур также просто: нажмите, чтобы создать одну, или нажмите на существующую, чтобы удалить ее.
При желании вы можете контролировать процесс, а также легко «заблокировать» свои любимые атрибуты.Редактировать вершины фигур также просто: нажмите, чтобы создать одну, или нажмите на существующую, чтобы удалить ее.
Шаблоны PolyGen готовы к использованию в качестве обоев для мобильных устройств или рабочего стола, аватаров или фонов в социальных сетях. Пользователи поделились ими на арт-порталах и добавили в качестве иллюстраций в сообщения в блогах и социальных сетях. Узоры варьируются от красочных до спокойных, от простых до замысловатых, от абстрактных до фотореалистичных.
Какой узор вы собираетесь создать?
Посетите официальную галерею на Tumblr:
http: // PolyGenApp.tumblr.com/
Как PolyGen на Facebook:
http://facebook.com/PolyGenApp
Подпишитесь на PolyGen в Twitter:
http://twitter.com/PolyGenApp
Инструмент «Многоугольное лассо» — выделение в Photoshop
По умолчанию инструмент «Многоугольное лассо» скрывается за стандартным инструментом «Лассо» на панели «Инструменты». Чтобы добраться до него, щелкните инструмент «Лассо», затем удерживайте кнопку мыши нажатой, пока не появится всплывающее меню с дополнительными доступными инструментами.Выберите инструмент Polygonal Lasso Tool из списка:
Чтобы добраться до него, щелкните инструмент «Лассо», затем удерживайте кнопку мыши нажатой, пока не появится всплывающее меню с дополнительными доступными инструментами.Выберите инструмент Polygonal Lasso Tool из списка:
Инструмент «Многоугольное лассо» скрывается за стандартным инструментом «Лассо» на панели «Инструменты».
После того, как вы выбрали инструмент «Многоугольное лассо», он появится вместо стандартного инструмента «Лассо» на панели «Инструменты». Чтобы вернуться к инструменту «Лассо» позже, нажмите и удерживайте инструмент «Многоугольное лассо», затем выберите инструмент «Лассо» во всплывающем меню:
Какой из трех инструментов лассо, выбранных вами последним, появится на панели «Инструменты».Выберите остальные из раскрывающегося меню.
Вы можете циклически переключаться между тремя различными инструментами лассо в Photoshop (инструмент «Лассо», «Полигональное лассо» и «Магнитное лассо», которые мы рассмотрим позже), удерживая нажатой клавишу Shift и несколько раз нажимая букву L .
Плагин шорткодов, действий и фильтров: ошибка в шорткоде [ ads-basics-middle-2 ]
Рисование прямых многоугольных выделений
Рисование выделений с помощью инструмента «Многоугольное лассо» во многом похоже на рисование прямолинейных контуров с помощью инструмента «Перо» .Начните с щелчка где-нибудь вдоль края объекта или области, которую нужно выделить, затем отпустите кнопку мыши. Это добавляет к документу точку, обычно называемую точкой привязки или точкой крепления. Когда вы отодвинете инструмент «Многоугольное лассо» от точки, вы увидите тонкую прямую линию, выходящую из курсора мыши, немного похожую на паука, плетущего паутину, с другим концом линии, прикрепленным к точке привязки. Щелкните еще раз, чтобы добавить вторую точку, затем отпустите кнопку мыши. Линия будет «привязана» к новой точке, и теперь обе точки соединятся прямой линией.
Продолжайте перемещаться по объекту или области, щелкая, чтобы добавить новую точку в любом месте, где линия должна изменить направление, прикрепляя конец линии к каждой новой точке по мере продвижения. В отличие от стандартного инструмента «Лассо», а также многих других инструментов выделения Photoshop, нет необходимости удерживать кнопку мыши нажатой при перемещении от точки к точке. Просто щелкните, чтобы добавить точку, отпустите кнопку мыши, перейдите к следующему месту, где линия должна изменить направление, затем щелкните, чтобы добавить новую точку:
В отличие от стандартного инструмента «Лассо», а также многих других инструментов выделения Photoshop, нет необходимости удерживать кнопку мыши нажатой при перемещении от точки к точке. Просто щелкните, чтобы добавить точку, отпустите кнопку мыши, перейдите к следующему месту, где линия должна изменить направление, затем щелкните, чтобы добавить новую точку:
Щелкните, чтобы добавить точки вокруг объекта или области, где необходимо изменить направление линии.
После того, как вы обошли объект или область, завершите выбор, еще раз щелкнув начальную точку, которую вы добавили. Photoshop преобразует все прямые линии в контур выделения. Когда вы достаточно приблизитесь к начальной точке, чтобы завершить выбор, в правом нижнем углу значка курсора появится маленький кружок. Я увеличил изображение, чтобы круг было легче рассмотреть:
Маленький кружок появляется в правом нижнем углу значка курсора, когда вы достаточно близко к начальной точке, чтобы завершить выбор.
Вы также можете закрыть выделение, просто дважды щелкнув в любом месте с помощью инструмента «Многоугольное лассо». Photoshop автоматически закроет выделение прямой линией от точки, на которой вы щелкнули, до начальной точки.
Photoshop автоматически закроет выделение прямой линией от точки, на которой вы щелкнули, до начальной точки.
Вот фотография, которую я открыл в Photoshop, показывает большой пустой рекламный щит, висящий на стене здания. Я хочу добавить фотографию на рекламный щит, а это значит, что сначала мне нужно выбрать ее:
Пустой рекламный щит.
На первый взгляд может показаться, что рекламный щит имеет форму прямоугольника, так зачем использовать инструмент «Многоугольное лассо», если инструмент «Прямоугольная область» должен работать нормально? Давайте попробуем.Я нажимаю на клавиатуре букву M , чтобы быстро выбрать инструмент Rectangular Marquee Tool, затем щелкаю в верхнем левом углу рекламного щита, чтобы начать выделение, и перетаскиваю его в нижний правый угол. Чтобы завершить выбор, отпущу кнопку мыши:
Попытка выделить рекламный щит с помощью инструмента Rectangular Marquee Tool.
Как мы видим, даже если рекламный щит, вероятно, показался бы нам прямоугольным, если бы мы стояли прямо перед ним, угловая перспектива фотографии искажает его форму, и инструмент Rectangular Marquee Tool в конечном итоге выполняет довольно паршивую работу. выбирая это.
выбирая это.
Я нажму Ctrl + D (Win) / Command + D (Mac), чтобы удалить мой неудачный контур выделения. На этот раз попробуем выбрать рекламный щит с помощью инструмента Polygonal Lasso Tool. Я возьму инструмент Polygonal Lasso Tool из панели инструментов, как мы видели ранее, затем, чтобы начать свой выбор, я щелкну в верхнем левом углу рекламного щита и отпущу кнопку мыши. Это устанавливает мою начальную отправную точку для выбора. Я перейду в верхний правый угол и нажму, чтобы добавить вторую точку.Photoshop соединяет две точки вместе тонкой прямой линией. Я нажимаю, чтобы добавить третью точку в правом нижнем углу, затем щелкаю, чтобы добавить четвертую точку в нижнем левом углу, прикрепляя прямую линию к каждой новой точке, когда я обхожу рекламный щит. Опять же, я не удерживаю кнопку мыши при перемещении от точки к точке. Я просто нажимаю, чтобы добавить точки, а затем каждый раз отпускаю кнопку мыши:
Щелкая в каждом из четырех углов с помощью инструмента «Многоугольное лассо», начиная с верхнего левого угла и двигаясь по часовой стрелке.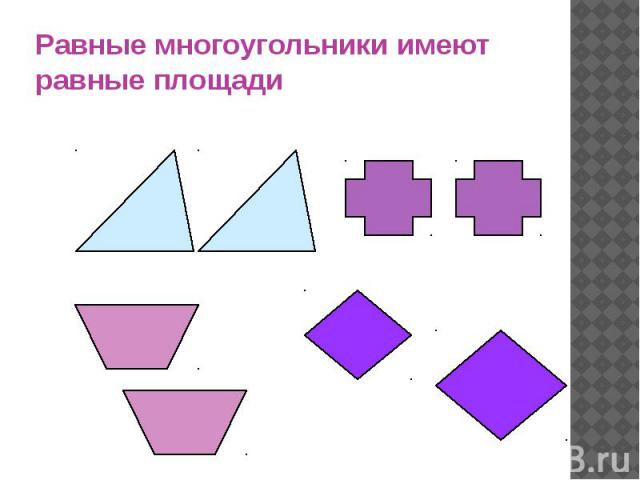
Если вы ошиблись и щелкнули, чтобы добавить точку не в том месте, нет необходимости начинать заново. Просто нажмите клавишу Backspace (Win) / Delete (Mac) на клавиатуре, чтобы отменить последнюю добавленную точку. Если вам нужно отменить несколько точек, продолжайте нажимать Backspace (Win) / Delete (Mac), чтобы отменить точки в обратном порядке, в котором они были добавлены.
Чтобы завершить свой выбор, я снова щелкну по начальной начальной точке для выбора в верхнем левом углу рекламного щита, затем отпущу кнопку мыши.Photoshop преобразует все прямые линии между точками в мой контур выделения, и, как мы видим, на этот раз мы смогли сделать гораздо лучшую работу по выбору рекламного щита:
Инструмент «Многоугольное лассо» упростил выбор билборда.
Теперь, когда рекламный щит выбран, я открываю изображение, которое хочу добавить к нему:
Фотография будущего билборда.
Я нажму Ctrl + A (Win) / Command + A (Mac), чтобы быстро выделить все изображение, затем Ctrl + C (Win) / Command + C (Mac) , чтобы скопировать его в буфер обмена. Чтобы добавить изображение на рекламный щит, я вернусь к своей исходной фотографии, затем перейду в меню Edit вверху экрана и выберу команду Paste Into :
Чтобы добавить изображение на рекламный щит, я вернусь к своей исходной фотографии, затем перейду в меню Edit вверху экрана и выберу команду Paste Into :
Команда «Вставить в» в Photoshop позволяет нам вставлять изображение прямо в выделенную область.
Это помещает вторую фотографию прямо в выделенную область, и после небольшого изменения размера с помощью команды Photoshop Free Transform изображение появляется на рекламном щите для всеобщего обозрения:
Кому бы не понравилось быть больше, чем жизнь на рекламном щите?
Для более подробного объяснения того, как вставить одно изображение в другое, обязательно ознакомьтесь с нашим учебным курсом «Размещение изображения внутри другого изображения в Photoshop ».
Далее мы рассмотрим, как инструмент «Многоугольное лассо» справляется с чем-то более сложным, чем четырехсторонний рекламный щит, и что происходит, когда мы сталкиваемся с закругленной или изогнутой частью объекта!
Не все, что вы хотите выделить с помощью инструмента «Многоугольное лассо», будет таким же простым, как четырехсторонний рекламный щит, но шаги всегда одинаковы. Просто щелкните, чтобы добавить точки вдоль объекта в те места, где контур выделения должен изменить направление, затем щелкните обратно в начальной начальной точке, чтобы завершить выделение.
Просто щелкните, чтобы добавить точки вдоль объекта в те места, где контур выделения должен изменить направление, затем щелкните обратно в начальной начальной точке, чтобы завершить выделение.
Вот фото старого здания. Я хочу заменить небо на фотографии, а это значит, что мне нужно выделить небо, нарисовав часть выделенной области вокруг верхней и боковых сторон здания. Поскольку здание почти полностью состоит из прямых плоских поверхностей, инструмент Polygonal Lasso Tool должен упростить задачу:
Чтобы выделить небо на фотографии, мне нужно выделить стороны и верх здания.
Я начну свой выбор где-нибудь с левой стороны здания, щелкнув мышью, чтобы задать начальную точку, затем я медленно пройду по внешней стороне здания, щелкая, чтобы добавить точки по мере необходимости.Я немного увеличу , чтобы было легче увидеть, что я делаю, нажав несколько раз Ctrl ++ (Win) / Command ++ (Mac). Чтобы прокрутить изображение внутри окна документа, нажмите и удерживайте пробел , который временно переключает вас на Ручной инструмент , затем щелкните и перетащите изображение, чтобы переместить его. Отпустите клавишу пробела, чтобы вернуться к инструменту «Многоугольное лассо»:
Отпустите клавишу пробела, чтобы вернуться к инструменту «Многоугольное лассо»:
.
Лучше закройте окна. Инструмент «Многоугольное лассо» без труда поднимается по стенам зданий.
Переключение между инструментом «Многоугольное лассо» и стандартным инструментом «лассо»
Пробираясь по верху здания, я наткнулся на проблему. Часть конструкции на крыше на самом деле закруглена, что является плохой новостью для инструмента Polygonal Lasso Tool, поскольку он может рисовать только прямые выделения. К счастью, Photoshop позволяет легко переключаться между инструментом «Многоугольное лассо» и стандартным инструментом «лассо» в таких случаях, как этот. Просто удерживайте нажатой клавишу Alt (Win) / Option (Mac), затем начните перетаскивание с помощью мыши.Это временно переключает вас на стандартный инструмент Lasso Tool, и с его помощью мы можем легко обвести любые закругленные или изогнутые области объекта:
Удерживая Alt (Win) / Option (Mac), начните перетаскивание, чтобы временно переключиться на стандартный инструмент «Лассо».
Обведя край закругленной или изогнутой поверхности, отпустите клавишу Alt / Option, затем отпустите кнопку мыши. Вы снова переключитесь на инструмент Polygonal Lasso Tool, после чего вы можете продолжить движение вокруг объекта и щелкнуть, чтобы добавить больше точек:
Отпустите клавишу Alt (Win) / Option (Mac), затем отпустите кнопку мыши, чтобы вернуться к инструменту Polygonal Lasso Tool.
Как только я закончу рисовать выделение вокруг здания, я уберу все краевые пиксели неба по бокам и вверху фотографии, щелкнув инструментом «Многоугольное лассо» в серой области монтажного стола вокруг Фото. Если вы не видите область монтажного стола, нажмите несколько раз Ctrl + — (Win) / Command + — (Mac), чтобы уменьшить масштаб, пока не появится монтажный стол. Photoshop не выбирает монтажный стол, он выбирает только пиксели изображения:
Щелчок внутри области монтажного стола вокруг изображения — хороший способ убедиться, что вы выбрали все краевые пиксели.
Чтобы завершить выбор, я еще раз щелкну по исходной начальной точке, и теперь небо на фотографии выделено:
Небо готово к замене.
Я собираюсь вернуться к уровню масштабирования 100%, нажав Ctrl + Alt + 0 (Win) / Command + Option + 0 (Mac). Если мы посмотрим на мою панель «Слои», то увидим, что мой документ состоит из двух слоев. Фотография здания находится на верхнем слое, а фотография темного облачного неба находится на фоновом слое под ним:
Облака, которыми я хочу заменить небо, находятся на слое под изображением здания.
Выбрав верхний слой, я собираюсь удерживать клавишу Alt (Win) / Option (Mac) и щелкнуть значок Layer Mask в нижней части панели слоев. Это преобразует мой выбор в маску слоя , и мы видим, что миниатюра маски слоя была добавлена к верхнему слою. Обычно выбранный объект или область остаются видимыми в документе, в то время как все, что не было выделено, скрывается от просмотра, но, удерживая нажатой клавишу Alt / Option, я инвертировал маску слоя, которая скроет небо.![]() (выбранная область) и оставить здание (невыделенную область) видимым:
(выбранная область) и оставить здание (невыделенную область) видимым:
Черные области в маске слоя скрыты от просмотра в документе.Белые области остаются видимыми.
Когда небо на фотографии здания теперь скрыто, облака на фотографии ниже видны в документе:
Если вам не нравится погода в Photoshop, просто подождите несколько минут. Это изменится.
Удаление выделения
В приведенном выше примере контур выделения исчез, когда мы преобразовали его в маску слоя, но обычно, когда вы закончили с выделением, созданным с помощью инструмента Polygonal Lasso Tool, вы можете удалить его, перейдя в меню Select в верхней части экрана и выбрав Отменить выбор , или вы можете нажать сочетание клавиш Ctrl + D (Win) / Command + D (Mac).Вы также можете просто щелкнуть в любом месте документа с помощью инструмента «Многоугольное лассо» или любого другого инструмента выделения Photoshop.
Как использовать инструмент Photoshop «Многоугольник» для обновления портретов
Загрузите файлы проекта здесь
Дополнительные руководства по редактированию фотографий
Такие многоугольные портреты сейчас очень популярны, но прежде чем мы углубимся в это руководство, сначала предупреждаем: это займет некоторое время.
Нет волшебных фильтров, которые бы справились с этой задачей.Вместо этого каждая треугольная форма, которую вы видите на изображении, была терпеливо вычерчена вручную, поэтому для достижения приличного уровня детализации потребуется не менее часа или двух.
К счастью, после того, как начальные шаги выполнены и все настроено, построение треугольников — это тип повторяющейся работы, которую можно выполнять, слушая радио или даже наполовину смотря телевизор. Все эти усилия служат только для того, чтобы сделать конечный эффект более полезным.
Мы предоставили несколько начальных изображений, но гораздо лучше использовать один из ваших собственных снимков.Подойдет любой портрет, и это не обязательно должен быть человек — животные и домашние животные тоже подойдут.
Подробнее: Лучшие приложения для редактирования фотографий для устройств iOS и Android
Основная техника здесь очень проста. Сначала мы выбираем треугольную часть портрета.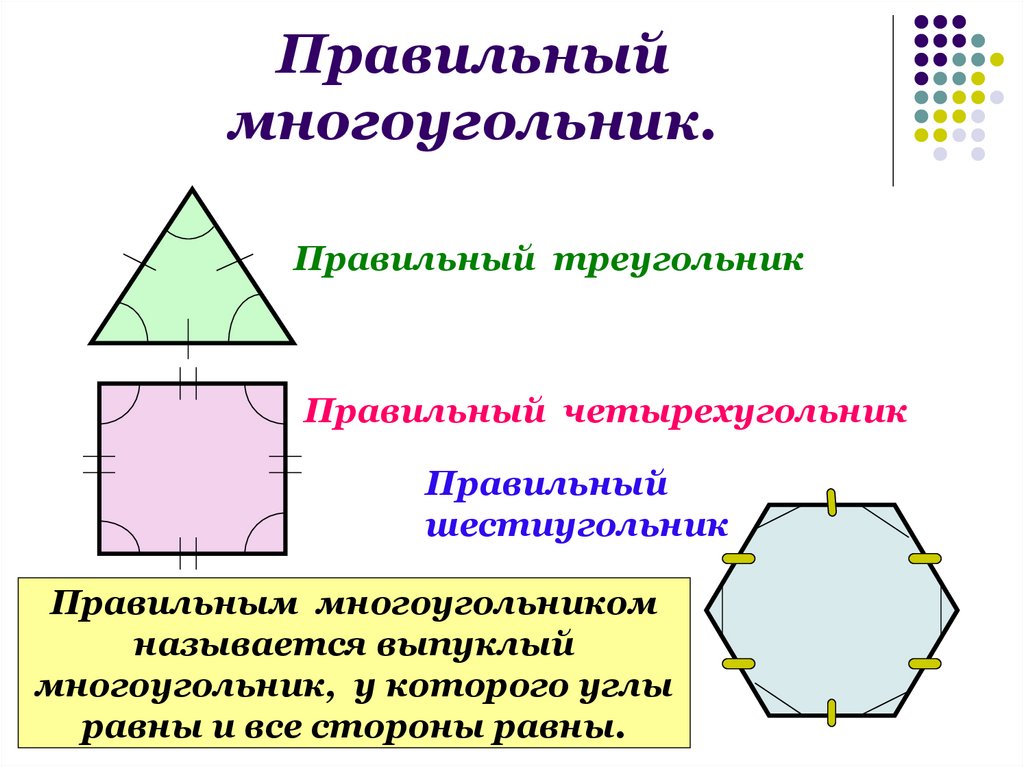 Затем мы применяем фильтр «Среднее», который показывает среднее значение для всех цветов в выделенной области, как если бы они смешивались в большом горшке. Затем мы просто повторяем этот процесс, пока он не закончится.
Затем мы применяем фильтр «Среднее», который показывает среднее значение для всех цветов в выделенной области, как если бы они смешивались в большом горшке. Затем мы просто повторяем этот процесс, пока он не закончится.
К счастью, мы можем сэкономить время, просто записав быстрый экшен Photoshop, который сделает всю действительно тяжелую работу за нас. Мы даже можем назначить это действие сочетанию клавиш, так что единственное, что нам нужно сделать вручную, — это нарисовать каждый из треугольников.
• Получите больше идей фотосессии
Пошаговое руководство: приведите форму в Photoshop
Узнайте, как создать низкополигональный эффект, и узнайте, как действия могут значительно сэкономить время
1.Настройка и действие
Откройте изображение и на панели «Слои» нажмите «Новый слой». Выберите инструмент «Многоугольное лассо» и создайте случайный треугольник. Выберите «Окно»> «Действия», щелкните значок «Новый набор» и назовите его, затем щелкните значок «Новое действие». Назовите действие, назначьте функциональную клавишу и нажмите «Запись».
Назовите действие, назначьте функциональную клавишу и нажмите «Запись».
2. Размытие до среднего
Точно соблюдайте этот бит. Щелкните слой «Фон», затем нажмите Ctrl + J, чтобы скопировать выделение на новый слой. Перейдите на панель «Слои» и, удерживая нажатой клавишу Ctrl, щелкните миниатюру слоя с треугольником, чтобы загрузить фигуру в качестве выделения.Перейдите в Фильтр> Размытие> Среднее, затем нажмите Ctrl + D, чтобы снять выделение.
3. Сделайте края более четкими
Нажмите кнопку «Fx» на панели «Слои» и выберите «Обводка». Установите Размер: 1, Положение: Внутри, Режим наложения: Разница, Непрозрачность: 100% и установите белый цвет, чтобы края были более четкими. Нажмите «ОК», затем нажмите «Остановить» на панели «Действия». Перетащите два верхних слоя в корзину.
БЫСТРЫЙ СОВЕТ!
Используя инструмент «Многоугольное лассо», дважды щелкните, чтобы отправить выделение обратно в начальную точку. Backspace удаляет предыдущую точку.
Backspace удаляет предыдущую точку.
4. Включите сетку
Перейдите в «Настройки» и щелкните «Направляющие, сетки и фрагменты». Установите подходящий размер сетки, например 5 пикселей. Перейдите в меню «Просмотр»> «Показать»> «Сетка», затем «Просмотр»> «Привязать к» и установите флажок «Сетка». Сделайте треугольное выделение с помощью Polygonal Lasso — оно должно привязаться к сетке. Нажмите сочетание клавиш «Действие».
5. Заполните портрет
Выберите треугольник, запустите действие и повторяйте, пока не закончите.Попробуйте разделить лицо на разные по тональности и детализации участки. Каждый треугольник должен встречаться в угловых точках соседнего, чтобы стороны совпадали. Используйте треугольники меньшего размера в деталях, например, в глазах.
6. Настройте стили
Дважды щелкните Стиль обводки. Установите режим наложения: Умножение, Непрозрачность: 10%. Нажмите «Наложение градиента», выберите «От черного к белому», режим наложения: мягкий свет, непрозрачность: 20%. Щелкните правой кнопкой мыши> Копировать стиль слоя, щелкните верхний и нижний треугольные слои, удерживая клавишу Shift, щелкните правой кнопкой мыши> Вставить стиль слоя.
Щелкните правой кнопкой мыши> Копировать стиль слоя, щелкните верхний и нижний треугольные слои, удерживая клавишу Shift, щелкните правой кнопкой мыши> Вставить стиль слоя.
Как правильно
Чтобы низкополигональный эффект выглядел правильно, каждую форму треугольника нужно аккуратно стыковать с соседней, а точки выровнять так, чтобы ни один треугольник не пересекал стороны другого. Мы также должны убедиться, что все аккуратно соединено. Вот почему мы включаем «привязку к сетке», чтобы точки сетки становились немного липкими. По-прежнему требуется много терпения, чтобы точно нанести каждую точку (особенно на таком портрете, который состоит из более тысячи слоев).После завершения изучите изображение, и если вы заметите какие-либо пробелы, удалите слой и повторите выделение.
Подробнее: Как удалить и заменить небо в Photoshop
Эволюция изображения
Что это?
Имитация отжига, подобная алгоритму оптимизации, повторная реализация
Отличная идея Роджера Алсинга. Цель состоит в том, чтобы получить изображение , представленное как набор перекрывающихся многоугольников различных цветов и прозрачностей .
Цель состоит в том, чтобы получить изображение , представленное как набор перекрывающихся многоугольников различных цветов и прозрачностей .
Мы начинаем со случайных 50 невидимых полигонов. На каждом шаге оптимизации мы случайным образом изменяем один параметр (например, компоненты цвета или вершины многоугольника) и проверьте, больше ли такой новый вариант похож на исходное изображение. Если это так, мы сохраняем его и продолжаем видоизменять его.
Фитнес — это сумма попиксельных отличий от исходного изображения. Чем меньше число, тем лучше.
Отображаемая пригодность теперь выражается в процентах от того, насколько близко новое изображение к исходному (1-текущая разница / максимальная разница).Лучшее из возможных — 100%.
Эта новая приспособленность нормализована, чтобы было легче сравнивать разные изображения и разные размеры.
Эта реализация основана на описании Роджера Алсинга, но не на его коде. Вероятно, есть некоторые тонкие различия в том, как выполняются мутации, как представлены полигоны и как вычисляется приспособленность, когда я пытался выяснить, как пусть он работает достаточно быстро в среде JavaScript +
Как это выглядит через некоторое время?
- 50 полигонов (4 вершины)
- ~ 15 минут
- 644 полезные мутации
- 6120 кандидатов
- 88.
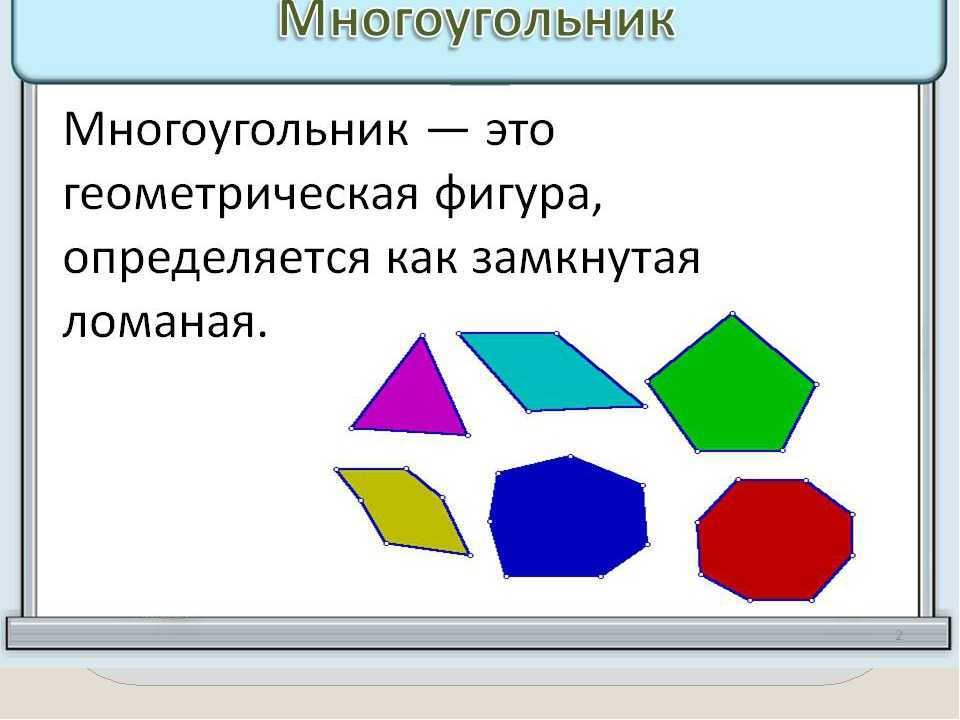 74% фитнес
74% фитнес
- 50 полигонов (6 вершин)
- ~ 15 минут
- 646 полезных мутаций
- 6024 кандидата
- 89,04% пригодность
- 50 полигонов (10 вершин)
- ~ 15 минут
- 645 полезных мутаций
- 5367 кандидатов
- 87,01% пригодность
- 50 полигонов (6 вершин)
- ~ 45 минут
- 1476 полезных мутаций
- 23694 кандидата
- 93.35% фитнес
- 50 полигонов (6 вершин)
- ~ 60 минут
- 1595 полезных мутаций
- 28 888 кандидатов
- 93,46% фитнес
- 50 полигонов (6 вершин)
- ~ 120 минут
- 1966 полезных мутаций
- 50 500 кандидатов
- 93.89% фитнес
- 50 полигонов (6 вершин)
- ~ 4 часа
- 4134 полезные мутации
- 807 890 кандидатов
- 95,59% фитнес
- Спасибо Сергею.
- 50 полигонов (6 вершин)
- ~ 2 дня
- 7 425 полезных мутаций
- 5 288 801 кандидат
- 96.
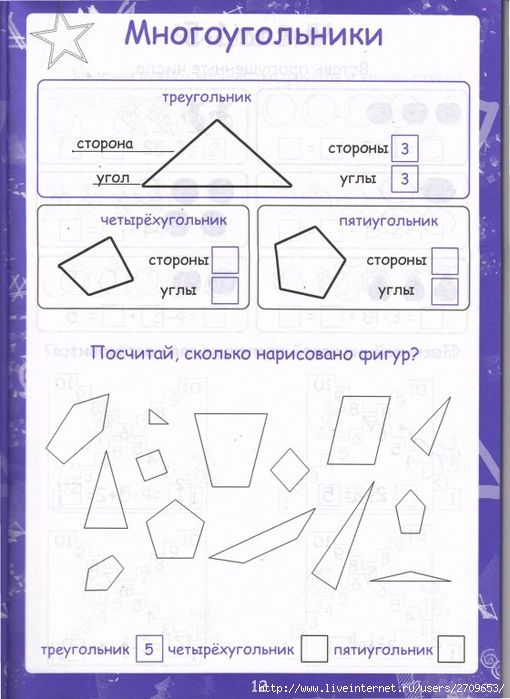 36% фитнес
36% фитнес - Спасибо Джулиану.
- 1000 полигонов (12 вершин)
- ~ 7 дней
- 21135 полезных мутаций
- 8 143 969 кандидатов
- 97,12% пригодность
- Спасибо Богдану.
На всех образах работает?
Это зависит от успеха. Лучше всего выглядят цветные изображения с четко определенными характеристиками.
- 50 полигонов (6 вершин)
- 4358 полезных мутаций
- 227 852 кандидата
- 95,97% фитнес
- Спасибо Quialiss.
- Изображения из разных прогонов.
- 50 полигонов (6 вершин)
- 718+ полезных мутаций
- 22 440+ кандидатов
- 95.24% фитнес
- Изображения из разных прогонов.
- 100 полигонов (6 вершин)
- 9686 полезных мутаций
- 1,220,569 кандидатов
- 96,21% фитнес
- Спасибо Стивену.
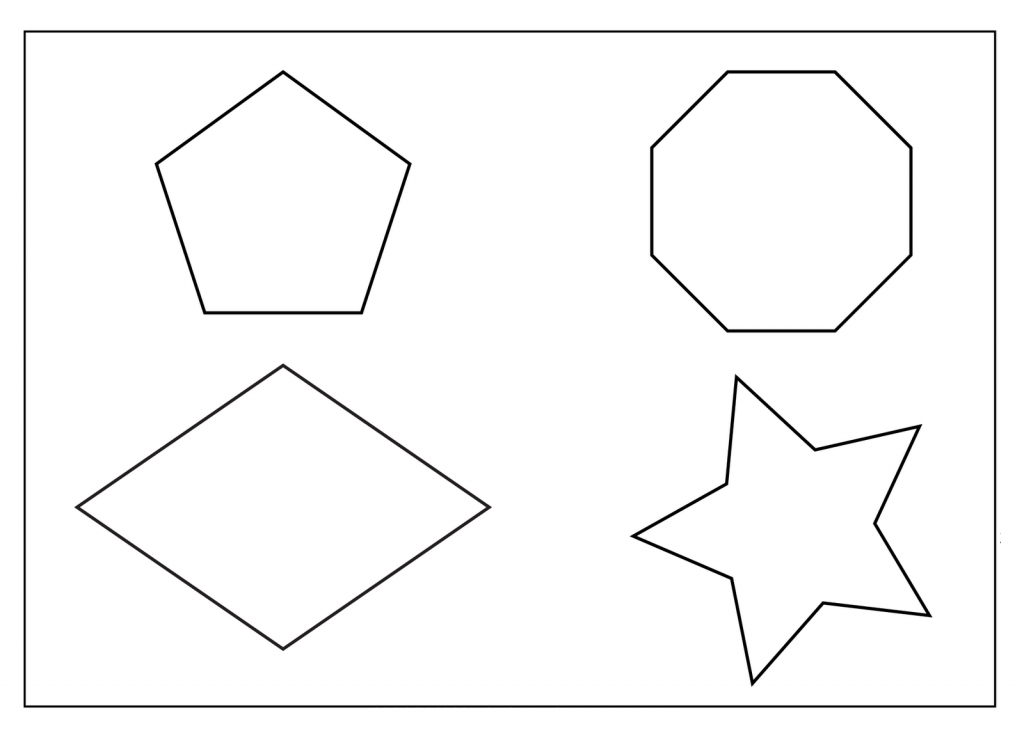
- 100 полигонов (5 вершин)
- 10490 полезных мутаций
- 2 161 018 кандидатов
- 95.03% фитнес
- Спасибо Асе, Уиллу, Нику и Юку.
- Изображения из разных прогонов.
- 50 полигонов (6 вершин)
- 6280 полезных мутаций
- 683 806 кандидатов
- Спасибо alexs за финальное изображение.
- Изображения из разных прогонов.
- 100 полигонов (5 вершин)
- 6974 полезные мутации
- 2,056,467 кандидатов
- 95.68% фитнес
- Спасибо Юку.
- 100 полигонов (6 вершин)
- 6,557 полезных мутаций
- 44 212 346 кандидатов
- 99,43% пригодность
- Спасибо Алексу.
- 50 полигонов (5 вершин)
- 8031 полезная мутация
- 1,099,366 кандидатов
- 96.
 14% фитнес
14% фитнес - Спасибо Karol Masztalerz.
- 50 полигонов (6 вершин)
- 4296 полезных мутаций
- 2404942 кандидата
- 97,6% фитнес
- Спасибо Кайлу.
- 50 полигонов (6 вершин)
- 10605 полезных мутаций
- 11 104 153 кандидата
- 93.84% фитнес
- Спасибо KRHAiNOS.
- 50 полигонов (6 вершин)
- 11147 полезных мутаций
- 1,021,165 кандидатов
- 95,04% пригодность
- Спасибо Саймону.
См. Также видео об эволюции логотипа Firefox. Спасибо Brooss.
- Объем распределенных вычислений: исходный размер изображения 600 пикселей X 900 пикселей, разделенных на 24 части, каждая по 150 X 150 пикселей
- 24 x 100 полигонов (6 вершин)
- 109 438+ полезных мутаций (всего)
- 8243441+ кандидатов (всего)
- Фитнес: мин.
 95.01%, макс 99,08%, среднее 96,59%, медиана 96,65%
95.01%, макс 99,08%, среднее 96,59%, медиана 96,65% - Спасибо Agro momusuindo.net (Индонезия).
- Окончательное изображение с полным разрешением
- 6278 полезных мутаций
- 267 623 кандидата
- 96,95% фитнес
- 4208 полезных мутаций
- 8 451 873 кандидата
- 97.88% фитнес
- 6250 полезных мутаций
- 10418975 кандидатов
- 98,38% пригодность
- 6281 полезная мутация
- 226 689 кандидатов
- 96,75% фитнес
- Спасибо Маринке за персонажей Южного парка.
- 100 полигонов (5 вершин)
- 7310 полезных мутаций
- 5 430 510 кандидатов
- 96.53% фитнес
- Спасибо Магнусу Хансену.
- 95,79% пригодность
- 1 день 9 часов
- Спасибо Кристиану Гроссеру.
Что такое импорт / экспорт ДНК?
Предупреждение: еще одна экспериментальная (которая вообще не тестировалась) функция. Большинство ошибок должны быть исправлены сейчас.
Большинство ошибок должны быть исправлены сейчас.
Нажмите Экспорт ДНК , чтобы скопировать полигональное представление текущего лучшего изображения в буфер обмена.Вы можете использовать его для сохранения состояния оптимизации, например, чтобы отправить его кому-нибудь по почте или разместить в сети.
Если у вас есть такая сохраненная строка ДНК, вы можете позже вставить ее в буфер обмена и нажать Импортировать ДНК . Это должно воспроизвести состояние оптимизации с момента сохранения через экспорт.
Обратите внимание, что ДНК не зависит от исходного изображения. Это означает, что если вы использовали собственное изображение, вы также должны настроить это изображение (через форму изображения) для воспроизведения полное состояние.(Или вы можете поиграть с переключением изображений / ДНК на полпути)
Формат ДНК очень простой (все числа — INT, кроме ALPHA, которая имеет FLOAT):
ЧИСЛО_OF_VERTICES NUMBER_OF_POLYGONS R G B АЛЬФА X0 Y0 X1 Y1 ... XN YN ... R G B АЛЬФА X0 Y0 X1 Y1 ... XN YN ...
Нажмите Экспортировать ДНК как SVG , чтобы получить векторное изображение из вашей лучшей на данный момент ДНК. Спасибо Мартину за экспорт SVG.
Требования
Протестировано и работает (пример скорости мутации для Моны Лизы в начале оптимизации на моем ноутбуке):
- Firefox 29 (~ 222 мутации в секунду)
- Хром 34 (~ 209 мутаций в секунду)
- Explorer 11 (~ 182 мутации в секунду)
Не стесняйтесь улучшать мою реализацию.Код довольно уродливый, хотя и некрасивый по соображениям производительности.
Фотоскан — Редактирование ортофотоплана — GeoCue Group
Photoscan имеет функцию назначения только выбранных пользователем изображений для определенной области. Это полезно для очистки областей ортофокуса, которые имеют: размытость, движущиеся транспортные средства, плохое сшивание изображений и т. Д. Созданные полигоны также могут использоваться для определения подмножества области проекта для экспорта.
Монтаж
1.Для начала убедитесь, что вы выбрали просмотр ортофотоплана, нарисуйте многоугольник вокруг области ортофотоплана, в которой есть проблемы. Используйте инструмент Draw Polygon , который находится на панели инструментов. Щелкните левой кнопкой мыши по области, которую необходимо отредактировать, и дважды щелкните, чтобы закончить. (Рисунок 1)
фигура 1
2. Щелкните правой кнопкой мыши многоугольник и выберите Назначить изображения. (рисунок 2)
фигура 2
3. Что касается заменяющих изображений для выбранной области, можно назначить одну фотографию или несколько фотографий.Когда вы щелкаете по доступным фотографиям в окне «Назначить изображения», изображения изменяются в области многоугольника. Выберите фотографии, которые изменяют область до желаемого вида. Когда вы закончите, нажмите ОК. (Рисунок 3)
Рисунок 3
4. Чтобы применить изменения, которые вы выбрали для ортофотоплана: вы должны обновить ортофотоплан после назначения изображений в выбранной области. Нажмите кнопку Обновить ортофотоплан . Эта кнопка будет выделена только после того, как вы назначили изображения.(Рисунок 4)
Чтобы применить изменения, которые вы выбрали для ортофотоплана: вы должны обновить ортофотоплан после назначения изображений в выбранной области. Нажмите кнопку Обновить ортофотоплан . Эта кнопка будет выделена только после того, как вы назначили изображения.(Рисунок 4)
Рисунок 4
5. После нажатия этой кнопки и принятия изменений она снова станет серой. Теперь ортомозиум должен отражать изменения, которые вы выбрали в окне ортофотоплана Photoscan и экспортировать.
Определение области проекта
1. Для начала нарисуйте многоугольник вокруг области, которая будет использоваться в качестве границ для экспорта ортофотоплана. Используйте инструмент «Нарисовать многоугольник», расположенный на панели инструментов.
Заколдованные многоугольники | План-конспект занятия по математике (подготовительная группа) на тему:
Непосредственно-образовательная деятельность
«Заколдованные многоугольники»
Комплексное комбинированное занятие
в старше -подготовительной группе
Разработала воспитатель СПб ГБУ
«Центр содействия семейному воспитанию №2»
Кудрявцева Евгения Анатольевна
Конспект комплексного занятия по формированию познавательных представлений у дошкольников.
Тема: «Заколдованные многоугольники»
Цель: Продолжать знакомить детей с многоугольниками, их взаимно-однозначным соответствием.
Задачи:
1.Продолжать знакомить детей с многоугольниками, его признаками, сторонами, углами, вершинами.
2.Познакомить детей со способами рисования многоугольника в тетради.
3.Продолжать учить понимать количественные отношения между числами в пределах 10.
4.Активизация словаря детей за счёт слов: многоугольник, вершина, сторона, угол.
5.Учить детей увеличивать и уменьшать число на 1.
Материал к занятии:.
-Демонстрационный материал -набор геометрических фигур.
– Чудесный мешочек.
-Набор игрушек: свинка, парты , доска.
-Мяч.
-Обручи
-Числовые домики
-Раздаточный материал: наборы геометрических фигур.
Ход занятия
Сюрпризный момент: Стук в дверь, Появляется свинка Пеппа с чудесным мешочком в руках.
-Здравствуйте, ребята.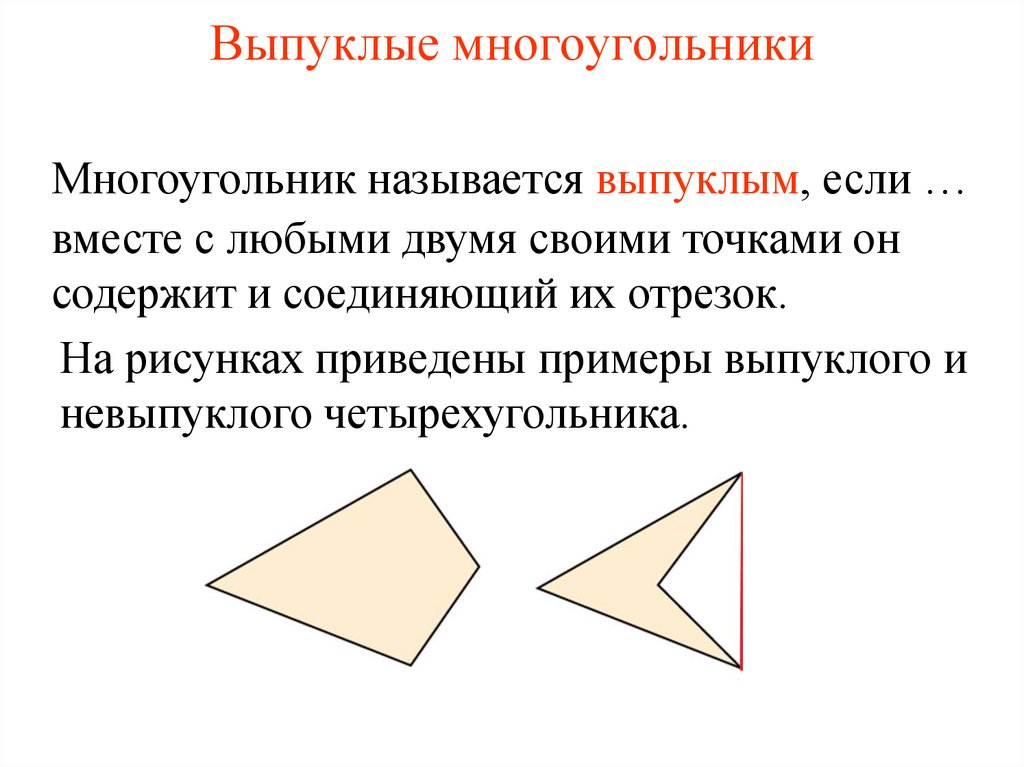
-Скажи пожалуйста, что у тебя в мешочке?
-У меня заколдованные фигуры.
-А как же их можно расколдовать?
– Расколдовать их можно следующим способом. Вы, ребята подходите ко мне, вынимаете из мешочка по одной фигуре, называете её.
Ответы детей.
-Скажите пожалуйста, как называются эти геометрические фигуры одним словом?
-Все эти геометрические фигуры называются многоугольники.
-Сегодня вместе со свинкой Пеппа мы узнаем почему они так называются.
У всякого многоугольника есть вершины, углы, стороны.
От того, сколько вершин, углов, сторон зависит название многоугольника.
Свинка Пеппа: Я дотрагиваюсь волшебной палочкой до многоугольника, авы , ребята считаете и называете , сколько углов, сторон, вершин у многоугольника.
-Ответы детей: 4 стороны, 4вершины, 4 стороны, стороны попарно равны.- прямоугольник.
-5углов, 5 сторон, 5 вершин- это пятиугольник .и т.д.
-Свинка Пеппа: -Молодцы, ребята, расколдовали все фигуры и я знаю, почему они называются многоугольники.
Игра «Сложи узор»
Дети делятся на пары.
Перед ними наборы геометрических фигур и две карточки, на каждой рядиз семи геометрических фигур, расположенных по-разному, с помощью жеребьёвки выбирается ведущий.Один из играющих берёт какой-нибудь предмет, прячет в руке, тот , кто отгадает, в какой руке предмет, становится ведущим. Ведущий берёт одну из карточек и начинает называть геометрические фигуры в ряду. Другой ребёнок раскладывает фигуры согласно инструкции. После того, как ребёнок разложил геометрические фигуры, дети проверяют, правильно ли он выполнил задание.
Игра «Назови предмет»
Дети делятся на две команды .
Одна команда находит предмет прямоугольной формы, другая –квадратной.
За каждый названный предмет, дети получают фишку.
В конце игры выясняется.
Сколько каждая команда набрала очков?
Какая команда больше назвала предметов?
Сколько всего предметов четырехугольной формы назвали все дети?
-Появляется свинка Пеппа:-«Я, очень люблю рисовать.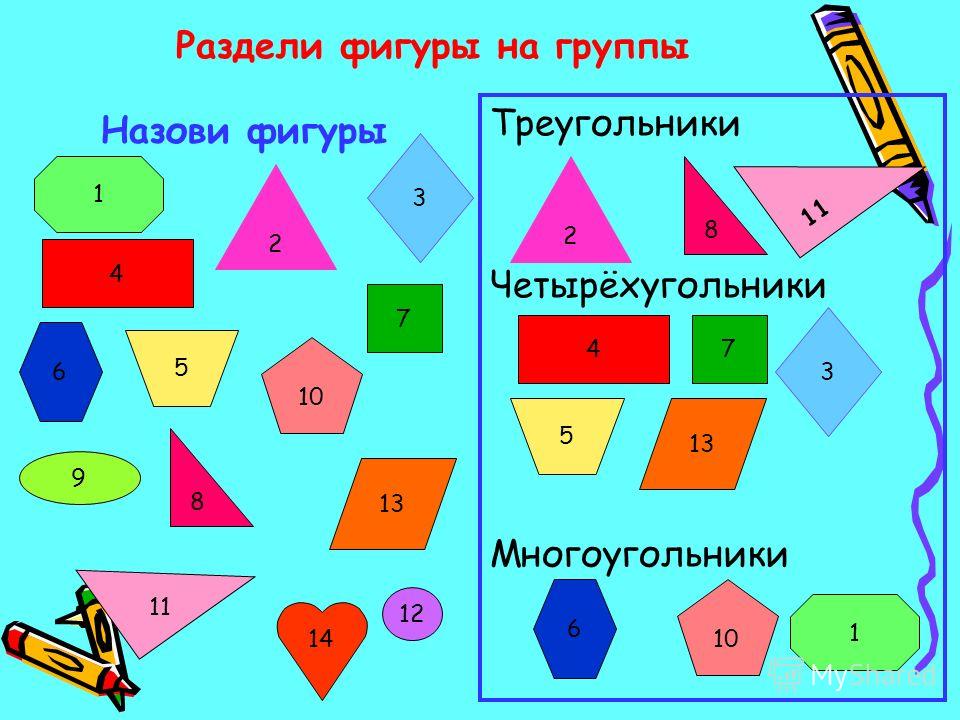
-Мы, тебя сегодня научим рисовать многоугольники.
-В-ль: Давайте все вместе попробуем нарисовать пятиугольник.
-Поставлю 5 точек для вершин, соединяю их прямыми линиями, между собй- получили стороны многоугольника.
-Какая фигура получилась(пятиугольник).
-Проверим, правильно ли мы нарисовали пятиугольник.
(Дети проверяют, считая вершины, углы, стороны)
-Теперь каждый из вас нарисует многоугольник.
-Сначала поставьте в тетрадях точки для вершин, затем соедините их линиями
В-ль: Какие многоугольники вы нарисовали?(ромб, прямоугольник, трапецию).
Многоугольники нарисавали.
-Свинка Пеппа, а ты хочешь с нами в мяч поиграть.
Игра «Назови числа»
Бросая мяч свинка Пеппа бросает мяч и просит увеличить (или уменьшить), названное число на 1..Ребёнок, поймавший мяч, называет число, затем сам называет любое число, просит уменьшить его и бросает мяч кому либо из играющих.
Игра с домиками.
Свинка Пеппа, а не желаешь выбрать себе домик, в котором будешь жить.
У каждого из играющих свой дом с определённым количеством окон, а в обруче нужная цифра.
Под музыку каждый бегает по группе, как только музыка закончилась, надо поставить свой дом в определённый обруч, с нужным количеством окон.
Итог занятия:
Свинка Пеппа. Ребята, спасибо вам огромное.
-Я запомнила, как называются геометрические фигуры, которые вам принесла и мы их вместе « расколдовали».
-Они называются –многоугольники, поняла почему они так называются.
-Вместе с вами научилась рисовать многоугольники
-Я научилась увеличивать и уменьшать число на 1.
-Научилась считать кол-во окошек в домиках и соотносила с нужной цифрой.
-Спасибо, вам ребята большое. Я многому у вас научилась.
2. Устный счет
3.
4.Целеполагание.
5.Момент осознания учащимися З. и У.
6.Взаимоконтроль и взаимопроверка.
7.
8.Закрепление знаний и способов действий.
9.Разминка для глаз
10.
11.Итог урока. Рефлексия.
| Работа в парах. –Возьмите карточки, такие, как на экране. Поработаем в парах. Первый в паре находит и называет числа на карточке в порядке возрастания, затем меняетесь, второй – в порядке убывания. Чья пара будет готова, покажите жестом «Я готов».
– Давайте подготовим наши руки к работе: Вот помощники мои. Их как хочешь, поверни. По дороге белой, гладкой, Скачут пальцы как лошадки. Чок-чок-чок-чок. Скачет резвый табунок.
– А теперь откройте тетради, запишите число. Сосчитайте примеры на карточке, запишите в тетрадь и закрасьте фигуру. – Кто получился? Проверьте.
– Исследуйте весь рисунок. Ответы на вопросы вы будете показывать на веере чисел. Сколько на всем рисунке квадратов? Треугольников? Кругов? Прямоугольников? – Какая фигура лишняя? Почему? – А кто-нибудь из вас знает, как называются эти фигуры одним словом?
– Как вы думаете, какая будет тема урока? – Итак, тема сегодняшнего урока «Многоугольники» – А что бы вы хотели узнать на уроке, что научиться делать?
– Мы узнаем сегодня, что такое многоугольники,
научимся находить и показывать вершины, стороны, углы многоугольников,
узнаем, что можно сконструировать с помощью многоугольников.
– Вспоминаем сказку. Испекла старуха колобок и поставила на окно студиться. Что дальше произошло?
– Катится колобок, катится, а навстречу ему заяц. Задумчивый такой сидит. – Что с тобой , заяц? – спрашивает колобок? – Да вот, не знаю какая фигура здесь лишняя. Поможешь мне, не буду тебя есть. – Ребята, поможем колобку? Дидактическая игра “Что лишнее?” – Сколько фигур в каждом ряду на экране? Исследуйте каждый ряд, какая фигура лишняя? Докажите.
– Как называется эта фигура? Почему треугольник назвали треугольником?
– А квадрат и прямоугольник являются четырехугольниками? Почему? – Как называется эта фигура?
– Как назвать все эти фигуры одним словом? – Сделайте вывод самостоятельно: какие фигуры называются многоугольниками?
– Катится колобок дальше. – Возьмите конверт под цифрой 1. В нем – геометрические фигуры, на которых написаны буквы. Соберите из них слово. Работаем группой. – Какое слово получилось? – Что мы будем сейчас делать? – Перед вами несколько кратких записей к задаче. Выберите правильную и самостоятельно запишите решение и ответ задачи. – Поменяйтесь тетрадями, проверьте.
Музыкальная физминутка
Катится колобок дальше. Навстречу ему волк. – Колобок, Колобок, я тебя съем! — Не ешь меня, Серый Волк – Вот нарисуешь мне многоугольники, пропущу тебя дальше. – Ребята, скорей, надо выручать колобка. Работа с ноутбуками. – включите ноутбуки. На рабочем столе
выберите программу paint с красным ярлычком. Нажмите левой кнопкой мыши 2
раза. Посмотрите, здесь есть набор фигур. – Теперь научимся показывать элементы многоугольника: вершины, стороны и углы. Что такое вершины? – Как вы думаете, с помощью каких инструментов мы сможем показать вершины треугольника? – Обозначьте вершины треугольника удобным для вас способом. Закрасьте вершины. – А как мы можем показать стороны треугольника? – Как покажем углы? – Молодцы! Выключите ноутбуки.
– Катится колобок дальше, вдруг видит Медведь сидит у светофора и плачет. -Медведь, – говорит ему Колобок. – Ты, что плачешь? – Да понимаешь, Колобок, хочу на другую сторону опушки перейти да не могу. Помоги мне». Поможем, ребята, Медведю? Вы будете
поднимать «сигналы» . Если высказывание, которое я назову верное, то
поднимайте зеленую карточку, а если неверное – красную. • Геометрическая фигура, которая имеет 3 стороны и 3 угла называется четырехугольник. · В 7угольнике 10 углов. • Геометрическая фигура, которая имеет 4 стороны и 4 угла называется четырехугольник. • Круг – это многоугольник. • Многоугольники – это треугольник, шестиугольник, восьмиугольник. – Ребята, а как же волку правильно перейти на другую сторону опушки? Как вы переходите улицу?
– Катится колобок дальше, вдруг перед ним яма. Ребята, как узнать сколько проволоки нужно, чтобы огородить яму? Что сначала нужно сделать?
– Все ли 4 стороны мы будем измерять? – А почему достаточно измерений только 2 сторон? Измерьте ваши цветные прямоугольники. Чему равны длины? – Как найдем периметр? – Запишите в тетрадь.
– А сейчас, для того, чтобы наши глазки были зоркими сделаем разминку для них: – зажмурьте глаза, а потом откройте, поморгайте, 2 раза – сделайте круговые движения глазами: налево-вверх-направо-вниз-направо-вверх-налево-вниз, 2 раза – вытяните вперед руку, следите взглядом за
ногтем пальца, приближая его к носу, а потом медленно отодвиньте его обратно,
2 раза.
– Катится колобок дальше, а навстречу ему лиса. Колобок, Колобок, я тебя съем! — Не ешь меня, Лиса. – Вот поможешь мне построить фигуры из многоугольников, пропущу тебя дальше. – Сейчас мы будем строить многоугольники из набора фигур. Работаем в группе. Достаньте фигуры из конверта № 2. Как называются предложенные вам фигуры? Прочитайте задание и постройте многоугольник.
– Какой многоугольник у вас получился? – Вот такие многоугольники построила я.
– Мы с вами учились составлять многоугольники из частей, а теперь я вам предлагаю сделать фигурку из многоугольников. В конверте № 3 у вас игра «Танграмм». Это большой квадрат, разрезанный на части. Пофантазируйте! Группой вам нужно из предложенных геометрических фигур выполнить аппликацию-конструкцию, наклеить ее на лист, а потом рассказать про свою работу по плану. План: 1. Название работы. 2. Что изображено? 3. Какие фигуры использовали? Выставка работ. – Я тоже составила фигурки.
– Какой вывод сделаем? Что можно составить из многоугольников?
– Прикатился домой Колобок, бабушка обрадовалась, но поругала его за непослушание. Колобок попросил у нее прощения и пообещал никуда больше не убегать. – Ребята , скажите, можно уходить из дома без спроса, не предупредив родителей? Вот и закончилось наше путешествие с Колобком. Мы помогли Колобку и героям сказки , а сами узнали много интересного. – Что вам понравилось на уроке, ребята? Чему мы учились сегодня? Какие фигуры называются многоугольниками? У какого многоугольника меньшее количество углов?
– Сейчас мы построим большой дом настроения. С чего начинают строительство дома? – Заложили фундамент и начинаем
строительство стен. – Возьмитесь за руки. Давайте построим четырехугольник. Получился крепкий, большой и красивый четырехугольник, как наш дружный класс. – Спасибо вам за прекрасный урок. |
Устный счет в паре
Индивидуальная работа на карточке.
Человечек. Сверяются с результатом на слайде. Показывают на веерах чисел.
3; 12; 1; 5+3
Круг. Нет углов – многоугольники
Ответы детей.
– узнать, что такое многоугольник.
– Колобок полежал, полежал, взял да и покатился — с окна на лавку, с лавки на пол, пó полу к двери, прыг через порог — да в сени, из сеней на крыльцо, с крыльца на двор, со двора за ворота, дальше и дальше.
– в каждом ряду по 4 фигуры. а) треугольник б) квадрат в) четырехугольник г) четырехугольник (Треугольник.) Потому что у него 3 угла. – Это квадрат – Это прямоугольник. – Это четырехугольник.
Да. 4 угла.
(Пятиугольник, потому что 5 углов, шестиугольник – 6 углов и т.д.)
Многоугольники
Вывод: Фигуры, которые имеют 3 и более углов
называются многоугольниками.
– Задача. – Решать задачу.
Решают задачу. Записывают в тетрадь.
Взаимопроверка
Дети работают по инструкции с ноутбуками.
– Это точки. – Карандаш, круг.
Выполняют практические действия.
– Карандаш, прямая линия
– Карандашом, кривая линия.
Красная
Красная Зеленая
Красная Зеленая
– Посмотреть направо, налево, нет машин,
можно идти.
– Нужно измерить длину каждой стороны. – Нет. Достаточно только 2. – В прямоугольнике противоположные стороны равны. – см, см. – Каждое число умножим на 2 и результаты сложим.
Треугольники. Практическая работа.
3-угольник, 4, 5, 6-угольники
Практическая работа в группе. Выставка работ.
Из многоугольников можно составить другие
многоугольники и интересные фигурки.
нет
Дети выбирают кирпичик и прикрепляют на доску. Остаются у доски.
– с фундамента.
| <Cлайд 1> и такие же карточки у детей на партах.
Слайд 2
Дети проверяют название фигур, нажимая на
мышку.
Конверт № 1 с геометрическими фигурами.
Работа в паре
Работа с ноутбуками. Программа paint
Работа с сигнальными карточками.
Воспитательный момент. Правила перехода улицы.
Работа в группе
Конверт с треугольниками № 2 Слайд 7>
<Слайд 8>
|
Умение выполнять устно и письменно арифметические действия с числами
Называть геометрические фигуры, их сходства и отличия
Овладение основами математической
речи.
Умение вычленять лишние фигуры. Называть геометрические фигуры, их сходства и отличия
Умение анализировать текст арифметической задачи: выделять условие и вопрос, данные и искомые числа, и решать текстовые задачи
Умение работать с ноутбуком; Овладение умениями
распознавать и изображать простейшие геометрические фигуры.
Овладение основами математической речи. Знать: элементы многоугольника
Умение применять полученные математические знания для решения учебно-практических задач
Умение конструировать многоугольники, определять их вид.
| Познавательные: развивать внимание, концентрацию внимания Регулятивные: принимать и сохранять учебную задачу Коммуникативные: умение строить монологическое высказывание и слушать собеседника
Регулятивные: Целеполагание Постановка учебной задачи на основе соотнесения того что уже известно и усвоено учащимися, и того, что еще неизвестно
Умение в сотрудничестве с учителем определять тему, ставить задачи, планировать свои действия в соответствии с поставленной задачей Коммуникативные: умение с достаточной полнотой и точностью выражать
свои мысли в соответствии с задачами.
Познавательные: осуществлять сравнение и умение делать выводы; выделять существенные признаки, устанавливать аналогии.
Регулятивные: -умение определять последовательности промежуточных целей с учетом конечного результата. -умение преобразовывать информацию из одной формы в другую
Коммуникативные: умение формировать коммуникативно – речевые действия, понимать возможность различных позиций других людей, отличных от собственной допускать возможность существования у людей различных точек зрения, в том числе не совпадающих с его собственной, формировать собственное мнение
Регулятивные: адекватно оценивать правильность выполнения действия
Познавательные: формировать умение использовать алгоритм при построении многоугольника, умение сравнивать различные виды многоугольников, выбирать удобный способ определения вида (подсчет углов, сторон или вершин) Регулятивные: осуществлять контроль в форме сличения способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона
Познавательные: умение структурировать знания. Контроль своей деятельности, проверка правильности выполнения работы партнера. Регулятивные: выделение и осознание того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения прогнозирование результатов выполнения.
Коммуникативные: умение ориентироваться на позицию партнера в общении и взаимодействии управлять поведением партнера, контролировать, оценивать действия партнера, договариваться и приходить к общему решению в совместной деятельности Регулятивные: адекватно воспринимать оценку товарищей.
Познавательные: освоение начальных форм познавательной и личностной рефлексии: рефлексия способов и условий действия, их контроль и оценка; критичность.
Регулятивные: адекватная оценивать свою деятельность на уроке и работу класса. Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли, аргументировать свою точку зрения
| Формируется учебно-познавательный интерес к учебному материалу
Установка на здоровый образ жизни
Формируется уважительное
отношение к иному мнению.
Формируется понимание необходимости учения
Формируется учебно- познавательный интерес к новому учебному материалу и способам решения новой задачи Формируется ориентация на самоанализ и самоконтроль результата, способность к самооценке на основе критерия успешности
Развивается самостоятельность
Формируется способность адекватной оценки товарищей
Развиваются навыки сотрудничества со сверстниками
Установка на здоровый образ жизни
Формируется
ориентация на понимание причин успеха.
Установка на здоровый образ жизни
Формируется ориентация на самоанализ и самоконтроль результата, способность к самооценке на основе критерия успешности
Развивается самостоятельность
Формируется способность адекватной оценки товарищей
Развиваются навыки сотрудничества со сверстниками
Формируется ориентация на понимание причин
успеха в учебной деятельности, в том числе на самоанализ и самоконтроль
результата, на понимание предложений и оценок учителя, товарищей.
|
Рисуйте многоугольники « Папа Карп
Есть много путей, как заинтересовать ребенка математикой, как подготовить его заранее к восприятию сложных математических знаний из программы средних и старших классов.
Рисование многоугольников с диагоналями – одно из самых очевидных средств.
Это настолько просто, что доступно и в дошкольном возрасте. В то же время, и более старшие ребята могут найти в таком занятии ценные для себя впечатления и новые математические знания и навыки.
Вот четырехугольник, в котором проведены обе его диагонали. Простая и понятная картинка.
С данного шага естественно начинать.
Для малыша наметить 4 точки, соединить их прямыми линиями по сторонам фигуры, а затем провести и две диагонали – это уже достаточно сложная задача.
Мы знакомимся с понятиями “вершина”, “сторона”, “диагональ”, “четырехугольник”. И привыкаем к ним.
И привыкаем к ним.
Давайте не спеша познакомимся с разными видами четырехугольников. Давайте почувствуем вкус к такому рисованию. Давайте будем использовать не только простой карандаш, но и цветные фломастеры или цветные карандаши…
В процессе этих экспериментов мы обнаружим, что не всегда в четырехугольнике можно провести обе диагонали внутри него.
Вот, скажем, изображены четырехугольник и шестиугольник. Некоторые их диагонали окажутся внутри контуров фигур. А некоторые “не влезут” внутрь, а пройдут снаружи.
Такие фигуры называют “невыпуклыми”. Вполне логичное название.
В курсе школьной геометрии изучают лишь выпуклые многоугольники. Но для рисования, конечно, годятся любые, самые разные.
Далее перейдем к пятиугольникам.
И уже уместно разъяснить ребенку общий принцип в названиях: сколько углов – “стольки и угольник”.
Раз тут 5 углов, значит, фигуру надо назвать “пятиугольник”.
Обратим внимание: углов стало всего на один больше (по сравнению с четырехугольником), а диагоналей сделалось уже значительно больше!
Всяких разных пятиугольников желательно нарисовать много.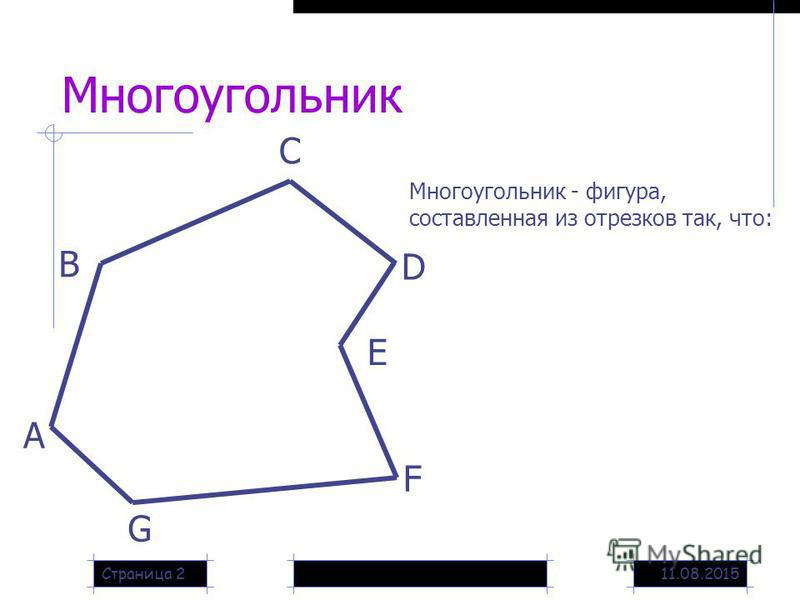 Спешить нам некуда. Для ребенка важно именно прожить данный тип фигур в образах, познакомиться на собственном опыте с различными вариациями общей схемы. Это маленькое исследование.
Спешить нам некуда. Для ребенка важно именно прожить данный тип фигур в образах, познакомиться на собственном опыте с различными вариациями общей схемы. Это маленькое исследование.
Ну а потом можно двигаться и дальше – увеличивая количество вершин по одной.
Вот я нарисовал здесь уже семиугольник.
Ух, сколько у него диагоналей!
Кстати, а как не забыть провести именно все диагонали? Как не пропустить ни одной?
Желательно, чтобы малыш сам придумал для себя удобный и эффективный метод.
Можно и подсказать чуть-чуть. Например, обратить внимание на то, сколько у фигуры вершин и сколько из каждой вершины должно выходить линий к другим вершинам. Две из этих линий будут сторонами многоугольника. А остальные – диагоналями.
И вот, оказывается, интересное дело: внутри данного семиугольника мы видим разные другие фигуры, образованные его сторонами и диагоналями.
И продолжаем исследование: постепенно увеличиваем количество вершин (углов). Вот уже я нарисовал девятиугольник.
Мне такие картинки напоминают кристаллы.
Их интересно разглядывать, вертеть во все стороны, рисовать линиями различной толщины…
Эти эксперименты – прекрасное средство подружиться с геометрией. Ее естественная и строгая красота постепенно открывает себя рисующему ребенку. Он привыкает к линиям, фигурам, узорам…
Однако есть и особая фишка.
Правильные многоугольники!
То есть такие, у которых все стороны равны между собой и все внутренние углы равны друг другу.
Вот правильный шестиугольник.
Как его нарисовать?
Как он устроен?
И посмотрите, как много можно в нем найти одинаковых элементов и структур!
Правильный шестиугольник является одной из самых важных, самых ключевых фигур в школьной геометрии. И поэтому познакомиться с ним следует особенно внимательно и особенно подробно.
Если ребенок уже владеет измерением углов в градусах, то имеет смысл показать, как с помощью транспортира мы получаем на окружности 6 точек – 6 вершин правильного шестиугольника.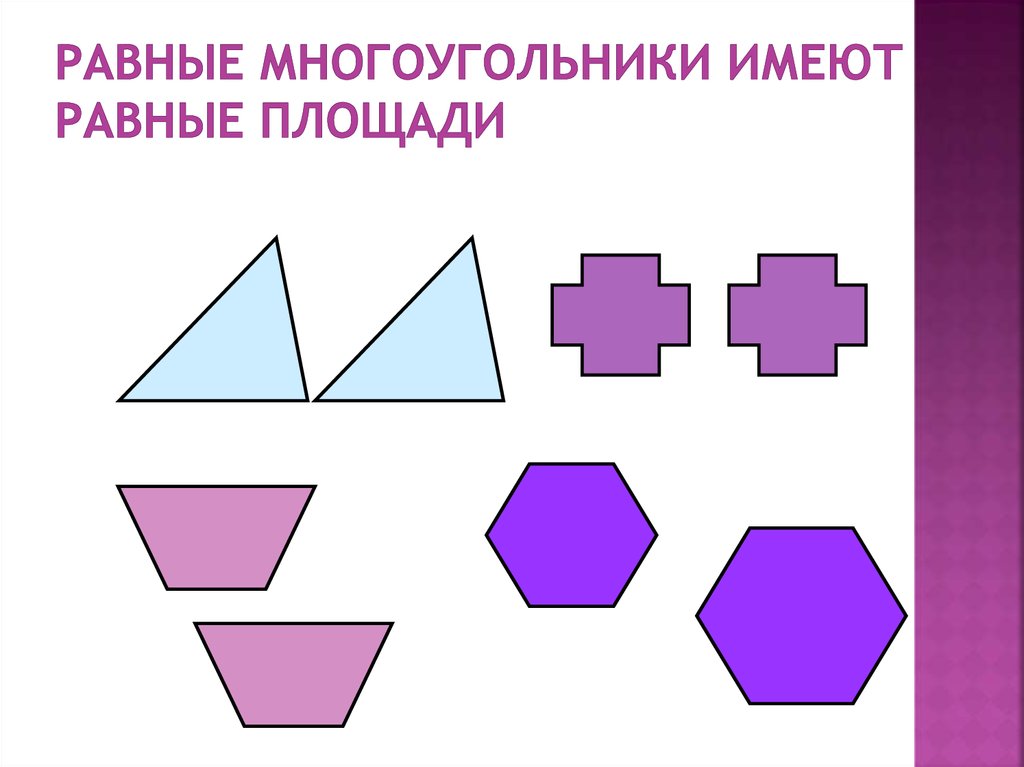
Заодно узнаем и удивительный факт: стороны правильного шестиугольника по длине равны радиусу окружности, на основе которой мы его строим.
Да, все это подробно изучается в школьном курсе геометрии 7-9 классов. Но почему бы не познакомиться с такими красивыми и жизненными штуками гораздо раньше? Они ведь очень просты для понимания.
Научиться рисовать правильные многоугольники полезно вообще по жизни.
Вот правильный десятиугольник.
Сначала я нарисовал окружность. С помощью транспортира провел из центра радиусы через равные углы – отметил на окружности точки на равных расстояниях друг от друга. А потом соединил эти точки – и получил стороны десятиугольника.
Диагонали здесь – особая история. Как видите, их стало уже очень много!
Красота!
Я специально провел диагонали тонкими линиями. Так получилось аккуратнее и точнее. Да и раскрасить можно такую картинку, если кому-нибудь захочется.
Ясное дело, правильный десятиугольник – это не предел. Углов (сторон) бывает и 11, и 12, и 15…
Углов (сторон) бывает и 11, и 12, и 15…
Когда мои дети были маленькими, я довольно много занимался с ними такими штуками – начиная со среднего дошкольного возраста.
Для каждого ребенка следует подбирать свой маршрут знакомства с многоугольниками.
Кому-то понравится рисовать и подсчитывать диагонали. И даже кто-то, возможно, сумеет вывести формулу для их числа – в зависимости от числа углов.
А кто-то увлечется созданием разнообразных контуров многоугольников. Это тоже увлекательное и полезное занятие. Оно ближе к процессу художественного творчества.
И не забудьте, что нарисованный многоугольник можно закрасить или хотя бы просто заштриховать.
Еще раз хочу подчеркнуть: наша цель не в том, чтобы маленький ребенок выучил всякие сведения про многоугольники задолго до того, как их будет изучать в курсе школьной геометрии, а в том, чтобы дети познакомились и подружились с геометрическими фигурами, чтобы не спеша прочувствовали их пространственную логику и красоту.
Что-то ребенок запомнит сразу и навсегда. А что-то забудет, конечно. Это не очень существенно.
В любом случае, мы так закладываем основы геометрического мышления.
И мы наглядно видим связь математики и жизни.
Потому что нарисованный многоугольник – это не какая-то далекая абстракция. Это простая игра с понятными образами, это построение красивых структур из линий, это нечто близкое и доступное.
| Этапы урока | Действия учителя | Направление действий учеников | Методический комментарий |
| I. Организационный момент | – Здравствуйте.
Прозвенел звонок и смолк. Начинается урок |
Садятся. | |
| II.
Устный счёт 1. Игра “Молчанка” |
Учитель показывает карточки: | Закрепление навыков счета в пределах
пяти.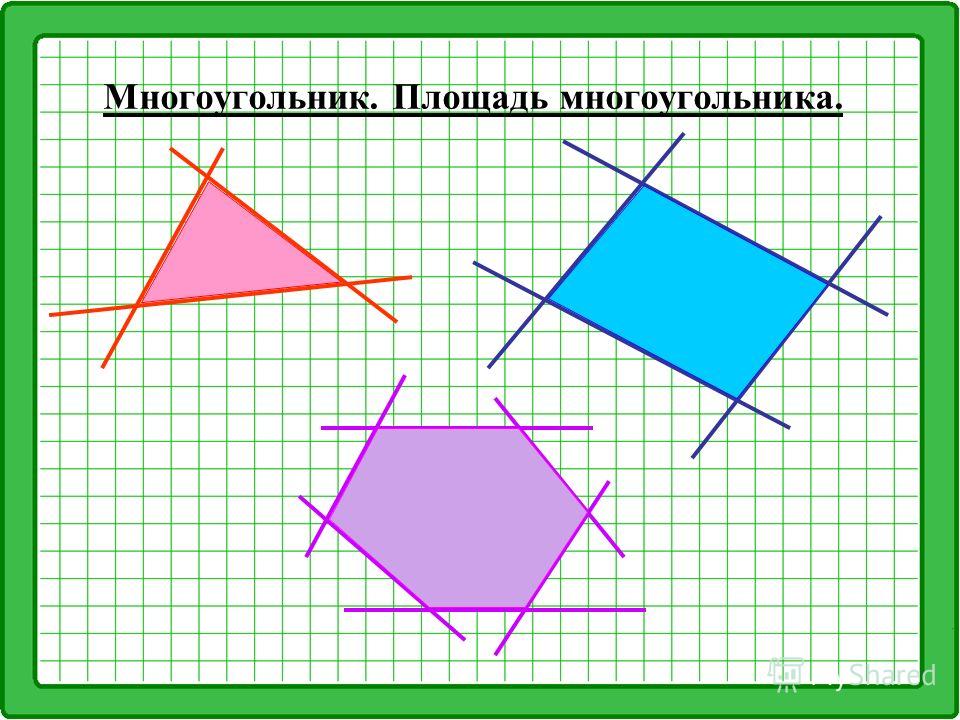 Карточки: 2 – [ ] = 1 |
|
| – Какое число пропущено? | Учащиеся с помощью веера показывают ответы к выражениям на карточках | ||
| – Какой знак пропущен? | Учащиеся подбирают нужный знак из разрезного материала и показывают | ||
| 2. Работа с геометрическим материалом | – При помощи чего создано изображение? | – Изображение создано при помощи линий. | Слайд 1 |
| – Что это за линии? | – Это ломаные лини. | ||
| – На какие две группы можно разделить эти ломаные линии? | – На замкнутые и незамкнутые. |
Если дети не смогут назвать восьмиугольник или по ошибке назовут его “шестиугольник”, не страшно. В конце урока можно вернуться к этому слайду и еще раз назвать фигуры. | |
| – Какие фигуры образуют замкнутые ломаные линии? | – Квадрат, треугольник, восьмиугольник | ||
| – Как бы вы по– другому назвали эти
фигуры? – Это верно, ребята, но эти фигуры могут иметь и другое название. А какое, мы узнаем немного позже. |
– Геометрические фигуры | ||
| – Посмотрите на экран. Определите, какая фигура пропущена? |
– Пропущен круг. | Слайд 2 | |
| – Подумайте, какая фигура здесь лишняя? | – Лишний круг. |
При помощи анимации круг появляется на
слайде Слайд 3 |
|
| – Почему? | – Потому что у круга нет углов, а у треугольника и квадрата есть углы. | При помощи анимации круги исчезают | |
| III. Физкультминутка | Раз – поднялись, потянулись. Три – согнулись, разогнулись. Три – в ладоши три хлопка, Головою три кивка. На четыре – руки шире. Пять – руками помахать. Шесть – за парту тихо сесть. |
Дети выполняют упражнения по показу учителя | |
| IV. Целеполагание | – Ребята, вы любите сказки? | – Да, любим. | Слайд 4 (фигуры появляются постепенно) |
Сегодня героями сказки станут круг и
квадрат.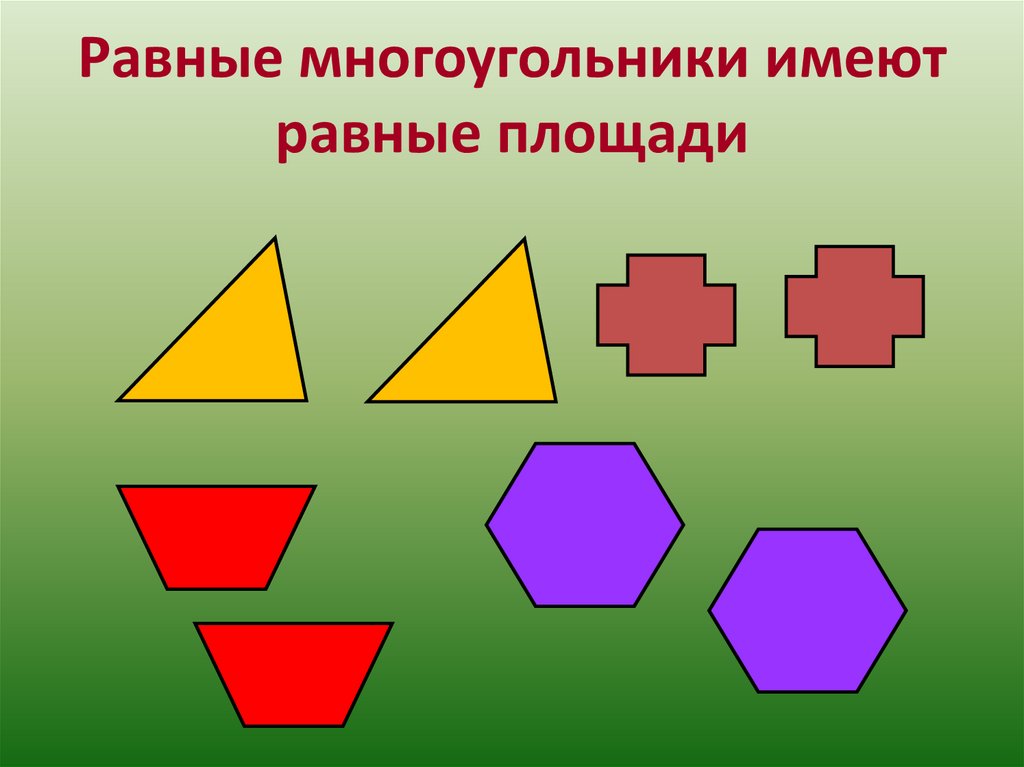 – Жили– были два брата: Вот настала ночь, и к брату, натыкаясь на столы, младший лезет воровато, срезать старшему углы. Но наутро младший брат страшной мести был не рад. Поглядел он: нет квадрата. Онемел, стоял без слов… Вот так месть! Теперь у брата восемь новеньких углов! |
Слушают сказку | Слайд 5 | |
| – Сколько сторон было у квадрата? | – Было четыре стороны. |
||
| – Сколько углов? | – Было четыре угла | ||
| – Сколько стало сторон? | – Стало восемь сторон. | ||
| – Сколько стало углов? | – Восемь углов. | ||
| – Как считаете, это много или мало углов? | – Это много углов. | ||
| – как эту фигуру можно назвать по-другому? | – Многоугольник | Слайд 6 Многоугольник |
|
| – Назовите тему урока | – Многоугольник | ||
| – Что хотите узнать? Чему научиться? | Высказывания учащихся | ||
V.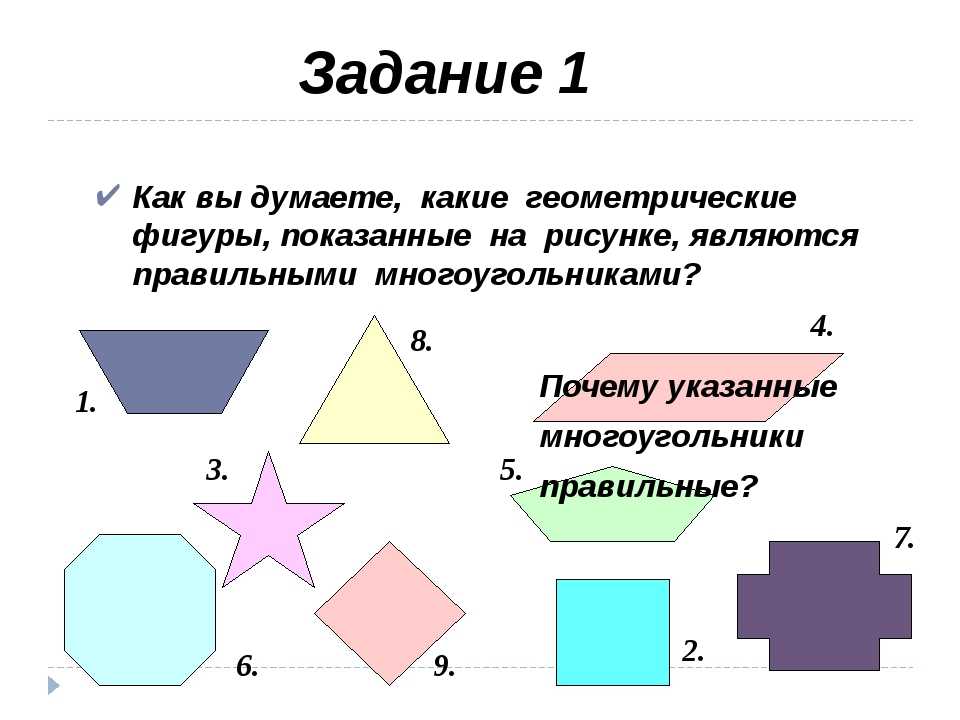 Работа по теме урока
Работа по теме урока |
– Откройте учебник на стр. 50 | Открывают учебники | |
| – Кто может прочитать тему урока? | Отвечает хорошо читающий ученик. | ||
| – Как считаете, какие фигуры могут
называться многоугольниками?
– Посмотрите на рисунок в учебнике. |
– Фигуры, у которых много углов. | ||
| – Какие фигуры видите слева? | – Круги. | Работа по иллюстрации учебника стр. 50 | |
| – Какие фигуры видите справа? | – Четырехугольники | ||
| – Чем эти фигуры отличаются? | – У круга нет углов, а у
четырехугольников есть углы. |
||
| – Как можно назвать четырехугольники? | – Многоугольники | ||
| – Какие фигуры изображены ниже? | – Треугольники и четырехугольники. | ||
| – Почему их так назвали? | – Потому что у треугольника три угла, а у четырехугольника – четыре угла. | ||
| – Сколько у них сторон? | – Три стороны у треугольника и четыре у четырехугольника. | ||
| – Сколько вершин? | – Три вершины и четыре вершины. | ||
| – Можно ли назвать треугольник многоугольником? | – Можно | ||
| – Знаете ли вы фигуру, у которой углов меньше, чем у треугольника? | – Нет. |
||
| – Какой следует вывод? | – Треугольник – это многоугольник с наименьшим количеством сторон, углов, вершин. | ||
| – Приготовьте счетные палочки. | |||
| Из палочек выложите многоугольник у которого вершин на 1 больше, чем у четырехугольника. | Учащиеся выполняют задание | Работа в парах | |
| – Сколько вершин у этой фигуры? Сколько сторон? | – Пять вершин, пять сторон. | ||
| – Как называется эта фигура? | – Пятиугольник | Проверка задания | |
| VI. Физкультминутка | Мы делили апельсин Много нас, а он один.  Эта долька для ежа, Эта долька для чижа, Эта долька для утят, Эта долька для котят. Эта долька для бобра, А для волка кожура. |
Движение, имитирующее деление на
дольки.
Загибают пальчики на руках Пальчики вразлет |
Подготовка рук к работе в тетради |
| VII. Работа в тетради на печатной основе | – Откройте, пожалуйста, тетради на стр. 20 | – Открывают тетради | Обязательно повторить гигиенические требования работы с тетрадью (осанка, положение тетради, рук, ног) |
| – Найдите на странице изображения многоугольников. | Находят ряд многоугольников | ||
| – Какую фигуру называют пятиугольником? | – Фигуру, у которой пять углов. |
||
| – Найдите пятиугольники и раскрасьте синим цветом | Выполняют задание | ||
| – Какой многоугольник называем
треугольником? – Найдите и раскрасьте треугольники. |
– Многоугольник, у которого три угла | ||
| – Сколько раскрасили пятиугольников? | – Два пятиугольника | ||
| – Сколько раскрасили треугольников? | – Два треугольника | ||
| VIII. Итог урока. Рефлексия | – О чем говорили на уроке? | – Говорили о многоугольниках | |
| – Какие фигуры можно назвать многоугольниками? | – Фигуры, у которых есть углы | ||
| – Назовите самый маленький
многоугольник – Посмотрите еще раз на экран. |
– Треугольник | Слайд 1 | |
| – Какие многоугольники вы здесь увидели? | – Треугольники, четырехугольник, восьмиугольник | ||
| Если вам на уроке сегодня было все
понятно, поднимите пятиугольник, если вы испытывали трудности, поднимите
четырехугольник, если многое не понятно, поднимите треугольник. Спасибо за работу! |
Учащиеся оценивают свою работу | На парте перед каждым ребенком лежат треугольник, квадрат и пятиугольник |
Конспект по математике в подготовительной группе «Путешествие с Элли» | Дошкольное образование
Автор: Удякова Анна Сергеевна
Организация: МБДОУ №4
Населенный пункт: Оренбургская область, г. Бугуруслан
Цель: продолжать учить составлять число 10 из единиц; познакомить с обозначением числа 10; закрепить навыки счета в прямом и обратном порядке в пределах 10; дать представление о многоугольнике на примере треугольника и четырёхугольника; закреплять умение ориентироваться в пространстве с помощью условных обозначений на плане, определять направление движения объектов, отражать в речи их пространственное положение.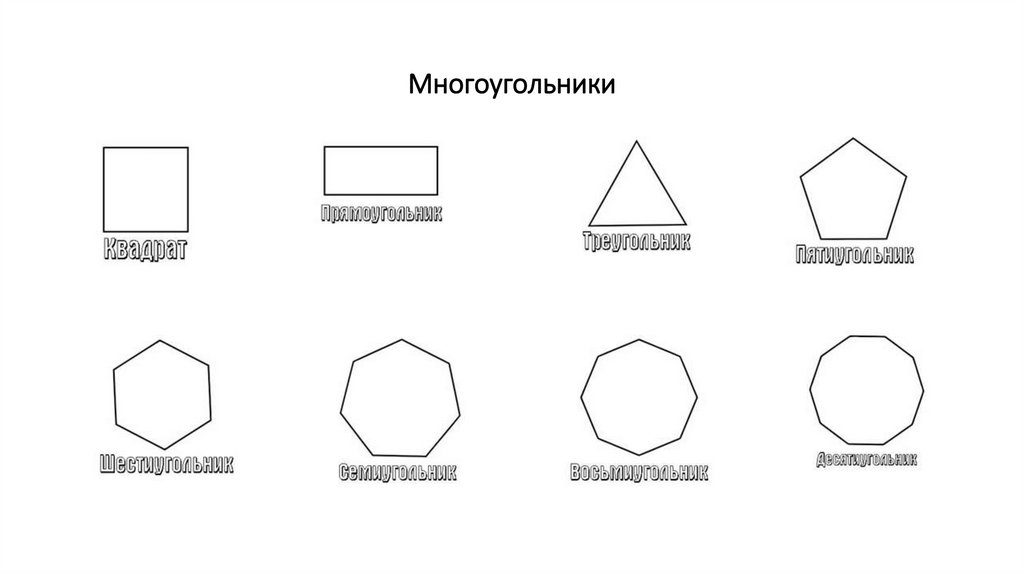
Дидактический наглядный материал
Демонстрационный материал: мяч, конверты с заданиями, карточки с цифрами от 0 до 9, карточки с изображением разного количества предметов (до10), треугольники, четырёхугольники, магнитная доска, картинка с изображением Дровосека, составленного из разных многоугольников.
Раздаточный материал: листы бумаги, цветные карандаши, многоугольники (треугольники разных видов, квадрат, прямоугольник, ромб).
Ход:
I часть.
Ребята, сегодня к нам пришла девочка. Она никак не может добраться до дома.(Напоминаю детям отрывок из сказки, в которой девочка Элли с другом Тотошкой после урагана попала в другую страну).Давайте, поможем ей вернуться домой. Для этого нам с вами нужен план. Рассматриваем план возвращения домой.
Путь Элли обозначен на плане цифрами, в группе на этих же местах как на плане спрятаны конверты с заданиями.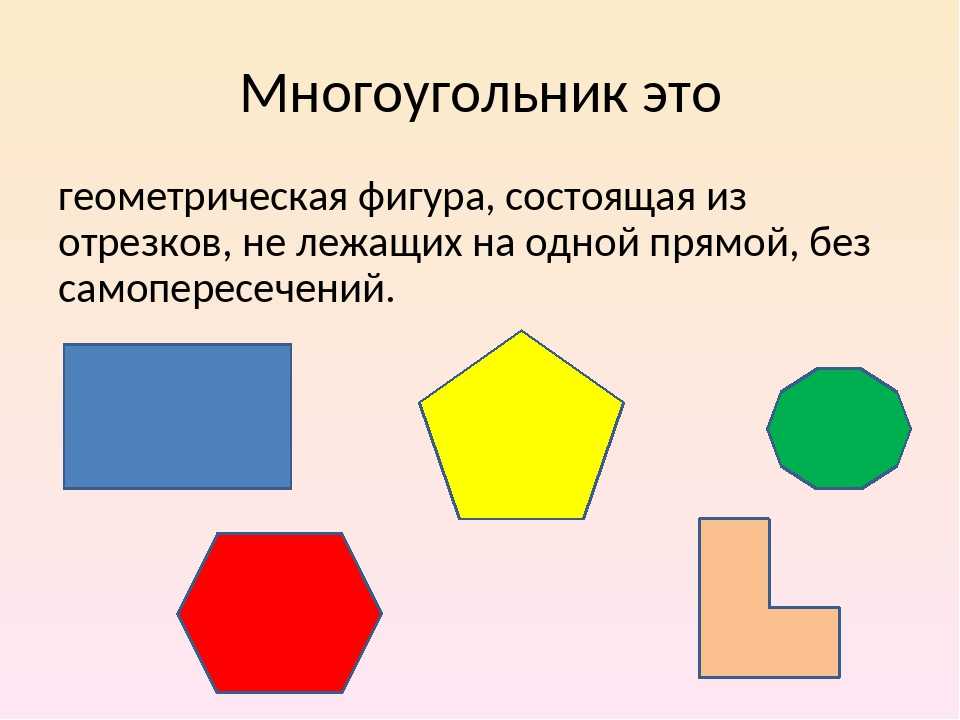 Вы должны найти на плане цифру 1, а в группе конверт – с цифрой 1.
Вы должны найти на плане цифру 1, а в группе конверт – с цифрой 1.
1 задание: «Весёлый кубик». Дети становятся в круг и передают кубик с цифрами, проговаривая слова: «Ты быстрей беги наш кубик, быстро, быстро по рукам, у кого остался кубик, тот считает дальше сам». У кого остановился кубик, тот называет цифру, расположенную сверху кубика, и продолжает считать от этой цифры.
II часть.
– Теперь найдите на плане цифру 2 и определите , в каком направлении надо рисовать стрелку (слева направо из нижнего левого угла в нижний правый угол) Теперь найдите 2 конверт.
2 задание: Маленькие человечки страны Оз просят «сшить» им 10 шапочек –колпачков разного цвета.
Дети на листочках рисуют 10 треугольных шапочек-колпачков разного цвета.
– Сколько шапочек вы «сшили»? Сколько какого цвета? Как вы составили число 10? Скольким жителям вы помогли?
III часть.
– Теперь найдите на плане цифру 3 и определите , в каком направлении надо рисовать стрелку (из нижнего правого угла в верхний левый угол) Теперь найдите 3 конверт.
3 задание: разложить на доске карточки с цифрами от 1 до 9 и назвать их по порядку.
Чтение стихотворения С.Маршака «Весёлый счет»:
Сказал весёлый круглый ноль (показать карточку с цифрой 0)
Соседке единице:
– С тобою рядышком позволь
Стоять мне на странице.
Она окинула его
Сердитым, гордым взглядом:
– Ты, ноль, не стоишь ничего,
Не стой со мною рядом! (поставить карточку с цифрой 0 перед единицей)
– Ребята, цифр всего 10, а чисел можно составить очень много.
Ответил ноль:
– Я признаю, что ничего не стою,
Но можешь стать ты десятью,
Коль буду я с тобою.
Так одинока ты сейчас,
Мала и худощава,
Но будешь больше в десять раз,
Когда я встану справа.
(поставить после цифры 9 карточки с цифрами 1 и 0)
– Сколько цифр обозначает число10? Как называются эти цифры?
А сейчас найдите карточку с изображением 10 предметов поставьте рядом с числом 10. Запомните, что если 0 стоит после 1, то эти цифры обозначают число 10.
IV часть.
– Найдите на плане цифру 4. В каком направлении надо рисовать стрелку? (из левого верхнего угла в правый верхний угол) Найдите 4 конверт…
4 задание: собрать Дровосека из геометрических фигур.
На доске в два ряда расположены треугольники и четырёхугольники.
– Какие фигуры расположены в первом ряду? Что между ними общего? (у треугольников три стороны и три угла) Какие фигуры во втором ряду? Что между ними общего? Каким словом можно назвать все эти фигуры? Сколько углов у фигур?
– Посмотрите, кто изображён на картине? (Дровосек) Из каких многоугольников он составлен?
Дети по образцу собирают Дровосека из многоугольников.
V часть.
– Найдите на плане цифру 5. В каком направлении надо рисовать стрелку? (из правого верхнего угла вниз в середину) Найдите 5 конверт…
5 задание: «Весёлый кубик» (т.ж. как и в 1 задании только счёт ведётся в обратном порядке)
-Молодцы, ребята, вы справились со всеми заданиями. Какое полезное дело мы совершили? Кому помогли? Что вы расскажите дома?
Приложения:
- file0.docx.. 17,5 КБ
Что такое многоугольник? | TheSchoolRun
Можете ли вы отличить шестиугольники от семиугольников? Ваши восьмиугольники из ваших десятиугольников? Мы объясняем, как учат многоугольникам в начальной школе, с примерами правильных и неправильных вариантов каждой многогранной формы.
или Зарегистрируйтесь, чтобы добавить к своим сохраненным ресурсам
Что такое многоугольник?
Многоугольник — это плоская двумерная (2D) фигура с прямыми сторонами, которая полностью замкнута (все стороны соединены). Боковые стороны должны быть прямыми. Многоугольники могут иметь любое количество сторон.
Боковые стороны должны быть прямыми. Многоугольники могут иметь любое количество сторон.
| Многоугольник | Многоугольник не является фигурой с изогнутыми сторонами. | Не полностью замкнутая фигура не является многоугольником. |
Правильные и неправильные многоугольники
Правильный многоугольник — это многоугольник, в котором все стороны имеют одинаковую длину и под одинаковыми углами .
Ан неправильный многоугольник — это многоугольник с сторонами и/или углами различной длины и размеров . (Although they still must be straight and joined up.)
Primary-school polygons
Polygons taught in primary school include:
| Regular | Irregular | |
| Треугольник (3 стороны) | ||
| Quadrilateral (4 sides) | ||
| Pentagon (5 sides) | ||
| Шестигранник (6 сторон) | ||
| Шестиугольник 4 | 440015||
| Octagon (8 sides) | ||
| Nonagon (9 sides) | ||
| Decagon (10 сторон) |
*Правильный четырехугольник имеет специальное название. Называется квадрат.
Называется квадрат.
*Треугольники бывают разных типов: 9Равносторонний треугольник 0023 является правильным треугольником , а прямоугольный треугольник и равнобедренный треугольник являются примерами неправильных треугольников.
When and how polygons are taught in primary school
| What is taught | How it might be taught | |
| Year 1 | Children are taught to name common 2D формы, включая многоугольники, такие как квадраты, прямоугольники, треугольники, пятиугольники, шестиугольники и восьмиугольники. | Дети могут изучать фигуры, выполняя задания на сопоставление, прогулку по фигуре на территории школы, карточки и игры. Они будут смотреть на реальные примеры форм, а также фотографии. |
| 2-й класс | Детей научат определять свойства фигур, такие как количество сторон и вершин (углов). | Дети будут считать количество сторон и углов фигуры. Они будут описывать фигуры с помощью свойств, например: Эта фигура имеет 3 угла и 3 стороны. Какова форма? |
| 3-й класс | Дети расширят свои знания о многоугольниках, включив в них различные типы треугольников и четырехугольников. Они познакомятся с семиугольниками, девятиугольниками и девятиугольниками. Знание свойств формы будет включать углы и симметрию этих многоугольников. | Дети будут описывать формы и определять их, используя их свойства, включая симметрию и углы. Их могут попросить отсортировать фигуры в соответствии с их свойствами, используя диаграммы Венна и диаграммы Кэрролла. |
| 4-й класс | Детей учат сравнивать длины и углы многоугольников, чтобы определить, правильные они или неправильные. Будут использоваться слова «многоугольник», «правильный» и «неправильный». | Детям будет дан набор многоугольников, которые нужно отсортировать на правильные и неправильные; это может быть выполнение практических заданий или использование ИКТ. |
| 5 класс | Детей научат различать правильные и неправильные многоугольники на основе рассуждений о равенстве сторон и углов. | Детям будет предложено отсортировать фигуры и объяснить, почему многоугольник правильный, используя свойства углов и сторон. |
| 6 класс | В конце KS2 дети начинают находить неизвестные углы в правильных многоугольниках. | Детям покажут, как вычислять неизвестные углы в многоугольниках, используя их знания об углах и заданную формулу. |
Расчет размера углов многоугольника в 6-м классе
Важно помнить, что все внутренние углы правильного многоугольника равны.
В 6 классе дети используют это знание и следующую формулу для вычисления размера углов.
Размер каждого внутреннего угла правильного многоугольника = (n-2) x 180º ÷ n
Где n – количество сторон.
Например:
- Правильный пятиугольник имеет 5 сторон
- (5-2) x 180 = 3 x 180 ÷ 5 = 540º ÷ 5 = 108º
Больше похоже на это
Рисование 2D-фигур
Как называются 2D- и 3D-фигуры?
2D and 3D shape Bingo
2D shapes: Pentagons and hexagons
Count the sides of 2D shapes
Mystery 3D shape net
Properties of 3D shapes
What правильной и неправильной формы?
Правильные и неправильные многоугольники
Полигоны
Многоугольник — это плоская фигура с прямыми сторонами.

Многоугольник?
Многоугольники — это двумерные фигуры. Они состоят из прямых линий, а форма «замкнутая» (все линии соединяются вверх).
| Полигон (прямые стороны) | Не Полигон (имеет кривую) | Не a Полигон (открытый, не закрытый) |
Полигон происходит от греческого. Poly- означает «много», а -gon означает «угол».
Типы полигонов
Обычные или нестандартные
У правильного многоугольника все углы равны и все стороны равны, в противном случае он неправильный
| Обычный | Нестандартный |
Вогнутая или выпуклая
Выпуклый многоугольник не имеет углов, направленных внутрь. Точнее, внутренний угол не может быть больше 180°.
Точнее, внутренний угол не может быть больше 180°.
Если какой-либо внутренний угол больше 180°, то многоугольник является вогнутым . ( Подумайте: в вогнутой части есть «пещера» )
| Выпуклая | Подбарабанье |
Простой или сложный
Простой многоугольник имеет только одну границу и не пересекает сам себя. Сложный полигон пересекает сам себя! Многие правила о многоугольниках не работают, когда они сложные.
| Простой многоугольник (это пятиугольник) | Комплексный полигон (он же Пентагон) |
Дополнительные примеры
| Неправильный шестигранник | Вогнутый восьмиугольник | Сложный многоугольник (“Звездный многоугольник”, в данном случае – пентаграмма) |
Играй с ними!
Попробуйте интерактивные полигоны. .. сделайте их правильными, вогнутыми или сложными.
.. сделайте их правильными, вогнутыми или сложными.
Имена полигонов
| Если это правильный многоугольник … | |||
| Имя | Стороны | Форма | Внутренний уголок |
|---|---|---|---|
| Треугольник (или Треугольник) | 3 | 60° | |
| Четырехугольник (или тетрагон) | 4 | 90° | |
| Пентагон | 5 | 108° | |
| Шестигранник | 6 | 120° | |
| Семиугольник (или Септагон) | 7 | 128,571° | |
| Октагон | 8 | 135° | |
| Нонагон (или Эннеагон) | 9 | 140° | |
| Декагон | 10 | 144° | |
| Hendecagon (или Undecagon) | 11 | 147,273° | |
| Додекагон | 12 | 150° | |
| Трискайдекагон | 13 | 152,308° | |
| Тетракайдекагон | 14 | 154,286° | |
| Пятиугольник | 15 | 156° | |
| Шестигранник | 16 | 157,5° | |
| Семиугольник | 17 | 158,824° | |
| Октакадекагон | 18 | 160° | |
| Эннеадекагон | 19 | 161,053° | |
| Икосагон | 20 | 162° | |
| Триаконтагон | 30 | 168° | |
| Тетраконтагон | 40 | 171° | |
| Пятиугольник | 50 | 172,8° | |
| Гексаконтагон | 60 | 174° | |
| Гептаконтагон | 70 | 174,857° | |
| Октаконтагон | 80 | 175,5° | |
| Эннеаконтагон | 90 | 176° | |
| Шестиугольник | 100 | 176,4° | |
| Чилиагон | 1000 | 179,64° | |
| Мириагон | 10 000 | 179,964° | |
| Мегагон | 1 000 000 | ~180° | |
| Гуголгон | 10 100 | ~180° | |
| н-угольник | п | ( n −2) × 180 ° / n | |
Вы можете сделать имена, используя этот метод:
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример: 62-сторонний многоугольник является Hexacontadigon | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
НО, для многоугольников с 13 или более сторонами можно (и проще) писать “ 13-угольник “, “ 14-угольник ” . .. “ 100-угольник” и т. д.
.. “ 100-угольник” и т. д.
Вспоминая
Четырехугольник (4 стороны)
A Quad Четырехколесный велосипед
Пентагон (5 сторон)
“ Pentagon ” в Вашингтоне, округ Колумбия, имеет 5 сторон
Шестигранник (6 сторон)
H Oneycomb имеет H эксагон
Септагон (7 сторон)
Think Sept agon это “Seven- agon”
Октагон (8 сторон)
У гноя Octo 8 щупалец
Нонагон (9 сторон)
Think Non agon это “Nine- agon”
Десятиугольник (10 сторон)
Думаю Декабрь агон имеет 10 сторон,
точно так же как наша декабрь имал система имеет 10 цифр
Что такое многоугольник? Определение, форма, типы, формулы, примеры
Что такое многоугольник?
Двумерная замкнутая фигура, образованная путем соединения трех или более прямых линий, называется многоугольником. Их также называют «плоскими фигурами». Пример: Квадрат – это многоугольник, образованный соединением 4 прямых линий одинаковой длины.
Их также называют «плоскими фигурами». Пример: Квадрат – это многоугольник, образованный соединением 4 прямых линий одинаковой длины.
Части многоугольника
Многоугольник состоит из трех частей:
- Стороны : Отрезок, соединяющий две вершины, называется стороной.
- Вершины : Точка, в которой встречаются две стороны, называется вершиной.
- Уголки : внутренние и внешние. Внутренний угол — это угол, образованный внутри замкнутой поверхности многоугольника путем соединения сторон.
Что такое правильные многоугольники?
Если все стороны и внутренние углы многоугольника равны, то они называются правильными многоугольниками. Примерами правильных многоугольников являются квадрат, равносторонний треугольник и т. д. В правильных многоугольниках конгруэнтны не только стороны, но и углы. Это значит, что они равноугольные.
Свойства правильных многоугольников
Ниже перечислены свойства правильных многоугольников:
- Все его стороны равны.
- Все его внутренние углы равны.
- Сумма его внешних углов равна 360°.
Периметр правильного многоугольника
У правильного многоугольника все стороны равны. А периметр многоугольника это сумма всех сторон. Итак, у правильного многоугольника с n сторонами периметр = n раз больше длины стороны.
Например, если сторона правильного многоугольника равна 6 см, а количество сторон равно 5, периметр = 5 ✕ 6 = 30 см
Сумма внутренних углов правильного многоугольника
Пусть существует n-сторонний правильный многоугольник . Поскольку стороны правильного многоугольника равны, сумма внутренних углов правильного многоугольника = (n − 2) × 180°
Например, стороны правильного многоугольника равны 6.
Итак, сумма внутренние углы 6-стороннего многоугольника = (n − 2) × 180° = (6 − 2) × 180° 9\circ}{n}$.
Количество диагоналей правильного многоугольника
Количество диагоналей в многоугольнике с n сторонами = $\frac{n(n-3)}{2}$, поскольку каждая вершина соединяется с (n – 3) вершинами. А чтобы не было двойного счета, делим на два.
А чтобы не было двойного счета, делим на два.
Например, если количество сторон правильного прямоугольника равно 4, то количество диагоналей = $\frac{4\times1}{2}=2$.
Количество треугольников правильного многоугольника
Если стороны правильного многоугольника равны n, то количество треугольников, образованных соединением диагоналей из одного угла многоугольника = n – 2
Например, если количество сторон равно 4, то количество образованных треугольников будет
(4 – 2) = 2.
Линии симметрии правильного многоугольника
Линия симметрии может быть определена как ось или воображаемая линия, проходящая через центр фигуры или объекта и делящая его на одинаковые половины. Поскольку все стороны правильного многоугольника равны, количество линий симметрии = количеству сторон = $n$
Например, у квадрата 4 стороны. Итак, количество линий симметрии = 4 9\circ$, мы каждый раз будем получать одно и то же изображение.
Различные правильные многоугольники
Ниже приведен список правильных многоугольников:
Забавный факт!
Круг — это правильная двумерная фигура, но это не многоугольник, поскольку у него нет прямых сторон.
Решенные примеры
Пример 1. Найдите количество диагоналей правильного многоугольника с 12 сторонами.
Решение : Количество диагоналей n-стороннего многоугольника = $n\frac{(n-3)}{2}$$=$$12\frac{(12-3)}{2}=54$ 9\circ}{n}$
Правильный ответ: имеет (n – 3) линий симметрии.
Правильный многоугольник имеет n осей симметрии.
1080°
1160°
1200°
1260°
Правильный ответ: 1260°
$n=9$ в правильном девятиугольнике. Итак, сумма внутренних углов = $(n-2)\times180°
=7\times180°=1260°$
18
19
20
22
Правильный ответ: 18
Каждый внешний угол = 20° . Количество сторон = $\frac{360°}{каждый внешний угол}=\frac{360°}{20}=18$.
Часто задаваемые вопросы
В чем разница между правильным и неправильным многоугольником?
Правильный многоугольник — это равносторонний и равноугольный многоугольник, такой как квадрат, равносторонний треугольник и т. д. С другой стороны, неправильный многоугольник — это многоугольник, у которого не все стороны равны или углы не равны, например воздушный змей , разносторонний треугольник и т. д.
д. С другой стороны, неправильный многоугольник — это многоугольник, у которого не все стороны равны или углы не равны, например воздушный змей , разносторонний треугольник и т. д.
Почему ромб не является правильным многоугольником?
Ромб не является правильным многоугольником, потому что противоположные углы ромба равны, а у правильного многоугольника все углы равны. 9\circ}{Каждый внешний угол}$
2,222 Math Polygons Стоковые фотографии и изображения
Символ треугольник, прямоугольник, пятиугольник, шестиугольник, шестиугольник, восьмиугольник. шестиугольник значок формы многоугольника.
Геометрические фигуры и формулы, абстрактный фон (3D визуализация)
Реалистичные геометрические фигуры прозрачный набор цветов с изолированными геометрическими объектами разного цвета на прозрачном фоне.
Абстрактный открытый школьный учебник с иконками школьных предметов
Футуристический светящийся низкополигональный знак бесконечности, состоящий из звезд, линий, треугольников на темно-синем фоне.
Милые дети изучают базовый урок математики
Счастливые милые детишки изучают трехмерную геометрию
Правильные многогранники, также известные как платоновые тела
Иллюстрация фигур разных цветов со счастливым мультяшным лицом, отлично подходит для детей, изучающих базовую геометрию
Набор основных геометрических фигур.
Сетка поверхности. 3D иллюстрации.
Набор основных геометрических фигур
Смешные дети изучают основные фигуры
Правильный многогранник с четырьмя гранями. тетраэдр
Абстрактный акварельный фон с геометрическими цветными объектами и интересными формами
Мультяшная иллюстрация основных геометрических фигур комических персонажей с надписями для детского образования
Значок многоугольного числа в кости. плоская иллюстрация многоугольной векторной иконки кубика для веб-дизайна
Симпатичные дети держат набор геометрических фигур. векторная иллюстрация листа начального школьного образования. маленькие мальчики и девочки с квадратом, треугольником, звездой и кругом на белом фоне
маленькие мальчики и девочки с квадратом, треугольником, звездой и кругом на белом фоне
Аннотация черного квадрата пятиугольной геометрической структуры контур фона
Милые дети изучают основной урок математики формы
Построение круга, описанного на треугольнике
Образовательная карикатура основных геометрических фигур с надписями и изображениями собак и щенков животных для детей дошкольного и младшего возраста
Мультяшный набор рабочих человечков с математическими символами. нарисуйте милые миниатюрные сцены рабочих геоматричных форм. нарисованная вручную векторная иллюстрация для школьного дизайна.
Абстрактный акварельный фон с геометрическими цветными объектами и интересными формами
Набор синих векторных полигональных чисел с длинной тенью. низкополигональная иллюстрация плоского дизайна.
Мультипликационная иллюстрация основных геометрических фигур для обучения детей младшего возраста
Шестигранник: правильное тело с шестью квадратными гранями
Набор восьмиугольных иконок. геометрия восьмиугольная черная восьмиугольная восьмиугольная линия восьмиугольника. векторная иллюстрация. изолированные на белом фоне.
геометрия восьмиугольная черная восьмиугольная восьмиугольная линия восьмиугольника. векторная иллюстрация. изолированные на белом фоне.
Правильный многогранник с двенадцатью гранями. додекаэдр
3d геометрические фигуры. изометрические линейные формы, кубический конус, цилиндр, пирамида, низкополигональные объекты. векторный минимальный изометрический набор
Набор простых геометрических фигур. Иконки геометрических примитивов
Абстрактный акварельный фон с геометрическими цветными объектами и интересными формами
Буква p низкополигональная конструкция, абстрактное геометрическое изображение алфавита, многоугольная векторная иллюстрация шрифтовой каркасной сетки, сделанная из точек и линий на белом фоне
Найдите правильную тень, образовательная игра для детей, звезда
Милые дети изучают базовый урок математики
Мультяшная иллюстрация обучающих основных геометрических фигур для детей дошкольного или младшего школьного возраста с изображением животных
Shape 2d: изучение двухмерных фигур для детей
Набор основных геометрических фигур
Значки геометрических фигур: круг, треугольник, квадрат, пятиугольник и многоугольная звезда. векторная иллюстрация.
векторная иллюстрация.
Милые дети изучают основные геометрические фигуры. Урок математики
Обучающая мультяшная иллюстрация основных геометрических фигур с надписями и фантастическими персонажами роботов для детей
Забавные дети изучают основные фигуры
Правильный многогранник из двадцати граней. икосаэдр
Белая геометрия Набор трехмерных фигур. элементы векторного дизайна для социальных сетей и визуального контента, веб-дизайн и дизайн пользовательского интерфейса, плакаты и художественный коллаж, брендинг.
Реалистичный металлический золотой роскошный куб рекламный пьедестал рекламный сценический дисплей 3d вектор
Абстрактное изолированное синее изображение математических знаков. многоугольная иллюстрация выглядит как звезды на пустынном ночном небе в космосе или осколки летящего стекла. цифровой дизайн для веб-сайта, сети, интернета.
Изометрические формы. 3d геометрическая форма, многоугольные объекты плоской геометрии, такие как призматическая пирамидальная цилиндрическая сфера. векторный изометрический набор
векторный изометрический набор
Набор основных геометрических фигур
Мультяшный набор эскизов рабочих человечков с математическими символами. нарисуйте милые миниатюрные сцены рабочих геоматричных форм. нарисованная вручную векторная иллюстрация для школьного дизайна.
Модель символа пи сетки с треугольным мозаичным значком. проволочная рамка многоугольная сетка символа пи. векторный коллаж из треугольных частей различных размеров и цветовых оттенков. абстрактный 2d-сетчатый символ пи,
Черно-белая образовательная мультяшная иллюстрация основных геометрических фигур с надписями и символами животных для детей
Правильный многогранник с шестью гранями. шестигранник
Геометрические фигуры граней. красочные фигуры пирамиды. детские развивающие геометрические игры. набор комических примитивных персонажей. веселые мультики. милые многоугольники и круги. вектор игрушки композиции
Обучающая карикатура с изображением основных геометрических фигур с надписями и символами птиц и животных для детей
Обучающая иллюстрация с изображением основных геометрических фигур с надписями и символами морских животных для детей
Набор геометрических фигур. изометрические виды. векторная иллюстрация
изометрические виды. векторная иллюстрация
Фигуры трассировки. 2D детские геометрические фигуры. 6 карточек. практика почерка. обучение формирует образовательную деятельность детского сада. домашнее обучение. распечатать а4 дошкольная игра детский сад.
Набор значков геометрической формы. черный силуэт и линия большой коллекции основных фигур. вектор, изолированный на белом
Набор основных геометрических фигур
Набор основных геометрических фигур
Абстрактный акварельный фон с геометрическими цветными объектами и интересными формами
Абстрактный акварельный фон с геометрическими цветными объектами и интересными формами
Правильные многогранники, также известные как Платоновые тела
Компасы, состоящие из линий с черным фоном, 3D-рендеринг. компьютерный цифровой рисунок.
2d геометрические фигуры. Основные геометрические фигуры для детей. 6 карточек. обучение формирует образовательную деятельность детского сада. домашнее обучение. распечатать а4 дошкольная игра детский сад.
распечатать а4 дошкольная игра детский сад.
Яркий сетчатый эллипс с эффектом светового пятна. белая проволочная туша треугольной сети в векторном формате на черном фоне. абстрактная двухмерная сетка с треугольными линиями, точками,
Счетная игра для детей дошкольного возраста. обучающая математическая игра. посчитай сколько круглых, квадратных и треугольных предметов и напиши результат!
Компасы, состоящие из линий с черным фоном, 3D-рендеринг. компьютерный цифровой рисунок.
Мультяшный набор рабочих человечков с математическими символами. нарисуйте милые миниатюрные сцены рабочих геоматричных форм. нарисованная вручную векторная иллюстрация для школьного дизайна.
Набор основных геометрических фигур
Набор основных фигур, иллюстрация геометрической формы в плоском стиле – вектор
Образовательная мультяшная иллюстрация основных геометрических фигур с надписями и забавными персонажами животных для детей
Геометрические фигуры с метками. набор из 12 основных фигур. простая плоская векторная иллюстрация.
набор из 12 основных фигур. простая плоская векторная иллюстрация.
2d геометрические фигуры. Основные геометрические фигуры для детей. 6 карточек. обучение формирует образовательную деятельность детского сада. домашнее обучение. распечатать а4 дошкольная игра детский сад.
Линия изометрических фигур. простые геометрические формы для школьного обучения и дизайна. цилиндр, призма и пирамида, конус и сфера 3d набор векторной математики. схема изолированных форм для обучения математике
Правильный многогранник двадцати граней. икосаэдр
Мультяшные человечки с математическими символами. нарисуйте милые миниатюрные сцены рабочих геоматричных форм. нарисованная вручную векторная иллюстрация для школьного дизайна.
Набор основных геометрических фигур
Свойства трехмерных фигур. геометрические фигуры 3д.
Геометрические фигуры и формулы, абстрактный фон (3d визуализация)
Сетка поверхности. 3D иллюстрации.
Мультяшные человечки с математическими символами.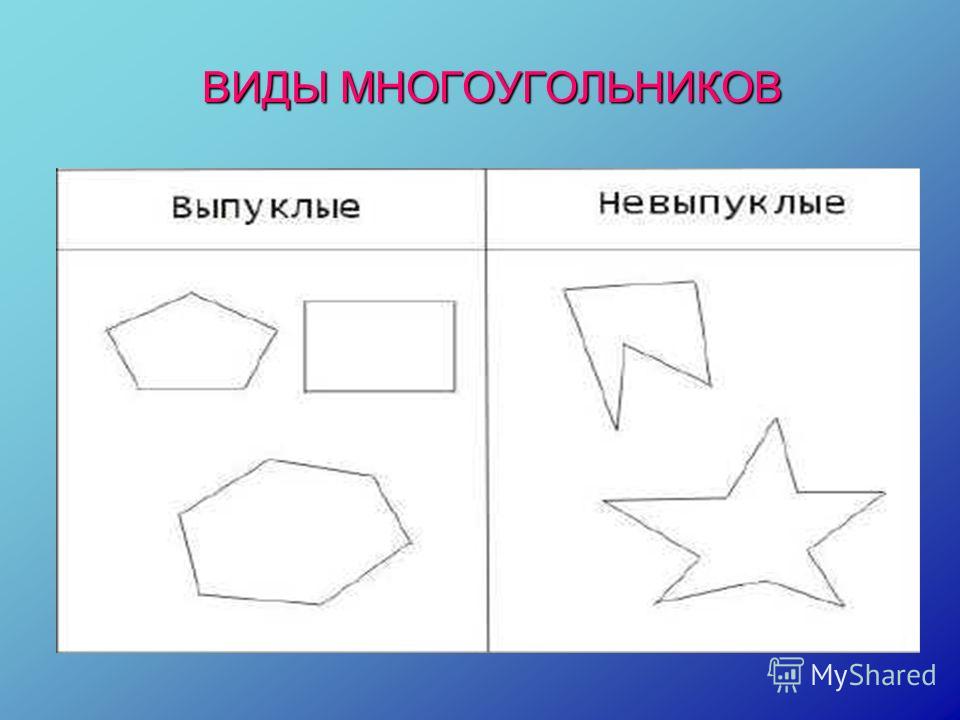 нарисуйте милые миниатюрные сцены рабочих геоматричных форм. нарисованная вручную векторная иллюстрация для школьного дизайна.
нарисуйте милые миниатюрные сцены рабочих геоматричных форм. нарисованная вручную векторная иллюстрация для школьного дизайна.
Формы трассировки. 2D детские геометрические фигуры. 6 карточек. практика почерка. обучение формирует образовательную деятельность детского сада. домашнее обучение. распечатать а4 дошкольная игра детский сад.
Правильные многогранники, также называемые платоновыми телами
Набор основных геометрических фигур
Набор простых геометрических фигур, включая основные: прямоугольник, круг, треугольник
Основные геометрические фигуры грани. милые детские развивающие фигурки с надписями. детские узорчатые цветные смайлики. круг и многоугольники с забавными улыбками. набор векторных абстрактных форм
Симпатичные дети изучают базовый урок математики.
Основные фигуры – значок набора острых углов, векторная геометрическая коллекция. векторные иллюстрации знак, изолированные на белом фоне.
Милые дети держат в руках набор геометрических фигур. векторная иллюстрация листа начального школьного образования. маленькие мальчики и девочки с квадратом, треугольником, звездой, прямоугольником, ромбом, кругом на белом фоне
векторная иллюстрация листа начального школьного образования. маленькие мальчики и девочки с квадратом, треугольником, звездой, прямоугольником, ромбом, кругом на белом фоне
Симпатичные геометрические персонажи. абстрактные базовые рисунки со счастливыми лицами, руками и ногами. крест и шестиугольник. забавные узорчатые формы. каракули прямоугольник и круг. набор векторных смайликов
Векторный рисунок сине-черной промышленной системы, созданный с помощью линий и трехмерных кубов. современная геометрическая композиция может быть использована в качестве шаблона и макета.
Трендовый изометрический геометрический узор желтого цвета с яркими блоками и кубиками. технический план можно использовать в веб-дизайне, а также в качестве обоев или фона. идеальный фон для ваших дизайнерских проектов.
Сетка поверхности. 3D иллюстрации.
Простые изометрические формы. многоцветные изолированные геометрические элементы, математические объекты для школьного обучения и дизайна. куб, призма 3d векторный набор. красочные абстрактные формы для изучения геометрии
куб, призма 3d векторный набор. красочные абстрактные формы для изучения геометрии
Обучающая мультяшная иллюстрация основных геометрических фигур с надписями и персонажами морских животных для детей.
Двухмерные геометрические фигуры. Основные геометрические фигуры для детей. 6 карточек. обучение формирует образовательную деятельность детского сада. домашнее обучение. распечатать а4 дошкольная игра детский сад.
Бумажный шаблон додекаэдра, схема обрезки, изолированная на белом
Классификация фигур в иерархии | Урок математики для детей
ЧТО ТАКОЕ КЛАССИФИКАЦИЯ ФОРМ В ИЕРАРХИИ (ЧЕТЫРЕХСТОРОННИЕ И ТРЕУГОЛЬНИКИ)
Каковы свойства фигур? 2D-формы плоские и могут занимать площадь. Когда все стороны прямые, фигура представляет собой многоугольник. Эти формы имеют такие свойства, как длины сторон и углы.
Чтобы лучше понять классификацию фигур в иерархии (четырехугольники и треугольники)…
ЧТО ТАКОЕ КЛАССИФИКАЦИЯ ФОРМ В ИЕРАРХИИ (ЧЕТЫРЕХСТОРОННИЕ И ТРЕУГОЛЬНИКИ). Каковы свойства фигур? 2D-формы плоские и могут занимать площадь. Когда все стороны прямые, фигура представляет собой многоугольник. Эти формы имеют такие свойства, как длины сторон и углы.
Чтобы лучше понять классификацию фигур в иерархии (четырехугольники и треугольники)…
Каковы свойства фигур? 2D-формы плоские и могут занимать площадь. Когда все стороны прямые, фигура представляет собой многоугольник. Эти формы имеют такие свойства, как длины сторон и углы.
Чтобы лучше понять классификацию фигур в иерархии (четырехугольники и треугольники)…
ДАВАЙТЕ РАЗЪЯСНИМ!
Вечеринка треугольников
У нас вечеринка треугольников! У нас есть много знакомых предметов, все с тремя прямыми сторонами. Одна – фишка со всеми сторонами одинаковой длины. Еще один парус для нашей модели парусника. Он имеет три разные длины сторон и один угол 90°. Мы знаем, что треугольники могут иметь острые углы, то есть углы меньше 90°, тупые углы больше 90° или прямые углы, равные 90°. Когда все стороны треугольника имеют одинаковую длину, он равносторонний. Если только две из них имеют одинаковую длину, то она равнобедренная, а если все длины разные, то разносторонняя. Какие треугольники являются нашими объектами? Фишка представляет собой равносторонний треугольник из-за трех равных сторон. Парус представляет собой прямоугольный треугольник, потому что все длины различны, а его длина равна 9.угол 0°. Попробуйте сами: какой треугольник является вешалкой, если у него две стороны одинаковой длины и один угол больше 90°?
Парус представляет собой прямоугольный треугольник, потому что все длины различны, а его длина равна 9.угол 0°. Попробуйте сами: какой треугольник является вешалкой, если у него две стороны одинаковой длины и один угол больше 90°?
Вечеринка треугольников У нас вечеринка треугольников! У нас есть много знакомых предметов, все с тремя прямыми сторонами. Одна – фишка со всеми сторонами одинаковой длины. Еще один парус для нашей модели парусника. Он имеет три разные длины сторон и один угол 90°. Мы знаем, что треугольники могут иметь острые углы, то есть углы меньше 90°, и тупые углы больше 9°.0° или прямые углы, равные 90°. Когда все стороны треугольника имеют одинаковую длину, он равносторонний. Если только две из них имеют одинаковую длину, то она равнобедренная, а если все длины разные, то разносторонняя. Какие треугольники являются нашими объектами? Фишка представляет собой равносторонний треугольник из-за трех равных сторон. Парус представляет собой прямоугольный треугольник, потому что все длины различны, а угол равен 90°. Попробуйте сами: какой треугольник является вешалкой, если у него две стороны одинаковой длины и один угол больше 9 градусов?0°?
Попробуйте сами: какой треугольник является вешалкой, если у него две стороны одинаковой длины и один угол больше 9 градусов?0°?
Подвешивание картин
Мы учимся в художественном классе, и нам нужно повесить картины в соответствующие рамки одинаковой формы. Все кадры отсортированы по наиболее конкретной категории 2D-формы, но нам все еще нужно отсортировать изображения. Все рамки имеют четыре прямые стороны, поэтому мы знаем, что все они четырехугольники. Некоторые кадры имеют один набор параллельных сторон; это трапеции. Другие имеют два набора параллельных сторон; это параллелограммы. У некоторых параллелограммов прямые углы, значит, они прямоугольники. Ваш друг показывает на стопку рамок, представляющих собой параллелограммы с четырьмя равными сторонами, но без прямых углов. Это ромбы или ромбы, если они у нас есть. Последняя стопка еще более конкретна, с 4 прямыми углами и 4 равными сторонами. Это квадраты! Ваша первая картинка имеет четыре прямые стороны, две пары параллельных сторон разной длины.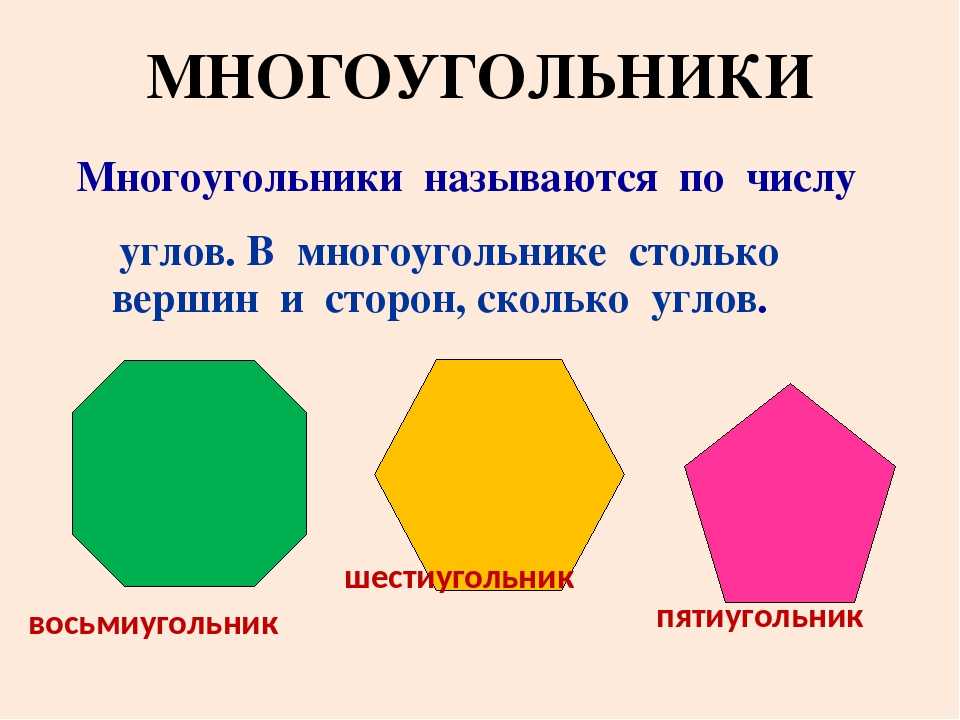 Это означает, что наиболее конкретная категория, которую мы можем выбрать, — это параллелограмм. Вот где мы найдем подходящую рамку! Попробуйте сами: есть картинка с четырьмя равными сторонами и без прямых углов. Какова наиболее специфическая категория формы для изображения?
Это означает, что наиболее конкретная категория, которую мы можем выбрать, — это параллелограмм. Вот где мы найдем подходящую рамку! Попробуйте сами: есть картинка с четырьмя равными сторонами и без прямых углов. Какова наиболее специфическая категория формы для изображения?
Развешивание картин Мы учимся в художественном классе, и нам нужно повесить картины в соответствующие рамки одинаковой формы. Все кадры отсортированы по наиболее конкретной категории 2D-формы, но нам все еще нужно отсортировать изображения. Все рамки имеют четыре прямые стороны, поэтому мы знаем, что все они четырехугольники. Некоторые кадры имеют один набор параллельных сторон; это трапеции. Другие имеют два набора параллельных сторон; это параллелограммы. У некоторых параллелограммов прямые углы, значит, они прямоугольники. Ваш друг показывает на стопку рамок, представляющих собой параллелограммы с четырьмя равными сторонами, но без прямых углов. Это ромбы или ромбы, если они у нас есть.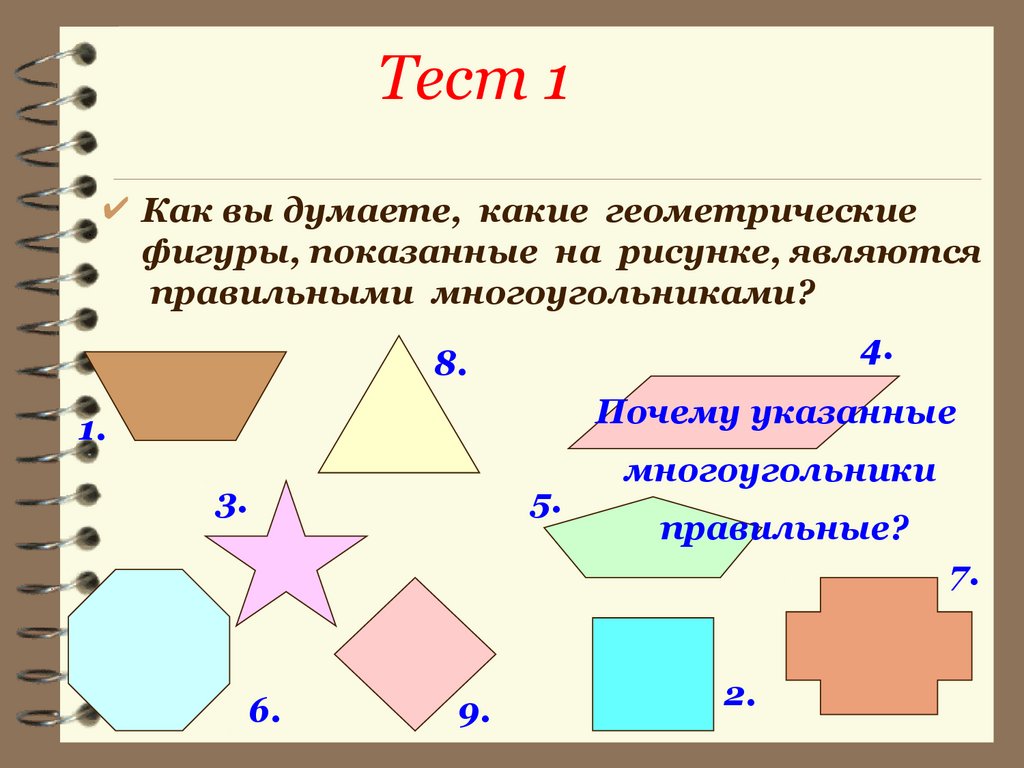 Последняя стопка еще более конкретна, с 4 прямыми углами и 4 равными сторонами. Это квадраты! Ваша первая картинка имеет четыре прямые стороны, две пары параллельных сторон разной длины. Это означает, что наиболее конкретная категория, которую мы можем выбрать, — это параллелограмм. Вот где мы найдем подходящую рамку! Попробуйте сами: есть картинка с четырьмя равными сторонами и без прямых углов. Какова наиболее специфическая категория формы для изображения?
Последняя стопка еще более конкретна, с 4 прямыми углами и 4 равными сторонами. Это квадраты! Ваша первая картинка имеет четыре прямые стороны, две пары параллельных сторон разной длины. Это означает, что наиболее конкретная категория, которую мы можем выбрать, — это параллелограмм. Вот где мы найдем подходящую рамку! Попробуйте сами: есть картинка с четырьмя равными сторонами и без прямых углов. Какова наиболее специфическая категория формы для изображения?
Упаковка для летнего лагеря
Предположим, вы собираете вещи для летнего лагеря и решили рассортировать свои вещи по форме. У вас есть книга, вешалка для одежды и воздушный змей. Глядя на фигуры, вы замечаете, что все они имеют прямые ребра, поэтому вы помещаете их все в стопку полигонов. У вешалки три стороны, так что вы знаете, что это треугольник. Книга и бумажный змей имеют четыре стороны, поэтому они являются четырехугольниками. У книги все углы прямые, значит, она тоже прямоугольник. Но какой формы воздушный змей? У него прямые стороны, поэтому это многоугольник. Воздушный змей имеет четыре стороны, так что это тоже четырехугольник. Более того, он имеет две пары смежных сторон одинаковой длины, что делает его воздушным змеем! Попробуйте сами: к каким категориям может принадлежать фигура с четырьмя сторонами равной длины, без прямых углов и без параллельных сторон?
Воздушный змей имеет четыре стороны, так что это тоже четырехугольник. Более того, он имеет две пары смежных сторон одинаковой длины, что делает его воздушным змеем! Попробуйте сами: к каким категориям может принадлежать фигура с четырьмя сторонами равной длины, без прямых углов и без параллельных сторон?
Упаковка для летнего лагеря Предположим, вы собираете вещи для летнего лагеря и решили рассортировать свои вещи по форме. У вас есть книга, вешалка для одежды и воздушный змей. Глядя на фигуры, вы замечаете, что все они имеют прямые ребра, поэтому вы помещаете их все в стопку полигонов. У вешалки три стороны, так что вы знаете, что это треугольник. Книга и бумажный змей имеют четыре стороны, поэтому они являются четырехугольниками. У книги все углы прямые, значит, она тоже прямоугольник. Но какой формы воздушный змей? У него прямые стороны, поэтому это многоугольник. Воздушный змей имеет четыре стороны, так что это тоже четырехугольник. Более того, он имеет две пары смежных сторон одинаковой длины, что делает его воздушным змеем! Попробуйте сами: к каким категориям может принадлежать фигура с четырьмя сторонами одинаковой длины, без прямых углов и без параллельных сторон?
Использование иерархии
Саша и Дерек пытаются объяснить другу свое местонахождение. Саша говорит, что они в Лос-Анджелесе, но Дерек говорит, что они в Калифорнии. Откуда мы знаем, кто прав? Они оба! Мы можем понять это, используя иерархию. На самом высоком уровне они находятся в Калифорнии. Точнее, они находятся в городе Лос-Анджелес. Точнее, они в Голливуде! Итак, зная, что кто-то находится в Голливуде, мы также знаем, что он находится в Лос-Анджелесе и Калифорнии, потому что это уровни выше Голливуда в нашей иерархии местоположений. Попробуйте сами: подумайте о своей школе. Какова его иерархия расположения?
Саша говорит, что они в Лос-Анджелесе, но Дерек говорит, что они в Калифорнии. Откуда мы знаем, кто прав? Они оба! Мы можем понять это, используя иерархию. На самом высоком уровне они находятся в Калифорнии. Точнее, они находятся в городе Лос-Анджелес. Точнее, они в Голливуде! Итак, зная, что кто-то находится в Голливуде, мы также знаем, что он находится в Лос-Анджелесе и Калифорнии, потому что это уровни выше Голливуда в нашей иерархии местоположений. Попробуйте сами: подумайте о своей школе. Какова его иерархия расположения?
С помощью Иерархии Саша и Дерек пытаются объяснить другу свое местонахождение. Саша говорит, что они в Лос-Анджелесе, но Дерек говорит, что они в Калифорнии. Откуда мы знаем, кто прав? Они оба! Мы можем понять это, используя иерархию. На самом высоком уровне они находятся в Калифорнии. Точнее, они находятся в городе Лос-Анджелес. Точнее, они в Голливуде! Итак, зная, что кто-то находится в Голливуде, мы также знаем, что он находится в Лос-Анджелесе и Калифорнии, потому что это уровни выше Голливуда в нашей иерархии местоположений.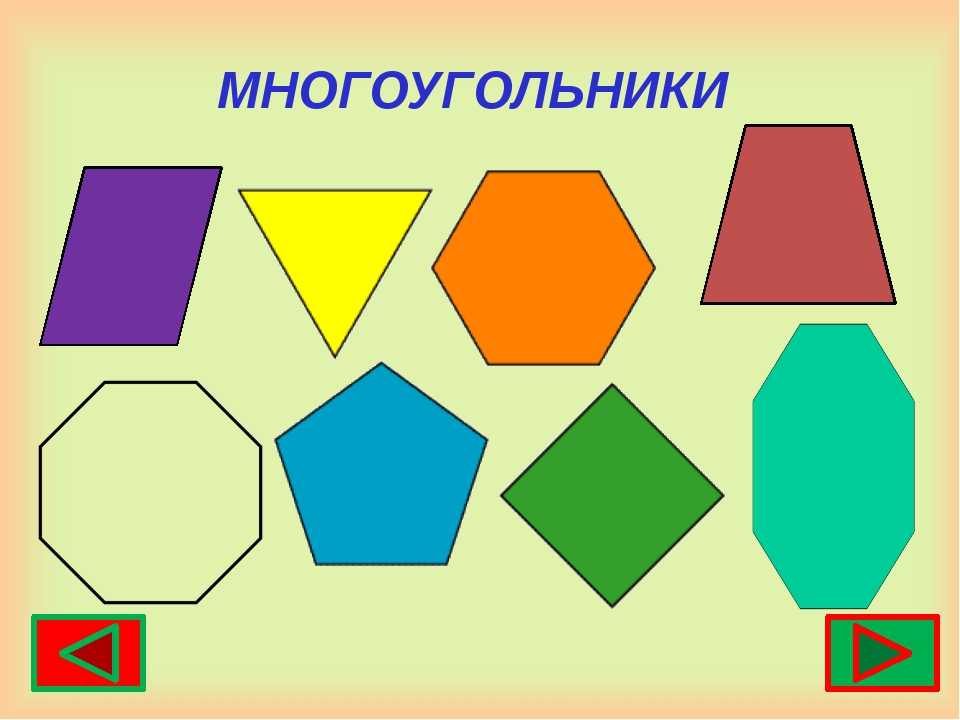 Попробуйте сами: подумайте о своей школе. Какова его иерархия расположения?
Попробуйте сами: подумайте о своей школе. Какова его иерархия расположения?
КЛАССИФИКАЦИЯ ФОРМ В ИЕРАРХИИ (ЧЕТЫРЕХСТОРОННИЕ И ТРЕУГОЛЬНИКИ) СЛОВАРЬ
Свойство
Характеристика, истинная для геометрической формы в данной категории.
Категория
Классификация форм с определенным набором свойств.
Многоугольник
Замкнутая форма со всеми прямыми сторонами.
Угол
Измерение поворота между двумя линиями с общей конечной точкой.
Прямоугольный
Угол, равный 90°.
Острый угол
Угол от 0° до 90°.
Тупой угол
Угол от 90° до 180°.
Треугольник
Трехсторонний многоугольник.
Равносторонний треугольник
Треугольник, у которого все стороны имеют одинаковую длину.
Равнобедренный треугольник
Треугольник с двумя равными сторонами.
Разносторонний треугольник
Треугольник, стороны которого не имеют одинаковой длины.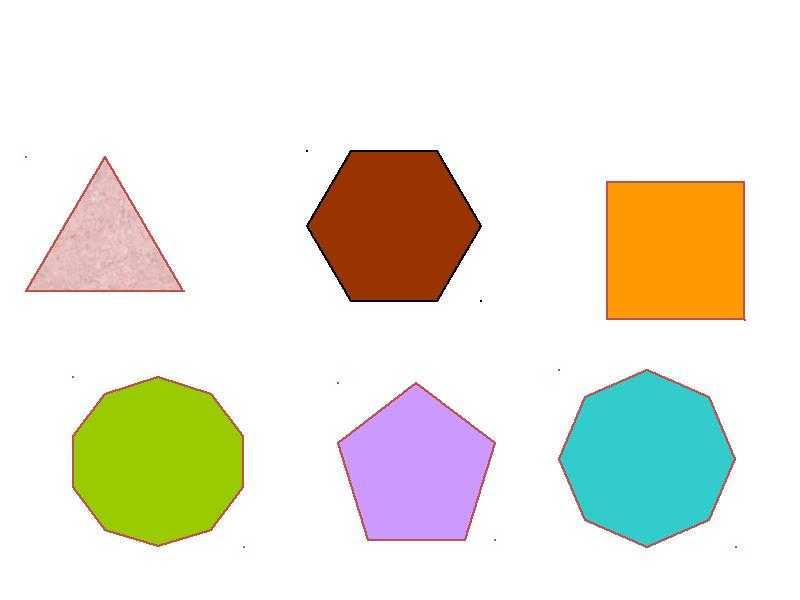
Четырехугольник
Четырехсторонний многоугольник.
Параллелограмм
Четырехугольник с двумя наборами параллельных сторон.
Иерархия
Метод категоризации, при котором вещи сортируются во все более и более определенные группы, а подгруппы сохраняют все свойства супергруппы.
Супергруппа
Группа, которую можно разделить на более мелкие подгруппы в зависимости от свойства сортируемых элементов.
Подгруппа
Группа с более специфичным свойством, чем супергруппа. Например, из супергруппы «все штаты США» есть подгруппа «штаты западного побережья».
Прямоугольник
Параллелограмм со всеми прямыми углами.
Ромб
Четырехугольник с 4 равными сторонами и двумя парами параллельных сторон.
Трапеция (включительно)
Четырехугольник по крайней мере с одним набором параллельных сторон.
Трапеция (эксклюзивная)
Четырехугольник, у которого ровно одна пара параллельных сторон.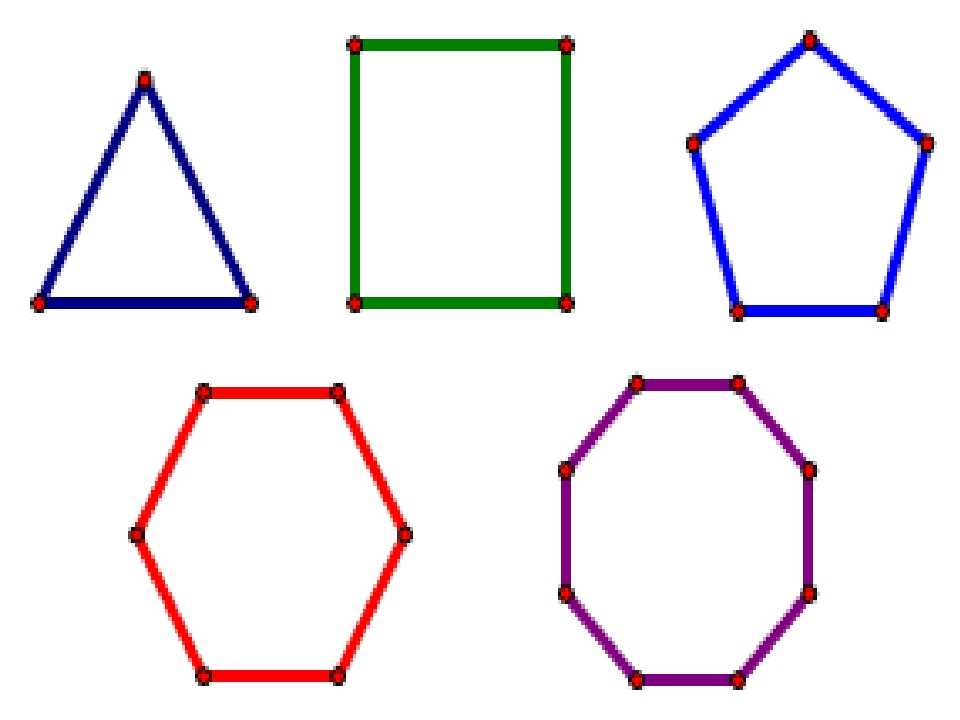
Пятиугольник
Пятиугольник.
Шестиугольник
Шестиугольник.
Семиугольник
Многоугольник с семью сторонами.
Восьмиугольник
Восьмиугольник.
Нонагон
Девятиугольник.
КЛАССИФИКАЦИЯ ФОРМ В ИЕРАРХИИ (ЧЕТЫРЕХСТОРОННИЕ И ТРЕУГОЛЬНИКИ) ВОПРОСЫ ДЛЯ ОБСУЖДЕНИЯ
Что означает, что параллелограмм является подгруппой четырехугольника?
Это означает, что параллелограмм обладает всеми свойствами четырехугольника, а также свойствами, характерными для параллелограмма.
Почему квадрат одновременно и параллелограмм, и воздушный змей?
Квадрат наследует свойства воздушного змея (два набора смежных сторон одинаковой длины) через ромб (четыре равные стороны) и свойства параллелограмма (два набора параллельных сторон) через прямоугольник (все углы прямые) . Поскольку квадрат сохраняет свойства, определяющие его супергруппы, квадрат также является параллелограммом и воздушным змеем.
Может ли треугольник быть четырехугольником? Объяснять.
Нет. Треугольник и четырехугольник классифицируются по свойству «количество сторон». Треугольник — это фигура, имеющая ровно три стороны, а четырехугольник — фигура, имеющая ровно четыре стороны. Это означает, что фигура не может быть одновременно треугольником и четырехугольником.
Является ли параллелограмм трапецией? Объясните
(Исключительное определение) Нет. Трапеция — это фигура с ровно одним набором параллельных сторон, поэтому параллелограмм не может быть трапецией. (Включающее определение) Да. Трапеция — это фигура, имеющая по крайней мере один набор параллельных сторон, поэтому параллелограмм — это подгруппа трапеции.
Как бы вы определили иерархию?
Иерархия — это система классификации, основанная на наборах свойств, которые становятся все более и более конкретными по мере продвижения вниз по иерархии. Все подгруппы сохраняют все свойства своих супергрупп, поэтому в геометрии фигуры наследуют свойства категорий над ними в иерархии.
Вернуться к уроку
Практическая геометрия – Часть I
Сообщение в гостевом блоге Стефани Мурман из Teaching in Room 6
Стандарты измерения и геометрии охватывают все уровни обучения. Вы можете подумать, что из-за этого многократного воздействия учащиеся легко усвоят концепции. Однако это не так. Идентификация различных многоугольников и объемных фигур, разбивка их на основные линии и углы, определение периметра и площади фигуры иногда бывает сложной задачей для учащихся. Особенно, когда большую часть времени ученики выполняют работу по учебнику.
Стремясь помочь своим ученикам лучше усвоить стандарты измерения и геометрии, я изо всех сил старался оторваться от книги и использовать практические стратегии для введения и закрепления понятий. Вот несколько занятий и уроков, которые я делал в прошлом, чтобы научить своих учеников измерению и геометрии. На следующей неделе во второй части этого поста я поделюсь еще несколькими.
Многоугольники
Идентификация различных двумерных фигур может быть довольно скучной, если просто заглянуть в книгу.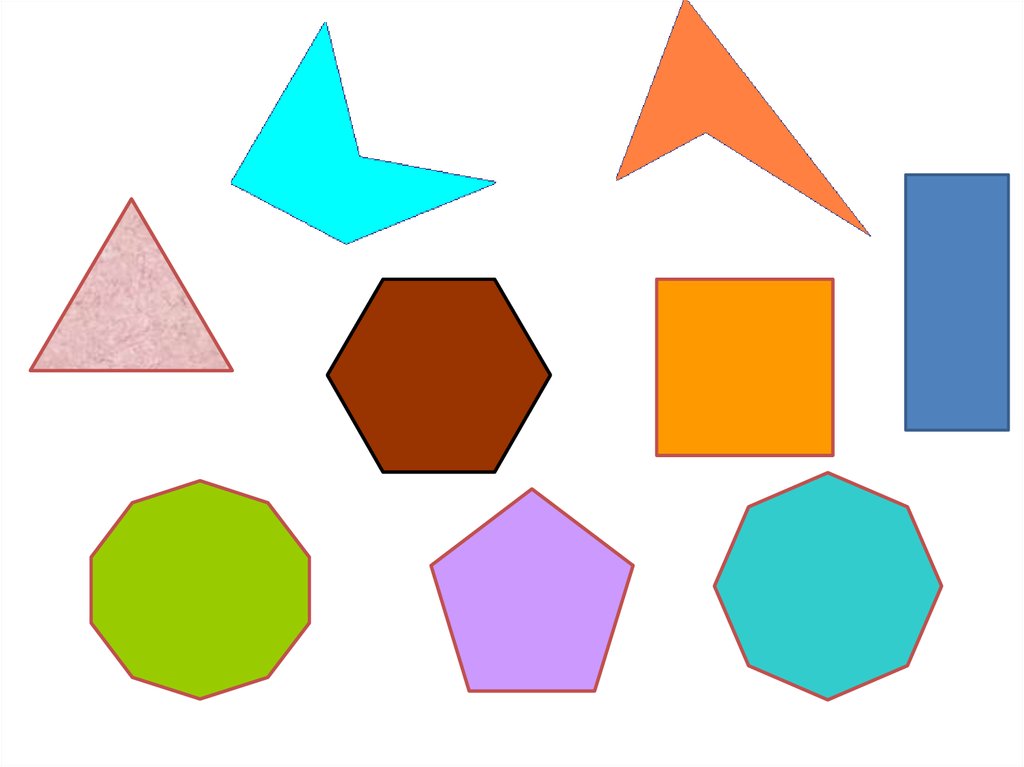 Одна вещь, которую я сделал, чтобы мои ученики более активно участвовали в их обучении, — это достала мою надежную стопку журналов.
Одна вещь, которую я сделал, чтобы мои ученики более активно участвовали в их обучении, — это достала мою надежную стопку журналов.
Учащиеся делят свою работу на 5 столбцов, по одному на каждый изучаемый нами базовый многоугольник. Если вы изучаете больше (например, равносторонний треугольник, разносторонний, равнобедренный или различные типы четырехугольников), просто разделите свою работу на соответствующее количество столбцов. Вверху страницы я предлагаю учащимся нарисовать правильный многоугольник, и мы перечислим атрибуты. Затем они выключены. Учащиеся ищут в журнале изображения многоугольников, вырезают их и приклеивают под соответствующим заголовком столбца.
Твердые фигуры
Как только учащиеся войдут в мир трехмерных объемных фигур, использование книги определенно не поможет. Итак, есть несколько вещей, которые я делаю, чтобы дети думали и узнавали о твердых фигурах.
Я всегда представляю цифры с картинками. Мы смотрим на обычные твердые тела, и я прошу учеников назвать мне объекты, которые они видели и которые соответствовали бы этим формам.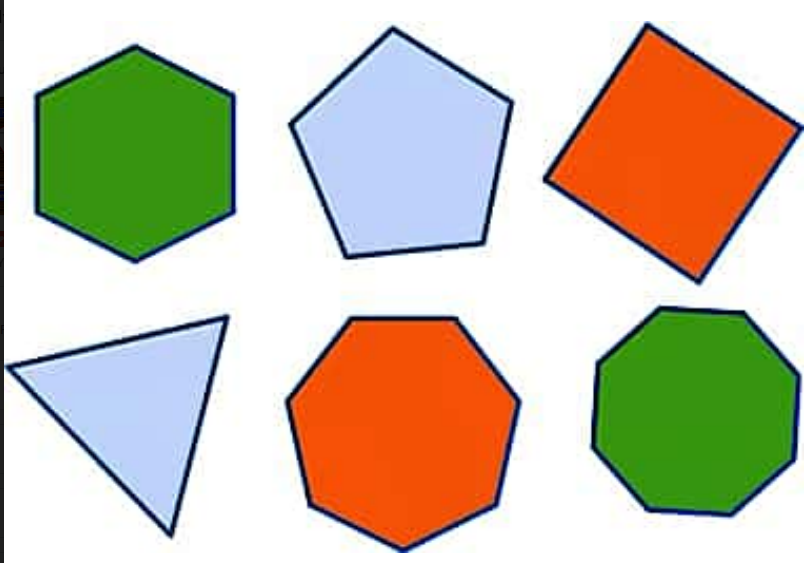 Дети всегда упоминают такие вещи, как конусы мороженого для формы конуса, банка из-под газировки для цилиндра, игральные кости для куба, пирамида для квадратной пирамиды и книга для прямоугольной призмы. Затем вечером я отправляю их домой и ищу настоящие объекты, подходящие под категории. Они записывают все объекты, которые могут, и приносят один по своему выбору. На следующий день мы все классифицируем найденные объекты. Вы можете загрузить эту таблицу, нажав на изображение; диаграмма — это страница 2 бесплатного пакета, который также включает в себя рабочий лист для действий на следующей неделе.
Дети всегда упоминают такие вещи, как конусы мороженого для формы конуса, банка из-под газировки для цилиндра, игральные кости для куба, пирамида для квадратной пирамиды и книга для прямоугольной призмы. Затем вечером я отправляю их домой и ищу настоящие объекты, подходящие под категории. Они записывают все объекты, которые могут, и приносят один по своему выбору. На следующий день мы все классифицируем найденные объекты. Вы можете загрузить эту таблицу, нажав на изображение; диаграмма — это страница 2 бесплатного пакета, который также включает в себя рабочий лист для действий на следующей неделе.
Студенты всегда любят еду. На самом деле создание цельных фигурок из зефира и зубочисток — прекрасный способ заставить детей думать. Мы обсуждаем вершины, ребра и грани каждой объемной фигуры, и ученики приступают к их построению.
Сети твердых тел
Используя описанные выше зефирные фигурки, я предлагаю учащимся разобрать их и создать сети. Для них это ОЧЕНЬ сложно, в основном потому, что когда вы вынимаете несколько зубочисток из зефира, у них не хватает краев! Студенты должны выяснить, что они должны добавить зубочистки и зефир, чтобы создать целое. Интересно посмотреть, кто поймет это понятие.
Интересно посмотреть, кто поймет это понятие.
Еще одна вещь, которую я проделал с сетями, это дать ученикам лист бумаги и позволить им создавать сети. Дети должны выяснить, что круги на цилиндре должны быть того же диаметра, что и длина прямоугольника. Им нужно использовать все квадраты одинакового размера для куба. Все должно быть очень точно, иначе ничего не получится!
Углы и линии
Я большой любитель кинестетического обучения. Из-за этого я использую множество движений и жестов при обучении понятий, чтобы помочь детям лучше понять. Когда дело доходит до углов, мы много двигаемся! Используя свои руки, я прошу учеников показать мне каждый тип угла и линии как можно лучше. Дети действительно увлекаются! Когда я говорю «параллельные линии», их руки всегда поднимаются над головой по двум прямым линиям. Когда я говорю «луч», их рука вытягивается и указывает в одном направлении. У «тупого угла» есть две руки, одна из которых вытянута прямо из тела, а другая под большим углом.
 Физминутка для рук.
Физминутка для рук.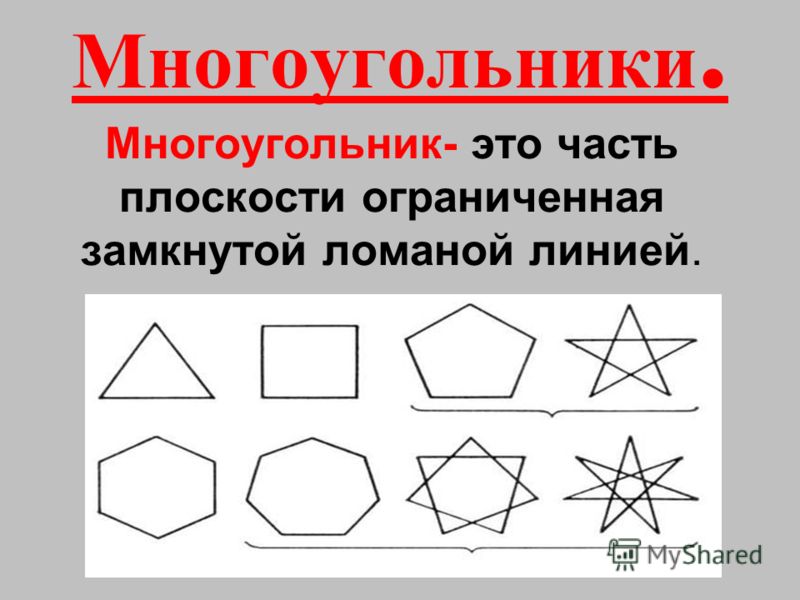 Музыкальная физминутка
Музыкальная физминутка Моделирование
Моделирование
 Вдруг видит на
дорожке перед ним геометрические фигуры кто-то рассыпал. Помогите Колобку
собрать их.
Вдруг видит на
дорожке перед ним геометрические фигуры кто-то рассыпал. Помогите Колобку
собрать их. Найдите треугольник, и нажмите на
него левой кнопкой. А теперь на листе нажмите на левую кнопку, и не отпуская
ее тяните вправо и вниз. Получился треугольник.
Найдите треугольник, и нажмите на
него левой кнопкой. А теперь на листе нажмите на левую кнопку, и не отпуская
ее тяните вправо и вниз. Получился треугольник.


 У вас на партах кирпичики разного цвета. Зеленый означает
«на уроке было все понятно», синий – «интересно, но не все понятно», красный
«было трудно». Выберите ваш кирпичик и выходите к доске.
У вас на партах кирпичики разного цвета. Зеленый означает
«на уроке было все понятно», синий – «интересно, но не все понятно», красный
«было трудно». Выберите ваш кирпичик и выходите к доске.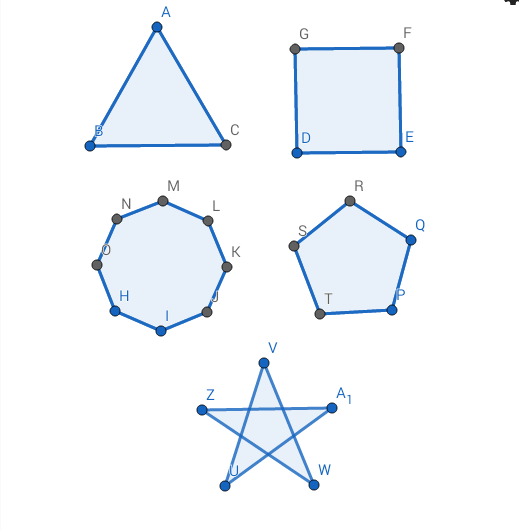 Научиться
его чертить. Составлять фигуры из многоугольников.
Научиться
его чертить. Составлять фигуры из многоугольников.
 По светофору переходить на зеленый свет по зебре.
По светофору переходить на зеленый свет по зебре.

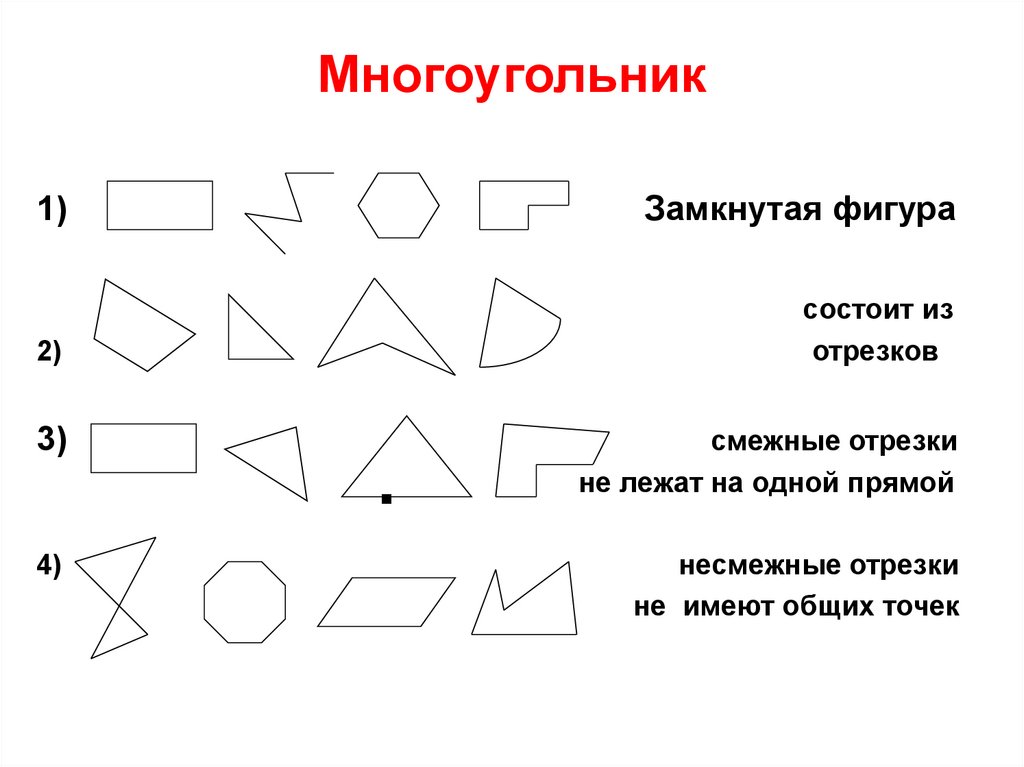


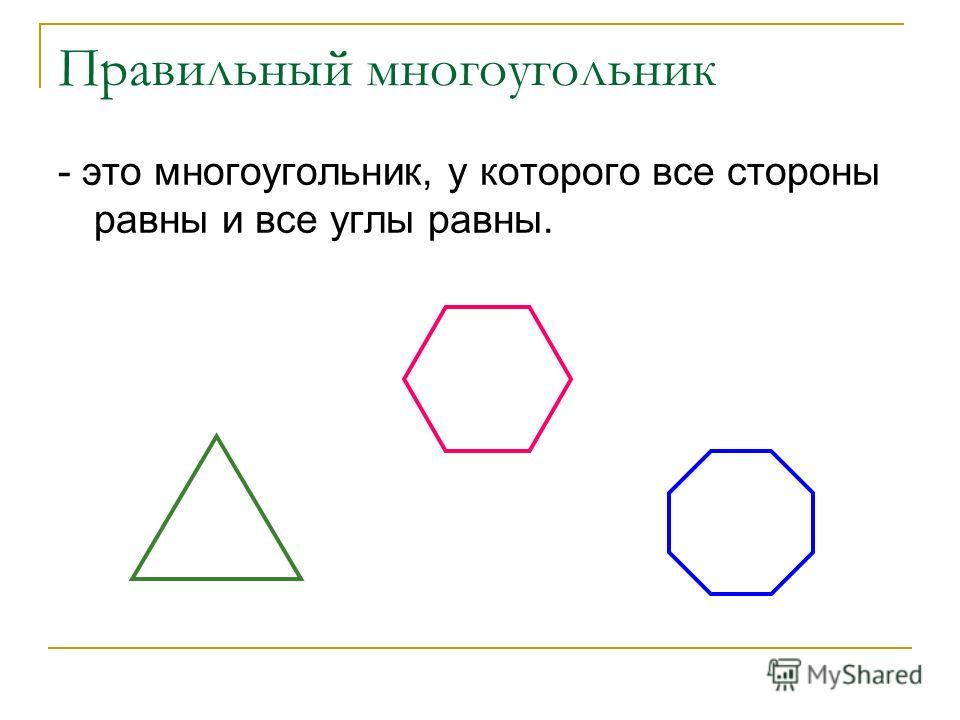





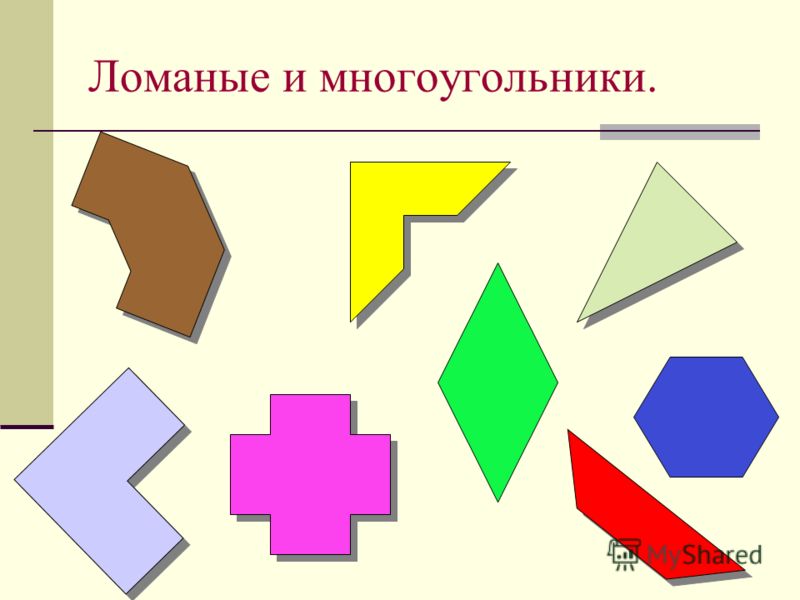 ..
..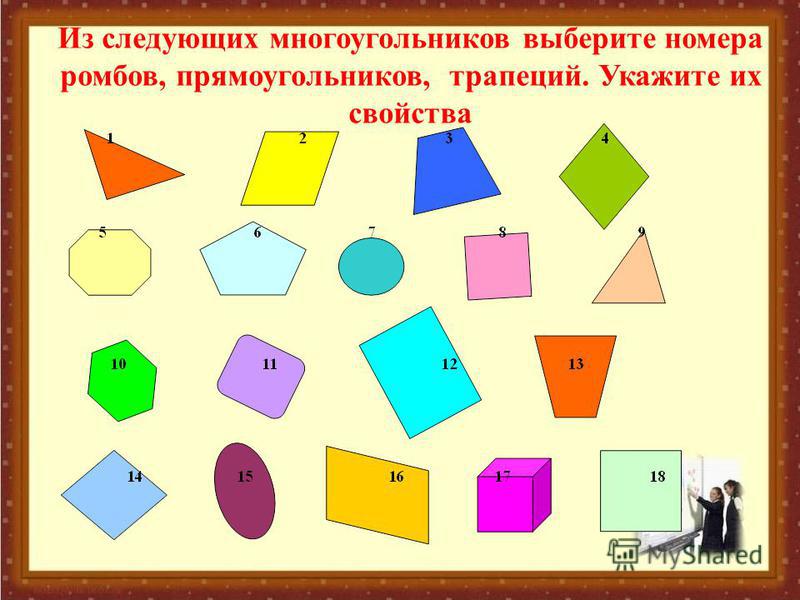 д..
д..