Разное

Калькулятор кругов эйлера: Операции над множествами | Онлайн калькулятор

Содержание

Круги Эйлера онлайн – 4 Июля 2016 – Примеры решений задач

Круги Эйлера, диаграммы Венна

Геометрическое моделирование множеств. Калькулятор.

Для наглядного представления множеств и отношений между ними используется диаграммы Венна (иногда их называют кругами Эйлера или диаграммами Эйлера – Венна).

Универсальное множество изображают в виде прямоугольника, а множества, входящие в универсальное множество,  –  в виде кругов внутри прямоугольника; элементу множества соответствует точка внутри круга.

С помощью диаграмм Венна удобно иллюстрировать операции над множествами.

Калькулятор для построения кругов Эйлера.

Правила вввода основных обозначений операций над множествами:

ОперацияОбозначение
 математическоев калькуляторе
Дополнение$\bar{A}$        A’
Пересечение(A∩B)(A intersection B)
Объединение(А⋃B)(A union B)
Симметрическая разность(A∆B)(symmetric difference of A and B)
Относительное дополнение(A\B)(A\B)

 

ОШИБКИ при вводе формул

ПравильноНе правильно
(A union B) intersection (A union C)(AunionB)intersection(AunionC)

 

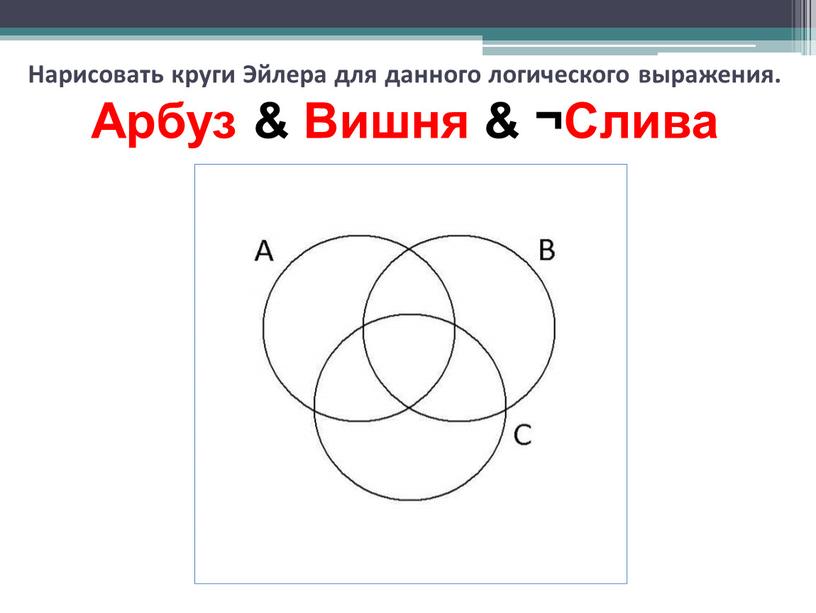
Пример.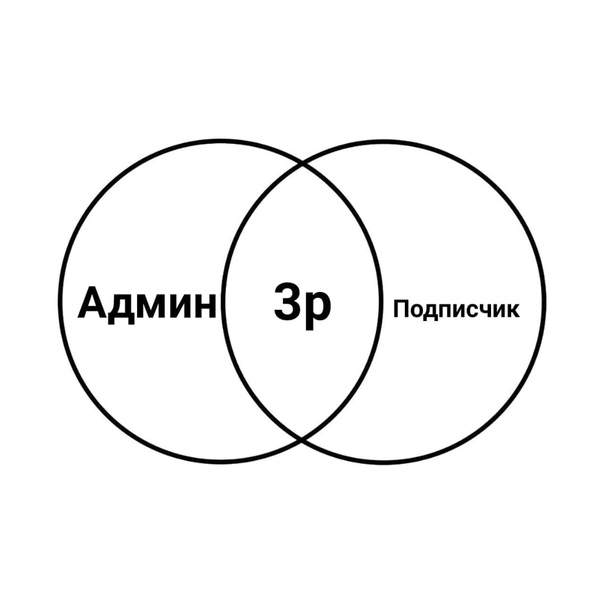 Изобразить множество D с помощью кругов Эйлера  (нарисовать диаграмму Эйлера-Венна):

 

№

Множество D

Вводим в калькулятор

1

$(A\cap B) \cup  C$

(A intersection B) union C

2

$(A\cap B) \cup  \bar{C}$

(A intersection B) union C’

3

$(A\cap \bar{B}) \cup  C$

(A union B’) intersection C

4

$(А\cap B) \cup  (А\cap C)$

(A intersection B) union (A intersection C)

В таблице показано: как правильно вводить в калькулятор выражения  для операций над множествами.

калькулятор онлайн круги эйлера

Вы искали калькулятор онлайн круги эйлера? На нашем сайте вы можете получить ответ на любой математический вопрос здесь.

Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и круги эйлера калькулятор онлайн, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели – у нас уже есть решение. Например, «калькулятор онлайн круги эйлера».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как калькулятор онлайн круги эйлера,круги эйлера калькулятор онлайн,круги эйлера онлайн калькулятор,онлайн круги эйлера калькулятор,онлайн решение круги эйлера.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и калькулятор онлайн круги эйлера. Просто введите задачу в окошко и нажмите «решить» здесь (например, круги эйлера онлайн калькулятор).

Где можно решить любую задачу по математике, а так же калькулятор онлайн круги эйлера Онлайн?

Решить задачу калькулятор онлайн круги эйлера вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать – это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Расчет значения функции Эйлера

Функция Эйлера – такая функция от целого положительного числа, значение которой равно количеству натуральных чисел, меньших заданного числа  и взаимно простых с ним.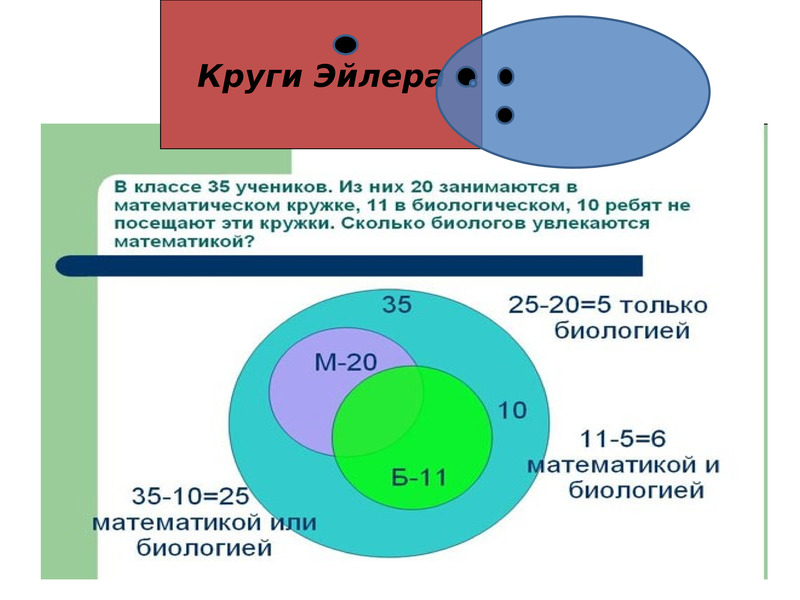

При этом полагают, что число 1 взаимно просто со всеми натуральными числами.

Если заданное число N является простым то логично предложить что функция Эйлера будет равна N-1, так как все числа меньше N, являются взаимно простыми  к заданному.

Например, значение функции Эйлера числа 33 равно 20. Как такое получилось?

Разложим 33 на множители получим  3*11.  Запомним их и будем сравнивать с рядом чисел от 1 до 32.

Напомним, что  взаимно простыми числами являются таки числа, которые не имеют общих делителей.

Считаем  взаимно простые числа: 1,2 ,3(не учитывем),4,5,6(делится на 3),7,8,9,10,11(делится на 11),12,13,14,15,16,17,18,19,20,21(делится на три),22(делится на 11),23,24,25,26,27,28,29,30,31,32

Посчитаем сколько получилось  зачеркнутых чисел? 

Их 12, ряд чисел содержит  32 элемента ( от 1 до 33) тогда количество незачеркнтуых (взаимно простых) чисел будет 32-12 =20

Есть еще простой способ рассчитывать значения функции

Разложим  произвольное число  например 4832 на простые множители.

Получим  

Функция Эйлера равна 

То есть, если у  вас число N  представлено в виде простых сомножителей вида  

то функция Эйлера будет равна

 

Вот еще пример 

Рассчитаем значение фунции числа 100

тогда значение функции Эйлера равно 

Применимость числа Эйлера в теории чисел и криптографии достаточно велико, но мы будем её использовать для расчета линейных диофантовых уравнений с двумя неизвестными.

Напоследок, представляем таблицу значений функции Эйлера для первых 500 чисел

1 1 101 100 201 132
301		 252 401 400
2 1 102 32 202 100 302 150 402 132
3 2 103 102 203 168 303 200
403		 360
4 2 104 48 204 64 304 144 404 200
5 4 105 48 205 160 305 240 405 216
6 2 106 52 206 102 306 96 406 168
7 6 107 106 207 132 307 306 407 360
8 4
108		 36 208 96 308 120 408 128
9 6 109 108 209 180 309 204 409 408
10 4 110 40 210 48 310 120 410 160
11 10 111 72 211 210 311 310 411 272
12 4 112 48 212 104 312 96 412 204
13 12 113 112 213 140 313 312 413 348
14 6 114 36 214 106 314 156 414 132
15 8 115 88 215 168 315 144 415 328
16 8 116 56 216 72 316 156 416 192
17 16 117 72 217 180 317 316 417 276
18 6 118 58 218 108 318 104 418 180
19 18 119 96 219 144 319 280 419 418
20 8 120 32 220 80 320 128 420 96
21 12 121 110 221 192 321 212 421 420
22 10 122 60 222 72 322 132 422 210
23 22 123 80 223 222 323 288 423 276
24 8 124 60 224 96 324 108 424 208
25 20 125 100 225 120 325 240 425 320
26 12 126 36 226 112 326 162 426 140
27 18 127 126 227 226 327 216 427 360
28 12 128 64 228 72 328 160 428 212
29 28 129 84 229 228 329 276 429 240
30 8 130 48 230 88 330 80 430 168
31 30 131 130 231 120 331 330 431 430
32 16 132 40 232 112 332 164 432 144
33 20 133 108 233 232 333 216 433 432
34 16 134 66 234 72 334 166 434 180
35 24 135 72 235 184 335 264 435 224
36 12 136 64 236 116 336 96 436 216
37 36 137 136 237 156 337 336 437 396
38 18 138 44 238 96 338 156 438 144
39 24 139 138 239 238 339 224 439 438
40 16 140 48 240 64 340 128 440 160
41 40 141 92 241 240 341 300 441 252
42 12 142 70 242 110 342 108 442 192
43 42 143 120 243 162 343 294 443 442
44 20 144 48 244 120 344 168 444 144
45 24 145 112 245 168 345 176 445 352
46 22 146 72 246 80 346 172 446 222
47 46 147 84 247 216 347 346 447 296
48 16 148 72 248 120 348 112 448 192
49 42 149 148 249 164 349 348 449 448
50 20 150 40 250 100 350 120 450 120
51 32 151 150 251 250 351 216 451 400
52 24 152 72 252 72 352 160 452 224
53 52 153 96 253 220 353 352 453 300
54 18 154 60 254 126 354 116 454 226
55 40 155 120 255 128 355 280 455 288
56 24 156 48 256 128 356 176 456 144
57 36 157 156 257 256 357 192 457 456
58 28 158 78 258 84 358 178 458 228
59 58 159 104 259 216 359 358 459 288
60 16 160 64 260 96 360 96 460 176
61 60 161 132 261 168 361 342 461 460
62 30 162 54 262 130 362 180 462 120
63 36 163 162 263 262 363 220 463 462
64 32 164 80 264 80 364 144 464 224
65 48 165 80 265 208 365 288 465 240
66 20 166 82 266 108 366 120 466 232
67 66 167 166 267 176 367 366 467 466
68 32 168 48 268 132 368 176 468 144
69 44 169 156 269 268 369 240 469 396
70 24 170 64 270 72 370 144 470 184
71 70 171 108 271 270 371 312 471 312
72 24 172 84 272 128 372 120 472 232
73 72 173 172 273 144 373 372 473 420
74 36 174 56 274 136 374 160 474 156
75 40 175 120 275 200 375 200 475 360
76 36 176 80 276 88 376 184 476 192
77 60 177 116 277 276 377 336 477 312
78 24 178 88 278 138 378 108 478 238
79 78 179 178 279 180 379 378 479 478
80 32 180 48 280 96 380 144 480 128
81 54 181 180 281 280 381 252 481 432
82 40 182 72 282 92 382 190 482 240
83 82 183 120 283 282 383 382 483 264
84 24 184 88 284 140 384 128 484 220
85 64 185 144 285 144 385 240 485 384
86 42 186 60 286 120 386 192 486 162
87 56 187 160 287 240 387 252 487 486
88 40 188 92 288 96 388 192 488 240
89 88 189 108 289 272 389 388 489 324
90 24 190 72 290 112 390 96 490 168
91 72 191 190 291 192 391 352 491 490
92 44 192 64 292 144 392 168 492 160
93 60 193 192 293 292 393 260 493 448
94 46 194 96 294 84 394 196 494 216
95 72 195 96 295 232 395 312 495 240
96 32 196 84 296 144 396 120 496 240
97 96 197 196 297 180 397 396 497 420
98 42 198 60 298 148 398 198 498 164
99 60 199 198 299 264 399 216 499 498
100 40 200 80 300 80 400 160 500 200

Удачных расчетов!

  • Расчет квадратного, кубического и 4 степени уравнения онлайн >>

Расчет значения функции Эйлера

Функция Эйлера – такая функция от целого положительного числа, значение которой равно количеству натуральных чисел, меньших заданного числа  и взаимно простых с ним.

При этом полагают, что число 1 взаимно просто со всеми натуральными числами.

Если заданное число N является простым то логично предложить что функция Эйлера будет равна N-1, так как все числа меньше N, являются взаимно простыми  к заданному.

Например, значение функции Эйлера числа 33 равно 20. Как такое получилось?

Разложим 33 на множители получим  3*11.  Запомним их и будем сравнивать с рядом чисел от 1 до 32.

Напомним, что  взаимно простыми числами являются таки числа, которые не имеют общих делителей.

Считаем  взаимно простые числа: 1,2 ,3(не учитывем),4,5,6(делится на 3),7,8,9,10,11(делится на 11),12,13,14,15,16,17,18,19,20,21(делится на три),22(делится на 11),23,24,25,26,27,28,29,30,31,32

Посчитаем сколько получилось  зачеркнутых чисел? 

Их 12, ряд чисел содержит  32 элемента ( от 1 до 33) тогда количество незачеркнтуых (взаимно простых) чисел будет 32-12 =20

Есть еще простой способ рассчитывать значения функции

Разложим  произвольное число  например 4832 на простые множители.

Получим  

Функция Эйлера равна 

То есть, если у  вас число N  представлено в виде простых сомножителей вида  

то функция Эйлера будет равна

 

Вот еще пример 

Рассчитаем значение фунции числа 100

тогда значение функции Эйлера равно 

Применимость числа Эйлера в теории чисел и криптографии достаточно велико, но мы будем её использовать для расчета линейных диофантовых уравнений с двумя неизвестными.

Напоследок, представляем таблицу значений функции Эйлера для первых 500 чисел

1 1 101 100 201 132 301 252 401 400
2 1 102 32 202 100 302 150 402 132
3 2 103 102 203 168 303 200 403 360
4 2 104 48 204 64 304 144 404 200
5 4 105 48 205 160 305 240 405 216
6 2 106 52 206 102 306 96 406 168
7 6 107 106 207 132 307 306 407 360
8 4 108 36 208 96 308 120 408 128
9 6 109 108 209 180 309 204 409 408
10 4 110 40 210 48 310 120 410 160
11 10 111 72 211 210 311 310 411 272
12 4 112 48 212 104 312 96 412 204
13 12 113 112 213 140 313 312 413 348
14 6 114 36 214 106 314 156 414 132
15 8 115 88 215 168 315 144 415 328
16 8 116 56 216 72 316 156 416 192
17 16 117 72 217 180 317 316 417 276
18 6 118 58 218 108 318 104 418 180
19 18 119 96 219 144 319 280 419 418
20 8 120 32 220 80 320 128 420 96
21 12 121 110 221 192 321 212 421 420
22 10 122 60 222 72 322 132 422 210
23 22 123 80 223 222 323 288 423 276
24 8 124 60 224 96 324 108 424 208
25 20 125 100 225 120 325 240 425 320
26 12 126 36 226 112 326 162 426 140
27 18 127 126 227 226 327 216 427 360
28 12 128 64 228 72 328 160 428 212
29 28 129 84 229 228 329 276 429 240
30 8 130 48 230 88 330 80 430 168
31 30 131 130 231 120 331 330 431 430
32 16 132 40 232 112 332 164 432 144
33 20 133 108 233 232 333 216 433 432
34 16 134 66 234 72 334 166 434 180
35 24 135 72 235 184 335 264 435 224
36 12 136 64 236 116 336 96 436 216
37 36 137 136 237 156 337 336 437 396
38 18 138 44 238 96 338 156 438 144
39 24 139 138 239 238 339 224 439 438
40 16 140 48 240 64 340 128 440 160
41 40 141 92 241 240 341 300 441 252
42 12 142 70 242 110 342 108 442 192
43 42 143 120 243 162 343 294 443 442
44 20 144 48 244 120 344 168 444 144
45 24 145 112 245 168 345 176 445 352
46 22 146 72 246 80 346 172 446 222
47 46 147 84 247 216 347 346 447 296
48 16 148 72 248 120 348 112 448 192
49 42 149 148 249 164 349 348 449 448
50 20 150 40 250 100 350 120 450 120
51 32 151 150 251 250 351 216 451 400
52 24 152 72 252 72 352 160 452 224
53 52 153 96 253 220 353 352 453 300
54 18 154 60 254 126 354 116 454 226
55 40 155 120 255 128 355 280 455 288
56 24 156 48 256 128 356 176 456 144
57 36 157 156 257 256 357 192 457 456
58 28 158 78 258 84 358 178 458 228
59 58 159 104 259 216 359 358 459 288
60 16 160 64 260 96 360 96 460 176
61 60 161 132 261 168 361 342 461 460
62 30 162 54 262 130 362 180 462 120
63 36 163 162 263 262 363 220 463 462
64 32 164 80 264 80 364 144 464 224
65 48 165 80 265 208 365 288 465 240
66 20 166 82 266 108 366 120 466 232
67 66 167 166 267 176 367 366 467 466
68 32 168 48 268 132 368 176 468 144
69 44 169 156 269 268 369 240 469 396
70 24 170 64 270 72 370 144 470 184
71 70 171 108 271 270 371 312 471 312
72 24 172 84 272 128 372 120 472 232
73 72 173 172 273 144 373 372 473 420
74 36 174 56 274 136 374 160 474 156
75 40 175 120 275 200 375 200 475 360
76 36 176 80 276 88 376 184 476 192
77 60 177 116 277 276 377 336 477 312
78 24 178 88 278 138 378 108 478 238
79 78 179 178 279 180 379 378 479 478
80 32 180 48 280 96 380 144 480 128
81 54 181 180 281 280 381 252 481 432
82 40 182 72 282 92 382 190 482 240
83 82 183 120 283 282 383 382 483 264
84 24 184 88 284 140 384 128 484 220
85 64 185 144 285 144 385 240 485 384
86 42 186 60 286 120 386 192 486 162
87 56 187 160 287 240 387 252 487 486
88 40 188 92 288 96 388 192 488 240
89 88 189 108 289 272 389 388 489 324
90 24 190 72 290 112 390 96 490 168
91 72 191 190 291 192 391 352 491 490
92 44 192 64 292 144 392 168 492 160
93 60 193 192 293 292 393 260 493 448
94 46 194 96 294 84 394 196 494 216
95 72 195 96 295 232 395 312 495 240
96 32 196 84 296 144 396 120 496 240
97 96 197 196 297 180 397 396 497 420
98 42 198 60 298 148 398 198 498 164
99 60 199 198 299 264 399 216 499 498
100 40 200 80 300 80 400 160 500 200

Удачных расчетов!

круги эйлера – Видео

Круги Эйлера в реальной жизни.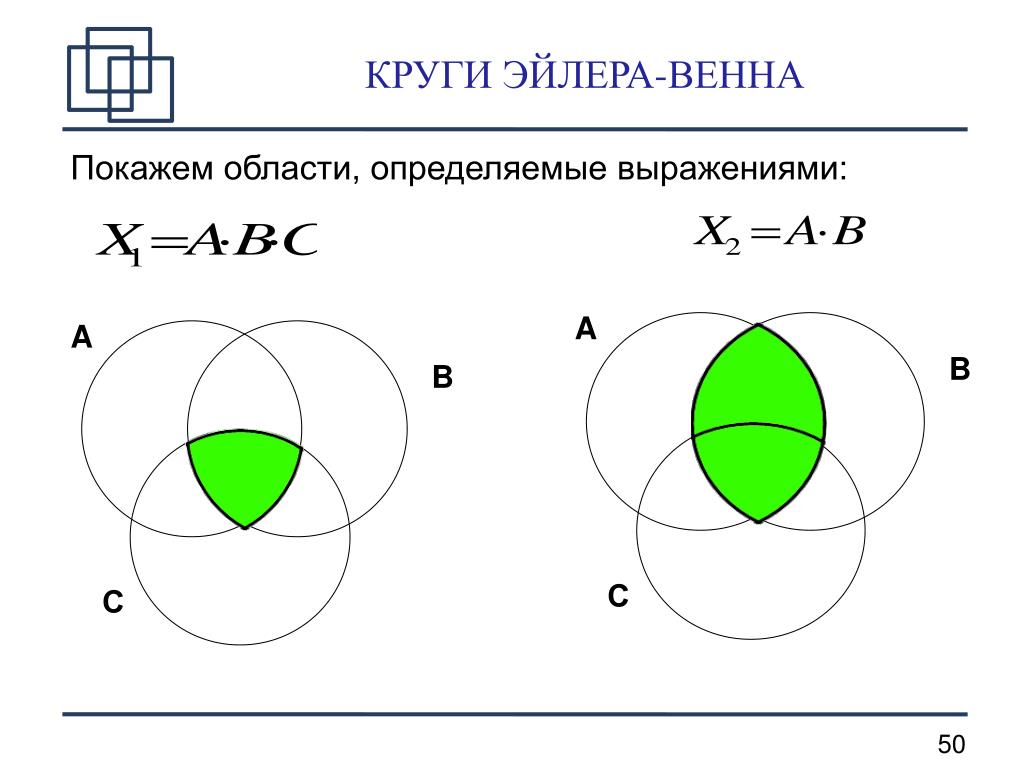 Математика на QWERTY

QWERTY
20-08-2020

Простое объяснения решения задач при помощи кругов Эйлера

Misha Rybakov
19-12-2018

Круги Эйлера

GetAClass – Просто математика
11-11-2017

Решение задач с помощью кругов Эйлера

Андрей Никитин
13-05-2017

Круги Эйлера-Венна

Smart Bilim
22-04-2015

Множества. Круги Эйлера

Marianna L
20-08-2016

Круги Эйлера | Урок нестандартных задач №4

Уроки Нестандартных Задач
13-02-2020

Круги Эйлера (диаграммы Венна) – просто и доступно.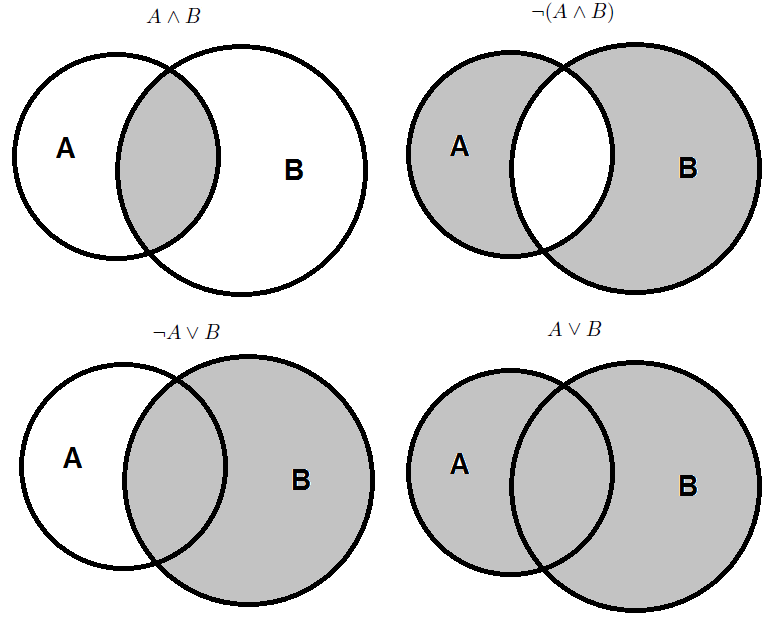

school info vids
29-01-2017

Диаграммы Эйлера. Решение заданий №17

Информатик БУ
17-03-2015

Множества. Круги Эйлера.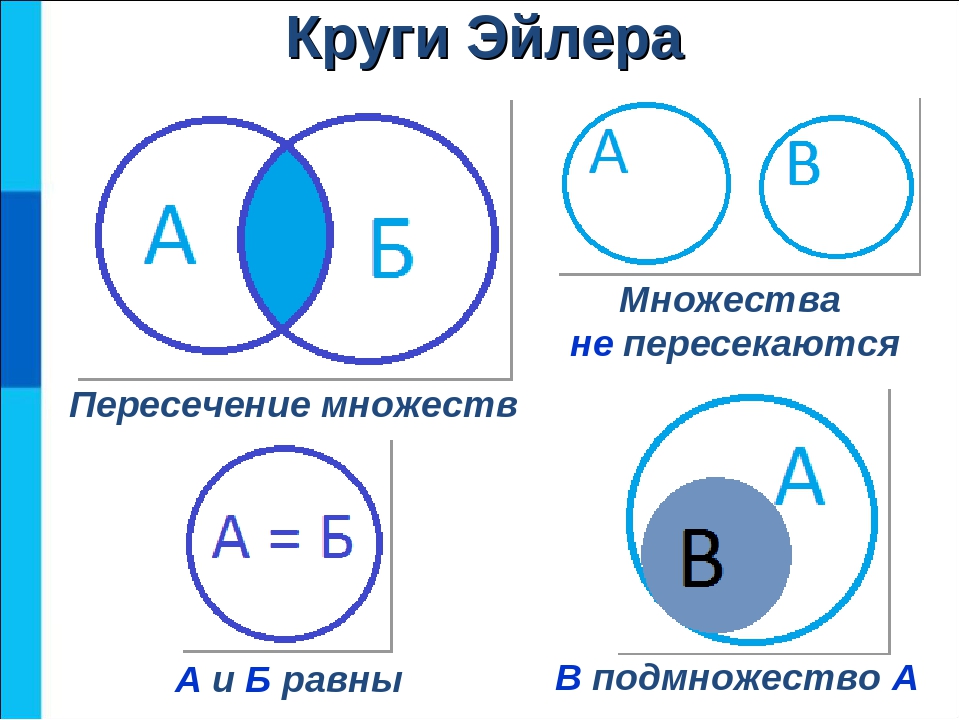 Математика 5, 6, 7, 8, 9, 10, 11 класс. Подготовка к ЕГЭ, ОГЭ, ЦТ, экзамену

Математика
09-04-2020

Логика для чайников

Pavel Tavankov
26-03-2014

Решение логических задач на круги Эйлера

Дмитрий Кросс
01-03-2016

Решение задач с помощью кругов Эйлера. Задача 1

Математика. В помощь учащимся
27-06-2019

3 круга Эйлера

Sergey Valerevich
10-11-2019

Круги Эйлера. Решение задач на поиск информации в Интернет. Информатика

Юлия Шелякина
18-10-2020

Игры с кругами Эйлера – Венна

Валентина Овинцовская
13-12-2018

Решение задач с помощью кругов Эйлера 6 класс

ФИЗМАТ & ИЛЬЯ ОЛЕГОВИЧ
27-04-2020

Логика и множества. Круги Эйлера

Заочная Школа Фрактал
13-10-2020

Информатика. Круги Эйлера. ОГЭ Задание №8. ЕГЭ задание №17.

Информатика в школе
26-03-2020

круги Эйлера

– информатика –
07-04-2020

Круги Эйлера в Логике. 10 класс

Информатик || Лосев А.В.
13-11-2020

6. Круги Эйлера

BrainStory Me
03-05-2017

Круги Эйлера 6 класс Пояснения и примеры

Максим Зойкин
15-12-2018

Практикум. Логические отношения между понятиями.

Азат Сабирзянов
05-04-2014

3 (х).
  • Из приведенной ниже таблицы вы можете заметить, что sech не поддерживается, но вы все равно можете ввести его, используя идентификатор `sech (x) = 1 / cosh (x)`.
  • Если вы получаете сообщение об ошибке, дважды проверьте свое выражение, добавьте скобки и знаки умножения, где это необходимо, и обратитесь к таблице ниже.
  • Приветствуются все предложения и улучшения. Пожалуйста, оставьте их в комментариях.

    • В следующей таблице перечислены поддерживаемые операции и функции:

    9 0028 acsc (x)
    Тип Получить
    Константы
    e e
    pi `pi`
    i i (мнимая единица)
    Операции
    a + b a + b
    ab ab
    a * b `a * b`
    a ^ b, a ** b` a ^ b`
    sqrt (x), x ^ (1/2) `sqrt (x)`
    cbrt (x), x ^ (1/3) `root (3 ) (x) `
    root (x, n), x ^ (1 / n)` root (n) (x) `
    x ^ (a / b)` x ^ (a / b) `
    x ^ a ^ b` x ^ (a ^ b) `
    abs (x)` | x | `
    Функции
    e ^ x `e ^ x`
    ln (x), журнал (x) ln (x)
    ln (x) / ln (a) `log_a (x)`
    Тригонометрические функции
    sin (x) sin (x)
    cos (x) cos (x)
    tan (x) tan (x), tg (x)
    кроватка (x) кроватка (x), ctg ( x)
    сек (x) сек (x)
    csc (x) csc (x), cosec (x)
    Обратные тригонометрические функции
    asin (x) , arcsin (x), sin ^ -1 (x) asin (x)
    acos (x), arccos (x), cos ^ -1 (x) acos (x)
    атан (x), arctan (x), tan ^ -1 (x) atan (x)
    acot (x), arccot ​​(x), cot ^ -1 (x) acot (x)
    asec (x), arcsec (x), sec ^ -1 (x) asec (x)
    acsc (x), arccsc (x), csc ^ -1 (x)
    Гиперболические функции
    sinh (x) sinh (x)
    cosh (x) cosh (x)
    tanh (x) tanh (x)
    coth (x) coth (x)
    1 / cosh (x) sech (x)
    1 / sinh (x) csch (x)
    Обратные гиперболические функции
    asinh (x), arcsinh (x), sinh ^ -1 (x) asinh (x)
    acosh (x), arccosh (x), cosh ^ – 1 (x) acosh (x)
    atanh (x), arctanh (x), tanh ^ -1 (x) atanh (x)
    acoth (x), arccoth (x) , детская кроватка ^ -1 (x) acoth (x)
    acosh (1 / x) asech (x)
    asinh (1 / x) acsch (x)

    Карты расстояний по Большому кругу, маршруты аэропортов и градусы / минуты / секунды

    Эта страница предназначена для того, чтобы помочь вам вычислить ответы на некоторые общие географические вопросы и нарисовать карты с помощью простых координат. Если у вас возникнут проблемы или вы получите неожиданный результат, дайте мне знать!

    Преобразователь координат

    Эта форма попытается прочитать введенное вами значение и преобразовать его в три формата: десятичные градусы, градусы-минуты и градусы-минуты-секунды.

    Вычислить расстояние по большому кругу между двумя точками

    Этот калькулятор найдет расстояние между двумя парами координат с очень высокой степенью точности (используя очень неприятную формулу Винсенти, которая учитывает сплющенную форму земли).Кнопка «Нарисовать карту» покажет вам две точки на карте и проведет большой круговой маршрут между ними.

    Рассчитать расстояние между двумя адресами

    Этот калькулятор найдет расстояние по прямой (большой круг) между двумя местоположениями любого типа: почтовые адреса, названия городов, почтовые индексы и т. Д. (Координаты местоположений предоставляются API геокодирования Google.) ПРИМЕЧАНИЕ. Если вам просто нужны координаты адреса, используйте утилиты геокодирования.

    Нарисуйте прямой маршрут между аэропортами

    Эта форма просто покажет вам два аэропорта – представленные трехбуквенным кодом ИАТА или четырехбуквенным кодом ИКАО – на карте вместе с линией, представляющей кратчайший маршрут между ними (и расстояние, конечно).

    Нарисовать маршруты между несколькими аэропортами

    В форме ниже вы можете ввести список маршрутов (пар аэропортов), разделенных запятыми, чтобы увидеть все маршруты и расстояния до них на одной карте.Например: PDX-MSP, BOS-MIA, ATL-DEN, DEN-PHX

    .

    Диапазон протяжки колец вокруг точки

    Этот «генератор кругов» нанесет точку на карту – с заданным набором координат или другим местоположением (код аэропорта, почтовый индекс, пара города / штата или пара координат) – и нарисует вокруг нее круг или круги. точка. Чтобы создать несколько колец, разделите значения в поле «радиус» запятыми: например, «10 миль, 50 миль, 100 миль». (Если вам нужно создать кольца вокруг нескольких точек одновременно, вы можете отправить данные в форму нормальной карты с добавленным полем «circle_radius»; см. Страницу о триангуляции и кольцах диапазона для получения дополнительной информации.)

    Если вам нужно поместить кольца диапазонов вокруг нескольких точек на одной карте, вы можете предоставить свои данные в виде текстового файла или электронной таблицы и включить поле «circle_radius»; см. пример страницы для получения дополнительной информации.

    Найдите координаты на заданном расстоянии и пеленге

    Эта форма сообщит вам, какая точка лежит на любом расстоянии и по направлению от другой точки вдоль траектории большого круга. Если вы не указываете единицы в самом поле расстояния (например,, “100 миль”), по умолчанию будут километры. (Используемая здесь формула была адаптирована из “Sprong” Дейла Бикеля из FCC.)

    (Примечание: эта страница раньше называлась «Географические калькуляторы», пока компания Blue Marble не пригрозила подать в суд на GPS-визуализатор за использование этой общей фразы, которая, по-видимому, была зарегистрирована как торговая марка в единственном числе с заглавной буквы.)


    Вернуться на главную страницу GPS-визуализатора


    Окружность (периметр) круга с помощью калькулятора

    Окружность (периметр) круга с помощью калькулятора – Math Open Reference

    Расстояние по краю круга.Также «периферия», «периметр».

    Попробуйте это Перетащите оранжевые точки, чтобы переместить и изменить размер круга. Окружность показана синим цветом. Обратите внимание на изменение радиуса, и длина окружности рассчитывается для этого радиуса.

    Иногда вы видите слово «окружность» в значении изогнутой линии, идущей по кругу. В других случаях это означает длину этой линии, например, «окружность составляет 2,11 см».

    Слово «периметр» также иногда используется, хотя обычно оно относится к расстоянию вокруг многоугольников, фигуры, составленные из отрезков прямых линий.


    Если вы знаете радиус

    Учитывая радиус круга, окружность можно рассчитать по формуле где:
    R – радиус окружности
    π – Пи, приблизительно 3,142

    См. Также вывод формулы окружности


    Если известен диаметр

    Если известен диаметр окружности, длина окружности может быть найдена по формуле
    , где:
    D – диаметр окружности
    π – Пи, приблизительно 3.142

    См. Также вывод формулы окружности


    Если вы знаете район

    Если вам известна площадь круга, длину окружности можно найти по формуле
    , где:
    A – площадь круга
    π равно Пи, приблизительно 3,142

    См. Также вывод формулы окружности

    Калькулятор

    Воспользуйтесь калькулятором выше, чтобы вычислить свойства круга.

    Введите любое одно значение, и остальные три будут рассчитаны.Например: введите радиус и нажмите «Рассчитать». Будут рассчитаны площадь, диаметр и окружность.

    Точно так же, если вы войдете в область, будет вычислен радиус, необходимый для получения этой области, а также диаметр и окружность.

    Сопутствующие меры

    • Радиус Радиус – это расстояние от центра круга до любой точки по периметру. См. Радиус круга.
    • Диаметр Расстояние по окружности.Видеть Диаметр круга больше.

    Другие темы в круге

    Общий

    Уравнения окружности

    Углы по окружности

    Дуги

    (C) Открытый справочник по математике, 2011 г.
    Все права защищены.

    Калькулятор длины окружности

    Формула окружности круга

    Длина окружности вычисляется по формуле: 2 x π x радиус , где π – математическая константа, равная примерно 3. 14159. Первоначально он был определен как отношение длины окружности круга к его диаметру (см. Вторую формулу ниже о том, почему) и появляется во многих формулах в математике, физике и повседневной жизни.

    На практике часто легче измерить диаметр, чем радиус. Если вы знаете диаметр, он в 2 раза больше радиуса, поэтому просто разделите его на два, чтобы получить радиус, или используйте эту формулу: π x диаметр .

    Результат расчета выражается в единицах измерения радиуса или диаметра окружности.

    Как рассчитать длину окружности?

    Расчет становится простым после того, как вы измерили радиус или диаметр окружности, используя приведенные выше формулы или, если вы предпочитаете более простой способ, используя наш калькулятор длины окружности выше. Чтобы убедиться, что вы правильно измеряете диаметр, это должно быть самое большое измерение, которое вы можете получить. Если, слегка перемещая измерительный инструмент, вы получите больший диаметр, то сделайте это.


    Пример: найти длину окружности

    Чтобы вычислить длину окружности, нужно знать только радиус или диаметр круга.Если задан радиус, применить формулу просто. Например, окружность круга с радиусом 4 дюйма просто равна 2 x 3,14159 x 4 = 25,13 дюйма.

    Если вместо этого указан диаметр, сначала разделите его на два, затем повторите описанный выше процесс. Например, если диаметр составляет 16 футов, тогда радиус будет 16/2 = 8 футов. Таким образом, окружность составляет 2 x 3,14159 x 8 = 50,26 футов.

    Практическое применение

    Круги часто используются архитекторами для строительства спортивных треков, зон отдыха, зданий и кольцевых развязок.Знаменитое колесо обозрения представляет собой круг. Круглые части, например цилиндры, трубки, шестерни и другие детали используются инженерами для изготовления часов, велосипедов, автомобилей, поездов, кораблей, самолетов и даже ракет. Изобретение колесной тележки было одним из революционных событий в ранней истории человечества. Число π применяется при вычислении важных статистических распределений, таких как нормальное распределение (гауссово распределение).

    Калькулятор периметра

    – вычисляет периметр квадрата, прямоугольника, треугольника, круга, параллелограмма, трапеции, эллипса…

    Как рассчитать периметр любой формы?

    Существуют разные правила расчета параметра для разных геометрических форм. Наш калькулятор периметра поддерживает множество основных форм, и ниже вы можете прочитать подробную информацию о каждой из них, включая формулу расчета периметра. Выполняя расчет, не забывайте проводить каждое измерение в одной и той же единице или преобразовывать ее в одну и ту же единицу, чтобы получить достоверные результаты.

    Периметр квадрата

    Формула для периметра квадрата: сторон x 4 , как показано на рисунке ниже:

    Это самая простая форма для расчета, так как вам нужно всего лишь одно измерение.Для этого вам даже не понадобится калькулятор. Однако это также редко встречается в практических вопросах.


    Периметр прямоугольника

    Формула для периметра прямоугольника: (ширина + высота) x 2 , как показано на рисунке ниже:

    Для прямоугольника нужны два измерения – ширина и длина. Убедитесь, что оба находятся в одном блоке, или при необходимости преобразуйте один из них. Благодаря простоте формы, измерения легко проводить, а калькулятор периметра упрощает расчет только при больших числах.

    Периметр треугольника

    Формула для периметра треугольника: сторона a + сторона b + сторона c , но есть много правил, с помощью которых можно вычислить. Визуализация на рисунке ниже:

    Наш калькулятор периметра также поддерживает следующие правила: SAS (сторона, угол, сторона), SSA (сторона, сторона, угол), ASA (угол, сторона, угол), а также гипотенуза и правило стороны для прямоугольных треугольников.

    Окружность круга

    Формула длины окружности: 2 x π x радиус , но диаметр круга равен d = 2 x r, поэтому можно записать его другим способом: 2 x π x (диаметр / 2) . Наглядно на рисунке ниже:

    Во многих практических ситуациях легче точно измерить диаметр, чем радиус. Кроме того, во многих инженерных схемах по умолчанию задается диаметр окружности, а не радиус.

    Периметр параллелограмма

    Формула для периметра параллелограмма: (ширина + высота) x 2 , как показано на рисунке ниже:

    Периметр параллелограмма рассчитывается по той же формуле, что и прямоугольник, поскольку в обеих формах противоположные стороны равны по длине.

    Периметр трапеции

    Формула для периметра трапеции: основание 1 + основание 2 + сторона a + сторона b , как показано на рисунке ниже:

    Для трапеции нужно больше размеров, так как это более сложная форма, в которой все стороны могут иметь разную длину.

    Окружность эллипса (овала)

    Не существует единой формулы для определения длины окружности эллипса, так как на удивление трудно вычислить ее точно. Мы используем точный способ вычисления, который приводит к точному вычислению после бесконечного количества вычислений. Если количество вычислений меньше бесконечного, есть небольшая ошибка. Оно быстро сходится к истинному значению, поэтому мы делаем всего несколько шагов.

    Сначала калькулятор вычисляет h = (большой радиус – малый радиус) 2 / (большой радиус + малый радиус) 2 . Затем он вычисляет периметр как равный π x (большой радиус + малый радиус) x (1 + h * 0.25 + h 2 * (1/64) + h 3 * (1/256) + h 4 * (25/16384) + h 5 * (49/65536) + h 6 * (441/1048576) . Наглядно на рисунке ниже:

    Периметр сектора

    Формула для периметра сектора: 2 x радиус + радиус x угол x (π / 360) . Наглядно на рисунке ниже:

    Сектор – это просто часть круга, поэтому формула аналогична. Дополнительная сложность возникает из-за необходимости рассчитать, какую часть круга составляет сектор.

    Периметр восьмиугольника

    Формула для периметра правильного восьмиугольника: сторона x 8 , как показано на рисунке ниже:

    Это одна из самых простых форм для вычисления периметра – требуется только одно измерение, и простое умножение на восемь – это все, что нужно сделать. Правильные восьмиугольники можно встретить в технике, озеленении и озеленении, а также в архитектуре.

    Где пригодится калькулятор периметра?

    Помимо очевидного – заданий на уроке геометрии или домашних заданий, калькулятор периметра может иметь множество практических применений.Например, в спорте – вы можете решить, что вам нужно ходить или бегать по 10 км в день, чтобы оставаться в хорошей физической форме. Однако что делать, если рядом нет хороших трасс? Вы можете просто выбрать большое здание или любой прямоугольный квартал или набор блоков, рассчитать их периметр и затем разделить на него 10 км, чтобы определить, сколько кругов вам нужно сделать.

    Калькулятор также может быть полезен в различных проектах DIY дома или в саду, в том числе в таких вещах, как украшение дома, рукоделие и т. Д.Работа в инженерии и некоторых ремеслах часто заканчивается расчетом периметра.

    Калькулятор площади круга

    Формула площади круга

    Формула для площади круга: π x радиус 2 , но диаметр круга d = 2 xr 2 , поэтому можно записать его другим способом: π x (диаметр / 2) 2 . Наглядно на рисунке ниже:

    π – это, конечно, знаменитая математическая константа, равная примерно 3.14159, который изначально определялся как отношение длины окружности к ее диаметру. Вышеуказанная формула используется в нашем калькуляторе площади круга.

    Как рассчитать площадь круга?

    Вычислить легко, если вы измерили радиус или диаметр окружности, или если вы знаете это из планов и схем: просто подставьте числа в формулы выше, используйте наш калькулятор площади круга выше. Если вы измеряете его вручную, помните, что диаметр – это наибольшее измерение, которое вы можете получить от круга.


    Пример: найти площадь круга

    Задача 1: Зная радиус петли, найдите ее площадь. Например, если радиус составляет 5 дюймов, то по первой формуле площади вычислите π x 5 2 = 3,14159 x 25 = 78,54 кв. Дюйма

    Задача 2: Найдите площадь круга с диаметром 12 см. Примените второе уравнение, чтобы получить π x (12/2) 2 = 3,14159 x 36 = 113,1 см 2 (квадратные сантиметры).

    Практическое применение

    Геометрия круга имеет широкий спектр практических применений.Круги используются при планировании спортивных трасс, зон отдыха, зданий и кольцевых развязок, поэтому знание их местности важно при строительстве, ландшафтном дизайне и т. Д. Знаменитое колесо обозрения – это круг, как и колеса вашего автомобиля или велосипеда. Круглые части, например цилиндры, трубы, шестерни и другие детали используются инженерами в часах, велосипедах, автомобилях, поездах, кораблях, самолетах и ​​даже ракетах.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *