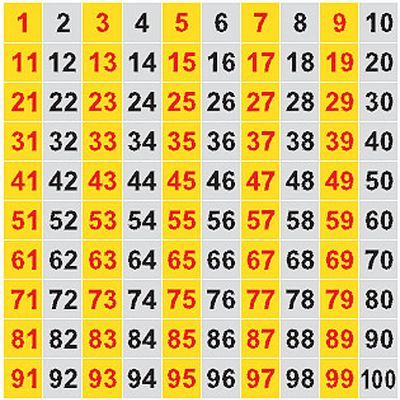
Какие четные числа какие нечетные: Чётные и нечётные числа — урок. Математика, 2 класс.
Биологи научили пчел отличать четные числа от нечетных – Газета.Ru
Биологи научили пчел отличать четные числа от нечетных – Газета.Ru | Новости
close
100%
Медоносные пчелы способны отличать четные числа от нечетных, выяснила команда биологов и специалистов по зрительной обработке из Мельбурнского королевского технологического университета и других исследовательских центров. О результатах эксперимента ученые рассказали в статье в журнале Frontiers in Ecology and Evolution.
Исследователи обучили одну группу пчел ассоциировать четные числа с водой, в которой был разведен сахар, а нечетные — с водой с хинином, а вторую — наоборот. В процессе обучения ученые показывали пчелам карточки с четным и нечетным количеством фигур. В итоге пчелы смогли отличать четные числа от нечетных в 80% случаев. Когда исследователи использовали карточки, которые не показывали пчелам ранее, точность немного упала, но все равно осталась высокой — около 70%.
Обучение в группах шло с разной скоростью, отмечают авторы работы. Те пчелы, которые ассоциировали четные числа со сладкой водой, обучались быстрее. Интересно, что у людей тоже есть факторы, влияющие на обработку четных и нечетных чисел — на четные мы быстрее реагируем при выполнении действий правой рукой, а на нечетные — левой. Кроме того, дети обычно ассоциирую слово «четный» со словом «правый», а «нечетный» — с «левый».
Чтобы определить, насколько задача по различению четных и нечетных чисел вообще может быть сложна, исследователи разработали простую нейросеть всего из пяти нейронов. Даже этого оказалось достаточно для такой задачи.
«Классификация четности не требует большого и сложного мозга, как у человека. Однако это необязательно означает, что пчелы и простая нейронная сеть использовали один и тот же механизм для решения задачи», — отметили авторы исследования.
Возможно, пчелы объединяли элементы в пары, чтобы найти непарный элемент, или подсчитывали общее их количество — точного ответа ученые дать не могут.
Подписывайтесь на «Газету.Ru» в Новостях, Дзен и Telegram.
Чтобы сообщить об ошибке, выделите текст и нажмите Ctrl+Enter
Новости
Дзен
Telegram
Георгий Бовт
Не догонишь – не похоронишь
О том, как мы хотели перегнать Америку, но потом передумали
Алексей Мухин
Хромая утка по-пекински
О возможном конфликте США и Китая
Мария Дегтерева
Там чудеса, там леший бродит
О бюрократии и чиновничестве в России
Иван Глушков
Холодное блюдо
О гастрономическом путешествии на Таймыр
Дмитрий Самойлов
Праздник за праздником
О Дне народного единства и Дне Октябрьской революции
Найдена ошибка?
Закрыть
Спасибо за ваше сообщение, мы скоро все поправим.
Продолжить чтение
Четные цифры списком
4.6
Средняя оценка: 4.6
Всего получено оценок: 541.
4.6
Средняя оценка: 4.6
Всего получено оценок: 541.
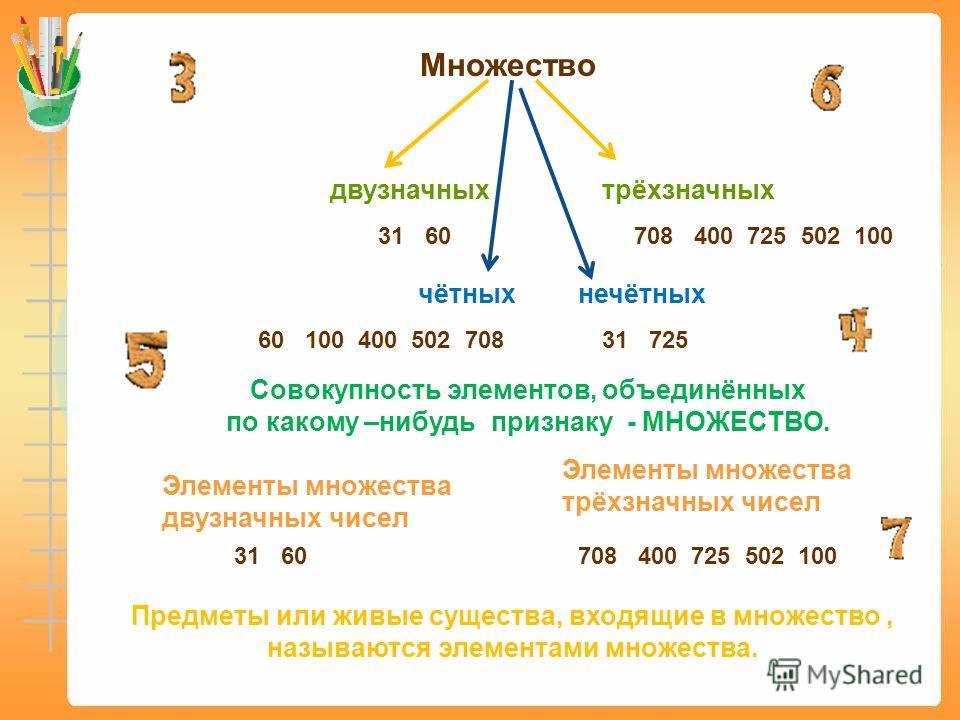
Четные числа – достаточно интересная и простая тема в курсе математики. Многие ученики не задумываясь, пользуются основными свойствами четных чисел, что иногда вызывает ошибки. Чтобы разобраться в вопросе раз и навсегда – разберем тему четных чисел во всех подробностях.
Что такое четное число?
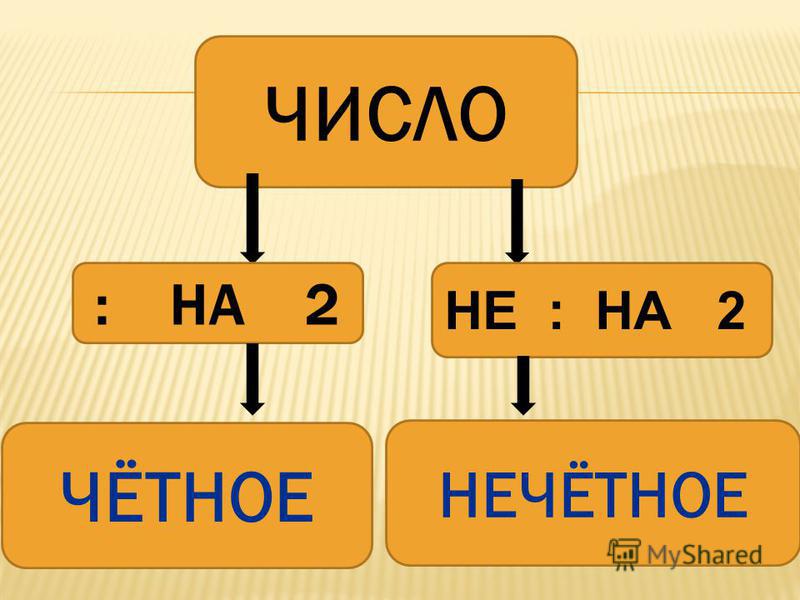
Четным числом называют любое целое число, которое делиться на два нацело. Для того, чтобы лучше понять, какие числа относятся к четным, вспомним классификацию чисел по множествам.
Ноль в натуральные числа не входит, а потому первое множество чисел, где встречается ноль – целые числа.
Формула четного числа
Существует формула четного числа, она выглядит так:
k=2m – где k – четное число, m – любое целое число. Если любое целое число подставить в формулу, то результатом будет всегда четное значение.
Можно обратить внимание на число 2 в формуле, именно это значение делает любой конечный результат формулы четным. Так же есть формула нечетного числа: k=2m+1.
Сколько всего четных чисел?
Полного списка четных чисел нет и никогда не будет. Как мы помним, чисел – бесконечное множество. Это значит, что четных чисел так же бесконечно много. Но часто у учеников возникает вопрос: сколько существует четных цифр.
Список четных цифр привести можно: 0,2,4,6,8 – всего пять значений.
Четные числа на числовой прямой
Еще один интересный вопрос в изучении темы, это четные числа на числовой прямой. Интересно посмотреть, являются ли отрицательные числа и ноль – четными. Ответ прост – да, являются. Исходя из определения, мы знаем, что четным числом может быть только целое значение. Попробуем подставить в формулу четных чисел 0:
k=2*0=0
Значение нуля сохранилось, а значит ноль – число четное.
Теперь подставим в формулу целое отрицательное число:
k=2*(-5)=-10 – получилось отрицательное число, то есть отрицательные числа так же могут быть четными. Это значит, что на числовой прямой, четные числа расходятся в обе стороны от нуля, а так же число ноль является четным числом.
Что мы узнали?
Мы поговорили о четных числах. Разобрались, сколько четных чисел существует в математике. Привели формулу четного числа.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
Алина Шабунина
5/5
Майрам Мажидова
4/5
Новиков Елисей
5/5
Лира Нургалиева
5/5
Алексей Кабанов
5/5
Захар Никулин
5/5
Лизочка Толстых
4/5
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 541.
А какая ваша оценка?
Деятельность по изучению и исследованию закономерностей
Обзор страницы :
- Обзор
- Концепции и результаты
- Концепции и результаты содержания по математике и естественным наукам
- Решение проблем и исследование концепций и результатов
- Педагогические идеи
- Последовательность действий
- Основные вопросы
- Связанные ресурсы
- Ресурсы расширения
- Виды деятельности
- Группы пар – четные, нечетные, кратные трем
- Группы квадратов – четные и нечетные группы квадратов
- Нечетные и четные бусины – группы бусин
- В-образные формы – нечетные формы
- Четные и нечетные числа
- Суперчетные числа
- Идеи расширения
Очень маленькие учащиеся распознают четные и нечетные модели.
На этой странице содержится информация о планировании и использовании действий для нечетных, четных и сверхчетных шаблонов и чисел. Он включает в себя понятия по математике для: шаблонов, алгебры, представления, диаграмм, геометрии, решения проблем, рассуждений, визуального представления,
Паттерн — повторяющийся дизайн, последовательность, структура, изменение свойств, формы, положения или изменение количества.
Концепции и результаты
Математическая
Понятия
- Шаблоны могут быть представлены словами, изображениями, символами, числами, таблицами, диаграммами, диаграммами, графиками, уравнениями, формулами, моделями, симуляциями, анимацией, видео
- Различные способы передачи и представления паттернов имеют разные преимущества.
- Четное число, которое можно без остатка разделить на два.
- Нечетное число, у которого при делении на два остается единица.
- Пары — это группы по два человека.
- Расположение и симметричность узоров можно использовать для идентификации четных и нечетных групп.
- Даже шаблоны могут быть описаны как пары.
- Четный и нечетный номинал
- Формула — это уравнение, которое устанавливает правило относительно шаблона.
- Последовательность — это порядок, в котором числа или предметы следуют друг за другом.n
- Суперчетные числа — это числа, при многократном делении которых на два получается частное, равное единице.
База знаний о математических концепциях, заблуждениях и результатах
- Анализ данных
- Шаблоны и алгебра
Результаты
- Определить закономерность и сгруппировать ее как четную или нечетную.
- Расширение шаблонов.
- Рассуждайте и объясняйте узоры как нечетные или четные, используя пары, симметрию, четные и нечетные числа, символы и другие визуальные и невизуальные представления.
- Определите и используйте правила для создания и расширения четных и нечетных шаблонов.
Решение проблем и исследование концепций и результатов
- Решение проблем
- Дознание и расследование
Педагогические идеи
Последовательность действий
- Группы пар – четные, нечетные, кратные трем
- Группы квадратов – четные и нечетные группы квадратов
- Нечетные и четные бусины – группы бусин
- В-образные формы – нечетные формы
- Четные и нечетные числа
- Суперчетные числа
- Идеи расширения
Основные вопросы
- Что такое пара?
- Какие группы образуют пары?
- Что четное?
- Что странного?
- Какие группы не образуют пары?
Связанные ресурсы
- Задачи по сохранению и оценке
- Пустой лист диаграммы
- Нечетное плюс нечетное три способа: конкретный, полуконкретный (знаковый), абстрактный
- Обучающее видео – доказательство нечетного + нечетного четного конкретно
- Шаблоны
Действия
Группы пар
Какие из групп пар нечетные, а какие четные?
Объясните, как вы определили, что четно, а что нечетно.
Объясните, что убеждает вас в равноправии группы.
Объясните, что убеждает вас в том, что группа странная.
Нечетные и четные квадраты
Для каждого из этих шаблонов покажите, какие из них четные, а какие нечетные без счета.
Четные шаблоны:
Нечетные шаблоны:
Откуда вы знаете?
Нечетные и четные бусины
Для каждой группы бусинок покажите, какие группы четные и нечетные без счета.
Четные шаблоны:
Нечетные шаблоны:
Откуда вы знаете?
V-образные формы
Ниже приведены четыре V-образные формы.
V-образные формы нечетные или четные?
Введите количество точек в каждом шаблоне в таблице.
Номер шаблона | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Количество точек |
Сколько точек в следующем узоре V?
Можно ли сделать V-образный узор из 100 точек?
Сколько точек в шестом образце V?
Числа четные и нечетные
Номера цветового кода четные и нечетные.
- Начните с нуля и напишите числа на пути.
- Раскрасьте блоки с четными номерами в один цвет, а блоки с нечетными номерами в другой цвет.
Что общего у чисел разного цвета?
Задумайте число, которое не находится на пути.
Какого цвета она была бы, если бы была?
Выберите один из цветов, которые вы использовали, и напишите правило для описания этих чисел?
Каково правило для остальных чисел?
Как узнать, какого цвета большее число, например 321?
Подсказка
Правила могут быть созданы с начальным номером, номером операции и номером изменения.
Пуск – работа – изменение
- 0 + 2
- (0 + 2) + 2
- (0 + 2 + 2) + 2
- (0 + 2 + 2 + 2) + 2
Суперчетные числа
Числа являются суперчетными, если их можно представить четными группами пар.
- Напишите четные числа на пути.
- Color perfect даже номера одного цвета.
Сколько суперчетных чисел меньше 100? … 1000?
Шаблоны четных и нечетных квадратов
Используйте приведенные ниже квадраты для рисования различных фигур с разным количеством квадратов. Затем решите, четное или нечетное количество квадратов в каждом шаблоне. Как насчет всех узоров вместе?
Заметки доктора Роберта Суитленда
[Домашняя страница: homeofbob.com & thehob.net]
Как учить нечетные и четные числа без рабочих листов
Обучение четным и нечетным числам часто рассматривается как навык «могут ли они» или «не могут ли они». Могут ли они определить нечетные числа? Могут ли они определить четные числа? И хотя распознавание нечетных и четных чисел важно, наше внимание должно быть сосредоточено на понимании моделей нечетных и четных чисел, а также на той роли, которую нечетные и четные числа играют в реальной жизни.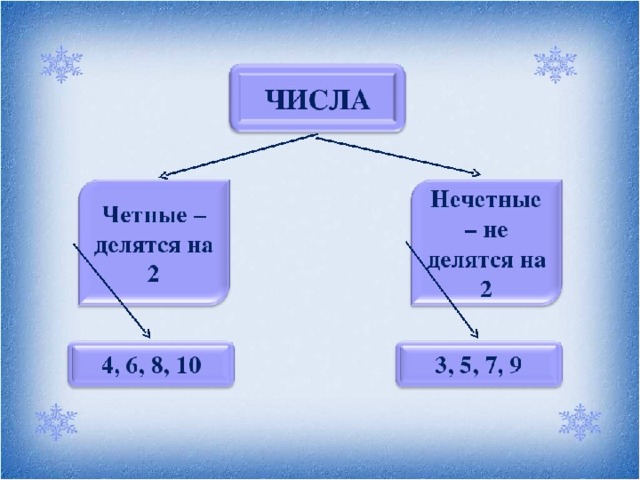
Когда вы думаете о четных и нечетных числах, что первое приходит на ум? Вот некоторые из них, которые всплывают у меня во взрослом возрасте:
- Четные числа можно расположить парами, а нечетные всегда имеют одно лишнее
- другая сторона
- При счете есть закономерность: нечетный, четный, нечетный, четный, нечетный, четный… и т.д.
- Нечетное количество учеников в классе — проблема для партнерской работы!
- Когда вы выстраиваете объекты в ряд, нечетное количество объектов будет иметь один объект в центре
- Четные числа заканчиваются на 0, 2, 4, 6 и 8
- Нечетные числа заканчиваются на 1, 3, 5, 7, и 9
Некоторые из этих фактов являются математическими фактами, связанными с нечетными и четными числами, но некоторые из них являются реальными связями. Нечетные и четные числа находят применение во многих областях математики, а также в реальной жизни. Важно, чтобы мы давали учащимся время изучить их и понять, как они выглядят в контексте.
Прежде чем мы начнем с четных и нечетных чисел
Подготовьте сцену
Я хочу, чтобы вы знали заранее, что идеи, которыми я собираюсь поделиться, не являются идеями, когда вы будете планировать и готовить рабочие листы или центральные действия. Я нашел ЛУЧШИЙ подход к обучению четным и нечетным числам путем исследования и обсуждения.
Это означает, что мы не можем точно планировать, что мы делаем каждый день, так как мы позволяем нашим ученикам руководить нами. Тем не менее, у нас может быть набросок и запланированные действия, чтобы создать основу нашей исследовательской единицы, которую я попытаюсь представить в этой статье.
Не говорите «четные» и «нечетные»
Одна вещь, которую я хочу сказать, прежде чем я перейду к своим любимым способам изучения нечетных и четных чисел со студентами: Я никогда не использую слова «четные» и «нечетные». до начала наших исследований . Вместо этого я позволяю учащимся исследовать закономерности и органично замечать понятия «нечетных» и «четных» чисел.
Только после того, как учащиеся определили понятия «нечетное» и «четное», как они это понимают, я даю им математические имена для обозначения их идей.
Органическое введение
Существует множество естественных возможностей для начала изучения нечетных и четных чисел. Вот несколько способов, которыми это началось в моем собственном классе:
- Повернуться и поговорить со сверстником (у нас было нечетное количество учеников, поэтому один ученик заговорил со мной)
- Разделить класс на пары для игры (один день работало ровно, а на следующий день студент отсутствовал, так что группа должна была стать трио)
- Пыталась разделить коллекцию между двумя студентами, но остался один больше
- Изучаем удвоения и замечаем, что каждое второе число является суммой удвоения (2, 4, 6, 8… и т. д.) надо быть начеку. Если вы действительно боретесь, вы всегда можете искусственно создать возможность начать свое исследование.
Начало работы
Допустим, вы использовали пример, когда учащиеся пытались разделить сумму поровну, но осталась одна сумма.
Есть несколько следующих шагов, которые вы могли бы предпринять, чтобы начать свое исследование, но, скорее всего, все они начнутся с наводящего вопроса (чуть позже я углублюсь в наводящие вопросы).Вы можете спросить: «Это всегда происходит? Когда вы делите что-то между двумя людьми, всегда ли остается что-то одно?» Независимо от их ответа (потому что вы, скорее всего, получите диапазон), вы можете продолжить с «Интересно, есть ли способ, которым мы могли бы проверить?»
Это идеальный сегвей для ваших исследований!
Совместное использование четных и нечетных чисел
Поскольку мы начали со сценария двух студентов, пытающихся поделиться объектами, я бы сделал свое первое исследовательское задание, непосредственно связанное с этим сценарием.
Материалы
Для этого исследования я даю учащимся полоску бумаги с написанными на ней числами. В зависимости от вашего уровня обучения ваши номерные полосы будут выглядеть по-разному. Это может быть 1-6, 1-10, 1-20 или сотня.
Вы также можете легко различать, предлагая разные полоски разным ученикам.Я предлагаю учащимся различные манипуляторы на выбор для этого занятия (контролируемый выбор может быть отличным мотиватором!):
- Бобы
- Кубики Unifix
- Камни-“самоцветы”
- Жетоны животных
- Мини-ластики
- Двусторонние жетоны
- Практически любые мелкие предметы, которые не могут кататься исследовать. Некоторые из ваших учеников захотят быть систематическими и начнут с одного. Другие студенты выбирают свои номера случайным образом. Это хорошо!
Если ученик решает начать с восьми, его задача состоит в том, чтобы отсчитать восемь своих манипуляций. Затем они работают, чтобы разделить это число на две равные группы. Если они могут разделить число на две равные группы, они обводят число на своей полосе с номером. Если они не могут, они ставят «x» через него.
На этом первом шаге не говорите учащимся, КАК разделить стопку поровну (т.
е. не моделируйте для них этот шаг). Позвольте учащимся сначала поэкспериментировать с разработкой собственных стратегий. Мы можем собраться вместе примерно через 5-10 минут, чтобы зарегистрироваться и позволить учащимся поделиться своими стратегиями друг с другом. Затем учащиеся могут вернуться к своей работе и, возможно, использовать более эффективную стратегию, которую они изучили.Дайте учащимся время изучить несколько чисел. Это может быть как совместное упражнение, так и самостоятельное. Если ваши ученики моложе и/или у них недостаточно внимания, чтобы делать это в течение длительного периода времени, подумайте о том, чтобы разбить его на два разных периода времени или в течение двух дней.
Обсуждение
Обсуждение — это место, где мы начинаем синтезировать идеи, которые сформировались во время исследования. Попросите учащихся принести группе свои полоски с цифрами. Разместите на доске или на полу собственную полосу с большими цифрами, чтобы учащиеся могли ее видеть.
Когда все расселены, пора просить добровольцев. Позвольте учащимся выбрать одно число, которое они исследовали, и сообщите группе, смогли ли они поделиться им или нет. Затем вы можете спросить группу, пробовал ли кто-нибудь еще этот номер и получил ли он такой же результат. Это важный шаг, потому что вполне вероятно, что у вас будут учащиеся, которые неточно подсчитали или поделились своими счетчиками. Когда вы заметили ошибку, это отличный шанс вернуться к этому числу со всей группой и сделать это вместе.
Совет для профессионалов: отметьте кружки другим цветом, чем крестики. Это может лучше помочь учащимся визуально различать их.
После того, как вы отметили все числа от 1 до 10, посмотрите, заметит ли кто-нибудь из ваших учеников какие-либо закономерности. Если они не делают эти наблюдения самостоятельно, спросите : «Что вы заметили в этих числах?»
Когда учащиеся смогут замечать схему ABAB: нечетный, четный, нечетный, четный, мы можем дополнительно проверить их с помощью таких вопросов, как — Думаешь, это всегда работает?
Пусть учащиеся расскажут, всегда ли, по их мнению, эта закономерность верна, а затем спросят: «Как мы можем это проверить?» Это может помочь вам в следующем исследовании!
Дополнительные визуальные способы изучения нечетных и четных чисел
Разделение суммы на две группы — это только один из способов изучения нечетных и четных чисел.
Есть так много красивых изображений, которые учащиеся могут использовать для изучения чисел. Мы можем углубить понимание учащимися, если позволим им создать несколько изображений одной и той же идеи и соединить эти разные представления.Нечетные и четные числа с десятью рамками
Предоставление учащимся возможности использовать десять рамок для исследования нечетных и четных чисел — отличный способ подчеркнуть идею «одного лишнего» нечетных чисел. Это означает, что мы собираемся заполнить кадр иначе, чем когда мы пытаемся использовать 5 в качестве эталона для десяти. В этом упражнении мы заполняем массив цифрами 2, а не 5 и 5.
Удивительно видеть, как их моменты «ага» возникают благодаря использованию такого знакомого математического манипулятора/организатора. Совместное создание якорной диаграммы после исследования — отличный способ записать полученные знания и вернуться к ним позже.
Нечетные и четные числа с башнями
Я люблю строить башни с узорами вместе со своими учениками, чтобы изучать нечетные и четные числа.
Для этого задания вам понадобятся два соединительных кубика разного цвета. Если у меня есть синие и оранжевые кубики, мне нужно выбрать один для начала. Я буду использовать этот цвет в качестве основания моей башни каждый раз.Моей первой башней будет один синий куб. Но моя вторая башня будет синим кубом с оранжевым кубом наверху. Тогда моя третья башня будет синей, оранжевой, синей. Вы видите, куда это идет?
Мне нравится, что это усиливает шаблон четных и нечетных чисел ABAB. Они могут видеть, как цвета меняются взад и вперед, и что вершины их башен меняют цвет от одного к другому.
Четные и нечетные числа с помощью игральных костей
Глядя на игральные кости, ученики могут увидеть, как четные и нечетные числа представлены в повседневных предметах. Многие могут заметить, что нечетные числа на костях имеют точку посередине, а четные числа — нет.
Создание узоров из точек после шести (но с использованием этой идеи средней точки для нечетных чисел) также является очень интересным упражнением для учащихся.
Я очень рекомендую это!Браслеты против часов
Я никогда не забуду, как мой специалист по математике рассказала мне о своей работе в детском саду. Студенты делали наручные часы из маленьких вырезанных кружочков. Не владея языком «четных» и «нечетных», они все же смогли понять и объяснить, что могут делать часы только с определенными числами (коэффициентами). Почему?
Ну, нечетные числа будут иметь одинаковое количество кругов с каждой стороны, а затем ОДИН в середине, который может быть циферблатом часов. Даже цифры могли быть только браслетом, потому что у них не было «центра», чтобы сделать из них часы. Гениально, верно?
В течение нескольких дней (возможно, недель) ученики называли их номерами часов и номерами браслетов. Эти термины имели для них огромное значение. «Нечетный» и «четный» были представлены только тогда, когда ученик со старшим братом или сестрой упомянул об этом. Перенос понимания на эти новые термины был БОЛЬШИМ, и все потому, что им было дано время для глубокого изучения этих чисел.
Расширения для нечетных и четных чисел
В зависимости от вашего уровня обучения учащиеся начнут замечать дополнительные закономерности в нечетных и четных числах:
- Числа, оканчивающиеся на 0, 2, 4, 6 и 8, всегда четные
- Числа, оканчивающиеся на 1, 3, 5, 7 и 9, всегда нечетные )
- Нечетный + Нечетный = Четный (то же верно для вычитания)
- Нечетный + Четный = Нечетный (то же верно для вычитания)
- Нечетный x Нечетный = Нечетный
- Нечетный x Четный = Четный
- С учетом того, что кратные определенным числам всегда будут четными
- С учетом того, что все простые числа (кроме 2) будут нечетными
Если учащиеся сталкиваются с этими шаблонами, важно исследовать их мышление, как мы это делали раньше. «Ты думаешь, это всегда так? Как мы можем проверить?»
Нечетные и четные числа в контексте
Возвращаясь к началу этой статьи, важно, чтобы мы всегда давали математический контекст.
Есть несколько следующих шагов, которые вы могли бы предпринять, чтобы начать свое исследование, но, скорее всего, все они начнутся с наводящего вопроса (чуть позже я углублюсь в наводящие вопросы).
Вы также можете легко различать, предлагая разные полоски разным ученикам.
е. не моделируйте для них этот шаг). Позвольте учащимся сначала поэкспериментировать с разработкой собственных стратегий. Мы можем собраться вместе примерно через 5-10 минут, чтобы зарегистрироваться и позволить учащимся поделиться своими стратегиями друг с другом. Затем учащиеся могут вернуться к своей работе и, возможно, использовать более эффективную стратегию, которую они изучили.
Есть так много красивых изображений, которые учащиеся могут использовать для изучения чисел. Мы можем углубить понимание учащимися, если позволим им создать несколько изображений одной и той же идеи и соединить эти разные представления.
Для этого задания вам понадобятся два соединительных кубика разного цвета. Если у меня есть синие и оранжевые кубики, мне нужно выбрать один для начала. Я буду использовать этот цвет в качестве основания моей башни каждый раз.
Я очень рекомендую это!
