Какие четные числа: Чётные и нечётные числа — урок. Математика, 2 класс.
Что такое «четные» и «нечетные» числа | Новости Горного Алтая
Числа всегда оказывали влияние на человека. Нумерологи искали совпадения и пытались выяснить, каким образом число влияет на судьбу и будущее. Философы, математики и мыслители – это другое дело. Они старались выявить закономерность и определить, какие числа оказывают влияние, проводили многочисленные вычисления и составляли таблицы. Но есть еще и простые люди, которые верили в различные сказания и сказки. Они старались найти объяснение тому, почему в сказках всегда три героя или есть цифра «семь». курсы по математике позволят подтянуть свои знания в этой области и узнать много всего интересного. А мы сегодня поговорим про четные и нечетные числа.
Понятие «четность» и «нечетность»
Если в более сознательном возрасте мы прекрасно понимаем, о чем речь, то школьникам не так просто во всем разобраться, хоть дома и в дошкольных учреждениях они слышали понятия.
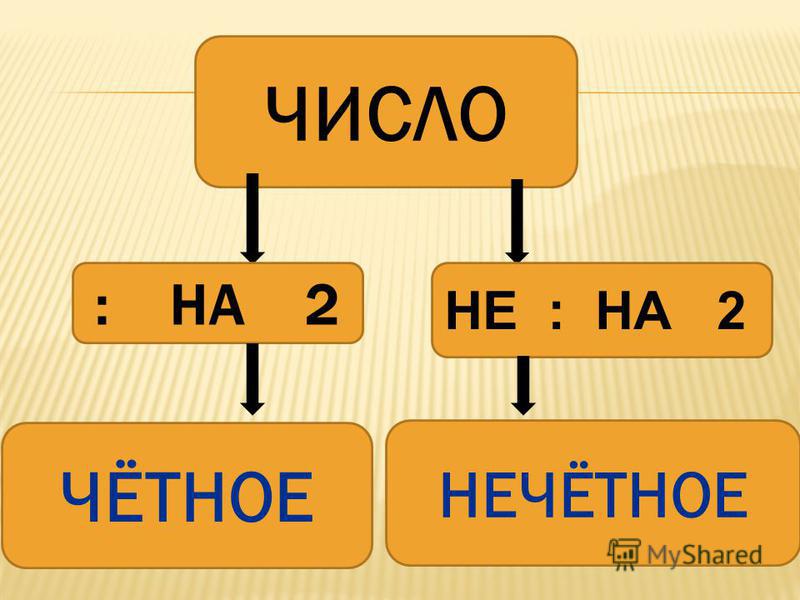
Четными числами называют целые числа, которые можно с легкостью разделить на два и получится целое число без какого-либо остатка.
Что касается нечетных чисел, то их поделить без остатка не получится.
Понять подобное разграничение проще на примерах. Что касается школ, то учителя стараются объяснить «четность» и «нечетность» на съедобных примерах, чтобы детям было проще во всем разобраться.
К примеру, учитель говорит, что перед учеником лежит пять яблок. И каким образом их можно разделить на половину?
Ученик начинает думать, каким образом у него получится разделить. В итоге он приходит к выводу, что разделить поровну не получится, потому что одно яблоко будет лишним, и чтобы у всех было все одинаково, нужно одно яблоко разделить ровно на половину. В результате остается остаток.
После этого учитель может предложить разделить шесть яблок пополам. Ученик без проблем это сделает, потому что каждой стороне достанется ровно по 3-и яблока.
Чтобы понять, каким образом расположены четные и нечетные числа, стоит внимательно посмотреть на цифровой ряд. Они будут между собой чередоваться. К примеру, 1- нечетное число, следующее число 2 и оно уже будет четным.
Числа чередуются между собой, и запомнить все не составит труда.
Постепенно стоит переходить к двухзначным, а после и к трехзначным числам. Если проводить занятия регулярно, то все это можно довести до автоматизма.
Немного истории
Если заглянуть в историю, то становится понятно, что данные понятия пришли к нам из глубокой древности. На первых порах люди придавали этому мистические значения. У каждого народа были свои традиции, которые были связаны с числом цветов, которые дарили друг другу. Несмотря на то, что прошло много времени и люди стали современными, традиции, связанные с четностью и нечетностью так и остались. К примеру, на территории Европы считают, что подарив человеку четное количество цветов, можно подарить ему счастье. Такой букет приносит радость и благополучие.
На территории нашей страны все совершенно иначе. Четное количество цветов приносят только на кладбище. Живому человеку не принято дарить 2-а или 4-е цветка. Букеты составляются с нечетным количеством цветов.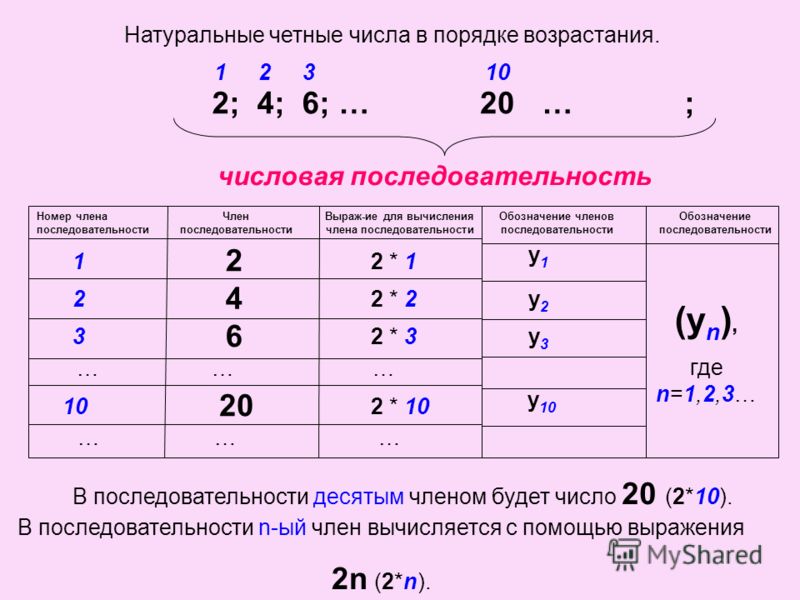
Подобная традиция имеет историческое обоснование. Ученые считают, что связано это с язычеством. Наши предки считали, что все четные числа связаны со злом и приносят смерть. Именно поэтому и стали дарить четное количество цветов, чтобы отогнать все несчастья.
Во многих древних культурах парные числа обозначают стандартную закономерность. Они связаны с завершением и это завершение непрерывно связано с жизнью. К примеру, какие-то народы боятся числа 13-ть, а какие-то считают, что оно приносит счастье и успех.
Стоит отметить, что все нечетные числа нестабильны. Они говорят человеку о том, что нужно двигаться. А вот четные приносят покой и умиротворение.
Четные и нечетные числа
Во вселенной существуют пары противоположностей, которые являются важным фактором ее устройства. Основные свойства, которые нумерологи приписывают четным (1, 3, 5, 7, 9) и нечетным (2, 4, 6, 8) числам, как парам противоположностей, следующие:
1 – активный, целеустремленный, властный, черствый, руководящий, инициативный;
2 – пассивный, восприимчивый, слабый, сочувствующий, подчиненный;
3 – яркий, веселый, артистичный, удачливый, легко добивающийся успеха;
4 – трудолюбивый, скучный, безынициативный, несчастный, тяжелый труд и частое поражение;
5 – подвижный, предприимчивый, нервный, неуверенный, сексуальный;
6 – простой, спокойный, домашний, устроенный; материнская любовь;
7 – уход от мира, мистика, тайны;
8 – мирская жизнь; материальная удача или поражение;
9 – интеллектуальное и духовное совершенство.
Нечетные числа обладают гораздо более яркими свойствами. Рядом с энергией “1”, блеском и удачливостью “3”, авантюрной подвижностью и многогранностью “5”, мудростью “7” и совершенством “9” четные числа выглядят не столь ярко. Насчитывается 10 основных пар противоположностей, существующих во Вселенной. Среди этих пар: четное – нечетное, один – много, правое – левое, мужское – женское, добро – зло. Один, правое, мужское и доброе ассоциировалось с нечетными числами; много, левое, женское и злое – с четными.
Нечетные числа обладают некой производящей серединой, в то время как в любом четном числе есть воспринимающее отверстие как бы лакуна внутри себя. Мужские свойства фаллических нечетных чисел вытекают из того факта, что они сильнее четных. Если четное число расщепить пополам, то, кроме пустоты, посередине ничего не останется. Нечетное число разбить непросто, потому что посередине остается точка. Если же соединить вместе четное и нечетное числа, то победит нечетное, так как результат всегда будет нечетным.
Именно поэтому нечетные числа обладают мужскими свойствами, властными и резкими, а четные – женскими, пассивными и воспринимающими.
Нечетных чисел нечетное число: их пять. Четных чисел четное число – четыре.
Нечетные числа – солнечные, электрические, кислотные и динамичные. Они являются слагаемыми; их с чем либо складывают. Четные числа – лунные, магнетические, щелочные и статичные. Они являются вычитаемыми, их уменьшают. Они остаются без движения, потому что имеют четные группы пар (2 и 4; 6 и 8).
Если мы сгруппируем нечетные числа, одно число всегда останется без своей пары (1 и 3; 5 и 7; 9). Это делает их динамичными. Два подобных числа (два нечетных числа или два четных) не являются благоприятными.
четное + четное = четное (статичное) 2+2=4
четное + нечетное = нечетное (динамичное) 3+2=5
нечетное + нечетное = четное (статичное) 3+3=6
Некоторые числа дружественны, другие – противостоят друг другу. Взаимоотношения чисел определяются отношениями между планетами, которые ими управляют (подробности в разделе “Совместимость чисел”).
Когда два дружественных числа соприкасаются, их сотрудничество не очень продуктивно. Подобно друзьям, они расслабляются – и ничего не происходит. Но когда в одной комбинации находятся враждебные числа, они заставляют друг друга быть настороже и побуждают к активным действиям; таким образом, эти два человека работают намного больше. В таком случае, враждебные числа оказываются на самом деле друзьями, а друзья – настоящими врагами, тормозящими прогресс. Нейтральные числа остаются неактивными. Они не дают поддержки, не вызывают и не подавляют активность.
Знать определение, список от 1 до 100, свойства здесь
Четные числа противоположны нечетным числам. Определение четных и нечетных чисел является важным навыком, которому дети должны научиться, чтобы лучше понять нашу систему счисления и подготовиться к операциям с целыми числами. Это также поможет детям в изучении деления, простых чисел и квадратных корней. В этой статье мы изучим, что такое четные числа, определение четных чисел, список четных чисел, четные числа от 1 до 100, нечетные и четные числа, сумму четных чисел, сумму первых n четные числа , медиана четных чисел, что такое четное простое число, свойства четных чисел, примеры решения четных чисел и часто задаваемые вопросы
четные числа четные числа являются частью системы счисления.
Понимание четных чисел является базовой математикой и важной темой алгебры. Все числа, оканчивающиеся на 0, 2, 4, 6 и 8, являются четными числами . Например, такие числа, как 14, 26, 32, 40 и 88, являются четными числами. Если мы разделим число на две группы с равным количеством элементов в каждой, то число будет четным числом. Понятие четных чисел преподается в начальной школе для детей, чтобы различать четные и нечетные числа. С другой стороны, нечетные числа — это целые числа, которые не делятся на 2 или оканчиваются на 1, 3, 5, 7 и 9..
Четное число — это целое число, которое можно разделить на два на два равных целых числа Числа 0, 2, 4, 6 и 8 — четные числа. Список четных чисел бесконечен, потому что счет продолжается до бесконечности. Любое число, которое точно делится на 2, называется четным числом. т. е. если число при делении на 2 не оставляет остатка, то число называется четным числом.
Как узнать, четное число или нечетное? Четное число — это число, которое делится на два и оставляет 0 в остатке.
Число, которое не делится на два, называется нечетным числом. В случае нечетного числа остаток всегда равен «1». Четность — это качество, которое позволяет нам классифицировать целое число как четное или нечетное в математике.
В системе счисления есть два вида чисел: натуральные числа и целые числа. Натуральные числа можно определить как основные счетные числа, начинающиеся с 1, а целые числа — это набор чисел, начинающийся с 0.
Следовательно, наименьшее четное целое число равно 0, а наименьшее четное натуральное число равно 2. 2 также является единственным четным простым числом.
Изучите различные концепции биномиальной теоремы здесь.
Список четных чисел Мы можем легко определить четное число в диапазоне от 1 до 10, от 1 до 20, от 1 до 50 и от 1 до 100. Знание четного числа в этих диапазонах поможет вам решить многие математические задачи. Вы можете легко решать такие задачи, как GCD, LCM, факторизация и т.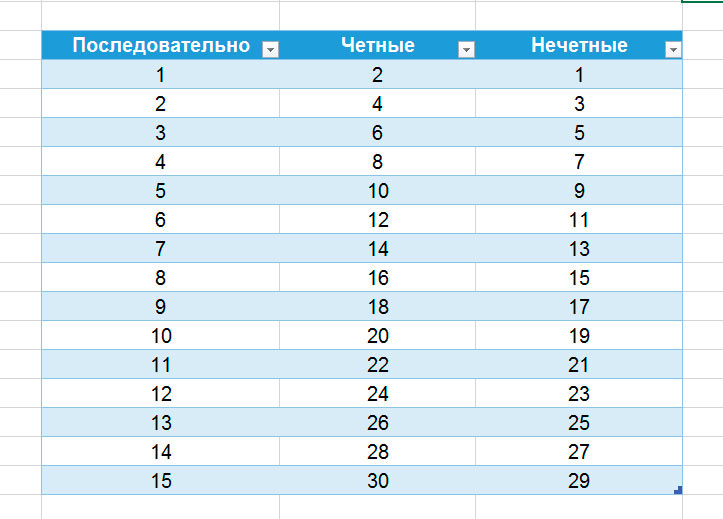
д.
Существует пять четных чисел от 1 до 10. Список четных чисел от 1 до 10: 2, 4, 6, 8 и 10.
| Even Numbers from 1-10 |
| 2 |
| 4 |
| 6 |
| 8 |
| 10 |
Есть 10 четных чисел до 20. Список четных чисел от 1 до 20: 2, 4, 6, 8, 10, 12, 14, 16, 18 и 20
| Even Numbers from 1-20 | |
| 2 | 12 |
| 4 | 14 |
| 6 | 16 |
| 8 | 18 |
| 10 | 20 |
Всего 25 четных чисел до 50.
Список четных чисел от 1 до 50: 2, 4, 10, 6, 8, 8, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48 и 50.
| Even Numbers from 1-50 | ||||
| 2 | 12 | 22 | 32 | 42 |
| 4 | 14 | 24 | 34 | 44 |
| 6 | 16 | 26 | 36 | 46 |
| 8 | 18 | 28 | 38 | 48 |
| 10 | 20 | 30 | 40 | 50 |
Свойства четных чисел Некоторые из важных свойств четных чисел приведены ниже:
Свойство сложения четных чиселДавайте разберемся со свойствами сложения четных чисел ниже:
- 9 Свойство сложения двух четных чисел: Это свойство утверждает, что при сложении двух четных чисел результатом всегда будет четное число. Например. 10 + 4 = 14
- Свойство сложения одного нечетного и одного четного числа: Это свойство указывает, что при сложении четного и нечетного числа результат всегда будет нечетным. Например. 9 + 4 = 13
- Свойство сложения двух нечетных чисел: Это свойство утверждает, что при сложении двух нечетных чисел всегда получается четное число. Например. 7 + 3 = 10
Давайте разберемся со свойствами вычитания четных чисел ниже:
- Свойство вычитания двух четных чисел: Это свойство указывает, что при вычитании двух четных чисел результатом всегда будет четное число.
Например. 10 – 4 = 6 - Свойство вычитания одного нечетного и одного четного числа: Это свойство утверждает, что при вычитании четного и нечетного числа результат всегда будет нечетным. Например. 9 – 4 = 5
- Свойство вычитания двух нечетных чисел: Это свойство утверждает, что при вычитании двух нечетных чисел всегда получается четное число. Например. 7 – 3 = 4
Например. 10 – 4 = 6Давайте попробуем узнать свойства умножения четных чисел ниже:
- Свойство умножения двух четных чисел: Это свойство утверждает, что при умножении двух четных чисел , результатом всегда будет четное число. Например. 10 × 4 = 40
- Свойство умножения одного нечетного и одного четного числа: Это свойство гласит, что при умножении четного числа на нечетное число всегда получается четное число. Например. 7 × 6 = 42
- Свойство умножения двух нечетных чисел : Это свойство гласит, что при умножении двух нечетных чисел всегда получается нечетное число. Например. 7 × 5 = 35
Например. 7 × 5 = 35Разница между нечетным числом и четным числом составляет следующее:
| нечетные числа | Даже числа | .| Целое число, которое нельзя разделить на 2, является нечетным числом | Целое число, которое можно разделить на 2, является четным числом. | При делении на нечетное число остается напоминание 1 | При делении на четное число остается напоминание 0 | Все числа, оканчивающиеся на 1, 3, 5, 7 и 9, являются нечетными. | Все числа, оканчивающиеся на 0, 2, 4, 6 и 8, являются четными числами. | Нечетные числа не могут быть сгруппированы в пары. | Четные числа можно объединять в пары. | Если последняя цифра заданного числа нечетная, число нечетное. | Если последняя цифра заданного числа четная, то число четное. |  |
Простые числа — это положительное целое число, которое не делится без остатка ни на одно целое число, кроме самого себя и 1. Простое число не может делиться ни на какие другие числа без остатка. За исключением числа 2, все простые числа нечетные, так как четное число делится на 2, что делает его составным. Следовательно, расстояние между любыми двумя простыми числами в строке не меньше 2,9.0005
Прочтите эту статью о среднем арифметическом.
Решенные примеры для четных чиселТеперь давайте посмотрим некоторые решенные примеры для четных чисел, которые часто задают на многих экзаменах.
Q1: Здесь объясняются примеры четных и нечетных чисел. Являются ли следующие числа четными или нечетными? 18, 22, 35, 165
Решение:
Мы знаем, что четные числа делятся на 2. Итак, давайте проверим приведенные выше числа для теста на делимость.
18: Мы знаем, что 9 x 2 = 18. Следовательно, 18 четно.
22: Мы знаем, что 11 х 2 = 22. Следовательно, 22 четно.
35 : 35 не делится на 2. Следовательно, 35 нечетно.
165: 165 не делится на 2. Следовательно, 165 нечетно.
Q2: Какова медиана 1, 2, 3, 4, 5, 6, 7, 8, 9, 10?
Решение:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
Ясно, что число членов четно, и два числа, разделяющие все множество 5 и 6.
Медиана = (5+6) / 2
= 11/ 2
= 5,5
Следовательно, медиана ряда равна 5,5.
Q3: Верно или неверно: число 341 — четное число.
Решение: 341 не делится на 2. Значит, 341 не четное число. Итак, приведенное выше утверждение неверно.
Q4: Выберите правильный ответ. Сумма двух четных чисел
- всегда будет четным числом
- всегда нечетное число
- иногда бывает нечетным, а иногда четным
- может быть ни нечетным, ни четным
результат всегда четное число.
Например,
10 + 4 = 14
Следовательно, правильный ответ – вариант 1. Четное число + Четное число = Четное число
В5: Как проверить, является ли число четным или нечетным?
Решение:
Есть два способа определить, четное число или нечетное. Они следующие:
Метод 1. В местоположении единицы проверьте цифру числа:
Чтобы определить, является ли число нечетным или четным, мы должны проверить его на месте «единицы» или «единицы». или последняя цифра номера.
Нечетные числа — это те, которые заканчиваются цифрами 1,3,5,7 и 9.
7,11,283,5735,9859 и так далее.
Данное число является нечетным, так как число 2835 заканчивается цифрой 5 (нечетное число).
Кроме того, четными считаются числа, оканчивающиеся цифрами 0, 2, 4, 6 и 8.
Данное число является четным, поскольку число 2838 оканчивается цифрой 8 (четное число).
Способ 2.
По группировке:
Всего на этой картинке 11 точек. Все точки не связаны. На картинке не хватает одной точки.
Нечетные числа — это числа, которые нельзя поставить вместе парами.
Нечетные числа — это любые числа, которые не делятся точно на два.
Теперь 12 точек. Поскольку все точки парные и не осталось ни одной непарной точки, мы можем сделать вывод, что 12 — четное число.
Мы можем сделать вывод, что четные числа — это все те, которые можно разделить на пары.
Надеюсь, эта статья о четных числах была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
Часто задаваемые вопросы о четных числах
Q.1 Четное или нечетное число?
Ответ 1 Все числа, оканчивающиеся на 0, 2, 4, 6 и 8, являются четными числами. С другой стороны, нечетные числа — это целые числа, которые не делятся на 2 или оканчиваются на 1, 3, 5, 7 и 9.
В.2 Что называется нечетным числом?
Ответ 2 Числа, которые нельзя разделить на пары поровну, называются нечетными.
Q.3 Какое число является четным и простым?
Ответ 3 Простые числа — это положительное целое число, которое не делится без остатка ни на одно целое число, кроме самого себя и 1. Простое число нельзя разделить ни на какое другое число без остатка. За исключением числа 2, все простые числа нечетные, так как четное число делится на 2, что делает его составным.
Q.4 Что не является простым числом?
Ответ 4 Простое число — это натуральное число больше 1, которое не является произведением двух меньших натуральных чисел. Простое число — это положительное натуральное число, имеющее только два положительных натуральных делителя — единицу и само число. Простые числа — это подмножество натуральных чисел.
Q.
5 Как число является четным?
Ответ 5 Четное число — это целое число, которое можно разделить на два на два равных целых числа Числа 0, 2, 4, 6 и 8 — четные числа.
Скачать публикацию в формате PDFОбразец умножения четных и нечетных чисел
Ключевые понятия
- Четные и нечетные числа
- Образцы умножения четных и нечетных чисел
4.5 Образцы умножения: четные и нечетные числа.
Четные числа : Четные числа — это целые числа, которые можно разделить на 2 без остатка.
- В четных числах 0, 2, 4, 6 или 8 стоят на месте единиц.
. Увластное число может быть сформировано только путем умножения тремя способами:
- даже x Odd
- ODD x даже
- даже x даже
нечетные номера 9000: нечетные номера. разделить на 2, чтобы ничего не осталось.
- В нечетных числах 1, 3, 5, 7 или 9 стоят на месте единиц.
Нечетное число может быть образовано путем умножения только одним способом:
- Нечетное x нечетное = нечетное.
4.5.1 Четные и нечетные числа
Четные числа : Четные числа — это целые числа, которые можно разделить на 2 без остатка.
Примеры для четных чисел:
- В четных числах 0, 2, 4, 6 или 8 стоят на месте единиц.
Например: 12, 24, 26, 48, 20
Пример: В таблице выделены четные числа от 1 до 100
Нечетные числа : используйте шаблоны, чтобы понять действие
Пример для нечетных чисел:
- Нечетные числа имеют 1, 3, 5 , 7 или 9 в разряде единиц.
Например: 11, 23, 35, 37, 49.
Пример: В таблице выделены нечетные числа от 1 до 100
4.5.2 Шаблоны умножения четных и нечетных чисел.
Марти говорит, что произведение четного числа на нечетное всегда четно. Он правильный?
Решение:
Четные числа больше 0 можно изобразить двумя равными группами.
Подумайте о 2 x 5 и 2 x 7.
2 – четное число.
2 x 5 означает 2 равные группы по 5.
2 x 5 = 10.
2 x 7 означает 2 равные группы по 7.
2 x 7 = 14.
Всегда есть 2 равные группы.
Обобщение:
Все четные числа кратны 2.
Подумайте о 6 x 3.
Вы можете думать о 6 как о 3 группах по 2.
Используя свойства, мы можем писать.
6 x 3 = (2 x 3) x 3 как
6 x 3 = 2 x (3 x 3)
Таким образом, 6 x 3 = 2 x 9
6 равных групп по 3 = 2 равных группы 9
Итак, изделие будет четным.
Пример 2:
Марти говорит, что произведение двух нечетных чисел всегда нечетно. Он правильный?
Решение:
Нечетное число не может быть разделено на 2 без остатка.
Подумайте о 5 x 7.
5 нельзя разделить на 2 так, чтобы не осталось ни одного.
7 нельзя разделить на 2 без остатка.
35 нечетно.
Оба множителя нечетные.
Нечетные числа нельзя разделить на две равные группы, чтобы не осталось ни одной.
Итак, нечетное число x нечетное число = нечетное число
Упражнение:
- Если умножить два нечетных числа, будет ли произведение четным или нечетным. Объясните на примере?
- 8 х 6 =?
8 можно разделить на 2? ______.
6 можно разделить на 2? _____.
8 x 6 является четным или нечетным.
8 х 6=____. - Обведите четные числа.
4. Определите четные или нечетные числа для приведенных ниже чисел:
5. Майк говорит, что следующие закономерности верны.
а. Нечетное x четное = нечетное
б. Четное x нечетное = четное
Правильно ли он объясняет.
6. Найдите произведение и напишите, четное оно или нечетное.
7. Мерси делает сумки для вечеринки по случаю дня рождения Скайлар. Она кладет 6 мешков по 4 игрушки в каждом. Сколько игрушек положила Мерси?
8.