Как записать условия задачи по математике 4 класс: Краткая запись условия задач в 1-4 классе начальной школы
Страница 86 – ГДЗ Математика 4 класс. Моро, Бантова. Учебник часть 1
- Главная
- ГДЗ
- 4 класс
- Математика
- Моро, Бантова. Учебник
- Числа, которые больше 1000. Умножение и деление
- Страница 86. Часть 1
Вернуться к содержанию учебника
Числа, которые больше 1000. Умножение и деление
Вопрос
395. Два куска одинаковой ткани стоят 360 р. В одном из них 5 м, а в другом – 4 м. Сколько стоит каждый кусок ткани?
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
396.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
397. Определи заранее, сколько цифр должно получиться в записи частного, и выполни деление.
| 6336 : 2 | 58135 : 7 | 251052 : 6 | 136012 : 4 |
| 6336 : 9 | 34472 : 8 | 411258 : 3 | 254105 : 6 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
398. Ребята заполнили водой два больших аквариума: в один они влили 300 л воды, а в другой – 312 л.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
399.
| 23 м 06 см = см | 2355 кг = т кг |
| 1 мин 6 с = с | 62335 кг = т кг |
| 1 ч 45 мин = мин | 584 мм = см мм |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
400.
| 10 км 875 м + 925 м | 17 м 30 см • 6 |
| 12 т 015 кг – 98 кг | 25 ц 80 кг : 3 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
401.
Реши только те уравнения, в которых неизвестное число должно быть найдено делением.
| : 9 = 9000 | 100 • = 6800 | 101 + = 101 |
| • 5 = 4500 | 7000 : = 100 | – 0 = 999 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
402. Вычисли и выполни проверку.
| 1) 201500 : 5 25600 : 8 3070 • 8 |
| 2) 67030 + 15097 + 4378 70100 – 29306 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
403. Во время экскурсии в один автобус сели 48 человек, а в другой – на 6 человек меньше.
Сколько человек должны перейти из первого автобуса во второй, чтобы в них пассажиров стало поровну?
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Вычисли.
| 8 м2 26 дм2 + 74 дм2 | 9 см 2 мм • 5 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Ребусы
Ответ
Поделись с друзьями в социальных сетях:
Вернуться к содержанию учебника
Реши задачи № 153 ГДЗ Математика 4 класс Моро М.
И. – Рамблер/класс Реши задачи № 153 ГДЗ Математика 4 класс Моро М.И. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания “Останкино”?
От двух остановок, расстояние между которыми 1 км, отошли два пешехода. Один из них прошёл 140 м, а другой — 160 м.
Каким стало расстояние между пешеходами?
1) Дополни условие, чтобы чертёж к задаче был таким:
2) Измени условие задачи, чтобы чертёж стал таким:
3) Реши обе задачи и сравни их решения.
ответы
1) …навстречу друг другу.
2) …в противоположных направлениях.
1) 1000 – (140 + 160) = 700 м. Ответ: 700 м.
2) 1000 + (140 + 160) = 1300 м. Ответ: 1300 м.
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
3 класс
5 класс
Репетитор
Химия
похожие вопросы 5
Выполни деление № 60 ГДЗ Математика 4 класс Моро М.И.
Выполни деление с объяснением.
564:4 471 : 3 296 : 2 792 : 4 (Подробнее…)
ГДЗМатематика4 классМоро М.
И.
Answer the following questions.
1. Where and when did the King and the Queen live? (Подробнее…)
ГДЗАнглийский язык4 классВерещагина И.Н.
ЕГЭ Математика 11 класс. Ященко И. В. Тренировочная работа 13 Вопрос 9 Найдите вероятность того, что Толя не выиграет.
Привет. Выручайте с ответом по математике…
Коля и Толя играют в кости. Они бросают кубик по одному разу, выигрывает тот, у кого (Подробнее…)
ЕГЭМатематикаЯщенко И.В.Семенов А.В.11 класс
ЕГЭ Математика 11 класс. Ященко И. В. Тренировочная работа 13 Вопрос 10 Найдите вероятность того, что будут дежурить мальчик и девочка.
Привет всем! Нужен ваш совет, как отвечать…
В классе 12 мальчиков и 13 девочек. 1 сентября случайным образом определяют двух (Подробнее…)
ЕГЭМатематикаЯщенко И.В.
Как вы решили №32.4? Поделитесь гдз по алгебре 7 класс Мордкович?
Разложите многочлен на множители:
а) 7kn – 6k – 14n + 12; в) 9m2 – 9mn – 5m + 5n;
б) 7х + 7а – 6ах – 5а2; (Подробнее…)
ГДЗАлгебра7 классМордкович А.Г.
Как превратить текстовые задачи в математические – Объяснение!
Примеры
Purplemath
Самое сложное в решении текстовых задач — использовать ту часть, где вам нужно взять английские слова и перевести их в математику. Обычно, как только вы получаете математическое уравнение, все в порядке; фактическая математика часто довольно проста. Но вычисление фактического уравнения может показаться почти невозможным. Далее следует список советов и подсказок. Однако имейте в виду: до действительно узнать, “как сделать” словесные задачи, вам нужно будет практиковаться, практиковаться, практиковаться.
Как преобразовать текстовые задачи в математические?
Шаги для создания текстовых задач:
- Прочитайте упражнение полностью.
- Работать организованно.
- Найдите ключевые слова.
- Примените свои знания «реального мира».
Содержание продолжается ниже
MathHelp.com
Словесные задачи по алгебре
Шаг 1 в эффективном переводе и решении текстовых задач состоит в том, чтобы полностью прочитать задачу. Не начинайте пытаться решить что-либо, когда вы прочитали только половину предложения. Сначала попытайтесь прочувствовать всю проблему; попытайтесь сначала посмотреть, какая информация у вас есть, а затем выяснить, что вам еще нужно.
Шаг 2 – работать организованно. Определите, что вам нужно, но чего у вас нет. Назовите вещи. Выберите переменные для обозначения неизвестных, четко обозначив эти переменные тем, что они означают. Аккуратно рисуйте и подписывайте картинки. Объясните свои рассуждения по ходу дела. И убедитесь, что вы точно знаете, о чем на самом деле просит проблема.
Вам нужно сделать это по двум причинам:
- Четкая работа поможет вам ясно мыслить, а
- выяснение того, что вам нужно, поможет вам перевести ваш окончательный ответ обратно на английский язык.
Относительно пункта (а) выше:
Может быть очень неприятно (и смущающе) потратить пятнадцать минут на решение словесной задачи на тесте только для того, чтобы в конце понять, что вы больше не имеете ни малейшего представления о том, что ” x ” означает, поэтому вам придется решать всю задачу заново. Я сделал это на тесте по математике — слава богу, это был короткий тест! — и, поверь мне, ты не захочешь сделать это с собой. Потратить пятнадцать секунд на то, чтобы маркировать вещи, — это лучшее использование вашего времени, чем потратить пятнадцать секунд на то, чтобы пометить вещи.0007 минут переработка всего упражнения!
Шаг 3 — поиск «ключевых» слов. Определенные слова обозначают определенные математические операции.
Некоторые из этих слов легкие. Если в упражнении говорится, что один человек «добавил» свои шарики в кучку, принадлежащую кому-то другому, и спрашивается, сколько шариков сейчас в этой кучке, вы знаете, что будете складывать два числа.
Какие общие ключевые слова для текстовых задач?
Ниже приводится список наиболее распространенных ключевых слов для текстовых задач:
Дополнение:
увеличено на
больше
вместе взятых, вместе
всего
сум, плюс
прибавлено к
сравнительные («больше чем» и т. д.)
Вычитание:
уменьшить на
минус, меньше
разница между/из
меньше, меньше
осталось, осталось после
сохранить (старомодный термин)
сравнительные значения (“меньше чем” и т. д.)
Умножение:
раз, умноженное на
произведение
, увеличенное/уменьшенное на коэффициент (последний тип может включать как сложение, так и вычитание и умножение!) получил по три” и т.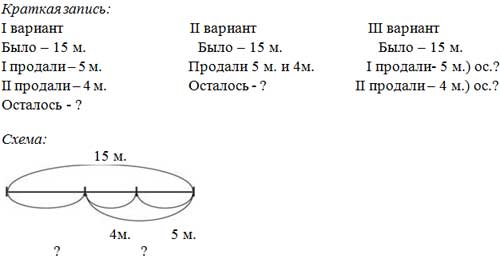
д.)
Деление:
на, соотношение
из
, частное
процентов (делить на 100)
равные части, разделенные
средние
Равно
есть, есть, было, были, будет
дает, дает
продан за, стоимость
Обратите внимание, что «за» в «Подразделении» означает «разделить на», например: «Я проехал 90 миль на трех галлонах бензина, поэтому я получил 30 миль на галлон». Кроме того, «а» иногда означает «деленное на», например: «Когда я заправился, я заплатил 12,36 доллара за три галлона, поэтому бензин стоил 4,12 доллара за галлон».
Предупреждение: конструкция «меньше чем» в «вычитании» в английском языке является обратной по сравнению с математикой. Если вам нужно, например, перевести «1,5 меньше x “, возникает искушение написать “1,5 – x “. Не делайте этого!
Вы можете увидеть, насколько это неправильно, используя эту конструкцию в ситуации “реального мира”: Рассмотрим утверждение, “Он зарабатывает на 1,50 доллара в час меньше, чем я”.
Вы не вычисляете его заработную плату, вычитая свою заработную плату из 1,50 доллара. Вместо этого вы вычитаете 1,50 доллара из своей заработной платы. Так что помните: конструкция “меньше чем” является обратной.
( Технически, конструкция «больше чем» в «Сложение» также является обратным по математике от английского, но порядок сложения не имеет значения, поэтому можно складывать в обратном порядке, потому что результат будет одинаковым в любом случае. .)
Также обратите внимание, что порядок важен в конструкциях “частное/отношение” и “разность между/из”. Если в задаче написано «отношение х и х », это означает « х разделить на х », а не « х разделить на х ». Если в задаче написано «разность x и y », это означает « x − y », а не « y − x ».
Иногда от вас ожидают, что вы привнесете свои знания «реального мира» в упражнение.
Например, предположим, вам сказали, что «Шелби отработал восемь часов MTThF и шесть часов WSat». Вы должны были бы понять, что это означало, что она работала по восемь часов каждый из четырех дней в понедельник, вторник, четверг и пятницу; и шесть часов для каждого из двух дней среды и субботы. Предположим, вам сказали, что Шелби зарабатывает «полтора часа» за любые часы, которые она отработала больше сорока в данную неделю. Ожидается, что вы знаете, что «полтора раза» означает в 1,5 раза больше ее базовой ставки; если ее базовая ставка составляет двенадцать долларов в час, то она будет получать 1,5 × 12 = 18 долларов за каждый час сверхурочной работы.
Вы должны знать, что “дюжина” – это двенадцать; можно ожидать, что вы знаете, что «счет» равен двадцати. От вас потребуется знать количество дней в году, количество часов в сутках и другие основные единицы измерения.
Вы также должны знать, что «периметр» указывает длину вокруг внешней стороны плоской формы, такой как прямоугольник (поэтому вы, вероятно, будете добавлять длины), а «площадь» указывает размер внутренней части плоская форма (так что вы, вероятно, будете умножать длину на ширину или применять какую-то другую формулу).
А «объем» — это внутренности трехмерной формы, такой как куб или сфера (так что вы, вероятно, будете умножать).
Вероятно, самым большим источником ошибок является использование переменных без определений. Когда вы выбираете букву для обозначения чего-либо, четко запишите, что означает эта последняя буква. «S» означает «Шелби» или «часы работы Шелби»? Если первое, то что это означает на практике? (И, если вы не можете придумать какое-либо осмысленное определение, то, возможно, вам нужно замедлиться и немного больше подумать о том, что происходит в слове «проблема».)
Во всех случаях не стесняйтесь использовать свои знания “реального мира”. Иногда вы не будете уверены в своем переводе английского языка в математическое выражение или уравнение. В этих случаях попробуйте подставить числа. Например, если вы не уверены, следует ли вам делить или умножать, попробуйте выполнить этот процесс с обычными числами. Например, предположим, что вы не уверены, следует ли представлять «половину (неизвестной суммы)» умножением на половину или делением на половину.
Если вы используете цифры, вы можете быть уверены. Выберите простое число, например десять. Половина десяти — это пять, поэтому мы ищем операцию (т.е. умножение или деление), которая дает нам ответ 5. Сначала попробуем деление:
десять разделить на половину:
10/(1/2) = (10/1)×(2/1) = 20
Что ж, это явно неправильно. Как насчет того, чтобы пойти другим путем?
десять умножить на половину:
(10)×(1/2) = 10 ÷ 2 = 5
Вот так! Вы, , знаете, , что половина десяти равна пяти, и теперь вы можете видеть, какие математические операции дают вам правильное значение. Итак, теперь вы знаете , что выражение, которое вы хотите, определенно “(1/2) x “.
У вас есть опыт и знания; не бойтесь применять свои навыки в этом новом контексте!
URL: https://www.purplemath.com/modules/translat.htm
Страница 2
Словесные задачи — Руководство по исследованиям и практике
Введение
Словесные задачи описываются как «словесные описания проблемных ситуаций, в которых возникает один или несколько вопросов, ответ на которые может быть получен путем применения математических операций к имеющимся числовым данным».
в постановке задачи» (Verschaffel, Greer, & De Corte, 2000). Решение текстовых задач включает в себя:
- Хорошо организованное и гибкое использование как концептуальных, так и процедурных знаний
- Стратегии и метапознание
- Положительные эмоции и убеждения (De Corte, Greer, & Verschaffel, 1996; Schoenfeld, 1992)
Является ли решение текстовых задач таким же, как математическое моделирование?
Решение текстовых задач , а не считается тем же, что и математическое моделирование. Математическое моделирование, как правило, является более сложным процессом, включающим определение вопросов, на которые необходимо ответить о реальном мире, создание предположений, определение переменных, преобразование явления в математическую модель, оценку решения и повторение процесса для уточнения и расширения модели (COMAP). и СИАМ, 2016 г.). Процесс решения словесной задачи не обязательно такой сложный, так как сама задача обычно дает читателю вопрос, на который нужно ответить, и информацию, необходимую для ответа на него, и не требует моделирования уровня осмысления и интерпретации.
Однако эти различия относительны и зависят от способностей учащегося и характера решения, необходимого для решения задачи.
Понимание задачи
Что затрудняет решение задач для учащихся?
Основные трудности учащихся при решении текстовых задач объясняются их «приостановкой осмысления» (Schoenfeld, 1991; Verschaffel, Greer, & De Corte). Вместо того, чтобы обдумывать контекст словесной задачи, чтобы понять ее, многие студенты просто ищут простое применение арифметики, необходимое для получения ответа, независимо от того, имеет ли он смысл или нет. В следующем видео Каплинский (2013) воспроизводит результат начала 19Исследование 80-х годов, проведенное в Институте исследований математики во Франции.
Учителя математики часто обеспокоены способностью учащихся перенести полученные в классе знания в мир за пределами классной комнаты, но эта «приостановка осмысления» показывает, что обратное также затруднено – учащиеся с трудом применяют свои знания и понимание мира.
снова в кабинете математики. Выученные годами арифметики, почти всегда включающей очевидные операции и ожидание, что каждая задача имеет правильный ответ, у учащихся развивается «навязчивое стремление к вычислениям» (Stacey & MacGregor, 19).99), которые могут помешать развитию алгебраического мышления, которое обычно необходимо для решения текстовых задач. Некоторые (но не все) результаты исследований показывают, что «принуждение к вычислениям» усиливается по мере того, как учащиеся стареют и у них формируется представление о том, что математика представляет собой набор правил (Radatz, 1983; Stern, 1992, оба цитируются в Verschaffel, Greer, & De Corte, 2000, стр. 5).
Учащиеся также могут испытывать затруднения при решении текстовых задач, потому что у них есть проблемы с академической лексикой, математической лексикой или и тем, и другим. Из-за этих трудностей изучающие английский язык и учащиеся с низким социально-экономическим статусом получают более низкие баллы по стандартным оценочным пунктам, чем те, кто хорошо владеет английским языком (Abedi & Lord, 2001).
Что затрудняет словесные задачи для учителей?
Некоторые учителя игнорируют или с трудом применяют свои практические знания при решении текстовых задач, как и ученики (Verschaffel, De Corte, & Borghart, 1997). Во время обучения учителя часто пытаются помочь учащимся «убрать то, что нам на самом деле не нужно» (Chapman, 2006, стр. 219) и свести проблему к числам, ключевым словам или фразам, обозначающим операции или отношения. Это игнорирование реальных аспектов текстовых задач может способствовать приостановке осмысления учащимися и их принуждению к вычислениям.
Большинство учителей считают или предполагают, что учащимся будет труднее решить задачу со словами, чем решить алгебраическое уравнение, представляющее ту же математику без слов. Из-за этого они верят в преподавание текстовых задач только после того, как учащиеся освоят решение подобных задач в виде уравнений. Традиционные учебники по математике подкрепляют это убеждение, помещая текстовые задачи в конце практических наборов.
Это убеждение или предположение оказалось ложным , по крайней мере, при некоторых условиях. При тестировании учащиеся показали, что они могут добиться большего успеха в решении словесных или вербальных задач, чем в эквивалентных чисто символических задачах (Nathan & Koedinger, 2000a, 2000b). Другие исследования показывают, что навыки алгоритмических вычислений могут не соответствовать способности учащихся концептуализировать взаимосвязь между числами в текстовых задачах (Fuchs et al., 2006).
Рекомендации
Использование текстовых задач для обучения студентов математике
Словесные задачи предназначены не только для приложений уже известной математики. На самом деле, самый действенный способ использования текстовых задач в классе — это помощь учащимся в изучении математики. Помещая математику в контекст, понятный учащимся, текстовые задачи побуждают учащихся следовать стратегиям решения, которые имеют для них смысл и чаще приводят к правильным ответам (Koedinger & Nathan, 2004).
Затем эти стратегии можно сделать более формальными и символическими с помощью дополнительных инструкций.
Это очевидно для воспитателей маленьких детей. В ранней математике задачи почти всегда помещаются в реалистичные контексты, понятные детям. Нет причин, чтобы это заканчивалось в раннем детстве. Учащиеся всех уровней должны заниматься математикой в разумном контексте, прежде чем она станет формальной и символической.
Привлекайте учащихся к рассуждениям
Вместо того, чтобы игнорировать контекст текстовых задач, учителя должны проводить время со студентами, чтобы разобраться в текстовых задачах и их вспомогательном контексте. Учителя должны сопротивляться принуждению учащихся к вычислениям, сосредоточив внимание на отношениях между известными и неизвестными в текстовых задачах, а не спешить с поиском ответа (Kieran, 2014). Некоторые типы текстовых задач могут быть особенно полезны для развития рассуждений, потому что в них либо отсутствует очевидная стратегия, либо нет одного правильного ответа, либо они могут быть «сложными» для учащихся, которые предполагают, что проблема проста.
Некоторые примеры:
- Пит организовал вечеринку по случаю своего десятого дня рождения. Он пригласил 8 друзей-мальчиков и 4 подруг. Сколько друзей Пит пригласил на свой день рождения?
- У Карла 5 друзей, а у Жоржа 6 друзей. Карл и Жорж решают вместе устроить вечеринку. Они приглашают всех своих друзей. Все друзья присутствуют. Сколько друзей на вечеринке?
- Кэти, Ингрид, Ганс и Том получили от дедушки коробку с 14 плитками шоколада, которые они поделили между собой поровну. Сколько плиток шоколада получил каждый внук?
- Дедушка дает своим 4 внукам коробку с 18 воздушными шарами, которые они делят поровну. Сколько шариков получит каждый внук?
- У лавочника есть два контейнера для яблок. В первом контейнере 60 яблок, во втором 90 яблок. Он кладет все яблоки в новый, больший контейнер. Сколько яблок в этом новом контейнере?
- Какой будет температура воды в сосуде, если в него налить 1 кувшин воды температурой 80 градусов по Фаренгейту и 1 кувшин воды температурой 40 градусов по Фаренгейту? (Нешер, 1980)
Verschaffel, De Corte и Lasure (1994) использовали эти текстовые задачи, чтобы увидеть, будут ли ученики рассуждать по-разному с нечетными и четными элементами.
Их исследования и последующие исследования показали, что подавляющее большинство учащихся — иногда более 90 процентов — вычисляют и дают ответы на вопросы с четными номерами точно так же, как и на вопросы с нечетными номерами, без каких-либо дополнительных рассуждений о реальном мире. соображения. Дайте учащимся общее предупреждение, например, «эти задачи не так просты, как кажутся» 9.0055 существенно не помог ученикам . Вместо этого учителя могут способствовать рассуждению учащихся, предоставляя поддержку, характерную для каждой проблемы, например, поощряя учащихся объяснять свой ответ и объяснять, почему он имеет смысл, рисовать изображение своего решения или рассматривать гипотетическое, но контрастирующее решение другого ученика. Хотя эти стратегии могут увеличить число студентов, правильно рассуждающих об этих проблемах, во многих исследованиях они редко давали правильные ответы гораздо более чем 50 % студентов (см. главу 3, Verschaffel, Greer, De Corte). Другими словами, эти стратегии полезны, но вряд ли сами по себе гарантируют успех всем учащимся.
Бесчисленные задачи со словами
Возможно, самый прямой способ противостоять принуждению учащихся к вычислениям — дать им задачи со словами без чисел. Брайан Бушарт, учитель начальных классов и координатор учебной программы по математике из Техаса, популяризировал идею «бесчисленных задач со словами» после того, как его коллега опробовал этот подход на некоторых учениках третьего класса. Задачи на бесчисленное количество слов не совсем новы, как в книге « задач без рисунков » (Гиллан, 1909 г.) представил нечто отдаленно похожее в начале 20 века. Подход Бушарта идет гораздо дальше, сосредоточив внимание на учебных шагах и возможностях для студенческого дискурса, которых не было в подходах вековой давности. Сообщение в блоге Бушарта (2014 г.) и последующий сборник ресурсов (без даты) описывают как его процесс решения бесчисленных текстовых задач, так и многочисленные примеры для различного содержания и уровней обучения.
Пример 1: Одношаговая задача со словами
В качестве примера задачи с бесчисленными словами рассмотрим этот элемент, вышедший из теста PARCC 4-го уровня (PARCC, 2016a):
Кувшин содержит 2 литра сока.
Стакан наполнен 180 миллилитрами сока из кувшина. Сколько миллилитров сока осталось в кувшине после наполнения стакана?
Вместо того, чтобы давать учащимся эту задачу в письменном виде, учителя могут представить бесчисленное количество вариантов этой задачи на серии слайдов:
Слайд 1 : В кувшине есть немного сока.
Слайд 2 : В кувшине есть немного сока. Стакан наполняется соком из кувшина.
Слайд 3 : В кувшине есть немного сока. Стакан наполняется соком из кувшина. Сколько сока осталось в кувшине после наполнения стакана?
Слайд 4 : Кувшин содержит 2 литра сока. Стакан наполняется соком из кувшина. Сколько сока осталось в кувшине после наполнения стакана?
Слайд 5 : Кувшин содержит 2 литра сока. Стакан наполнен 180 миллилитрами сока из кувшина. Сколько сока осталось в кувшине после наполнения стакана?
Слайд 6 : Кувшин содержит 2 литра сока.
Стакан наполнен 180 миллилитрами сока из кувшина. Сколько миллилитров сока осталось в кувшине после наполнения стакана?
Учителя могут регулировать количество слайдов в зависимости от способностей учащихся, сложности задачи и количества времени, которое учитель желает посвятить выработке и обмену мнениями учащихся. В этом примере учитель может остановиться после слайда 1, чтобы убедиться, что учащиеся знают, что такое кувшин, и чтобы учащиеся оценили вместимость кувшина. После слайда 2 учитель может попросить учащихся объяснить, что произойдет с количеством сока в кувшине, а также взаимосвязь между соком в кувшине и соком в стакане. С каждым последующим слайдом учитель может продолжать исследовать смыслообразование учащихся и понимание взаимосвязей между величинами, описываемыми задачей.
Пример 2: Многошаговая текстовая задача
Учителя также могут использовать бесчисленные словесные задачи с многошаговыми словесными задачами. Рассмотрим этот многошаговый вопрос, полученный из теста PARCC 5-го класса (PARCC, 2016b):
Дана готовит суп из фасоли.
Рецепт, который у нее есть, рассчитан на 10 порций и использует 3/4 фунта бобов. Сколько всего фунтов фасоли ей нужно, чтобы приготовить 5 порций супа? У нее 1/16 фунта бобов в одном контейнере и 1/4 фунта бобов в другом контейнере. Сколько еще фунтов фасоли нужно Дане, чтобы приготовить 5 порций супа?
Как и в примере 1, учитель может представить бесчисленное количество вариантов этой текстовой задачи на серии слайдов.
Слайд 1 : Дана готовит суп из фасоли. Рецепт, который у нее есть, рассчитан на несколько порций и использует определенное количество бобов.
Учитель может использовать слайд 1, чтобы убедиться, что учащиеся понимают основной контекст. Студенты могут заметить, что «Если она хочет сварить больше супа, ей понадобится больше бобов», или прийти к другим выводам, которые помогут установить взаимосвязь между количеством супа и количеством бобов.
Слайд 2 : Дана готовит суп из фасоли. Рецепт, который у нее есть, рассчитан на несколько порций и использует определенное количество бобов.
Какое количество фасоли ей нужно, чтобы приготовить меньшее количество порций супа?
На слайде 2 учащиеся должны заметить, что для меньшего количества супа требуется меньше бобов. Учащиеся могут начать строить предположения, например: «Если она хочет в два раза меньше супа, ей понадобится в два раза меньше бобов».
Слайд 3 : Дана готовит суп из фасоли. Рецепт, который у нее есть, рассчитан на несколько порций и использует определенное количество бобов. Какое количество фасоли ей нужно, чтобы приготовить меньшее количество порций супа? У нее уже есть небольшое количество бобов. Сколько еще фасоли нужно Дане, чтобы сварить суп?
После просмотра слайда 3 учащиеся должны столкнуться с еще более сложной взаимосвязью: Дане не только нужно меньше бобов, потому что она варит меньше супа, чем предусмотрено рецептом, но у нее уже есть несколько бобов, которые ей понадобятся. . Наблюдения и предположения учащихся на этом этапе должны предложить две операции, такие как первый шаг, включающий деление, чтобы найти количество бобов, необходимых в сокращенном рецепте, и второй шаг, чтобы вычесть количество бобов, которое уже есть у Даны.
Учитывая эту многоступенчатую сложность, учащимся было бы полезно нарисовать или иным образом проиллюстрировать свое мышление.
Слайд 4 : Дана готовит суп из фасоли. Рецепт, который у нее есть, рассчитан на 10 порций и использует определенное количество бобов. Сколько фасоли ей нужно, чтобы приготовить 5 порций супа? У нее уже есть небольшое количество бобов. Сколько еще фасоли нужно Дане, чтобы приготовить 5 порций супа?
На слайде 4 указано количество порций, но не бобов. Имея эту информацию, учащиеся могут пересмотреть свои наблюдения, чтобы прояснить, что количество бобов, указанное в рецепте, нужно разделить на 2 с вычитанием дополнительного количества, чтобы найти, сколько еще бобов нужно Дане.
Слайд 5 : Дана готовит суп из фасоли. Рецепт, который у нее есть, рассчитан на 10 порций и использует 3/4 фунта бобов. Сколько всего фунтов фасоли ей нужно, чтобы приготовить 5 порций супа? У нее уже есть небольшое количество бобов.
Сколько еще фунтов фасоли нужно Дане, чтобы приготовить 5 порций супа?
На слайде 5 учащиеся уже должны были решить, что количество бобов в рецепте нужно разделить на 2, и теперь они могут сосредоточиться на нахождении 3/4 ÷ 2. Учащиеся также могут заметить, что задача теперь дает понять, что все измерения фасоли в фунтах.
Слайд 6 : Дана готовит суп из фасоли. Рецепт, который у нее есть, рассчитан на 10 порций и использует 3/4 фунта бобов. Сколько всего фунтов фасоли ей нужно, чтобы приготовить 5 порций супа? У нее 1/16 фунта бобов в одном контейнере и 1/4 фунта бобов в другом контейнере. Сколько еще фунтов фасоли нужно Дане, чтобы приготовить 5 порций супа?
На слайде 6 задача со словами представлена в ее исходной форме, и учащиеся могут быть удивлены тем, что небольшое количество бобов, которое уже было у Даны, представлено в виде двух сумм, которые необходимо рассматривать вместе. Из-за сложности этой задачи может быть не самое подходящее время для введения этой информации, но пятиклассник, который обдумал задачу и дошел до нее, должен быть в состоянии рассуждать с двумя небольшими количествами бобов, либо добавляя сначала их, а затем вычитая сумму из 3/8 или выполняя два вычитания.
Добавить аутентичность
Учащиеся успешнее решают текстовые задачи, когда от них требуется аутентичный подход к контексту. Например, DeFranco and Curcio (1997, цит. по Verschaffel, Greer, De Corte) дали группе из 20 учеников шестого класса следующую текстовую задачу: «328 пожилых людей собираются в путешествие. Автобус вмещает 40 человек. Сколько нужно автобусов, чтобы все пожилые люди смогли поехать?» Позже исследователи дали студентам аналогичную задачу, но они представили ее в виде таблицы фактов с количеством людей и размером фургонов, а также инструкциями по совершению телефонного звонка, имитирующего размещение реального заказа на определенное количество автомобилей. требуемые транспортные средства. В первом сценарии только 2 из 20 студентов ответили правильно и правильно рассуждали, а остальные остались за делением. Во втором сценарии, используя более аутентичную обстановку, 16 из 20 студентов ответили правильно и аргументировали оставшихся, либо округлив до следующего целого фургона, либо попросив «например, машину или что-то в этом роде» для перевозки небольшого количества оставшихся.
пассажиры.
Решение проблемы языковой сложности
Сложная языковая сложность может быть решена путем уменьшения сложности или предоставления учащимся дополнительной поддержки. Учащимся, которые борются с языком текстовых задач, может быть полезно переписать задачу, используя более простой, знакомый язык или родной язык учащегося (Бернардо, 1999). Подобные модификации, как правило, помогают учащимся, изучающим английский язык, и учащимся с низким уровнем SES больше, чем их сверстникам, владеющим английским языком и имеющим более высокий уровень SES, а это означает, что эта стратегия может помочь сократить разрыв в успеваемости (Abedi & Lord, 2001).
Учителя также могут оказать дополнительную поддержку. Рекомендации по обучению изучающих английский язык включают сосредоточение внимания на рассуждениях и дискурсе учащихся, а не на правильности использования языка, и использование знаний и опыта изучающих язык в качестве ресурсов (Moschkovich, 2012). Веб-сайт Understanding Language (ell.
stanford.edu) является рекомендуемым ресурсом для понимания того, как помочь изучающим язык в математике.
Ссылки
Abedi, J., & Lord, C. (2001). Языковой фактор в тестах по математике. Прикладные измерения в образовании, 14(3), 219–234. https://doi.org/10.1207/S15324818AME1403_2
Бернардо, ABI (1999). Преодоление препятствий к пониманию и решению текстовых задач по математике. Педагогическая психология, 19 (2), 149–163. https://doi.org/10.1080/01443419
203
Бушарт, Б. (без даты). Бесчисленные словесные задачи. Получено 16 ноября 2017 г. с https://bstockus.wordpress.com/numberless-word-problems/
Bushart, B. (6 октября 2014 г.). Бесчисленные текстовые задачи [сообщение в блоге]. Получено 16 ноября 2017 г. с https://bstockus.wordpress.com/2014/10/06/numberless-word-problems/ 9.0003
Чепмен, О. (2006). Практика в классе для контекста задач по математике. Образовательные исследования по математике, 62 (2), 211–230. https://doi.org/10.1007/s10649-006-7834-1
COMAP и SIAM.
(2016). GAIMME: Руководство по оценке и обучению математическому моделированию. Бедфорд, Массачусетс. Получено с http://www.comap.com/Free/GAIMME/index.html
De Corte, E., Greer, B., & Verschaffel, L. (1996). Преподавание математики и обучение. В DC Berliner & RC Calfee (Eds.), Справочник по педагогической психологии (стр. 49).1–549). Нью-Йорк, штат Нью-Йорк: Lawrence Erlbaum Associates.
ДеФранко, Т.С., и Курсио, Ф.Р. (1997). Проблема деления с остатком в двух контекстах: детские решения в ограничительных и реальных условиях. Сосредоточьтесь на проблемах обучения по математике, 19 (2), 58–72.
Фукс, Л. С., Фукс, Д., Комптон, Д. Л., Пауэлл, С. Р., Ситалер, П. М., Капицци, А. М., … Флетчер, Дж. М. (2006). Когнитивные корреляты навыков третьего класса в арифметике, алгоритмических вычислениях и арифметических текстовых задачах. Журнал педагогической психологии, 98(1), 29–43. https://doi.org/10.1037/0022-0663.98.1.29
Gillan, SY (1909). Задачи без фигур. Милуоки, Висконсин: SY Gillan & Company.
Получено с http://www.schoolinfosystem.org/pdf/2008/10/problemswithoutfigures.pdf
Каплинский, Р. (2013). Сколько лет пастуху? Получено 3 ноября 2017 г. с https://www.youtube.com/watch?v=kibaFBgaPx4
Киран, К. (2014). Что говорят нам исследования о развитии алгебраических рассуждений в школьной алгебре? Рестон, Вирджиния. Получено с http://www.nctm.org/Research-and-Advocacy/Research-Brief-and-Clips/Algebraic-Reasoning-in-School-Algebra/
Koedinger, KR, & Nathan, MJ (2004). Настоящая история, стоящая за задачами истории: влияние представлений на количественные рассуждения. Журнал наук об обучении, 13 (2), 129–164. https://doi.org/10.1207/s15327809jls1302_1
Мошкович, Дж. Н. (2012). Математика, Common Core и язык. Понимание языка: язык, грамотность и обучение в предметных областях. Получено с http://ell.stanford.edu/publication/mathematics-common-core-and-language
Натан, М.Дж., и Кёдингер, К.Р. (2000a). Исследование взглядов учителей на развитие алгебры учащихся.
Познание и обучение, 18 (2), 209–237. https://doi.org/10.1207/S1532690XCI1802_03
Натан М.Дж. и Кёдингер К.Р. (2000b). Представления учителей и исследователей о развитии алгебраического мышления. Журнал исследований в области математического образования, 31 (2), 168–190. https://doi.org/10.2307/749750
Нешер, П. (1980). Стереотипный характер школьных текстовых задач. Для изучения математики, 1 (1), 41–48. Получено с http://flm-journal.org/Articles/flm_1-1_Nesher.pdf
ПАРКЦ. (2016а). Math Spring Operational 2016 Grade 4 Выпущенные элементы. Партнерство по оценке готовности к колледжу и карьере. Получено с https://parcc-assessment.org/content/uploads/released_materials/05/Grade_04_Math_Item_Set.pdf
PARCC. (2016б). Math Spring Operational 2016 Grade 5 Выпущенные элементы. Партнерство по оценке готовности к колледжу и карьере. Получено с https://parcc-assessment.org/content/uploads/released_materials/05/Grade_05_Math_Item_Set.pdf 9.0003
Радац, Х. (1983).
Untersuchungen zum Lösen eingekleideter Aufgaben. Zeitschrift Fur Mathematic-Didaktik, 4 (2), 205–2017. https://doi.org/10.1007/BF03339231
Schoenfeld, AH (1991). О математике как осмыслении: неформальная атака на неудачный развод формальной и неформальной математики. В Дж. Ф. Воссе, Д. Н. Перкинсе и Дж. В. Сигале (ред.), Неформальное мышление и образование (стр. 311–343). Хиллсдейл, Нью-Джерси: Lawrence Erlbaum Associates.
Шенфельд, А. Х. (1992). Обучение математическому мышлению: решение проблем, метапознание и осмысление математики. В Д. А. Гроувс (ред.), Справочник по исследованиям в области преподавания и обучения математике (стр. 334–370). Рестон, Вирджиния: Национальный совет учителей математики.
Стейси, К., и МакГрегор, М. (1999). Изучение алгебраического метода решения задач. Журнал математического поведения, 18 (2), 149–167. https://doi.org/10.1016/S0732-3123(99)00026-7
Стерн, Э. (1992). Warum werden Kapitänsaufgaben «gelöst»? Dav Verstehen von Textaufgaben aus phychologischer Sicht.