Как выучить таблицу степеней: Таблица степеней от 1 до 10 по алгебре для 7 класса: распечатать в хорошем качестве – Всё о детях – беременность, воспитание, уроки для детей

Содержание

Таблица степеней от 1 до 10 по алгебре для 7 класса: распечатать в хорошем качестве

В начальной школе мы учили наизусть таблицу умножения, но давайте зайдем немного дальше. В этой статье мы узнаем о таблице степеней от 1 до 10, расскажем, как ей пользоваться и что с ее помощью можно сделать

Наталия Юмагулова

Учитель математики

Сложение, вычитание, деление и умножение — первые арифметические действия, которые ученики начинают изучать в школе. С погружением в познание математики учителя начинают знакомить школьников с возведением чисел в степень. Для простоты понимания этой темы математики разработали таблицу степеней. В статье расскажем, как применять ее на практике, но для начала вспомним немного теории.

Возведение числа в степень — произведение нескольких равных множителей. Есть и более простое определение — многократное умножение числа на себя: aⁿ, где a — основание, n — показатель степени.

Важно!

Возведение числа в степень — произведение нескольких равных множителей.

Рассмотрим пример:

3² = 3 × 3 = 9

3 — основание, 2 — показатель степени

Чтобы решить эту задачу, нам необходимо число 3 умножить само на себя 2 раза.

А вот другая задача — найдите значение выражения: 7⁸. Здесь арифметическое действие становится довольно длительным. Мы не сомневаемся, что вы справитесь с умножением числа 7 самого на себя 8 раз, но с помощью таблицы степеней вы справитесь в один миг.

В ТЕМУ

Как пользоваться таблицей степеней

Пользоваться таблицей степеней очень просто. Например, нам необходимо посчитать 7⁸. ^{В 1-м столбце находим число, которое нужно возвести в степень, — 7^С. В 1-й строке ищем показатель степени — 8. Ответ смотрим на пересечении столбца и строки и получаем ответ: 7⁸ = 5764801. Для удобства таблицу можно скачать и пользоваться ею при подготовке к ЕГЭ по математике.}
В 1-м столбце таблицы степеней находится основание, в 1-й строке — показатель. Изображение: Наталия Юмагулова.
Задачи с использованием таблицы степеней

Задача №1
Найдите значение выражения:
8⁴ × 8³
Упростим выражение, используя свойство умножения степеней, а затем с помощью таблицы получим ответ:
8⁴ × 8³ = 8⁴⁺³ = 8⁷ = 2097152
Задача №2
Найдите значение выражения:
49³
Основание 49 заменим на основание 7, так как 49 = 7². Применим свойство возведения степени в степень и данные таблицы:
49³ = (7²)³ = 7⁶ = 117649
В ТЕМУ
Задача №3
Решите уравнение:
х⁵ = 59049
х⁵ = 9⁵
х = 9
Ответ: х = 9
Популярные вопросы и ответы
Почему таблицу степеней изучают на алгебре в 7-м классе?
Так как программа 7-го класса по алгебре включает в себя понятие степени и все, что с ним связано.
Зачем нужна таблица степеней?
Таблица степеней нужна для экономии времени при выполнении громоздких вычислений.
Можно ли запомнить таблицу степеней?
Всю таблицу, наверно, могут выучить только люди с феноменальной памятью. В школе рекомендуется к запоминанию лишь та часть таблицы, которая чаще встречается для преобразований выражений.
В школе рекомендуется к запоминанию лишь та часть таблицы, которая чаще встречается для преобразований выражений. Изображение: Наталия Юмагулова.
Где в повседневной жизни можно использовать таблицу степеней?
В информатике: если использовать таблицу степеней двойки, то перевод в десятичную систему счисления целых двоичных чисел будет значительно проще. ^{Таблица степеней десяти используется для записи и вычислений больших величин, измерений, расстояний в химии, географии и физике. Например: площадь Земли равна 510 × 10⁶ км².}
https://uchim.org/matematika/tablica-stepenej – uchim.org
Таблица степеней
Пример: 2³=8
Степень:
Число 2 3 4 5 6 7 8 9 10
2 4 8 16 32 64 128 256 512 1 024
3 9 27 81 243 729 2 187 6 561 19 683 59 049
4 16 64 256 1 024 4 096 16 384 65 536 262 144 1 048 576
5 25 125 625 3 125 15 625 78 125 390 625 1 953 125 9 765 625
6 36 216 1 296 7 776 46 656 279 936 1 679 616 10 077 696 60 466 176
7 49 343 2 401 16 807 117 649 823 543 5 764 801 40 353 607 282 475 249
8 64 512 4 096 32 768 262 144 2 097 152 16 777 216 134 217 728 1 073 741 824
9 81 729 6 561 59 049 531 441 4 782 969 43 046 721 387 420 489 3 486 784 401
10 100 1 000 10 000 100 000 1 000 000 10 000 000 100 000 000 1 000 000 000 10 000 000 000
11 121 1 331 14 641 161 051 1 771 561 19 487 171 214 358 881 2 357 947 691 25 937 424 601
12 144 1 728 20 736 248 832 2 985 984 35 831 808 429 981 696 5 159 780 352 61 917 364 224
13 169 2 197 28 561 371 293 4 826 809 62 748 517 815 730 721 10 604 499 373 137 858 491 849
14 196 2 744 38 416 537 824 7 529 536 105 413 504 1 475 789 056 20 661 046 784 289 254 654 976
15 225 3 375 50 625 759 375 11 390 625 170 859 375 2 562 890 625 38 443 359 375 576 650 390 625
16 256 4 096 65 536 1 048 576 16 777 216 268 435 456 4 294 967 296 68 719 476 736 1 099 511 627 776
17 289 4 913 83 521 1 419 857 24 137 569 410 338 673 6 975 757 441 118 587 876 497 2 015 993 900 449
18 324 5 832 104 976 1 889 568 34 012 224 612 220 032 11 019 960 576 198 359 290 368 3 570 467 226 624
19 361 6 859 130 321 2 476 099 47 045 881 893 871 739 16 983 563 041 322 687 697 779 6 131 066 257 801
20 400 8 000 160 000 3 200 000 64 000 000 1 280 000 000 25 600 000 000 512 000 000 000 10 240 000 000 000
21 441 9 261 194 481 4 084 101 85 766 121 1 801 088 541 37 822 859 361 794 280 046 581 16 679 880 978 201
22 484 10 648 234 256 5 153 632 113 379 904 2 494 357 888 54 875 873 536 1 207 269 217 792 26 559 922 791 424
23 529 12 167 279 841 6 436 343 148 035 889 3 404 825 447 78 310 985 281 1 801 152 661 463 41 426 511 213 649
24 576 13 824 331 776 7 962 624 191 102 976 4 586 471 424 110 075 314 176 2 641 807 540 224 63 403 380 965 376
25 625 15 625 390 625 9 765 625 244 140 625 6 103 515 625 152 587 890 625 3 814 697 265 625 95 367 431 640 625
Свойства степени – 2 части
<noscript><img loading='lazy' src='/800/600/http/i.pinimg.com/originals/5e/b1/67/5eb167ed35a30c560a4592eb808baf01.jpg' /></noscript> youtube.com/embed/4FrlQUHlDrg” frameborder=”0″ allowfullscreen=””/>
Таблица основных степеней по алгебре в компактном виде (картинка, удобно, чтобы распечатать), сверху числа, сбоку степени:
(можно открыть в новом окне, нажав на картинку)
Полную математическую таблицу можно бесплатно скачать, просто сохранив картинку выше с помощью правой кнопки мыши.
Всё для учебы » Математика в школе » Таблица степеней по алгебре
Если страница помогла, сохраните её и поделитесь ссылкой с друзьями:
Ссылка: https://uchim.org/matematika/tablica-stepenej

Измерение углов
Измерение углов
Концепция угла
Понятие угла — одно из важнейших понятий геометрии. Понятия равенства, суммы и разности углов важны и используются во всей геометрии, но предмет тригонометрии основан на измерении углов.
Существуют две широко используемые единицы измерения углов. Более привычной единицей измерения являются градусы. Окружность разделена на 360 равных градусов, так что прямой угол равен 90°. Пока мы будем рассматривать только углы от 0° до 360°, но позже, в разделе о тригонометрических функциях, мы будем рассматривать углы больше 360° и отрицательные углы.
Градусы могут быть разделены на минуты и секунды, но это деление уже не так универсально, как раньше. Каждый градус делится на 60 равных частей, называемых минутами. Итак, семь с половиной градусов можно назвать 7 градусов и 30 минут, записав 7° 30′. Каждая минута далее делится на 60 равных частей, называемых 9.0004 секунды,
и, например, 2 градуса 5 минут 30 секунд записывается как 2° 5′ 30″. Деление градусов на минуты и угловые секунды аналогично делению часов на минуты и секунды времени.
Части градуса теперь обычно указываются в десятичном виде. Например, семь с половиной градусов теперь обычно записывают как 7,5&deg.
Когда для анализа нарисован один угол на плоскости xy , мы нарисуем его за стандартная позиция с вершиной в начале координат (0,0), одна сторона угла вдоль оси x , а другая сторона над осью x .
радианы
Другой распространенной единицей измерения углов являются радианы. Для этого измерения рассмотрим единичную окружность (окружность радиуса 1), центр которой является вершиной рассматриваемого угла. Тогда угол отсекает дугу окружности, и длина этой дуги является мерой угла в радианах. Легко конвертировать между измерением в градусах и измерением в радианах. Длина окружности всего круга 2
π , отсюда следует, что 360° равняется 2 π радиан. Следовательно,
1° равно π /180 радиан
и
1 радиан равен 180/ π градусов
Большинство калькуляторов можно настроить на использование углов, измеряемых в градусах или радианах. Убедитесь, что вы знаете, какой режим использует ваш калькулятор.
Краткая заметка об истории радианов
Хотя слово «радиан» было придумано Томасом Мьюиром и/или Джеймсом Томпсоном примерно в 1870 году, математики давно измеряли углы таким способом. Например, Леонард Эйлер (1707–1783) в своих « элементах алгебры » прямо сказал, что углы измеряются длиной дуги, отсеченной в единичной окружности. Это было необходимо, чтобы дать его знаменитую формулу с комплексными числами, которая связывает функции знака и косинуса с показательной функцией. e ^iθ = cos θ + i sin θ
где θ — это то, что позже было названо измерением угла в радианах. К сожалению, объяснение этой формулы выходит далеко за рамки этих заметок. Но для получения дополнительной информации о комплексных числах см. мой Краткий курс комплексных чисел.
Радианы и длина дуги
Альтернативное определение радианов иногда дается как отношение. Вместо того, чтобы взять единичную окружность с центром в вершине угла θ , возьмем любую окружность с центром в вершине угла. Тогда радианной мерой угла является отношение длины стягиваемой дуги к радиусу r окружности. Например, если длина дуги равна 3, а радиус окружности равен 2, то мера радиана равна 1,5.
Причина, по которой это определение работает, заключается в том, что длина стягиваемой дуги пропорциональна радиусу окружности. В частности, определение в терминах отношения дает ту же цифру, что и приведенная выше, с использованием единичного круга. Однако это альтернативное определение более полезно, поскольку его можно использовать для связи длин дуг с углами. Длина дуги равна радиусу r , умноженное на угол θ , где угол измеряется в радианах.
Например, дуга θ = 0,3 радиана в окружности радиусом r = 4 имеет длину 0,3 умножить на 4, то есть 1,2.
Радианы и площадь сектора
Сектором окружности называется та часть окружности, которая ограничена двумя радиусами и дугой окружности, соединяющей их концы. Площадь этого сектора легко вычислить по радиусу r окружности и угол θ между радиусами, если он измеряется в радианах. Так как площадь всего круга равна πr ² , а сектор относится ко всему кругу как угол θ к 2 π , поэтому
Углы общие
Ниже приведена таблица общих углов как в градусах, так и в радианах. Обратите внимание, что измерение в радианах дается как π . Его, конечно, можно было бы представить десятичным числом, но радианное измерение часто появляется с коэффициентом 9.0004 № .
Уголок градусов радиан
90° № /2
60° № /3
45° № /4
30° № /6
Упражнения
Эдвин С.
Кроули написал книгу «Тысяча упражнений в плоской и сферической тригонометрии», Университет Пенсильвании, Филадельфия, 1914 г. Задачи этого краткого курса взяты из этого текста (но не все 1000 из них!) Он дал свои задачи с точностью до пяти знаков, поэтому учащимся пришлось поработать над их решением, и они использовали таблицы логарифмов, чтобы помочь в умножении и делении. Студенты должны были уметь пользоваться таблицей синусов-косинусов, тангенсов, логарифмов, логарифмических синусоидальных и логарифмических таблиц. Теперь мы можем использовать калькуляторы! Это означает, что вы можете сосредоточиться на концепциях, а не на трудоемких вычислениях.
Кроули использовал не десятичную запись для долей градуса, а минуты и секунды.
Каждый набор упражнений включает, во-первых, формулировки упражнений, во-вторых, несколько советов по решению упражнений и, в-третьих, ответы на упражнения.

1. Выразите следующие углы в радианах.
(а). 12 градусов 28 минут, то есть 12° 28′.
(б). 36° 12′.
2. Сократите следующие числа радианов до градусов, минут и секунд.
(а). 0,47623.
(б). 0,25412.
3. Учитывая угол a и радиус r, найти длину стягивающей дуги.
(а). a = 0° 17′ 48″, r = 6,2935.
(б). a = 121° 6′ 18″, r = 0,2163.
4. Зная длину дуги l и радиус r, найти угол, опирающийся на центр.
(а). l = 0,16296, r = 12,587.
(б). l = 1,3672, r = 1,2978.
5. Зная длину дуги l и угол a , на который она опирается в центре, найти радиус.
(а). a = 0° 44′ 30″, l = 0,032592.
(б). a = 60° 21′ 6″, l = 0,4572.
6. Найдите длину с точностью до дюйма дуги окружности 11 градусов 48,3 минуты, если радиус равен 3200 футов.
7. Железнодорожная кривая образует дугу окружности 9 градусов 36,7 минуты, радиус от центральной линии пути составляет 2100 футов. Если ширина колеи 5 футов, найдите разницу в длине двух рельсов с точностью до полдюйма.
9. На сколько человек изменит широту, пройдя на север одну милю, если предположить, что Земля представляет собой сферу радиусом 3956 миль?
10. Вычислите длину одной угловой минуты в футах по большому кругу Земли. Какова длина одной угловой секунды?
14. На окружности радиусом 5,782 метра длина дуги 1,742 метра. На какой угол он сужается в центре?
23. Известно, что воздушный шар диаметром 50 футов вытягивается из глаза под углом 8 1/2 минут. Как далеко это?

Подсказки
1. Чтобы преобразовать градусы в радианы, сначала преобразуйте количество градусов, минут и секунд в десятичную форму. Разделите количество минут на 60 и прибавьте к количеству градусов. Так, например, 12 ° 28 ‘это 12 + 28/60, что равно 12,467°. Далее умножить на π и разделите на 180, чтобы получить угол в радианах.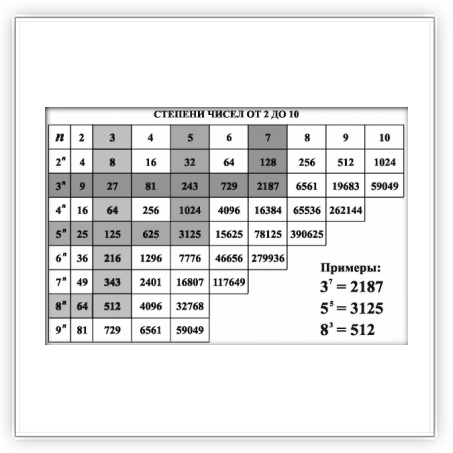
2. И наоборот, чтобы преобразовать радианы в градусы, разделите π и умножьте на 180. Таким образом, 0,47623, деленное на π и умноженное на 180, дает 27,286°. Вы можете преобразовать доли градуса в минуты и секунды следующим образом. Умножьте дробь на 60, чтобы получить количество минут. Здесь 0,286 умножить на 60 равно 17,16, поэтому угол можно записать как 27° 17,16′. Затем возьмите любую оставшуюся долю минуты и снова умножьте на 60, чтобы получить количество секунд. Здесь 0,16 умножить на 60 примерно равно 10, поэтому угол можно также записать как 27° 17′ 10″.

3. Чтобы найти длину дуги, сначала переведите угол в радианы. Для 3(a) 0°17’48” составляет 0,0051778 радиан. Затем умножьте на радиус, чтобы найти длину дуги.
4. Чтобы найти угол, разделите его на радиус. Это дает вам угол в радианах. Это можно преобразовать в градусы, чтобы получить ответы Кроули.
5. Как упоминалось выше, радиан умножить на радиус = длине дуги, поэтому, используя буквы для этой задачи, ar = l, , но a необходимо сначала преобразовать из градусов в радианы. Итак, чтобы найти радиус r, сначала преобразуйте угол a в радианы, а затем разделите его на длину l дуги.
6. Длина дуги равна произведению радиуса на угол в радианах.

7. Помогает нарисовать фигуру. Радиус внешней направляющей равен 2102,5, а радиус внутренней направляющей равен 209.7.5.
9. У вас есть окружность радиусом 3956 миль и дуга этой окружности длиной 1 миля. Какой угол в градусах? (Средний радиус Земли был известен довольно точно в 1914 году. Посмотрите, сможете ли вы узнать, каким Эратосфен считал радиус Земли еще в третьем веке до нашей эры.)
10. Угловая минута равна 1/60 градуса. Преобразовать в радианы. Радиус равен 3956. Какова длина дуги?
14. Поскольку длина дуги равна радиусу, умноженному на угол в радианах, отсюда следует, что угол в радианах равен длине дуги, деленной на радиус. Радианы легко перевести в градусы.
23. Представьте, что диаметр воздушного шара является частью дуги окружности, в центре которой вы находитесь. (Это не совсем часть дуги, но довольно близко.) Эта дуга имеет длину 50 футов. Вы знаете угол, так каков радиус этого круга?
Ответы
1. (а). 0,2176. (б). 0,6318.
2. (а). 27° 17′ 10 дюймов (б). 14,56 ° = 14 °33,6′ = 14°33’36”.
3. (а). 0,03259 (б). 2,1137 умножить на 0,2163 равно 0,4572.
4. (а). 0,16296/12,587 = 0,012947 радиан = 0° 44′ 30″.
(б). 1,3672/1,2978 = 1,0535 радианы = 60,360° = 60° 21,6′ = 60° 21′ 35″.
5. (а). л/год = 0,032592/0,01294 = 2,518.
(б). л/год = 0,4572/1,0533 = 0,4340.
6. ra = (3200′) (0,20604) = 659,31′ = 659′ 4 дюйма.
7. Угол a = 0,16776 радиан. Разница в длинах есть 2102.5 a – 1997.5 a , что составляет 5 a. Таким образом, ответ равен 0,84 фута, что с точностью до дюйма равно 10 дюймам.
9. Угол = 1/3956 = 0,0002528 радиан = 0,01448° = 0,8690′ = 52,14″.
10. Одна минута = 0,0002909 радиан. 1,15075 мили = 6076 футов. Поэтому одна секунда будет соответствовать 101,3 фута.
14. a = л/об = 1,742/5,782 = 0,3013 радиан = 17,26° = 17°16′.
23. Угол a равен 8,5′, что составляет 0,00247 радиана. Значит радиус равен r = л/год = 50/0,00247 = 20222′ = 3,83 мили, почти четыре мили.
О разрядах точности.
Кроули старается давать свои ответы примерно с той же точностью, что и данные в вопросах. Это важно, особенно сейчас, когда у нас есть калькуляторы. Например, в задаче 1 исходная точка равна 12°28′, что имеет точность около четырех знаков, поэтому ответ 0,2176 также должен быть дан с точностью только до четырех знаков. (Обратите внимание, что начальные нули не учитываются при подсчете цифр точности.) Ответ 0,21758438 предполагает восемь цифр точности, и это может ввести в заблуждение, поскольку данная информация не была такой точной.
Другой пример см. в задаче 3(а). Данные равны 0°17’48” и 6,2935 с точностью до 4 и 5 цифр соответственно. Поэтому ответ должен быть дан только с точностью до 4 цифр, поскольку ответ не может быть более точным, чем наименее точные данные. Таким образом, ответ, который может дать калькулятор, а именно 0,032586547, следует округлить до четырех цифр (не считая ведущих нулей) до 0,03259.
Хотя окончательные ответы должны быть выражены с соответствующим количеством цифр точности, вы все равно должны сохранить все цифры для промежуточных вычислений.
Направлений обучения | Линнский университет
Изучайте программы и планируйте свое будущее!
Откройте для себя совершенно новый стиль обучения с нашим инновационным подходом к образованию.
Получить подробности
Подготовьтесь к своему будущему. Начните или продвиньтесь по карьерной лестнице.
В Lynn University мы предлагаем степени младшего специалиста, бакалавра и магистра, а также сертификаты и докторскую степень.
Студенты бакалавриата могут воспользоваться преимуществами неограниченного партнерства в области обучения, чтобы исследовать новые горизонты и новые карьеры. Аспирантам нравится гибкая и удобная учебная программа, идеально подходящая для работы и семейных обязанностей.
Кроме того, вы можете сэкономить время и деньги с помощью ускоренного обучения и получить инновационный подход к обучению с помощью iPad.
17%
иностранные студенты
Удобно
GRE/GMAT не требуются для поступления, и многие программы можно пройти онлайн.
18-1
соотношение студентов и преподавателей
Направления обучения
Реклама и связи с общественностью (B.A.)
Реклама и связи с общественностью (A.A.)
Прикладные науки (A.A.)
Авиация (A.A.)
Авиационный менеджмент (B.S.)
Авиационный менеджмент (B. S.) (онлайн-подразделение)
Авиационный менеджмент (MBA)
Авиационные операции (BS450) 904 B.S.) (онлайн-подразделение)
Авиационная безопасность (B.S.) (онлайн-подразделение)
Behavioral Science (AA)
Биологические науки (M.S.)
Биология (B.S.)
Деловое администрирование (B.S.) (онлайн-подразделение)
Деловое администрирование (A.A.)
Клиническое консультирование по вопросам психического здоровья (MS)
Коммуникации (BA)
Коммуникации и СМИ (BA) (онлайн-подразделение)
Коммуникации и СМИ: цифровые медиа (STEM) (M.S.)
0
0
0
Коммуникации и медиа: медиа-исследования и практика (STEM) (MS)
Коммуникации и медиа: стратегическая коммуникация (STEM) (M.S.)
Композиция (B.M.)
Композиция (M.M.)
Компьютерная анимация (B.F.A.)
Уголовное правосудие (B.A.)
Уголовное правосудие (B.A.) (онлайн-подразделение)
Уголовное правосудие (M. S.)
Кибербезопасность (B.S.)
Аналитика данных (B.S.)
Аналитика данных (B.S.) 9 (онлайн-подразделение 450)
Цифровые медиа (сертификат)
Драма (BFA)
Дошкольное образование (B.S.)
Дошкольное образование (B.S.) (онлайн-подразделение)
Руководство в сфере образования (Ed.D.)
Руководство в сфере образования: School School -12 (M.Ed.)
Классы начального образования K-6 (B.S.)
Классы начального образования K-6 (B.S.) (онлайн-подразделение)
Начальное образование K-6 (A.S.)
Предпринимательский менеджмент (MBA)
Предпринимательский менеджмент (сертификат)
Предпринимательство (B.S.)
Предпринимательство (B.S.) (онлайн-подразделение)
Экологическая политика и менеджмент (B.S.) (онлайн-подразделение)
Экологическая наука и политика (B.S.)
Управление производством мероприятий (B.S.)
Высшее студенческое образование (M. Ed.)
Мода и розничная торговля (B.S.)
Кинопроизводство (B.F.A.)
Финансовая оценка и управление инвестициями (MBA)
Финансовая оценка и управление инвестициями (сертификат)
ForInvestigations (B.S.)
Графический дизайн (BFA)
Графический дизайн (A.S.)
Управление здравоохранением (B.S.)
Управление здравоохранением (MBA)
Управление здравоохранением (сертификат)
Менеджмент в сфере здравоохранения (бакалавр) (онлайн-подразделение)
Менеджмент в сфере гостеприимства (бакалавр)
Менеджмент в сфере гостеприимства (MBA)
Менеджмент в сфере гостеприимства (сертификат)
Управление человеческими ресурсами (MBA)
Управление человеческими ресурсами (сертификат)
Управление персоналом (B.S.) (онлайн-подразделение)
Управление международным бизнесом (B.S.)
Управление международным бизнесом (B.S.) (онлайн-подразделение)
Управление международным бизнесом (MBA)
Международный бизнес-менеджмент (сертификат)
Инвестиционный менеджмент (B. S.)
Инвестиционный менеджмент (B.S.) (онлайн-подразделение)
Лидерство и менеджмент (MBA)
Гуманитарные науки (B.A.) (онлайн-подразделение)
904.9 Маркетинг (B.S.S.) )
Маркетинг (MBA)
Маркетинг (сертификат)
Маркетинг (B.S.) (онлайн-подразделение)
Медиа-менеджмент (MBA)
Медиа-исследования и практика (сертификат)
Мультимедийная журналистика (B.A.)
Исполнение: Instrumental Collaborative Piano (M.M.)
Исполнение: Instrumental Collaborative Piano (PPC)
Исполнение: Piano (B.M.)
Исполнение: Piano (M.M.)
Piano (4P.0P.0P.P.0449)
Исполнение: струнные, деревянные духовые, духовые, арфа и перкуссия (B.M.)
Исполнение: струнные, деревянные духовые, духовые, арфа и перкуссия (M.M.)
Исполнение: струнные, деревянные духовые, духовые, арфа и перкуссия (P.P.C.)
Политология (B.A.)
Профессиональный пилот (B. S.)
Профессиональный пилот (B.S.) (онлайн-подразделение)
Психология (B.S.)
Психология (B.S.) (онлайн-подразделение)
9M49 Psychology (онлайн-подразделение)
Психология Администрирование (MPA)
Социальное влияние и предпринимательство с Watson Institute (B.S.)
Управление социальными инновациями (MBA)
Спортивный менеджмент (B.S.)
Спортивный менеджмент (MBA)
Спортивный менеджмент (сертификат)
Стратегические коммуникации (сертификат)
Необъявленная специальность (B.S.)
Визуальное искусство и дизайн (B.F.A.)
Анимация визуальных эффектов (STEM) (MFA)
Академический каталог
Ищете дополнительную информацию о программе? Посмотрите наш академический каталог.
Обзорный каталог
Свяжитесь с нами
Свяжитесь с нашим приемным отделением
Часы приема
Понедельник-пятница, 9:00-17:00
Познакомьтесь с вашим консультантом
Узнайте больше о своем консультанте по приему, получите помощь в процессе приема или запланируйте личную встречу.
Я подаю заявление на
Академическое подразделение
Дневной бакалавриатВыпускникОнлайн
Тип студента
Первый год: внутреннийПервый год: международныйПеревод: внутреннийПеревод: международный
Моя фамилия начинается с
ABCDEFGHIJKLMNOPQRSTUVWXYZ
Я живу в
Страна
AfghanistanAlbaniaAlgeriaAndorraAngolaAntigua and BarbudaArgentinaArmeniaAustraliaAustriaAzerbaijanBahamasBahrainBangladeshBarbadosBelarusBelgiumBelizeBeninBhutanBoliviaBosnia and HerzegovinaBotswanaBouvet IslandBrazilBruneiBulgariaBurkinaBurma (Myanmar)BurundiCambodiaCameroonCanadaCape VerdeCentral African RepublicChadChileChinaColombiaComorosCongoCongo, Democratic Republic ofCosta RicaCroatiaCubaCyprusCzech RepublicDenmarkDjiboutiDominicaDominican RepublicEast TimorEcuadorEgyptEl SalvadorEquatorial GuineaEritreaEstoniaEthiopiaFijiFinlandFranceFrench Southern TerritoriesGabonGambiaGeorgiaGermanyGhanaGreeceGrenadaGuatemalaGuineaGuinea-BissauGuyanaHaitiHeard Island and McDonald IslandsHondurasHungaryIcelandIndiaIndonesiaIranIraqIrelandIsraelItalyIvory CoastJamaicaJapanJordanKazakhstanKenyaKiribatiKorea, NorthKorea, SouthKuwaitKyrgyzstanLaosLatviaLebanonLesothoLiberiaLibyaLiechtensteinLithuaniaLuxembourgMacedoniaMadagascarMalawiMalaysiaMaldivesMaliMaltaMarshall IslandsMauritaniaMaur itiusMexicoMicronesiaMoldovaMonacoMongoliaMontenegroMoroccoMozambiqueNamibiaNauruNepalNetherlandsNew ZealandNicaraguaNigerNigeriaNorwayOmanPakistanPalauPanamaPapua New GuineaParaguayPeruPhilippinesPolandPortugalQatarRomaniaRussian FederationRwandaSaint Kitts and NevisSaint LuciaSaint Vincent and the GrenadinesSamoaSan MarinoSao Tome and PrincipeSaudi ArabiaSenegalSerbiaSeychellesSierra LeoneSingaporeSlovakiaSloveniaSolomon IslandsSomaliaSouth AfricaSouth Georgia and the South Sandwich IslandsSouth SudanSpainSri LankaSudanSurinameSwazilandSwedenSwitzerlandSyriaTajikistanTanzaniaThailandTogoTongaTrinidad and TobagoTunisiaTurkeyTurkmenistanTuvaluUgandaUkraineUnited Arab EmiratesUnited KingdomUnited StatesUruguayUzbekistanVanuatuVatican CityVenezuelaVietnamYemenZambiaZimbabwe
County
AlachuaBakerBayBradfordBrevardBrowardCalhounCharlotteCitrusClayCollierColumbiaDeSotoDixieDuvalEscambiaFlaglerFranklinGadsdenGilchristGladesGulfHamiltonHardeeHendryHernandoHighlandsHillsboroughHolmesIndian RiverJacksonJeffersonLafayetteLakeLeeLeonLevyLibertyMadisonManateeMarionMartinMiami-DadeMonroeNassauOkaloosaOkeechobeeOrangeOsceolaPalm BeachPascoPinellasPolkPutnamSanta RosaSarasotaSeminoleSt.