Как выглядит абак фото: Что такое Абак | Древняя счетная доска

Что такое Абак | Древняя счетная доска

Абак, или счетная доска похож на привычные деревянные счеты. Этот счетный прибор широко использовался еще с древних времен, в разных видах он был представлен практически во всех странах мира. Известно, что первые абаки применялись еще в третьем тысячелетии до нашей эры.

Содержание:

• Что такое абак
• Древний Вавилон
• Древняя Греция и Древний Рим
• Страны Европы эпохи Средневековья
• Американский континент
• Китай
• Япония
• Русский абак
• Современные счеты

Что такое абак

Все разновидности инструмента имеют схожую конструкцию: у них есть полосы со счетным материалом. В разных вариантах эту функцию выполняют косточки, камешки, бусинки и прочие мелкие предметы.

Появление абака было связано с развитием государств и торговых связей. Счет на пальцах, веревки с узелками и прочие примитивные приспособления не могли удовлетворить возрастающие потребности в вычислении.

Развитие же письменного счета в древности сдерживалось отсутствием подходящего материала. Традиционные восковые и глиняные таблички для этого мало подходили, пергамент стоил дорого, а бумага появилась значительно позже.

В результате появился абак – инструмент, который в разы упростил и облегчил устные вычисления. Он широко применялся в Древней Греции, Древнем Риме и Древнем Китае примерно с V века до нашей эры.

Древний Вавилон

Археологические исследования свидетельствуют, что впервые абак изобрели в Древнем Вавилоне примерно в VI век до н.э. Счетное устройство тех времен имело вид деревянной доски, покрытой песком. На песке чертили борозды, в которые помещали камешки для обозначения цифр.

В Древнем Вавилоне применялась шестидесятеричная система счисления. Поскольку уложить 60 камешков в каждую бороздку было затруднительно, древние вавилоняне придумали оригинальный выход – разделили счетную доску горизонтальной полосой. В одной части помещали камешки (от 1 до 9), соответствующие единицам, во второй части – соответствующие десяткам (от 1 до 5). Как только в бороздке набиралось 59 камешков, их снимали, а в следующее углубление помещали один камень.

Древняя Греция и Древний Рим

Древние греки внесли существенные изменения в конструкцию вавилонской доски для арифметических вычислений. Вместо дощечки с песком они стали использовать пластину с прорезями, по которым двигались камешки. Древнегреческие абаки изготавливали из мрамора или дерева, их было удобно брать с собой в дорогу. Они использовались для счета по пятеричной системе счисления.

В Древнем Риме абаки стали изготавливать не только из камня или дерева, но и из бронзы, стекла, слоновой кости. До наших дней сохранился древнеримский абак, представляющий собой доску с восемью прорезанными желобками, разделенными на две неравные части (длинную и короткую).

Страны Европы эпохи Средневековья

В европейских странах абак начали массово применять примерно с X столетия. Вместо камешков в европейском абаке начали использоваться жетоны с числовыми обозначениями.

Правила счета с применением этого инструмента подробно описаны в трудах многих ученых того времени. Самые известные из них – работы французского ученого и священнослужителя Герберта, который подробно описал производство всех видов арифметических вычислений с помощью абака.

Активное использование абака в европейских странах продлилось до XVIII столетия. В течение всей эпохи Средневековья абацисты (так называли приверженцев этой методики вычислений) активно боролись с так называемыми алгоритмиками, которые пытались внедрить алгоритмические методы совершения арифметических действий.

Американский континент

Свой абак изобрели и народы американского континента. У ацтеков этот счетный инструмент имел вид деревянного каркаса, в котором натягивались нити с нанизанными кукурузными зернами. Рама была разделена на две части горизонтальной перекладиной. В одной части на нитях было по три зерна, на другой – по четыре.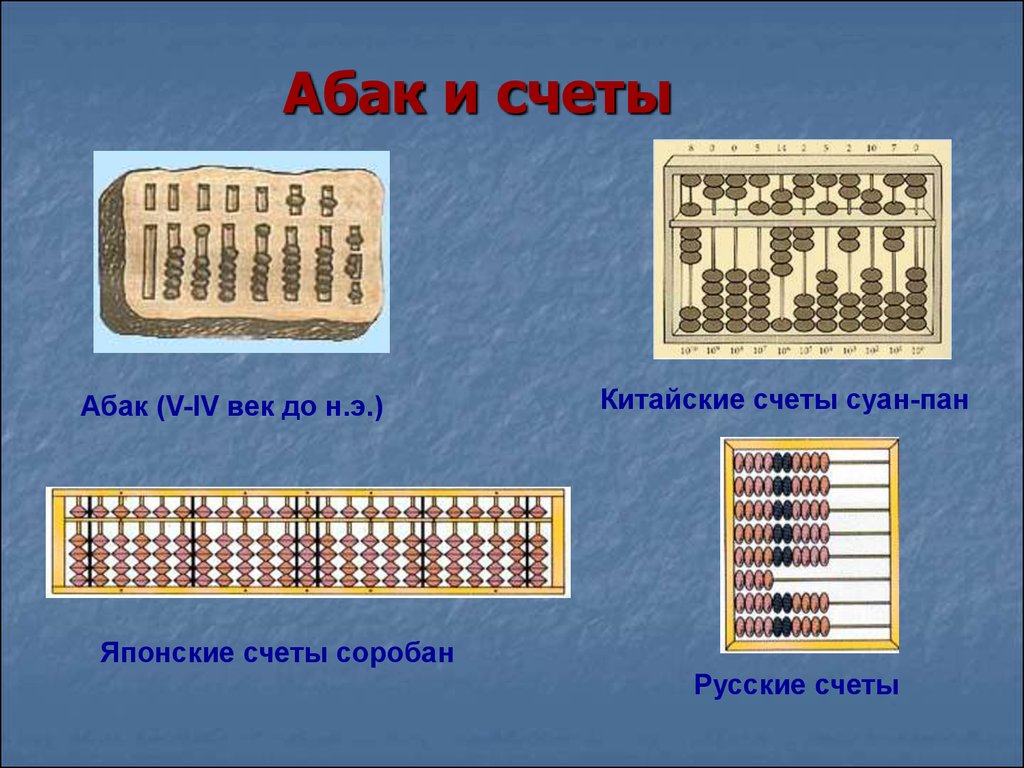 Известно, что такие приспособления использовались у ацтеков примерно в X-XI столетии.

Китай

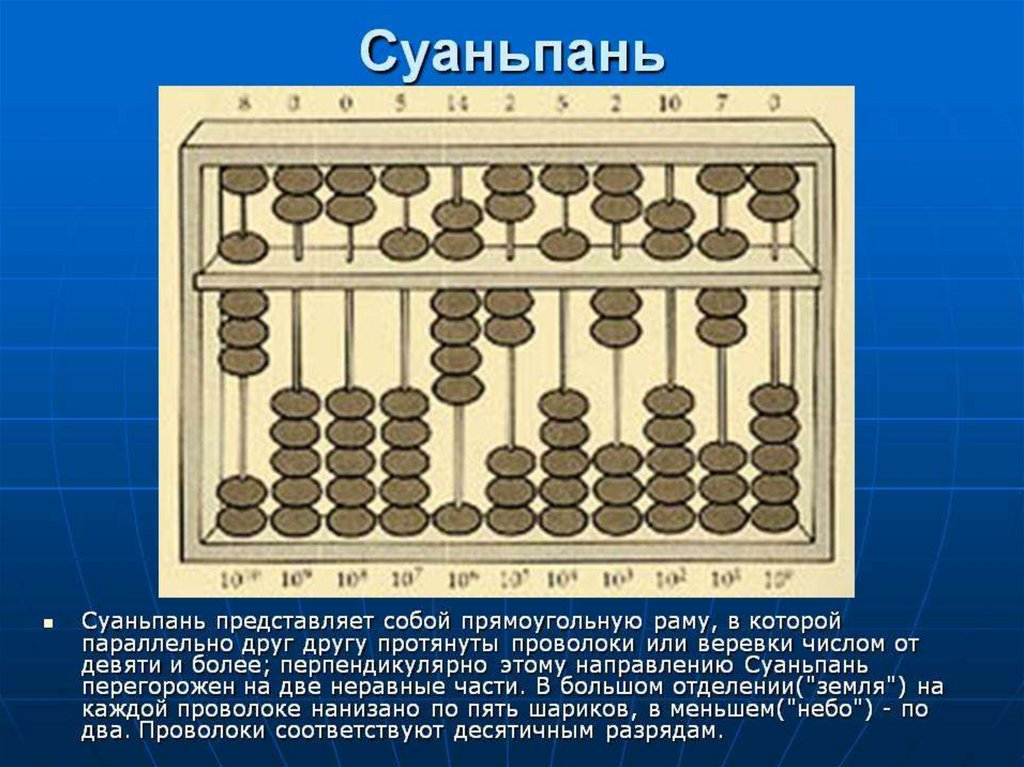
Древнекитайский аналог абака носил название суаньпань, он был предназначен для пятеричной системы счисления. Счетный инструмент представлял собой деревянную рамку, которая была поделена по горизонтали на две неравные части. Внутри каркаса натягивали проволочки или веревки в количестве 9 штук и более.

В нижнем (большем) отделении на проволочки нанизывали по пять бусинок, в верхней (меньшей) секции – по две. Нижнее отделение называлось «земля», а верхнее – «небо».

Япония

Японский аналог абака называется соробан. Его прародителем является китайский суаньпань, который попал в Японию в XV – XVI веках. Соробан имеет более простую конструкцию, у японской счетной доски всего одна косточка в верхнем отделении.

Русский абак

Русский вариант абака – всем известные счеты – был изобретен на рубеже XV-XVI столетий. Он был предназначен для десятичной системы и позволял применять четверти, десятые и сотые, что является его главным отличием от классических конструкций.

Современные счеты

Русские счеты в практически неизменном виде применялись в торговле до конца XX века. Обучение их применению входило в школьную программу СССР. Из употребления счеты вытеснили массово появившиеся электронные калькуляторы, однако и сегодня их можно встретить в некоторых торговых заведениях.

Сегодня для обучения детей скоростному устному счету активно применяется японский вариант абака – соробан. В Японии и Китае он уже давно является элементом школьной программы и применяется на уроках математики в младших классах.

См. также Что такое ментальная арифметика и для чего она нужна

Рейтинг: 5/5 – 4 голосов

Что такое абакус? Как считать на абакусе?

Содержание

1. Как выглядит абак?
2. Распределяем числа
3. Как проводить сложение и вычитание на абакусе?
4. Как умножать и делить на абакусе?
5. Насколько быстро можно работать на абакусе?

Многие люди слова абакус и соробан слышат, чуть ли не впервые. А ведь эта система подсчетов использовалась в Древней Греции, Риме и Китае еще за пять веков до нашей эры. Легкая система подсчета положила начало нашим классическим счетам с костяшками, но абак намного проще и понятней в использовании.

Детям система устного счета абакус полезна не только тем, что они научатся быстро считать и понимать цифры, со временем они обучаются ими пользоваться ментально, в воображении. Эта «игра» позволяет научить даже первоклашку очень быстро считать и выполнять абсолютно все арифметические действия, сначала с помощью специального прибора, а потом и в уме, для этого ему нужно будет только научиться считать до десяти.

Как выглядит абак?

Специальные счеты, используемые в системе ментального счета абакусе, называются абак, линейка или также абакус. Они имеют классический вид:

Это рамка со спицами, на которые надеты костяшки, по пять штук на каждой. Количество спиц на разных абакусах отличается, а вот костяшек на каждой из них пять, кроме того, одну костяшку на каждой спице отделяет поперечная планка.

Считающий в воображении сам рассчитывает название каждой спицы, на рисунке выше подписано распределение без десятичных знаков, но если они нужны, то первые левые спицы отводятся под них, а уже потом начинаются единицы. (Абакус и абакус с десятичными знаками)

 

Распределяем числа

Чтобы понять, как считать на абакусе, надо просто разобраться, как на нем распределяются цифры. В дальнейшем мы будем использовать распределение на спицах, начиная с единицы, так как будем работать с целыми числами. Чтобы работать с десятичными, нужно для начала разобраться в элементарной арифметике.

Первая правая спица, когда одна костяшка сверху – наименьшее десятичное значение, в подсчетах, если мы считаем миллиарды, значит, наименьшее – миллиард, если десятичные дроби, то тысячные. Далее спицы считаются с умножением на 10.

Для пользования спицами надо запомнить, как распределяется число на абакусе:

• на спице пять костяшек;
• костяшка над планкой это 5, если она опущена – это говорит что число больше пяти, если поднята, значит меньше;
• костяшки ниже планок – 1, 2, 3, 4, сколько поднято костяшек, столько и надо учесть;
• если костяшка 5 опущена, то прибавляется число костяшек, поднятых снизу, если они не подняты, то значит на спице 5.

Например, число 15 будет выглядеть вот так:

66 вот так:

А 81549 вот так:

Кажущаяся сложность пропадает практически через пять минут, ребенок очень быстро начинает разбираться в самых сложных числах. Главное – понять принцип работы этого прибора.

Как проводить сложение и вычитание на абакусе?

Считать на абакусе достаточно просто. Для понимания возьмем пример 26+34 и сложим его на линейке абаке.

Устанавливаем первое число 26 :

Раскладываем все числа на простые цифры, не забывая, к какой спице они относятся: 2 и 3 к десяткам, а 6 и 4 к единицам. Производим сложение простых чисел. 6+4 и 2+3.

Теперь сдвигаем единицы на первой спице 6+4 =10, то есть на 1 спице надо показать 0, и развести все костяшки по местам, а к двум костяшкам на второй спице добавить еще одну, получим 30:

Но мы добавляли не 4, а 34, поэтому на второй спице надо добавить еще 3 костяшки и показать цифру 6, для этого опускаются снизу 2 костяшки и «5».

Итого мы получаем 60.

Сложение всегда начинается с меньшего числа с переходом к большему. Если костяшек на спице получается больше чем 9, тогда на соседней спице добавится еще одна.

В случае с вычитанием система та же, начинаем с меньшего, только если вычитается от меньшей цифры большая, тогда они меняются местами, а с соседней спицы убирается костяшка.

Например, 15-13:

• ставим 15;
• раскладываем число на простые цифры 1 и 5 и 1 и 3, от 1 отнимаем 1, от 5 отнимаем 3 и получаем 2:

Эта система расчетов при должной сноровке занимает около двух-трех секунд. Со временем сама линейка уже будет не нужна, она сама будет возникать в мыслях.

Как умножать и делить на абакусе?

Умножение на линейке тоже достаточно простое, для этого нужно только освоить таблицу умножения от 1 до 10 и запомнить одно правило: десятки умножаем на единицы, потом единицы умножаем на единицы. Если ребенок уже разобрался, как считать на абакусе, все действия будут занимать не больше минуты.

Для примера возьмем простое задание 11х5, которое решается в два действия:

1. 10х5=50.
2. 1х5=5.

Для начала на абакусе набирается ответ на первый пример, 50:

потом к нему добавляется ответ на второй пример, 5:

И в результате мы видим на абаке ответ 55.

Для проведения более сложных действий, когда берутся более сложные примеры, тогда задание решается в последовательности: десятки умножаются на десятки, единицы на десятки, десятки на единицы, единицы на единицы. То есть, сначала все цифры, постепенно от большего к меньшему перемножаются и набираются последовательно на абаке.

Например, 611 Х24:

Решается это так, нули прячутся и берутся цифры без них, а их количество определяет, на сколько спиц надо сдвинуться влево, кроме того, если результат получился двузначный, значит надо сместиться еще на одну спицу:

1. 6х2=12 – при умножении результат набираем на той спице, к которой относится число и сдвигаемся вправо на столько спиц, сколько нулей в числе, на которое умножают, в нашем случае в 20 один ноль, то есть результат 12 набирается не на сотнях, а на тысячах. Но если результат имеет две цифры, тогда надо сместиться еще на одну спицу. То есть, в нашем случае 12 набирается на спицах, отвечающих на десять тысяч и тысячи.(12000)
2. 1х2=2 – единица относится к десяткам, в 20 один ноль, то есть сдвигаемся на одну спицу и добавляем ответ в сотнях.(12200)

1х2=2 единица относится к единицам, а в 20 один ноль, то есть исходя из правил, добавляем ответ в десятках.(12220)

3. Теперь переходим к следующему порядку и умножаем сотни на единицы, десятки на единицы и единицы на единицы.
4. 6х4=24 – в 4 нет нолей, мы сдвигаемся только на одну спицу, так как в ответе две цифры, и добавляем 2 костяшки к тысячам и 4 к сотням. (14620)
5. 1х4=4 – добавляем в десятки 4 костяшки. (14660)
6. 1х4=добавляем теперь 4 костяшки в единицы. (14664)

Последнее действие можно не делать, но сначала нужно проверить: берем калькулятор, умножаем 611х24, получаем 14664 и радуемся своей сноровке.

Деление проводится по такому же принципу, только производится не сложение результатов на линейке, а вычитание. Сдвигание по спицам происходит слева направо.

Насколько быстро можно работать на абакусе?

Даже на самые сложные действия ребенок, как и взрослый, потратит не больше одной минуты, главное во всем этом деле – практика и понимание, как считать на абакусе. Чем чаще и больше заниматься, тем проще будет перейти на систему ментального вычисления, без каких либо приспособлений. Для начала со сложными примерами понадобится еще ручка и бумага, чтобы расписать последовательность действий и не запутаться, но пара дней практики – и ничего кроме абака уже не понадобится.

Главное – не стесняться перепроверять результат и показывать маленькие победы. Это позволяет стимулировать желание пользоваться этой древней системой. А она, в свою очередь, развивает память, фантазию и логику.

Счеты | Encyclopedia.com

gale

просмотров обновлено 27 июня 2018

---

Счеты — самое древнее из известных счетных устройств. Он выдержал испытание временем и до сих пор используется в некоторых странах. Счеты состоят из деревянной рамы, стержней и бусин. Каждый стержень представляет собой разное разрядное значение — единицы, десятки, сотни, тысячи и так далее. Каждая бусина представляет собой число, обычно 1 или 5, и ее можно перемещать по стержням. Сложение и вычитание можно легко выполнять, перемещая бусины по проволоке счетов.

Слово счеты на латыни. Оно взято из греческого слова abax , что означает «плоская поверхность». Предшественники счетов — счетные доски — были именно такими: плоскими поверхностями. Часто это были просто доски или столы, по которым можно было перемещать гальку или камни, чтобы показать сложение или вычитание. Самые ранние счетные таблицы или доски могли быть просто линиями, нарисованными на песке. Они превратились в настоящие столы с канавками для перемещения счетчиков.

Поскольку счетные доски часто изготавливались из материалов, которые со временем портились, их было найдено немного. Самая старая из найденных счетных досок называется Саламинской табличкой. Он был найден на острове Саламин, греческом острове, в 189 г.9. Его использовали вавилоняне около 300 г. до н. э. К тому же периоду времени были найдены рисунки людей, использующих счетные доски.

Есть свидетельства использования счетов в Древнем Риме (753 г. до н. э. – 476 г. н. э.). Было найдено несколько ручных счетов того времени. Они очень маленькие, помещаются на ладони. У них есть прорези с бусинами, которые можно перемещать в прорезях вперед и назад, как счетчики на счетной доске. Поскольку их было обнаружено такое небольшое количество, они, вероятно, не получили широкого распространения. Однако они напоминают китайские и японские счеты, предполагая, что использование счетов распространилось из Греции и Рима в Китай, а затем в Японию и Россию.

Суанпан

В Китае счеты называют “суанпан”. Мало что известно о его раннем использовании, но правила его использования появились в тринадцатом веке. Суанпан состоит из двух палуб, верхней и нижней, разделенных перегородкой. В верхней колоде по две бусинки в каждом столбце, а в нижней колоде по пять бусинок в каждой колонке. Каждая из двух бусинок в колонке единиц в верхней колоде стоит 5, а каждая бусина в нижней колоде стоит 1. Крайний правый столбец — это колонка единиц. Следующий столбец слева — это столбец десятков и так далее. Затем счеты можно читать так же, как если бы вы читали число. Каждый столбец можно рассматривать как поместите значение и общее количество бусинок в каждом столбце как цифру для этого значения места.

Бусины перемещаются к среднему лучу, чтобы показывать разные числа. Например, если три бусинки из нижней колоды в колонке единиц были перемещены к середине, на счетах отображается цифра 3. Если одна бусина из верхней колоды и три бусинки из нижней колоды в колонке единиц были перемещены в средней, это равно 8, так как бусина из верхней колоды стоит 5,

Чтобы сложить числа на счетах, бусинки перемещаются к середине. Чтобы вычесть цифры, бусины перемещаются обратно к краям рамки. Посмотрите на следующий простой расчет (12 + 7 = 19) с использованием suanpan.

Счеты слева показывают число 12. В нижней колоде в разряде десятков есть одна бусинка, поэтому цифра в десятках равна 1. В нижней колоде в разряде единиц две бусинки, поэтому цифра в колонке единиц равна 2. Затем это число читается как 12. Чтобы добавить 7 на счеты, просто переместите одну бусину в колонке единиц верхней колоды (5) и еще две бусины в колонке единиц нижней колоды. (2). Теперь суанпан показывает 9в колонке единиц и 10 в колонке десятков равно 19.

Соробан

Японские счеты называются соробан. Хотя соробан не использовался широко до семнадцатого века, он все еще используется сегодня. Японские ученики впервые изучают счеты в подростковом возрасте, а иногда посещают специальные школы счетов. Были даже проведены конкурсы между пользователями соробана и современного калькулятора. Чаще всего побеждает соробан. Умелый человек обычно быстрее считает на соробане, чем на калькуляторе.

Соробан мало чем отличается от китайских счетов. Вместо двух рядов бус в верхней колоде всего один ряд. В нижней колоде вместо пяти рядов бусинок всего четыре. Бусины равны тому же количеству, что и в китайских счетах, но с одной бусиной меньше, числа не переносятся. Например, на суанпане число 10 можно показать, переместив две бусины в верхней колоде столбца единиц или только одну бусину в верхней колоде столбца десятков. На соробане 10 можно показать только в колонке десятков. Бусины в колонке единиц в сумме дают только 9(одна бусина по 5 и четыре бусины по 1).

Схоты

Русские счеты называются схоты. Он вошел в употребление в 1600-х годах. Мало что известно о том, как это произошло. Схоты отличаются от других счетов тем, что не разделены на колоды. Также бусины на шоте передвигаются по горизонтальным, а не вертикальным проволокам. Каждая проволока состоит из десяти бусин, и каждая бисерина стоит 1 в столбце единиц, 10 в столбце десятков и так далее. В счетах также есть провод для четверти рубля, российской валюты. Две средние бисерины в каждом ряду темного цвета. Шоти показывает 0, когда все бусины сдвинуты вправо. Бусины перемещаются слева направо, чтобы показать числа. Скоты до сих пор используются в современной России.

см. также Калькуляторы; Математические устройства, ранние.

Келли Дж. Мартинсон

Библиография

Пуллан, Дж. М. История счетов. New York: Frederick A. Praeger, Inc., 1969.

---

СЧЕТЫ ПРОТИВ КАЛЬКУЛЯТОРА

В конце 1946 года служащий японской почты, хорошо умеющий пользоваться соробаном (японскими счетами), участвовал в соревновании с американским солдатом в сложение, вычитание и умножение чисел. Американец использовал самый современный на тот момент электромеханический калькулятор. В четырех из пяти состязаний японский чиновник с соробаном был быстрее, уступая лишь в задачах на умножение.

---

Математика Мартинсон, Келли Дж.

Гейл

просмотров обновлено 08 июня 2018

Счеты — древняя счетная машина. Этому простому устройству около 5000 лет, и считается, что оно возникло в Вавилоне. По мере того, как понятия ноль и арабские числа получили широкое распространение, основные математические функции упростились, а использование счетов уменьшилось. В большинстве стран мира для математических вычислений используются арифмометры, калькуляторы и компьютеры, но сегодня Япония, Китай, Ближний Восток и Россия все еще используют счеты, и школьников в этих странах часто учат пользоваться счетами. В Китае счеты называются суан пан, что означает счетный поднос. В Японии счеты называются соробан. У японцев ежегодно проводятся экзамены и соревнования по вычислениям на соробане.

До изобретения счетных машин люди использовали пальцы рук и ног, делали отметки в грязи или песке, делали зарубки в костях и дереве или использовали камни для счета, подсчета и учета количества. Первые абаки представляли собой неглубокие лотки, заполненные слоем мелкого песка или пыли. Цифры наносились и легко стирались пальцем. Некоторые ученые считают, что термин счеты происходит от семитского слова, обозначающего пыль, abq .

Современные счеты изготавливаются из дерева или пластика. Он прямоугольный, часто размером с крышку обувной коробки. Внутри прямоугольника находится не менее девяти вертикальных стержней, на которые нанизаны подвижные бусины. Счеты основаны на десятичной системе. Каждый стержень представляет собой столбцы записанных чисел. Например, начиная справа и двигаясь влево, первый стержень представляет единицы, второй стержень представляет десятки, третий стержень представляет сотни и так далее. Горизонтальная перекладина расположена перпендикулярно стержням, разделяющим счеты на две неравные части. Подвижные борта располагаются либо над, либо под перекладиной. Бусины над перекладиной называются небесными, а нижние – земляными. Каждая бусина неба имеет ценность в пять единиц, а каждая бусина земли – в одну единицу. В китайском суан пан две бусины неба и пять бусинок земли, а в японском соробане одна бусина неба и четыре бусины земли.

Эти две абаки немного отличаются друг от друга, но ими манипулируют и используют одинаково. Русская версия счетов имеет множество горизонтальных стержней с подвижными неразделенными бусами, по девять в колонке.

Для работы соробан или суан сковороду кладут горизонтально, а все бусины отодвигают к внешним краям

от перекладины. Обычно небесные бусины двигаются указательным пальцем, а земные бусины – большим пальцем. В первом случае одна земляная бусина должна быть прижата к перекладине. Во-вторых, потребуются две бусины земли. Для номера пять к перекладине будет прижата только одна небесная бусина. Для числа шесть потребуется одна бусина неба (пять единиц) плюс одна бусина земли (одна единица). Число 24 будет состоять из четырех бусинок земли на первом стержне и двух бусинок земли на втором стержне. Таким образом, число 26 будет состоять из одной бусины неба и одной бусины земли на первом стержне и двух бусинок земли на втором стержне. Сложение, вычитание, умножение и деление можно выполнять на счетах.

Опытные пользователи счетов могут решать длинные задачи на умножение и деление и даже находить квадратный или кубический корень из любого числа.

См. также Арифметика; Математика.

Научная энциклопедия Гейла

Гейл

просмотров обновлено 27 июня 2018

Счеты — древняя счетная машина. Этому простому устройству около 5000 лет, и считается, что оно возникло в Вавилоне. По мере того, как понятия ноль и запись арабских чисел получили широкое распространение, основные математические функции упростились, а использование счетов уменьшилось. В большинстве стран мира для математических вычислений используются арифмометры, калькуляторы и компьютеры, но сегодня Япония, Китай, Ближний Восток и Россия все еще используют счеты, и школьников в этих странах часто учат пользоваться счетами. В Китае счеты называются суан пан, что означает счетный поднос. В Японии счеты называются соробан. У японцев ежегодно проводятся экзамены и соревнования по вычислениям на соробане.

До изобретения счетных машин люди использовали пальцы рук и ног, делали отметки в грязи или песке, делали зарубки в костях и дереве или использовали камни для счета, подсчета и учета количества. Первые абаки

представляли собой неглубокие лотки, заполненные слоем мелкого песка или пыли. Цифры наносились и легко стирались пальцем. Некоторые ученые считают, что термин счеты происходит от семитского слова, обозначающего пыль, abq .

Современные счеты изготавливаются из дерева или пластика. Он прямоугольный, часто размером с крышку обувной коробки. Внутри прямоугольника находится не менее девяти вертикальных стержней, на которые нанизаны подвижные бусины. Счеты основаны на десятичной системе. Каждый стержень представляет собой столбцы записанных чисел. Например, начиная справа и двигаясь влево, первый стержень представляет единицы, второй стержень представляет десятки, третий стержень представляет сотни и так далее. Горизонтальная перекладина перпендикулярно стержням, разделяющим счеты на две неравные части. Подвижные борта располагаются либо над, либо под перекладиной. Бусы над перекладиной называются небом бусы, а бусины внизу называются земляными бусами. Каждая бусина неба имеет ценность в пять единиц, а каждая бусина земли – в одну единицу. В китайском суан пан две бусины неба и пять бусинок земли, а в японском соробане одна бусина неба и четыре бусины земли. Эти две абаки немного отличаются друг от друга, но ими манипулируют и используют одинаково. Русская версия счетов имеет множество горизонтальных стержней с подвижными неразделенными бусами, по девять в колонке.

Для работы соробан или суан сковороду кладут горизонтально, а все бусины отодвигают к внешним краям от перекладины. Обычно небесные бусины двигаются указательным пальцем, а земные бусины – большим пальцем. В первом случае одна земляная бусина должна быть прижата к перекладине. Во-вторых, потребуются две бусины земли. Для номера пять к перекладине будет прижата только одна небесная бусина. Для числа шесть потребуется одна бусина неба (пять единиц) плюс одна бусина земли (одна единица). Число 24 будет состоять из четырех бусинок земли на первом стержне и двух бусинок земли на втором стержне. Таким образом, число 26 будет состоять из одной бусины неба и одной бусины земли на первом стержне и двух бусинок земли на втором стержне. Сложение , вычитание , умножение и деление могут выполняться на счетах. Опытные пользователи счетов могут решать длинные задачи на умножение и деление и даже находить квадратный корень из из или кубический корень из любого числа.

См. также Арифметика; Математика.

Научная энциклопедия Гейла

Гейл

просмотров обновлено 14 мая 2018 г.

Счеты — древняя счетная машина. Считается, что этот простой аппарат появился в Вавилоне около 5000 лет назад. Сегодня счеты по-прежнему широко используются в Японии, Китае, на Ближнем Востоке и в России. В Китае счеты называются 9.0013 suan pan, означает «поднос для подсчета». В Японии это называется соробан . японских школьников до сих пор учат пользоваться соробаном , и ежегодно проводятся соревнования по поиску самых умелых вычислителей.

Историки считают, что первые счеты представляли собой неглубокие лотки, заполненные мелким песком или пылью. Номера записывались и легко стирались пальцем. На самом деле слово абак, возможно, произошло от семитского слова, означающего «пыль», abq.

Современные счеты изготавливаются из дерева или пластика. Он состоит из прямоугольной рамки размером с крышку обувной коробки. Внутри рамы находится не менее девяти вертикальных стержней, нанизанных на подвижные бусины. Горизонтальная перекладина, перпендикулярная стержням, разделяет счеты на две неравные части. Бусины над перекладиной называются небесными, а те, что ниже перекладины, называются земными.

Числовое значение каждой бусины зависит от ее положения на счетах. Каждая бусина небес имеет ценность в пять раз больше, чем бусина земли под ней. Каждый стержень представляет собой столбцы записанных чисел. Бусины на самом дальнем правом вертикальном стержне имеют свои значения, умноженные на единицу. На этом стержне каждая бусина земли — одна, а каждая бусина неба — пять. Бусины на втором стержне справа, однако, имеют значение, умноженное на 10. На этом стержне каждая земная бусина представляет 10, а каждая небесная бусина – 50. Бусины на третьем стержне справа имеют свое значение, умноженное на 100, так что каждая бусина земли представляет 100, а каждая бусина неба — 500, и так далее.

Для работы счеты кладут горизонтально и все бусины сдвигают к внешним краям, от перекладины. Затем бусины сдвигаются вверх или вниз, чтобы представить число. Число 7, например, представлено перемещением одной бусины неба (стоимостью 5) вниз к перекладине и двух бусинок земли (стоимостью по одной) вверх к перекладине. Число 24 представлено перемещением вверх двух бусинок земли на втором стержне (стоимостью 10 каждая) и четырех бусинок земли на первом стержне (стоимостью 1 каждая). Счеты позволяют решать сложные задачи на сложение, вычитание и даже на умножение и деление. Опытные пользователи могут даже найти квадратный корень из любого числа.

[ См. также Арифметика; Математика ]

UXL Encyclopedia of Science

буря

просмотров обновлено 23 мая 2018

Счеты, древнее счетное устройство, вероятно, возникло в Вавилоне около 2400 г. до н.э. Это был первый в мире калькулятор, современные версии которого используются до сих пор.

Счеты представляют собой деревянную или металлическую прямоугольную раму с вертикальными стержнями, содержащими подвижные бусины. До появления счетов в качестве вычислительных инструментов использовались камни. У этого было два основных недостатка: при вычислении легко было потерять след, а найти или транспортировать большое количество камней было сложно. Напротив, счеты были очень портативным и простым в использовании устройством, которое оказалось отличной альтернативой мешку с камнями.

Счеты использовались на всем Ближнем Востоке и на востоке вплоть до Японии. Количество вертикальных стержней и бусин на каждом стержне варьировалось от культуры к культуре, но основная функция счетов — подсчет стоимости и количества товаров — оставалась неизменной.

Китайские счеты, наиболее распространенная сегодня форма, делят рамку горизонтальной перекладиной. Считается, что классическая версия, известная как suan-pan, или «счеты 2/5», возникла примерно в 1200 году н. э. Область выше горизонтальная перекладина, небо, содержит две бусины на вертикальную перекладину; каждый имеет значение пять. В нижней области, или земле, каждый вертикальный стержень содержит пять бусин, каждая со значением один. Каждый вертикальный стержень представляет единицу из десяти. Вычисление выполняется путем перемещения шариков к горизонтальному разделителю или от него. В середине 1800-х счеты 2/5 были заменены счетами 1/5, а к 1930-х годов наиболее широко используемой формой счетов были японские счеты соробан, или 1/4 счеты.

Хотя карманные калькуляторы и другие устройства заменили счеты в большинстве стран мира, многие азиатские владельцы магазинов и школьники до сих пор используют счеты для основных арифметических функций, таких как сложение, вычитание и умножение.

см. также Кости Нейпира; Логарифмическая линейка.

Берта Кугельман Моримото

Библиография

Меннингер, Карл. Числовые слова и числовые символы. Кембридж, Массачусетс: Массачусетский технологический институт Press, 1969.

Интернет-ресурсы

Университет Райерсона, факультет электротехники и вычислительной техники, Счеты: искусство счета с помощью бусин . .

Компьютерные науки Моримото, Берта Кугельман

Оксфорд

просмотра обновлено 17 мая 2018 г.

счеты (мн. счеты).
1. Пластина с плоской вершиной, также называемая tailloir , верхняя часть капители колонны, на которой держится архитрав. Греко-дорические счеты – самые простые, они состоят из квадратного неформованного блока, называемого plinthus , но счеты различаются в зависимости от используемого порядка.

2. Плоская плита, поддерживаемая подиумом или ножками, использовавшаяся в качестве буфета или для демонстрации тарелок и т. д. в древности.

3. Панно на античной стене.

Словарь архитектуры и ландшафтной архитектуры ДЖЕЙМС СТИВЕНС КЕРЛ н. (мн. -cus·es) 1. продолговатая рамка с рядами проволок или желобков, по которым скользят бусины, используемая для счета.2. Архит. плоская плита на вершине капители, поддерживающая архитрав.

abacus

Оксфордский карманный словарь современного английского языка

oxford

просмотров обновлено 21 мая 2018

счеты продолговатая рамка с рядами проволок или желобков, по которым скользят бусины, используемые для счета; возможно, это развитие классической счетной доски, она широко использовалась в Европе в средние века и до сих пор используется в некоторых странах.

Слово в этом смысле восходит к концу 17 века; это записано на позднем среднеанглийском языке, обозначая доску, усыпанную песком, на которой можно рисовать фигуры, и происходит через латынь от греческого abax , abak- ‘плита, чертёжная доска’, семитского происхождения и, вероятно, связан с ивритом ‘āḇāq ‘пыль’.

Оксфордский словарь фраз и басен ELIZABETH KNOWLES

oxford

просмотров обновлено 11 июня 2018 г. Одна форма состоит из бусинок, нанизанных на проволоку и расположенных столбиками.

Всемирная энциклопедия

Оксфорд

просмотра обновлено 21 мая 2018 г.

счеты XVI. — Л. счеты , ф. гр. абакс , абак- стол.

Краткий Оксфордский словарь английской этимологии T. F. HOAD

Подробнее Из encyclopedia.

com

Сложение Сложение, обозначенное знаком +, представляет собой метод комбинирования чисел. Результат сложения двух чисел называется их суммой. Добавление натуральных чисел Consi… Натуральные числа , Натуральные числа — это обычные числа, 1, 2, 3,. . . с которыми люди считают. Иногда их называют счетными числами. Натуральные числа… Цинь Чиу-шао, Цинь Чиу-Шао (род. Сычуань, Китай, ок. 1202 г.; г. Гуандун, Китай, ок. 1261 г.), математика. Цинь цзю-чиу-шао (литературное название Дао-ку) было описано… Ноль, Ноль часто отождествляется с «ничто», но это не очень хорошая аналогия. Ноль может быть отсутствием качества, но может быть и отправной точкой, такой… Двигаться, двигаться /moōv/ • v. 1. [внутр.] идти в определенном направлении или образом; изменить положение: она встала и подошла к двери он позволил своим глазам пройтись по ней… Арифметика Арифметика — это раздел математики, связанный с числовыми манипуляциями с числами с помощью операций сложения, вычитания, умножения…

About this article

All Sources –

Updated Aug 13 2018 About encyclopedia. com content Print Topic

You Might Also Like

NEARBY TERMS

abaculus

abaciscus

ABAC

ABAA

аб.

Ab-

ab ovo

ab иници.

AB 1586 Антидискриминационный закон штата Калифорния для трансгендеров

AAZPA

AAWC

AAVS

Aavik, Juhan

Aavid Thermal Technologies, Inc.

AAVC

Aav, Evald

AAV

AAUW Legal Advocacy Fund

AAUW

AAUP

AAUN

AAU

AATUF

AATTA

AATT

счеты

Abad Casasempere, Amalia, and Companions, Bb.

Абад-и-Кейпо, Мануэль (1751–1825)

Abadeh

Abadi, Jennifer Felicia 1967 (?) –

Abadía Méndez, Miguel (1867–1947)

Abadie, Paul

Abady, Josephine (C. 1950–2002)

Abadys, Nickephine (c. 1950–2002)

---

Abadys, Nickephine (C. 1950–2002)

---

– Nickedy, Josephine.

Abagtha

Abaijah, Josephine (1942–)

Abaijah, Josephine (1942—)

Abailard, Pierre

Abair, Mindi

Abajian, Kathryn J. 1944- (Kathryn jabalena, Abalena, Abalena, Abalena, Abalena, Abalena, Abalena, Abalena, Abalena, Abalena, Abalena, Abalena, Abalena, Abalena, Abalena, Abalena, Abalena, Abalena, Abalena. 1930–)

Abakanowicz, Magdalena (1930—)

Abakuá

Abalos, José de

Ábalos, Rafael 1956-

abamurus

Abana

Abandon Ship

abandoned

abandoned channel

abandonment facies association

Abacus -Первый в мире калькулятор | История компьютеров

Содержание

1.	Введение
2.	Краткая история Abacus
3.	Основы счетов
4.	Техника счетов
5.	Заключение
6.	Часто задаваемые вопросы

11 ноября 2020 г.

Время считывания: 5 минут

Введение

Помните ENIAC, первый в мире компьютер? Очевидно.

Вы бы купили его для повседневной работы? Очевидно нет.

В эту современную эпоху технологий то, что было запущено вчера, сегодня может устареть. Итак, как можно ожидать, что мы будем использовать 66-летний компьютер?

А что, если мы скажем вам, что вы, как и весь мир, до сих пор пользуетесь первым созданным калькулятором.

Счеты, инструмент для расчета или счета с использованием скользящих счетчиков и стержней, действительно являются первым в мире калькулятором. Счеты использовались в Европе, Китае, России.

Старая версия счетов представляла собой неглубокий лоток, состоящий из песка, и цифры можно было легко стереть при необходимости, но современные счеты сделаны из дерева или пластика. Представляет собой прямоугольную коробку, состоящую из девяти вертикальных стержней, нанизанных на бусины.

Горизонтальная перекладина, расположенная перпендикулярно вертикальным стержням, делит их на неравные части. Бусины над горизонтальной перекладиной называются бусами Неба, а бусины, расположенные ниже перекладины, называются бусами Земли.

Хотя счеты появились в Вавилоне, они прошли долгий путь от Ближнего Востока до Японии и Китая. Когда он путешествовал из одной страны в другую, он также был транзитным. В Китае это называется Суанпан . В Suanpan у него есть \(\frac{2}{5}\) колоды.

Известный японский математик Секи Кава заменил колоды \(\frac{2}{5}\) на колоды \(\frac{1}{4} \) и назвал это Soroban . Современные счеты, которые мы используем сегодня, относятся к типу счетов Сорабана.

---

Загружаемый PDF

Вот несколько дополнительных моментов, которые рассказывают о краткой истории Abacus. Для их просмотра нажмите на кнопку Скачать.

📥

Счеты: краткая история от Вавилона до Японии

Скачать

---

Краткая история счетов

Слово «абак» происходит от греческого слова «abax», что означает «табличная форма». Говорят, что он был изобретен в древнем Вавилоне между 300 и 500 г. до н.э. . Абак был первой счетной машиной.

Раньше это были пальцы, камни или любой другой природный материал.

Широко использовался в разных странах от Ближнего Востока до Японии, Китая, России, а также Европы.

Когда индуистская система счисления ввела ноль, а также стала использоваться система счисления Арби, использование счетов уменьшилось, и они стали ограничиваться подсчетом только значения места чисел.

Счеты на протяжении веков

Рис. Линия показывает эволюцию счетов от счетной доски до современных счетов.

Временную шкалу можно разделить на три категории:

• Новое время: с 1200 г. н.э. по настоящее время.

  Пример: Суан Пан или Китайские счеты, Соробань или Японские счеты, Шоты или Русские счеты.

Месопотамская

Месопотамская или шумерская цивилизация была одной из древнейших цивилизаций в истории человечества. Между 2700 г. до н.э. и 2300 г. до н.э. шумеры использовали первые счеты для счета. Считается, что древневавилонские ученые использовали эти счеты для сложения и вычитания. Старовавилонские ученые, такие как Куррицио, считают, что древние вавилоняне использовали свою шестидесятеричную систему счисления на счетах для вычислений.

Греческий

Имеются археологические свидетельства использования счетов в греческом языке в V веке до н.э. Греческие счеты представляли собой деревянную или мраморную раму, состоящую из небольших металлических счетов. Самая старая счетная доска, обнаруженная на греческом острове, возраст которой предположительно составляет 300 лет до нашей эры. Это мраморная плита размером 149 см x 75 см x 4,5 см, на которой были отмечены 5 групп. В середине плиты отмечают 5 параллельных линий и разделяют их вертикальной чертой. Ниже этой линии есть широкое пространство и горизонтальная трещина. Ниже трещины

снова представляют собой одиннадцать параллельных наборов линий, разделенных перпендикулярно вертикальной линией.

Так как она была обнаружена на греческом острове Саламин, то и получила название Саламинская табличка.

Рис. Фотография таблички Саламин. Сейчас хранится в Национальном музее эпиграфики в Греции.

Китайский

Китайские счеты называются Suanpan, что означает счетный лоток. Он имеет длину 20 см и имеет более семи стержней. Жесткие деревянные бусины расположены из двух частей, по две бусины в каждом стержне в верхней части и по пять бусинок в каждом стержне в нижней части. Под каждым стержнем написано несколько цифр, указывающих на место.

Китайские счеты появились во времена династии Хань, в то время бусины были овальными.

Во времена более поздней династии Мин соотношение суанпан составляло 2:5, что означает, что на верхней палубе было две бусины, а на нижней — пять бусинок.

Римский

Римские счеты представляли собой гладкий стол и некоторые счетчики, первоначально сделанные из гальки. Позже папа Сильвестр вновь ввел абак с некоторыми изменениями, и после этого он стал широко использоваться в Европе. Вместо счетной доски в этих счетах использована проволока и бусины.

В течение 1-го века нашей эры римские счеты снова были реконструированы с восемью длинными канавками, состоящими из пяти бусин, и восемью более короткими канавками, каждая из которых не имеет или имеет одну бусину. Группы обозначаются буквой I для единиц, X для десятков и т. д. Бусины меньшей канавки обозначались пятью единицами, пятью десятками и т. д. Короткие канавки по бокам используются для обозначения унций, что означает дробь.

Японский

Японские счеты известны как Соробан. Он был завезен из Китая в 14 веке. Но японские счеты — это счеты 1:4, верхняя колода имеет одну бусину, а нижняя колода — четыре бусины. Бусинка на верхней колоде имеет значение пять, а каждая бусина нижней колоды имеет значение один. Бусины были ромбовидными.

В Японии было два других вида счетов: счеты 3:5, известные как 天三算盤, и счеты типа 2:5.

Счеты все еще широко используются в Японии, которые были модифицированы и модернизированы.

Русский

Русские счеты, известные как «счеты», имеют одну колоду и десять бусинок на каждой проволоке, за исключением одной с четырьмя бусами. Эти счеты часто используются с вертикальным перемещением слева направо. 5-я и 6-я бусины разного цвета для удобства просмотра, и левая бусина тысячи тоже разного цвета.

Счеты широко использовались в Советской России до 1990-х годов.

Индийский

Счеты широко использовались в древней Индии. Мы можем найти ясное свидетельство использования счетов в книге «Абхидхармакошавасья» Васубандху, буддийского ученого и философа. Здесь также упоминается использование Sunya или Zero.

Счеты Сегодня

Счеты до сих пор широко используются в азиатских и некоторых западных школах. В Японии и Китае соревнование по абакусу имеет большое значение.

Счеты в настоящее время в основном используются для обучения детей разрядам в системах счисления и умножению.

Счеты теперь доступны в виде портативного вычислительного устройства. В 21 веке счеты теперь используются только как инструмент обучения.

---

Основы счетов

Мы можем использовать счеты для решения всех видов арифметических операций, таких как сложение, вычитание, умножение и деление. Он состоит из стержней, и каждый стержень содержит несколько бусин.

Существует множество видов счетов, но наиболее широко используются японские счеты или соробан. Он имеет 4 бусинки на нижней палубе и 1 бусину на верхней палубе. Каждый стержень может представлять любое число от 0 до 9, то есть 10 чисел. Бусины над горизонтальной перекладиной известны как бусины Неба, а нижняя — как бусины Земли. Мы должны считать или вычислять, перемещая бусины вверх и вниз.

Рис. Строение японских счетов.

• В Соробане бусины располагаются по разрядности справа налево.

• Если бусины не касаются горизонтальной полосы, это означает, что число не отображается. Чтобы показать или сосчитать любое число, мы должны передвигать бусинки. Бусины, которые касаются полосы, представляют собой число в соответствии с их положением.

На приведенных выше счетах отображается число 6912 или шесть тысяч девятьсот двенадцать.

Чтобы узнать больше об Abacus Basics, ознакомьтесь с Abacus from Basics.

---

Техника счетов

Счет

 Расположите счеты: бусины на абаке будут в исходном положении, что означает, что бусины не будут касаться планки счета. И показывает цифру ноль.

B. Назначьте каждому вертикальному стержню название места: Крайний правый стержень называется «Единицы», за которым следуют десятки, сотни и т. д. Мы также можем назначить десятичный разряд. Если мы хотим представить десятичное число, такое как 10,5, то крайний правый столбец будет десятым разрядом, ранее это был разряд единицы, за которым следовали разряды целых чисел, таких как единицы и десятки.

C. Начинайте считать: Мы всегда должны начинать считать с нижней колоды. Число один должно быть представлено перемещением одной бусины своего места по направлению к горизонтальной полосе счисления. Таким же образом, перемещая бусины в сторону счетной полосы, мы можем составить любое число.

Поскольку в нижнем ряду всего четыре бусины, чтобы получить число больше 4, мы должны переместить бусину нижней колоды в исходное положение и опустить небесную бусину к шкале счета. Чтобы получить 6 небесных бусин, нужно, чтобы одна земляная бусина касалась счетной планки.

Сложение и вычитание

A. Чтобы сложить число, давайте возьмем 1234 с другим числом, нам нужно сначала сделать число 1234, перемещая бусины согласно их месту. Теперь мы должны начать добавлять слева, что является самым высоким местом, в данном случае это тысячный разряд, и должны добавлять 1 и 5. И постепенно к более низким местам. Поскольку разряд десятков перенесен (3 + 7 = 10), поэтому необходимо добавить одну бусину на разряд сотен и переместить бусину десятков на исходное место, сделав значение равным нулю. Таким же образом нужно добавить и свое место.

Теперь нужно читать с левой стороны, 1234+5678= 6912

B. Вычитание — это процесс, обратный сложению. Мы должны сначала сделать большее число, передвигая бусины таким же образом. И приходится занимать, а не переносить.

Вычитание будет 932-867=65

Чтобы узнать больше,

• Счеты Сложение

Умножение и деление

Чтобы сделать умножение, мы должны присвоить числа слева. Возьмем 34×12, так что мы должны присвоить слева направо, ”3” “4” “х” “1” “2” “=” “произведение” и для знака х и = нужно оставить стержни нулевыми должность.

 Чтобы умножить числа, мы должны умножить первый столбец на первый столбец другого числа и снова 1-й столбец на второй столбец другого числа.

Чтобы разделить, возьмем 34 на 2, мы должны взять 2 в крайнем левом столбце и оставить два столбца пустыми или равными нулю, а затем 34.

Чтобы узнать больше,

• Счеты Умножение
• Отдел счетов

---

Заключение

Счеты — старейшее счетное оборудование. Начиная с 5000 лет назад и заканчивая 21 веком, счеты претерпели множество изменений. Он начался с лотка с песком и превратился в компьютеризированное вычислительное устройство.

Это огромное путешествие, но единственное назначение счетов остается прежним, облегчая вычисления.

Хотя счеты сейчас заменены электронными калькуляторами и компьютерами, как инструмент обучения математике, его роль по-прежнему неоспорима. Не только для технического прогресса, но и по-прежнему очень полезного и важного для слепых людей, и его называют счетами Кранмера.

---

О Cuemath

Cuemath, удобная для учащихся платформа математики и кодирования, проводит регулярные онлайн-занятия в прямом эфире для академиков и развития навыков, а их приложение Mental Math для iOS и Android является универсальным решение для детей, чтобы развить несколько навыков.

Ознакомьтесь со структурой оплаты для всех классов и запишитесь на пробный урок уже сегодня!

---

Часто задаваемые вопросы (FAQ)

Что такое счеты?

Счеты — это ручное вспомогательное средство для счета, состоящее из бусин, которые можно перемещать вверх и вниз на ряде палочек или веревок внутри обычно деревянной рамы. Сами по себе счеты не считают; это просто средство, помогающее человеку считать, запоминая то, что было подсчитано.

Где были изобретены счеты?

Тип абака, наиболее часто используемый сегодня, был изобретен в Китае примерно во 2 веке до н. э. Однако устройства, подобные абаку, впервые засвидетельствованы в древней Месопотамии около 2700 г. до н.э.!

Где впервые использовались счеты?

Счеты (множественное число abaci или abacuses), также называемые счетной рамкой, представляют собой вычислительный инструмент, использовавшийся на древнем Ближнем Востоке, в Европе, Китае и России за столетия до принятия письменной арабской системы счисления. Точное происхождение абака до сих пор неизвестно.

Каковы преимущества обучения использованию счетов?

Математические навыки закладывают прочную основу для поступления в высшие классы.

Обучение счету улучшает навыки

• Визуализация (фотографическая память)
• Концентрация
• Навыки слушания
• Память, Скорость
• Точность
• Творчество
• Уверенность в себе
• Уверенность в себе, приводящая к развитию всего мозга

Полезно ли детям пользоваться счетами?

Да, счеты — отличный инструмент для обучения детей основам математики.