Как умножать легко: Как быстро умножать числа без калькулятора

Как быстро умножать числа без калькулятора

Не любишь математику? Ты просто не умеешь ею пользоваться! На самом деле, это увлекательная наука. И наша подборка необычных методов умножения подтверждает это.

Умножай на пальцах, как купец

Этот метод позволяет умножать числа от 6 до 9. Для начала согни обе руки в кулаки. Затем на левой руке отогни столько пальцев, на сколько первый множитель больше числа 5. На правой проделай то же самое для второго множителя. Посчитай количество разогнутых пальцев и умножь сумму на десять. А теперь перемножь сумму загнутых пальцев левой и правой руки. Сложив обе суммы, получишь результат.

Пример. Умножим 6 на 7. Шесть больше пяти на один, значит на левой руке отгибаем один палец. А семь – на два, значит на правой – два пальца. В сумме – это три, а после умножения на 10 – 30. Теперь перемножим четыре загнутых пальца левой руки и три – правой. Получим 12. Сумма 30 и 12 даст 42.

Вообще-то здесь речь идет о простой таблице умножения, которую хорошо бы знать наизусть. Но этот метод хорош для самопроверки, да и пальцы размять полезно.

Умножай, как Ферроль

Этот способ получил название по фамилии немецкого инженера, который им пользовался. Метод позволяет быстро перемножить числа от 10 до 20. Если потренируешься, то сможешь делать это даже в уме.

Суть простая. В итоге всегда будет получаться трехзначное число. Так что сначала считаем единицы, потом – десятки, затем – сотни.

Пример. Умножим 17 на 16. Чтобы получить единицы, умножаем 7 на 6, десятки – складываем произведение 1 и 6 с произведением 7 и 1, сотни – умножаем 1 на 1. В итоге получим 42, 13 и 1. Для удобства запишем их в столбик и сложим. Вот и итог!

Умножай, как японец

Этот графический способ, которым пользуются японские школьники, позволяет легко перемножить двух- и даже трехзначные числа. Чтобы опробовать его, приготовь бумагу и ручку.

Пример. Умножим 32 на 143. Для этого нарисуем сетку: первое число отразим тремя и двумя линиями с отступом по горизонтали, а второе – одной, четырьмя и тремя линиями по вертикали. В местах пересечения линий поставим точки. В итоге у нас должно получиться четырехзначное число, поэтому условно разделим таблицу на 4 сектора. И пересчитаем точки, попавшие в каждый из них. Получаем 3, 14, 17 и 6. Чтобы получить ответ, лишние единички у 14 и 17 прибавим к предыдущему числу. Получим 4, 5 и 76 – 4576.

Умножай, как итальянец

Еще один интересный графический способ используется в Италии. Пожалуй, он проще японского: точно не запутаешься при переносе десятков. Чтобы перемножить большие числа с его помощью, нужно начертить сетку. По горизонтали сверху записываем первый множитель, а по вертикали справа – второй. При этом на каждую цифру должна приходиться одна клетка.

Теперь перемножим цифры каждого ряда на цифры каждой колонки. Результат запишем в клетку (разделенную надвое) на их пересечении. Если получилось однозначное число, то в верхнюю часть клетки пишем 0, а в нижнюю – полученный результат.

Осталось сложить все числа, оказавшиеся в диагональных полосках. Начинаем с нижней правой клетки. Десятки при этом прибавляем к единицам в соседнем столбике.

Вот как мы умножили 639 на 12.

Весело, правда? Нескучной тебе математики! И помни, что гуманитарии в ИТ тоже нужны!

Быстрее, еще быстрее

Даже великие ученые иногда ошибаются. Когда в середине 1950-х годов советский математик Андрей Колмогоров высказал гипотезу: сложность перемножения N-значных чисел пропорциональна N². Всего через несколько лет его гипотеза была опровергнута, а чуть позже появился новый, еще более быстрый алгоритм, причем его создатели высказали гипотезы о том, что быстрое умножение чисел пропорционально N log (N) и это теоретический предел. Совсем недавно, похоже, этого предела удалось достичь. О том, в каких областях используется умножение по-настоящему больших чисел, как был достигнут предел скорости и нельзя ли его преодолеть, для британского издания The Conversation один из авторов недавнего открытия, австралийский математик Дейвид Харви, написал статью под названием «Мы нашли способ быстрее перемножать по-настоящему большие числа». Издание

N + 1 предлагает своим читателям полный перевод этой статьи.

Перемножить два числа — легко, верно?

В начальной школе нас учат, как умножить одно большое число на другое, — вот как в примере выше.

Способы умножения, подобные этому, появились тысячи лет назад, их знали уже древние шумеры и египтяне.

Но можно ли считать этот способ умножения двух больших чисел друг на друга наилучшим?

При перемножении больших чисел мы должны умножить каждую цифру первого множителя на каждую цифру второго множителя. Если каждый из множителей состоит из N цифр, то всего получается N² (или N × N) умножений. В нашем примере N = 3, поэтому требуется проделать 3² = 9 операций.

Примерно в 1956 году выдающийся советский математик Андрей Колмогоров выдвинул гипотезу, что это и есть

лучший из всех возможных способов умножить одно число на другое.

То есть вне зависимости от того, как именно вы считаете, объем работы, которую вам придется проделать, будет пропорционален как минимум N². Увеличьте множители в два раза — и вам придется проделать в четыре раза больше вычислений.

Колмогоров был уверен, что существуй способ хоть чуть-чуть сократить этот путь, его наверняка бы уже открыли. Как-никак люди перемножают числа на протяжении тысяч лет.

Это великолепный пример логической ошибки, известной как «аргумент к незнанию».

Более быстрый способ

Уже через несколько лет гипотеза Колмогорова была впечатляюще опровергнута.

В 1960 году Анатолий Карацуба, в то время 23-летний российский студент-математик, открыл хитрый алгебраический трюк, позволивший сократить необходимое число умножений.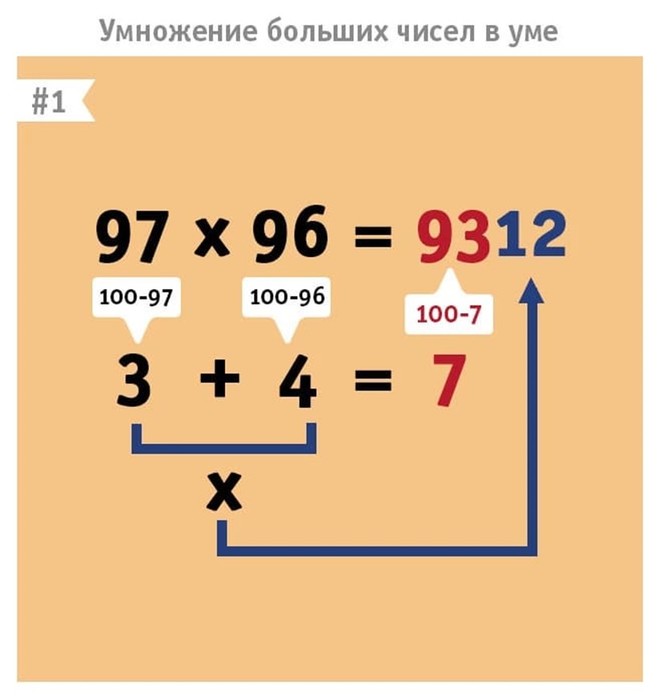

Например, чтобы перемножить два четырехзначных числа, вместо необходимых 4² = 16 перемножений метод Карацубы позволяет обойтись всего девятью. При применении его метода увеличение множителей в два раза потребует проделать всего лишь в три раза больше вычислений.

Это давало впечатляющую экономию по мере того, как длина множителей росла. В случае с числами длиной в тысячи знаков метод Карацубы требовал в 17 раз меньше вычислений, чем при обычном умножении.

Но зачем вообще кому-то надо перемножать такие большие числа?

На самом деле эти операции применяются сплошь и рядом. Одна из наиболее наглядных и экономически значимых областей — криптография.

Большие числа в нашей жизни

Всякий раз, когда вы устанавливаете защищенное интернет-соединение, — например, заходите в личный кабинет на сайте своего банка или задаете поисковый запрос, — ваше устройство совершает головокружительное количество вычислений, в том числе с числами длиной в сотни, а то и тысячи знаков.

Скорее всего, ваше устройство использует трюк Карацубы, чтобы справиться с этой арифметикой. Это все часть изумительной программной экосистемы, позволяющей нашим веб-страницам грузиться как можно быстрее.

Но для некоторых менее доступных широкому пониманию целей математикам приходится перемножать куда бóльшие числа, состоящие из миллионов, миллиардов и даже триллионов знаков. Для таких грандиозных объемов даже алгоритм Карацубы работает слишком медленно.

Настоящий прорыв случился в 1971 году, когда вышла работа немецких математиков Арнольда Шёнхаге и Фолькера Штрассена. Они показали, как можно использовать недавно открытое быстрое преобразование Фурье (FFT) для перемножения огромных многозначных чисел. Сегодня их метод повсеместно используется для обработки чисел длиной в миллиарды знаков.

Быстрое преобразование Фурье стало одним из важнейших алгоритмов ХХ столетия. Одна из повседневных областей его применения — цифровое аудио: когда вы слушаете MP3-файл, или музыкальный стриминговый сервис, или онлайн-радио, именно FFT занимается декодированием звука за кадром.

Еще более быстрый способ?

В своей работе 1971 года Шёнхаге и Штрассен выдвинули еще одну поразительную гипотезу. Чтобы объяснить ее суть, мне придется ненадолго погрузиться в детали.

Первая часть их гипотезы гласит: должен быть работающий способ перемножить N-значные числа с помощью некоторого количества фундаментальных операций, по большей части пропорциональных N log (N) (то есть N раз по натуральному логарифму от N).

Их собственный алгоритм не до конца достиг этой цели: у них получилось N, умноженное на log (N) и умноженное на log (log N) (логарифм от логарифма от N). Тем не менее, чисто интуитивно они чувствовали, что что-то упускают и что N log (N) достижим.

За десятилетия, прошедшие после 1971 года, нескольким исследователям удалось улучшить алгоритм Шёнхаге и Штрассена. В частности, алгоритм, разработанный Мартином Фюрером в 2007 году, дразняще близко подошел к ускользающему значению N log (N).

Вторая (и куда более сложная) часть их гипотезы гласит, что N log (N) является фундаментальным пределом скорости вычислений — что ни один другой алгоритм не позволит производить перемножение больших чисел быстрее.

Звучит знакомо, не правда ли?

Достигнут ли предел?

Несколько недель назад мы с Йорисом ван дер Ховеном опубликовали результаты исследования, описывающие новый алгоритм умножения, достигающий, наконец, заветного значения N log (N) и тем самым подтверждающий первую, «простую» часть гипотезы Шёнхаге и Штрассена.

Наше исследование еще не прошло рецензирование, так что некоторые сомнения остаются. Это стандартная практика у математиков — распространять результаты исследования еще до того, как получены финальные рецензии.

Вместо использования одномерного быстрого преобразования Фурье — базовой предпосылки всех работ по этой проблеме начиная с 1971 года — наш алгоритм использует многомерные FFT. В них нет ничего нового: широко распространенный формат изображений JPEG зависит от двухмерного FFT, а трехмерные FFT широко применяются в физике и инженерном деле.

Мы в своем исследовании использовали FFT с 1729 измерениями. Это довольно трудно визуализировать, но с точки зрения математики это мало чем отличается от двухмерного преобразования.

Огромные, по-настоящему огромные числа

Новый алгоритм в своем нынешнем виде не очень годится для конкретных вычислений, потому что доказательство, приведенное в нашей статье, работает только для абсурдно больших чисел. Если каждый знак одного из таких чисел записать на атоме водорода, то в обозримой Вселенной не хватит места, чтобы оно уместилось целиком.

С другой стороны, мы надеемся улучшить его и приспособить для чисел с какими-нибудь миллиардами и триллионами знаков. Если нам это удастся, этот алгоритм может стать незаменимым инструментом в арсенале математических вычислений.

Если гипотеза Шёнхаге и Штрассена верна целиком, тогда, с теоретической точки зрения, новый алгоритм станет конечным пунктом этого пути — ничего более совершенного придумать уже не удастся.

Лично я буду очень удивлен, если окажется что Шёнхаге и Штрассен ошибались. Но не следует забывать, что в свое время случилось с Колмогоровым. Математика порой способна преподносить сюрпризы.

Перевод с английского Дмитрия Иванова

Советы по умножению в уме, чтобы быстрее считать в уме

Приемы и советы по умножению в уме, приведенные в этом посте, позволят вам выполнять вычисления в уме быстрее, чем калькулятор, полностью в уме. Существует много умственных стратегий умножения, но рассмотренные здесь стратегии умственного умножения можно применять для умножения любого набора чисел. Изучение советов по умственному умножению в этом посте будет похоже на обучение езде на велосипеде. Однажды выучив его, действительно очень трудно его забыть.

Прежде чем мы продолжим, вы должны освоить умножение однозначных чисел. Предварительным условием является знание таблицы умножения однозначных чисел от 1 x 1 до 9 x 9, прежде чем приступать к умственному умножению больших чисел. Если вы немного заржавели, добавьте этот пост в закладки и убедитесь, что вы сначала выучили свою таблицу умножения с одной цифрой. Если вы хорошо разбираетесь в умножении однозначных чисел, можете читать дальше.

Этот пост является второй частью серии математических трюков в уме. Настоятельно рекомендуется прочитать первый пост этой серии — Уловки ментальной арифметики для быстрой математики, прежде чем приступить к изучению того, как выполнять ментальную арифметику в умножении.

Секрет трюков с умножением в уме

В первой части «Уловок с ментальной арифметикой» мы узнали, что арифметика в уме становится труднее, если считать справа налево. Следовательно, секрет ментальной арифметики заключается в том, чтобы делать наоборот и вместо этого считать слева направо. Решая слева направо, вы начнете называть ответ, прежде чем закончите полный расчет. Вычисление слева направо поначалу может показаться немного странным, но после небольшой практики оно станет естественным. В этом посте мы увидим, как применить это к умственному умножению.

Что такое множимое и множитель?

Прежде чем мы приступим к умножению в уме, давайте быстро определим, что такое множимое и множитель. Возьмем, к примеру, задачу на умножение 43 x 23. Здесь число 43 является множимым — числом, которое нужно умножить. Число 23 — это множитель — число, на которое умножается первое число.

В этом посте есть несколько трюков с умножением для ментальной арифметики. Каждый метод мысленного умножения будет иметь два примера. Первый пример, видимый всем, познакомит вас с трюком умножения. Второй пример, видимый только вошедшим в систему пользователям, будет иметь варианты, не описанные в первом примере. Так что войдите или зарегистрируйтесь бесплатно, чтобы получить доступ ко всему контенту.

Трюки с умножением для однозначного числа

Общее умственное умножение для однозначного множителя

Общий метод умственного умножения заключается в умножении слева направо. Хотя общий метод можно применять для любого числа, лучше всего он работает, когда числа не заканчиваются на 7, 8 и 9. У нас есть отдельная техника для чисел, оканчивающихся на 7, 8 и 9. А пока давайте применим метод умственного умножения для умножения 5321 x 4.

Правило простое. Умножать слева направо. Одна цифра за раз.

Умножение слева направо выполняется быстрее, потому что вам нужно запомнить меньшее количество чисел, чтобы потом их вспомнить и использовать. Вы сразу начнете называть ответ с самого первого шага расчета.

Теперь попробуйте умножить 7142 x 6. Процедура такая же, как и раньше, и вы можете найти ее ниже:

Умножение в уме с округлением до 1-разрядного множителя

Использование приемов умножения в уме после округления полезно, когда числа заканчиваются на 7, 8 или 9. Это значительно упрощает умножение. Давайте посмотрим, как применить это на примере. Умножьте 68 x 3.

1. Округлите число

2. Умножьте слева направо

3. Умножьте сумму, которую вы округлили,

4. Вычтите числа из двух предыдущих шагов

Если вы попытаетесь сделать так, как вы обычно делаете это на бумаге, вы поймете, что это занимает больше времени, чем то, что вам нужно сейчас, чтобы сделать это в своей голове. Если у вас еще нет скорости, не волнуйтесь. Это придет с практикой. В конце есть практические упражнения и рабочие листы для умственного умножения, которые вы можете скачать и попрактиковаться.

Теперь попробуйте умножить 96 x 7. Процедура такая же, как и раньше, и вы можете найти ее ниже:

Умножение в уме двузначных чисел

Общие приемы умножения

Давайте теперь посмотрим, как выполнять умножение в уме для теперь двухзначные числа. Трюки с умножением, которые мы видели ранее, нужно немного изменить. Давайте посмотрим, как это сделать на примере. Умножить 36 x 32.

1. Разбить множимое

2. Умножить слева направо

3. Сложите отдельные ответы вместе, чтобы получить окончательный ответ

Вы можете решить ту же проблему, разбив множитель вместо множимого. Ваш выбор будет зависеть от того, что дает вам более простой процесс сложения на шаге 3. Попробуйте выбрать число с меньшей цифрой, потому что в большинстве случаев это обычно приводит к тому, что вы добавляете меньшие числа.

Теперь попробуйте умножить 26 x 23. Процедура такая же, как и раньше, и вы можете найти ее ниже:

Округление для двузначного множителя

Как и в случае однозначных множителей, округление и умножение полезно, когда числа заканчиваются на 7, 8 или 9. Давайте посмотрим, как это сделать, на примере. Умножить 87 x 99:

1. Округлить число

2. Умножить округленное значение и сумму, округленную слева направо

3. Вычесть два числа

Теперь попробуйте умножить 41 x 57. Процедура такая же, как и раньше, и вы можете найти ее ниже:

Умножение в уме с использованием коэффициентов

Как и при округлении, один из приемов умножения заключается в том, чтобы перед умножением числа разложить его на множители. Давайте посмотрим, как это сделать, попытавшись умножить 45 x 22.

1. Разложить число на множители

2. Умножить число на первый множитель (слева направо)

4. Умножить произведение на второй множитель (слева направо)

В трюках с умножением, которые мы видели ранее, вам нужно будет запомнить произведение первой цифры, чтобы сложить/вычесть с произведением второй цифры. Однако при умственном умножении с использованием множителей вы просто умножаете второй множитель на первый продукт, поэтому вам не нужно запоминать столько чисел, сколько вы вычисляете.

Теперь попробуйте умножить 21 x 63, используя метод множителей. Процедура такая же, как и раньше, и вы можете найти ее ниже:

Рабочие листы с упражнениями на умножение в уме

Ниже вы можете скачать рабочие листы с упражнениями на умножение в уме в формате PDF, чтобы применить описанные приемы умножения.

Стать человеком-калькулятором

Вы научились основным приемам умножения. Но Мы коснулись только поверхности, и еще многое предстоит осветить. Если вы действительно хотите стать человеком-калькулятором и вывести свои математические способности в уме на новый уровень, посмотрите это видео. В видео я поделюсь историей о том, как я на самом деле боролся с математикой и как я добился того, что имею сегодня. Вы узнаете секрет, который сократит вашу кривую обучения и ускорит ваш путь к мастерству ментальной математики.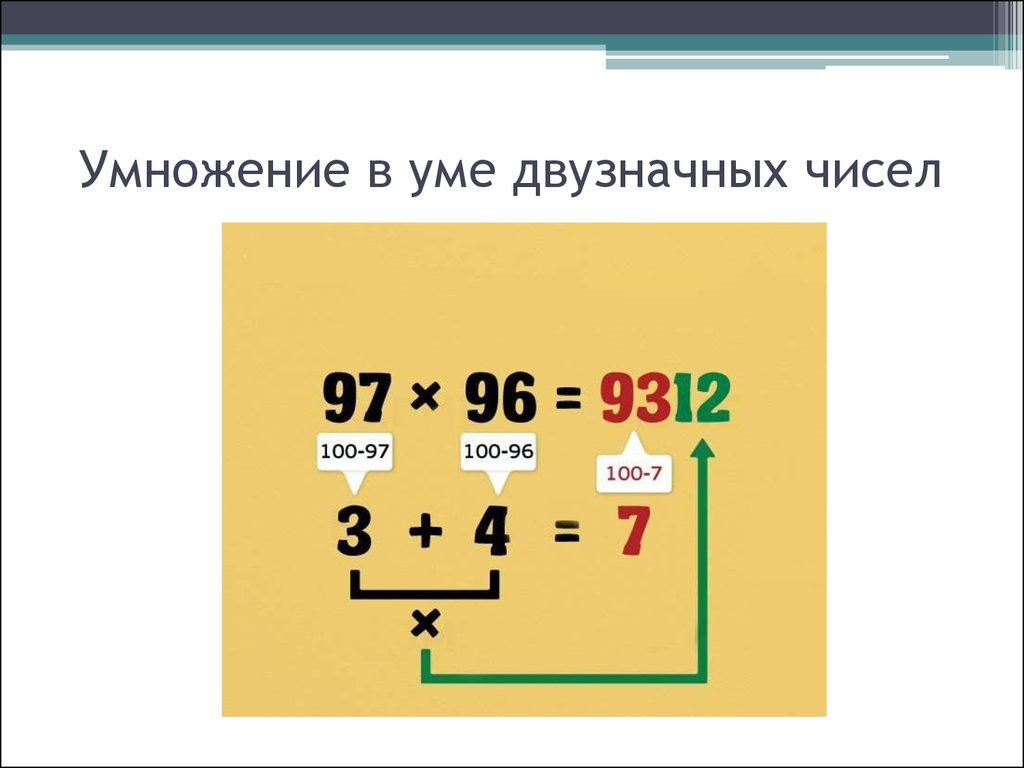 Чтобы посмотреть видео кликните здесь.

Заключение

Вопросы, уточнения и отзывы оставляйте в комментариях. Потребуется практика, прежде чем применение трюков с умножением станет легким и легким. Поначалу вам будет трудно запомнить все числа в голове, когда вы будете считать. Но практика поможет вам улучшить кратковременную память на числа. Заставьте себя выполнять мысленные вычисления слева направо для повседневных вычислений и используйте калькулятор только для перепроверки своих чисел. Ваша скорость и способности будут улучшаться по мере того, как вы будете практиковаться.

Быстро умножить | МатЧат

Сообщения с пометкой «Быстро умножить»

Как умножать четные числа на 5 — БЫСТРО!

Время для математического трюка…

В: Как молниеносно умножить четное число на 5?

A:  Поделите число на 2, затем прибавьте «0».

Пример:   5 x 24

Разделите 24 на 2, чтобы получить 12.

Прикрепите «0» к 12, чтобы получить 120. Вуаля, ничего в рукаве. Это так просто.

Почему это работает? Подсказка: подумайте о том, как мы умножаем на 10. Затем подумайте о том, как умножение на 5 сравнивается с умножением на 10. x 16

B) 5 x 8

C) 5 x 28

D) 5 x 64

E) 5 x 142

F) 5 x 2 468

G) 5 x 6,042

H) 5 x 86 432

к) 5 х 888 888

Ответы:

A) 5 x 16 = 80

B) 5 x 8 = 40

C) 5 x 28 = 140

D) 5 x 64 = 320

E) 5 x 142 = 710

F) 5 x 2,468 = 12 340

г) 5 x 6,042 = 30,210

H) 5 x 86 432 = 432,160

j) 5 x 888 888 = 4,4444409

K) 5 x 2,4888 = 4,4444409

K) 5 x 2,4888 = 4,4444409

K) 5 x 88888 = 44444409

j) это:

Нравится Загрузка…

Категория:

Изучение фактов о математике, Развлечение с математикой, Математические приемы, Умножение, Трюки с умножением, Без категорий

Как умножить на 25 в уме

Это простой прием, которому может легко научиться любой. Это всего лишь уловка для
, умножение числа на 25.

Если бы кто-то спросил вас, чему равно 25, умноженное на 36, у вас, вероятно, возникло бы искушение
дотянуться до калькулятора и начать нажимать кнопки. Но что примечательно, вы,
, вероятно, сможете еще быстрее продумать это в уме.

Так как 25 составляет одну четвертую от 100, то умножение на 25 это то же самое, что
умножение на 100 и деление на 4. Или еще проще:
сначала делим на 4, потом прибавляем два нуля.

Вот пример:

Задача: 36 x 25
Сначала разделите 36 на 4, чтобы получить 9.
Затем добавьте два нуля, чтобы получить: 900.
Это, как ни странно, и есть ответ.

Другой пример: 88 x 25
Сначала разделите 88 на 4, чтобы получить 22.
Затем добавьте два нуля, чтобы получить: 2200.

А теперь попробуй про себя эти задачи:

а) 25 х 12
б) 25 х 28
в) 25 х 48
г) 25 х 60
д) 25 х 84
е) 25 х 96

Вот ответы:
9 а) 180 300 ) 700
c) 1200
d) 1500
e) 2100
f) 2400

Но, вы говорите, что если число, с которого вы начинаете, не делится на 4.
Нет проблем. Просто используйте этот факт:
, если остаток равен 1, это то же самое, что 1/4 или 0,25
, если остаток равен 2, это то же самое, что 2/4 или 0,50
, если остаток равен 3, то есть то же, что 3/4 или .75

Итак, возьмем такую ​​задачу: 25 x 17
разделив 17 на 4, вы получите 4 остатка 1.
Но это то же самое, что и 4,25
Теперь просто переместите десятичную дробь на два разряда вправо (то же самое, что и при умножении на 100)
Ответ составляет: 425

Другой пример: 25 x 18
разделив 18 на 4, вы получите 4 остатка 2.
Но это то же самое, что и 4,50
Теперь переместите десятичную дробь вправо на два знака.
Ответ: 450

Другой пример: 25 x 19
разделив 19 на 4, вы получите 4 в остатке 3.
Но это то же самое, что 4,75
Теперь переместите запятую на два знака вправо.
Ответ: 475

А теперь подумайте над этим:
A) 25 x 21
B) 25 x 26
C) 25 x 35
D) 25 x 42
E) 25 x 63
F) 25 x 81

и вот ответы:

A) 525
B) 650
C) 875
D) 1,050
E) 1 575
F) 2 025

Нравится это:

, как загрузка .