Как пользоваться абакус: Что такое счеты абакус и для чего они

как научиться считать самому / TeachMePlease

Ментальная арифметика — это мгновенное совершение арифметических операций в уме. Сначала они выполняются с помощью японских счётов — соробана, на которых ученик впоследствии считает в воображении. Существует множество организаций, предлагающих обучить данной технике. Мы же разберёмся, можно ли изучить её самостоятельно.

Инструменты счёта

Начинается обучение ментальной арифметике со счёта на соробане — японском варианте счёт. Они представляют собой доску с вертикальными спицами и пятью нанизанными на них костяшками. Отличительная черта соробана — горизонтальная перегородка, которая отделяет четыре костяшки в столбцах от пятой.

Четыре нижние косточки японцы называют «земными», они означают единицы. Пятая, верхняя костяшка, «небесная», считается сразу за пять единиц.

Для обучения ментальной арифметике необходимо обзавестись именно соробаном, а не просто счётами. Учиться считать можно также на бумаге с помощью изображения соробана или использовать специализированные сайты и приложения, но такое выполнение вычислений будет менее наглядным.

Основы работы с числами

В начале занятий соробан нужно привести в нулевую позицию, косточки соробана не должны касаться разделителя: верхние необходимо поднять к рамке, а нижние — наоборот опустить.

Для совершения действий с соробаном традиционно используют большой и указательный пальцы: первый перемещает бусины из нижнего ряда к разделителю, второй — выполняет остальные манипуляции.

Первая спица справа — это единицы (от 1 до 9). Чтобы отложить цифры от 1 до 4 необходимо перемещать косточки под разделителем в правом крайнем столбце вверх, для обозначения цифры 5 опускаем 1 костяшку из верхнего правого ряда. Числа от 6 до 9 обозначаем как 5, то есть 1 опущенная костяшка из верхнего ряда, плюс от 1 до 4 костяшек, поднятых к разделителю из нижнего ряда: 6 — это 5+1, 7 — это 5+2.

Переходим к десяткам (числа от 1 до 99): они находятся на следующей спице.

Двигаясь на столбец влево, мы меняем разряд — от единиц переходим к десяткам, далее к сотням, тысячам, десяткам тысяч и так далее.

Например, чтобы набрать число 129 необходимо поднять 1 косточку снизу в столбце сотен, 2 костяшки на столбце десятков, и 5 — опустить одну косточку к разделителю сверху и поднять 4 снизу в столбце единиц.

Представление числа 129 на соробане

Изучив способы обозначения чисел, переходим к практике. Один человек вслух называет числа, а другой набирает их на доске. После того как навык доведён до автоматизма, можно переходить к арифметическим действиям.

Занятия с ребёнком можно сделать интереснее, называя числа со значением: например, посчитать количество дней в неделе, году, набрать номер дома, квартиры, годы рождения родственников, количество материков, стран, человек, населяющих город и страну.

Простые сложение и вычитание

Главное правило счёта на соробане: «считать нужно слева направо», что не соответствует привычному нам способу вычисления.

Внимание: техники счёта могут отличаться, мы используем те, что встречаются в рекомендации японской организации The Abacus Committee.

Начинать вычисления стоит с чисел, сумма и разность которых даёт не более 9 при сложении и не менее 1 при вычитании.

Примеры вроде 1+6, 2+7, 12+24 или 123+432 подойдут на первых порах.

• Начнём со сложения единиц: для примера 1+2 поднимите на крайней правой спице 1 костяшку вверх, а затем добавьте к ней ещё 2. 
• Для примера:12+32. Откладываем в колонке десятков — 1 косточку, в единицах — 2. Затем к 1 костяшке придвигаем 3, к 2 костяшкам единиц ещё 2. 

Изучать вычитание также стоит с простых примеров:

• Рассмотрим вычитание на единицах. Простой пример: 4 – 2 = 2. Из четырёх поднятых костяшек убираем 2 и получаем результат.
• Простой пример с десятками: 24 – 13 = 11. Из столбца десятков убираем 1 костяшку остаётся 1. Переходим к единицам: от 4 костяшек отнимаем 3, у нас остаётся 1 костяшка. Результат готов.
• По тому же принципу работаем с сотнями: 432 – 322 = 110. Из столбца сотен от 4 отнимем 3, из 3 вычтем 2 останется 1, из 2 вычтем 2 — все костяшки из столбца единиц возвращаются в нулевую позицию.

Для более сложных вычислений необходимо познакомиться с принципом дополнительных чисел.

Дополнительные числа

Высокая скорость работы на соробане зависит от того, насколько механизированы действия считающего. Смысл заключается в том, чтобы снять лишнюю нагрузку с ума и выполнять арифметические действия механически, без размышлений или колебаний, отсюда и сравнение людей, обладающих этим навыком, с калькулятором. И если со сложением и вычитанием простых чисел всё ясно, то с более сложными примерами нужно освоить концепцию дополнительных чисел. Нужно просто запомнить, что:

• цифру 5 можно разложить на дополнительные числа: 4 и 1, 5 и 2.
• цифру 10 можно разложить на дополнительные числа: 9 и 1, 8 и 2, 7 и 3, 6 и 4, 5 и 5.

При сложении дополнительное число вычитается. При вычитании — дополнительное число прибавляется. Как это работает на практике рассмотрим далее.

Сложное сложение

Пример: 4 + 8 = 12 

Как решать?

1. Установите 4 костяшки в столбце единиц.
2. Для 8 костяшек места уже не найдётся.
3. Вспоминаем принцип дополнительных чисел: число 10 даёт наша 8 и цифра 2. 
4. Вычтите дополнительную цифру 2 из 4.
5. Добавьте единицу в столбик десятков.
6. Результат — 12. 

Процесс решение примера 4+8 на соробане

Принцип вычисления на соробане в привычной записи можно представить так:

4 + 8 = 12 превращаем в 4 – 2 +10 = 12

Важно запомнить: в сложных заданиях на сложение всегда вычитайте дополнительное число.

Сложное вычитание

Пример: 12 – 7 = 5.

Как решать?

1. Установите 1 костяшку на столбец с десятками, добавьте 2 к единицам.
2. Вспомните, что 7 — это 10 и 3.
3. Уберите 1 костяшку из столбца десятков.
4. Прибавьте в столбце единиц к 2 костяшкам дополнительные 3. Получается 5 — верните в нулевую позицию нижние костяшки и опустите «небесную».

Принцип вычисления на соробане в привычной записи можно представить так:

12 – 7 = 5 мы превращаем в 12 – 10 + 3 = 5

Важно запомнить: в подобных вычислениях на вычитание всегда прибавляйте дополнительное число.

Порядок столбцов при счёте

В приведённых выше примерах мы использовали по 2 столбца — для десятков и единиц. Особое внимание стоит уделить тому, в каком порядке стоит добавлять и убирать костяшки из столбцов.

Для сложения:

1. Вычтите дополнительное число и соответственное количество костяшек из правого столбца.
2. Затем добавьте костяшку в левый стержень.

Для вычитания:

1. Сначала вычтите числа в левом столбце.
2. Добавьте дополнительное число на правый стержень.

Умножение

Есть несколько возможных способов умножения на соробане, мы рассмотрим один из самых распространённых.

Обратите внимание: чтобы умножать на соробане, нужно хорошо знать таблицу умножения.

Также необходимо запомнить следующие термины, которые мы рассмотрим на примере a x b = c, где:

a — это множимое;

b — это множитель;

с — произведение.

Пример: 43 x 8 = 344.

Шаг 1

В первом столбце слева устанавливаем множитель — 8, отступаем один столбец и откладываем множимое — 43.  Отступаем 2 столбца — с этого столбца начнём записывать результат.

Шаг 2

Умножаем 3 на 8. Результат 24 записываем в 7 и 8 столбцах. Завершая операцию, убираем цифру 3 с доски, сдвинув костяшки вверх.

Шаг 3

Умножьте 4 на 8. Результат 32 запишите следующим образом: 3 в 6 столбец — перед прошлым результатом, а 2 сложите с результатом в 7 столбце, то есть с 2. Три цифры в результате дают ответ — 344. 

Сложнее выполнить умножение с двумя двузначными числами, рассмотрим это на следующем примере:

Пример: 35 x 18

Шаг 1 

Откладываем множитель, то есть 18 с начала доски. Делаем отступ и откладываем 35. 

Шаг 2

Умножаем 1 на 5, записываем результат через 2 пробела.

Шаг 3

Умножаем 8 на 5, получаем 40. 4 записываем под прошлым результатом, т.е. складываем с 5. В столбцах результата остаётся цифра 90.

Шаг 4 

Умножаем 3 на 1 и записываем результат — 3 — перед предыдущими столбцами. Получается 390. 

Шаг 5

Умножаем 3 на 8, результат 24 записываем под первыми двумя цифрами прошлого результата. Получаем 630. 

Деление

Для деления мы также используем стандартные математические термины a ÷ b = c, где:

a — делимое;

b — делитель;

c — частное.

Делимое набирается на спицах в правом конце соробана, делитель — в левом конце. Результат записывается посередине.

Между делимым и делителем рекомендуют оставить минимум 4 пустых столбца для записи результата.

Также существуют правила размещения первой цифры частного:

• Если количество цифр в делителе меньше (или равно) количеству цифр в делимом, расположите первую цифру частного, отступив 2 столбца слева от делимого.
• Если количество цифр в делителе больше, нежели в делимом, начните располагать частное, отступив 1 столбец слева от делимого.

Пример: 72 ÷ 2

1. Помещаем делитель 2 в левую часть счёт, делимое — 72 — в правую.
2. Делим первое число 7 на 2. Цифра 2 помещается в 7 полностью три раза — поднимаем 3 костяшки в соответствии с правилом №1, отступив 2 столбца влево от делимого.
3. Умножим полученное число 3 на делитель — 2. Результат — 6 — вычтем из первой цифры делимого — 7. Убираем лишние костяшки, остаётся единица.
4. Остаток от делимого — 12 делим на делитель — 2. Полученный результат — 6 помещаем в следующий свободный столбец для записи результата. Получаем в итоге — 36. 

Полезные ресурсы

• Подвигать косточки на соробане: ссылка
• Посмотреть пошаговое решение примеров: ссылка
• Приложение «Игры соробан»: ссылка

Мы разобрали самые простые способы вычисления на соробане. Чтобы выполнять манипуляции с трёхзначными и дробными числами необходимо на высоком уровне научиться работать с однозначными и двузначными числами.

Следующей ступенью после тщательного освоения каждой техники счёта становится его представление соробана в уме и мысленное выполнение вычислений. Последовательно, правильно и адаптировано для каждого возраста учат считать подготовленные тренеры в специализированных центрах. Подобрать такой в своём городе вы можете на TeachMePlease.

Абакус онлайн бесплатно без регистрации

С каждым годом все больше людей интересуются ментальной арифметикой, ведь эта наука обладает огромным количеством преимуществ. Кто-то посещает очные курсы по освоению быстрого счета в уме, а кто-то хочет изучить его самостоятельно и ищет приложение с абакусом онлайн, которым можно пользоваться бесплатно. Существуют ли такие программы и как выбрать среди них наиболее подходящую? Ответим в данной статье.

Счеты абакус и ментальная арифметика

Ментальная арифметика – это методика, позволяющая не только научиться быстро считать в уме, но и развить свой интеллект. Она задействует сразу два полушария мозга человека, благодаря чему удается тренировать разные интеллектуальные способности: память и запоминание, внимание, логику, фантазию, креативное мышление. Именно разностороннее развитие интеллекта и способностей к математике являются причиной популярности и высокой востребованности этой методики.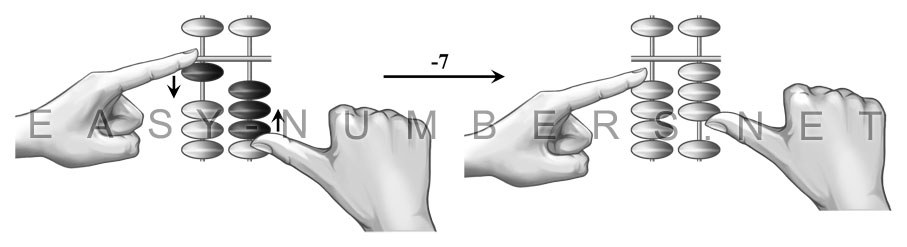

Конечно, добиться видимого эффекта от ее изучения не удастся без определенных усилий и временных затрат. Чтобы в совершенстве овладеть ментальной арифметикой, придется регулярно заниматься, оттачивая навыки вычислений на специальных счетах – абакусе. Только доведя умение считать на этом инструменте до автоматизма, можно будет перейти к самому интересному этапу – счету в уме.

Проблема состоит в том, что постоянно носить счеты с собой не всегда удобно. Поэтому многие находятся в поиске специальных приложений или сайтов, с помощью которых можно считать на абакусе в режиме онлайн. Поговорим об особенностях и преимуществах таких программ и интернет-ресурсов.

Абакус онлайн

В век информационных технологий многие повседневные задачи удается переложить на плечи умных устройств. Именно они предоставляют нам массу возможностей, дают доступ не только к развлекательным, но и к образовательным ресурсам. Так современные смартфоны позволяют отправлять сообщения, узнавать новости, играть и даже считать на абакусе абсолютно бесплатно, если скачано подходящее приложение или присутствует доступ в интернет.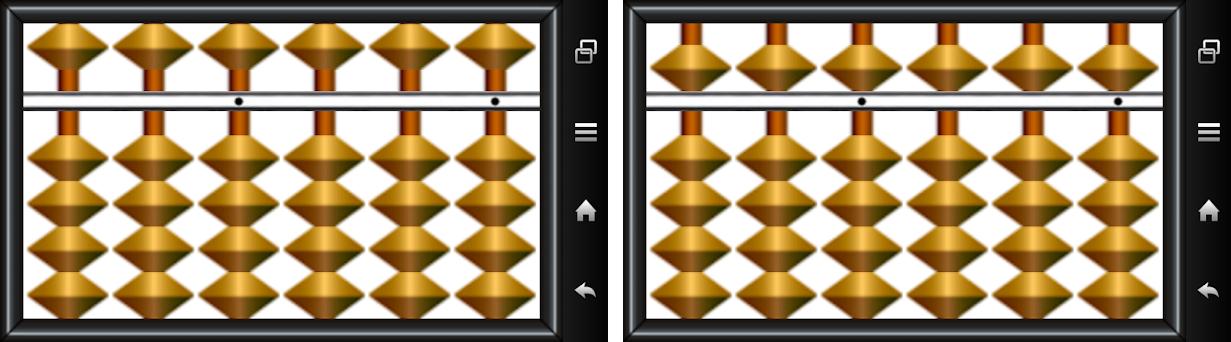

Именно благодаря современным гаджетам можно осваивать ментальную арифметику тогда, когда это удобно. Во время поездки в общественном транспорте, в путешествии, в перерыве от работы или учебы и в любой другой момент удастся попрактиковаться в использовании счетов, ведь личный смартфон стал неотъемлемой частью нашего быта, а потому всегда находится под рукой.

Остается только выбрать специальное приложение или сайт для тренировок в режиме онлайн. При этом, важно обращать внимание на интерфейс и иные параметры программы, чтобы удалось сделать занятия максимально комфортными. Но как же выбрать подходящий виртуальный абакус?

Ментальные счеты без регистрации бесплатно

Как и любое другое приложение, виртуальный абакус может иметь свои плюсы и минусы. К недостаткам таких программ можно отнести:

• большое количество всплывающей рекламы. Рекламные заставки, появляющиеся в самый неподходящий момент, являются одним из тех факторов, которые больше всего раздражают пользователей.
• необходимость приобрести программу или оплатить доступ на ресурс. Далеко не все приложения и сайты бесплатны, что также является минусом.
• отсутствует возможность пользоваться приложением без регистрации. Доступ к некоторым программам со счетами будет недоступен, пока пользователь не зарегистрируется.
• неудобный интерфейс. Некоторыми приложениями некомфортно пользоваться из-за неудобно расположенных кнопок или слишком яркого оформления.
• нет пользовательских настроек. Невозможность менять визуальные или звуковые параметры является серьезным недостатком для пользователей.

Одной из программ, в которой можно пользоваться абакусом бесплатно без регистрации, является приложение от образовательного онлайн-портала Amavit. В этом приложении нет раздражающей рекламы, а внешний вид счетов и иные параметры можно настроить на свой вкус. Все это сделает освоение ментальной арифметики более комфортным.

Курсы ментальной арифметики online

Чтобы научиться считать ментально, нужно регулярно заниматься, оттачивая навыки устных вычислений. Но далеко не всегда удается добиться значительного успеха при самостоятельных тренировках. Кому-то не удается освоить азы использования абакуса, а кто-то не может перейти к устному счету без поддержки наставника. Именно поэтому большинство людей, изучающих эту технику, предпочитают заниматься с помощью тренера.

Однако посещать очные занятия также не всегда удобно. Загруженность и отсутствие большого количества свободного времени из-за работы или учебы, необходимость добираться до места проведения занятий, постоянные разъезды и путешествия – все это препятствует посещению тренировок. А ведь для того, чтобы добиться видимого результата, нужно заниматься регулярно.

Но выход есть, ведь теперь курсы ментальной арифметики можно проходить в режиме online на платформе Amavit. Чтобы начать заниматься, нужно пройти простую регистрацию и выбрать удобное время для проведения занятий. Студентам доступны различные пакеты уроков, среди которых без труда удастся выбрать наиболее подходящий. Запишитесь на пробное занятие уже сейчас и начните осваивать ментальный счет вместе с Амавит.

Ментальная математика

 

Вводное занятие «Знакомство с ментальной арифметикой (счет в воображении)»

 Теория: Понятие «ментальная арифметика». История возникновения ментальной арифметики в Японии и Китае. Практика: Физкультминутка. Пальчиковая гимнастика. Рассматривание абакуса . Игры со счётами.

3. Тема «Знакомство с абакусом»

 Теория: Строение абакуса. Практика. Физкультминутка. Пальчиковая гимнастика. Дыхательные упражнения. Перекладывание косточек.

4. Тема «Набор чисел, использование пальцев, пятерка, «птичка» Теория: Что такое пятёрка на счётах. Как складывать пальцы при передвижении косточек. Термин «птичка» Практика: Физкультминутка. Пальчиковая гимнастика. Набор чисел на абакусе.

 5. Тема «Использование «старших» разрядов для отображения чисел» Теория: Что такое «старший разряд» для отображения чисел. Ряд десятков на абакусе. Чтение загадки про числа. Набор чисел на абакусе.

 6.Тема «Пятерка – старший брат, другой разряд – друзья» Теория: Термины и понятия: пятерка – старший брат, другой разряд – друзья. Практика: Набор чисел на абакусе.

 7. Тема «Знакомство с флеш-картами» Теория: Что такое флеш-карта и ими пользоваться. Практика: Набор чисел на абакусе с использованием флеш-карт.

 8. Тема «Повторение отображения чисел» Теория: Отображение чисел на флеш-картах. Практика: Набор чисел на абакусе с использованием флеш-карт. 

9. Тема «Работа с флеш-картами, набор чисел на абакусе» Теория: Отображение чисел на флеш-картах. Техника работы с абакусом. Практика: Набор чисел на абакусе с использованием флеш-карт.

10. Тема «Простые операции: сложение и вычитание (+\- 1, +\- 5, когда не требуются правила)» Теория: Правильная постановка пальцев при простом сложении и вычитании. Обнуление. Практика: Простое сложение и вычитание на счётах.

11. Тема «Ментальная карта и как с ней работать» Теория: Что такое ментальная карта. Способы работы с ментальной картой. Практика: Физкультминутка. Пальчиковая гимнастика. Игра.

12. Тема «Простые операции: сложение и вычитание (+\- 1, +\- 5, когда не требуются правила)» Теория: Правильная постановка пальцев при простом сложении и вычитании. Обнуление. Практика: Простое сложение и вычитание на счётах и ментальной карте. 

13. Тема «Простые операции: сложение и вычитание (+\- 1, 2, +\- 5, когда не требуются правила)» Теория: Правильная постановка пальцев при простом сложении и вычитании. Обнуление. Практика: Простое сложение и вычитание на счётах и ментальной карте.

14. Тема «Простые операции: сложение и вычитание (+\- 1,2, 3, +\- 5, когда не требуются правила)» Теория: Правильная постановка пальцев при простом сложении и вычитании. Обнуление. Практика: Простое сложение и вычитание на счётах и ментальной карте.

15. Тема ««Простые операции: сложение и вычитание (+\- 1,2, 3, 4 +\- 5, когда не требуются правила)» Теория: Правильная постановка пальцев при простом сложении и вычитании. Обнуление. Практика: Простое сложение и вычитание на счётах и ментальной карте. 

16. Тема «Повторение: отображение чисел, набор чисел на счетах. Примеры с двузначными числами» Теория: Как набирать двузначное число. Двузначные числа на флеш картах. Практика: Отображение чисел, набор чисел на счетах. 

17. Тема «Повторение: счеты, отображение и набор, сложение и вычитание без правил» Теория: Строение абакуса. Отображение и набор чисел. Практика: Простое сложение и вычитание на счётах и ментальной карте. 

18. Тема «Повторение: состав числа 5» Теория: Состав числа 5. Практика: Физкультминутка. Пальчиковая гимнастика. Упражнения для глаз. Математические загадки. 

19. Тема «Правило: +4 = -1+5» Теория: Знакомство со счётом с правилами. Правило: +4 = -1+5. Практика:Сложение при помощи правила на абакусе и ментальной карте.

20. Тема «Правило: +3 = -2+5» Теория: Знакомство со счётом с правилами. Правило: +3 = -2+5. Практика: Сложение при помощи правил на абакусе и ментальной карте.  

 21. Тема «Правило: +2 = -3+5» Теория: Знакомство со счётом с правилами. Правило: +2 = -3+5. Практика: Сложение при помощи правил на абакусе

22. Тема «Правило: +1 = -4+5» Теория: Знакомство со счётом с правилами. Правило: +1 = -4+5. Практика:  Сложение при помощи правил на абакусе и ментальной карте. 

23. Тема «Повторение. Решение примеров с применением известных правил»  Выполнение заданий в рабочей тетради.

24. Тема «Правило: -4 = -5, +1» Теория: Знакомство со счётом с правилами. Правило: -4 = -5, +1. Практика: Выполнение заданий в рабочей тетради.

25. Тема «Правило: -3 = -5+2» Теория: Знакомство со счётом с правилами. Правило: -3 = -5+2. Практика: Вычитание при помощи правил на абакусе и ментальной карте.

26. Тема «Правило: -2 = -5+3» Теория: Знакомство со счётом с правилами. Правило: -2 = -5+3. Практика: Вычитание при помощи правил на абакусе и ментальной карте.

27. Тема «Правило: -1 = -5+4» Теория: Знакомство со счётом с правилами. Правило: -1 = -5+4. 

записаться на урок — Amakids

Головной мозг человека разделен на левое и правое полушарие. Исследования показывают, что форма двух полушарий похожа, но функции у них разная. Левое полушарие имеет тесные связи с работой языка, абстрактного мышления и логического мышления. Правое полушарие имеет дело с объектом мышления: изображение, формы, творческое мышление и интуиция.

Большинство людей считают, что функции левого полушария преобладают над функциями правого полушария, а физиологи и психологи считают, что потенциал правого полушария должен использоваться больше. Идеальным методом является одинаковое использование обоих полушарий.

Альберт Эйнштейн, всемирно известный ученый и мыслитель, шокировал научное сообщество, когда предложил «теорию относительности». С помощью творчества и воображения правого полушария, он представлял взаимодействие пространства и времени в его сознании и преодолел ограничение в трех измерениях. В то же время, он также использовал дедукцию и логику левого полушария, чтобы доказать и выяснить научную и математическую ценность теорий. Поэтому, когда левое и правое полушария головного мозга объединяются и эффективно используются вместе, результаты могут быть поразительными.

Все мы хотим, чтобы наш ребенок был успешным человеком! Как воспитать своего ребенка таким? — эти вопросы занимают каждого любящего родителя.

Курсы ментальная арифметика

На сегодняшний день, много центров и клубов, предлагающих развивающие занятия для детей. Все они предлагают одностороннее развитие ребенка — это музыка, творчество, подготовка к школе, театральные студии, шахматы и т.д. Во всем этом сложно разобраться, что же лучше подойдет нашему ребенку, что бы стать разносторонне развитым, ведь заниматься абсолютно всем невозможно.

На самом деле ему необходимо научиться извлекать их из памяти нужную информацию в нужный момент, уметь оценивать, анализировать, делать выводы – и, самое, главное! – достигать поставленных целей. Самым эффективным инструментом в любых руках для достижения поставленных целей является Интеллект. Ведь это нечто большее, чем книжная ученость, умение петь, играть в шахматы или умение хорошо сдавать тесты. Это умение пользоваться своими знаниями. А эффективный интеллект – это способность получать, обрабатывать и использовать знания с максимальным эффектом, способность действовать в направлении желаемых целей.

Курс ментальной арифметики направлен на развитие интеллектуальных способностей , дети закладывают твердую основу для дальнейших академических успехов и развития личности. В результате освоения программы ментальная арифметика ребенок, например, может сложить пятизначные числа за несколько секунд, но это не единственный результат.

 

Благодаря ментальной арифметике развивается и улучшается:

• Концентрация внимания
• Фотографическая память
• Точность и быстрота реакции
• Уверенность в себе
• Творческое мышление
• Слух и наблюдательность
• Воображение и представление
• И как следствие успехи в учебе.

В начале обучения основная часть работы заключается в интенсивном использовании ребенком счетов Абакус (Соробан). На всех стадиях обучения ребенок использует обе руки для операций с косточками счетов, стимулируя работу обоих полушарий головного мозга. Дети постигают все 4 вида математических операций сложение, вычитание, умножение и деление. При равном участии обоих полушарий головного мозга процесс обучения и размышления становится гораздо более эффективным. На каждой тренировке постепенно ослабляется привязка ребенка к счетам и стимулируется его собственное воображение, благодаря чему уже через несколько занятий, он сможет производить простейшие расчеты в уме, лишь представляя Абакус (Соробан) перед собой и мысленно совершая движения косточками (так называемая работа с воображаемыми счетами).

Ребенок, обучаемый по программе ментальная арифметика, начинает решать математическую задачу, воспринимая числа как картинки, так как каждое конкретное число будет вызывать у него ассоциацию соответствующего изображения на косточках счетов.

Развивающий центр для детей AMAKids предлагает курс ментальной арифметики для детей в возрасте от 4 до 16 лет. Группы формируются по возрастам. Для младшей группы длительность обучения составляет 2,5 года, а для старшей – 2 года. Каждый месяц формируется и начинает обучаться новый класс желающих. Но присоединиться к уже начавшей занятия группе – невозможно.

Все, что не обходимо для процесса обучения, а именно счеты, учебные материалы и тетради, уже включено в стоимость курса.

Первая возрастная категория детей – это 4-6 лет, вторая – 7-10 лет, третья 11-16 лет. Класс младшей группы состоит из 4-6 человек, старшие допускает 6-10 человек. Дети обязательно проходят пробное занятие. Это нужно для того, чтобы сформировать равные группы. Основное требование для учеников – умение считать до 10.

Периодичность занятий удобная. Это по 2 урока в день 1 раз в неделю. Но ежедневная домашняя тренировка должна быть не менее 15 минут. Постепенно ребенок накапливает навыки. Каждый день тренируется одно правило.

Для домашних занятий ребенку нужен доступ к компьютеру. Он получает логин и пароль для входа в программу вместе с рабочими материалами и счетами Абакус (Соробан) еще вначале занятий.

Для младшей группы обязательно участие родителей в тренировках, контроль правильности выполнения домашнего задания. Для старшей группы участие родителей не обязательно, но в расписании ребенка желательно выделить определенное время для тренировок, привязанное к режимному моменту (например, перед ужином). Ощутимые результаты и одновременную работу двух полушарий мозга вы сможете увидеть через 2-3 месяца регулярных занятий. После успешного прохождения программы обучения ребенок получает соответствующий сертификат нашего центра.

Занятия по нашей методике помогут раскрыть и выразить экстраординарные способности каждого ребенка, развить креативность через инновационное обучение.

 

Как пользоваться счетами абакус — инструкция для первоклассников

Среди необычных дидактических пособий для детей свое место занимают счеты абакус, которые помогут улучшить математические навыки и весело и с пользой провести время. Предлагаем познакомиться с тем, что они собой представляют и как ими пользоваться.

Блок: 1/6 | Кол-во символов: 276
Источник: https://Razvivashka.online/poznavatelnoe/abakus-kak-polzovatsya

Что это такое?

Сами счеты, которые положены в основу методики, появились более 2,5 тысячелетий назад. Также можно встретить названия «абак» или «соробан». Эти счеты исполняли в древнейших государствах функции современных калькуляторов и помогали отсчитывать десятки. Впоследствии они стали использоваться в ментальной арифметике.

Внешний их вид довольно прост: абак представляет собой рамку прямоугольной формы, которая разделена перекладинами с нанизанными на них косточками. Вверху, над разделительной полосой, расположена всего одна линия, каждый элемент которой означает пять. Снизу находятся ряды с четырьмя косточками, обозначающими единицу.

Линии косточек означают поочередно единицы (первая правая), десятки (вторая правая), сотни, тысячи. Если первая правая косточка поднята, то на счетах выложена цифра 1 или наименьшее десятичное значение (если расчеты ведутся, например, в миллиардах). Распределение чисел таково:

• нижние косточки – это 1,2,3 и 4, соответственно, если подняты 2 из них, то счеты показывают число два;
• если верхняя косточка поднята, число меньше, чем 5; если опущена на разделительную линию – больше;
• верхняя опущена, три нижние подняты – это число 8.

Аналогичным образом можно выложить любое число.

Блок: 2/6 | Кол-во символов: 1228
Источник: https://Razvivashka.online/poznavatelnoe/abakus-kak-polzovatsya

История возникновения Абакус

Трудно себе представить счет без цифр. Самым ранним счетным устройством были человеческие пальцы рук, а иногда и ног. Но когда возникла необходимость посчитать что — либо большее, придумали новую счетную систему.

Абакус является одним из многих счетных устройств, изобретенных, чтобы посчитать большие числа.

Сегодня хотелось бы рассказать о самых древних и используемых по сей день системах вычисления. Это три основные счетные системы: Суан Пэн, Соробан и Русские счеты. У каждого из них есть свои отличия, давайте кратко рассмотрим каждое.

Суан Пэн

Абакус (Абак), или в китайском языке Suan-Pan, представляет собой деревянную дощечку с шарами. На верхней палубе находилось по 2 косточки, на нижней по 5 (2/5). Так было вплоть до 1850 года, после стиль немного изменился: на верхней палубе осталось по 1 бусинке, а на нижней 5 (1/5).

Соробан (современный Абакус)

В японском языке счеты назывались Соробан. У них было соотношение бусинок ¼. Техники подсчета в японской и китайской системе счета похожи, но имеют свои отличия. В нашей стране есть школы, которые обучают как той, так и другой системе подсчета. В статье представлена информация именно о Соробане, так как она активно используется как в Японии, так и в нашей стране для обучения деток.

Русские счеты

Были изобретены в 17 веке и используются до сих пор. Дизайн счет напоминает модель пары человеческих рук (каждый ряд имеет 10 бусин, соответствующей 10 пальцам на двух руках).

Модификация Ли Кай Чена

В 1958 году китайский ученый Ли Кай Чен объединил абакус и соробан в одни счеты и опубликовал руководство для новых счетчиков. По словам автора, умножение и деление на много легче использовать с помощью модифицированных счетов. Так можно вычислить даже кубические корни чисел.

На фото видно, что сверху находится японский Соробан, а снизу китайский Суан Пэн.

Блок: 2/6 | Кол-во символов: 1839
Источник: https://chesnachki.ru/ot-6-ti-i-starshe/shkolniki/scheti-abakus.html

Преимущества использования

Работа со счетами не только помогает развивать мелкую моторику дошкольника, но и тренирует сразу оба полушария его головного мозга, позволяет наладить взаимосвязи между ними. Кроме того, можно выделить несколько достоинств методики:

1. Интерес. Малышам нравится перебирать косточки, при правильном подходе родителей из абакуса можно сделать тренажер, занятия на котором будут искренне нравиться ребенку.
2. Использование счетов позволяет избежать заучивания и стимулирует образное мышление.
3. При регулярных тренировках со временем удастся перевести ребенка от работы с реальным абакусом к воображаемой.
4. Дети учатся находить нестандартные варианты решения проблемы.
5. Постепенно обретают уверенность в себе, становятся более самостоятельными.
6. Очень хорошо развивается мышление.

Вот почему счеты считаются мощнейшим пособием в ментальной арифметике, то есть обучении быстрому счету.

Блок: 3/6 | Кол-во символов: 900
Источник: https://Razvivashka.online/poznavatelnoe/abakus-kak-polzovatsya

Как выглядят счеты?

Современные счеты, японские счетчики или Соробан имеют один шар вверху и четыре внизу.

Верхние косточки имеют значение 5 их еще называют небесные бусины. А нижний ряд (состоящий из 4-х косточек) имеет значение 1, его называют земными бусинами.  Между ними есть разделительная линия.

Значения шариков начинаются с крайнего правого столбца, и равняется 1. Справа налево значения бисера увеличиваются и равна 1, затем 10, 100 и т.д. На приведенной ниже фотографии показано значение каждого шарика на счетах.

Блок: 3/6 | Кол-во символов: 521
Источник: https://chesnachki.ru/ot-6-ti-i-starshe/shkolniki/scheti-abakus.html

Основы ментальной арифметики

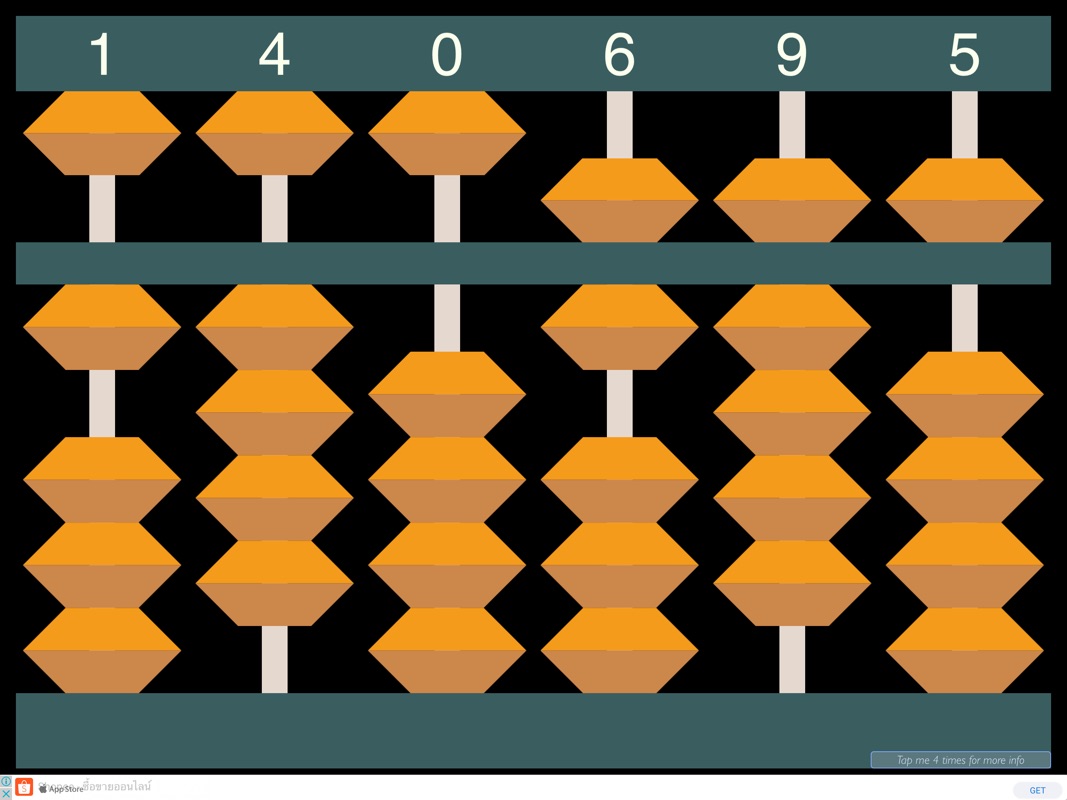
Как выглядят счеты абакус и из чего состоят вы уже знаете. Сейчас нужно понять, как набирать числа.

Располагаем соробан как на рисунке выше. Перед нами столбики, у стандартного соробана их 13. Мы будем использовать абакус с девятью столбиками (такой же как в приложении Simple Soroban). Начиная с крайне правого столбика, в этом столбце единицы. Т. е. здесь можно составить цифру от 0 до 9. Следующий столбец — это десятки, здесь числа от 10 до 90. В последующих соответственно сотни, тысячи и т. д. На верху соробана размещено по одной бусине, в соответствии со своим столбцом они обозначают число кратное пяти, т. е. в первом столбце это 5, во втором 50, в третьем 500 и так далее. Чтобы нам показать цифру пять, нужно опустить верхнюю бусину вниз, это будет пять. В исходном положении, когда верхние бусины в верху, а нижние внизу это ноль. Чтобы больше было понятно разберем несколько цифр:

• Чтобы составить цифру 7 нужно опустить верхнюю бусину в первом столбце, это будет 5 и поднять две бусины с низу, т.е. мы к 5 прибавили 2 получилось 7.
• Цифра 9 это опущенная верхняя бусина и 4 нижние бусины, поднятые вверх до разделительной планки.

Как только научились быстро набирать единицы, переходим к двухзначным числам, т.е. к десяткам.

Набираем число 73, для этого опускаем верхнюю бусину из второго столбика, это получилось 50, поднимаем еще две нижние бусины из этого же столбца с десятками, получилось 70. В первом столбце поднимаем три нижних бусины, и в итоге получаем 73.

Несколько раз потренируетесь и все будет понятно, потом переходите к сотням и так далее.

Все передвижения бусин нужно делать определенными руками и не менять последовательность. В столбце единиц мы все делаем правой рукой, при этом поднимаем бусины большим пальцем, а опускаем указательным. Например, когда мы хотим составить цифру 5 нужно указательным пальцем правой руки опустить верхнюю бусину. Если нужно составить цифру 2 нужно большим пальцем правой руки поднять две бусины из первого столбца. Запоминаем правило вверх это большой палец, вниз указательный. В столбце с десятками все тоже самое только левой рукой. Если смотрели видео как дети считаю, можно было заметит, как они крутят пальцами. Так они представляют, как передвигают бусины на счетах и тем самым производят у себя в голове, подсчет на воображаемом соробане.

Так как вся суть метода сводится к тому чтобы все вычисления происходили в уме и без каких-либо вспомогательных инструментов, нужно научится запоминать цифры и комбинации из бусин. Для этого нам понадобятся вспомогательные карточки, которые можно сделать самим. На одной стороне пишем цифру, а на другой ее графическое обозначение в виде фрагмента счет. Пример на фото ниже.

После того как научились пользоваться карточками и быстро называть цифры расположенные на них, переходим к простым арифметическим вычислениям, первое что мы разберем это сложение.

Блок: 4/8 | Кол-во символов: 2898
Источник: https://SemyaTut.ru/deti/obuchenie/mentalnaya-arifmetika.html

Как пользоваться пальцами?

Стандартные счеты могут использоваться для выполнения сложения, вычитания, умножения и деления. Их так же используют для извлечения квадратных и кубических корней.

Правильная техника пальцев имеет первостепенное значение для достижения мастерства в счетах.  В случае японской версии Абакуса (Соробана) используется только указательный и большой пальцы.

На картинке представлена вырезка из японского учебника, в котором рассказывается о правильной технике перемещения бусин. Он показывает большой палец, используемый для подсчета бусинок в нижней палубе, а указательный палец используется во всех других случаях.

Удобно земные шары добавлять большим пальцем, а вычитать указательным. А вот небесные шары лучше добавлять и вычитать только указательным пальцем одной руки.

Так же я предполагаю, что вас интересует как вместо счетов пользоваться пальцами. Об этом у меня есть отдельный раздел в статье «Как научиться ментальной арифметике дома».

Блок: 5/6 | Кол-во символов: 963
Источник: https://chesnachki.ru/ot-6-ti-i-starshe/shkolniki/scheti-abakus.html

Вычитание

Переходим к следующему действию, вычитанию. Для примера возьмем 83-56.

Выставляем на соробане число 83, что получилось сверяем по фото.

При вычитании все действия нужно производить в обратном порядке и начинать нужно с десяток. Нам нужно у десяток убрать 5 бусин, для этого поднимаем верхнюю бусину. От единиц нужно отнять 6, так как у нас только 3 единицы, берем из второго столбца десятку, т. е. опускаем одну бусину. В единицах нужно из 13 вычесть 6 получается 7, выставляем эту цифру на соробане.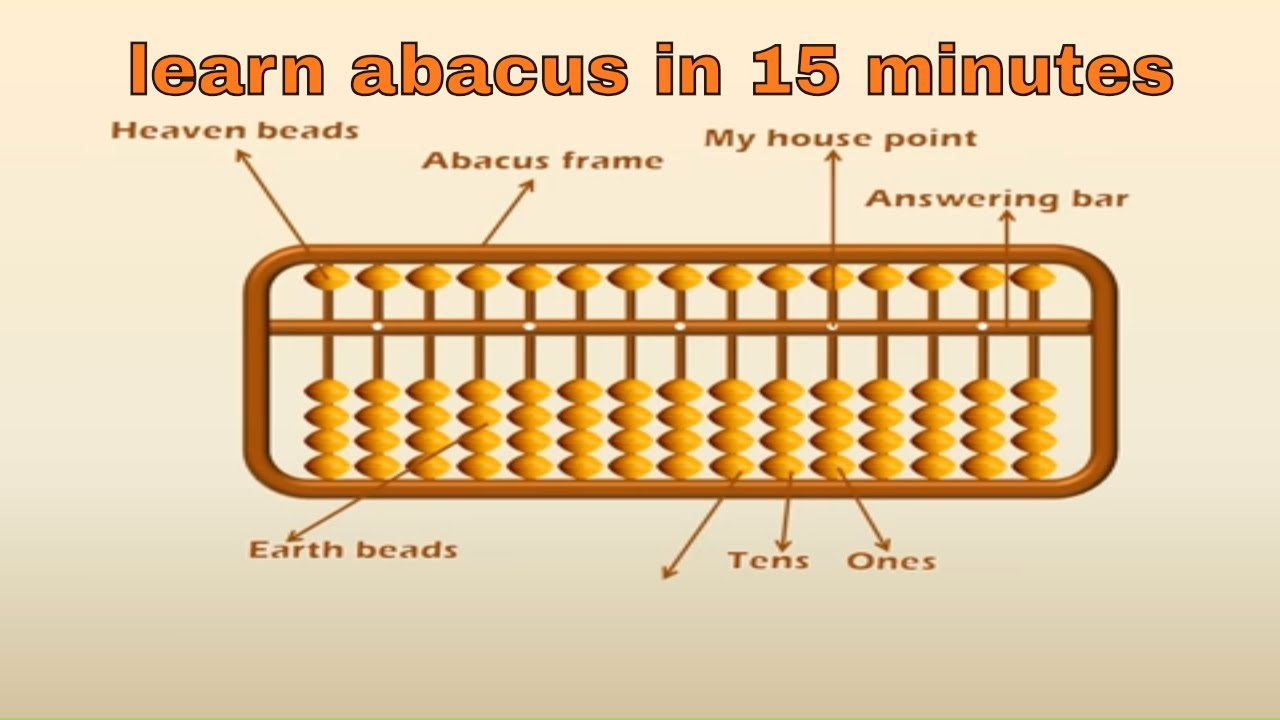 В итоге 83-56=27

Видео урок: Вычитание

Блок: 6/8 | Кол-во символов: 553
Источник: https://SemyaTut.ru/deti/obuchenie/mentalnaya-arifmetika.html

Видео-урок 1: как пользоваться счетами Абакус?

Как правило, видеоинформация усваивается лучше, чем описание. Поэтому предлагаю рассмотреть простой и понятный урок о том, с чего начинается работа над абакусом.

А на последок вам небольшое домашнее задание. Попробуйте самостоятельно посчитать, какие цифры расположены на счетах. Ссылка кликабельна.

Этот блог читают 10875 мам, пока
играют со своими детьми.

Блок: 6/6 | Кол-во символов: 403
Источник: https://chesnachki.ru/ot-6-ti-i-starshe/shkolniki/scheti-abakus.html

Кол-во блоков: 12 | Общее кол-во символов: 10758
Количество использованных доноров: 3
Информация по каждому донору:

1. https://Razvivashka. online/poznavatelnoe/abakus-kak-polzovatsya: использовано 3 блоков из 6, кол-во символов 2404 (22%)
2. https://SemyaTut.ru/deti/obuchenie/mentalnaya-arifmetika.html: использовано 3 блоков из 8, кол-во символов 4628 (43%)
3. https://chesnachki.ru/ot-6-ti-i-starshe/shkolniki/scheti-abakus.html: использовано 4 блоков из 6, кол-во символов 3726 (35%)

Японские счеты Соробан (Абакус)

Методика счета под названием Соробан сегодня распространяется со скоростью света. Ее цель – развить умственные способности детей, равномерно задействуя левое и правое полушария. Этой методике более 25 лет в Японии, 3 года она работает в постсоветских странах. Но самое интересное, что счетам, на основе которых она построена, уже более 2,5 тысяч лет. И только сейчас из далеких стран Азии этот инструмент счета начинает распространяться по всему миру.

Что такое абакус?

Абакус (Абак), или Соробан – это древние счеты, которые использовали в древних странах Азии и Европе. В Китае они назывались абак  (по-латыни «абакус»), в Японии – Соробан. Однако применяли их также в Древнем Риме и Греции. Абакус несколько видоизменялись в зависимости от страны, где они использовались, но суть оставалась прежней.

Счеты представляют собой рамку, разделенную перекладиной. В верхней части расположена одна линия косточек. Каждая косточка в ней означает «пять». Внизу расположены ряды косточек, в каждом из которых по 4 косточки. Каждая из них обозначает «один».

Косточки на счетах Соробан, или Абакус специально заострены, чтобы дети, перебирая их, развивали мелкую моторику. Счеты Абакус обозначают единицы, десятки, сотни, тысячи и миллионы. С помощью Соробан дети быстро осваивают устный счет и даже могут перемножить многозначные числа.

Как проходят занятия?

Методика обучения на счетах Соробан, или Ментальная арифметика, позволяет развить способности детей до небывалых высот. Основным инструментом при этом являются счеты Абакус.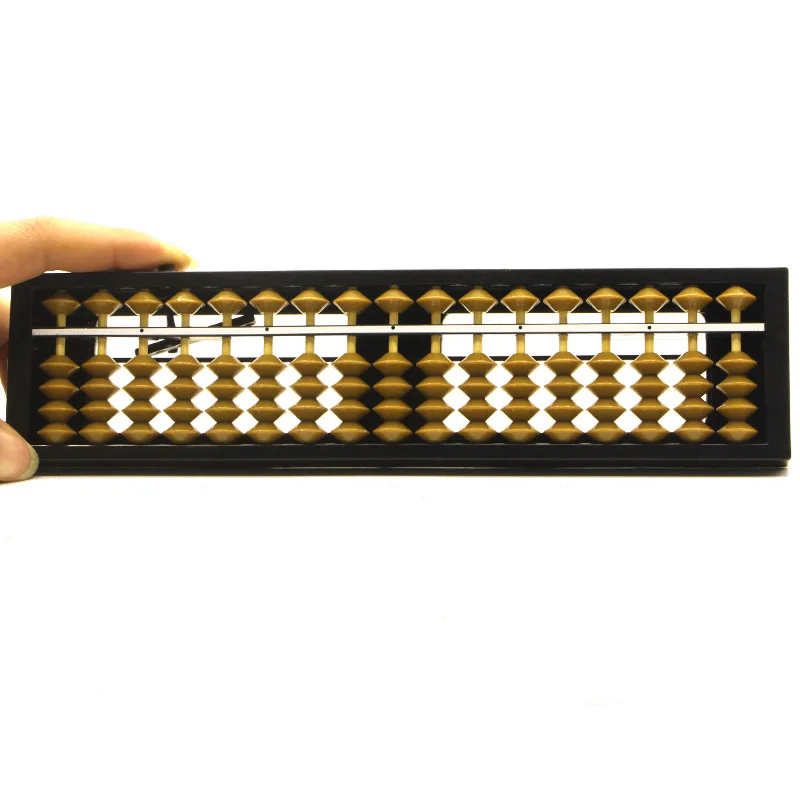 На первом этапе дети учатся пользоваться счетами.

На второй этапе дети представляют счеты Соробан в уме. Т.е. ребенок начинает представлять Соробан перед собой и производить вычисления в уме. При этом осваиваются 3 математические действия:

• сложение;
• вычитание;
• умножение;

Обучение продолжается 2 года. Лучше всего начинать обучение в возрасте ребенка от  5 до 11 лет. Этот возраст считается оптимальным.  Но это не означает, что методика Соробан недоступна для старших детей и взрослых, просто для обучения может потребоваться больше времени.

Занятия в центрах Соробан проходят в течение 2 часов 1 раз в неделю. На дом детям даются задания. Если они выполнены, тренер открывает доступ к следующим. Для выполнения задания достаточно четверти часа в сутки. Программа может корректироваться индивидуально в зависимости от того, как успевает каждый ребенок.

Как пользоваться?

Чтобы научиться пользоваться счетами, необходимо знать, что они из себя представляют. Счеты состоят из:

• рамки;
• разделительной полосы;
• верхних косточек;
• нижних косточек.

Посередине находится центральная точка. Верхние косточки обозначают пятерки, а нижние – единицы. Каждая вертикальная полоса косточек, начиная справа налево, обозначает один из разрядов цифр:

• единицы;
• десятки;
• сотни;
• тысячи;
• десятки тысяч и т. д.

Чтобы отложить число, необходимо на счетах придвинуть к разделительной линии косточки, по числовому обозначению соответствующие цифре каждого разряда. Например, чтобы отложить число 165, необходимо на первой линии справа придвинуть верхнюю косточку (она обозначает пятерку), на второй линии – верхнюю и одну нижнюю косточку (5+1=6), на третьей линии – одну нижнюю. Так мы получаем требуемое число.

Дальнейшие вычисления будут сопровождаться передвижением косточек по линиям соответственно разрядам.

Что дает ментальная арифметика?

Японские счеты под названием Соробан учат не только считать, хотя в этом дети добиваются небывалых успехов.  Малыши с легкостью вычисляют в уме 10-значные числа, умножают и вычитают. Но быстрый устный счет не главная цель.

Считать – лишь способ развивать умственные способности. Ментальная арифметика способствует:

• умению концентрироваться;
• активизации слуховой и зрительной памяти;
• совершенствованию интуиции и смекалки;
• умению нестандартно решать проблемы;
• проявлению самостоятельности и уверенности в себе;
• реализации способностей и успешной карьере в будущем.

В основе методики лежит сила воображения. Именно благодаря ей удается ускорить мышление, наладить ускоренные связи между правым и левым полушариями мозга. Дети, которые учились по методике Соробан, быстрее осваивают иностранные языки, хорошо учатся в школе, более целеустремленные.

Здесь Вы можете посмотреть видео учеников, обучающихся в школе Соробан™

Отзывы

Так ли это? Действительно ли метод обучения столь эффективен? Отзывы в основном положительные: дети уже через пару месяцев начинают быстро считать и лучше соображать.

В основном родители довольны: дети подтягиваются по предметам, становятся внимательнее и сосредоточеннее. Но у некоторых ребят случаются неудачи. В основном это связано с тем, что задания в школе Соробан следует выполнять ежедневно. Некоторых детей трудно усадить ежедневно за выполнение заданий, и  они не успевают усваивать курс.

Таким образом, родители должны внимательно следить за реакцией ребенка на обучение. Если ему нравится, он успевает, и занятия не становятся предметом для слез и переживаний, можно продолжать. Но если малышу не уроках не комфортно, он не успевает, стоит попросить руководителя определить индивидуальный курс или вовсе пока прекратить занятия. Каждому свое!

Немного секретов ментальной арифметики

Школьная пора одна из самых ярких и запоминающихся моментов в жизни каждого человека.

Но зачастую ребенку очень сложно эффективно распределять поступающую к нему информацию.

Постоянная зубрежка, многократное чтение, решение однотипных задач, могут повлиять на мотивацию ребенка к учебе.

Как разбудить жажду к знаниям? На этот вопрос мы ответим, сквозь призму Методики Ментальная арифметика.

Опыт, накопленный пред идущими поколениями, открывает для нас массу возможностей для помощи ребенку в освоении различных предметов.

В чем польза для школьной программы, от занятий ментальной арифметикой?

На занятиях по ментальной арифметике мы используем соробан или абакус. Это древний вычислительный инструмент, которые использовали в качестве калькулятора много веков назад.

На абакусе расположены косточки, которые ребенок передвигает, в зависимости от количества косточек и их расположения получается ответ, который ребенок переносит в числа.

После прохождения курса занятий, ребенку не нужно пользоваться абакусом, т.к он начинает представлять косточки в своем воображении, передвигая их, получает большие числа.

Самый заметный эффект от занятий это быстрый устный счет, который пригодиться везде.

В физике, геометрии, математике.

Главный результат тренировок:

-Развитие обоих полушарий мозга.

-Быстрое принятие решений.

-Фотографическая память

-Пространственное мышление и воображение.

-Легкое запоминание стихов.

-Уверенность в себе и своих силах

Причем навыком счета можно пользоваться везде, в вузе, колледже.

А когда у ребенка что-то хорошо получается, он делает это с удовольствием.

Как сделать занятия ментальной арифметикой более эффективными.

-Повторение-мать учения! Заниматься нужно по 15-25 минут, каждый день. Толку будет меньше если делать 2 раза в неделю 2 часа.

-Делать примеры на слух, слуховая и двигательная память самая долгосрочная.

-Проговаривать про себя правила, когда они начнут «отскакивать от зубов» любые сложные и быстрые примеры становятся более легкими.

-Поддержка родителей очень важна, нужно хвалить ребенка, даже если у него не получается.

На занятиях мы используем индивидуальный подход к каждому, каждого выделяем хвалим.

Повышается самооценка и ребенку хочется заниматься в классе. Приходя домой, родители часто берут все под строгий контроль и ругают и наказывают за неудачи. Отсюда нежелание делать домашнее задание.

Учителя в школе, за неимением возможности уделить каждому время, упускают особенности каждого ученика.

Но учится в школе важно, это важная ступень, облегчить можно дав ребенку преимущество.

Говорить ему о том, что он особенный, что он как суперкалькулятор, после занятий ментальной арифметикой. И если школьные уроки даются сложно, дайте ему 10 минут, чтобы посчитать ментально или на абакусе, перед выполнением заданий.

Во-первых, после тренировки он станет думать быстрее, во-вторых, на волне успеха ребенку легче будет воспринимать школьную нагрузку.

В чем особенности методики школы Rich Brain

-Все занятия проходят в игровой форме.

-Дети школьного возраста осваивают сложение и вычитание до трехзначных чисел за учебный год.

-Младшие дети до двузначных за календарный год.

-Мы используем элементы ТРИЗ решение изобретательских задач.

-Физминутки это Brain Fitness

-Для отработки всех правил используем платформу-тренажер по ментальной арифметике.

-Используем бонусную систему мотивации детей за домашнюю работу.

Приходите, будет интересно!

Как использовать китайские счеты

Вы когда-нибудь задумывались, как бы вы решали математические задачи, если бы у вас не было калькулятора, компьютера или даже карандаша и бумаги? На протяжении веков люди в Азии использовали древний счетный инструмент для выполнения математических операций. Китайское название калькулятора – «суанпан», но оно также известно как счеты. Это простое счетное устройство, построенное как минимум в XII веке, передавалось из поколения в поколение, сохранив первоначальную конструкцию и предназначение практически без изменений.

Введение в китайские счеты

Традиционные суанпан или китайские счеты состоят из прямоугольной деревянной рамы, разделенной горизонтальной перекладиной на верхнюю и нижнюю части. Ряд вертикальных проволок или стержней, нанизанных бусинами, простирается от верха до низа рамки. Часть проволоки над перекладиной традиционно называется «небом», но также называется верхней палубой. Область под баром, традиционно известная как «Земля», – это нижняя палуба.

Каждая проволока в рамке абака имеет семь бусинок, две из которых находятся на верхнем уровне и пять – на нижнем.Каждая из двух бусинок верхней деки имеет значение 5, в то время как каждая бусинка нижней деки имеет значение 1. Проволока представляет собой степень десяти. Начиная с правой стороны абака, первый провод представляет значения ниже 10, второй провод представляет значения от 10 до 99, а третий провод представляет от 100 до 999. Этот шаблон продолжается по оставшимся проводам, позволяя традиционным счетам с 13 проводами использовать представляют собой очень большие числа.

Инструкции для китайских счётов

Первым шагом при использовании китайских счётов является их очистка. Для этого нужно положить устройство на стол и переместить выступы верхней деки к верхней части рамы, а валики нижней деки – к верхней части рамы. каркас внизу.Чтобы сосчитать одно число на счетах, переместите соответствующее количество бусинок к полосе. Например, число 1 подсчитывается путем перемещения верхней бусинки в нижнюю часть проволоки до перекладины. Число 9 подсчитывается путем перемещения нижней бусины в верхнюю деку и четырех бусинок из нижней деки на планку. Число 10 подсчитывается путем перемещения верхней бусинки с нижней колоды проволоки десятков на планку.

Простое сложение выполняется на счетах путем подсчета бусинок для первого числа и последующего подсчета бусин для числа, которое нужно добавить.Например, чтобы решить 5 + 3, вы должны сначала переместить бусину в верхней колоде, чтобы представить 5, а затем переместите три бусинки из нижней колоды для значения 3. Затем бусинки будут представлять собой число 8, которое является решение 5 + 3. Если счет во время сложения приводит к значению больше 10 на любом проводе, то «перенос» осуществляется путем удаления бусинок с верхней и нижней дека текущей проволоки и перемещения одной бусинки вверх с нижней дека на провод слева.

Вычитание на счетах выполняется путем отсчета первого числа и удаления бусинок, представляющих второе число.Для задачи 9 – 2 вы опускаете одну бусину в верхней деке и поднимаете четыре бусины в нижней деке, чтобы обозначить число 9. Затем вы опускаете две бусинки в нижней деке, чтобы вычесть 2. Полученные бусинки представляют собой число 7, которое является решением для 9 – 2.

История китайских счётов

Счетные устройства, такие как счеты, использовались более 2000 лет. Есть записи о подобных инструментах, известных как счетные доски, которые использовались древними греками и римлянами.На этих досках имелись металлические канавки со скользящими счетчиками, которые перемещались горизонтально во время операций счета. Некоторые историки полагают, что римские купцы представили эти счетные доски китайцам в ходе торговых сделок, а затем китайцы довели этот инструмент до его нынешней формы.

Использование 100-бусных счётов в элементарной математике

Одним из лучших манипуляторов для первоклассников и второклассников являются простые «школьные» счеты (или 100-бусные счеты), у которых есть 10 проволок и 10 бусинок на каждой проволоке.

Это не значит, что китайские или японские счеты со специальной системой счета. Я говорю об использовании простых счётов из 100 бусинок для счета и обработки каждой бусинки как 1. Вам не нужно изучать какую-либо из этих сложных систем, которые использовались с различными счетами. Просто считайте, что каждая бусинка равна 1, и точка.

У вас есть 10 десятков или сотня на ваших счетах, и это имеет большое значение для объяснения десятков и единиц или двузначного числа детей в детском саду и в первом классе.

Лучше всего, если на счетах будет пять бусинок разного цвета, как на счетах справа. Тогда ребенок без труда узнает 6, 7 и 8 бусинок.

Идеи использования счеты

• Обучающие номера. Сыграйте в простую игру со счетами. Когда наступает ваша очередь, вы произносите число, например 42, и ребенок «набирает» его или показывает на счетах. Затем ребенок называет вам число, и вы показываете его на счетах.Продолжайте так по очереди.


• Более 10 дополнительно. Выберите, например, 6 бусинок на одной проволоке и 8 бисеринок на следующей. Вы можете показать, как пять и пять на этих двух проводах составляют десять, а некоторые остались.


• Узоры на вычитание (и сложение). Покажите ученику, как выполнять каждое из вычитаний
  10–5
  20–5
  60 – 5
  Ученик заметит, что они очень похожи – есть закономерность!


• Добавление 2-х значных номеров без перегруппировки (переноса). Чтобы сложить 23 + 45, ребенок может переместить 2 десятки и 4 десятки, затем 3 и 5 отдельных фигур. Вы можете показать ребенку, как складывать по отдельности десятки и единицы.


• Идея перегруппировки. Пусть ребенок исследует, что происходит с 28 + 9 и другими суммами, требующими перегруппировки.


• Умножение модели. Например, переместите 4 бусинки на на каждую из 5 соседних проводов, и получится 5 раз по 4!


• Модельное подразделение. Пожалуйста, смотрите пост Абакус и основное деление для более подробной информации.

Так что это не ракетостроение; это очень просто! Вы можете просмотреть выборку счетов Amazon здесь.

Как использовать Abacus – Science Class [Видео 2021]

Использование счеты

Чтобы прочитать счеты, вы посмотрите, какие бусинки куда перемещаются. Каждый столбец представляет собой разное разрядное значение. Крайний правый столбец представляет значение разряда отдельных единиц.Столбец рядом с ним представляет значение разряда десятков. Средний столбец представляет собой значение сотен разрядов.

Бусины внизу – это числа от 1 до 5, а бусинки наверху – это 5 и 10 соответственно. Вы перемещаете верхние бусинки вниз и нижние бусинки вверх, чтобы обозначить число. Если вы сдвинете одну нижнюю бусину вверх в столбце десятков, у вас будет номер 10. Если вы вытолкните две нижние бусинки из столбца сотен, у вас будет 200. Если вы сдвинете одну верхнюю бусину вниз из столбца десятков, вы получите есть 50.Чтобы представить число 15, вы должны нажать две верхние бусинки в крайнем правом столбце вниз и подтолкнуть пять нижних бусинок вверх. Вы также можете использовать два столбца, чтобы получить номер 15. Вы можете подтолкнуть одну нижнюю бусину вверх из второго столбца справа и пять нижних бусинок вверх в крайнем правом столбце.

Расчет с помощью бус

Теперь давайте посмотрим, как можно использовать счеты для решения своих математических задач.

Допустим, вы хотите вычислить 11 + 45. Вы бы начали с нажатия бусинок, чтобы получилось 11.Вы выталкиваете одну нижнюю бусину вверх из столбца десятков и одну нижнюю бусину вверх из столбца единиц.

Теперь, чтобы добавить 45, все, что вам нужно сделать, это добавить такое количество бусинок на свои счеты. Вы переместите четыре нижних бусинки вверх из столбца десятков и одну верхнюю бусину вниз в столбце единиц. Вы переместите одну верхнюю бусину вниз, поскольку каждая из этих верхних бусинок соответствует 5. Кроме того, не хватает нижних бусинок, чтобы подняться в столбце единиц.

Тогда ваш ответ – это число, указанное на ваших счетах. Чтение счеты дает 56 (50 из столбца десятков и 5 + 1 = 6 из столбца единиц).При достаточной практике вы сможете быстро и легко производить расчеты на своих счетах.

Другие примеры

Давайте теперь попробуем задачу на вычитание.

Допустим, вы хотите вычислить 107 – 35. Начните с перемещения бусинок, чтобы получилось 107. Переместите одну нижнюю бусину вверх из столбца сотен. Затем переместите одну верхнюю бусину вниз в столбце единиц и две нижние бусинки вверх.

Теперь, чтобы вычесть 35, вы уберете столько бусинок из своей задачи. Вы заметите, что у столбца десятков нет бусинок, которые можно было бы убрать.Вы можете изменить это, переместив одну нижнюю грань вниз в столбце сотен и заменив ее, переместив одну верхнюю грань вниз из столбца десятков и пять нижних граней вверх также в столбце десятков.

У вас еще есть 107 на счетах, просто вы используете другие бусинки. Но, переделав 107, теперь вы можете легко вычесть 35. Чтобы вычесть 35, нажмите три нижних бусинки вниз из столбца десятков и одну верхнюю бусину вверх из столбца единиц.

Теперь, когда вы читаете свои счеты, у вас есть 72 (50 + 20 из столбца десятков и 2 из столбца единиц).Итак, 107 – 35 равно 72.

Резюме урока

Давайте рассмотрим. Счеты похожи на ручной калькулятор со скользящими шариками для представления чисел. На нем есть ряды или столбцы бусинок, которые представляют цифры вашего числа. У вас будут единицы, десятки, сотни, тысячи и так далее.

Китайские счеты имеют столбики из бисера с верхней и нижней частью. В верхней части есть две бусинки, каждая из которых представляет собой 5. Если переместить эти две бусинки вниз, вы получите число 10.В нижней части есть пять бусинок, каждая бусинка представляет собой 1. Если вы переместите три бусинки вверх, вы будете представлять число 3. Вы представляете числа, перемещая бусинки вверх и вниз, чтобы встретиться друг с другом в середине. Чтобы выяснить, какое число показывает счет, просто сложите числа, представленные бусинками. Другая версия абака имеет ряды из десяти бусинок, каждая бусинка представляет 1, а каждая строка представляет различное разрядное значение.

Abacus Как использовать его для вычисления в первую очередь мысленно | by Online Tutors Helpline

Abacus – очень простой механический калькулятор.Он существует с древних времен. Это очень полезный инструмент для продавцов и аудиторов. Это полезное обучающее оборудование для слабовидящих, а также для всех, кто хочет изучить происхождение современного калькулятора. В этой теме мы говорим о счетах, как ими пользоваться?

Abacus – это инструмент со стержнями и бусинами, который используется для математических вычислений, таких как сложение, вычитание, умножение и деление. Просто перемещая бусинки слева направо, вы можете добавить миллиард или больше.Хотя у нас есть технология, позволяющая решать сложные математические задачи на Go, Abacus обучает ум вычислять без каких-либо внешних технологических инструментов, таких как гаджеты, мобильные устройства или калькуляторы. Это действительно весело, если ты знаешь счеты и как ими пользоваться?

4 простых способа улучшить программирование для детей, даже не задумываясь об этом

Счеты – это деревянный инструмент квадратной формы, состоящий из десяти различных проводов или струн, расположенных параллельно. Каждая из этих струн имеет десять движущихся шариков.Это инструмент, который помогает людям делать простые вычисления.

10 лучших веб-сайтов, которые помогут научиться программированию в Интернете Бесплатно

Сегодня он все еще широко используется в Африке, Японии, России, Китае и других странах в качестве визуального справочника для поощрения изучения математических понятий. Дети в азиатских странах получают образование Abacus еще в детстве, чтобы они могли сконцентрироваться и уменьшить свой страх в цифрах. Термин abacus происходит от греческого слова «abax», что означает «компьютерная доска» или «компьютерный планшет», согласно UCMAS.

Метод 9 способов повышения энергии и мотивации учащегося

Если вы хотите преподавать Abacus, и сначала вы должны знать. Теперь мы обсуждаем шаги абака, как им пользоваться?

Правильно выровняйте счет. В каждом столбце верхнего ряда должна быть одна или две бусинки в ряду, а в каждом столбце нижнего ряда должно быть четыре бусинки. Когда вы начнете, все бусинки будут вверху в верхнем ряду и вниз в нижнем ряду. Бусинки в верхнем ряду имеют номер 5, а каждая бусинка в нижнем ряду – номер 1.

Присвойте значение разряда каждому столбцу. Как и в современном калькуляторе, каждый столбик бусинок содержит «размеченное» значение, из которого вы строите число. Таким образом, самый дальний столбец справа будет содержать «единицы» (1–9), второй – «десятки» (10–99), третий дальше всего – сотню (100–999) и так далее.

Начинаем считать бисеринки в нижнем ряду. Переместите бусинку в положение «вверх», чтобы сосчитать цифру. «Один» – переместить одну бусину в самом дальнем столбце из нижнего ряда вправо, чтобы «вверх», «два» – потянуть 2 и т. Д.

Выполните «обмен 4/5». Поскольку в нижнем ряду всего четыре перфорации, чтобы перейти от «четырех» к «пяти», вы перемещаете принудительную перфорацию в верхнем ряду вниз в положение «вниз» и перемещаете четыре перфорации из нижнего ряда вниз. Счеты правильно интерпретируют это место как «пять».

Повторить более высокую числовую последовательность.

Как подготовить ребенка к первому дню школы или детского сада

Пожалуйста, введите свое первое число. Заявите, что вам нужно сложить 234 и 678.Введите 234 на счетах, поместив четыре бусины на единицу измерения, три на 10-ю и две на сотую.

Начинайте добавлять снизу. Первые числа, которые вы можете сложить, – это 2 и 6 из 100, где одна бусина перемещается от верхнего ряда столбца вниз до 6 и оставляет в общей сложности 8 на нижней бусине. Только, чтобы добавить 7 в 10-м положении, переместите верхнюю бусину снизу на 10 в 10-й и одну бусину.

Завершите обмен. Поскольку два числа складываются в разряде десятков до 10, вы должны довести 1 до 100, превратив его в 9 в этом столбце.Сначала соберите все бусинки на место, сделав его пустым.

Посчитайте бусинки для ответа. У вас останется 9 возрастов, 1 из десятков и 2 из них:

234 + 678 = 912.

Вычтите, изменив процесс сложения в обратном порядке. Лучше заимствуйте числа из предыдущего столбца, чем переносите их.

Мотивация детей: 10 вещей, которые я хотел бы знать в карантине

Умножение счётов требует определённой концентрации внимания и подсчёта.

Переместите то же количество бусинок, что и в первом вопросе умножения на слайде.Например, при умножении 6 * 4 перенесите в решетку шесть бусинок. Начните с бусинок вверху и сместите их вправо слева, чтобы ваши вычисления были более организованными и более простыми. Все бусинки на счетах должны быть размещены абсолютно слева, когда начнется расчет, чтобы вы не запутались.

Повторите вышеуказанный шаг для второго числа в уравнении. Для примера 6 * 4 вы переместите шесть бусинок четыре раза на противоположную сторону стойки. Спуститесь ко второму ряду счет, как только первый ряд полностью переместится, и продолжайте движение слева направо после того, как закончится ряд над ним.

Подсчитайте общее количество бусинок, которое вы прошли, чтобы получить ответ.

Меньшее число можно умножить аналогичным образом, посчитав одну бусину за малое число, например, пять или десять. Это предотвращает исчерпание бусинок в смете.

Как легко и эффективно обучать учеников начальной школы

Оставьте справа от делителя и делителя поля для своего ответа. Если вы делите на счетах, вы помещаете разделитель в левую колонку (и). Оставьте несколько пустых столбцов справа и поместите дивиденды рядом с ними в столбцах.Для выполнения работы, ведущей к ответу, используются остальные столбцы справа. Оставив их пустыми.

В крайнем левом столбце, например, чтобы разделить 34 на 2, оставьте два пустых столбца, а затем поместите 34 справа. Оставьте остальные столбцы в разделе ответов пустыми.

Рекордное частное. Рекордное частное. Разделите первое делимое число (3) на делитель (2) и поместите его в сегмент комментария первого пустого столбца. Два раза переходят в три, так что запишите там один.

Определите остальное.Затем в первом столбце ответа (1) вы должны вычесть частное на делимое в столбце один (2), чтобы вычислить баланс. После этого исключите товар (2) из ​​первой дивидендной доски.

Повторить процесс. Повторите процесс. В следующем пустом столбце ответа сегмент вставляет следующую цифру частного, удаляя произведение из делимого (исключая его здесь).

Как выбрать программу домашней школы для ваших детей

Давайте разберемся, как работают счеты и чем они могут быть опасны для математического потенциала вашего ребенка.

Использование абакуса похоже на игру на клавиатуре компьютера, которое помогает вам писать намного проще, но набирать их непросто. Понимание абстрактных уравнений разрушит когнитивные навыки вашего ребенка. Когда вы предлагаете ребенку добавить 15 и 19, он добавит их, даже если он не знает их настоящих значений. Семьи чувствуют себя хорошо, когда видят, как измеряется скорость младенца, но на этом этапе им нужно понимать, что скорость не имеет значения.

В младших классах ваш ребенок может получить отличные результаты, если будут проверены простые математические вычисления.Однако этот экзамен не может выявить темную сторону ума вашего ребенка. Из-за отсутствия базовых знаний о числах и математике у вашего ребенка может быть фобия к математике.

Было бы слишком поздно, когда вы это поняли. Это ухудшает социальный рост ребенка. Я говорю вам, потому что я внимательно изучил его результаты. Моя скромная просьба – не делать из них роботов; чтобы побудить их думать, рассуждать и исследовать. N0w, выбор за вами.

Я обнаружил, что Abacus – вещь положительная для человечества.Мозги готовы к числам, которые поддерживают все умнее и умнее. Тренировка на счетах в наше время позволяет нашей культуре поверить в твердую структуру нашего тела. Мало того, счеты как использовать стали фантастической работой в сфере образования для многих людей по всему миру. И родители начали уделять внимание интеллектуальной силе своих детей задолго до их возраста. Спасибо всем тем благородным педагогам, которые потратили необходимые ресурсы на то, чтобы заставить Abacus работать

Как пользоваться счетами

В двух словах

Все любят счеты *! Это такой элегантный и умный инструмент.

Но знаете ли вы, как помочь своему ребенку получить от этого максимум удовольствия? Если нет, то вот 13 практических советов, которые помогут вам показать ребенку, как пользоваться счетами.

* На этой странице мы обсуждаем простые счеты.

Если вы хотите научить своего ребенка пользоваться японскими счетами, соробаном , вы можете посмотреть эту серию видео.

Для самых маленьких (3-6 лет)

1. Просто поиграйте с ним: Перемещение бусинок помогает развивать координацию рук и глаз, и знакомить ребенка со счетным инструментом с раннего возраста может быть только хорошо.(Убедитесь, что вы следите за своим маленьким ребенком, так как бусинки, если они отсоединены, представляют опасность удушья, а деревянная рама довольно тяжелая и может поранить молодую ступню).

2. Выучить цвета: Пока ваш маленький ребенок играет с бусами, вы тоже можете играть и называть цвета по именам.

3. Осведомленность об образце: Вы можете сыграть в игру, в которой вы создаете узор, используя верхнюю половину счет, а затем ваш ребенок сопоставляет узор на нижней части.Умение распознавать узор – важный навык, который позже поможет вашему ребенку с пропуском таблиц подсчета и умножения.

4. Фигуры: Попросите ребенка попробовать двигать бусинки, чтобы получились простые формы – например, квадрат, прямоугольник или треугольник.

5. Научитесь пользоваться счетами для счета: Перемещайте бусинки в ряд по одной слева направо вместе с ребенком и при этом произносите или спойте числа от 1 до 10.

6. Практика счета с использованием реальных событий: Например, в первый день декабря вы можете начать счет к Рождеству.Вы и ваш ребенок можете начинать каждый день, перемещая бусинку и подсчитывая, сколько дней прошло – волнение нарастает по мере приближения числа 25!

7. Простое сложение: Ваш ребенок может весело провести время с простыми вопросами сложения, используя одну строку на счетах. Например, для суммы «5 + 3»: подсчитывается и перемещается 5 бусинок, затем подсчитываются и перемещаются еще 3 бусинки. Наконец, подсчитывается общее количество перемещенных бусинок, чтобы прийти к ответу: 8.

Для детей от 7 лет

8. «Рассчитывать на»: Этому важному навыку должны научиться маленькие дети. Используя пример сложения 5 и 3: после того, как первые 5 бусинок были перемещены поперек, последние 3 бусинки считаются не как «1, 2, 3», а как «6, 7, 8» с «1, 2, 3 ”счет выполняется пальцами.

9. Обратный отсчет: В преддверии захватывающего события начните обратный отсчет – например, до дня рождения вашего ребенка или до того, как семья уйдет в отпуск, может пройти десять дней.

10. Научитесь использовать счеты для вычитания: Как и в случае с сложением, основы вычитания можно изучить на счетах. Возьмем пример «7 минус 4»: 7 бусинок считается и перемещается. Затем 4 бусинки подсчитываются и перемещаются назад, и, наконец, подсчитываются оставшиеся бусинки, чтобы прийти к ответу: 3.

11. Схемы умножения: Для детей старшего возраста счеты могут быть хорошим инструментом для визуального изображения таблиц умножения. Например, если вы переместите 3 бусинки влево в каждом ряду и проигнорируете остальные 7 бусинок в каждом ряду, вы создадите форму бусинок 10 на 3, отображающую таблицу умножения на 3.

12. Угадайте число: Установите число на счетах и ​​посмотрите, сколько уходит времени ваш ребенок, чтобы угадать его (не глядя на счет). После каждого неудачного предположения говорите «выше» или «ниже». Затем поменяйтесь ролями и посмотрите, сколько догадок вы сделаете. Эта игра – интересный способ познакомить вашего ребенка с двузначными числами и понятиями «высшее и низшее», а также знакомит его с некоторыми основными элементами стратегического мышления.

13. Присвойте каждой строке на счетах разрядное значение – например, нижняя строка – это единицы, следующая – десятки, затем сотни и так далее.Это позволит вам знакомить ребенка с большими числами – например, вы можете указать, какой сейчас год, или даже сложить большие числа. Обратите внимание, что многим детям будет намного легче выполнять это упражнение, если вы повернете счеты на 90 градусов влево и положите их на стол. Это позволит вашему ребенку читать числа слева направо – так же, как мы представляем числа в письменной форме.

Сводка

Мы надеемся, что приведенные выше идеи дадут вам пищу для размышлений и помогут вашему ребенку научиться пользоваться счетами.

Прежде всего, веселитесь! В счетах есть что-то врожденное приятное – их трудно увидеть, не хочется дотронуться до них и услышать щелчок и щелканье бусинок, перемещающихся на место. В наши дни детей часто заставляют думать, что математика – это сложно и скучно, поэтому знакомить их с инструментом, который делает ее легкой и увлекательной , может быть только хорошим делом!

Как использовать AL Abacus в ЛЮБОЙ учебной программе – с видео

Используете ли вы Saxon или Singapore, Math Mammoth или Math U See, AL Abacus может помочь вашим детям лучше понять сложение и вычитание и развить более глубокое чувство чисел.(Если вы не читали мой предыдущий пост о том, почему я так люблю AL Abacus, вы можете сначала щелкнуть там, чтобы получить представление о том, что делают счеты, прежде чем погрузиться в этот пост.)

Я начал писать длинный сложный пост о том, как преподавать на счетах в вашей домашней школе, когда понял, что на самом деле я хотел просто сесть с вами и показать вам . Итак, я снял четыре коротких видеоролика , демонстрирующих, как использовать AL Abacus для обучения:

• начало добавления
• мысленная математика с двузначными числами
• как складывать трехзначные числа при перегруппировке
• как вычесть трехзначные числа при перегруппировке

Я также обрисовал пять шагов по использованию AL Abacus в любом уроке сложения или вычитания, а также то, как перевести вашего ребенка от использования счеты к решению задач на бумаге или мысленно.В конце концов, цель использования счётов – настолько хорошо понять математику, что вам не нужны счеты . Этот пост покажет вам, как это сделать!

Самое замечательное в счетах состоит в том, что вы действительно можете использовать их в любой программе по математике, чтобы помочь вашему ребенку закрепить основы восприятия чисел, сложения и вычитания. Для каждого из приведенных ниже видео я взял задачу из другой учебной программы (в данном случае, Singapore Primary Mathematics 2A) и «перевел» ее на счеты.

Видео: Как научить простому сложению на AL Abacus

Многие учебные программы представляют собой простые дополнения в виде груд неорганизованных предметов для подсчета. Использование счётов помогает вашему ребенку видеть числа как группы, а не просто предметы, которые нужно считать по одному.

Видео: Как преподавать мысленную математику на AL Abacus

Счеты отлично подходят для обучения детей использованию своего понимания числового значения для решения ментальных математических задач.

Видео: Как научить складывать многозначные числа на AL Abacus

Счеты упрощают перегруппировку и торговлю при обучении сложению или вычитанию многозначных чисел.

Видео: Как научить многозначное вычитание на AL Abacus

Теперь, когда у вас есть общее представление о том, как учить на счетах для обучения, вот пять шагов, которые помогут вам использовать счеты AL с по вашей учебной программе .

1. Решите, с какой стороны счет использовать.

Счеты имеют две стороны. Используйте пустую сторону (с кружком AL в верхнем правом углу) для мысленных вычислений до 100. Используйте сторону с надписью 1000, 100, 10, 1, если вы работаете с большими числами, или если вы занимаетесь перегруппировкой или торговлей (как в двузначном вертикальном сложении или вычитании).

Используйте эту сторону для вычисления в уме до 100.

2. Ознакомьте ребенка со счетами.

Прежде чем приступить к новой концепции, дайте ребенку время, чтобы понять, как работают счеты.Введите числа на счетах и ​​попросите ребенка сказать, какой номер изображен на бусинках. Затем назовите ребенку число и попросите его ввести правильное количество бусинок. (См. Мой предыдущий пост с изображениями чисел, введенных на счетах.) Например, если вы хотите научить своего ребенка складывать многозначные числа, вы должны попросить его ввести несколько трех- и четырехзначных чисел на стороне с надписью. абака.

3. Переведите на счеты концепцию, которую вы преподаете.

Здесь вам пригодятся учебник для учащихся или руководство для учителя.Взгляните на изображения, которые они используют для иллюстрации концепции, и переведите их на счеты, как я сделал в видео выше. Делайте это медленно, проработайте несколько примеров и убедитесь, что каждый шаг понятен вашему ребенку. Задайте множество вопросов, чтобы проверить понимание, особенно когда дело касается перегруппировки и торговли.

4. Позвольте вашему ребенку использовать счеты, поскольку он начинает использовать новую концепцию для решения задач.

Держите счеты под рукой и позвольте ребенку использовать их, выполняя первые несколько заданий с новой концепцией.Это поможет укрепить его понимание и действительно закрепит новую концепцию.

5. Поощряйте ребенка переходить к решению математических задач без счётов.

Как пошутила на этой неделе подруга, рассказывая об успехах своей дочери в математике: «Счеты помогают ей понять, что она делает. Но я не хочу, чтобы ей приходилось держать один в сумочке, когда она станет взрослой, чтобы внести изменения! ” Она абсолютно права! Цель использования счётов (или любого другого манипулятора) в том, чтобы в конечном итоге они больше не понадобились.Манипуляторы – это инструмент , который помогает детям понять, что они делают, чтобы они могли быстро решать проблемы на бумаге или мысленно.

Чтобы счеты не превратились в костыль, постепенно уменьшайте количество их использования ребенком по мере того, как он осваивает новую концепцию. Например, вот как вы можете отучить своего ребенка от счета при обучении сложению многозначных чисел:

• Сначала используйте счеты для решения каждой задачи, осторожно меняя бусинки, чтобы перегруппироваться.
• После того, как ваш ребенок полностью поймет концепцию перегруппировки, предложите ему ввести только первое слагаемое на счетах, а затем представьте, что добавит бусинки для второго слагаемого. Например, если ваш ребенок складывает 265 + 379, он может ввести 265 на проводах, но только визуализирует, как скользит вверх по бусинкам для 379.
• Как только она сможет надежно решать проблемы таким образом, уберите счеты. Вытаскивайте его только в том случае, если ваш ребенок запутался или застрял, но в противном случае поощряйте его решать задачи на бумаге.

Купите здесь AL Abacus, чтобы пожинать плоды для своих детей.

(Ссылки выше могут быть партнерскими ссылками. Когда вы покупаете товар по партнерской ссылке, вы помогаете поддерживать этот сайт без каких-либо дополнительных затрат для вас. Спасибо!)

Happy Math!

Как пользоваться счетами?

Какой твой любимый предмет в школе? Не говори обеда или перерыва! Это всеобщие фавориты! Что касается популярных предметов, некоторые студенты предпочитают английский.Другим студентам могут нравиться естественные науки или история. Дети, которые любят числа, могут найти математику своим любимым уроком дня.

По мере того, как вы становитесь старше, уроки математики становятся все сложнее. Вы когда-нибудь занимались алгеброй? Как насчет геометрии или тригонометрии? Если да, то вы знаете, что быстро выходите за рамки работы, которую вы можете делать в своей голове. Для более продвинутых предметов калькулятор необходим.

Еще до изобретения калькуляторов и компьютеров люди работали с системами счисления.Но как насчет самых первых людей на Земле? У них не было языка, не говоря уже о системах счисления, чтобы делать основную математику. Так как же они следили за вещами?

Первые люди, вероятно, обращались к объектам в природе, чтобы вести счет. Камни и палки можно легко использовать для подсчета и отслеживания объектов. Однако когда началась торговля, торговцам понадобился способ производить простые вычисления и считать большие числа.

Первые счетные устройства, вероятно, были сделаны из канавок, вырезанных в песке или дереве, в которых можно было перемещать небольшие предметы, такие как бусинки и камешки.Со временем эти устройства были заменены на каркас из бамбука или дерева. Они содержат стержни, нити или проволоку, по которым могут свободно скользить бобы или бусинки.

Это раннее устройство было известно как счетная рамка. Если у вас несколько счётов, они называются abaci или abacus. Человек, использующий счеты, известен как абакист.

Счеты использовались веками. Фактически, они все еще часто используются купцами и торговцами. Никто точно не знает, когда были изобретены счеты.Однако историки знают, что версии abaci появлялись в разных культурах на протяжении всей истории.

Например, шумерские счеты могли быть первыми. Он был изобретен еще в 2700 году до н. Э. Со временем версии абака использовались древними персами, греками, римлянами и китайцами.

Вы когда-нибудь использовали счеты? Если это так, то вы знаете, что бусинки можно перемещать, чтобы отслеживать подсчитанные объекты. Более сложные абачи могут даже помочь вам складывать, вычитать, умножать и делить!

Стандарты: CCRA.